Kapitel 1 Einleitung
1.1 Antriebstechnik
Der Begriff Antriebstechnik bezieht sich auf eine technische Disziplin, deren Sinn darin besteht mit Hilfe technischer Systeme Bewegung durch Kraftübertragung zu erzeugen. Es ist dabei offen um welche Art des Antrieb es sich handelt. Wie Abbildung 1.1 zeigt, kann eine Unterteilung von Antrieben anhand der Wirkprinzipien erfolgen.

Abbildung 1.1: Unterteilung von Antrieben nach Wirkprinzipien
1.2 Stand der Antriebstechnik
Die achtziger Jahre waren durch eine stark zunehmende industrielle Automatisierung gekennzeichnet. Dies setzte sich auch in den neunziger Jahren, wenngleich gebremst, durch die Konjunkturkrise und verschärft durch den notwendigen Strukturwandel in der Industrie, weiter fort. So beobachtet man in den letzten Jahren eine ständig weiter wachsende Nachfrage nach reaktionsschnellen, wartungsarmen und möglichst kleinen Antriebssystemen in hoher Schutzart. In der Vergangenheit standen hier Pneumatische, hydraulische und elektrische Antriebe in einer gewissen Konkurrenz. Wegen der einfacheren Steuerung und Regelung hat sich der Bereich der Elektroantriebe, besonders der drehzahlveränderbaren, allerdings laufend vergrössert. Der wichtigste Trend der letzten Jahre war der Systemgedanke. Nicht einzelne Komponenten stehen im Vordergrund, sondern das System „Elektrischer Antrieb“. Die Komponenten müssen in ein System eingebunden werden. Die neuen Kompaktantriebe (Umrichter, Maschine und Getriebe als Einheit) bestätigen diesen Trend. Elektrische drehzahlveränderbare Antriebe sind heutzutage ein wichtiger und bestimmender Bestandteil vieler Maschinen geworden. Ihr Verhalten beeinflusst in starkem Masse die Qualität und die Kosten der erzeugten Produkte. Die gewünschten Anpassungen der Antriebe an die optimalen Produktionsbedingungen erfordern immer mehr dezentrale drebzahlveränderbare Antriebslösungen. Dies stellte in der Vergangeheit und stellt auch heute noch ein grosses Entwicklungs- und Wachstumsgebiet dar. Für weiterführende Angaben zu Marktverbreitung und Anwendungsgebiete sei auf weiterführende Literatur (z.B. [1]) verwiesen. Daher wurden auch in den letzten Jahren für den Markt der drehzahlveränderbaren Drehstromantriebe (AC-Antriebe) hohe Zuwachsraten festgestellt [1]. Alle diese Antriebe werden über Stromrichter als Stellglieder gesteuert oder geregelt betrieben. Drehzahlveränderbare Antriebe gelten daher im Allgemeinen als Stromrichterantriebe. Die rein mechanischen Verstellmöglichkeiten der Drehzahl über Getriebe und die stufigen Verfahren, wie z.B. die Polumschaltung bei Asynchronmaschinen, werden in Zukunft sicher ihre Marktnischen behalten, aber an Bedeutung weiter verlieren. Fernziel ist sicher, alle Antriebe drehzahlvariabel arbeiten zu lassen. Dies stellt, insbesondere aufgrund des voranschreitenden Klimawandels, in allen Wirtschaftsbereichen einen starken technologischen Trend dar. In den letzten Jahren war dieser Trend auch sehr stark im Bereich der Mobilität, mit dem Übergang zur Elektromobilität, spürbar und wird sich mit grosser Wahrscheinlichkeit auch in Zukunft weiter fortsetzen. Drehzahlveränderbare Antriebe werden in vielen verschiedenen Branchen eingesetzt. Eine, keinesfalls vollständige Übersicht darüber liefert die folgende Aufzählung:
- Lebensmittel
- Anlagenbau
- Handhabung und Montage
- Bergbau
- Kunststoffverarbeitung
- Energietechnik
- Metallverarbeitende Industrie
- Transport und Mobilität (E-Mobilität)
- Werkzeugmaschinen
- Verpackungsindustrie
1.3 Eigenschaften elektrischer Antriebe
Elektrische Antriebe haben im Vergleich zu anderen Lösungen (z.B. pneumatische oder hydraulische Antriebe) folgende besondere Eigenschaften:
- einfache Energiezufuhr über Kabel
- hohe Verfügbarkeit
- sofortige Einsatzbereitschaft
- leichte Bedienbarkeit
- umweltschonender Betrieb
- geringe Leerlaufverluste und hoher Wirkungsgrad
- kleine Abmessungen mit guten Anbaumöglichkeiten
- lageunempfindliche Aufstellung (Staub, Wasser)
- einfache Anpassungen an den geforderten Drehmomentverlauf
- grosser Drehzahlbereich, verbunden mit einem grossen Stellbereich
- Nulldrehzahl ist möglich (Stillstandsbelastung)
- gute Regelbarkeit
- hohe kurzzeitige Überlastbarkeit
- Nutzbremsung (Energierückspeisung) möglich
- geräusch- und erschütterungsarmer Lauf
- einfache, messtechnische Erfassung der Betriebszustände
1.4 Die Qual der Wahl
In den letzten Jahren gab es eine schnelle Weiterentwicklung bei elektronischen Bauteilen, z.B. bei den verschiedenen hochsperrenden, modernen Halbleiterschaltern (Dioden, Transistoren, Thyristoren, GTO’s, IGBT’s und IGCT‘s) und beim Einsatz der Mikroprozessoren und Signalprozessoren. Diese Fortschritte auf dem Gebiet der Leistungs- und Informationselektronik sowie der verstärkte Trend zum an die Antriebsaufgabe genau angepassten Einzelantrieb bestimmen das Bild in fast allen Industriezweigen, im Handwerk und im Haushalt. Die verwirrende Vielfalt am Markt bei drehzahlveränderbaren Antrieben ist in Abbildung 1.2 zusammengefasst.
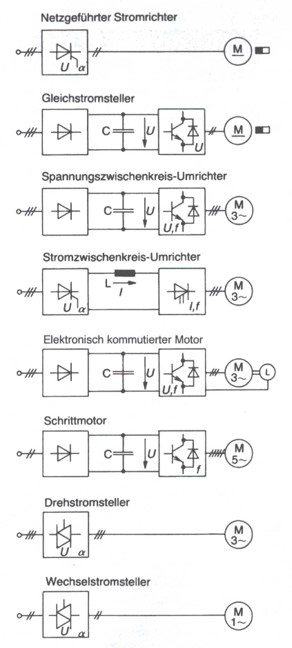
Abbildung 1.2: Übersicht verschiedener Antriebssysteme
1.5 Antriebskomponenten
Elektrische drehzahlveränderbare Antriebe bestehen im Normalfall aus folgenden Hauptkomponenten:
- Stromrichter als elektronisches Stellglied
- elektrische Maschine als elektromechanischer Energiewandler (inkl. Regelung)
- mechanisch gekoppelte Arbeitsmaschine als Verbraucher der mechanischen Energie
Die Aufgabe des Antriebssystems ist es Energie, welche vom Netz zur Verfügung gestellt wird, möglichst verlustarm in mechanische Energie umzuwandeln. Insbesondere aufgrund der wachsenden Anforderungen an die technologischen Prozesse muss der Antrieb drehzahlvariabel sein, wodurch sich die Arbeitsgeschwindigkeit stufenlos anpassen lässt.
1.6 Technologischer Wandel
Während lange Zeit der netzgeführte Stromrichter, zusammen mit der fremderregten Gleichstrommaschine mit Nebenschlussverhalten (GNM), das Feld beherrschte, wurde diese Lösung später vermehrt durch umrichtergespeiste Drehfeldmaschinen, asynchroner (DAM) oder synchroner (SYM) Bauart substituiert. Dies ist vor allem im mechanischen Aufbau der Gleichstrommaschine mit einem Stromwendeapparat begründet. Trotz stark verbesserter Standzeiten der Bürsten wird dennoch, aufgrund des mechanischen Verschleisses des Stromwendeapparates und der Bürsten, ein gewisser Wartungsaufwand erforderlich. Gleichzeitig ist der Stromwendeapparat anfällig bei gewissen Umgebungsbedingungen wie zum Beispiel aggressive Atmospäre, Rüttelkräfte, hohe Drehzahlen bzw. bei Stillstandsbelastung. Eine einfach aufgebaute Käfigwicklung einer Asynchronmaschine, sowie deren vollständige Kapselung ermöglichen den Betrieb bei hohen Drehzahlen und in nahezu jeder Umgebung.
Folglich war es Ziel der Bemühungen der letzten Jahre, die wartungsarme Drehfeldmaschine anstelle der stromwenderbehafteten Gleichstrommaschine einzusetzen. Neuere Halbleiterentwicklungen ermöglichten den Ersatz der aufwendigen Thyristorumrichter durch kompakte Transistorumrichter bis etwa 1000 kW, wobei die obere Grenze fliessend ist. Der Einsatz von Mikroprozessoren mit komplexen Regelalgorithmen kann dem Drehstromantrieb heute die gleichen Eigenschaften verleihen, die bisher nur mit dem Gleichstromantrieb erreicht wurden. Die neuentwickelten Kompaktantriebe mit Umrichter und Maschine als Einheit, stellen einen weiteren Meilenstein dar. Leistungsteil, Steuerteil und die elektronisch kommutierte Maschine (EK) sind als Einheit entwickelt und kommen vorwiegend als Servoantrieb zum Einsatz. Elektrische Direkt-Linearantriebe und direktwirkende Drehantriebe finden als Positionierantriebe im Werkzeugmaschinenbereich oder der Handhabungstechnik zunehmendes Interesse. Sie werden meist als Drehstrommaschinen ausgeführt.
1.7 Elektrotechnische Grundlagen
1.7.1 Bauelemente der Elektrotechnik
Es gibt eine Vielzahl von Bauelementen in der Elektrotechnik. Eine grundlegende Unterteilung besteht darin, sie in aktive und passive Bauelemente zu unterteilen. Die Zuordnung hängt dabei von der Wirkung des Bauelementes auf das elektrische Signal ab. Passive Bauelemente besitzen keine eingebaute (Hilfs-)leistungsquellen und können nur Energie aufnehmen und speichern. Ihre Ausgangsleistung kann nie grösser als die Eingangsleistung sein. Aktive Bauelemente hingegen zeigen meist in irgend einer Form eine Verstärkerwirkung, weshalb sie üblicherweise eine Hilfsenergiequelle benötigen. Typische Beispiele für passive Bauelemente sind:
- Widerstände
- Induktivitäten
- Kondensatoren
- Sicherungen
- Potentiometer
- Varistoren
- Fotowiderstände
- Dioden
Beispiele für aktive Bauelemente hingegen sind:
- Transistoren
- Spannungsquellen
- Batterien
- Operationsverstärker
Die drei wichtigsten passiven Bauelemente sind Widerstände, Kondensatoren und Induktivitäten (Spulen). Durch Widerstände fliesst nur dann ein Strom \(I\), wenn von aussen eine Spannung \(U\) angelegt wird. Der Widerstand fungiert dabei als konstanter Proportionalitätsfaktor zwischen Strom und Spannung. Dieser Zusammenhang wird durch das Ohmsche Gesetz dargestellt:
\[ U=R\cdot I \]
Jeder Leiter weist einen ohmschen Widerstand auf, der aus den geometrischen Abmessungen (Länge \(l\) sowie Querschnitt \(A\)) sowie einer Materialkonstante (spezifischer Widerstand \(\rho\)) berechnet werden kann.
\[ R=\rho\cdot \frac{l}{A} \]
Da an einem ohmschen Widerstand Ströme und Spannungen gleichzeitig auftreten, entsteht eine Verlustleistung \(P\), welche in thermische Energie umgewandelt wird und zur Erwärmung des Widerstandes beiträgt. Die Verlustleistung kann mit Hilfe der Gleichung
\[ P = U\cdot I = \frac{U^{2}}{R} = I^{2}\cdot R \] bestimmt werden. Ideale Kondensatoren und Induktivitäten sind per Definition verlustlos. Sie speichern jedoch Energie in magnetischen bzw. elektrischen Feldern, welche anschliessend wieder vollständig entnommen werden kann. Der klassische Aufbau eines Kondensators besteht aus zwei elektrisch leitfähigen Platten, die durch einen Isolator voneinander getrennt sind. Wird von aussen eine Spannung an die Platten angeschlossen, dann sammeln sich auf diesen Platten unterschiedlich geladene Ladungsträger. Die Kapazität (Speicherfähigkeit) eines Kondensators hängt massgeblich von der Fläche dieser Platten \(A\) sowie dem Abstand der Platten \(d\) und der Art des Isolators (Permittivität \(\varepsilon\)) ab. Die Permittivität ist eine Materialeigenschaft, welche beschreibt wie der Isolator mit dem elektrischen Feld, welches zwischen den Platten ausbildet, wechselwirkt. Auch für das Vakuum existiert eine Permittivität und stellt eine Naturkonstante (elektrische Feldkonstante \(\varepsilon_{0}=8.854\cdot10^{-12} \frac{As}{Vm}\)) dar. Die Permittivität eines Stoffes wird dann als Vielfaches der elektrischen Feldkonstante angegeben.
\[ \varepsilon = \varepsilon_{0}\cdot \varepsilon_{r} \] Bei dem dimensionslosen Faktor \(\varepsilon_{r}\) handelt es sich dabei um die materialabhängige Permittivitätszahl. Basierend darauf kann die Kapazität \(C\) eines Kondensators anhand der Gleichung
\[ C = \varepsilon\cdot \frac{A}{d} = \varepsilon_{0}\cdot \varepsilon_{r} \cdot \frac{A}{d} \]
berechnet werden. Umso grösser die Kapazität eines Kondensators, umso grösser fällt die Ladung \(Q\) aus, die bei gegebener Spannung \(U\) in einem Kondensator gespeichert werden kann.
\[ Q = C\cdot u \]
Der gespeicherte Energieinhalt \(W_{C}\) eines Kondensators kann mit Hilfe der Spannung \(u\) am Kondensator sowie der Kapazität bestimmt werden.
\[ W_{C} = \frac{C}{2}\cdot u^{2} \]
Soll das Verhalten von Strom und Spannung am Kondensator über der Zeit betrachtet werden, muss man auf Integral- bzw. Differentialgleichungen zurückgreifen. So gilt beispielsweise für den zeitlichen Verlauf des Kondensatorstromes \(i_{C}(t)\) in Abhängigkeit der Kondensatorspannung \(u_{C}(t)\) folgender Zusammenhang:
\[ i_{C}(t) = C\cdot \frac{du_{C}(t)}{dt} \]
Im Falle einer Spule handelt es sich um einen elektrischen Leiter, welcher so angeordnet wird, dass sich eine oder mehrere Wicklungen ergeben. Diese Wicklungen können auch auf ferromagnetische Materialien aufgewickelt werden, wodurch die Magnetwirkung verstärkt wird. Die Induktivität \(L\) (Einheit Henry \(H\)) einer solchen Spule beschreibt den Vorgang der Induktion, welche eine Wechselwirkung zwischen Magnetismus und Elektrizität darstellt. Dabei unterscheidet man zwischen Selbst- und Gegeninduktion, womit die Ursache der induzierten Spannung beschrieben wird. Ein elektrischer Strom in einem Leiter erzeugt ein Magnetfeld, welches, bei zeitlicher Änderung wiederum eine elektrische Spannung im gleichen Stromkreis hervorruft. Dieser Vorgang beschreibt die Selbstinduktion. Da ein Magnetfeld allerdings auch in Stromkreisen eine Spannung induziert, die sich in der Nähe befinden, wird in diesem Fall von einer Gegeninduktion gesprochen. Der Zusammenhang zwischen magnetischem Fluss \(\Phi\) und dem verursachenden Strom \(I\) wird anhand folgender Gleichung beschrieben:
\[ \Phi = L\cdot I \]
Die im Magnetfeld gespeicherte Energie \(W_{L}\) kann aus dem Strom \(i\) und der Induktivität bestimmt werden.
\[ W_{L} = \frac{L}{2}\cdot i^{2} \]
Auch im Fall der Spule kann der Zusammenhang zwischen Strom und Spannung über der Zeit mittels Differentialgleichung beschrieben werden:
\[ u_{L}(t) = L\cdot \frac{di_{L}(t)}{dt} \]
Die Beschreibungen mittels Integral- und Differential gelten ohne Einschränkungen für beliebige Zeitverläufe.
1.7.2 Gleich-, Wechsel- und Mischgrössen
Die üblichen mathematischen Methoden zur Beschreibung elektrischer Grössen können angewandt werden, wenn diese entweder reine Gleichgrössen sind oder sich nach der Periodendauer \(T\) identisch wiederholen. Um beliebige Signalverläufe betrachten zu können, werden Signalverläufe in folgende Kategorien eingeteilt:
- Gleichgrössen
- Wechselgrössen
- Mischgrössen
Bei Gleichgrössen (DC für direct current) handelt es sich um Signale, die über die Zeit konstant sind. Wechselgrössen (AC für alternating current) hingegen zeigen einen, nach Ablauf der Periodendauer identischen (nichtkonstanten) Signalverlauf, wobei der lineare Mittelwert Null ist. Mathematisch bedeutet dies, dass das Integral des Signalverlaufes über die Periodendauer \(T\) hinweg den Wert Null ergibt. Mischgrössen setzen sich aus Gleich- und Wechselgrössen zusammen.
1.7.3 Typische Kennwerte von periodischen Signalverläufen
Zur Beschreibung und Charakterisierung von periodischen Signalen \(x(t)\) werden üblicherweise Mittelwerte verwendet. Dazu gehört beispielsweise der lineare Mittelwert \(\overline{x}\):
\[ \overline{x} = \frac{1}{T}\int^{T}_{0}{x(t)\cdot dt} \]
Dabei gilt, dass der lineare Mittelwert einer reinen Wechselgrösse Null ist.
Der quadratische Mittelwert, RMS-Wert oder auch Effektivwert (\(X_{eff}\)) eines Signals \(x(t)\) berechnet sich anhand der Gleichung:
\[ X_{eff} = \sqrt{\frac{1}{T}\int^{T}_{0}{x^{2}(t)\cdot dt}} \]
Die Namensgebung des Effektivwertes beruht auf der Idee einen Messwert für eine Wechselgrösse zu definieren, welcher an einem ohmschen Widerstand die gleiche Energieabgabe hervorruft wie eine konstante Grösse mit gleichem Betrag. Bei harmonischen (Sinus-/Kosinus) Grössen beschreibt der Faktor \(\sqrt{2}\) den Zusammenhang zwischen quadratischem Mittelwert und Spitzenwert:
\[ \hat{x}=\sqrt{2}\cdot X_{eff} \]
1.7.4 Komplexe Zeiger in der Elektrotechnik
Komplexe Zeiger spielen in der Wechselstromrechnung eine signifikante Rolle, da sie den mathematischen Aufwand zur Berechnung des zeitlichen Verlaufes von Strömen, Spannungen und Leistungen deutlich reduzieren. Geht man beispielsweise von einem harmonischen Spannungsverlauf
\[ u(t) = \hat{u}\cdot sin(\omega\cdot t + \varphi_{u}) \]
aus, dann beinhaltet die Gleichung Informationen über den zeitlichen Verlauf der Spannung als auch über den Phasenwinkel (\(\varphi_{u}\)) zum Zeitpunkt \(t=0s\). Diese Funktion kann auch mit Hilfe der Eulerschen Formel \(e^{j\cdot y} = cos(y) + j\cdot sin(y)\) dargestellt werden:
\[ u(t) = Re \left\{\hat{u} \cdot e^{j\left(\omega t+\varphi{u} \right)} \right\} = Re\left\{\hat{u} \cdot e^{j\omega t}\cdot e^{j\varphi_{u}} \right\} \]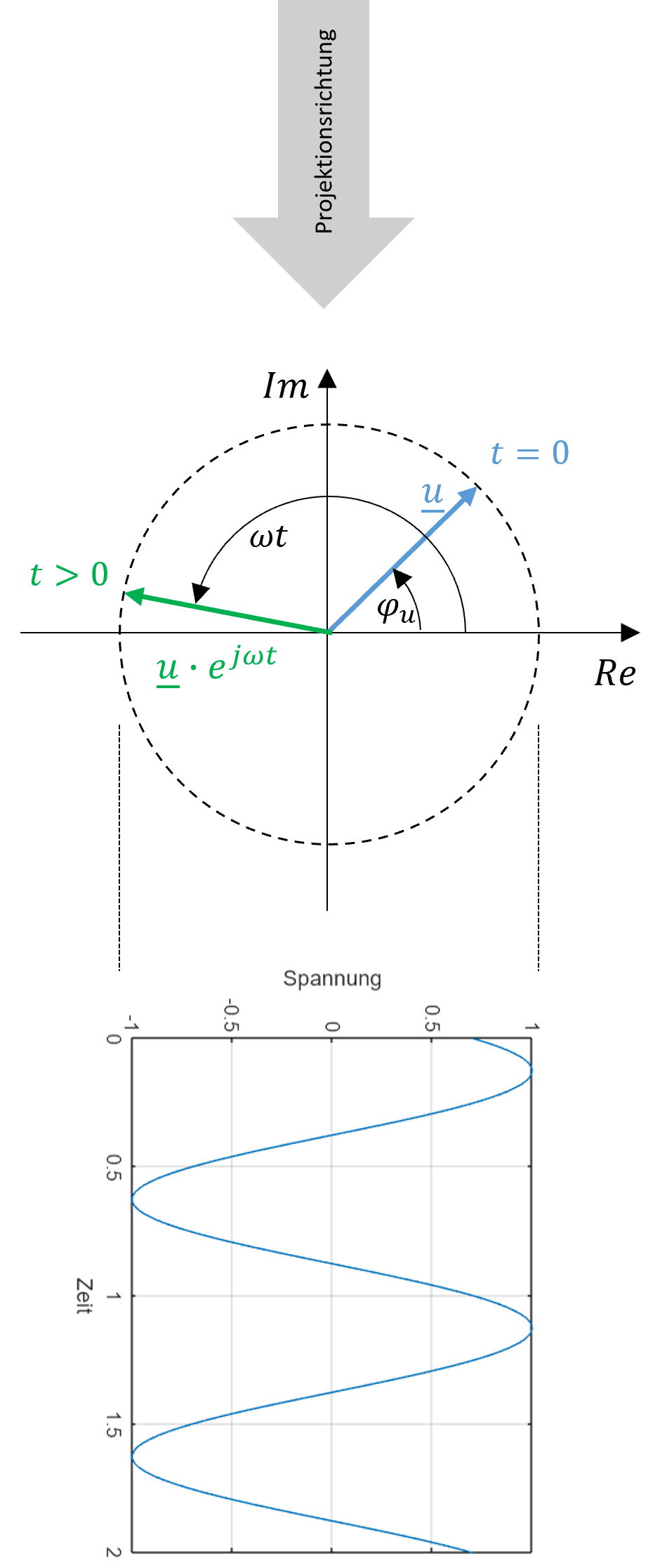
Abbildung 1.3: Beispielhafte Darstellung eines komplexen Spannungszeigers
Die Beschränkung der Darstellung auf den Realteil ist damit zu begründen, dass die Original-Zeitfunktion durch eine rechtwinklige Projektion des rotierenden Zeigers auf eine Achse (üblicherweise die Re-Achse) repräsentiert werden kann \(\left(u(t)=Re\left\{\underline{u}(t)\right\}\right)\). Bei komplexen Zeigern in der Elektrotechnik interessiert üblicherweise die gegenseitige Lage der einzelnen Wechselgrössen zum Zeitpunkt \(t=0s\), weshalb die Zeitabhängigkeit unberücksichtigt bleibt (vorausgesetzt alle Elemente der Schaltung erfahren die gleiche Frequenz).
\[ \underline{u} = \hat{u} \cdot e^{j\varphi_{u}} \]
Dadurch können die Kirchhoffschen Gesetze vektoriell angewandt werden.
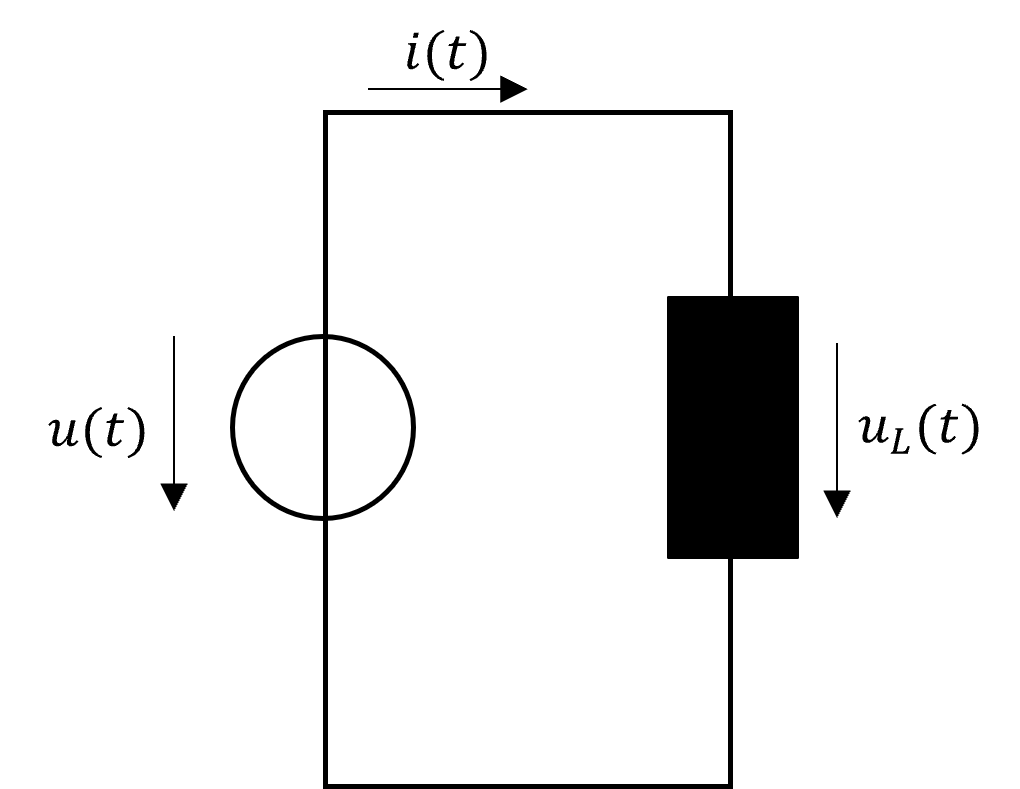
Abbildung 1.4: Ideale Spule an Wechselspannungsquelle
Betreibt man beispielsweise, wie in Abb. 1.4 dargestellt, eine Spule mit der Induktivität \(L\) an einer Spannungsquelle mit oben genanntem Spannungsverlauf, dann kann der Strom \(i(t)\) bestimmt werden:
\[ u(t)=L\frac{di}{dt} \rightarrow i(t) = \frac{1}{L}\int{u(t)dt} \]
Wendet man den Maschensatz an und setzt die Quellenspannung dem Spannungsfall über der Spule gleich, ergibt sich der Stromverlauf durch beidseitige Integration (auf die mathematisch korrekte Integrationskonstante wird verzichtet).
\[ i(t) = \frac{-\hat{u}}{L\cdot \omega t}\cdot cos(\omega t+\varphi_{u}) \]
Führt man diese Berechnung unter Verwendung komplexer Zeiger durch, kann das Ohm’sche Gesetz im komplexen Zahlenraum verwendet werden, indem die komplexe Impedanz \(\underline{Z}=j\omega L\) berücksichtigt wird.
\[ \underline{i}(t) = \frac{\underline{u}(t)}{\underline{Z}} = \frac{\underline{u}\cdot e^{j\cdot \omega t}}{j \omega L} = \underbrace{\frac{\hat{u}}{\omega L}\cdot e^{j\cdot \varphi_{u}}\cdot e^{-j\frac{\pi}{2}}}_{\underline{i} = \frac{\hat{u}}{\omega L}\cdot e^{j\left(\varphi_{u}- \frac{\pi}{2}\right)}} \cdot e^{j\omega t} = \underline{i}\cdot e^{j\cdot \omega t} \]
Dabei wurde der Zusammenhang \(j=e^{j\frac{\pi}{2}}\) in obiger Gleichung berücksichtigt. Da der Zusammenhang zwischen Strömen und Spannungen an den Bauelementen (Spule, Widerstand, Kapazität) in der komplexen Zeigerrechnung linear ist, kann theoretisch sowohl mit Spitzenwert- als auch mit Effektivwertzeigern gerechnet werden.