Kapitel 5 Gleichstrommotor

5.1 Allgemeines

Der Gleichstrommotor wurde in der Vergangenheit sehr häufig in Kombination mit entsprechenden Stromrichtern im Bereich der drehzahlvariablen Antriebe verwendet, da sich dessen Drehzahl in weiten Bereichen kontinuierlich verändern lässt, indem die Ankerspannung verstellt wird. Allerdings benötigt dieser einen mechanischen Stromwendeapparat, welcher trotz stark verbesserten Bürstenstandzeiten einen gewissen Wartungsaufwand mit sich bringt. Ausserdem ist dieser anfällig bei aggressiver Atmosphäre, hohen Drehzahlen bzw. bei Stillstandsbelastung. Aufgrund dessen wurde die Gleichstrommaschine in den letzten Jahren mehr und mehr von umrichtergespeisten Drehfeldmaschinen verdrängt. Vorteile der Gleichstrommaschinen sind:

• einfacher und kostengünstiger Aufbau der Stromrichter
• hohe Regeldynamik
• relativ hohe Leistungsdichte

Nachteilig hingegen sind:

• höherer Wartungsaufwand (z.B. Tausch der Bürsten)
• Aufgrund des aufwendigen Kommutators höherer Preis im Vergleich zu Asynchronmaschinen
• geringere Drehzahlen als Drehfeldmaschinen

5.2 Wirkprinzip

Das Wirkprinzip der Gleichstrommaschine basiert auf der Kraftwirkung auf einen stromdurchflossenen Leiter (siehe Bild 5.1), welcher sich in einem Magnetfeld befindet (Lorentzkraft):

\[ F=i\cdot \vec{B}\cdot l \] Wobei gilt:

• \(i\) Strom durch den Leiter
• \(\vec{B}\) magnetische Flussdichte
• \(l\) Länge des Leiters (im Magnetfeld befindlich)

Es ist dabei unerheblich ob die magnetische Flussdichte mit Hilfe eines Permamnentmagneten oder durch elektrische Erregung rezeugt wird.

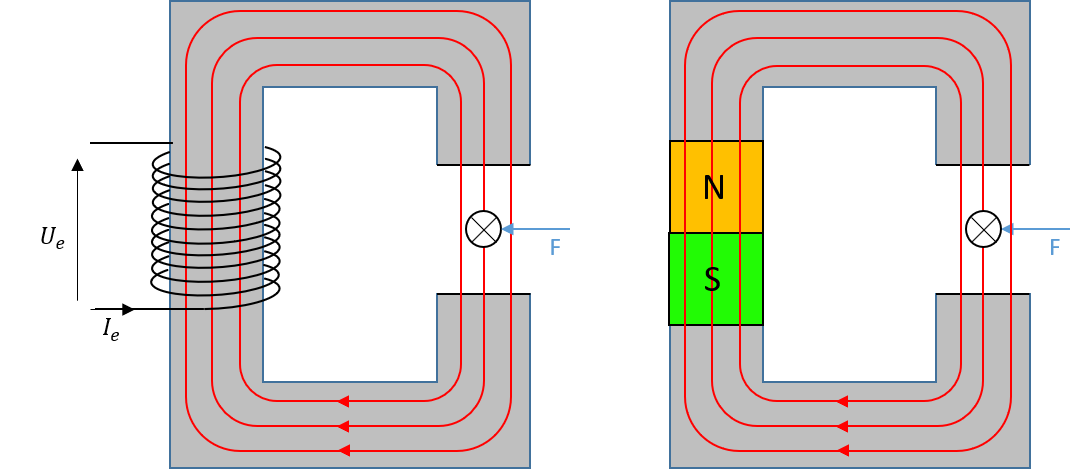
Abbildung 5.1: Wirkung der Lorentzkraft (links: elektr. erregt, rechts: permanenterregt

Zu einer Drehmomentbildung kommt es schlussendlich indem der stromdurchflossene Leiter zu einer drehend gelagerten Leiterschleife umgeformt wird.

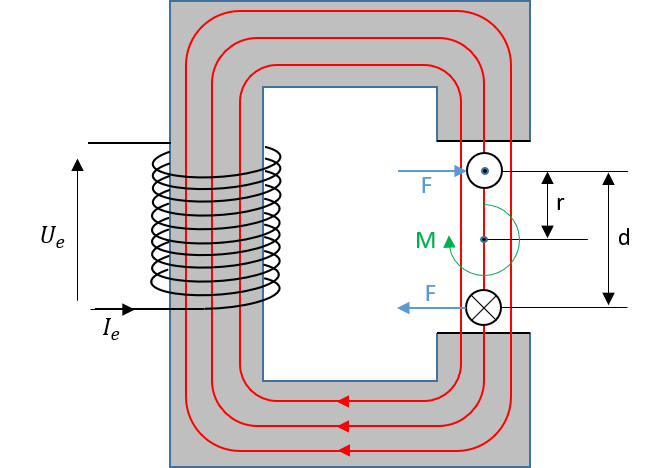
Abbildung 5.2: Entstehung des Drehmomentes in einer Leiterschleife

Somit ergibt sich das Drehmoment mit dem Ansatz:

\[ M=F\cdot r \]

Da die Leiterschleife aus einem Hin- und einem Rückleiter besteht, wobei sich die Stromrichtung in beiden unterscheidet, ergibt sich das gesamt auf die Leiterschleife wirkende Drehmoment \(M_{LS}\) aus zwei Kraftkomponenten gleicher Amplitude:

\[ M_{LS} = 2F\cdot r = 2F\cdot \frac{d}{2}=F\cdot d = i\cdot B\cdot d\cdot l \] Je nach Winkelposition \(\alpha\) der Leiterschleife im Magnetfeld verändert sich das wirksame Drehmoment, da die tangentiale Kraftkomponente die auf beide Leiter wirkt eine entsprechende Abhängigkeit zeigt.

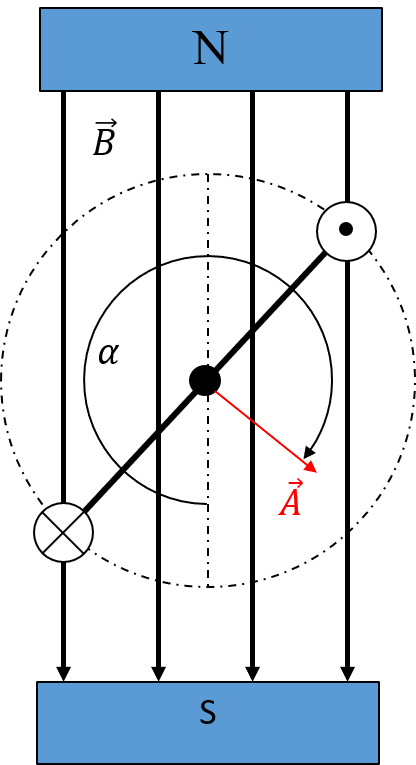
Abbildung 5.3: Abhängigkeit des Drehmomentes von der Position der Leiterschleife im Magnetfeld

Soll das Drehmoment somit in Abhängigkeit der Position bestimmt werden, muss obige Gleichung angepasst werden.

\[ M_{LS}(\alpha)=2\cdot F\cdot \frac{d}{2}\cdot \sin(\alpha) = F\cdot d \cdot \sin(\alpha) \] Gleichzeitig wird sich ein weiterer Effekt einstellen, der auf dem Induktionsgesetz basiert. Und zwar wird in der Leiterschleife eine Spannung induziert, da sich die Leiter innnerhalb des Magnetfeldes bewegen (Induktion durch Bewegung des Leiters) und sich somit die von der Leiterschleife eingeschlossene Fläche zeitlich ändert.

\[ \hat{u}_{LS} = \frac{d\Phi}{dt}=2\cdot \vec{B}\frac{d}{2}\omega\cdot l = B\cdot d\cdot l\cdot \omega = \Phi_{0}\cdot \omega \] Der Term \(\Phi_{0}=B\cdot d\cdot l\) beinhaltet konstruktiv bedingte Faktoren, die als konstant angesehen werden können (vorausgesetzt der Erregerstrom bleibt konstant) und den magnetischen Fluss repräsentieren, der die Leiterschleife bei senkrechter Ausrichtung und homogener Flussdichte durchdringen würde.

Um den zeitlichen Verlauf der induzierten Spannung beschreiben zu können, lässt sich dies mit Hilfe der Fläche der Leiterschleife beschreiben, die zum jeweiligen Zeitpunkt vom Magnetfeld durchsetzt wird. In Bild 5.4 wird dazu die senkrechte Projektionsfläche verwendet.

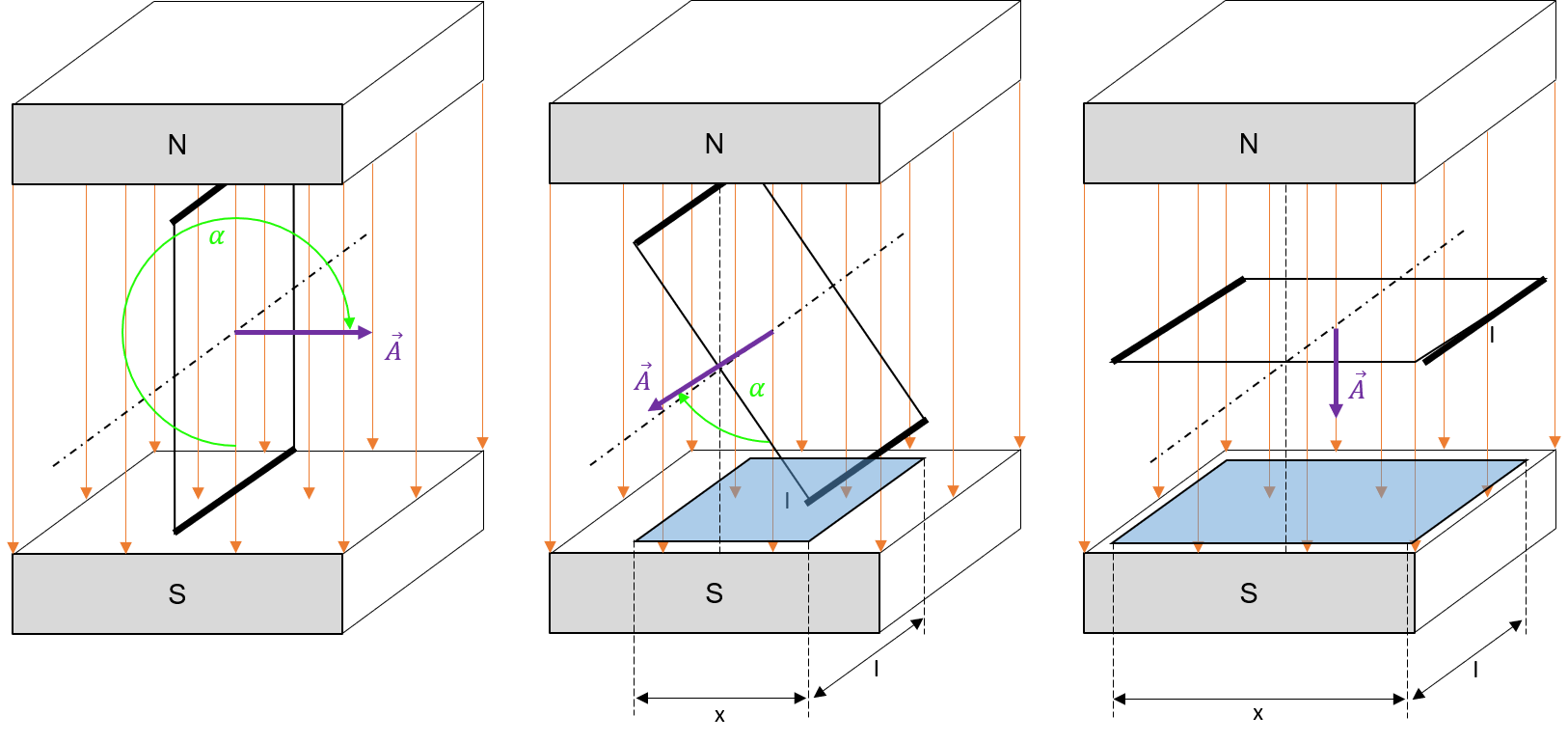
Abbildung 5.4: Vom Magnetfeld durchsetzte Fläche in Abhängigkeit von der Position der Leiterschleife

Der Fluss der von der Leiterschleife umfasst wird, lässt sich mit Hilfe des Modells in Bild 5.4 folgendermassen ausdrücken.

\[ \Phi = \vec{B}\cdot \vec{A} \]

Der Winkel \(\alpha\) wird bei den folgenden Betrachtungen als Winkel zwischen der vektoriellen Ausrichtung der Flussdichte \(\vec{B}\) und dem Normalenvektor \(\vec{A}\) der von der Leiterschleife aufgespannten Fläche betrachtet.

In Abhängigkeit von der Position der Leiterschleife lässt sich die Projektionsfläche folgendermassen beschreiben.

\[ A = l\cdot x \] und \[ x(\alpha) = d\cdot \cos(\alpha) \] Somit gilt:

\[ \Phi(\alpha) = B\cdot l\cdot d\cdot \cos(\alpha) \] Da die Winkelposition eine Funktion der Winkelgeschwindigkeit darstellt, lässt sich die obige Gleichung ebenfalls als Funktion der Zeit darstellen.

\[ \alpha(t) = \omega \cdot t = 2\cdot \pi \cdot n \cdot t \] Folglich gilt:

\[ \Phi(t) = \vec{B}\cdot l\cdot d\cdot \cos(2\cdot \pi \cdot n \cdot t) \]

Daraus folgt der zeitliche Verlauf der induzierten Spannung :

\[ u_{LS}(t)=-\frac{d\Phi(t)}{dt}=2\cdot \pi \cdot n \cdot B\cdot l\cdot d\cdot \sin(2\cdot \pi \cdot n \cdot t) = \omega \cdot B\cdot l\cdot d\cdot \sin(\omega \cdot t) \] Die obigen Überlegungen lassen mehrere Schlüsse zu:

• Die Drehzahl (Winkelgeschwindigkeit) ist direkt proportional zur Amplitude der induzierten Spannung.
• Das verwendete Modell einer einzelnen Leiterschleife in einem homogenen Magnetfeld lässt eine kontinuierliche Rotation nicht zu, da das sich einstellende Drehmoment einen sinusförmigen Verlauf aufweist. Die Leiterschleife würde somit in der neutralen Zone (\(\alpha=0^{\circ}\)) stehenbleiben.

Aufgrund dessen ist eine weitere konstruktive Massnahme notwendig, die eine kontinuierliche Drehbewegung ermöglicht.

5.3 Aufbau

Der grundsätzliche, vereinfachte Aufbau einer Gleichstrommaschine ist in Bild 5.5 [3] dargestellt.

Abbildung 5.5: Schnittzeichnung einer DC-Maschine (Polpaarzahl p=1) (Auszug aus dem Online Skript von Prof. Dr.-Ing. J. Böcker, Universität Paderborn)

Der Hauptpol mit der darauf befindlichen Erregerwicklung (bzw. Feldspule) erzeugt die notwendige Flussdichte im Luftspalt der Maschine. Die Ankerwicklung wird über Spulen und einen Kommutator mit Strom (Ankerstrom) versorgt. Grundsätzlich ist es möglich über den Umfang des Luftspaltes mehrere Hauptpole zu verteilen. Die Anzahl der Pole wird mit Hilfe der sog. Polpaarzahl \(p\) zum Ausdruck gebracht.

5.3.1 Kommutator und Ankerwicklungsschema

Ein Kommutator für eine Windungsschleife besteht im einfachsten Fall aus zwei voneinander isolierten Ringhälften. Die Verbindung dieser Ringhälften mit dem Ankerstromkreis erfolgt über Bürsten, die darauf schleifen. Beim Nulldurchgang der induzierten Spannung (in der sog. neutralen Zone), die darauhin ihr Vorzeichen ändert, sorgen die Bürsten ebenfalls für eine Stromrichtungsänderung. Dadurch wird die auf entsprechende Ankerwicklung wirkende Kraftrichtung umgedreht und die aktuelle Drehrichtung kann beibehalten werden.

Abbildung 5.6: Grundsätzliches Funktionsprinzip des Kommutators (Auszug aus Online Skript Elektrische Maschinen , Universität Clausthal)

Durch die kontinuierliche Stromrichtungsänderung in der Leiterschleife, sorgt für eine Gleichrichtung der an ben Bürsten abgreifbaren Spannung. Es entsteht eine pulsierende Gleichspannung. Wird die in Bild 5.6 [4] gezeigte einzelne Leiterschleife durch mehrere ersetzt und der Kommutator entsprechend durch mehrere Ringteile ersetzt, wird die pulsierende Gleichsspannung weiter geglättet. Der Kommutator sorgt somit dafür, dass die Ankerwicklungen unterhalb der Hauptpole, unabhängig von der aktuellen Winkelposition des Ankers (Rotors) immer von Strom einer definierten, gleichbleibenden Richtung durchflossen werden. Der Kommutator fungiert also quasi als mechanischer Frequenzwandler.

Bei der Wicklung des Ankerkreises unterscheidet man zwischen Wellen- und Schleifenwicklung (siehe Bild 5.7 [3] bzw. 5.8 [3]).

Abbildung 5.7: Schleifenwicklung für einen Motor mit Polpaarzahl \(p=2\) (Auszug aus dem Online Skript von Prof. Dr.-Ing. J. Böcker, Universität Paderborn)

Abbildung 5.8: Wellenwicklung für einen Motor mit Polpaarzahl \(p=2\) (Auszug aus dem Online Skript von Prof. Dr.-Ing. J. Böcker, Universität Paderborn)

Zur Vertiefung des Themas wird auf weiterführende Literatur verwiesen.

5.3.2 Ankerrückwirkung

Wie in Kapitel 5.3.1 erwähnt findet die sog. Stromwendung (Stromrichtungsänderung aufgrund der Anordnung des Kommutators) in der neutralen Zone statt. Dies kann dadurch begründet werden, dass lediglich in diesem Bereich des Luftspaltes die Flussdichte ebenfalls null ist (siehe Abb. 5.9).

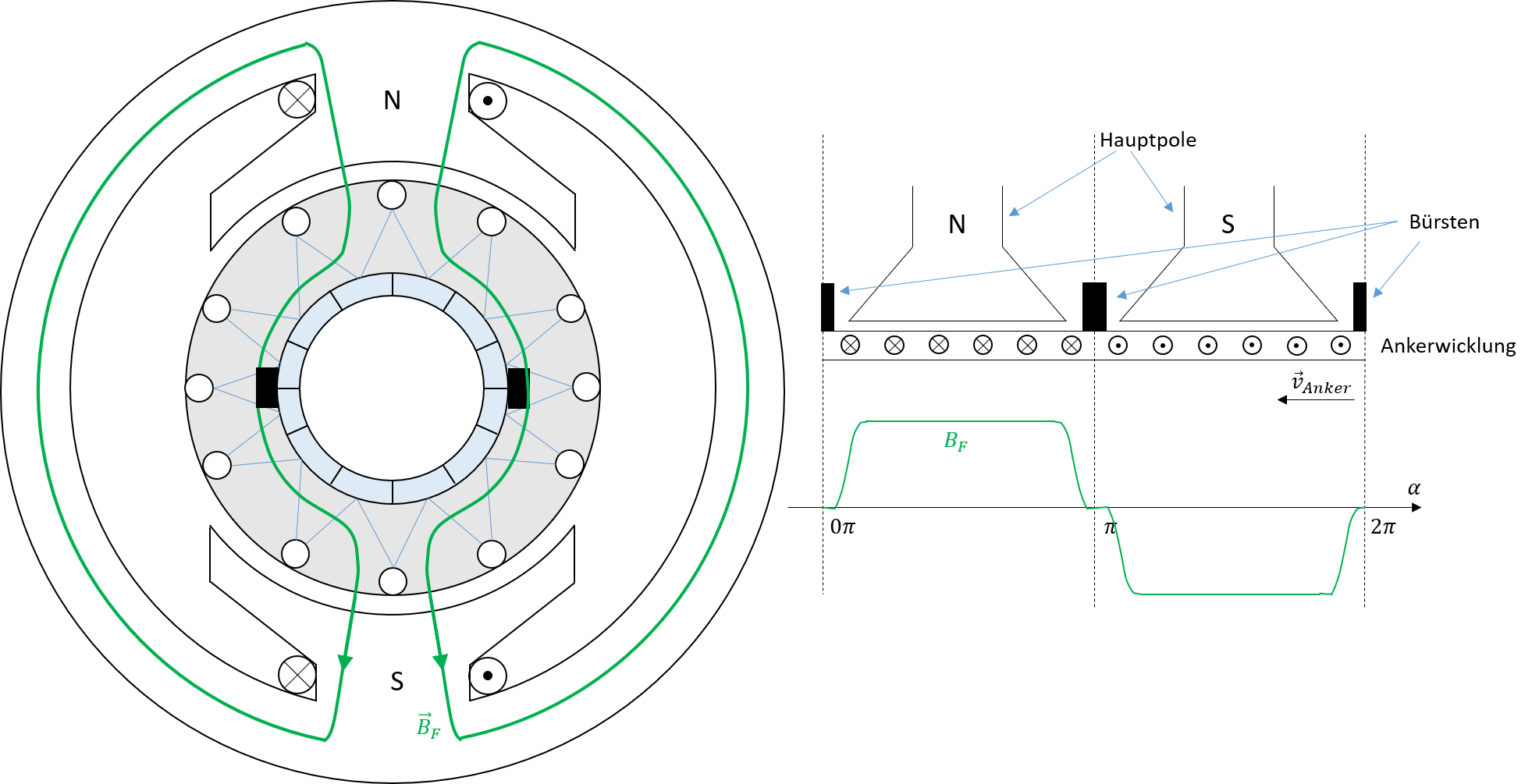
Abbildung 5.9: Qualitative Flussdichteverteilung ohne Ankerfeld (Maschine abgewickelt)

Die Annahme dieser Flussdichteverteilung im Luftspalt trifft allerdings nur zu, wenn die Ankerwicklung nicht von Strom durchflossen wird (unbelasteter Fall). Kommt es zur Belastung der Maschine und es stellt sich ein entsprechender Ankerstrom ein, bewirkt auch dieser ein zusätzliches Magnetfeld, welches sich dem Feld der Erregerspule überlagert. Dieses sogenannte Ankerquerfeld ist in Bild 5.10 dargestellt.

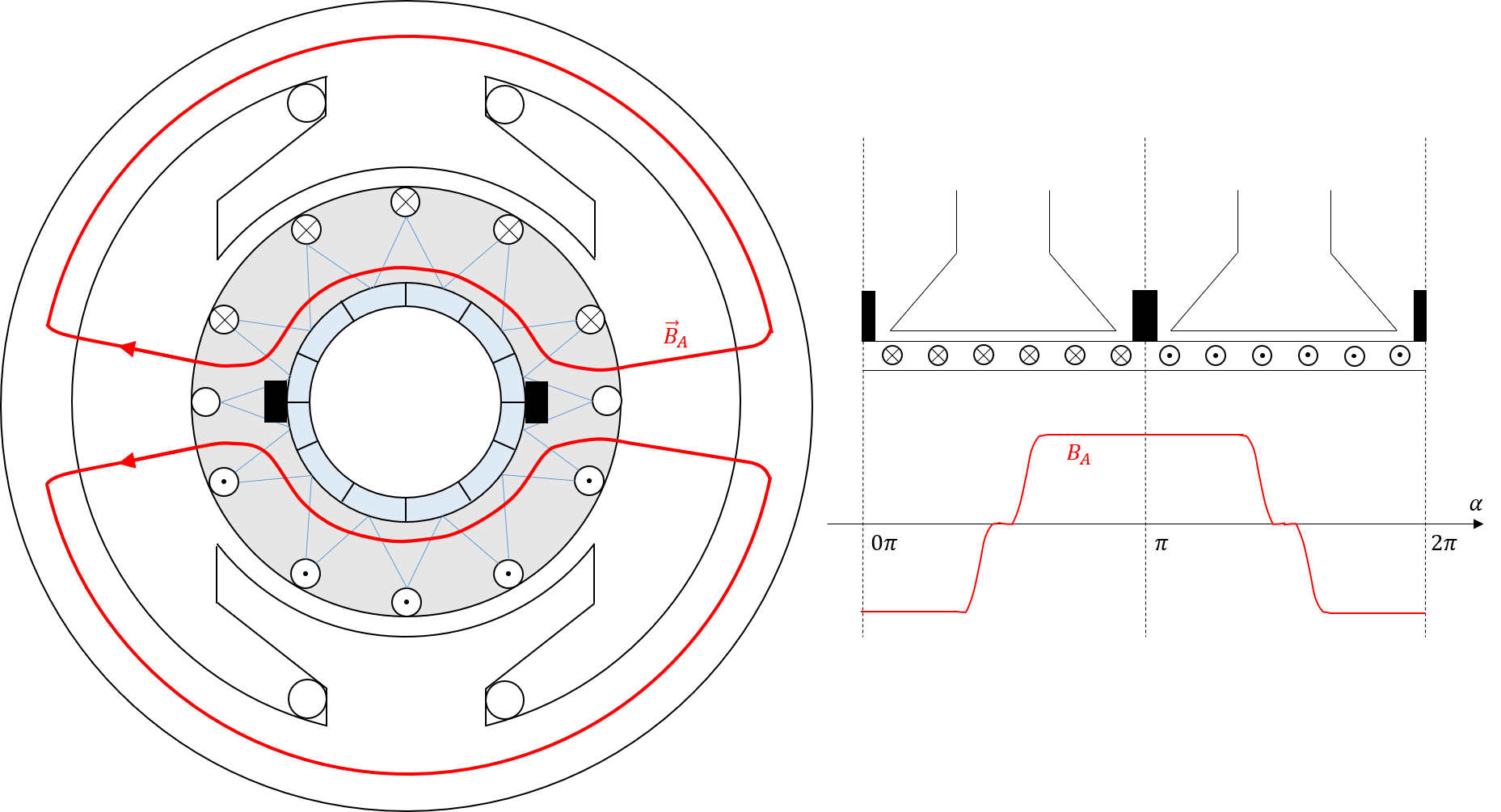
Abbildung 5.10: Flussdichteverteilung hervorgerufen durch Ankerstrom (Feldspulen unbestromt)

Die in den Bildern 5.9 und 5.10 lassen sich auch vektoriell darstellen, wodurch die Überlagerung beider Induktionen \(\vec{B}_{F}\) und \(\vec{B}_{A}\) wie in Bild 5.11 durch eine vektorielle Addition erfolgen kann. Daran ist zu Erkennen, dass eine Verschiebung der neutralen Zone um den Winkel \(\mu\) erfolgt.

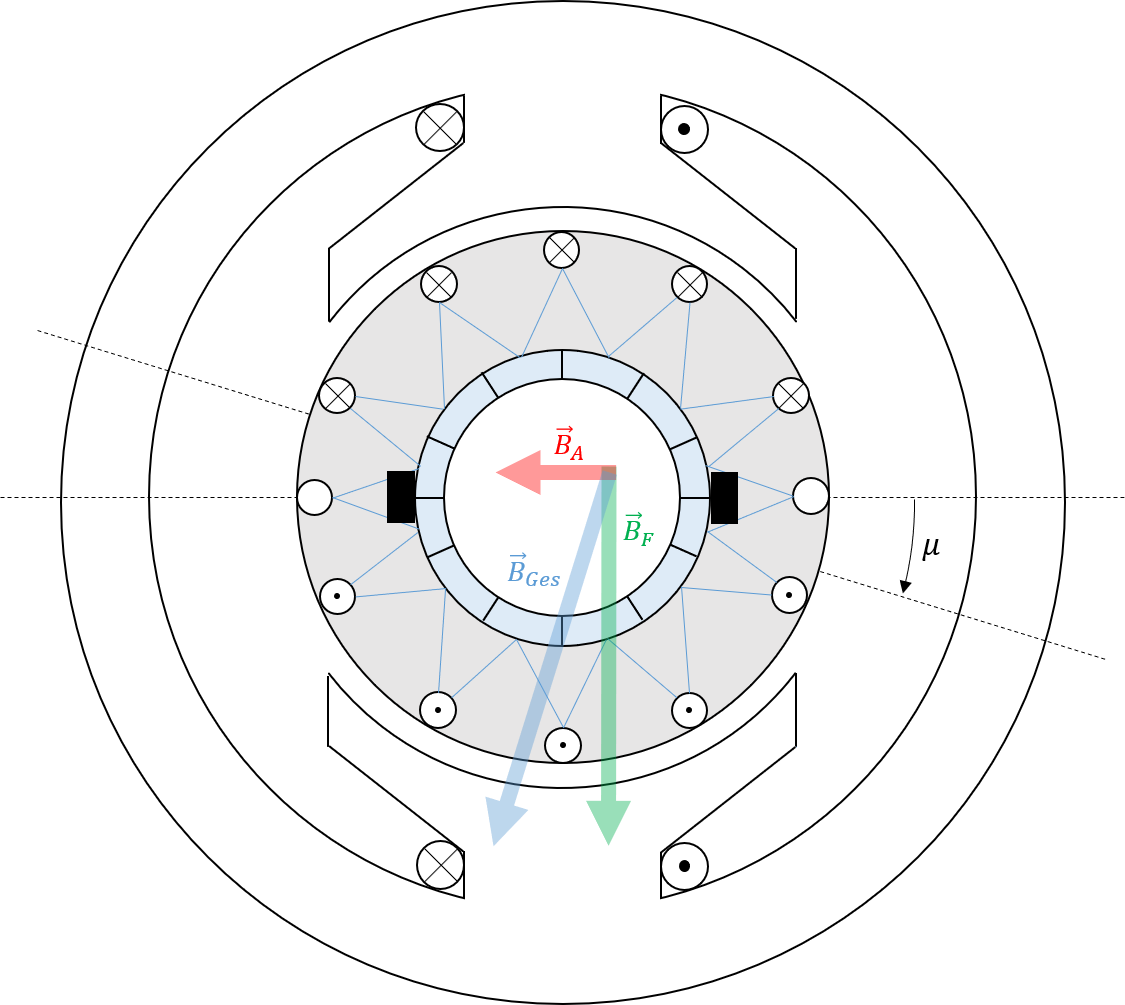
Abbildung 5.11: Verschiebung der neutralen Zone um den Winkel \(\mu\)

Der Verschiebungswinkel \(\mu\) ist folglich keine Konstante, sondern hängt massgeblich von der Amplitude sowie dem Vorzeichen (Motor- oder Generatorbetrieb) des Ankerstromes ab.

Wichtig an dieser Stelle zu erwähnen ist, das die Darstellung der vom Ankerstrom hervorgerufenen Flussdichteverteilung im Bild 5.10 keineswegs einen solchen Verlauf aufweist, da der grössere Luftspalt in den Pollücken zu entsprechenden Feldverzerrungen führt. Die grundsätzliche Überlegung (ein um \(90^{\circ}\) verschobener symmetrischer Induktionsverlauf) stimmt allerdings mit der Realität überein und stellt somit die Verhältnisse hinreichend genau dar.

Um gewährleisten zu können, dass die Stromwendung weiterhin in der neutralen Zone erfolgt, wäre eine mechanische Verschiebung der Bürstenposition denkbar. Dies ist jedoch sowohl aufwendig als auch sehr wartungsintensiv und fehleranfällig. Wird eine entsprechende Kompensation dieser Verschiebung der neutralen Zone nicht vorgesehen, hat dies insbesondere bei grösseren Maschinen negative Folgen. Es kommt zum sog. Bürstenfeuer, bei dem es im Bereich der Bürsten zur Funkenbildung kommt, welche sowohl die Bürsten als auch die Oberfläche des Kommutators beschädigen.

Um diesen negativen Effekt dennoch unterbinden zu können, werden stattdessen sog. Wendepolwicklungen bzw. Kompensationswicklungen vorgesehen. Beide Wicklungen werden dabei vom Ankerstrom selbst durchflossen.

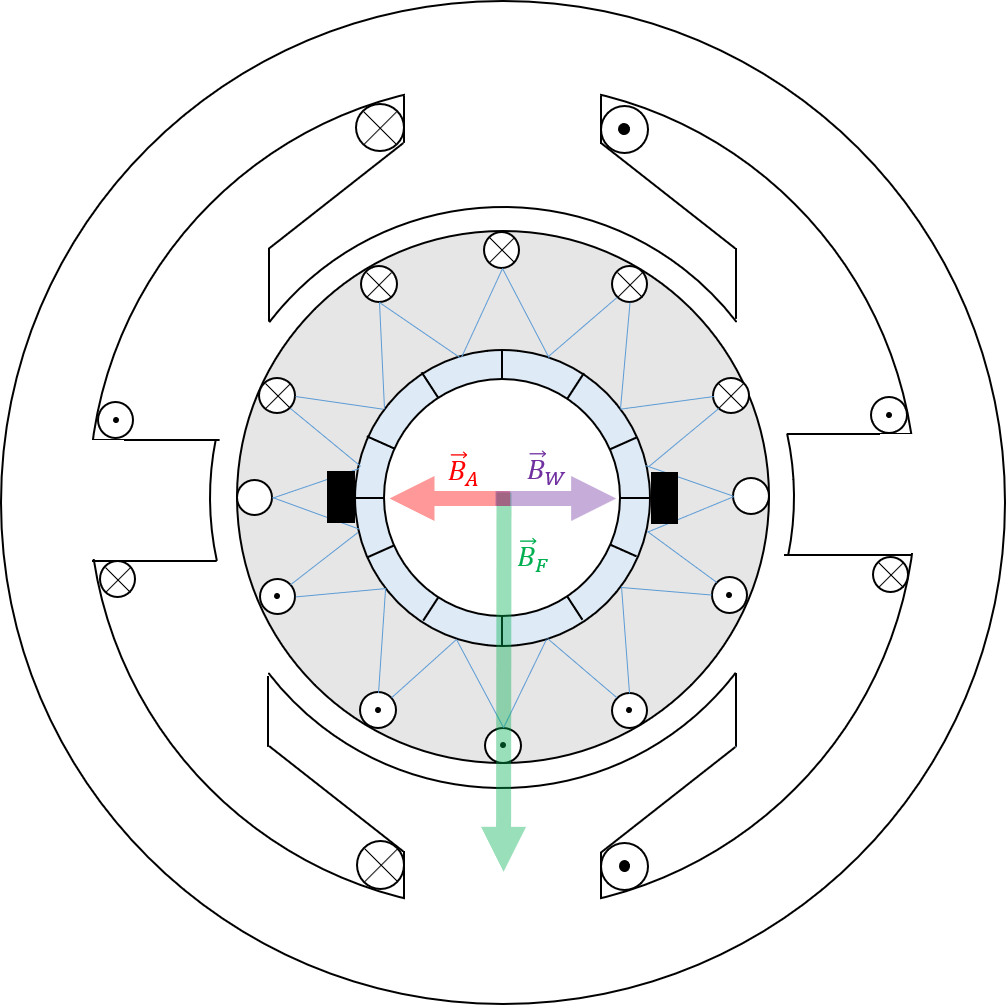
Abbildung 5.12: Auswirkungen der Wendepolwicklung

Die Wendepolwicklung wird in den Pollücken untergebracht (siehe Bild 5.12) und sorgt aufgrund Ihrer Anordnung für eine vollständige Kompensation des Ankerquerfeldes. Da sie ebenfalls vom Ankerstrom durchflossen wird, bleibt ihre kompensierende Wirkung auch bei sich ändernder Belastung erhalten.

Die Kompensationswicklung befindet sich in den Polschuhen und dient der Vermeidung von Spitzen in der Feldkurve. Da Kompensationswicklungen entsprechende Mehrkosten, aufgrund ihrer konstruktiven Komplexität, darstellen, werden sie meist bei Maschinenleistungen ab 5kW verwendet.

5.4 Grundgleichungen der DC-Maschine

Ganz allgemein lässt sich feststellen, dass in einem sich im Magnetfeld bewegenden Leiter eine elektrische Feldstärke entsteht. Diese lässt sich mit folgender Gleichung beschreiben:

\[ -\vec{E} = \vec{v} \times \vec{B} \]

Der konstruktive Aufbau der Maschine sorgt dafür, dass im Luftspalt einer elektrischen Maschine sowohl die Geschwindigkeit \(v\), die Flussdichte \(B\) als auch der Leiter senkrecht aufeinnader stehen. Unter Angabe der Leiterlänge \(l\) lässt sich die elektrische Feldstärke auch folgendermassen ausdrücken:

\[ E=\frac{U_{q}}{l} \]

Somit gilt:

\[ U_{q} = -E \cdot l = l\cdot B \cdot v \cdot \sin{90^{\circ}} \] Da die Maschine aus mehreren Ankerleitern besteht, die sich alle im Magnetfeld bewegen, lässt sich die an den Klemmen der Ankerwicklung im Leerlauf (\(I_{A}=0\)) abgreifbare innere Quellenspannung \(U_{q}\) mit Hilfe der Leiterzahl \(z\) bestimmen.

\[ U_{q} = z\cdot B\cdot l \cdot v \] Unter Verwendung des magnetischen Flusses

\[ B = \frac{\Phi}{A} = \frac{\Phi}{b_{p}\cdot l} \] und der Drehzahl \(n\)

\[ v = d \cdot \pi \cdot n \]

lässt sich die obige Gleichung entsprechend umformen:

\[ U_{q} = z\cdot \frac{\Phi}{b_{p}\cdot l} \cdot l \cdot d \cdot \pi \cdot n = z\cdot 2\cdot r \cdot \pi \cdot n \cdot \frac{\Phi}{b_{p}} \] Diese Formel wird oft durch entsprechende Maschinenkonstanten \(c_{Masch}\) bzw. \(c^{'}_{Masch}\) ausgedrückt:

\[ U_{q}=c_{Masch} \cdot n \cdot \Phi = z \cdot \frac{p}{\pi} \cdot \omega \cdot \Phi = c^{'}_{Masch} \cdot \omega \cdot \Phi \]

Dabei gelten folgende Festlegungen:

• \(z \dots\) Zahl der in Reihe liegenden Leiter
• \(\Phi \dots\) Erregerfluss \([Vs=Wb]\)
• \(b_{p}\dots\) Polbreite \([m]\)

Die obige Gleichung setzt sich somit aus einer konstruktiv bedingten Maschinenkonstante \(c_{Masch}\) und den veränderlichen Einflussgrössen \(\Phi\) und \(n\) bzw. \(\omega\) zusammen. Die Maschinenkonstante kann somit durch Messung bestimmt werden.

5.5 Leistung und Drehmoment

Durch eine entsprechende Belastung der Maschine stellt sich ein Ankerstrom \(I_{A}\) ein, welcher ein inneres Drehmoment hervorruft. Dieses innere Drehmoment \(M_{i}\) lässt sich recht einfach über die innere Leistung \(P_{i}\) bestimmt werden:

\[ M_{i} = \frac{P_{i}}{\omega} = \frac{U_{q}\cdot I_{A}}{2\cdot \pi \cdot n} \]

Indem man die obige Gleichung für die innere Quellenspannung einsetzt ergibt sich folgender Ausdruck für das innere Drehmoment:

\[ M_{i} = z\cdot \frac{p}{\pi}\cdot \frac{2\pi n}{2\pi n}\cdot I_{A}\cdot {\Phi}=z\cdot \frac{p}{\pi}\cdot I_{A}\cdot {\Phi}=c^{'}_{Masch} \cdot I_{A}\cdot {\Phi} \] Dabei gilt:

\[ c_{Masch}=c^{'}_{Masch} \cdot 2 \cdot \pi \] Die mechanische Leistung im Erzeugerzälpfeilsystem lässt sich folgenermassen bestimmen:

\[ P_{mech}=\omega \cdot M_{mech} \] Aufgrund der Induktivitäten im Anker- und Erregerkreis (\(L_{A}\) und \(L_{E}\)) wird in der Maschine während des Betriebes Energie gespeichert:

\[ w_{A}=\frac{L_{A}}{2}\cdot i^{2}_{A}, \qquad w_{E}=\frac{L_{E}}{2}\cdot i^{2}_{E} \]

Gleichzeitig kann folgende Energiebilanz aufgestellt werden:

\[ p_{El} = \frac{dw_{A}}{dt}+\frac{dw_{E}}{dt}+p_{V}+p_{mech} \] In den Leitungswiderständen des Anker- und Erregerkreises treten entsprechende Verluste auf. Die Verlustleistung der Maschine kann somit folgendermassen bestimmt werden:

\[ P_{V} = P_{VA}+P_{VE} = R_{A}\cdot i^{2}_{A}+R_{E}\cdot i^{2}_{E} \]

5.6 Betriebsverhalten der Gleichstrommaschine

5.6.1 Mathematisches Modell für den stationären Betrieb

Grundsätzlich lässt sich das Verhalten der Gleichsstrommaschine im stationären Betrieb \(\biggl( \frac{di_{A}}{dt} =\frac{di_{E}}{dt} = 0 \biggr)\) aus folgenden drei Grundgleichungen ableiten:

\[ U_{A} = R_{A}\cdot I_{A} + U_{q} \]

\[\begin{equation} U_{q} = c_{Masch}\cdot \Phi \cdot n \tag{5.1} \end{equation}\]

\[\begin{equation} M_{i} = \frac{c_{Masch}}{2\pi} \cdot \Phi \cdot I_{A} \tag{5.2} \end{equation}\]

Der magnetische Fluss kann dabei mit Hilfe des magnetischen Widerstandes des Feldkreises \(R_{mf}\) beschrieben werden:

\[ \Phi = \frac{N_{f}\cdot I_{f}}{R_{mf}} \]

Die Verschaltung der Wicklungen hat einen massgeblichen Einfluss auf das Betriebsverhalten der Maschine:

• Fremderregung: getrennte Quellen für Anker- und Erregerkreis
• Nebenschluss: Parallelschaltung von Erreger- und Ankerkreis
• Reihenschluss: Reihenschaltung von Erreger- und Ankerkreis
• Doppelschluss: Mischform

Die unterschiedlichen Maschinentypen sind in Abbildung 5.13 dargestellt.

Abbildung 5.13: Unterschiedliche Maschinentypen der Gleichstrommaschine

Dabei kann zwischen folgenden Widerständen unterschieden werden:

• \(R_{A}\) = Wicklungswiderstand der Ankerkwicklung
• \(R_{V}\) = Vorwiderstand im Ankerkreis
• \(R_{f}\) = Widerstand der Erregerwicklung
• \(R_{pf}\) = Parallelwiderstand der Erregerwicklung
• \(R_{vf}\) = Vorwiderstand der Erregerwicklung

5.6.2 Vollständiges mathematisches Modell

Zur Beschreibung dynamischer Vorgänge der Gleichstrommaschine gilt es die Spannungsabfälle an der Anker- und Erregerwicklung, wie im Bild 5.14 am Beispiel der fremderregten Gleichstrommaschine dargestellt, zu berücksichtigen.

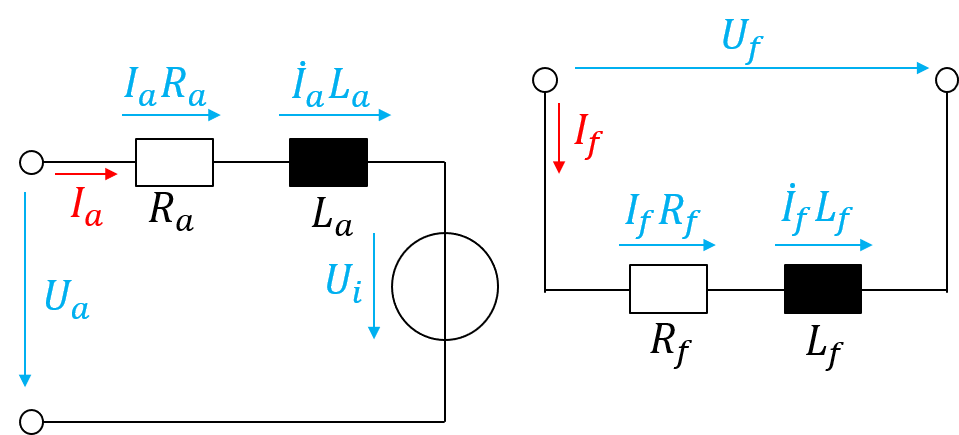
Abbildung 5.14: Ersatzschaltbild der fremderregten Gleichstrommaschine

\[\begin{equation} u_{A} = i_{A}\cdot R_{A} + L_{A}\cdot \frac{di_{A}}{dt} + u_{i} = i_{A}\cdot R_{A} + L_{A}\cdot \frac{di_{A}}{dt} + c_{Masch}\cdot n \cdot \Phi \tag{5.3} \end{equation}\]

\[ u_{f} = i_{f}\cdot R_{f} + L_{f}\cdot \frac{di_{f}}{dt} \]

\[ M_{i} = \frac{c_{Masch}}{2\pi} \cdot \Phi \cdot i_{A} \]

5.6.3 Nebenschlussmaschine

Um das stationäre Betriebsverhalten der Nebenschlussmaschine beschreiben zu können, werden alle differenzierten Grösssen vernachlässigt (zu Null gesetzt). Sollten im Anker- bzw. Erregerkreis zusätzliche Widerstände (\(R_{V}\) bzw. \(R_{vf}\)) verwendet, so müssen diese ebenfalls berücksichtigt werden. Wird davon ausgegangen, dass die Ankerspannung und der magnetische Fluss konstant bleiben, lässt sich die Drehzahl-Drehmoment-Kennlinie ableiten.

Für den Leerlauf gilt \(U_{q}=U_{A}\) da sich kein Ankerstrom einstellt und somit kein Spannungsabfall an den Wicklungswiderständen zu verzeichnen ist. Somit lässt sich die Leerlaufdrehzahl anhand der Gleichung (5.4) bestimmen:

\[\begin{equation} n_{0}=\frac{U_{A}}{c_{Masch}\cdot \Phi} \tag{5.4} \end{equation}\]

Ausgehend von Gleichung (5.1) kann somit die Drehzahl der Maschine anhand folgender Gleichung bestimmt werden:

\[\begin{equation} n = n_{0}-\frac{I_{A}(R_{A}+R_{V})}{c_{Masch}\cdot \Phi} = n_{0}-\frac{2\pi (R_{A}+R_{V})}{c^{2}_{Masch}\cdot \Phi^{2}} \cdot M_{i} \tag{5.5} \end{equation}\]

Die grafische Darstellung dieses Zusammenhanges ist in der Abbildung 5.15 dargestellt (bei konstantem Fluss und konst. Ankerspannung).

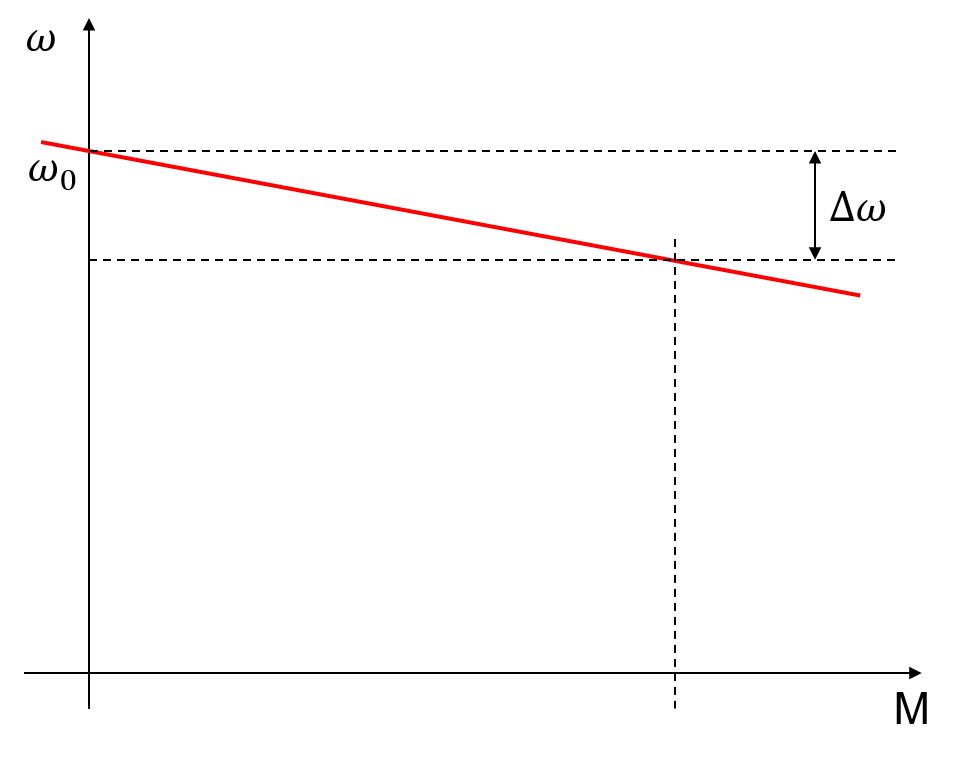
Abbildung 5.15: Stationäre Drehzahl-Drehmoment Kennlinie der Nebenschlussmaschine

Der Erregerstrom lässt sich folgendermassen bestimmen:

\[\begin{equation} I_{f} = \frac{U_{A}}{R_{f}+R_{vf}} \tag{5.6} \end{equation}\]

Folglich ist eine Veränderung der Drehzahl anhand folgender Massnahmen möglich:

• Vorwiderstand im Ankerkreis \(R_{V}\) verändern
• Flussänderung über den Erregerstrom \(I_{f}\) (z.B. durch Vorwiderstand \(R_{vf}\))

Eine Drehzahländerung über den Vorwiderstand \(R_{V}\) geht einher mit hohen Verlusten (Wärmeverluste an \(R_{V}\)) und ist lediglich bei belasteter Maschine möglich (siehe Abbildung 5.16). Mit Hilfe des Vorwiderstandes kann somit die Maschine an einem Gleichstromnetz konstanter Spannung angelassen werden, wodurch der Ankerstrom begrenzt wird. Dies geht einher mit einer Reduktion des zur Verfügung stehenden Drehmomentes. Die Kennlinie wird “weicher”.

Abbildung 5.16: Drehzahl-Drehmoment Kennlinie mit Vorwiderstand als Parameter

Soll eine Drehzahlerhöhung über die Nenndrehzahl hinaus ermöglicht werden, muss der Fluss durch eine Reduktion des Erregerstromes abgeschwächt werden. Bei konstanter Ankerspannung ist dies beispielsweise durch eine Erhöhung des Vorwiderstandes \(R_{vf}\) im Erregerkreis möglich. Anhand der Gleichung (5.4) lässt sich erkennen, dass dies mit einer Erhöhung der Leerlaufdrehzahl einhergeht. Gleichzeitig verändert sich die lastabhängige Drehzahlabhängigkeit (siehe Abbildung 5.17).

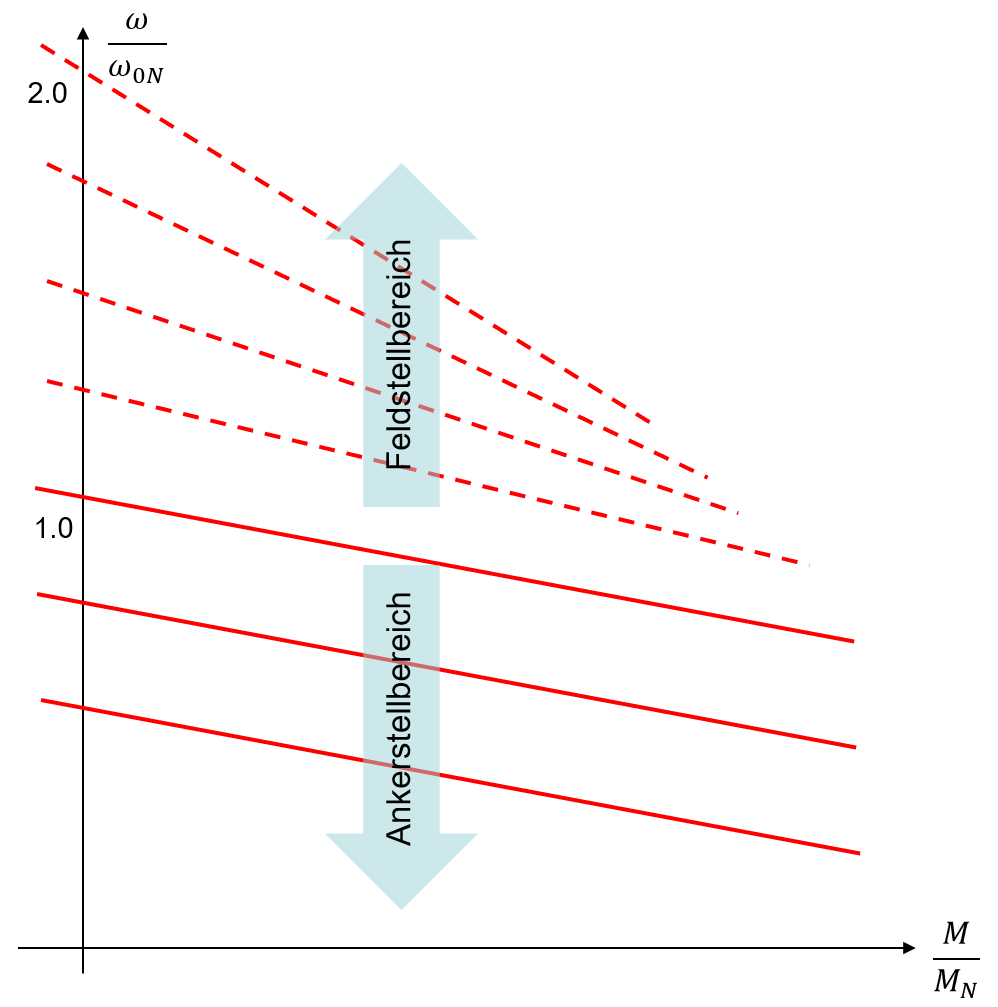
Abbildung 5.17: Drehzahl-Drehmoment Kennlinie im Anker- und Feldstellbereich

5.6.3.1 Betrieb als selbsterregter Gleichstromgenerator

Die Nebenschlussmaschine kann als Generator betrieben werden, da aufgrund der Remanenz des Eisens auch bei fehlendem Erregerstrom ein endliches Magnetfeld vorhanden ist. In diesem Fall wird die Erregerwicklung des Generators durch die von der selbst erzeugten Ankerspannung gespeist.

5.6.4 Fremderregte Gleichstrommaschine

Das Verhalten der fremderregten Gleichstrommaschine ist vergleichbar mit dem Verhalten der Nebenschlussmaschine, da auch hier der Fluss der Maschine verändert werden kann. Bei Einsatz entsprechender Stromrichter, die sowohl den Anker- als auch den Erregerkreis versorgen, kann allerdings auf entsprechende Vorwiderstände verzichtet werden, da sich somit Anker- als auch Erregerkreis, nahezu verlustlos, getrennt voneinander regeln lassen.

5.6.5 Reihenschlussmaschine

Im Falle einer Reihenschlussmaschine sind Anker- und Errgerwicklung in Reihen geschalten. Dadurch hängt der Fluss in der Maschine massgeblich vom Ankerstrom \(I_{A}\) ab (\(\Phi=f(I_{A})\)). Der Fluss lässt sich dabei im linearen Bereich ganz allgemein folgendermassen beschreiben:

\[\begin{equation} \Phi\cdot R_{mf} = \Theta= N_{f}\cdot I_{A} \tag{5.7} \end{equation}\]

Unter Berücksichtigung der Gleichung (5.1) kann somit die innere Quellenspannung bestimmt werden:

\[\begin{equation} U_{q} = c_{Masch}\cdot \frac{N_{f}}{R_{mf}} \cdot n \cdot I_{A} \tag{5.8} \end{equation}\]

Die Ankerspannung ergibt sich aus der Spannungssumme der inneren Quellenspannung und dem Spannungsabfall über dem Widerstand im Ankerkreis:

\[\begin{equation} U_{A} = c_{Masch}\cdot \frac{N_{f}}{R_{mf}} \cdot n \cdot I_{A} + R\cdot I_{A} \tag{5.9} \end{equation}\]

Daraus lässt sich die Drehzahl bestimmen:

\[\begin{equation} n = \frac{R_{mf}}{c_{Masch}\cdot N_{f}}\bigg(\frac{U_{A}}{I_{A}}-R\bigg) \tag{5.10} \end{equation}\]

Unter Berücksichtigung der Gleichung (5.2) lässt sich das innere Drehmoment bestimmen:

\[\begin{equation} M_{i} = \frac{c_{Masch}\cdot N_{f}}{2\cdot \pi \cdot R_{mf}}\cdot I^{2}_{A} \tag{5.11} \end{equation}\]

Mit Hilfe der Gleichungen (5.10) und (5.11) kann die Drehzahl-Drehmoment-Kennlinie bestimmt werden:

\[\begin{equation} n = \frac{R_{mf}}{c_{Masch}\cdot N_{f}} \Bigg(\frac{U_{A}}{\sqrt{M_{i}}}\cdot \sqrt{\frac{c_{Masch}\cdot N_{f}}{2\pi \cdot R_{mf}}}-R \Bigg) \tag{5.12} \end{equation}\]

Aus der Gleichung (5.12) wird ersichtlich, dass eine Variation der Ankerspannung \(k\cdot U_{An}\) zu einer Parallelverschiebung der Drehzahl-Drehmoment-Kennlinie führt, wie sie in Abbildung 5.18 dargestellt ist.

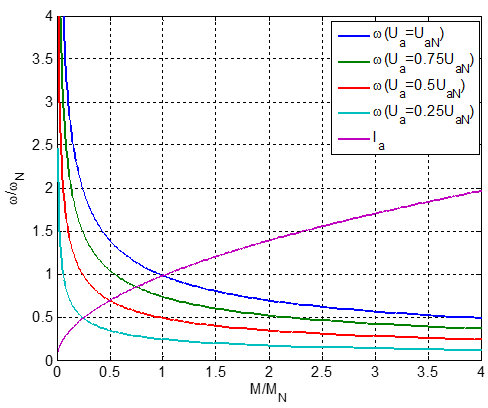
Abbildung 5.18: Drehzahl-Drehmoment Kennlinie der Reihenschlussmaschine mit Ankerspannung als Parameter

\[\begin{equation} \frac{n(k\cdot U_{An})}{n(U_{An})}=k\cdot n(U_{An}) \tag{5.13} \end{equation}\]

Der Reihenschlussmotor darf nicht unbelastet betrieben werden, da eine damit einhergehende Flussreduktion für eine fehlende innere Quellenspannung sorgt und der Motor somit durchgehen würde. Durch Umpolen der Erreger- oder Ankerwicklung kann die Drehrichtung des Motors beeinflusst werden. Aufgrund der Reihenschaltung von Erreger- und Ankerwicklung wirkt das erzeugte Drehmoment, unabhängig von der Stromrichtung immer in die gleiche Richtung, wodurch der Motor auch an Wechselspannung betreibbar ist (Universalmotor). Allerdings müssen für diese Betriebsart die Eisenteile des Motors geblecht ausgeführt werden. Dieser Maschinentyp findet häufig bei Haushaltsgeräten bzw. Elektrowerkzeugen Anwendung.

5.7 Umrichter für Gleichstrommaschinen

Da die Gleichstrommaschinen, insbesondere bei Anwendungen mit grossem Leistungsbedarf, nahezu vollständig von Drehfeldmaschinen verdrängt wurden, finden Gleichstrommaschinen heutzutage eher im Bereich kleinerer Leistungen Anwendung. Dies hat zur Folge, dass die in der Vergangenheit üblichen thyristorbasierten Stromrichter häufig durch Umrichter mit abschaltbaren Leistungshalbleitern ersetzt werden. Eine in diesem Fall häufig anzutreffende Umrichtervariante ist die H-Brücke, die in Abbildung 5.19 dargestellt ist.

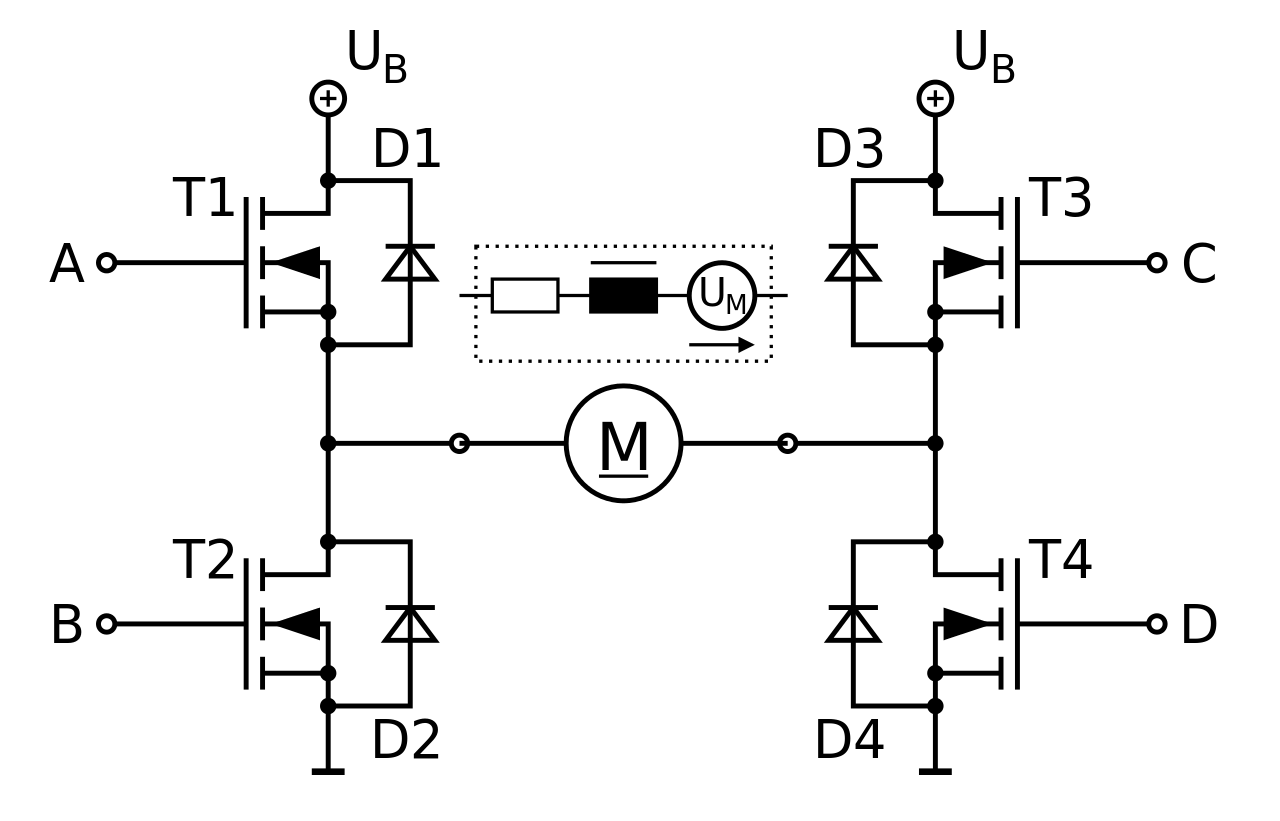
Abbildung 5.19: Vereinfachte Darstellung einer H-Brücke (Bildquelle: https://de.wikipedia.org/wiki/Vierquadrantensteller/media/File:Vierquadrantensteller.svg)

Als entsprechende Leistungshalbleiter kommen dabei üblicherweise Power-MOSFET’s oder IGBT’s zu Einsatz und die Versorgungsspannung (in der Abb. mit \(U_{B}\) gekennzeichnet) wird üblicherweise von einer sogenannten Zwischenkreiskondensator bereitgestellt, welcher wiederum von einem Gleichrichter gespeist wird. Diese Topologie ermöglicht es Strom in beide Richtungen durch den Motor zu treiben, wodurch sowohl motorischer als auch generatorischer Betrieb möglich ist. Eine Variation der mittleren Spannung wird durch Pulsweitenmodulation (PWM) ermöglicht. Grundsätzlich gilt, dass der Strom- und damit auch der Drehmomentrippel umso kleiner ausfällt, umso höher die PWM-Frequenz gewählt wird bzw. umso höher die Induktivität ist. Die Ansteuerung der Leistungshalbleiter erfolgt dabei üblicherweise mit Hilfe von Mikrocontrollern oder FPGA’s mit einer zwischengeschalteten Treiberstufe.

5.8 Systemtheoretische Beschreibung der Gleichstrommaschine

5.8.1 Elektromagnetismus

Üblicherweise werden die physikalischen bzw. mathematischen Modelle, die ein System beschreiben im Falle der Regelungstechnik systhemtheoretisch verallgemeinert. Somit ist es möglich Im Zusammenhang mit Systemen nur noch von Ein- und Ausgangssignalen zu sprechen. Die übliche Vorgehensweise ist dabei die Überführung bzw. Transformation der gegebenen Differentialgleichungen in den Laplace-Bereich. Eine ähnliche Vorgehensweise ist somit auch in Bezug auf die Gleichstrommaschine möglich. Ausgangspunkt bildet die Gleichung (5.3) zur Bestimmung der Ankerspannung der fremderregten DC-Maschine.

\[\begin{equation} U_{A}=R_{A}\cdot I_{A} +L_{A}\cdot s I_{A} + U_{i} \tag{5.14} \end{equation}\]

Durch Umstellen der Gleichung (5.14) nach dem Ankerstrom \(I_{A}\) ergibt sich folgende Struktur:

\[\begin{equation} I_{A}=\frac{\frac{1}{R_{A}}}{s\frac{L_{A}}{R_{A}}+1}\cdot \left( U_{A}-U_{i}\right) \tag{5.15} \end{equation}\]

Diese Gleichung spiegelt das Verhalten des Ankerstromes bei Veränderung der Ankerspannung wider. Der Bruchterm entspricht dabei einem Verzögerungsglied erster Ordnung (PT1) und kann durch eine Verstärkung \(V=\frac{1}{R_{A}}\) und eine Zeitkonstante \(T=\frac{L_{A}}{R_{A}}\) charakterisiert werden. Die Gleichung (5.15) kann, wie in der Regelungstechnik üblich, durch ein entsprechendes Blockschaltbild dargestellt werden.

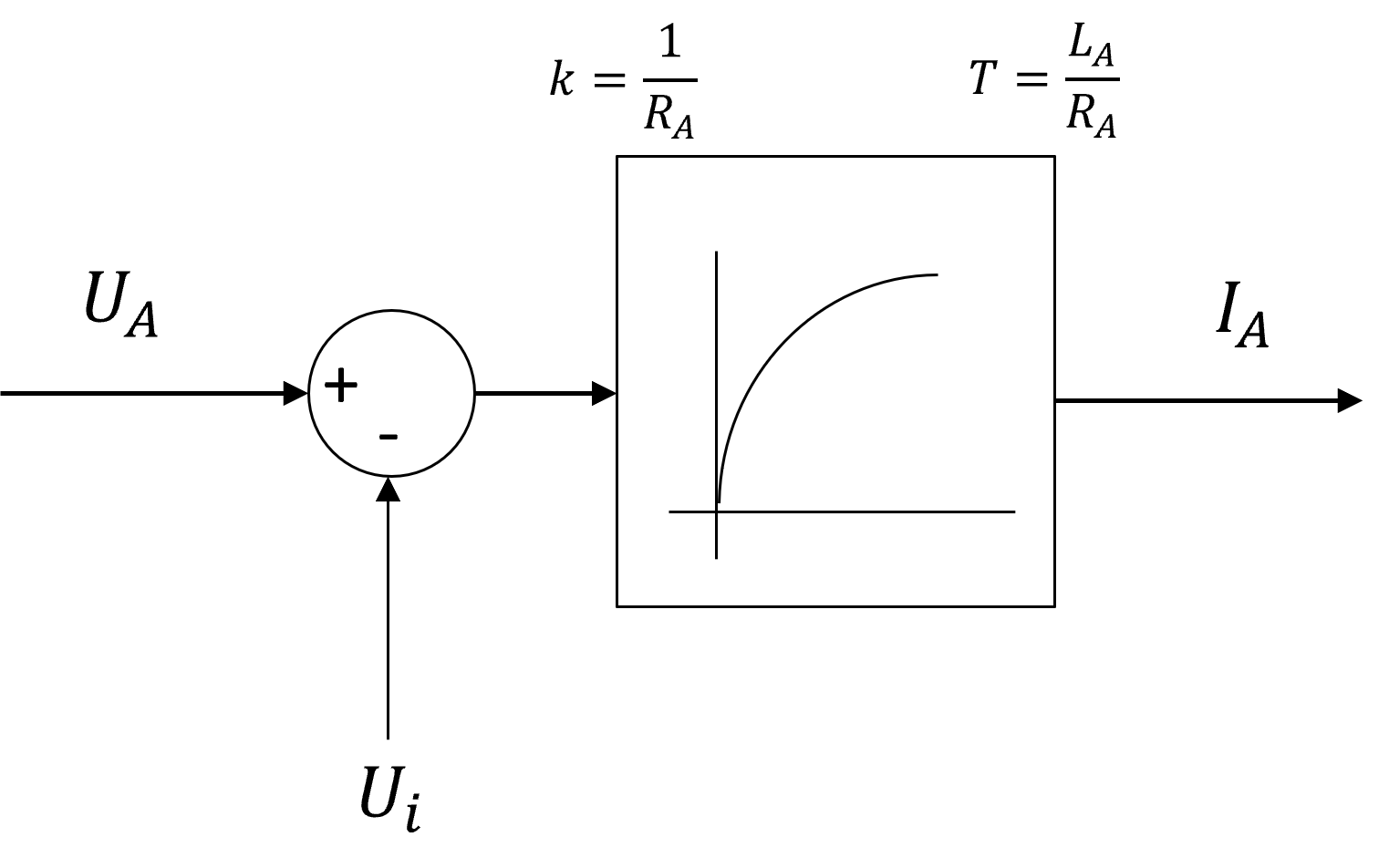
Abbildung 5.20: Blockschaltbild des Ankerkreises einer fremderregten Gleichstrommaschine

Das Blockschaltbild zeigt, dass die auf die Ankerspule wirkende Spannung der Spannungsdifferenz zwischen der eigentlichen Ankerspannung \(U_{A}\) und der induzierten Spannung \(U_{i}\) entspricht. Da der Erregerkreis der fremderregten DC-Maschine einen ähnlichen Aufbau aufweist, kann für den Erregerkreis analog vorgegangen werden und auch hier ein entsprechendes Blockschaltbild erzeugt werden, welches ebenfalls das Verhalten eines PT1-Gliedes aufweist.

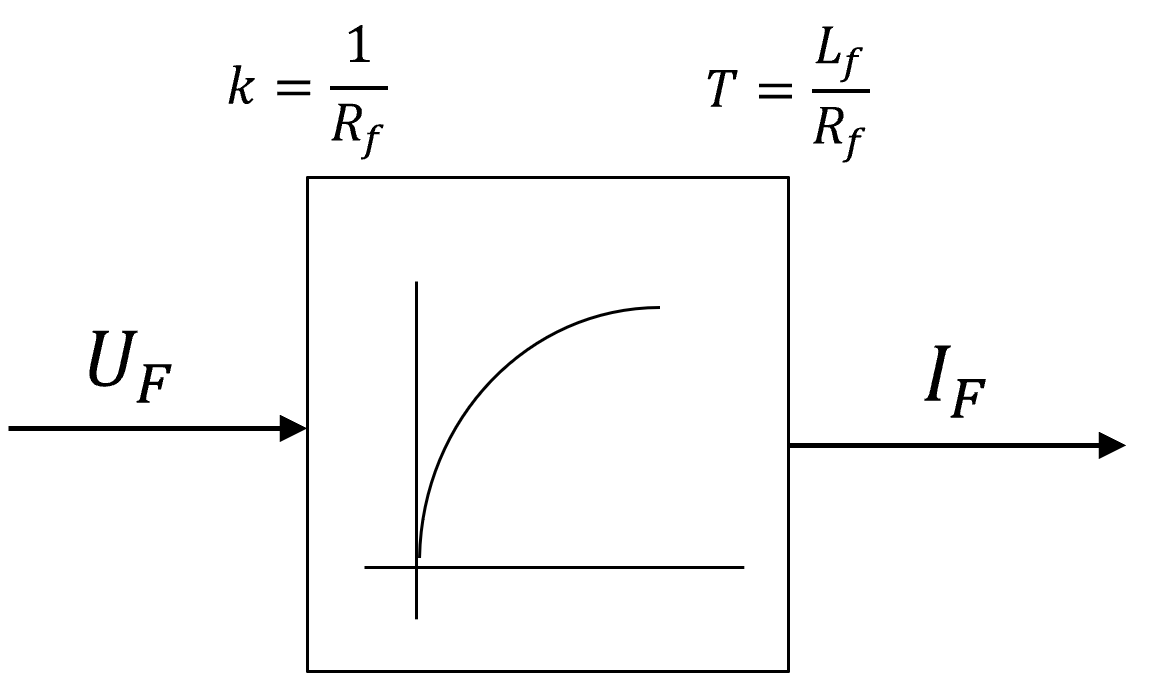
Abbildung 5.21: Blockschaltbild des Erregerkreises einer fremderregten Gleichstrommaschine

5.8.2 Mechanik

Wie bereits im Kapitel 3.1 vorgestellt, lässt sich die Mechanik eines elektrischen Antriebes mit Hilfe des dynamischen Grundgesetzes der Rotation beschreiben. Dieses besagt, dass die Summe aller Drehmomente dem Beschleunigungsmoment entspricht.

\[\begin{equation} \sum{M}=J\cdot \alpha = J\cdot \dot \omega = J \cdot \ddot \varphi \tag{5.16} \end{equation}\]

Dabei beschreibt \(\alpha\) die Winkelbeschleunigung, \(\omega\) die Winkelgeschwindigkeit, \(J\) das Trägheitsmoment und \(\varphi\) den Winkelweg der Rotation. Die Summe der Drehmomente setzt sich üblicherweise aus dem elektromagnetischen bzw. Luftspaltmoment \(M\) und dem Lastmoment \(M_{Last}\) zusammen. Es sei dabei zu beachten, dass sich das Lastmoment häufig aus mehreren einzelnen Komponenten (z.B. Reibmoment und Moment der Arbeitsmaschine) zusammensetzt. Da das Lastmoment dem Luftspaltmoment entgegenwirkt, wird es mit einem negativen Vorzeichen versehen. Somit kann Gleichung (5.16) vervollständigt werden.

\[\begin{equation} M-M_{Last}=J\cdot \ddot \varphi \tag{5.17} \end{equation}\]

Da die Mechanik mit einem eingangsseitigen Moment beaufschlagt wird und sich dadurch eine entsprechende Winkelbeschleunigung bzw. ein entsprechender Winkelweg ergibt, gilt es die Gleichung nach der gewünschten Ausgangssgrösse umzustellen.

\[\begin{equation} \varphi = \frac{1}{J}\int{\int{\left(M-M_{Last}\right)dt^{2}}} + \varphi_{0} \end{equation}\]

Das zugehörige Blockschaltbild ist in Abbildung 5.22 dargestellt.

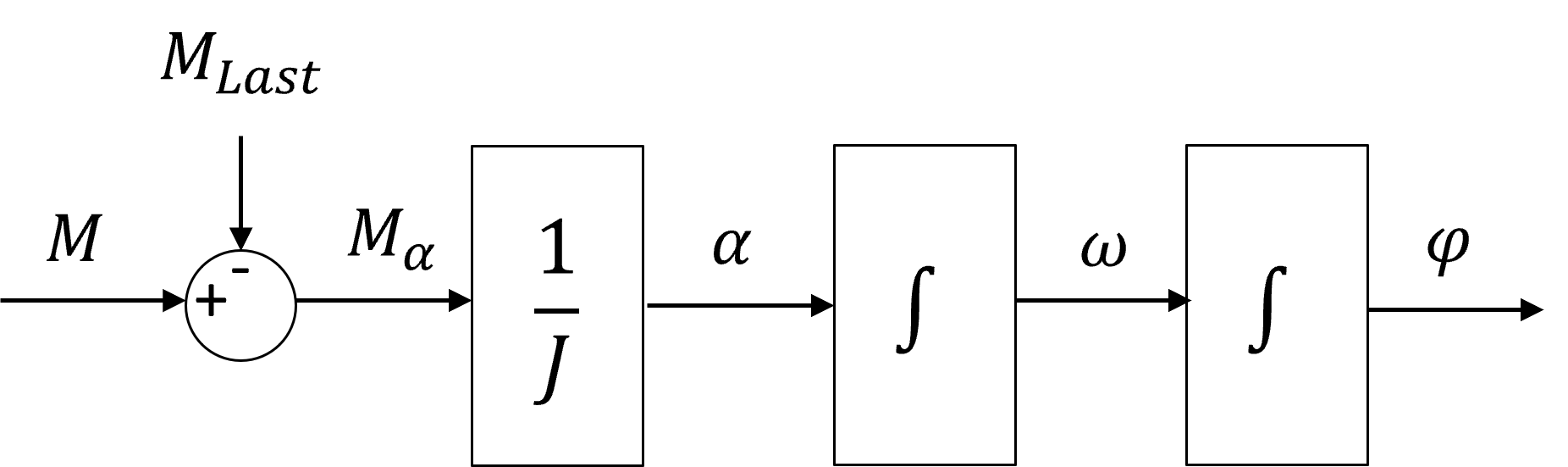
Abbildung 5.22: Blockschaltbild der Mechanik eines elektrischen Antriebs

5.8.3 Gesamtsystem

Werden alle vorgängig beschriebenen Teilsysteme (Anker- und Erregerkreis sowie Mechanik) zusammengeschaltet und die bereits erarbeiteten Gleichungen berücksichtigt, kann das Blockschaltbild der gesamten fremderregten Gleichstrommaschine dargestellt werden.

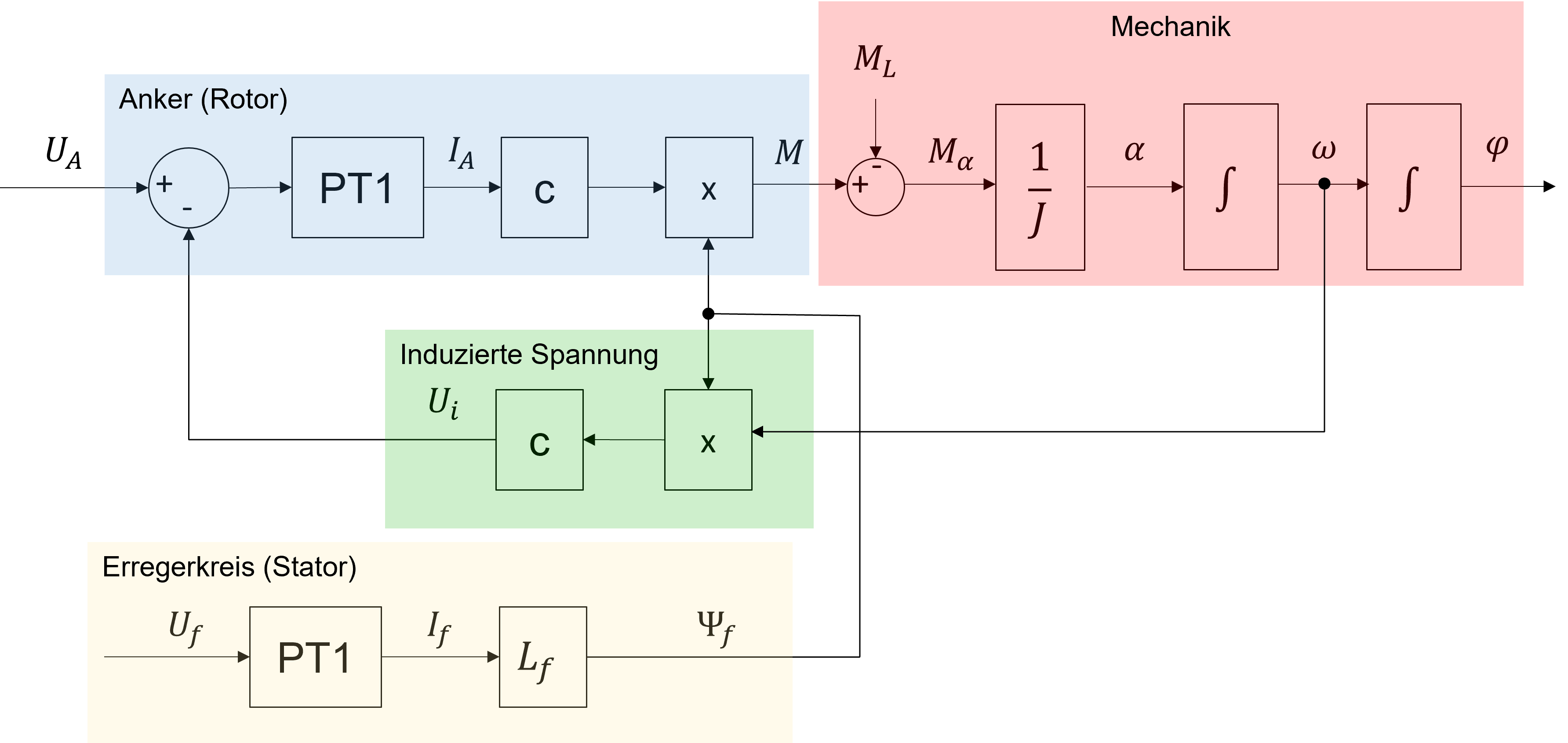
Abbildung 5.23: Blockschaltbild der fremderregten Gleichstrommaschine

Das Verhalten der Umrichter zur Bereitstellung der Anker- bzw. Erregerspannung ist im dargestellten Blockschaltbild nicht berücksichtigt. Das Blockschaltbild zeigt wie Paramter aus der Mechanik (Winkelgeschwindigkeit \(\omega\)) das elektrische Verhalten der Maschine beeinflussen.

5.9 Regelung der Gleichstrommaschine

Die klassische Methode zur Regelung von elektrischen Maschinen (inkl. Drehfeldmaschinen) ist die sog. Kaskadenregelung, bei der einzelne Regler kaskadiert angeordnet werden. Eine solche Regelstruktur ist in Abbildung 5.24 dargestellt.

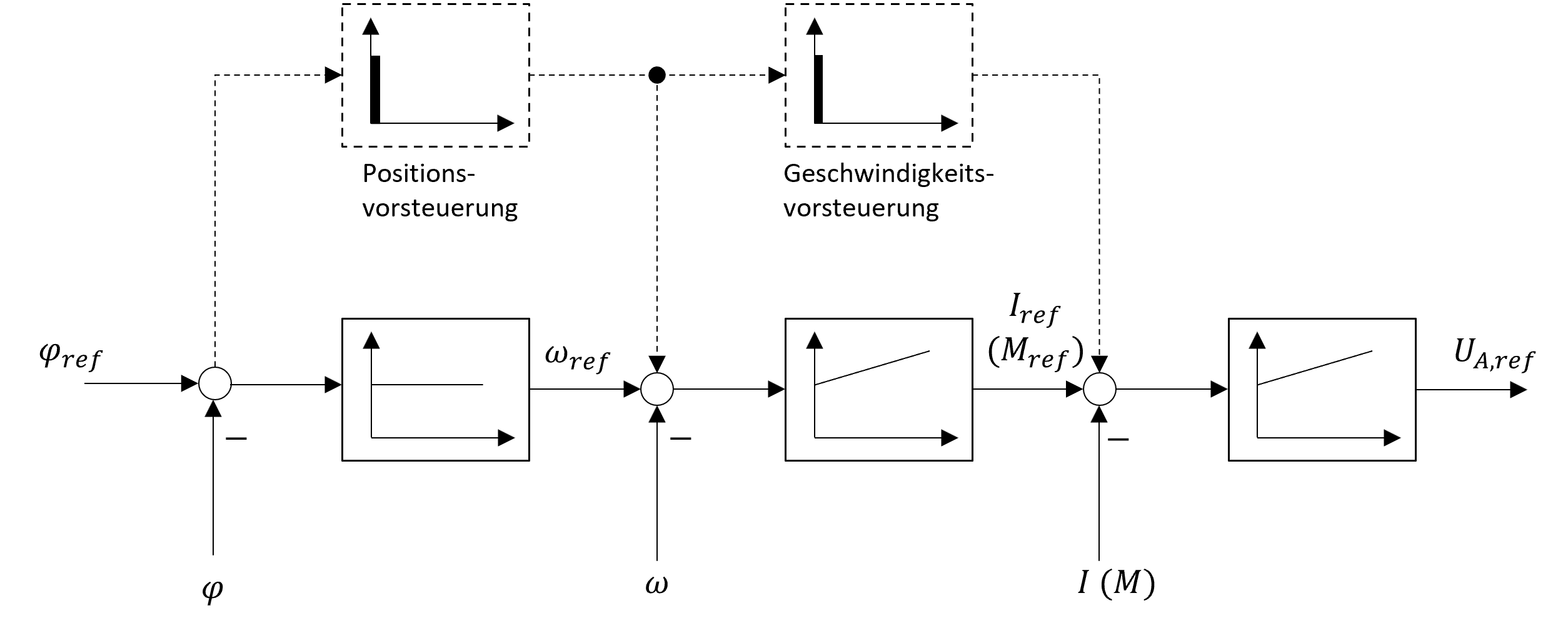
Abbildung 5.24: Kaskadierte Regelstruktur einer Gleichstrommaschine

Die Streckenzeitkonstanten der einzelnen kaskadierten Regelstrecken nehmen dabei von innen nach aussen hin zu. Aufgrund des einfachen und überschaubaren Aufbaus dieser Regelstruktur, ist die Einstellung der Regler relativ einfach und eventuelle Begrenzungen (z.B. Strombegrenzung) können einfach implementiert werden. Aufgrund dessen wird diese Methode der Regelung in der Industrie am häufigsten eingesetzt. Die gestrichelt gekennzeichneten Blöcke stellen eventuell vorhandene Vorsteuerungen dar, die dazu verwendet werden die Dynamik des Antriebssystems weiter zu verbessern.

5.9.1 Drehmomentregelung

Da der Ankerstrom einer Gleichstrommaschine direkt proportional zum elektrischen Drehmoment ist (mit gewisser Toleranz und bei konstantem Fluss), wird die Stromregelung häufig auch als Drehmomentregelung bezeichnet. Es handelt sich allerdings um eine Drehmomentsteuerung mit unterlagerter Stromregelung. Dieser Regelkreis stellt den innersten Regelkreis der in Abbildung 5.24 dargestellten Kaskadenregelung dar und regelt somit die Strecke mit der kleinsten Zeitkonstante des Gesamtsystems. Da der Stromrichter, welcher den Anker mit Spannung versorgt, mit Schaltfrequenzen im Kilohertzbereich arbeitet, wird dieser in erster Näherung als ideal angenommen, wodurch er in der weiteren Betrachtung vernachlässigt werden kann. Desweiteren wird davon ausgegangen, dass der magnetische Fluss in der Maschine konstant ist.

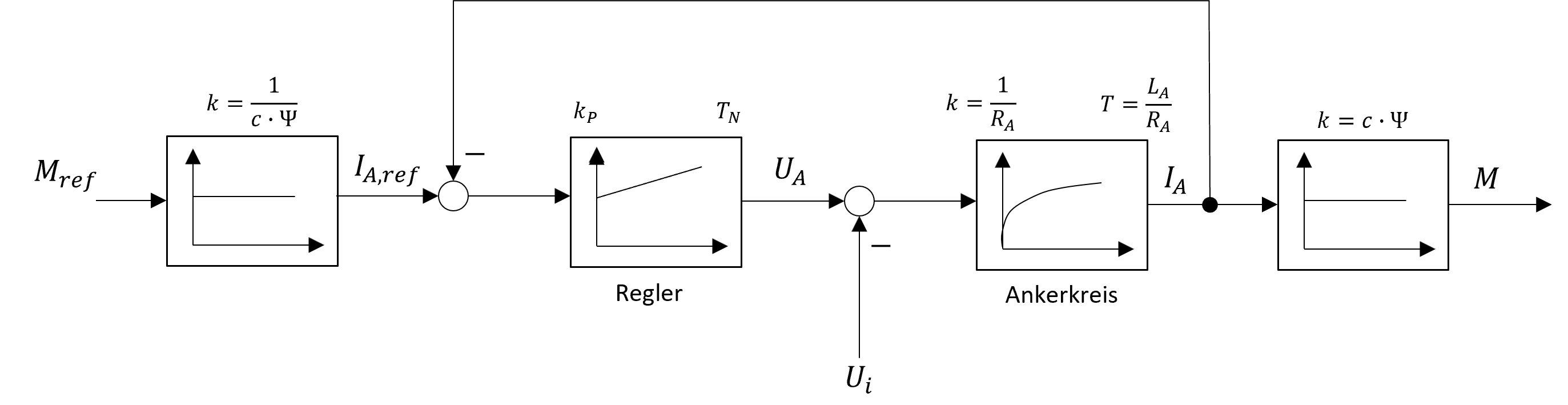
Abbildung 5.25: Drehmomentsteuerung mit unterlagertem Ankerstromregelkreis der fremderregten Gleichstrommaschine

Wie die Abbildung zeigt, wird zur Regelung der Ankerstromes ein PI-Regler verwendet, da der I-Anteil einen bleibenden Regelfehler verhindert. Die geschwindigkeitsabhängige induzierte Spannung \(U_{i}\) wirkt als Störgrösse, welche allerdings aufgrund der relativ grossen Zeitkonstante problemlos vom Regler ausgeregelt werden kann. Berücksichtigt man die Übertragungsfunktion des PI-Reglers, kann die Nachstellzeit des Regler relativ einfach bestimmt werden, indem sie der Ankerzeitkonstante gleichgesetzt wird. Aufgrund dessen verhält sich der geschlossene Regelkreis anschliessend wie ein Verzögerungsglied erster Ordnung. Bei der Wahl der Reglerverstärkung \(k_{P}\) muss hingegen die Verzögerung des Umrichters mit berücksichtigt werden und kann somit nicht beliebig hoch eingestellt werden. Die Reglereinstellung wird bei der Stromregelung üblicherweise nach dem sogenannten Betragsoptimum vorgenommen, bei dem es sich um eine Einstellregel handelt, die auf dem Frequenzkennlinienverfahren basiert und in Kapitel 10.1 näher erläutert wird.

Aufgrund des direkten Zusammenhanges zwischen dem Drehmoment und des magnetischen Feldes, wäre es auch möglich das Drehmoment zu regeln, indem der Ankerstrom \(I_{A}\) konstant gehalten und stattdessen der den Erregerstrom \(I_{f}\) als Stellgrösse verwendet wird. Da die Zeitkonstante des Erregerkreises allerdings in der Regel erheblich grösser ausfällt als die Zeitkonstante des Ankerkreises, würde dies in einer weniger dynamischen Regelung resultieren.

5.9.2 Drehzahlregelung

In Abbildung 5.26 ist der Drehzahlregelkreis mit optionaler Drehzahlvorsteuerung der Gleichstrommaschine dargestellt.

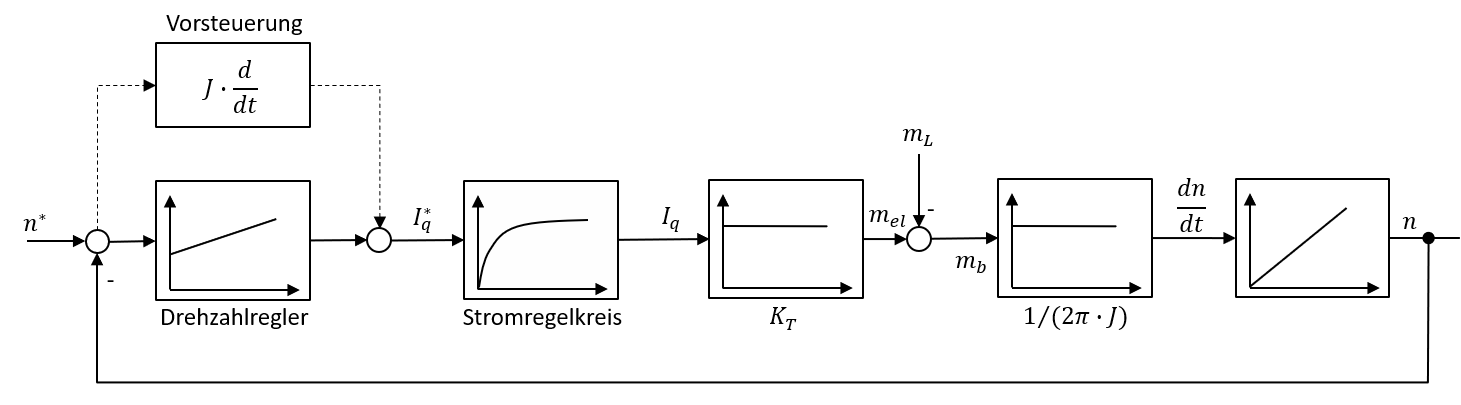
Abbildung 5.26: Drehzahlregelkreis mit unterlagertem, betragsoptimiertem Stromregelkreis

Die eigentliche Regelstrecke, bestehend aus dem unterlagerten Stromregelkreis, wird hier vereinfacht als Verzögerungsglied erster Ordnung dargestellt. Das eine solche Vereinfachung möglich ist, wird in Kapitel 10.2 erklärt. Das an der Motorwelle angreifende Lastmoment \(M_{L}\) wirkt als Störgrösse. Obwohl sich im Vorwärtszweig des Regelkreises bereits ein Intergrierglied befindet, ist es dennoch notwendig einen PI-Regler zu verwenden, da die Störgrösse vor dem Integrierglied angreift. In der klassischen Antriebstechnik hat sich als Einstellregel für den Drehzahlregelkreis das sogenannte symmetrische Optimum etabliert, welches ausführlich in Kapitel 10.2 beschrieben ist. Die optional dargestellte Vorsteuerung dient dazu die Dynamik des Regelkreises zu verbessern, indem das Beschleunigungsmoment, welches vom Trägheitsmoment der sich bewegenden Massen und der Winkelbeschleunigung abhängt, kompensiert wird und der Regler somit lediglich die Störgrösse (Lastmoment) und Modellabweichungen (z.B. drehzahlabhängige Reibung) ausregeln muss. Wird ein solcher Antriebs zur Positionsregelung verwendet, dann ist dies ein sehr wirksames Mittel um Schleppfehler zu minimieren. Dazu ist es allerdings notwendig, dass die Referenzdrehzahl analytisch (z.B. in Form einer Solltrajektorie) vorliegt, da die Ableitung der Referenzdrehzahl gebildet werden muss.

5.9.3 Lageregelung

Ist es notwendig die Rotorlage und damit die Position der Arbeistmaschine zu regeln, dann kommt ein P-Regler zum Einsatz, da der Vorwärtszweig des Regelkreises bereits ein Intergierglied beinhaltet und keine Störgrösse vor dem Integrierglied angreift.

Abbildung 5.27: Lageregelkreis mit unterlagertem Drehzahlregelkreis

Abbildung 5.27 zeigt das Blockschaltbild eines möglichen Lageregelkreises. Der Faktor \(K_{S}\) beschreibt dabei ein Proportionalglied, welches den Zusammenhang zwischen der Drehzahl \(n\) der Gleichstrommaschine und der Position der Arbeitsmaschine \(x\) herstellt. Dies könnte, am Beispiel eines Spindelantriebs, z.B. die Spindelsteigung darstellen, die die Umwandlung einer Rotation in eine Translation ermöglicht.

\[ v=K_{S}\cdot n=\frac{\omega\cdot K_{S}}{2\cdot \pi} \]

Die Übertragungsfunktion des offenen Lageregelkreises kann folgendermassen zusammengefasst werden:

\[\begin{equation} G_{O,x}(s)=k_{P,x}\cdot K_{S}\cdot \frac{1}{1+s\cdot T_{GW,n}}\cdot \frac{1}{s} \tag{5.18} \end{equation}\]

Die Faktoren \(k_{P,x}\) und \(K_{S}\) werden üblicherweise zur sogenannten Geschwindigkeitsverstärkung \(K_{v}\) zusammengefasst, welche eine wichtige Kenngrösse zur Beurteilung von Lageregelkreisen darstellt. Der \(K_{v}\)-Faktor beeinflusst unmittelbar die Grösse des Schleppfehlers bzw. Schleppabstandes, der beim Anfahren einer neuen Position auftritt. Je grösser der \(K_{v}\)-Faktor ist, umso kleiner ist der sich einstellende Schleppfehler (siehe Abbildung 5.28).

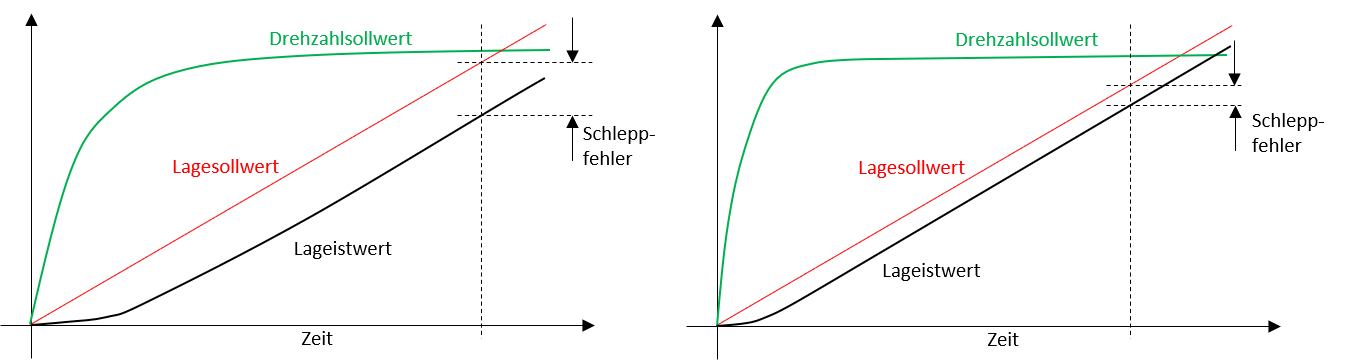
Abbildung 5.28: Einfluss der Proportionalverstärkung auf den Schleppfehler (links:geringe Verstärkung, rechts: grosse Verstärkung)

Der geschlossenen Lageregelkreis \(G_{W,x}(s)\) zeigt die Struktur eines Verzögerungsgliedes zweiter Ordnung (PT2).

\[\begin{equation} \begin{matrix} G_{W,x}(s)=\frac{G_{W,x}(s)}{1+G_{W,x}(s)}= \frac{k_{P,x}\cdot K_{S}\cdot \frac{1}{1+s\cdot T_{GW,n}}\cdot \frac{1}{s}}{1+k_{P,x}\cdot K_{S}\cdot \frac{1}{1+s\cdot T_{GW,n}}\cdot \frac{1}{s}} \\ G_{W,x}(s)=\frac{k_{P,x}\cdot K_{S}}{k_{P,x}\cdot K_{S}+s(1+s\cdot T_{GW,n})}=\frac{1}{1+s\cdot \frac{1}{k_{P,x}\cdot K_{S}}+s^{2}\cdot \frac{T_{GW,n}}{k_{P,x}\cdot K_{S}}} \end{matrix} \tag{5.19} \end{equation}\]

Durch Koeffizientenvergleich mit der Normalform der Übertragungsfunktion eines PT2-Gliedes \(\Biggl(G_{PT2}(s)=\frac{1}{1+s\cdot \frac{2D}{\omega_{0}}+s^{2}\cdot \frac{1}{\omega_{0}^{2}}}\Biggr)\) lassen sich sowohl die Resonanzfrequenz als auch die Dämpfung bestimmen:

\[\begin{equation} \omega_{0}=\sqrt{\frac{k_{P,x}\cdot K_{S}}{T_{GW,n}}} \tag{5.20} \end{equation}\]

\[\begin{equation} D=\frac{1}{2\cdot \sqrt{k_{P,x}\cdot K_{S}\cdot T_{GW,n}}}=\frac{1}{2\cdot \sqrt{K_{v}\cdot T_{GW,n}}} \tag{5.21} \end{equation}\]

Bei der Auslegung des Lagereglers wird dabei darauf geachtet, dass der Lageregelkreis ausreichend stark gedämpft wird. Diese Forderung kann berücksichtigt werden, indem die Dämpfung auf \(D\geq 0.7=\frac{1}{\sqrt{2}}\) eingestellt wird. Dieser Ansatz liefert die Einstellregel für die die Verstärkung des Lagereglers:

\[ k_{P,x}\leq \frac{1}{2\cdot T_{GW,n}\cdot K_{S}} \] Wird die Geschwindigkeitsverstärkung \(K_{v}\) so gewählt, das sich eine Dämpfung von \(D=0.707\) einstellt und der quadratische s-Term im Nenner der Führungsübertragungsfunktion \(G_{W,x}(s)\) (vgl. Gleichung (5.19)) vernachlässigt, dann verhält sich der geschlossene Lageregelkreis wie ein PT1-Glied mit der Zeitkonstante \(T_{GW,x}=2\cdot T_{GW,n}\).

5.10 Zusammenfassung

Werden die kaskadierten Regelkreise der Gleichstrommaschine entsprechend der empfohlenen Einstellregeln (siehe Kapitel 5.9.3, 10.1 und 10.2) eingestellt, dann wird der Einfluss der Zeitkonstante des vereinfachten Stromregelkreises \(T_{N,I}\) recht deutlich sichtbar, wenn man die Führungsübertragungsunktionen der unterlagerten Regelkreise betrachtet:

\[ G_{W,x}(s)\approx \frac{1}{1+s\cdot T_{GW,x}}=\frac{1}{1+s\cdot 2\cdot T_{GW,n}}=\frac{1}{1+s\cdot 2\cdot 4\cdot T_{GW,I}} = \frac{1}{1+s\cdot 2\cdot 8\cdot T_{N,I}} \]

Dies bedeutet, dass die erreichbare Geschwindigkeitsverstärkung des Lageregelkreises mit zunehmender Zeitkonstante des Stromregelkreises \(T_{N,I}\) sinkt. Für hochdynamische Positionierantriebe, die einen sehr geringen Schleppfehler aufweisen sind somit sehr schnelle Stromrichter notwendig. Die Dynamik des Umrichters wird dabei massgeblich von der Schaltfrequenz des Umrichters (neben der Topologie) beeinflusst.

References

3.

Böcker J (2020) Elektrische Antriebstechnik. Universität Paderborn, Paderborn, Deutschland

4.

Turschner D (1998) Elektrische Maschinen. TU Clausthal, Clausthal, Deutschland