Kapitel 10 Reglereinstellung
Bei der Einstellung von Reglern (Reglerentwurf) gibt es unterschiedliche Lösungskonzepte. Dabei unterscheidet man zwischen folgenden Methoden [6]:
- Heuristische Einstellregeln (Faustformelverfahren), die ohne ein mathematisches Modell der Regelstrecke auskommen. Hierbei wird der Regler an die Regelstrecke angeschlossen und mit Hilfe von Experimenten (z.B. Sprungantwort) nach geeigneten Reglerparametern gesucht.
- Reglerentwurf durch Loopshaping (Frequenzkennlinienverfahren) bei denen Kenntnis der einzelnen Übertragungslieder vorausgesetzt wird. Bei diesem verfahren wird die Frequenzkennlinie der Regelstrecke gezielt durch Wahl eines entsprecehnden Reglers beeinflusst.
- Reglerentwurf anhand des Pol-Nullstellenbildes des Regelkreises.
- Parameteroptimierung des Reglers, wobei die Güteanforderungen an einen Regelkreis durch ein Gütefunktional beschrieben werden und der Regelerentwurf somit als Optimierungsfunktion beschrieben wird.
In der klassischen Antriebstechnik haben sich Einstellregeln nach dem Frequenzkennlinienverfahren etabliert, da die Streckenparameter meistens bekannt sind oder messtechnisch ermittelt werden können. Bei der unterlagerten Stromregelung erfolgt die Reglereinstellung nach dem sogenannten Betragsoptimum und die Reglerparameter der überlagerten Drehzahlregelung werden nach dem symmetrischen Optimum eingestellt.
10.1 Betragsoptimum
Bei dem Betragsoptimum handelt es sich um eine Einstellregel die auf dem Frequnezkennlinienverfahren basiert und sich in der Antriebstechnik als Einstellregel für Strom- bzw. Drehmomentregelkreise etabliert hat, da sich mit einer solchen Einstellung ein gutes Führungsverhalten ergibt. Die eigentliche Entwurfsidee besteht darin, die massgebliche (grösste) Zeitkonstante der Regelstrecke mit Hilfe der Nachstellzeit des, üblicherweise verwendeten, PI-Reglers zu kompensieren und die Verstärkung des Reglers entsprechend den geforderten Güteanforderungen einzustellen. Basierend auf dieser Grundlage stellt sich ein Führungsfrequenzgang \(G_{W}(s)\) ein, der über einen möglichst grossen Frequenzbereich hinweg den Betrag Eins (1) aufweist, was darauf hindeutet, dass die Regelgrösse dem Wert der Führungsgrösse mit geringer zeitlicher Verzögerung folgen kann. Die Optimierung bezieht sich in diesem Zusammenhang auf die Optimierung der Einschwingzeit. Um das Betragsoptimum anwenden zu können, müssen gewisse Voraussetzungen erfüllt sein:
- Das Messglied der wird mit zur Regelstrecke gezählt, wodurch sich ein Standardregelkreis ergibt
- Die Parameter der Regelstrecke (Zeitkonanstanten und Verstärkungen) müssen bekannt sein
- Es wird davon ausgegangen, dass sich die Regelstrecke aus einer Zusammensetzung von Verzögerungsgliedern handelt
Das Vorgehen bei der Reglereinstellung nach dem Betragsoptimum soll anhand der in Kapitel 5.9.1 dargestellten, fremderregten Gleichstrommaschine erfolgen.

Abbildung 10.1: Modifizierter Stromregelkreis der fremderregten Gleichstrommaschine
In Abbildung 10.1 ist dargestellt, wie der zu betrachtende Stromregelkreis der fremderregten Gleichstrommaschine aussieht. Der Regelkreis wurde dazu im Vergleich zum Stromregelkreis in Abbildung 5.25 dahingehend modifiziert, dass das Verhalten des Stromrichters ebenfalls in Form eines Totzeitliedes berücksichtigt wird. Diese Totzeit beschreibt die Zeitdauer, die vergeht, bis der Stromrichter (z.B. H-Brücke) auf eine Änderung des Spannungs-Sollwertes reagiert. Sie ist indirekt proportional zur Schaltfrequenz des Stromrichters. Das Totzeitglied wiederum, wird dabei durch ein PT1-Glied ersetzt, dass sich dieses deutlich einfacher in der Regelstruktur berücksichtigen lässt. Desweiteren bleibt die Störgrösse (induzierte Spannung) in diesem Fall unberücksichtigt, da die Führungsübertragungsfunktion des Stromregelkreises von Interesse ist und die Störgrösse, aufgrund der deutlich grösseren Zeitkonstante der Mechanik, problemlos vom Regler kompensiert werden kann. Ausserdem wurde berücksichtigt, dass die Regelgrösse (Ankerstrom \(I_{A}\)) durch ein geeignetes Messglied (z.B. Stromwandler) zurückgekoppelt werden muss. Da eine solche Strommessung mit entsprechendem Rauschen einhergeht und gleichzeitig einen funktionsbedingten (Ein- und Ausschalten der Leistungshalbleiter) Rippel aufweist, wird dieses Messignal im Normalfall noch tiefpassgefiltert, was in der Abbildung ebenfalls durch ein entsprechendes PT1-Glied berücksichtigt wird. Die Übertragungsfunktionen des Stromrichters \(G_{SR}(s)\), der Ankerwicklung \(G_{A}(s)\) sowie des Messfilters \(G_{Filt}(s)\) können also alle durch die folgende, grundlegende Struktur der Übertragungsfunktion charakterisiert werden:
\[ G(s) = \frac{k}{1+s\cdot T} \]
Der Faktor \(k\) repräsentiert dabei die Verstärkung und der Faktor \(T\) die Zeitkonstante des jeweiligen Verzögerungsgliedes. Die Zeitkonstanten der einzelnen PT1-Glieder lassen sich folgendermassen abschätzen:
- \(T_{SR}\): Zeitkonstante des Stromrichters. Da die Stromrichter mit Frequenzen im Kilohertzbereich arbeiten, kann davon ausgegangen werden, dass sich die zugehörige Zeitkonstante im Mikrosekundenbereich bewegt.
- \(T_{A}=\frac{L_{A}}{R_{A}}\): Ankerzeitkonstante, die je nach Maschinengrösse im zwei- bis dreistelligen Millisekundenbereich liegt.
- \(T_{Filt}\): Da der vom Stromrichter erzeugte Rippel unterdrückt werden soll, liegt diese Zeitkonstante üblicherweise im Bereich \(T_{SR}<T_{Filt}<T_{A}\).
Die Verstärkungsfaktoren beschreiben dabei einen konstanten Faktor, mit dem ein entsprechendes Eingangssignal multipliziert werden muss, um ein zu erwartendes Ausgangssignal zu erhalten:
- \(k_{A}=1/R_{A}\) abhängig vom Ankerwiderstand der betrachteten DC-Maschine. Beschreibt quasi den konstanten Umwandlungsfaktor des Eingangssignals (Spannung) in ein zugehöriges Ausgangssignal (Strom).
- \(k_{SR}\) beschreibt die verstärkende Wirkung des Stromrichters. Da der Stromrichter üblicherweise einen Absolutwert als Spannungs-Sollwert erhält kann hier von einem Wert von 1 ausgegangen werden. Sollte der Stromrichter stattdessen einen normierten Spannungs-Sollwert erhalten, muss dieser Faktor entsprechend angepasst werden.
- \(k_{Filt}\) beschreibt das Übersetzungsverhältnis des Stromwandlers. Je nach verwendetem Messprinzip (z.B. Hallsensor, Shuntwiderstand, etc.) unterscheidet sich dieser Faktor.
Das Bodediagramm der Übertragungsfunktionen der drei beteiligten PT1-Glieder sind in der Abbildung 10.2 unter Verwendung sinnvoller Beispielwerte dargestellt.
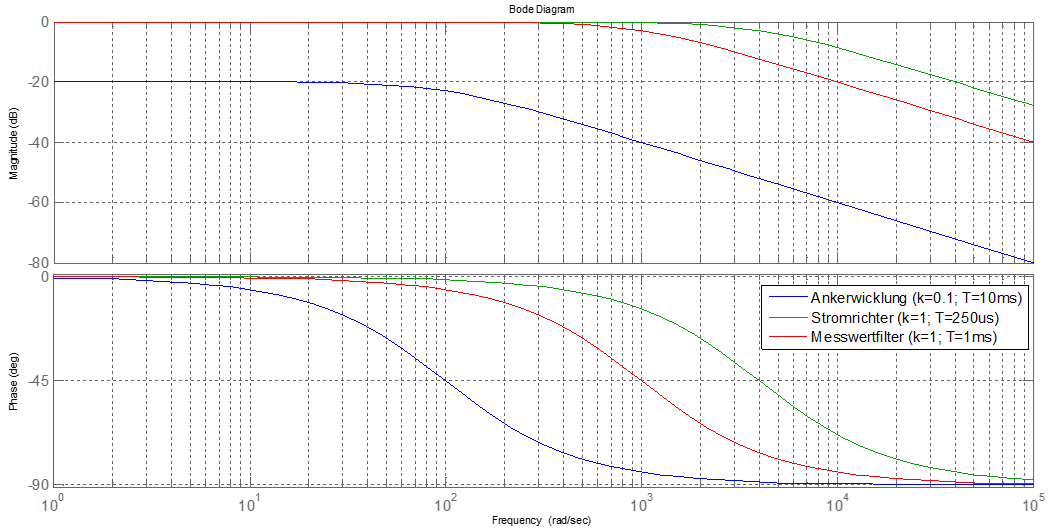
Abbildung 10.2: Bodediagramm der drei beteiligten PT1-Glieder
Die Übertragungsfunktion eines PI-Reglers lautet:
\[ G_{Regler}(s)=k_{P}\cdot \frac{1+s\cdot T_{N}}{s\cdot T_{N}} \]
Das zugehörige Bodediagramm eines solchen PI-Reglers ist in Abbildung 10.3 dargestellt.
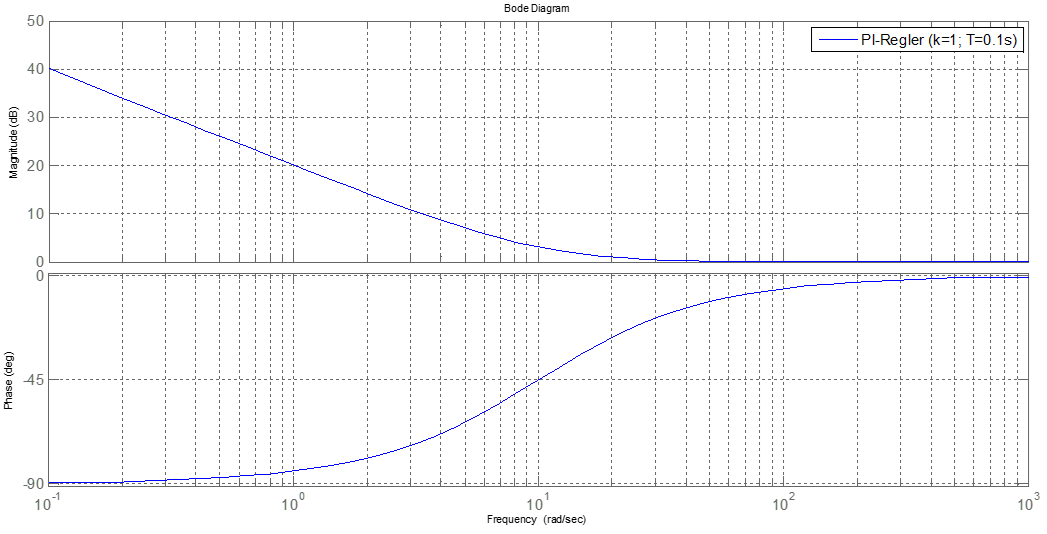
Abbildung 10.3: Bodediagramm eines PI-Reglers (beispielhafte Parameterwahl)
Der offene Regelkreis \(G_{0}(s)\) ergibt sich indem alle Übertragungslieder des Regelkreises miteinander multipliziert werden.
\[\begin{equation} G_{0}(s)=G_{Regler}(s)\cdot G_{SR}(s)\cdot G_{A}(s)\cdot G_{Filt}(s) \end{equation}\]
\[\begin{equation} G_{0}(s)=k_{P}\cdot k_{SR}\cdot k_{A}\cdot k_{Filt}\cdot \frac{1+s\cdot T_{N}}{s\cdot T_{N}}\cdot \frac{1}{1+s\cdot T_{SR}}\cdot \frac{1}{1+s\cdot T_{A}}\cdot \frac{1}{1+s\cdot T_{Filt}} \tag{10.1} \end{equation}\]
Da die Zeitkonstante des Messfilters \(T_{Filt}\) und des Stromrichters \(T_{SR}\) deutlich kleiner ausfallen als die des Ankerkreises ist es zulässig diese beiden Zeitkonstanten zu einer sog. Summenzeitkonstante \(T_{\sum}\) zusammenzufassen. Diese Zusammenfassung basiert auf dem Satz von der Summe kleiner Zeitkonstanten [7]. Dieser besagt, dass eine Ersatzzeitkonstante gebildet werden kann, die sich aus der Summe aller kleinen Zeitkonstanten zusammensetzt, wenn eine Regelstrecke höherer Ordnung vorliegt, die folgende Form aufweist:
\[ G(s)=\frac{K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{2}\cdot s)\dotsc (1+T_{n}\cdot s)} \]
Unterschieden wird dabei zwischen Regelstrecken mit einer oder zwei dominanten Zeitkonstanten. Gibt es nur eine dominante Zeitkonstante, gilt [8]:
\[\begin{equation} \begin{matrix} T_{\sum}=\sum\limits_{i=2}^{n}{T_{i}}, & T_{1}>>T_{\sum}, & G(s)=\frac{K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{\sum}\cdot s)} \end{matrix} \end{equation}\]
Im Falle von zwei dominanten Zeitkonstanten gilt [9]:
\[\begin{equation} \begin{matrix} T_{\sum}=\sum\limits_{i=3}^{n}{T_{i}}, & T_{1}>T_{2}>>T_{\sum}, & G(s)=\frac{K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{2}\cdot s)\cdot (1+T_{\sum}\cdot s)} \end{matrix} \end{equation}\]
Da, im Falle des Gleichstrommotors die Ankerzeitkonstante \(T_{A}\) deutlich grösser ausfällt als alle weiteren Zeitkonstanten, wird von einer Regelstrecke mit nur einer dominanten Zeitkonstante ausgegangen, wodurch sich Gleichung (10.1) vereinfacht:
\[\begin{equation} G_{0}(s)=k_{P}\cdot k_{SR}\cdot k_{A}\cdot k_{Filt}\cdot \frac{1+s\cdot T_{N}}{s\cdot T_{N}}\cdot \frac{1}{1+s\cdot T_{A}}\cdot \frac{1}{1+s\cdot T_{\sum}} \tag{10.2} \end{equation}\]
Die Summenzeitkonstante \(T_{\sum}\) ergibt sich dabei aus der Summe der zwei kleinen Zeitkonstanten:
\[ T_{\sum} = T_{Filt}+T_{SR} \]
Um nun eine möglichst grosse Bandbreite des Frequenzganges des offenen Regelkreises zu erhalten, wird die Nachstellzeit \(T_{N}\) des PI-Reglers auf die dominante Zeitkonstante (Ankerzeitkonstante \(T_{A}\) in diesem Fall) abgestimmt:
\[ T_{N}=T_{A} \]
Durch diese Parametereinstellung wird die Übertragungsfunktion des offenen Regelkreises weiter vereinfacht (Kürzen im mathematischen Sinn):
\[\begin{equation} G_{0}(s)= \frac{k_{P}\cdot k_{SR}\cdot k_{A}\cdot k_{Filt}}{s\cdot T_{A}}\cdot \frac{1}{1+s\cdot T_{\sum}} \tag{10.3} \end{equation}\]
Durch diese Kompensation wird somit der Einfluss (die verzögernde Wirkung) des Ankerkreises eliminiert und die Regeldynamik hängt nur noch von der, deutlich kleineren, Summenzeitkonstante \(T_{\sum}\) ab. Diese Wirkung ist ebenfalls in Abbildung 10.4 dargestellt.
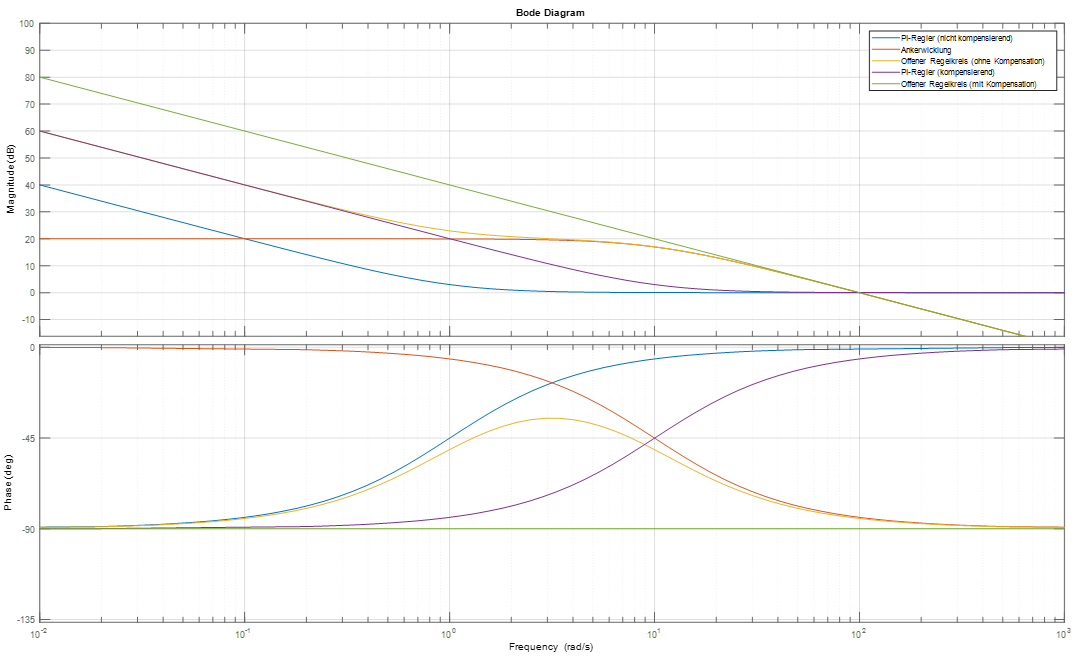
Abbildung 10.4: Bodediagramm verschiedener Übertragungsglieder zur Verdeutlichung der Wirkung der Kompensation der Ankerzeitkonstante über die Nachstellzeit des Reglers
Wird dieser modifizierte offene Regelkreis geschlossen, ergibt sich folgende Führungsübertragungsfunktion \(G_{W}(s)\) des Regelkreises.
\[\begin{equation} \begin{matrix} G_{W}(s)= \frac{G_{0}(s)}{1+G_{0}(s)}=\frac{k_{P}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}}{s\cdot T_{A}\cdot (1+s\cdot T_{\sum})+k_{P}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}} \\ G_{W}(s)= \frac{1}{1+s\cdot \frac{T_{A}}{k_{P}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}}+s^{2}\cdot \frac{T_{A}\cdot T_{\sum}}{k_{P}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}}} \end{matrix} \tag{10.4} \end{equation}\]
Gleichung (10.4) entspricht von der Struktur her einem Verzögerungsglied zweiter Ordnung (PT2):
\[ G(s)=\frac{1}{1+s\cdot a_{1}+s^{2}\cdot a_{2}} \]
Die optimale Reglerverstärkung \(k_{P}\) kann auf unterschiedliche Art und Weise bestimmt werden. Ein erster Ansatz kann über die Forderung nach einem Betrag der Führungsübertragungsfunktion \(|G_{W}(j\omega)|=1\) über einen möglichst weiten Frequenzbereich hinweg, gewählt werden.
\[ |G_{W}(j\omega)| = \left|\frac{1}{1+j\omega a_{1}+(j\omega)^{2}\cdot a_{2}}\right| = \frac{1}{\sqrt{(1-a_{2}\omega^{2})^{2}+(a_{1}\omega)^{2}}}=1 \] Das Nennerpolynom dieser Gleichung kann weiter modifiziert werden.
\[ |G_{W}(j\omega)| = \frac{1}{\sqrt{(1-2 \cdot a_{2}\cdot \omega^{2}+a_{2}^{2}\cdot \omega^{4})+a_{1}^{2}\cdot \omega^{2}}} \]
Da zur Beeinflussung des Betrages der Führungsübertragungsfunktion lediglich ein Freiheitsgrad zur Verfügung steht (Verstärkung \(k_{P}\)) kann der Forderung nicht völlig entsprochen werden. Der Term \(a_{2}^{2}\cdot \omega^{4}\) im nennerseitigen Wurzelausdruck wächst deutlich schneller mit der Kreisfrequenz \(\omega\), weshalb er bei der weiteren Parameteroptimierung vernachlässigt wird und sich obige Forderung somit durch folgende Gleichung formulieren lässt.
\[ 1=(1-2 \cdot a_{2}\cdot \omega^{2})+a_{2}^{2}\cdot \omega^{2} \]
Diese Gleichung liefert folglich einen Ausdruck zur Bestimmung der Reglerverstärkung.
\[ 2\cdot a_{2}\cdot \omega^{2}=a_{1}^{2}\cdot \omega^{2} \rightarrow 2\cdot a_{2} = a_{1}^{2} \]
Ausgehend von Gleichung (10.4) können die Streckenparameter \(a_{1}=\frac{T_{A}}{k_{P}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}}\) und \(a_{2}=\frac{T_{A}\cdot T_{\sum}}{k_{P}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}}\) ersetzt werden und mit Hilfe obiger Gleichung die, nach dem Betragsoptimum optimierte, Reglerverstärkung \(k_{P_{BO}}\) bestimmt werden.
\[\begin{equation} k_{P_{BO}}=\frac{T_{A}}{2\cdot T_{\sum}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}} \tag{10.5} \end{equation}\]
Wird die nach dem Betragsoptimum bestimmte Reglerverstärkung \(k_{P_{BO}}\) in die Führungsübertragungsfunktion des geschlossenen Stromregelkreises (Gleichung (10.4)) eingesetzt, beschreibt diese das Verhalten des optimierten Regelkreises.
\[\begin{equation} G_{W}(s)= \frac{1}{1+s\cdot 2 \cdot T_{\sum}+s^{2}\cdot 2\cdot T_{\sum}^{2}} \tag{10.6} \end{equation}\]
Um das Verhalten des, auf diese Art und Weise erzeugten, optimierten Regelkreises beschreiben zu können, liefert ein Koeffizientenvergleich mit der Standard-Übertragungsfunktion eines PT2-Gliedes (Gleichung (10.8)) Auskunft über die Resonanzfrequenz \(\omega_{0}\) als auch die damit einhergehende Dämpfung \(D\).
\[\begin{equation} \begin{matrix} \omega_{0}=\frac{1}{\sqrt{2}\cdot T_{\sum}} \\ D=\frac{1}{\sqrt{2}}=0.707 \end{matrix} \tag{10.7} \end{equation}\]
Die zweite Möglichkeit zur Bestimmung der optimalen Reglerverstärkung besteht darin, die Koeffizienten \(a_{1}\) bzw. \(a_{2}\) der Führungsübertragungsfunktion in Gleichung (10.4), die einem schwingungsfähigen System (PT2) entspricht, direkt durch Koeffizientenvergleich und Vorgabe einer bestimmten Dämpfung \(D\) mit Hilfe des Bodediagrammes zu bestimmen. Ausgangspunkt dieser Überlegung besteht darin, dass sich der Phasengang bei Veränderung der Reglerverstärkung nicht verändert. Allerdings ändert sich die Durchtrittsfrequenz \(\omega_{D}\). Die Durchtrittsfrequenz stellt die Frequenz dar, bei der der Amplitudengang der Führungsübertragungsfunktion \(G_{W}(\omega)\) die 0-dB Linie schneidet. Mit steigender Durchtrittsfrequenz wird der Phasenrand immer kleiner, was einer Zunahme der Schwingungsneigung entspricht.
Dazu kann die Gleichung (10.4) mit der allgemeinen Gleichung eines schwingungsfähigen PT2-Gliedes verglichen werden.
\[\begin{equation} G_{PT2}(s)= \frac{K}{1+ s\cdot \frac{2D}{\omega_{0}}+s^{2}\frac{1}{\omega_{0}^{2}}} \tag{10.8} \end{equation}\]
Durch Koeffizientenvergleich lässt sich somit eine Rechenvorschrift zur Bestimmung der Dämpfung \(D\) finden.
\[ \begin{matrix} \frac{1}{\omega_{0}^{2}} = \frac{T_{A}\cdot T_{\sum}}{k_{P}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}} \rightarrow \omega_{0}=\sqrt{\frac{k_{P}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}}{T_{A}\cdot T_{\sum}}} \\ \frac{2D}{\omega_{0}} = \frac{T_{A}}{k_{P}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}} \rightarrow D = \frac{1}{2}\sqrt{\frac{T_{A}}{T_{\sum}\cdot k_{P}\cdot k_{A}\cdot k_{Filt}\cdot k_{SR}}} \end{matrix} \]
Da sich eine Dämpfung von \(D=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}\) (entspricht einem Phasenrand in Höhe von \(65°\)) für die meisten Anwendungsfälle als ideal erwiesen hat (vgl. Gleichung (10.7)), kann diese zur Bestimmung der Reglerverstärkung \(k_{P_{BO}}\) verwendet werden und liefert, wie zu erwarten, das exakt gleiche Ergebnis wie bereits in Gleichung (10.5) angegeben. Es sei darauf hinzuweisen, dass die Forderung nach einer relativ starken Dämpfung in Höhe von \(D=\frac{1}{\sqrt{2}}\) nicht zwangsläufig für alle Anwendungen geeignet ist. Die obigen Gleichung erlauben allerdings eine problemlose Anpassung des Regelverhaltens an die besonderen Anforderungen. Steht einem zur Einstellung des Stromreglers hingegen nur das Bodediagramm der Regelstrecke, bestehend aus der Ankerwicklung und einem weiteren Verzögerungsglied 1. Ordnung zur Verfügung, dann ist die Bestimmung der Reglerparameter ebenfalls unter Verwendung des Betragsoptimums möglich. Das zweite Verzögerungsglied kann dabei zum Beispiel aus der Übertragungsfunktion des Stromrichters (PT1) und dem Messfilter (PT1) durch Summenbildung der Zeitkonstanten (Summenzeitkonstante \(T_{\sum}\)) gebildet worden sein. Ein solches Beispiel ist in Abbildung 10.5 dargestellt.
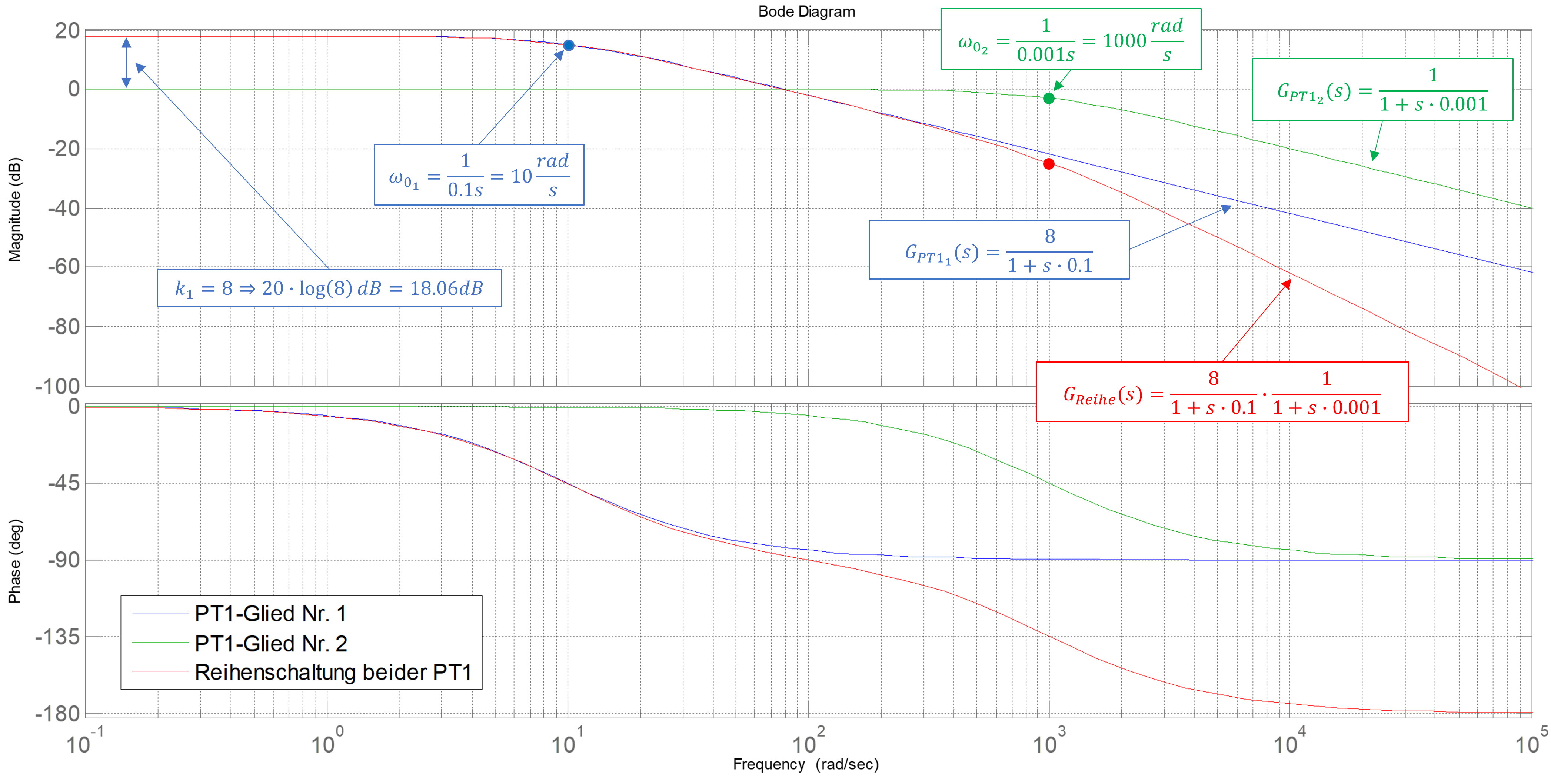
Abbildung 10.5: Bodediagramm zweier in Reihe geschalteter PT1-Glieder mit beispielhaften Parametern
Die Abbildung zeigt ein beispielhaftes PT1-Glied (\(G_{PT1_{1}}(s)\)) mit einer dominierenden Zeitkonstante (repräsentiert die Ankerwicklung) und ein zweites PT1-Glied (\(G_{PT1_{2}}(s)\)) mit einer deutlich kleineren Zeitkonstante \(T_{PT1_{2}}=T_{\sum}\) sowie deren Grenzfrequenzen (\(\omega_{0_{1}}\) und \(\omega_{0_{2}}\)). Die Reihenschaltung beider PT1-Glieder zeigt dabei deutlich die Eigenschaften beider PT1-Einzelglieder, sowohl in Form der entsprechenden Knickfrequenzen als auch die Summe der einzelnen Verstärkungen. Um einen PI-Regler nach dem Betragsoptimum für eine solche Regelstrecke zu entwickeln, gilt es auch hier die dominante Zeitkonstante der Strecke (\(T_{PT1_{1}}\)) mit der Nachstellzeit des Reglers zu kompensieren (\(T_{PT1_{1}}=T_{N}\)), wodurch sich eine Gesamt-Übertragungsfunktion (bestehend aus Regler und den zwei in Reihe geschalteten PT1-Gliedern) ergibt, die einen möglichst langen Abfall in Höhe von 20dB pro Dekade aufweist (siehe Abb. 10.6).

Abbildung 10.6: Bodediagramm zweier in Reihe geschalteter PT1-Glieder und PI-Regler mit optimierter Nachstellzeit
Um die Reglerverstärkung zu definieren nutzt man die Erkenntnisse bezüglich der Zusammenhänge zwischen der Durchtrittszeitkonstante \(T_{D}\) und der Summenzeitkonstante \(T_{\sum}\) eines schwingungsfähigen PT2-Gliedes.
\[ G_{PT2}(s)= \frac{K}{1+ s\cdot\frac{2D}{\omega_{0}}+s^{2}\frac{1}{\omega_{0}^{2}}}=\frac{K}{1+ s\cdot T_{D} + s^{2}\cdot T_{D}\cdot T_{\sum}} \]
Es sei dabei zu berücksichtigen, dass die Verstärkung \(K\) für ein Anheben bzw. Absenken des Amplitudenganges der Übertragungsfunktion sorgt. Dies liefert den Zusammenhang zwischen der dominierenden Zeitkonstante (Ankerzeitkonstante \(T_{A}\) in diesem Fall) und der Durchtrittszeitkonstante \(T_{D}\) und stellt somit die Verbindung obiger Gleichung mit der Gleichung (10.4) her.
\[ T_{D} = \frac{T_{A}}{K} \]
Auch hier liefert ein Koeffizientenvergleich eine Berechnungsvorschrift für die Dämpfung in Abhängigkeit der Summen- und der Durchtrittszeitkonstante.
\[\begin{equation} D=\frac{1}{2}\sqrt{\frac{T_{D}}{T_{\sum}}} \tag{10.9} \end{equation}\]
Da sich sowohl die Durchtritts- als auch die Summenzeitkonstante aus dem Bodediagramm ablesen lassen, ist es folglich möglich die Reglerverstärkung, welche für ein Anheben oder Absenken der Gesamt-Übertragungsfunktion verantwortlich ist, die Durchtrittszeitkonstante entsprechend einer gegebenen Forderung nach einer bestimmten Dämpfung einstellen. Das Vorgehen bei der Einstellung eines auf diese Art und Weise zu optimierenden Regelkreises ist in Abbildung 10.7 dargestellt.
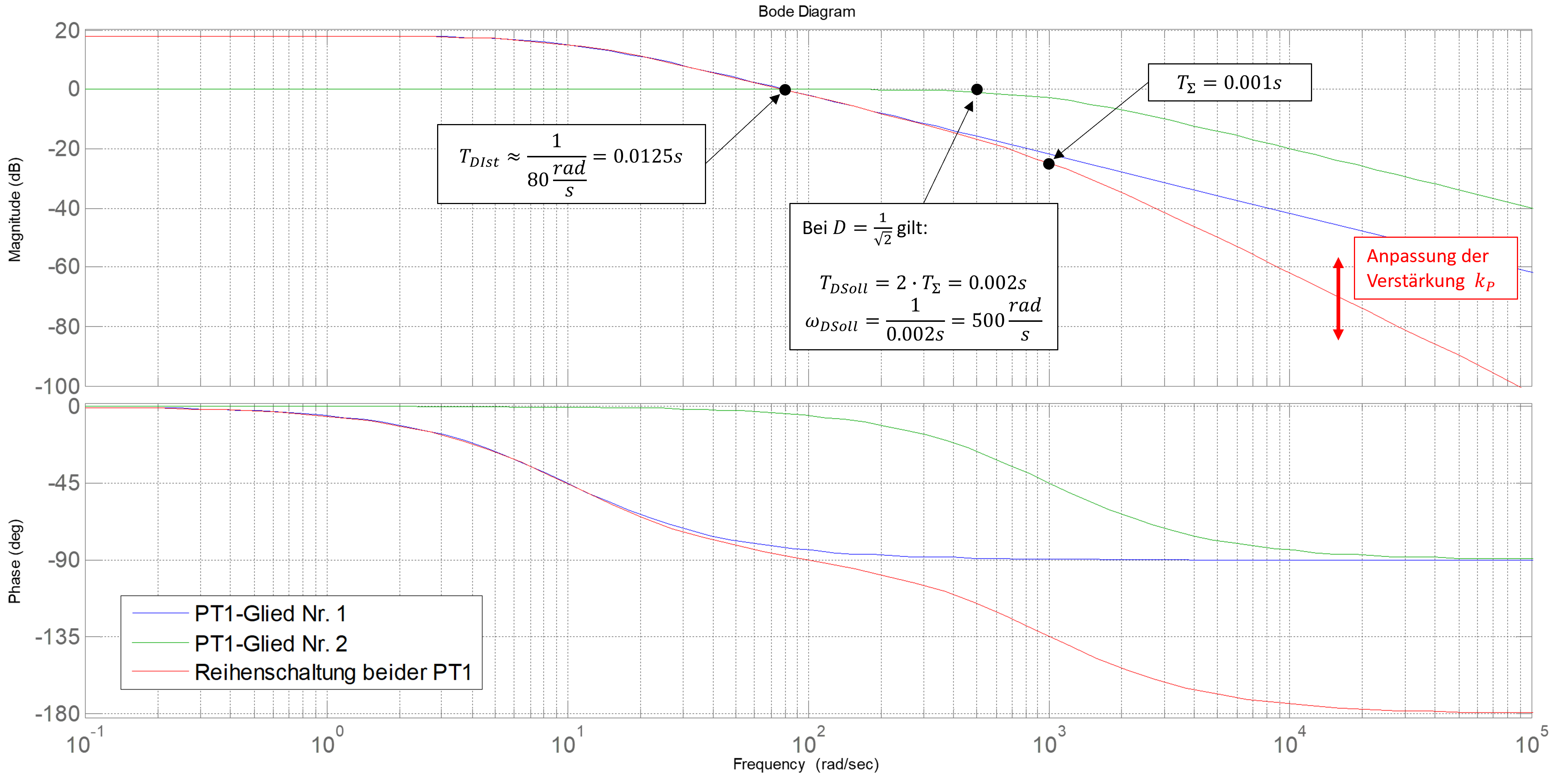
Abbildung 10.7: Beispiel zur Bestimmung der Reglerverstärkung anhand des Bodediagrammes
Aus der Abbildung ist ersichtlich, dass die Reglerverstärkung um ca. 18dB angehoben werden muss, um die Durchtrittsfrequenz an die gewünschte Position zu verschieben.
Erfolgt die Einstellung der Reglerparameter direkt an der Maschine durch heuristische Methoden (z.B. Analyse der Sprungantwort), dann sollte dies bei festgebremsten Motor erfolgen, um den Einfluss der induzierten Spannung (aufgrund der Rotation der Maschine) vernachlässigen zu können.
10.2 Symmetrisches Optimum
Beim symmetrischen Optimum (erstmals erwänt von Kessler 1958) handelt es sich ebenfalls um eine Auslegungsverfahren der Regelungstechnik für Eingrössensysteme, welches dann angewandt wird, wenn die Regelstrecke Verzögerungsglieder aufweist, die sich in je eine Gruppe grosser und kleiner Zeitkonstanten aufteilen lassen. Das Verfahren zielt darauf ab, die Durchtrittskreisfrequenz des offenen Regelkreises mittig zwischen die beiden Knickfrequenzen zu legen, um somit den Phasenrand zu maximieren, wodurch der geschlossene Regelkreis optimal gedämpft wird. Im Bereich der Antriebstechnik hat sich diese Einstellregel für den Drehzahlregelkreis etabliert, da sich somit ein gutes Störverhalten ergibt. Das Vorgehen bei der Anwendung des symmetrischen Optimums soll auch hier am Beispiel der Gleichstrommaschine erfolgen. Der betragsoptimal eingestellte Stromregelkreis wird dabei näherungsweise durch ein Verzögerungsglied erster Ordnung nachgebildet. Wie in Abbildung 10.8 zeigt, sind die Unterschiede in der Sprungantwort eines PT1 und PT2-Gliedes marginal, was für eine derartige Vereinfachung spricht.
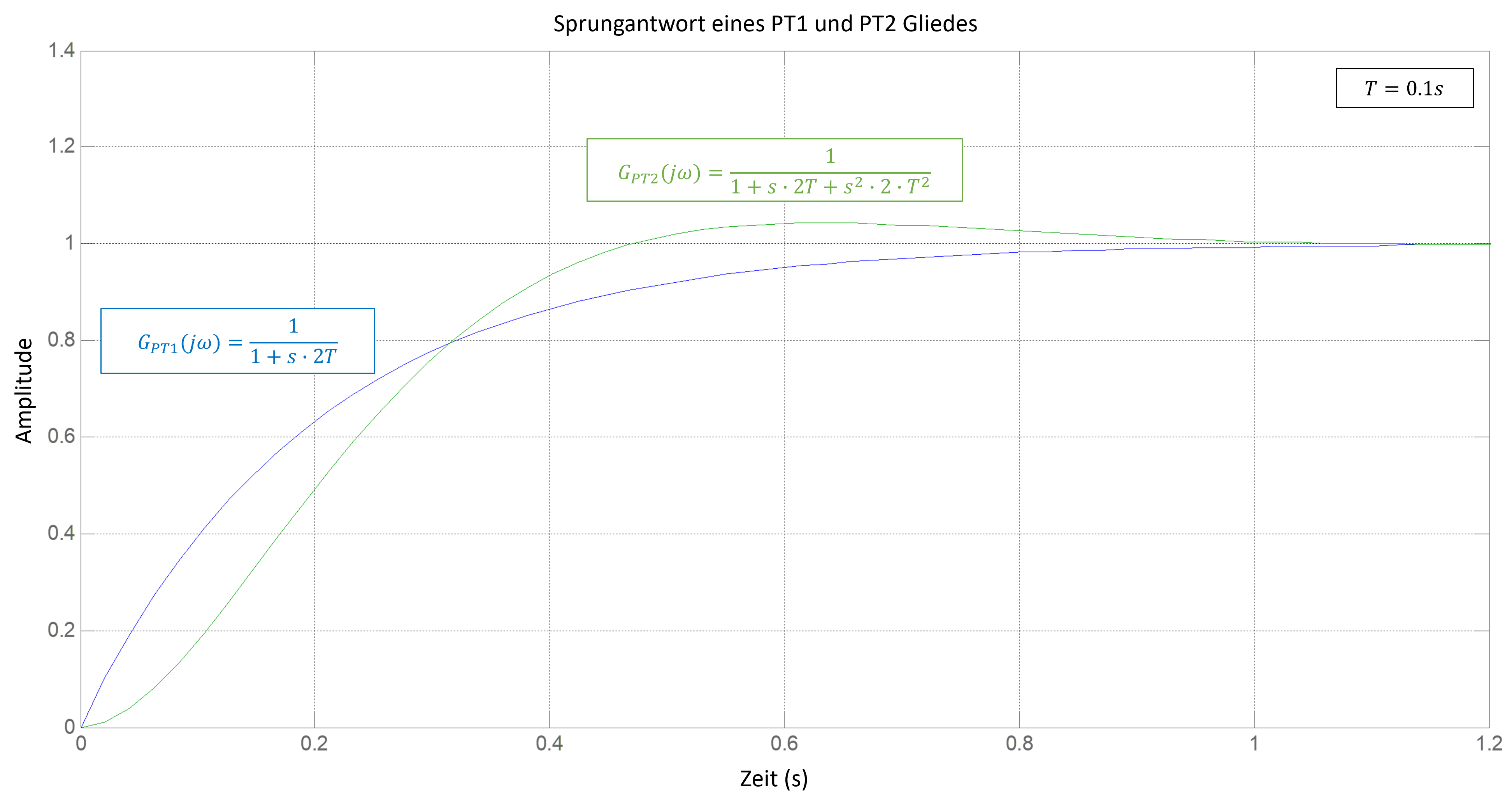
Abbildung 10.8: Sprungantwort eines PT1 und eines PT2 Gliedes gleicher Zeitkonstanten
Die Führungsübertragungsfunktion (vgl. Gleichung (10.6)) des Stromreglers wird somit vereinfacht durch ein PT1-Glied dargestellt.
\[\begin{equation} G_{W}(s)=\frac{1}{1+s\cdot 2\cdot T_{\sum}}=\frac{1}{1+s\cdot T_{GW,I}} \tag{10.10} \end{equation}\]
Um eine bleibende Regelabweichung zu vermeiden kommt ein PI-Regler zum Einsatz. Der Drehzahlregelkreis weist eine Regelstrecke auf, die aus einem verzögerten Integrator besteht (vgl. Abb. 10.9), wodurch die Reglereinstellung nach dem Betragsoptimum und der damit einhergehenden Kompensation der grössten Streckenzeitkonstante nicht möglich, da sich stattdessen eine ungedämpfte Dauerschwingung einstellen würde.

Abbildung 10.9: Drehzahlregelkreis mit unterlagertem, betragsoptimiertem Stromregelkreis
Die Übertragungsfunkton des offenen Regelkreises kann somit anhand des Blockschaltbildes bestimmt werden.
\[\begin{equation} G_{O,n}(s)=k_{P}\cdot \frac{1+s\cdot T_{N}}{s\cdot T_{N}}\cdot \frac{1}{1+s\cdot 2\cdot T_{\sum}}\cdot \frac{K_{T}}{J\cdot s} \tag{10.11} \end{equation}\]
Unter der Voraussetzung das der magnetische Fluss konstant auf seinem Nominalwert gehalten wird, beschreibt die Konstante \(K_{T}\) die sogenannte Drehmomentkonstante, die den Zusammenhang zwischen dem Ankerstrom und dem elektrischen Drehmoment herstellt. Vergleichbar mit dem Betragsoptimum, lässt sich die Einstellung des Reglers nach dem symmetrischen Optimum sowohl rein analytisch als auch mit Hilfe des Bodedigrammes des offenen Regelkreises vornehmen. Bei der rein analytischen Betrachtung wird die Übertragungsfunktion des geschlossenen Regelkreises bestimmt:
\[\begin{equation} \begin{matrix} G_{W,n}(s)=\frac{G_{O,n}(s)}{1+G_{O,n}(s)}=\frac{k_{P}\cdot \frac{1+s\cdot T_{N}}{s\cdot T_{N}}\cdot \frac{1}{1+s\cdot T_{GW,I}}\cdot \frac{K_{T}}{s\cdot J}}{1+k_{P}\cdot \frac{1+s\cdot T_{N}}{s\cdot T_{N}}\cdot \frac{1}{1+s\cdot T_{GW,I}}\cdot \frac{K_{T}}{s\cdot J}}\\ G_{W,n}(s)=\frac{k_{P}\cdot K_{T}+s\cdot k_{P}\cdot T_{N}\cdot K_{T}}{k_{P}\cdot K_{T}+s\cdot k_{P}\cdot K_{T}\cdot T_{N}+s^{2}\cdot J\cdot T_{N}+s^{3}\cdot J\cdot T_{GW,I}\cdot T_{N}} \end{matrix} \tag{10.12} \end{equation}\]
Die Faktoren der obigen Gleichung lassen sich folgendermassen zusammenfassen:
\[ \begin{matrix} a_{0}=k_{P}\cdot K_{T} && a_{1} = k_{P}\cdot K_{T}\cdot T_{N} \\ a_{2}=J\cdot T_{N} && a_{3}=J\cdot T_{GW,I}\cdot T_{N} \end{matrix} \]
Diese Zusammenfassung erzeugt aus Gleichung (10.12) folgende Gleichung:
\[\begin{equation} G_{W,n}(s)=\frac{a_{0} + s\cdot a_{1}}{a_{0}+s\cdot a_{1}+s^{2}\cdot a_{2}+s^{3}\cdot a_{3}} \tag{10.13} \end{equation}\]
Ähnlich wie beim Betragsoptimum kann auch hier der Ansatz gewählt werden, dass sich eine ideale Regelung ergibt, wenn für alle Frequenzen \(x(t)=w(t)\) bzw. \(x(s)=w(s)\) gelten würde. Dies bedeutet, dass der Betrag der Übertragungsfunktion \(|G_{W}(s)|=1\) für alle Frequenzen gelten müsste. Indem der Betrag der Führungsübertragungsfunktion (Gleichung (10.13)) gebildet und dem Wert 1 gleichgesetzt wird, lässt sich anschliessend durch geeignete Parameterwahl eine Berechnungvorschrift für die Reglerparameter (\(k_{P_{SO}}\) und \(T_{N_{SO}}\)) nach dem symmetrischen Optimum bestimmen:
\[\begin{equation} \begin{matrix} k_{P_{SO}}=\frac{J}{2\cdot k_{T}\cdot T_{GW,I}} \\ T_{N_{SO}}=\frac{2\cdot J}{k_{P_{SO}}\cdot K_{T}}=4\cdot T_{GW,I} \end{matrix} \tag{10.14} \end{equation}\]
Eine ausführliche Herleitung der obigen Berechnungsvorschrift findet sich in [10] auf Seite 62. Wird der Drehzahlregler nach der Einstellvorschrift (10.14) eingestellt, dann ergibt sich eine Sprungantwort, die ein deutliches Überschwingen aufweist (vgl. Abb. 10.10).
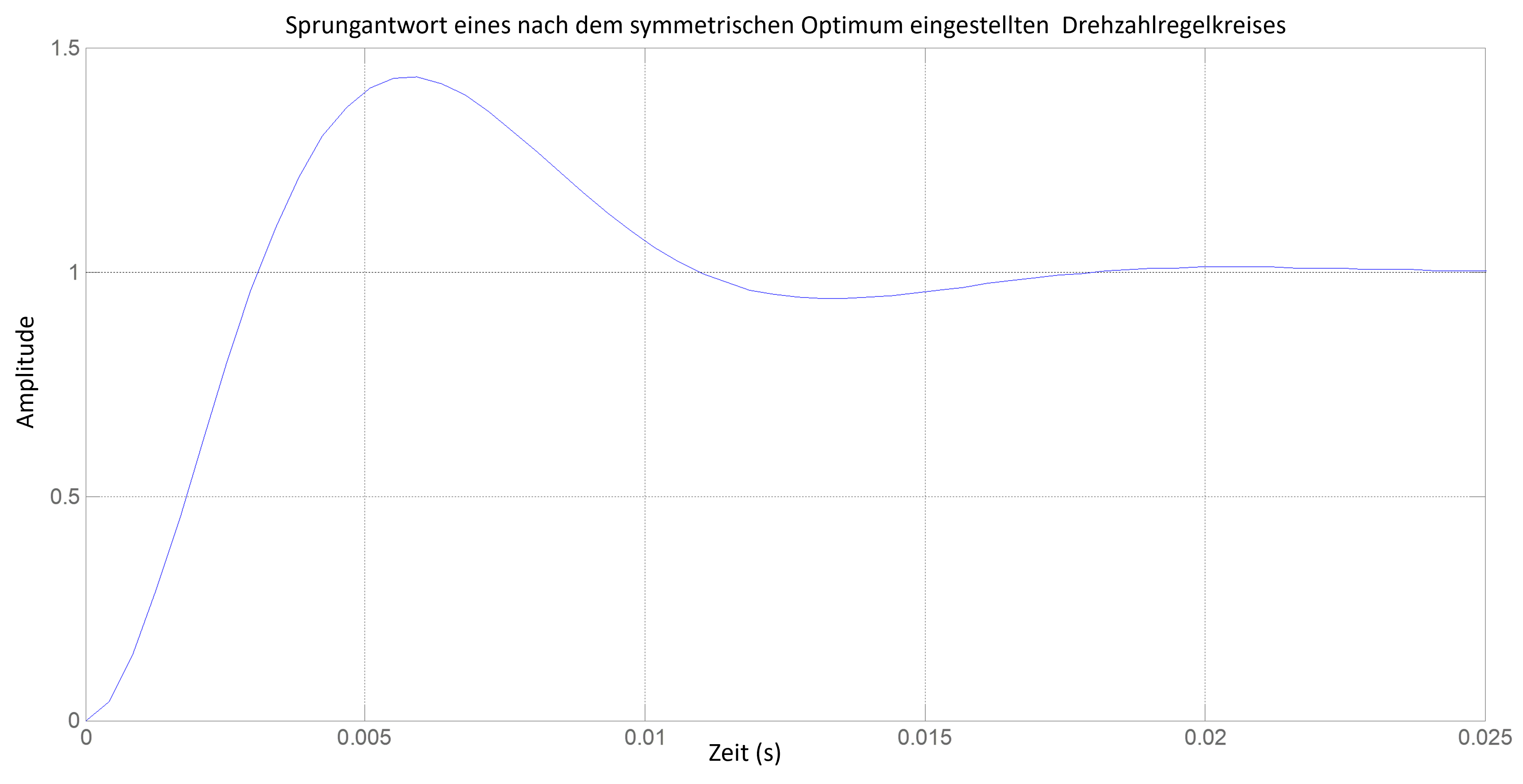
Abbildung 10.10: Sprungantwort eines nach dem symmetrischen Optimum eingestellten Drehzahlregelkreises
In der Praxis ist dieses Überschwingen meistens nicht zulässig. Man begegnet diesem Effekt indem man einen Sollwertfilter (PT1-Glied) vorsieht, dessen Zeitkonstante \(T_{SWFilt}\) auf die Nachstellzeit des Drehzahlreglers abgestimmt ist (vgl. Abb. 10.11):
\[ T_{SWFilt}=T_{N_{SO}}=4\cdot T_{GW,I} \]

Abbildung 10.11: Drehzahlregelkreis mit Sollwertfilter
Damit ist es möglich das Überschwingen auf ein zulässiges Mass in Höhe von ca. 8% zu begrenzen.
Die Reglereinstellung des Drehzahlregelkreises nach dem symmetrischen Optimum lässt sich auch anhand des Bodediagrammes bestimmen. Abbildung 10.12 zeigt die einzelnen Übertragungsglieder des vereinfachten Drehzahlregelkreises im Bodediagramm unter Verwendung willkürlicher Zeitkonstanten.
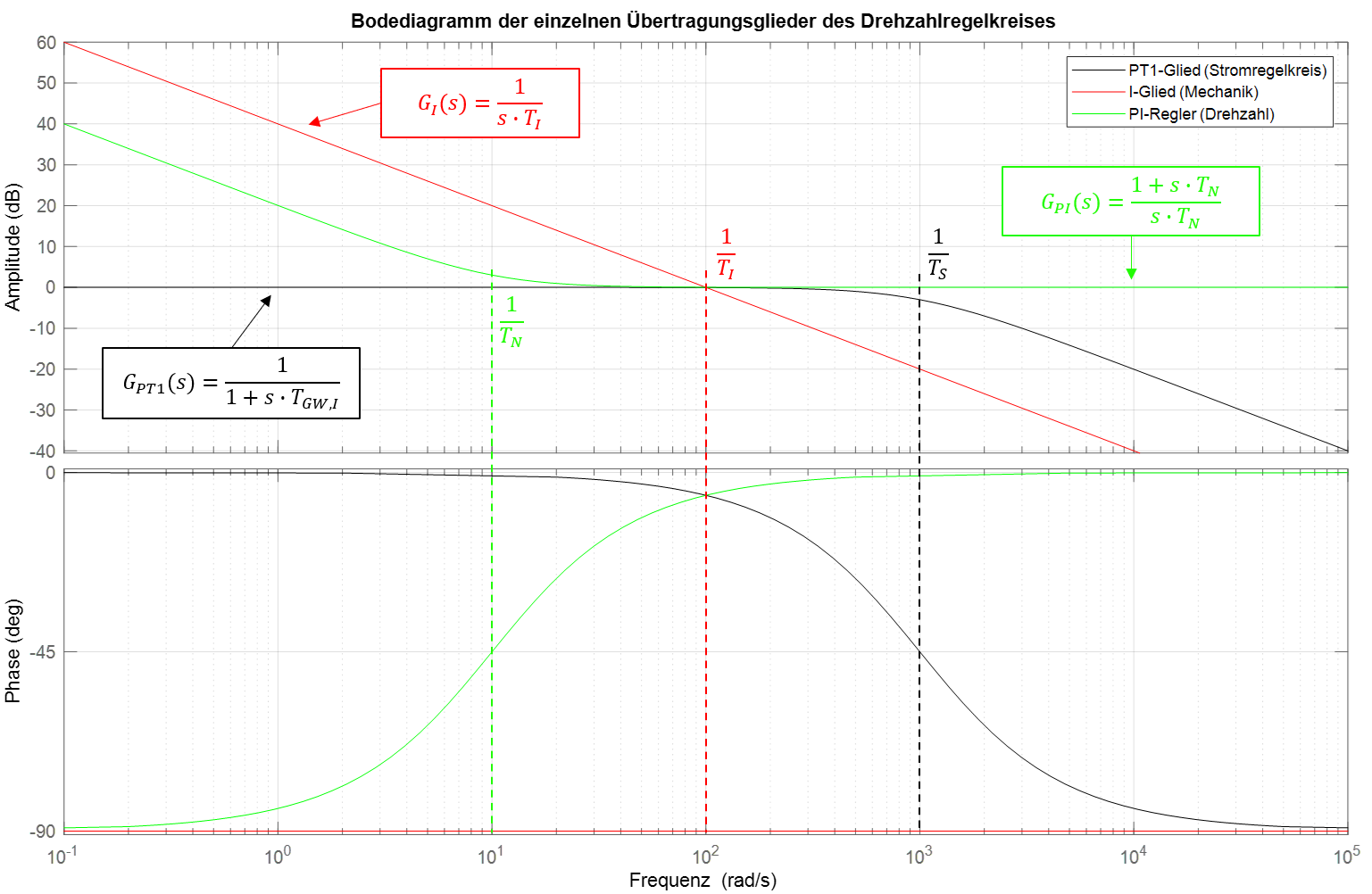
Abbildung 10.12: Bodediagramm der einzelnen Übertragungsglieder des Drehzahlregelkreises
Der Drehzahlregelkreis besteht dabei aus dem nach dem Betragoptimum eingestellten Stromregelkreis (PT1-Glied), dem Interierglied (I-Glied), gebildet durch die integrierende Wirkung der Mechanik, sowie dem Drehzahlregler (PI-Regler). Die Abbildung zeigt ausserdem die charakteristischen Knick- bzw. Durchtrittskreisfrequenzen der einzelnen Übertragungsglieder, die sich aus den Zeitkonstanten bestimmen lassen. Die Verstärkungen der einzelnen Übertragungsglieder wurden der Übersichtlichkeit halber zu Eins gewählt.
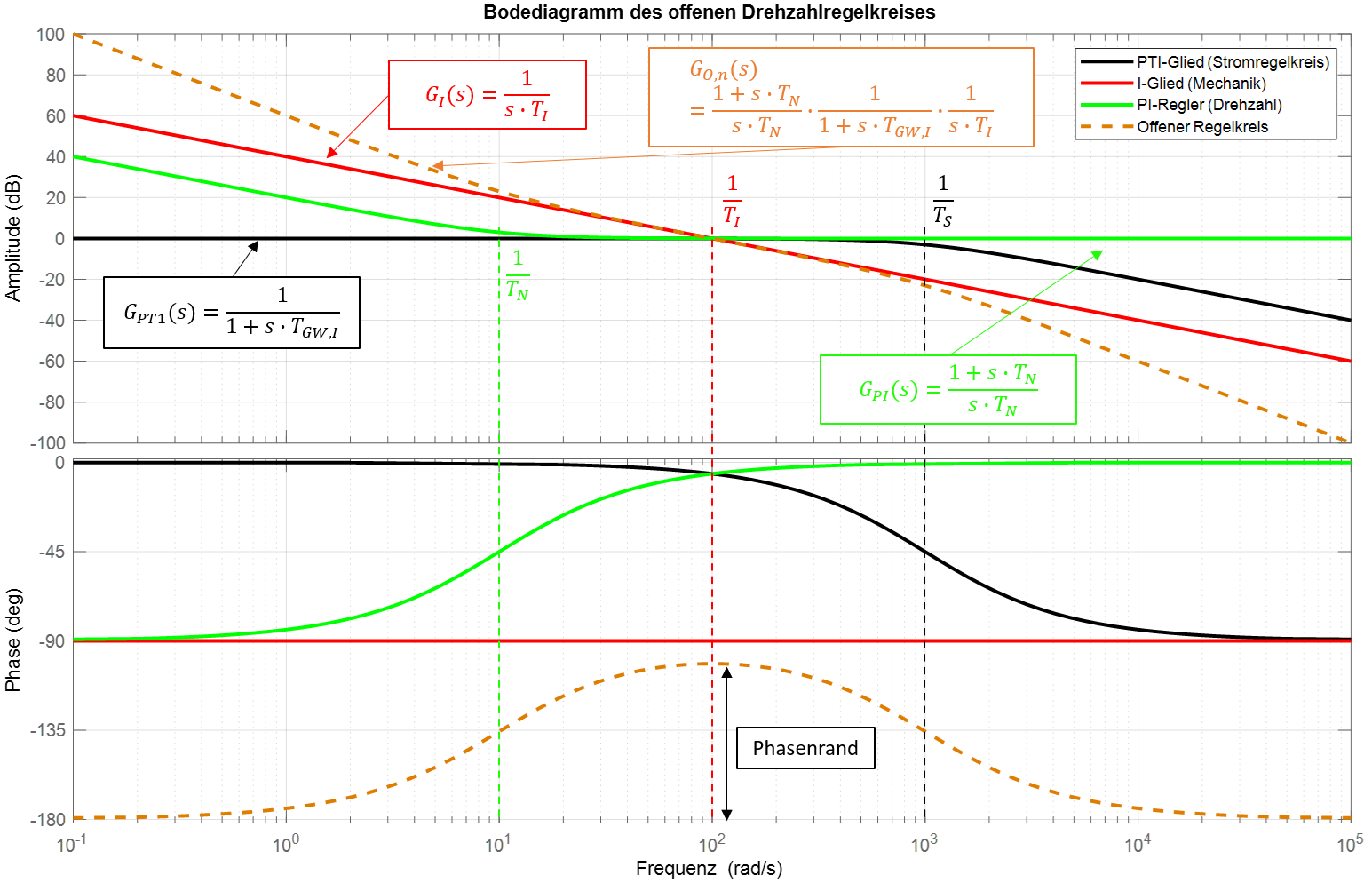
Abbildung 10.13: Bodediagramm der einzelnen Übertragungsglieder und des offenen Drehzahlregelkreises
Abbildung 10.13 stellt das Bodediagramm der einzelnen Übertragungsglieder sowie des offenen Drehzahlregelkreises dar. Der Amplitudengang des offenen Regelkreises setzt sich aus der Summe der Amplitudengänge der einzelnen Übertragungsglieder zusammen und weist somit an den charakteristischen Knick- bzw. Durchtrittskreisfrequenzen der einzelnen Übertragungsglieder ebenfalls seine charakteristischen Knickkreisfrequenzen auf. In diesem Beispiel wurden die Zeitkonstanten so gewählt, dass die Durchtrittskreisfrequenz genau mittig zwischen den Knickfrequenzen des PI-Reglers bzw. des Verzögerungsgliedes zum liegen kommt. Der Amplitudengang des offenen Regelkreises weist somit einen punktsymmetrischen Verlauf zur Durchtrittskreisfrequenz auf, der dieser Einstellregel seinen Namen gegeben hat. Die Knickkreisfrequenz des Verzögerungsgliedes \(\omega_{GW,I}=\frac{1}{T_{GW,I}}\) wird durch die Zeitkonstante des optimierten, unterlagerten Stromregelkreis gebildet und kann, ohne das Verhalten des Stromregelkreises zu beeinflussen, nicht verändert werden. Die Durchtrittszeitkonstante \(\omega_{D}=\frac{1}{T_{I}}=\frac{1}{J}\) ist durch die Trägheit des mechanischen Systems gegeben und kann ebenfalls nicht verändert werden. Die Abbildung zeigt ausserdem, dass der Phasenrand \(\varphi_{R}\) sein Maximum an der Stelle erreicht, an der die Phasen des PT1-Gliedes und des PI-Reglers sich schneiden. Verläuft die Durchtrittskreisfrequenz nicht exakt mittig zwischen beiden Knickfrequenzen, reduziert dies den Phasenrand. Der Phasenrand ist ausserdem direkt proportional zum Abstand der zwei Knickkreisfrequenzen (\(\omega_{GW,I}\) und \(\omega_{N}=\frac{1}{T_{N}}\)). Die Einstellregel des symmetrischen Optimums berücksichtigt diese Effekte, indem die Nachstellzeit \(T_{N}\) des Reglers, je nach gewünschter Dämpfung \(D\), in entsprechendem Abstand zur Knickfrequenz \(\omega_{GW,I}\) platziert wird und die Reglerverstärkung \(k_{P}\) dazu verwendet wird die Durchtrittskreisfrequenz des offenen Regelkreises \(\omega_{D}\) mittig zwischen den äusseren Knickkreisfrequenzen zu platzieren. Die Durchtrittskreisfrequenz kann durch die Reglerverstärkung beeinflusst werden, da diese für ein Anheben bzw. Absenken des Amplitudenganges des offenen Regelkreises sorgt. Um die Dämpfung bei der Reglereinstellung berücksichtigen zu können, wird ein Abstandsfaktor \(a>1\) eingeführt, der den Abstand zwischen den Knickkreisfrequenzen und der Durchtrittszeitkonstante beschreibt:
\[\begin{equation} a=\frac{T_{N}}{T_{D}}=\frac{T_{D}}{T_{GW,I}} \tag{10.15} \end{equation}\]
Der Zusammenhang zwischen der Dämpfung \(D\) und dem Abstandsfaktor \(a\) wird durch folgende Gleichung ausgedrückt:
\[\begin{equation} D=\frac{a-1}{2} \tag{10.16} \end{equation}\]