1.3.2 Konfidensinterval (teori), “p-hat”

1.3.2.1 Transformation

Vi er interesseret i at finde ud af, hvor præcist vores estimat $\hat p$ af den ukendte sandsynlighed $p$ i binomialfordelingen er (NB: Vi anvender ordene “sandsynlighed” og “andel” synonymt som betegnelse for $p$).

Vi ved, at estimatet $\hat p$ i sig selv sådan cirka kan beskrives ved hjælp af en normalfordeling $$\hat p\overset{a}{\sim} N\left(p,\sqrt{\frac{p(1-p)}{n}}\right)$$

Det kan vi alternativt også skrive som $$\frac{\hat p-p}{\sqrt{\hat p(1-\hat p)/n}}\overset{a}{\sim} N(0,1)$$ pga. normalfordelingens transformationsegenskab.

I det nedenstående gennemgår vi kort, hvordan vi kan udnytte det, til at sige noget om præcisionen af estimatet $\hat p$.

Overvejelserne følger samme fremgangsmåde som konstruktionen af konfidensintervallet for den ukendte middelværi $\mu$ i en normalfordeling.

1.3.2.2 Symmetri i $N(0,1)$-fordelingen

$N(0,1)$-fordelingen er symmetrisk omkring 0, og det kan vi udnytte.

Ser vi eksempelvis på 2,5%-fraktilen i $N(0,1)$-fordelingen, som vi ved beregning kan finde til $z_{2,5\%}$ = -1,96, så betyder det, at der per definition ligger 2,5% sandsynlighed til venstre for værdien -1,96

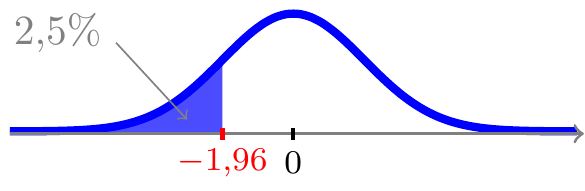
og pga. symmetrien også 2,5% sandsynlighed til højre for værdien 1,96

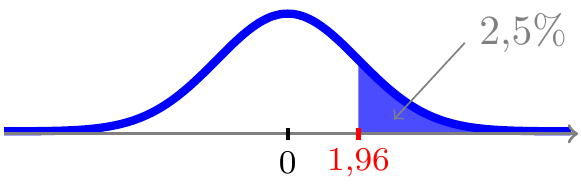
og dermed ligger der 95% sandsynlighed i intervallet $[-1,\!96;\;1,\!96]$

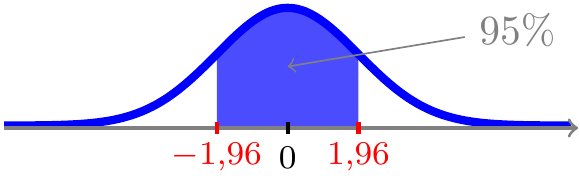
Det leder til nedenstående generelle overvejelse (tilfældet ovenfor svarer til $\alpha=5\%$).

For $0<\alpha<1$ ligger der per definition $\alpha/2$ sandsynlighed til venstre for $\alpha/2$-fraktilen $z_{\alpha/2}$

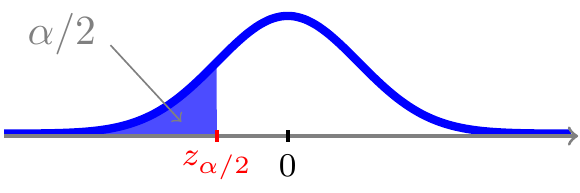
og pga. symmetrien også $\alpha/2$ sandsynlighed til højre for værdien $-z_{\alpha/2}$

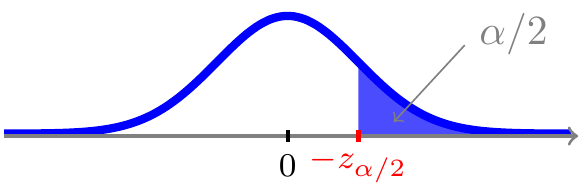
og dermed ligger der $1-\alpha$ sandsynlighed i intervallet $[z_{\alpha/2};\;-z_{\alpha/2}]$

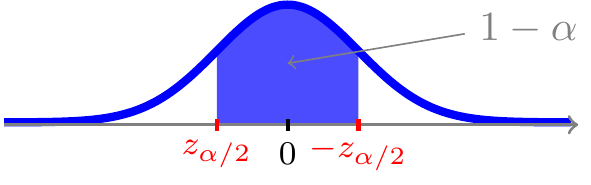
1.3.2.3 Præcision af $\hat p$

Vi er nu klar til at sige noget om præcisionen af vores estimat $\hat p$.

Vi ved, at størrelsen $\frac{\hat p-p}{\sqrt{\hat p(1-\hat p)/n}}$ sådan cirka er beskrevet ved en $N(0,1)$-fordeling.

Vi har ovenfor set, hvordan vi i $N(0,1)$-fordelingen kan konstruere et interval, som indeholder en vis mængde sandsynlighed.

Ved at bruge disse overvejelser på størrelsen $\frac{\hat p-p}{\sqrt{\hat p(1-\hat p)/n}}$ kan vi konstruere et interval, som indeholder $\frac{\hat p-p}{\sqrt{\hat p(1-\hat p)}{n}}$ med en vis sandsynlighed.

Ved at flytte lidt rundt på tingene (transformere) kan vi ændre det til et interval, som indeholder $\hat p$ med en vis sandsynlighed.

Vi får hermed konstrueret et interval som med en vis sandsynlighed indeholder vores estimat $\hat p$. Intervallet siger dermed noget om, hvor meget eller lidt vi skal forvente, at estimatet $\hat p$ vil variere, dvs. det siger noget om, hvor præcist vores estimat $\hat p$ er.

Mere formelt, så laver vi følgende overvejelse. For $0<\alpha<1$ ligger $\frac{\hat p-p}{\sqrt{\hat p(1-\hat p)/n}}$} ca. med sandsynlighed $1-\alpha$ i intervallet $\bigl[z_{\alpha/2};\;\;-z_{\alpha/2}\bigr]$

og dermed ligger $\hat p-p$ med sandsynlighed $1-\alpha$ i intervallet $\bigl[z_{\alpha/2}\sqrt{\hat p(1-\hat p)/n};\;\;-z_{\alpha/2}\sqrt{\hat p(1-\hat p)/n}\bigr]$

og dermed ligger $\hat p$ med sandsynlighed $1-\alpha$ i intervallet $

OPSUMMERING:

• Vi har nu fundet frem til det resultat, vi skal bruge til at sige noget om præcisionen af vores estimat $\hat p$.
• Udgangspunktet er, at vi gerne vil estimere sandsynligheden $p$ i en binomialfordeling.
• Resultatet siger, at med sandsynlighed $1-\alpha$ er forskellen mellem den ukendte størrelse $p$ og vores estimat $\hat p$ mindre end $-2z_{\alpha/2}\sqrt{\hat p(1-\hat p)/n}$ (= længden af intervallet $\bigl[p+z_{\alpha/2}\sqrt{\hat p(1-\hat p)/n};\;\;p-z_{\alpha/2}\sqrt{\hat p(1-\hat p)/n}\bigr]$).
• Ved at vælge en værdi af $\alpha$ tæt på 0, bliver $1-\alpha$ tæt på 1, og dermed siger resultatet, at afstanden mellem den ukendte værdi $p$ og vores estimat $\hat p$ med stor sandsynlighed (= $1-\alpha$) ligger indenfor en afstand på $-2z_{\alpha/2}\sqrt{\hat p(1-\hat p)/n}$ af hinanden.