1.2.2 Konfidensinterval (teori), “my-hat”

1.2.2.1 Transformation

Vi er interesseret i at finde ud af, hvor præcist vores gæt/estimat $\hat\mu$ af den ukendte middelværdi $\mu$ i normalfordelingen er. For at kunne sige noget om præcisionen af $\hat\mu$ er vi nødt til først at finde ud af, hvilken fordeling der kan bruges til at beskrive vores estimat.

Vi ved fra afsnit 1.2.1, at estimatet $\hat\mu$ kan beskrives ved hjælp af en normalfordeling $$\displaystyle\hat\mu\sim N\left(\mu,\sigma/\sqrt{n}\right)$$

Det kan vi alternativt også skrive som $$\frac{\hat\mu-\mu}{\sigma/\sqrt{n}}\sim N(0,1)$$ på grund af normalfordelingens transformationsegenskab.

Resultat: Transformation fra $N(\mu,\sigma)$ til $N(0,1)$

Hvis $X_1,...,X_n$ er indbyrdes uafhængige normalfordelte variable $N(\mu,\sigma)$, så er $$Z=\frac{\hat\mu-\mu}{\frac{\sigma}{\sqrt{n}}}$$ standardnormalfordelt $Z\sim N(0,1)$.

I størrelsen $\frac{\hat\mu-\mu}{\sigma/\sqrt{n}}$ indgår imidlertid to ukendte størrelser – både $\mu$ og $\sigma$. Hvis vi vil sige noget om estimatet af $\mu$ (dvs. $\hat\mu$), er vi nødt til først at fjerne den ukendte størrelse $\sigma$.

Det problem løser vi ved at indsætte vores estimat $\hat\sigma$ for $\sigma$, dvs. ved i stedet at se på $\frac{\hat\mu-\mu}{\hat\sigma/\sqrt{n}}$.

Det har imidlertid som konsekvens, at resultatet ovenfor ændrer sig fra $$\frac{\hat\mu-\mu}{\sigma/\sqrt{n}}\sim N(0,1)$$ til i stedet at blive $$\frac{\hat\mu-\mu}{\hat\sigma/\sqrt{n}}\sim t(n-1)$$ hvor $t(n-1)$ er den såkaldte $t$-fordeling} (“$t$ distribution”) med $n-1$ frihedsgrader (“degrees of freedom”).

Resultat: Transformation fra $N(\mu,\sigma)$ til $t$

Hvis $X_1,...,X_n$ er indbyrdes uafhængige normalfordelte variable $N(\mu,\sigma)$, så er $$Z=\frac{\hat\mu-\mu}{\frac{\hat\sigma}{\sqrt{n}}}$$ $t$-fordelt med $n-1$ frihedsgrader $Z\sim t(n-1)$.

Forskellen på de to resultater ovenfor er, at vi i det nederste resultat erstatter den ukendte teoretiske standardafvigelse $\sigma$ med vores estimat $\hat\sigma$. Det har som konsekvens, at standardnormalfordelingen $N(0,1)$ bliver skiftet ud med $t$-fordelingen.

Vi ved dermed nu, at vi kan at vores gæt $\hat\mu$ på den ukendte middelværdi $\mu$ i en normalfordeling kan beskrives ved hjælp af en såkaldt t-fordeling. Når vi lige har lært t-fordeling lidt bedre at kende, kan vi bruge det til at finde et udtryk for præcisionen af vores gæt $\hat\mu$.

1.2.2.2 t-fordelingen

$t$-fordelingen er vigtig, fordi den beskriver fordelingen af størrelsen $\frac{\hat\mu-\mu}{\hat\sigma/\sqrt{n}}$, og denne størrelse kan – som vi skal se om lidt – sammen med $t$-fordelingen bruges til at udtale sig om, hvor præcist et estimat $\hat\mu$ er.

Men først nogle facts om $t$-fordelingen. Fordelingen…

• er klokkeformet
• har centrum i 0
• er symmetrisk omkring 0
• har én parameter $f$, der kaldes “antal frihedsgrader”
• minder meget om standardnormalfordelingen $N(0,1)$ (begge fordelinger er symmetriske, klokkeformede og har centrum i 0)
• har lidt tungere haler end standardnormalfordelingen
• minder mere og mere om standardnormalfordelingen, desto større antallet af frihedsgrader $f$ er (og for passende store værdier af $f$ (> 30) vil t-fordelingen og standardnormalfordelingen for alle praktiske formål være ens)

$t$-fordelingen er som sagt symmetrisk omkring 0, og det kan vi udnytte. Ser vi eksempelvis på 2,5%-fraktilen i $t$-fordelingen med $f=10$ frihedsgrader, som vi ved beregning kan finde til $t_{2,5\%}(10)$=-2,23, så betyder det, at der per definition ligger 2,5% sandsynlighed til venstre for værdien -2,23

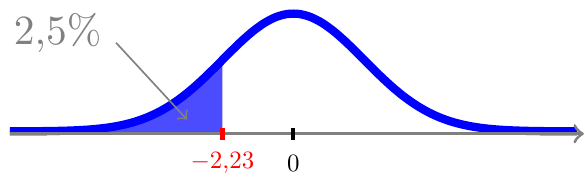
og pga. symmetrien også 2,5% sandsynlighed til højre for værdien 2,23

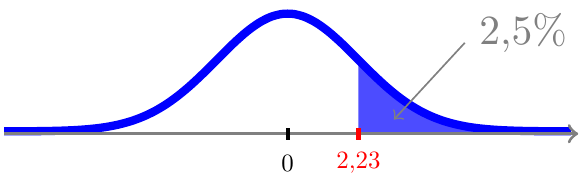
og dermed ligger der 95% sandsynlighed i intervallet [-2,23;;2,23]

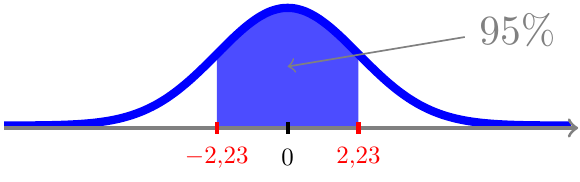
Symmetriovervejelserne ovenfor gælder ikke kun i det ovenstående eksempel med $f=10$. $t$-fordelingen er nemlig symmetrisk omkring 0 uanset antallet af frihedsgrader $f$. Det leder til nedenstående generelle overvejelse (tilfældet ovenfor svarer til $\alpha=5\%$).

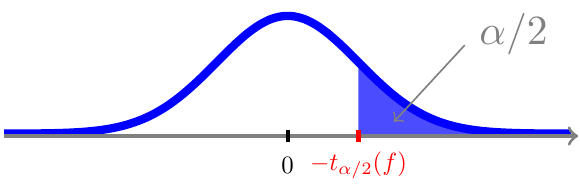
For $0<\alpha<1$ ligger der per definition $\alpha/2$ sandsynlighed til venstre for $\alpha/2$-fraktilen $t_{\alpha/2}(f)$

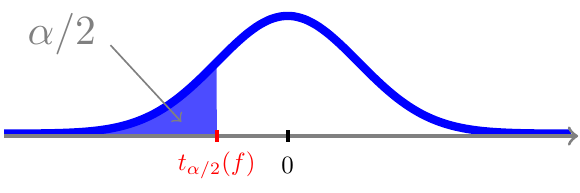
og pga. symmetrien også $\alpha/2$ sandsynlighed til højre for værdien $-t_{\alpha/2}(f)$

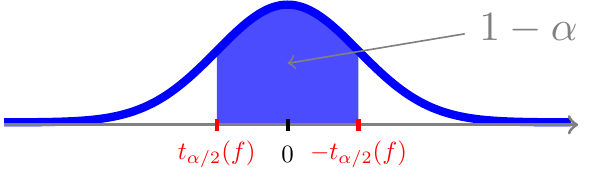
og dermed ligger der $1-\alpha$ sandsynlighed i intervallet $[t_{\alpha/2}(f);\;-t_{\alpha/2}(f)]$

1.2.2.3 Præcision af $\hat\mu$

Vi er nu endelig klar til at sige noget om præcisionen af vores middelværdiestimat $\hat\mu$.

Vi ved, at størrelsen $\frac{\hat\mu-\mu}{\hat\sigma/\sqrt{n}}$ er beskrevet ved en $t$-fordeling med $n-1$ frihedsgrader.

Vi har ovenfor set, hvordan vi i $t$-fordelingen kan konstruere et interval, som indeholder en vis mængde sandsynlighed.

Ved at bruge disse overvejelser på størrelsen $\frac{\hat\mu-\mu}{\hat\sigma/\sqrt{n}}$ kan vi konstruere et interval, som indeholder $\frac{\hat\mu-\mu}{\hat\sigma/\sqrt{n}}$ med en vis sandsynlighed.

Ved at flytte lidt rundt på tingene (transformere) kan vi ændre det til et interval, som indeholder $\hat\mu$ med en vis sandsynlighed.

Vi får hermed konstrueret et interval som med en vis sandsynlighed indeholder vores middelværdiestimat $\hat\mu$. Intervallet siger dermed noget om, hvor meget eller lidt vi skal forvente, at middelværdiestimatet $\hat\mu$ vil variere, dvs. det siger noget om, hvor præcist vores estimat $\hat\mu$ er.

Mere formelt, så laver vi følgende overvejelse. For $0<\alpha<1$ ligger $\frac{\hat\mu-\mu}{\hat\sigma/\sqrt{n}}$ med sandsynlighed $1-\alpha$ i intervallet $\bigl[t_{\alpha/2}(n-1);\;\;-t_{\alpha/2}(n-1)\bigr]$

og dermed ligger $\hat\mu-\mu$ med sandsynlighed $1-\alpha$ i intervallet $\bigl[t_{\alpha/2}(n-1)\hat\sigma/\sqrt{n};\;\;-t_{\alpha/2}(n-1)\hat\sigma/\sqrt{n}\bigr]$

og dermed ligger $\hat\mu$ med sandsynlighed $1-\alpha$ i intervallet $\bigl[\mu+t_{\alpha/2}(n-1)\hat\sigma/\sqrt{n};\;\;\mu-t_{\alpha/2}(n-1)\hat\sigma/\sqrt{n}\bigr]$

OPSUMMERING:

• Vi har nu fundet frem til det resultat, vi skal bruge til at sige noget om præcisionen af vores middelværdiestimat $\hat\mu$.
• Udgangspunktet er, at vi gerne vil estimere middelværdien $\mu$ i en normalfordeling.
• Resultatet siger, at med sandsynlighed $1-\alpha$ er forskellen mellem den ukendte størrelse $\mu$ og vores estimat $\hat\mu$ mindre end $-2t_{\alpha/2}(n-1)\hat\sigma/\sqrt{n}$ (= længden af intervallet $\bigl[\mu+t_{\alpha/2}(n-1)\hat\sigma/\sqrt{n};\;\;\mu-t_{\alpha/2}(n-1)\hat\sigma/\sqrt{n}\bigr]$).
• Ved at vælge en værdi af $\alpha$ tæt på 0, bliver $1-\alpha$ tæt på 1, og dermed siger resultatet, at afstanden mellem den ukendte værdi $\mu$ og vores estimat $\hat\mu$ med stor sandsynlighed (= $1-\alpha$) ligger indenfor en afstand på $-2t_{\alpha/2}(n-1)\hat\sigma/\sqrt{n}$ af hinanden.