2.2.2 I praksis

2.2.2.1 Beregning

Når vi skal estimere forskellen $\mu_1-\mu_2$ mellem middelværdierne i to grupper af normalfordelte observationer, kan vi bruge det nedenstående resultat til at sige noget om, hvor præcist vores estimat $\hat\mu_1-\hat\mu_2$ er.

Resultat: Konfidensinterval for $\mu_1-\mu_2$

Under antagelserne i det foregående afsnit vil forskellen $\mu_1-\mu_2$ mellem middelværdierne i de to grupper ligge i intervallet $$\left[\hat\mu_1-\hat\mu_2+t_{\alpha/2}(f)\cdot\sqrt{\frac{\hat\sigma_1^2}{n_1}+\frac{\hat\sigma_2^2}{n_2}};\quad\hat\mu_1-\hat\mu_2-t_{\alpha/2}(f)\cdot\sqrt{\frac{\hat\sigma_1^2}{n_1}+\frac{\hat\sigma_2^2}{n_2}}\right]$$ med sandsynlighed $1-\alpha$, hvor $t_{\alpha/2}(f)$ er $\alpha/2$-fraktilen i $t(f)$-fordelingen og $f$ er som anført i foregående afsnit.

Vi ser igen på prisen på Grøn Tuborg i Føtex og Bilka og beregner nu et konfidensinterval for forskellen mellem de forventede priser $\mu_1$ og $\mu_2$ i de to supermarkeder.

Sætter vi $\alpha=5\%$, finder vi, at et 95% ($=1-\alpha$) konfidensinterval for forskellen $\mu_1-\mu_2$ er givet som $$\begin{align*} &\mathrel{\phantom{=}}\left[\hat\mu_1-\hat\mu_2+t_{2,\!5\%}(f)\cdot\sqrt{\frac{\hat\sigma_1^2}{n_1}+\frac{\hat\sigma_2^2}{n_2}};\quad\hat\mu_1-\hat\mu_2-t_{2,\!5\%}(f)\cdot\sqrt{\frac{\hat\sigma_1^2}{n_1}+\frac{\hat\sigma_2^2}{n_2}}\right]\\ &=\bigl[0,\!286-1,\!97\cdot 0,\!0251;\quad 0,\!286+1,\!97\cdot 0,\!0251\bigr] = [0,\!24;\quad 0,\!34] \end{align*}$$

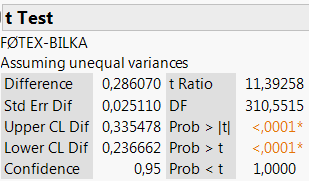
Figur 2.5: 95%-konfidensinterval for forskellen i middelværdier

Med 95% sandsynlighed vil den sande forskel mellem de forventede priser på Grøn Tuborg i Føtex og Bilka således ligge mellem 0,24 kr. og 0,34 kr.

På tilsvarende vis er eksempelvis et 99%-konfidensinterval givet som $[0,\!22\textsf{ kr.};\;0,\!35\textsf{ kr.}]$.

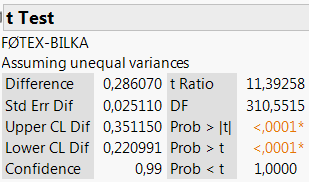
Figur 2.6: 99%-konfidensinterval for forskellen i middelværdier

Med 99% sandsynlighed vil den sande forskel mellem de forventede priser på Grøn Tuborg i Føtex og Bilka således ligge mellem 0,22 kr. og 0,35 kr.

Der ser dermed på baggrund af datamaterialet ud til at være tegn på en prisforskel på Grøn Tuborg mellem Føtex og Bilka på i hvert fald 20 øre.

2.2.2.2 Intuition

• Jo flere observationer $n_1$, desto smallere bliver konfidensintervallet, indtil et vist punkt hvorefter intervallets bredde reelt er uændret. Intuitionen er, at jo flere observationer i gruppe 1 (dvs. jo mere information om $\mu_1$) vi har til rådighed, desto mere præcist er vi i stand til at gætte på værdien af $\mu_1$ og dermed på værdien af $\mu_1-\mu_2$. Men uanset hvor meget information vi har fra gruppe 1, er der fortsat usikkerhed om $\mu_2$ og dermed også om $\mu_1-\mu_2$.
• Jo højere konfidensniveau $1-\alpha$, desto bredere bliver konfidensintervallet. Intuitionen er, at jo mere sikker vi vil være på, at intervallet indeholder den sande værdi $\mu_1-\mu_2$, desto bredere er vi nødt til at gøre intervallet.
• Jo højere standardafvigelse $\sigma_1$, desto bredere bliver konfidensintervallet, men med en vis mindstebredde uanset hvor lille $\sigma_1$ er. Intuitionen er, at jo mere usikkerhed, der er omkring hver enkelt observation i gruppe 1, desto mindre præcist er vi i stand til at gætte på værdien af $\mu_1$ og dermed på værdien af $\mu_1-\mu_2$. Selv med stort set ingen usikkerhed om $\mu_1$ er der fortsat usikkerhed om $\mu_1-\mu_2$, som skyldes usikkerheden omkring observationerne fra gruppe 2.