2.3.2 I praksis

2.3.2.1 Beregning

Når vi skal estimere forskellen \(p_1-p_2\) mellem andelene af 1’ere i to grupper, hvor hver observation har de to mulige udfald 1 og 0, kan vi bruge det nedenstående resultat til at sige noget om, hvor præcist vores estimat \(\hat p_1-\hat p_2\) er.

Resultat: Konfidensinterval for \(p_1-p_2\)

Under antagelserne i det foregående afsnit vil forskellen \(p_1-p_2\) mellem andelene i de to grupper ligge i intervallet \[\left[\hat p_1-\hat p_2+z_{\alpha/2}\cdot\sqrt{\frac{\hat p_1(1-\hat p_1)}{n_1}+\frac{\hat p_2(1-\hat p_2)}{n_2}};\quad\hat p:1-\hat p_2-z_{\alpha/2}\cdot\sqrt{\frac{\hat p_1(1-\hat p_1)}{n_1}+\frac{\hat p_2(1-\hat p_2)}{n_2}}\right]\] ca. med sandsynlighed \(1-\alpha\), hvor \(z_{\alpha/2}\) er \(\alpha/2\)-fraktilen i standardnormalfordelingen \(N(0,1)\).

Bemærk: For ethvert \(0<\alpha<1\) er \(z_{\alpha/2}<0\) og dermed \(-z_{\alpha/2}>0\), således at intervallet ovenfor altid er veldefineret.

Eksempel: Skat

Vi ser igen på svarene på spørgsmålet “Er topskatten for høj?” opdelt på henholdsvis mænd og kvinder og beregner nu et konfidensinterval for forskellen mellem andelen, der svarede “Ja” på spørgsmålet, hos de to køn (dvs. vi betegner de mulige udfald med 1=“Ja” og 0=“Nej”).

Sætter vi \(\alpha=5\%\), finder vi, at et 95% (\(=1-\alpha\)) konfidensinterval for forskellen \(p_1-p_2\) er givet som \[\begin{align*} &\mathrel{\phantom{=}}\left[\hat p_1-\hat p_2+z_{2,5\%}\cdot\sqrt{\frac{\hat p_1(1-\hat p_1)}{n_1}+\frac{\hat p_2(1-\hat p_2)}{n_2}};\quad\hat p_1-\hat p_2-z_{2,5\%}\cdot\sqrt{\frac{\hat p_1(1-\hat p_1)}{n_1}+\frac{\hat p_2(1-\hat p_2)}{n_2}}\right]\\ &=[0,\!039;\quad 0,\!158] \end{align*}\]

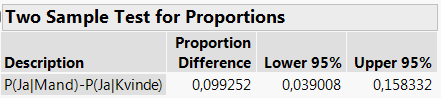
Figur 2.7: 95%-konfidensinterval for forskellen i andele

Med 95% sandsynlighed vil den sande forskel mellem andelen af “Ja”-sigere (dem der mener, at topskatten er for høj) blandt mænd og kvinder således ligge mellem 3,9% og 15,8 %.

På tilsvarende vis er eksempelvis et 99%-konfidensinterval givet som \([0,\!020;\;0,\!177]\).

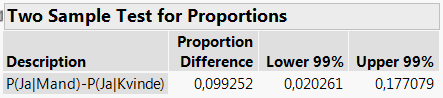
Figur 2.8: 99%-konfidensinterval for forskellen i andele

Med 99% sandsynlighed vil den sande forskel mellem andelen af “Ja”-sigere blandt mænd og kvinder således ligge mellem 2,0% og 17,7%.

Der ser dermed på baggrund af datamaterialet ud til at være tegn på en forskel blandt kønnene på andelen af “Ja”-sigere. En større andel af mænd end af kvinder ser ud til at mene, at topskatten er for høj.

2.3.2.2 Intuition

• Jo flere observationer \(n_1\), desto smallere bliver konfidensintervallet, indtil et vist punkt hvorefter intervallets bredde reelt er uændret. Intuitionen er, at jo flere observationer i gruppe 1 (dvs. jo mere information om \(p_1\)) vi har til rådighed, desto mere præcist er vi i stand til at gætte på værdien af \(p_1\) og dermed på værdien af \(p_1-p_2\). Men uanset hvor meget information vi har fra gruppe 1, er der fortsat usikkerhed om \(p_2\) og dermed også om \(p_1-p_2\).
• Jo højere konfidensniveau \(1-\alpha\), desto bredere bliver konfidensintervallet. Intuitionen er, at jo mere sikker vi vil være på, at intervallet indeholder den sande værdi \(p_1-p_2\), desto bredere er vi nødt til at gøre intervallet.