3.2 Metoden bag hypotesetest

Hypotesetest om en middelværdi $\mu$ i en normalfordeling og hypotesetest om en andel $p$ i en binomialfordeling foregår efter nøjagtig samme metode. Vi beskriver derfor i dette afsnit for overskueligheden skyld blot metoden med udgangspunkt i test af hypoteser om middelværdien $\mu$ .

Når vi skal undersøge en påstand om den forventede værdi $\mu$ af en normalfordelt variabel $N(\mu,\sigma)$ , tager vi udgangspunkt i et datamateriale bestående af $n$ observationer. Formålet er – på baggrund af datamaterialet – at undersøge en specifik påstand om den ukendte middelværdi $\mu$ .

Metoden kaldes hypotesetest om $\mu$ og består af følgende 5 trin:

Trin 1: “Antagelser” (“assumptions”)
Trin 2: “Hypoteser” (“hypotheses”)
Trin 3: “Teststørrelse” (“test statistic”)
Trin 4: “P-værdi” (“P-value”)
Trin 5: “Konklusion” (“conclusion”)

Eksempel: Ølsalg

Lad os her, som illustration af metoden, gennemgå hvordan vi kan undersøge påstanden om, at den forventede pris $\mu$ på Grøn Tuborg i Føtex er 3,50 kr.

3.2.1 Trin 1: Antagelser

Vi antager, at vores datamateriale består af $n$ indbyrdes uafhængige observationer, der alle stammer fra den samme normalfordeling $N(\mu,\sigma)$ .

I praksis kan vi undersøge om denne antagelse er rimelig ved at tegne et histogram og et normalfraktildiagram af datamaterialet og se på, om figurerne indikerer overensstemelse med normalfordelingen.

Eksempel: Ølsalg

Vi antager her, at de 157 ugentlige observationer af prisen på Grøn Tuborg i Føtex er indbyrdes uafhængige og alle kan beskrives af den samme normalfordeling $N(\mu,\sigma)$ .

Som vi har set i afsnit 1.2 viser et histogram af de 157 prisobservationer, at normalfordelingen med en vis rimelighed kan bruges til beskrivelse af prisen på Grøn Tuborg i Føtex.

3.2.2 Trin 2: Hypoteser

Den påstand vi ønsker at undersøge om den ukendte middelværdi $\mu$ udtrykker vi ved hjælp af den såkaldte nulhypotese $H_0$ (“null hypothesis”).

Hypoteser formuleres altid i par, dvs. at nulhypotesen altid suppleres af en såkaldt alternativhypotese $H_a$ (“alternative hypothesis”), som udtrykker det modsatte af nulhypotesen. Så snart man har formuleret sin nulhypotese, så er alternativhypotesen automatisk givet som “det modsatte af nulhypotesen”.

Idéen er nu, at enten er datamaterialet i overensstemmelse med nulhypotesen, eller også er det i overensstemmelse med alternativhypotesen. Hvorvidt det ene eller det andet er tilfældet afgør vi ved at se på en såkaldt teststørrelse.

Eksempel: Ølsalg

Påstanden om, at den forventede pris $\mu$ på Grøn Tuborg i Føtex er 3,50 kr., kan vi udtrykke ved at angive henholdsvis nul- og alternativhypotese som $H_0:\;\mu=3,\!50\hspace{1cm}H_a:\;\mu\ne 3,\!50$ Nulhypotesen ( $H_0$ ) udtrykker vores påstand om den forventede pris på Grøn Tuborg, mens alternativhypotesen ( $H_a$ ) udtrykker det modsatte af vores påstand.

3.2.3 Trin 3: Teststørrelse

Teststørrelsen bruger vi til at sammenligne vores datamateriale med den formulerede påstand $H_0$ . Vi ønsker at vurdere, om datamaterialet ser ud til at være i overensstemmelse med påstanden eller ej.

Som teststørrelse bruger vi udtrykket $Z=\frac{\hat\mu-\mu}{\frac{\hat\sigma}{\sqrt{n}}}$ Her repræsenterer $\hat\mu$ } det bedste gæt på værdien af den ukendte middelværdi baseret på datamaterialet, mens $\mu$ repræsenterer den sande (men ukendte) middelværdi baseret på den formulerede påstand.

Vi tænker dermed på tælleren $\hat\mu-\mu$ i teststørrelsen $Z$ som et mål for om datamateriale og påstand er i overensstemmelse med hinanden eller ej:

$\hat\mu-\mu=\textrm{"datamaterialets gæt på $\mu$"}\;-\;\textrm{"den påståede værdi af $\mu$"}$

Hvis påstanden $H_0$ er sand (falsk), vil vi forvente, at $\hat\mu$ og $\mu$ ligger forholdsvis tæt på (langt fra) hinanden.

En lille (stor) værdi af $Z$ er derfor udtryk for, at der er lille (stor) forskel på vores datamateriale og den formulerede påstand.

Normeringen $\frac{\hat\sigma}{\sqrt{n}}$ i vores teststørrelse $Z=\displaystyle \frac{\hat\mu-\mu}{\frac{\hat\sigma}{\sqrt{n}}}$ kan man tænke på som en teknisk bekvemmelighed, der gør, at vi ved hvilken fordeling, der beskriver teststørrelsen $Z$ , og at vi dermed kan regne sandsynligheder ud om $Z$ .

For at vurdere om den beregnede værdi af teststørrelsen $Z$ er lille eller stor, dvs. om datamaterialet er i god eller dårlig overenstemmelse med påstanden $H_0$ , har vi behov for at kunne afgøre, hvornår en værdi af $Z$ skal opfattes som “lille” henholdsvis “stor”. Det gør vi ved hjælp af den såkaldte P-værdi.

Eksempel: Ølsalg

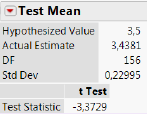
I tilfældet med prisen på Grøn Tuborg i Føtex estimeres normalfordelingens parametre til

$\hat\mu=3,44 kr.\hspace{1cm}\hat\sigma=0,23 kr.$ på baggrund af et datamateriale bestående af

$n=157$ observationer.

Figur 3.1: Nøgletal for Grøn Tuborg i Føtex

Under forudsætning af at nulhypotesen $H_0:\;\mu=3,\!50$ er sand, kan værdien af teststørrelsen beregnes til $Z=\frac{\hat\mu-\mu_0}{\frac{\hat\sigma}{\sqrt{n}}}=\frac{3,44-3,50}{\frac{0,23}{\sqrt{157}}}=-3,\!37$

3.2.4 Trin 4: P-værdi

Hvis vi antager, at påstanden $H_0$ er korrekt, så har vi set i kapitel 1, at teststørrelsen $Z$ er beskrevet ved en $t$ -fordeling med $n-1$ frihedsgrader.

Dermed kan vi under antagelse af at påstanden $H_0$ er sand beregne sandsynligheden for, at et datamateriale vil være i dårligere overensstemmelse med påstanden $H_0$ (som målt ved teststørrelsen $Z$ ) end tilfældet er med vores observerede datamateriale.

Denne sandsynlighed – kaldet P-værdien – vil vi herefter bruge som mål for, om datamaterialet ser ud til at være i overensstemmelse med påstanden $H_0$ eller ej. P-værdien kaldes også for signifikanssandsynligheden.

Hvis P-værdien er stor (lille), betyder det, at der er stor (lille) sandsynlighed for at observere et datamateriale, som er i dårligere overensstemmelse med påstanden $H_0$ end tilfældet er med vores datamateriale.

Med andre ord: En stor (lille) P-værdi betyder, at det er meget sandsynligt (usandsynligt) at observere et datamateriale, der passer dårligere med påstanden $H_0$ end vores givne datamateriale under forudsætning af at påstanden $H_0$ rent faktisk er korrekt. Meget tyder derfor på, at påstanden $H_0$ nok er (ikke er) korrekt.

Derfor vil vi opfatte en stor (lille) P-værdi som evidens for (imod) påstanden $H_0$ .

Eksempel: Ølsalg

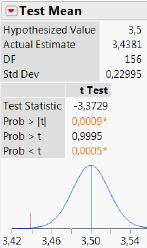
I tilfældet med prisen på Grøn Tuborg i Føtex er teststørrelsen $Z$ beskrevet ved en $t$ -fordeling med $n-1$ = 156 frihedsgrader.

Teststørrelsen blev beregnet til -3,37 og på baggrund af det kan P-værdien beregnes til 0,09% (vi skal senere i dette kapitel se, præcis hvordan P-værdien beregnes).

3.2.5 Trin 5: Konklusion

På baggrund af indholdet af trin 1 – trin 4 ovenfor kan vi afgøre, hvorvidt vores datamateriale underbygger påstanden formuleret i form af nulhypotesen $H_0$ eller ej.

Som praktisk beslutningsregel vil vi sammenholde den beregnede P-værdi med et på forhånd valgt signifikansniveau $\alpha$ } (“significance level”). Typisk bruger vi $\alpha=5\%$ .

Hvis P-værdien er…

mindre end $\alpha$ vil vi ikke tro på, at påstanden $H_0$ er sand. Vi vil derfor forkaste påstanden $H_0$ og i stedet tro på, at alternativhypotesen $H_a$ er sand
større end $\alpha$ vil vi ikke afvise, at påstanden $H_0$ kan være sand. Vi vil derfor ikke forkaste påstanden $H_0$

Eksempel: Ølsalg

Hvis vi anvender et signifikansniveau på $\alpha=5\%$ , vil vi forkaste nulhypotesen $H_0$ (fordi P-værdi = 0,09% < 5% = $\alpha$ ) $H_0:\;\mu=3,\!50$ dvs. forkaste at den forventede pris på Grøn Tuborg i Føtex er 3,50 kr. Vi vil i stedet tro på indholdet af alternativhypotesen $H_a:\;\mu\ne3,\!50$ dvs. tro på at den forventede pris på Grøn Tuborg i Føtex ikke er 3,50 kr.

På baggrund af det udførte hypotesetest er konklusionen, at der ikke på baggrund af vores datamateriale bestående af 157 ugentlige observationer af prisen på Grøn Tuborg i Føtex er belæg for en påstand om, at den forventede pris på Grøn Tuborg i Føtex er 3,50 kr.

Et naturligt opfølgende spørgsmål at stille sig selv er, hvilke påstande der så *er belæg for på baggrund af datamaterialet?!

Udover at prøve at lave hypotesetest med andre værdier end lige 3,50 i nulhypotesen $H_0$ , så findes der også andre måder at formulere nulhypotesen på end den, vi indtil videre har set på, og andre hypoteser kan muligvis give os andre indsigter i, hvad der er belæg for at hævde på baggrund af vores datamateriale.