3.3 Normalfordeling

3.3.1 Hypotesetest om \(\mu\)

3.3.1.1 Formulering af hypoteser

Hver gang man laver et hypotesetest om \(\mu\), skal man igennem alle fem trin (jf. afsnit 3.2). Indholdet af trin 1, trin 3 og trin 5 er dog altid det samme.

Der findes imidlertid forskellige måder at formulere sine hypoteser på (trin 2), og valget af hypotese påvirker også beregningen af P-værdien (trin 4). Derfor kan der være forskel på indholdet af trin 2 og tirn 4 afhængig af præcis hvilket hypotesetest om \(\mu\), man ønsker at lave.

Inden vi ser nærmere på de forskellige mulige hypoteser og de tilhørende beregninger af P-værdier, så lad os først lige opsummere de tre trin 1, 3 og 5, der altid er de samme.

Hypotesetest om \(\mu\) – Trin 1, 3, 5

Trin 1: Antagelser \(X_1,...,X_n\) er indbyrdes uafhængige observationer af en variabel, der er normalfordelt \(N(\mu,\sigma)\).

Trin 3: Teststørrelse Test af nulhypotesen \(H_0\) udføres ved hjælp af teststørrelsen \[Z=\frac{\hat\mu-\mu_0}{\frac{\hat\sigma}{\sqrt{n}}}\] hvor \(\mu_0\) er talværdien specificeret i nulhypotesen \(H_0\). Under forudsætning af at nulhypotesen \(H_0\) er sand, er teststørrelsen \(Z\) beskrevet ved en \(t\)-fordeling med \(n-1\) frihedsgrader.

Trin 5: Konklusion Hvis P-værdien er…

• mindre end signifikansniveauet \(\alpha\) forkaster vi nulhypotesen \(H_0\)
• større end signifikansniveauet \(\alpha\) forkaster vi ikke nulhypotesen \(H_0\)

Som nævnt kan hypoteser (nul- og alternativ) formuleres på flere forskellige måder. Vi skal her se på tre forskellige muligheder.

Hypotesetest om \(\mu\) – Trin 2

Når vi laver hypotesetest om \(\mu\), vil vi altid anvende én ud af tre nedenstående formuleringer af nulhypotesen \(H_0\) og alternativhypotesen \(H_a\):

• Nulhypotese om at middelværdien er lig \(\mu_0\): \[H_0:\;\mu=\mu_0\qquad\textrm{og}\qquad H_a:\;\mu\ne\mu_0\]
• Nulhypotese om at middelværdien er mindre end \(\mu_0\):: \[H_0:\;\mu\le\mu_0\qquad\textrm{og}\qquad H_a:\;\mu>\mu_0\]
• Nulhypotese om at middelværdien er større end \(\mu_0\): \[H_0:\;\mu\ge\mu_0\qquad\textrm{og}\qquad H_a:\;\mu<\mu_0\]

Bemærk at:

• \(\mu_0\) er blot notation for den talværdi, man ønsker at undersøge i forbindelse med sit hypotesetest
• \(\ne\) betyder “forskellig fra”. Udtrykket \(\mu\ne\mu_0\) betyder således, at enten er \(\mu>\mu_0\) eller også er \(\mu<\mu_0\)
• Test af nulhypotesen \(H_0: \mu=\mu_0\) (dvs. hvor \(H_a: \mu\ne\mu_0\)) kaldes for et 2-sidet test (“two-tailed test”), mens de to øvrige kaldes for 1-sidet test (“one-tailed”)
• Ved et 2-sidet test ser man på afvigelser fra nulhypotesen til begge (dvs. 2) sider i alternativhypotesen (\(H_a: \mu\ne\mu_0\)), mens man ved et 1-sidet test kun ser på afvigelser fra nulhypotesen til den ene side (dvs. enten \(H_a: \mu>\mu_0\) eller \(H_a: \mu<\mu_0\))
• I formuleringen af en nulhypotese om \(\mu\) der involverer ulighedstegn, er det ligegyldigt, om man erstatter \(\le\) med \(<\) og tilsvarende erstatter \(\ge\) med \(>\). Det vil sige at det er ligegyldigt, om man skriver

\[H_0: \mu\le\mu_0\qquad\textrm{og}\qquad H_a: \mu>\mu_0\]

eller

\[H_0: \mu<\mu_0\qquad\textrm{og}\qquad H_a: \mu\ge\mu_0\]

og tilsvarende er det ligegyldigt, om man skriver

\[H_0: \mu\ge\mu_0\qquad\textrm{og}\qquad H_a: \mu<\mu_0\] eller \[H_0: \mu>\mu_0\qquad\textrm{og}\qquad H_a: \mu\le\mu_0\]

3.3.1.2 Beregning af P-værdi

For at kunne drage en konklusion i et hypotesetest (i trin 5) kræver det, at vi først har beregnet en P-værdi (i trin 4).

Beregning af P-værdien bygger – uanset valget af hypotese – på den værdi af teststørrelsen \(Z=(\hat\mu-\mu_0)/(\hat\sigma/\sqrt{n})\), vi har beregnet i trin 3.

P-værdien bruges til at vurdere, om datamaterialet er foreneligt med nulhypotesen \(H_0\). Det gøres ved at se på, hvor stor sandsynligheden er for at observere noget, der er mere i modstrid med nulhypotesen \(H_0\) end vores datamateriale er.

P-værdien beregnes derfor som sandsynligheden for at få en værdi af teststørrelsen \(Z\), der er mere i modstrid med nulhypotesen \(H_0\) end værdien af teststørrelsen beregnet på baggrund af datamaterialet.

Hvis P-værdien er lille (stor), er det udtryk for, at datamateriale og nulhypotese stemmer dårligt (fint) overens. Hvordan P-værdien helt specifikt beregnes afhænger af det konkrete valg af nul- og alternativhypotese.

Når P-værdien er beregnet, kan man drage konklusionen på hypotesetestet. Hvis den beregnede P-værdi er lille…

• er det tegn på, at det er en meget usædvanlig værdi af vores teststørrelse, vi har beregnet på baggrund af datamaterialet (under forudsætning af at nulhypotesen \(H_0\) er sand)
• virker det rimeligt at tro, at nulhypotesen nok ikke er sand
• vil vi i trin 5 vælge at forkaste nulhypotesen \(H_0\), såfremt P-værdien er lille nok (= mindre end det valgte signifikansniveau \(\alpha\))

Hvis den beregnede P-værdi er stor…

• er det tegn på, at det ikke er en usædvanlig værdi af vores teststørrelse, vi har beregnet på baggrund af datamaterialet (under forudsætning af at nulhypotesen \(H_0\) er sand)
• virker det rimeligt at tro, at nulhypotesen nok er sand
• vil vi i trin 5 vælge ikke at forkaste nulhypotesen \(H_0\), såfremt P-værdien er stor nok (= større end det valgte signifikansniveau \(\alpha\))

\(\underline{\textrm{Test af }H_0: \mu=\mu_0}\)

HVIS nulhypotesen \(H_0\) er sand…

• vil vi regne med, at vores estimat \(\hat\mu\) ligger tæt på talværdien \(\mu_0\), og at teststørrelsen \(Z=(\hat\mu-\mu_0)/(\hat\sigma/\sqrt{n})\) derfor ligger tæt på 0
• vil store positive eller negative værdier af teststørrelsen \(Z\) være i modstrid med nulhypotesen \(H_0\)
• beregner vi P-værdien som sandsynligheden for, at teststørrelsen \(Z\) ligger længere væk fra 0 (i enten positiv eller negativ retning) end værdien beregnet ud fra datamaterialet.

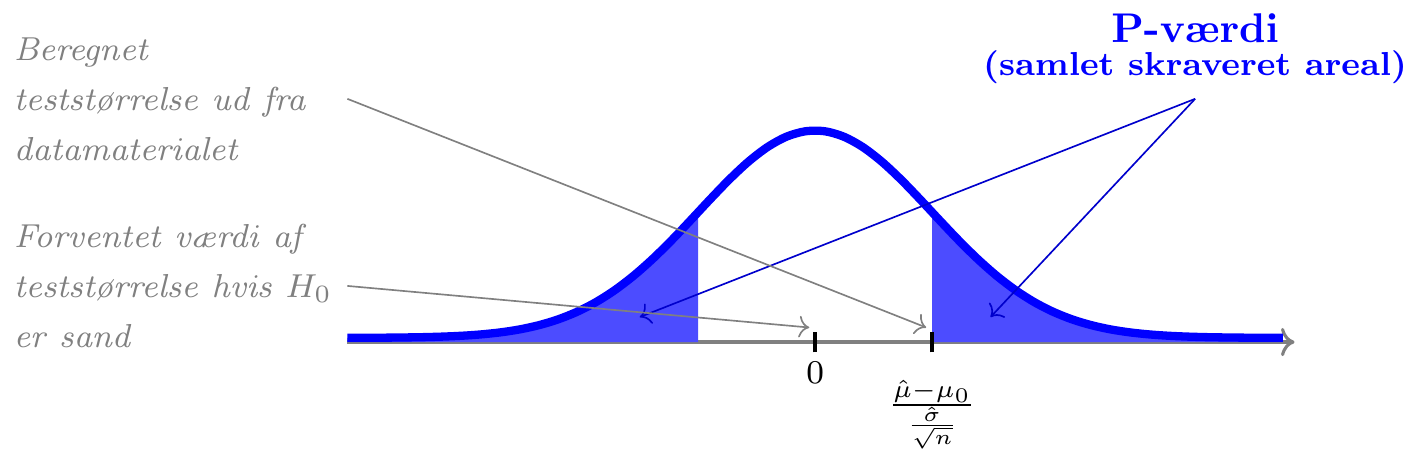
Eksempel: Ølsalg

Vi ser fortsat på prisen for 1 stk. Grøn Tuborg (33 cl glasflaske) i supermarkedskæden Føtex, der kan beskrives ved en normalfordeling med estimerede parametre \(\hat\mu\) =3,44 og \(\hat\sigma\) = 0,23 baseret på \(n=157\) observationer.

Hvis vi betragter hypoteserne \[H_0:\;\mu=3,\!48\hspace{1cm}H_a:\;\mu\ne3,\!48\] (dvs. \(\mu_0=3,\!48\)) så svarer det til at undersøge, om den forventede pris kan antages at være 3,48 kr. eller om den ikke kan.

Under forudsætning af at nulhypotesen \(H_0\) er sand kan teststørrelsen beregnes til \[z=\frac{\hat\mu-\mu_0}{\frac{\hat\sigma}{\sqrt{n}}}=\frac{3,44-3,48}{\frac{0,230}{\sqrt{157}}}=-2,\!28\] Herefter kan P-værdien beregnes som sandsynligheden for at observere noget, der er i dårligere overensstemmelse med \(H_0\) end værdien \(-2,\!28\), dvs. som \[P(Z>2,\!28)+P(Z<-2,\!28)=2,\!38\%\] hvor \(Z\) er beskrevet ved en \(t\)-fordeling med \(n-1=156\) frihedsgrader.

Ved et signifikansniveau på \(\alpha=5\%\) forkaster vi således nulhypotesen \(H_0\) (fordi \(\textsf{P-værdi}=2,\!38\% < 5\%=\alpha\)). Der er således ikke på baggrund af datamaterialet belæg for at hævde, at den forventede pris på Grøn Tuborg er 3,48 kr.

\(\underline{\textrm{Test af }H_0: \mu\le\mu_0}\)

HVIS nulhypotesen \(H_0\) er sand…

• vil vi regne med, at vores estimat \(\hat\mu\) er mindre end talværdien \(\mu_0\), og at teststørrelsen \(Z=(\hat\mu-\mu_0)/(\hat\sigma/\sqrt{n})\) derfor er mindre end 0
• vil store positive værdier af teststørrelsen \(Z\) være i modstrid med nulhypotesen \(H_0\)
• beregner vi P-værdien som sandsynligheden for, at teststørrelsen \(Z\) ligger længere væk fra 0 (i positiv retning) end værdien beregnet ud fra datamaterialet.

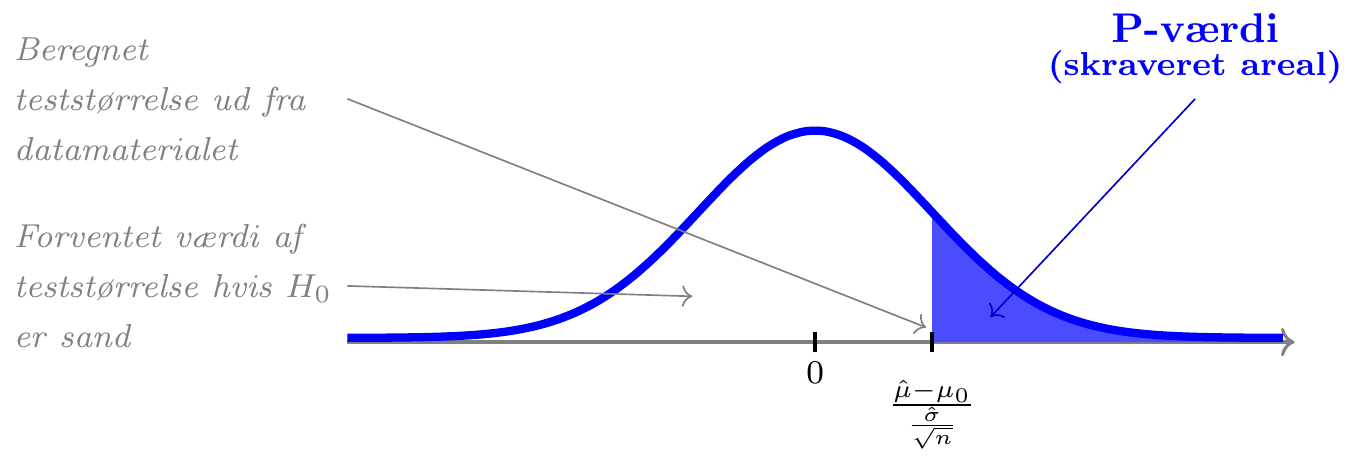
Eksempel: Ølsalg

Vi ser fortsat på prisen for 1 stk. Grøn Tuborg (33 cl glasflaske) i supermarkedskæden Føtex, der kan beskrives ved en normalfordeling med estimerede parametre \(\hat\mu=3,44\) og \(\hat\sigma=0,230\) baseret på \(n=157\) observationer.

Hvis vi betragter hypoteserne \[H_0:\;\mu\le3,\!48\hspace{1cm}H_a:\;\mu>3,\!48\] (dvs. \(\mu_0=3,\!48\)) så svarer det til at undersøge, om den forventede pris kan antages at være lavere end 3,48 kr. eller om den ikke kan.

Under forudsætning af at nulhypotesen \(H_0\) er sand kan teststørrelsen beregnes til \[z=\frac{\hat\mu-\mu_0}{\frac{\hat\sigma}{\sqrt{n}}}=\frac{3,44-3,48}{\frac{0,230}{\sqrt{157}}}=-2,\!28\]

Herefter kan P-værdien beregnes som sandsynligheden for at observere noget, der er i dårligere overensstemmelse med \(H_0\) end værdien -2,28, dvs. som \[P(Z>-2,\!28)=98,\!81\%\] hvor \(Z\) er beskrevet ved en \(t\)-fordeling med \(n-1=156\) frihedsgrader.

Ved et signifikansniveau på \(\alpha=5\%\) forkaster vi således ikke nulhypotesen \(H_0\) (fordi \(\textsf{P-værdi}=98,\!81\% > 5\%=\alpha\). Der er således ikke på baggrund af datamaterialet belæg for at afvise, at den forventede pris på Grøn Tuborg er lavere end 3,48 kr.

\(\underline{\textrm{Test af }H_0: \mu\ge\mu_0}\)

HVIS nulhypotesen \(H_0\) er sand…

• vil vi regne med, at vores estimat \(\hat\mu\) er større end talværdien \(\mu_0\), og at teststørrelsen \(Z=(\hat\mu-\mu_0)/(\hat\sigma/\sqrt{n})\) derfor er større end 0
• vil store negative værdier af teststørrelsen \(Z\) være i modstrid med nulhypotesen \(H_0\)
• beregner vi P-værdien som sandsynligheden for, at teststørrelsen \(Z\) ligger længere væk fra 0 (i *negativ* retning) end værdien beregnet ud fra datamaterialet

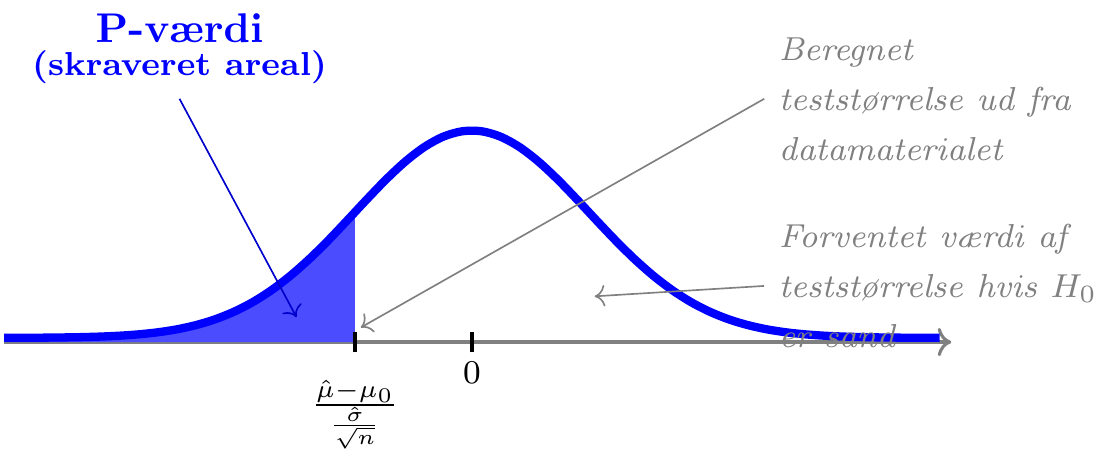
Eksempel: Ølsalg

Vi ser fortsat på prisen for 1 stk. Grøn Tuborg (33 cl glasflaske) i supermarkedskæden Føtex, der kan beskrives ved en normalfordeling med estimerede parametre \(\hat\mu\) = 3,44 og \(\hat\sigma\) =0,23 baseret på \(n=157\) observationer.

Hvis vi betragter hypoteserne \[H_0:\;\mu\ge3,\!48\hspace{1cm}H_a:\;\mu<3,\!48\] (dvs. \(\mu_0=3,\!48\)) så svarer det til at undersøge, om den forventede pris kan antages at være højere end 3,48 kr. eller om den ikke kan.

Under forudsætning af at nulhypotesen \(H_0\) er sand kan teststørrelsen beregnes til \[z=\frac{\hat\mu-\mu_0}{\frac{\hat\sigma}{\sqrt{n}}}=\frac{3,44-3,48}{\frac{0,230}{\sqrt{157}}}=-2,\!28\]

Herefter kan P-værdien beregnes som sandsynligheden for at observere noget, der er i dårligere overensstemmelse med \(H_0\) end værdien \(-2,\!28\), dvs. som \[P(Z<-2,\!28)=1,\!19\%\] hvor \(Z\) er beskrevet ved en \(t\)-fordeling med \(n-1=156\) frihedsgrader.

Ved et signifikansniveau på \(\alpha=5\%\) forkaster vi således nulhypotesen \(H_0\) (fordi \(\textsf{P-værdi}=1,\!19\% < 5\%=\alpha\)). Der er således ikke på baggrund af datamaterialet belæg for at hævde, at den forventede pris på Grøn Tuborg er højere end 3,48 kr.