Kapitel 2 Konfidensinterval (for to grupper)

2.1 Emne i dette kapitel

I mange sammenhænge er det relevant at sammenligne værdien af en variabel mellem to forskellige grupper:

Er der forskel på variablens værdier i de to grupper?
Hvis der er en forskel, hvad kan vi så sige om forskellen?

Vi har i kapitel 1…

set på, hvor præcist vi er i stand til at gætte på middelværdien $\mu$ af en variabel
vurderet præcisionen af vores gæt på middelværdien $\mu$ ved at beregne et konfidensinterval for $\mu$

I dette kapitel vil vi bruge samme type overvejelser til at…

se på, hvor præcist vi er i stand til at gætte på FORSKELLEN $\mu_1-\mu_2$ i middelværdien af en variabel MELLEM TO GRUPPER
vurdere præcisionen af vores gæt på forskellen i middelværdier $\mu_1-\mu_2$ ved at beregne et konfidensinterval for $\mu_1-\mu_2$

Ligeledes vil vi også i dette kapitel se på præcisionen af, og et konfidensinterval for, et gæt på en forskel $p_1-p_2$ mellem andele i to grupper.

Eksempel: Ølsalg

Hvis vi tegner en figur af den ugentlige gennemsnitspris for 1 stk. Grøn Tuborg (33 cl glasflaske) i de to supermarkedskæder Føtex og Bilka (datafil: Ølsalg.jmp) ser det ud til, at Grøn Tuborg i de fleste uger er billigere i Bilka end i Føtex: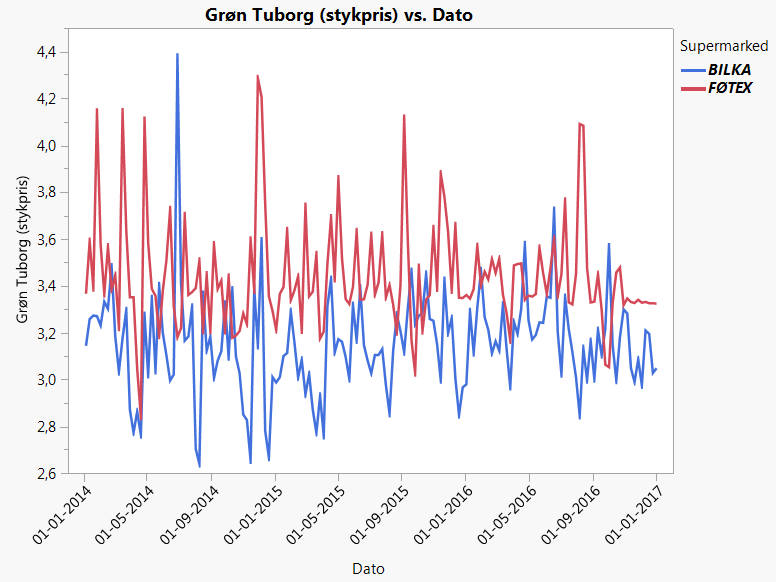

Figur 2.1: Prisen på 1 stk. Tuborg i Bilka og Føtex

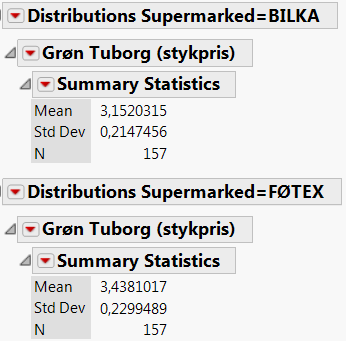
Figur 2.2: Prisen på 1 stk. Tuborg i Bilka og Føtex

Datamaterialet består af 157 ugers priser for hvert supermarked (= “gruppe”) med en estimeret middelværdi på $\hat\mu_1$ =3,44 kr. i Føtex (“gruppe 1”) og en estimeret middelværdi på $\hat\mu_2$ = 3,15 kr. i Bilka (“gruppe 2”).

Den forventede prisforskel er dermed $\hat\mu_1-\hat\mu_2$ = 3,44-3,15=0,29 kr., således at vi alt andet lige vil forvente, at Grøn Tuborg er 0,29 kr. billigere i Bilka end i Føtex.

Det er klart fra figuren ovenfor, at prisforskellen mellem de to supermarkeder varierer meget fra uge til uge. Spørgsmålet er derfor, hvor præcist et gæt $\hat\mu_1-\hat\mu_2$ = 0,29 kr. er på den forventede prisforskel i en given uge?

Med andre ord, hvilke forskelle i prisen på Grøn Tuborg mellem Føtex og Bilka skal vi rimeligvis forvente os på baggrund af datamaterialet? Er det rimeligt visse uger at forvente en forskel på mere end 0,50 kr.? Eller på mindre end 0,10 kr.? Det er det, vi skal se på i dette kapitel.

Eksempel: Skat

I en spørgeskemaundersøgelse om velfærd og skat udsendt til 975 personer har vi i kapitel 1 set på spørgsmålet “Er topskatten for høj?”.

Tegner vi søjlediagrammer af de indkomne svar opdelt på svar fra henholdsvis mænd og kvinder (datafil: Skat.jmp), ser det ser ud til, at mændene i højere grad end kvinderne mener, at topskatten er for høj: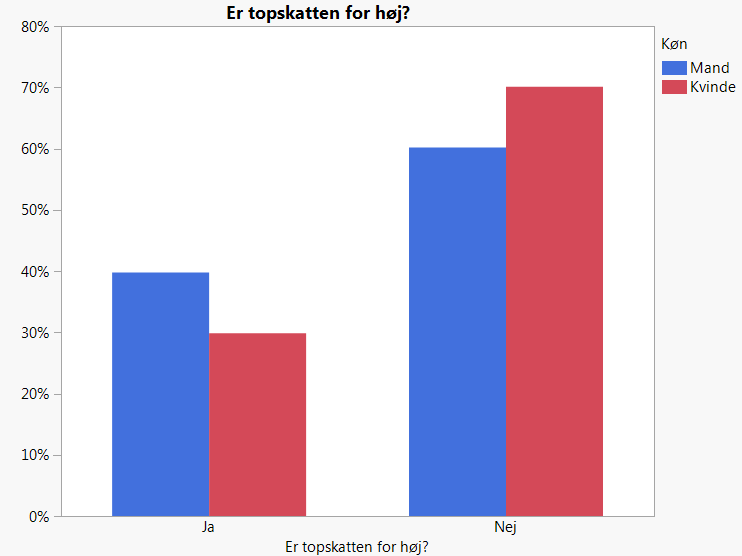

Figur 2.3: Svar på spørgsmålet: Er topskatten for høj? for mænd og kvinder

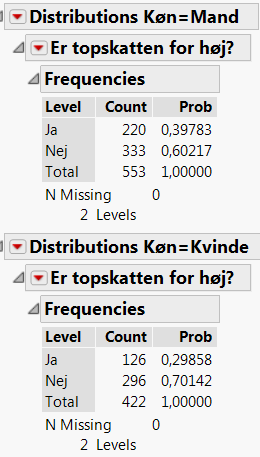
Figur 2.4: Svar på spørgsmålet: Er topskatten for høj? for mænd og kvinder

Af de adspurgte personer er 553 mænd (“gruppe 1”) og heraf mener $\hat p_1$ = 39,8%, at topskatten er for høj. Blandt de 422 adspurgte kvinder (“gruppe 2”) mener $\hat p_2$ = 29,9%, at topskatten er for høj. Forskellen mellem de to køn er $\hat p_1-\hat p_2$ = 9,9%$, dvs. at blandt mændene mener ca. 10% flere at topskatten er for høj end blandt kvinderne.

Spørgsmålet er nu, hvor præcist et gæt $\hat p_1-\hat p_2$ = 9,9% er på forskellen mellem andelen af mænd og andelen af kvinder, der mener topskatten er for høj blandt den samlede danske befolkning?

Med andre ord, er det på baggrund af datamaterialet rimeligt at forvente, at forskellen mellem de to andele ligger tæt på 10%? Eller er undersøgelsens resultat også foreneligt med en forskel på kun 5%? Eller på slet ingen forskel mellem kønnene? Det er det, vi skal se på i dette note.