Chapter 9 One-Way Between Subjects ANOVA
A one-way between subjects ANOVA is used to test differences in the means of the dependent variable (DV) among different levels of an independent variable (IV). The first check that must be made is if our data are of the correct form: a categorical (also called discrete) IV and an interval or ratio DV. Much of the grouping techniques used for the between subjects ANOVA will mirror the grouping techniques performed in the independent samples t-test. For clarity, I will be repeating much of what was already explained, though perhaps with slightly less detail.
Packages used: psych, tidyverse, ggplot2, qqplotr, viridis, car, lsr, onewaytests, emmeans
Optional packages: DescTools
The data: We will be using the InsectSprays dataset from R, which gives the count of insects after treatment with different insecticides. Lower counts indicate lower insect survival, and more effective insecticide.
## count spray
## 1 10 A
## 2 7 A
## 3 20 A
## 4 14 A
## 5 14 A
## 6 12 ALooking at the data, we can see that spray is a categorical variable, and count is a ratio variable. This allows us to perform an ANOVA, provided assumptions are met.
9.1 Descriptive Statistics
We can first take a look at the descriptive statistics for our data, broken down by treatment group. To do this, we will use the describeBy() function from the psych package.
#Call the package
library(psych)
#Get the descriptives by group
describeBy(bugs$count, group = bugs$spray)##
## Descriptive statistics by group
## group: A
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 12 14.5 4.72 14 14.4 5.19 7 23 16 0.27 -1.13 1.36
## ------------------------------------------------------------------------------------------------------------
## group: B
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 12 15.33 4.27 16.5 15.6 4.45 7 21 14 -0.35 -1.04 1.23
## ------------------------------------------------------------------------------------------------------------
## group: C
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 12 2.08 1.98 1.5 1.8 1.48 0 7 7 1.13 0.52 0.57
## ------------------------------------------------------------------------------------------------------------
## group: D
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 12 4.92 2.5 5 4.5 1.48 2 12 10 1.68 2.56 0.72
## ------------------------------------------------------------------------------------------------------------
## group: E
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 12 3.5 1.73 3 3.5 2.22 1 6 5 0.05 -1.41 0.5
## ------------------------------------------------------------------------------------------------------------
## group: F
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 12 16.67 6.21 15 16.5 6.67 9 26 17 0.39 -1.56 1.79From this, we can see the means of each group, along with min/max values and skew and kurtosis and other values.
We can also use a box plot to examine our data, and look for outliers in each of the groups. To do this, we will use ggplot2 to create boxplots by group. First, we define our data (data = bugs), x (x = spray), and y (y = count) values. The x value is our grouping variable, and our y value is the one we are comparing. The next line is the boxplot function (geom_boxplot()), and the last line prints each data point as a dot on the box plot (geom_jitter()).
#Call ggplot
library(ggplot2)
#Generate a boxplot
ggplot(data = bugs, aes(x = spray, y = count)) +
geom_boxplot() +
geom_jitter(width = .2)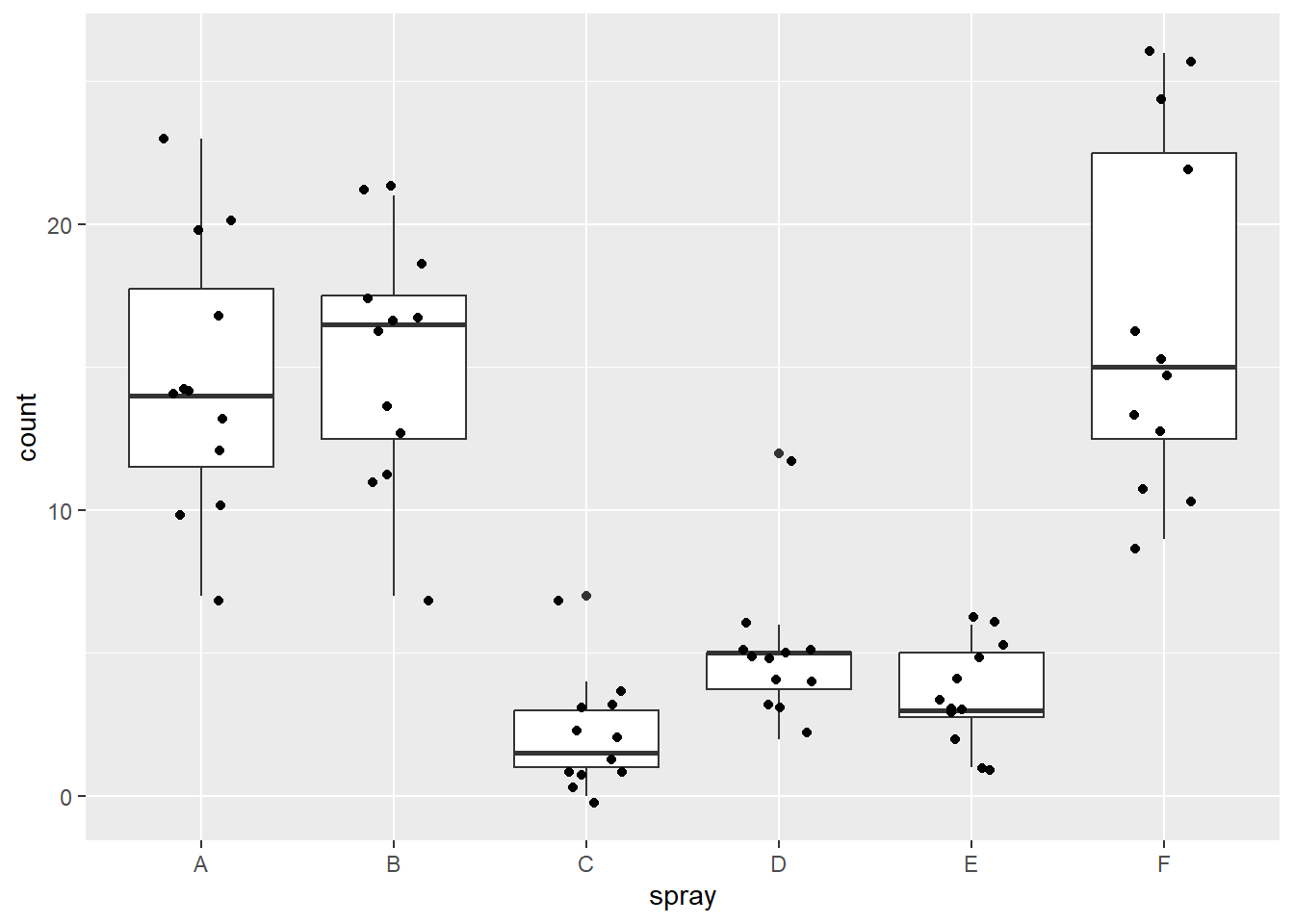
Looking at the boxplots, we can see that spray C and D appear to have two rather extreme outliers each, and sprays A and F have some data points that could be considered outliers.
9.2 Assumptions
We will test assumptions for each of the groups, rather than on the data as a whole. In order to get R to split by group, we will make use of the ‘pipe’(%>%) from the tidyverse package.
Shapiro-Wilk
We will begin by running a Shapiro-Wilk test to test each group for normality. The shapiro.test() will allow us to get the test, though we will need to assign it to an object and ask for the information in a table. Specifically, we will be asking for the W statistic, or Shaprio-Wilk statistic, and the p-value from the test.
In the code below, we first call the tidyverse package to allow us to split by group before moving on to running the Shapiro-Wilk test. Then, we specify our data (bugs) and send it on to the next line (%>%). We next specify which variable R should group by with the group_by() function - this time, it is the ‘spray’ variable. The line group_by(spray) takes our dataframe and groups it by spray type. Then, we send that on (%>%) to the Shapiro-Wilk test.
Running the Shapiro-Wilk test, we start with the summarise() function, and define what our columns will be. The first column is the Shapiro-Wilk statistic, named “S-W Statistic”, and we specify that the value in this column should be the statistic from the function: "S-W Statistic" = shapiro.test(count)$statistic. We see that we are still calling the shapiro.test() function on the ‘count’ column (shapiro.test(count)), but then we are including $statistic because that’s the value we want in this column. In the second column we specify that the values should be the p-value from the shapiro.test() function: "p-value" = shapiro.test(count)$p.value.
#Call tidyverse package
library(tidyverse)
#Run the Shapiro-Wilk test
bugs %>% #Call our dataframe and send it on
group_by(spray) %>% #Group by our grouping variable
summarise("S-W Statistic" = shapiro.test(count)$statistic, #Give us the statistics we want, in a table
"p-value" = shapiro.test(count)$p.value)## # A tibble: 6 × 3
## spray `S-W Statistic` `p-value`
## <fct> <dbl> <dbl>
## 1 A 0.958 0.749
## 2 B 0.950 0.641
## 3 C 0.859 0.0476
## 4 D 0.751 0.00271
## 5 E 0.921 0.297
## 6 F 0.885 0.101We can see that sprays A, B, E, and F have non-significant p-values, indicating that they do not have a distribution that is significantly different than a normal distribution. However, sprays C and D have significant p-values, indicating that they do have a distribution that is significantly different than a normal distribution, thus violating the assumption of normality. We will be continuing, to illustrate the other checks and how to run an ANOVA.
Histogram
We can also check the normality assumption visually, by generating histograms of each group. Given that we have six groups, we will be creating separate histograms for each group.
The stacked histogram is generated much the same as a unstacked one, with the exception of the function facet_grid(~ spray). This is what is generating one histogram per group. The facet_grid() function allows separate plots per group. If you’d like them as a vertical stack rather than side-by-side, use spray ~ .. At the end, theme_minimal() is addressing how the graphs look - getting rid of the grey background, for example.
#Generate side-by-side histograms
ggplot(data = bugs, aes(x = count)) +
geom_histogram() +
facet_grid(~ spray) +
theme_minimal()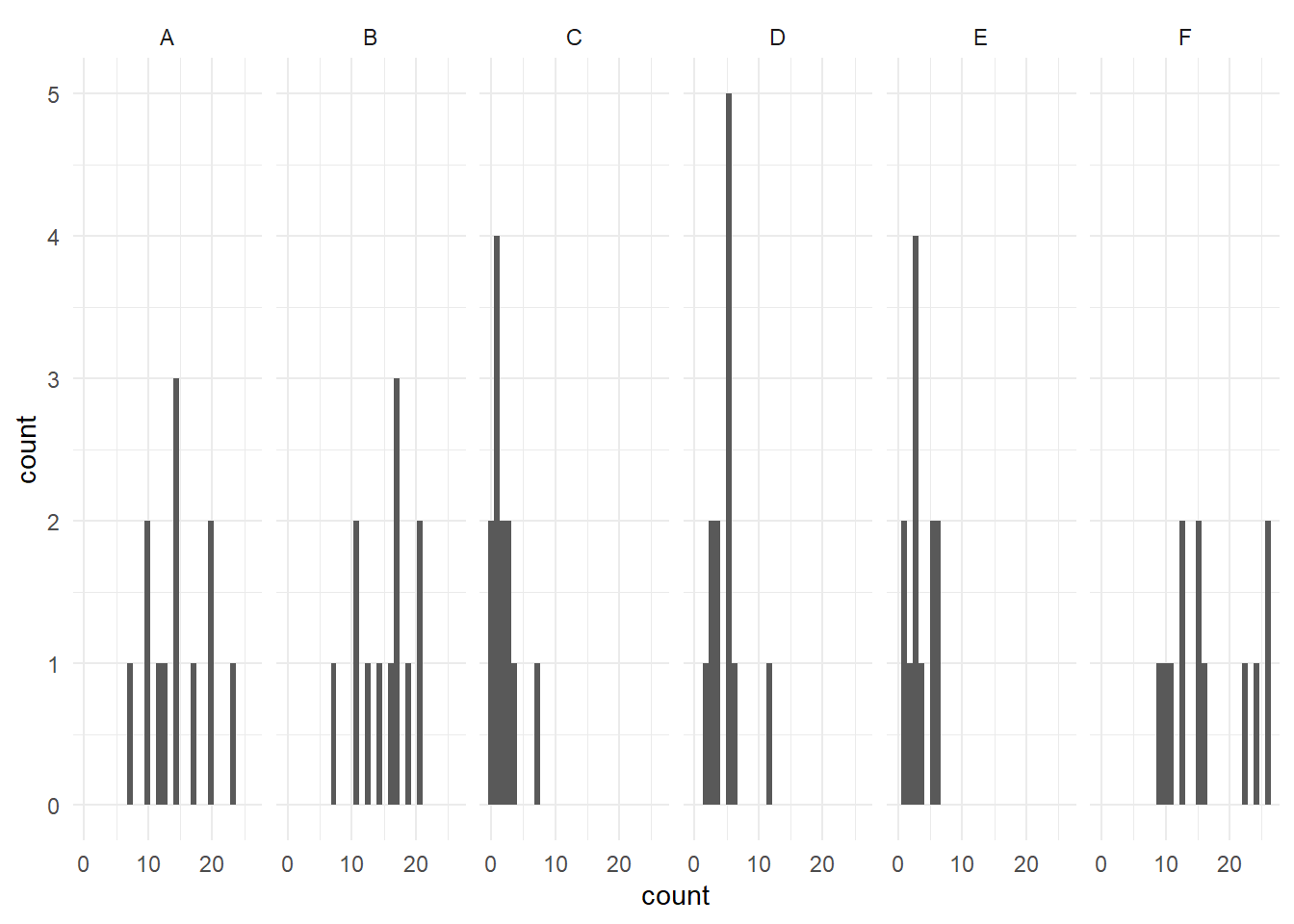
These histograms show that, visually, sprays C and D are not as normally distributed as the other sprays.
QQ Plot
Another visual inspection we can do involves a Q-Q plot. We will use the package qqplotr to make these, as an addition to ggplot2.
Breaking down the code we will use to generate the plot:
1. ggplot(data = bugs, mapping = aes(sample = count, color = spray, fill = spray)) + is our call to ggplot. We are defining what data to use (data = bugs), and then giving some arguments to the aes() function. sample = count says to use the variable ‘count’, color = spray is asking for each spray type to be a different color, and fill = spray corresponds to the filled in portion. To ensure colorblind friendliness, we will specify colors below.
2. stat_qq_band(alpha=0.5, conf=0.95, qtype=1, bandType = "ts") + is our first function using the qqploter package, and contains arguments about the confidence bands. This is defining the alpha level (alpha = 0.5) and the confidence interval (conf = 0.95) to use for the confidence bands. bandType = "pointwise" is saying to construct the confidence bands based on Normal confidence intervals.
3. stat_qq_line(identity = TRUE) + is another call to the qqplottr package and contains arguments about the line going through the qq plot. The argument identity = TRUE says to use the identity line as the reference to construct the confidence bands around.
4. stat_qq_point(col = "black") + is the last call to the qqplottr package and contains arguments about the data points. col = "black" means we’d like them to be black.
5. facet_wrap(~ spray, scales = "free") + is a similar argument to the bar plot above. This is sorting by group (~ spray), and creating a qq plot for each of our sprays. The scales = "free" refers to the scales of the axes; by setting them to “free” we are allowing them to freely vary between each of the graphs. If you want the scale to be fixed, you would use scale = "fixed".
6. labs(x = "Theoretical Quantiles", y = "Sample Quantiles") + is a labeling function. Here, we are labeling the x and y axis (x = and y = respectively).
7. scale_fill_viridis(discrete = TRUE) is specifying a color fill that is colorblind friendly as well as grey-scale friendly. Since these are discrete groups, we add discrete = TRUE.
8. scale_color_viridis(discrete = TRUE) is again using a colorblind friendly scale for the outlines, to match the fill.
9. Lastly, theme_bw() is giving an overall preset theme to the graphs - this touches on things such as background, axis lines, grid lines, etc.
#Call qqplotr
library(qqplotr)
#Call viridis
library(viridis)
#Perform QQ plots by group
ggplot(data = bugs, mapping = aes(sample = count, color = spray, fill = spray)) +
stat_qq_band(alpha = 0.5, conf = 0.95, bandType = "pointwise") +
stat_qq_line(identity = TRUE) +
stat_qq_point(col = "black") +
facet_wrap(~ spray, scales = "free") +
labs(x = "Theoretical Quantiles", y = "Sample Quantiles") +
scale_fill_viridis(discrete = TRUE) +
scale_color_viridis(discrete = TRUE) +
theme_bw()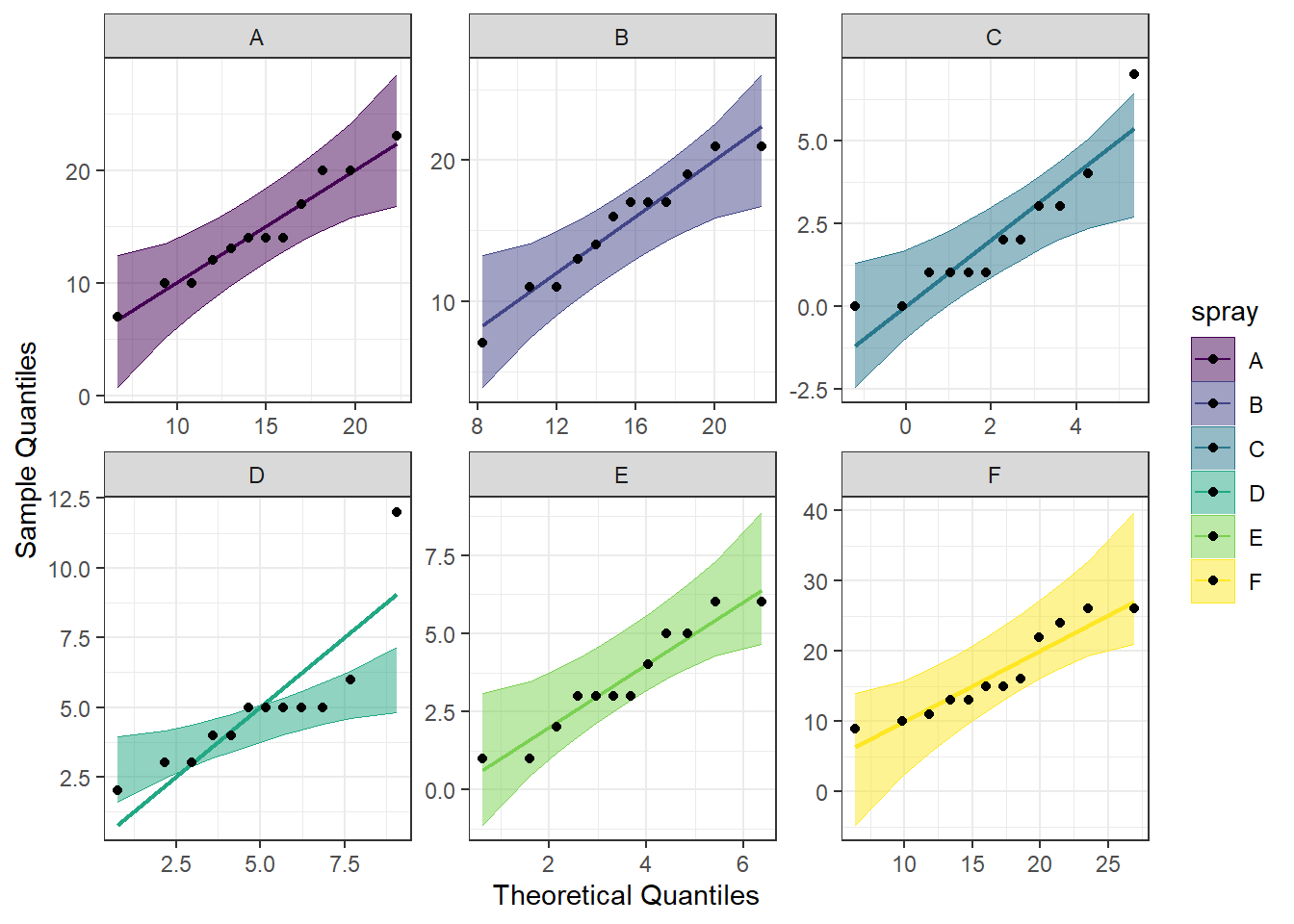
Looking at the Q-Q plot, what becomes more obvious is the pull the outliers have on the data in sprays C and D.
Detrended QQ Plot
We can also make a detrended Q-Q plot using the same code but adding detrend = TRUE to all of the stat_qq_ functions.
#Perform detrended QQ plots by group
ggplot(data = bugs, mapping = aes(sample = count, color = spray, fill = spray)) +
stat_qq_band(alpha = 0.5, conf = 0.95, bandType = "pointwise", detrend = TRUE) +
stat_qq_line(identity = TRUE, detrend = TRUE) +
stat_qq_point(col = "black", detrend = TRUE) +
facet_wrap(~ spray, scales = "free") +
labs(x = "Theoretical Quantiles", y = "Sample Quantiles") +
scale_fill_viridis(discrete = TRUE) +
scale_color_viridis(discrete = TRUE) +
theme_bw()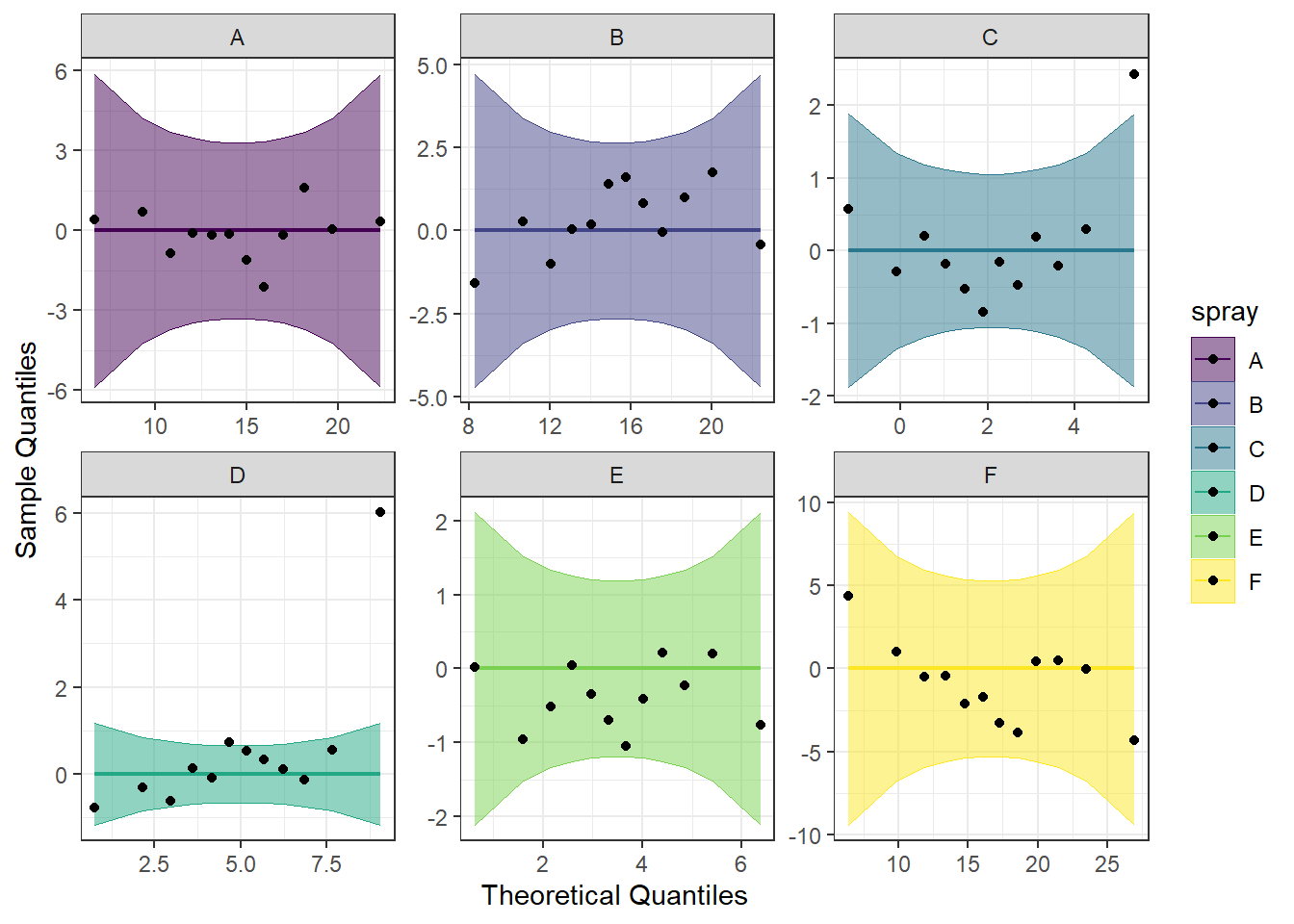
Looking at both the regular and detrended Q-Q plots, we can see that sprays A, B, E, and F seem to be pretty normally distributed. We can also see that C and D are not, potentially due to the effect of one or two extreme outliers.
9.2.2 Homogeneity of Variance
We will test the homogeneity of variance between the spray types with the Levene’s Test and the Brown-Forsyth Test. Both tests use the same function from the package car, leveneTest(), but with the argument center = we can differentiate between the two.
#Call the car package
library(car)
#Perform Levene's Test
LT_bugs <- leveneTest(count ~ spray, data=bugs, center="mean")
#Perform Brown-Forsythe test
BFT_bugs <- leveneTest(count ~ spray, data=bugs, center="median")
#Print both of them
print(LT_bugs)## Levene's Test for Homogeneity of Variance (center = "mean")
## Df F value Pr(>F)
## group 5 6.4554 6.104e-05 ***
## 66
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Levene's Test for Homogeneity of Variance (center = "median")
## Df F value Pr(>F)
## group 5 3.8214 0.004223 **
## 66
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1We see that both values are significant, indicating that we reject the null that the variances are the same. The assumption of homogeneity of variances is not met.
9.3 Run the one-way between subjects ANOVA
Were this not for illustrative purposes, we would reconsider running an ANOVA due to the fact that both the normality and homogeneity of variance assumptions have been violated. However, we will proceed, in order to work through the code.
There are a number of different approaches that can be taken when running a one-way between subjects ANOVA, two of which will be given as examples here: the aov() function and the lm() function.
AOV
Using the aov() function, we first assign the formula to an object (model_b1 here), so we can later get summary statistics. We put in that we want count modeled as a function of spray (count ~ spray), and that our data is the bugs dataframe (data = bugs). When we run the first line, we don’t see any output, because we have assigned it to an object. However, if we ask for the summary of that model (summary(model_b1)), we get the output seen below.
## Df Sum Sq Mean Sq F value Pr(>F)
## spray 5 2669 533.8 34.7 <2e-16 ***
## Residuals 66 1015 15.4
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1From the output, we can see that the ANOVA is significant, with p < 0.001 and an F( with 5 and 66 degrees of freedom) of 34.7. It also provides us with the Sum of Squares and Mean Squares.
LM
Setting up an ANOVA using lm() (lm = linear model) is pretty much the same, except for switching out the function we use. We are again assigning the output to an object (model_b2 this time), then specifying the formula (count ~ spray) and our data (data = bugs). After running the first line, nothing appears, since the output was assigned to the model_b2 object. However, we can ask for a summary, which looks much like a summary we would get after doing a regression. To get an ANOVA table, we run the anova() function on the object.
##
## Call:
## lm(formula = count ~ spray, data = bugs)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.333 -1.958 -0.500 1.667 9.333
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 14.5000 1.1322 12.807 < 2e-16 ***
## sprayB 0.8333 1.6011 0.520 0.604
## sprayC -12.4167 1.6011 -7.755 7.27e-11 ***
## sprayD -9.5833 1.6011 -5.985 9.82e-08 ***
## sprayE -11.0000 1.6011 -6.870 2.75e-09 ***
## sprayF 2.1667 1.6011 1.353 0.181
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.922 on 66 degrees of freedom
## Multiple R-squared: 0.7244, Adjusted R-squared: 0.7036
## F-statistic: 34.7 on 5 and 66 DF, p-value: < 2.2e-16## Analysis of Variance Table
##
## Response: count
## Df Sum Sq Mean Sq F value Pr(>F)
## spray 5 2668.8 533.77 34.702 < 2.2e-16 ***
## Residuals 66 1015.2 15.38
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Looking at the summary, we get a coefficients table. This will be addressed in another course, so for now we will just pass this by. Running an ANOVA on the model gives us an ANOVA table - this looks nearly identical to the one obtained with aov() with the exception of the number of decimal places provided. We again get significance, an F statistic with degrees of freedom, and Sum of Squares and Mean Square.
Since we had unequal variances, thereby violating the homogeneity of variances assumption, we should do either a Welch or a Brown-Forsythe test for equal means. For the Brown-Forsythe test, we will be using the bf.test() function from the onewaytests package. As before, we specify our formula (count ~ spray) and our data (data = bugs) to the function, and get our output. The Welch’s test is done with the oneway.test() function in base R. Along with the formula and data specification, we add var.equal = FALSE to indicate we do not have equal variances.
##
## Attaching package: 'onewaytests'## The following object is masked from 'package:Hmisc':
##
## describe## The following object is masked from 'package:psych':
##
## describe##
## Brown-Forsythe Test (alpha = 0.05)
## -------------------------------------------------------------
## data : count and spray
##
## statistic : 34.70228
## num df : 5
## denom df : 39.31889
## p.value : 2.051138e-13
##
## Result : Difference is statistically significant.
## -------------------------------------------------------------##
## One-way analysis of means (not assuming equal variances)
##
## data: count and spray
## F = 36.065, num df = 5.000, denom df = 30.043, p-value = 7.999e-12Looking at the output, we can first see that both tests are significant, indicating that at least one spray is different than the others, taking into account the fact that we have violated the homogeneity of variances assumption. Additionally, note the denominator degrees of freedom: it is no longer a whole number. This is how the unequal variances are taken into account.
Given that p < 0.05 for the ANOVA, we reject the null hypothesis and conclude that at least one spray is different than the others in terms of number of insects surviving.
We can also calculate \(\eta^{2}\) using the etaSquared() function from the lsr package. Conveniently, it does not matter which method we used to create our model (aov() vs lm()), both will be understood by the function. This simply requires feeding the model object to the etaSquared() function. Since this is a one-way ANOVA, the eta squared and partial eta squared are identical; later ANOVAs will make use of one over the other.
## eta.sq eta.sq.part
## spray 0.724439 0.724439## eta.sq eta.sq.part
## spray 0.724439 0.724439We can see that \(\eta^{2}\) = 0.72, which would be considered a large effect size.
9.4 Post-hoc tests
Since there is a significant main effect, we will be performing multiple comparisons to determine where the differences in the DV are (ie, is spray C the only one different than all the rest, or are sprays C and D different than A, B, E, and F?)
9.4.1 Pairwise comparisons
We can do pairwise comparisons between each set of sprays to see which are different from each other. Depending on which PostHoc method you choose (Bonferroni, Tukey, Scheffe are given as examples) will dictate which function you will run. Each have slightly different ways of adjusting the p-values to account for the additional testing being performed. All the different adjustments should produce similar results. We first look at the emmeans() package, and then give options to run each example individually.
9.4.2 Using emmeans() for Pairwise Comparisons
The emmeans() function has a wide range of versatility both in what model objects it can accept (both our aov() and lm() models, for example) as well as what type of post-hoc comparisons it can perform. For the pairwise comparisons, we just need to specify which adjustment method we would like for it to use under the adjust = argument. I will be modelling three different methods: Bonferroni, Tukey’s HSD, and Scheffe as examples.
Looking at the code below, you can see that for each adjustment, we are assigning it to an object. We can use that object later for contrasts or plotting if desired. The emmeans() function first takes an ANOVA model (model_b1 here). Then, we specify that we want to do pairwise comparisons, and our grouping variable is spray (pairwise ~ spray). Lastly, we have how we want the p-values adjusted (adjust = "bonferroni", for example).
#Call emmeans package
library(emmeans)
#Compute expected marginal means post-hoc tests
posthocs <- emmeans(model_b1, pairwise ~ spray, adjust = "bonferroni")
posthocs2 <- emmeans(model_b1, pairwise ~ spray, adjust = "tukey")
posthocs3 <- emmeans(model_b1, pairwise ~ spray, adjust = "scheffe")
#Bonferroni adjustment results
posthocs## $emmeans
## spray emmean SE df lower.CL upper.CL
## A 14.50 1.13 66 12.240 16.76
## B 15.33 1.13 66 13.073 17.59
## C 2.08 1.13 66 -0.177 4.34
## D 4.92 1.13 66 2.656 7.18
## E 3.50 1.13 66 1.240 5.76
## F 16.67 1.13 66 14.406 18.93
##
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## A - B -0.833 1.6 66 -0.520 1.0000
## A - C 12.417 1.6 66 7.755 <.0001
## A - D 9.583 1.6 66 5.985 <.0001
## A - E 11.000 1.6 66 6.870 <.0001
## A - F -2.167 1.6 66 -1.353 1.0000
## B - C 13.250 1.6 66 8.276 <.0001
## B - D 10.417 1.6 66 6.506 <.0001
## B - E 11.833 1.6 66 7.391 <.0001
## B - F -1.333 1.6 66 -0.833 1.0000
## C - D -2.833 1.6 66 -1.770 1.0000
## C - E -1.417 1.6 66 -0.885 1.0000
## C - F -14.583 1.6 66 -9.108 <.0001
## D - E 1.417 1.6 66 0.885 1.0000
## D - F -11.750 1.6 66 -7.339 <.0001
## E - F -13.167 1.6 66 -8.223 <.0001
##
## P value adjustment: bonferroni method for 15 tests## $emmeans
## spray emmean SE df lower.CL upper.CL
## A 14.50 1.13 66 12.240 16.76
## B 15.33 1.13 66 13.073 17.59
## C 2.08 1.13 66 -0.177 4.34
## D 4.92 1.13 66 2.656 7.18
## E 3.50 1.13 66 1.240 5.76
## F 16.67 1.13 66 14.406 18.93
##
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## A - B -0.833 1.6 66 -0.520 0.9952
## A - C 12.417 1.6 66 7.755 <.0001
## A - D 9.583 1.6 66 5.985 <.0001
## A - E 11.000 1.6 66 6.870 <.0001
## A - F -2.167 1.6 66 -1.353 0.7542
## B - C 13.250 1.6 66 8.276 <.0001
## B - D 10.417 1.6 66 6.506 <.0001
## B - E 11.833 1.6 66 7.391 <.0001
## B - F -1.333 1.6 66 -0.833 0.9603
## C - D -2.833 1.6 66 -1.770 0.4921
## C - E -1.417 1.6 66 -0.885 0.9489
## C - F -14.583 1.6 66 -9.108 <.0001
## D - E 1.417 1.6 66 0.885 0.9489
## D - F -11.750 1.6 66 -7.339 <.0001
## E - F -13.167 1.6 66 -8.223 <.0001
##
## P value adjustment: tukey method for comparing a family of 6 estimates## $emmeans
## spray emmean SE df lower.CL upper.CL
## A 14.50 1.13 66 12.240 16.76
## B 15.33 1.13 66 13.073 17.59
## C 2.08 1.13 66 -0.177 4.34
## D 4.92 1.13 66 2.656 7.18
## E 3.50 1.13 66 1.240 5.76
## F 16.67 1.13 66 14.406 18.93
##
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## A - B -0.833 1.6 66 -0.520 0.9981
## A - C 12.417 1.6 66 7.755 <.0001
## A - D 9.583 1.6 66 5.985 <.0001
## A - E 11.000 1.6 66 6.870 <.0001
## A - F -2.167 1.6 66 -1.353 0.8699
## B - C 13.250 1.6 66 8.276 <.0001
## B - D 10.417 1.6 66 6.506 <.0001
## B - E 11.833 1.6 66 7.391 <.0001
## B - F -1.333 1.6 66 -0.833 0.9827
## C - D -2.833 1.6 66 -1.770 0.6802
## C - E -1.417 1.6 66 -0.885 0.9773
## C - F -14.583 1.6 66 -9.108 <.0001
## D - E 1.417 1.6 66 0.885 0.9773
## D - F -11.750 1.6 66 -7.339 <.0001
## E - F -13.167 1.6 66 -8.223 <.0001
##
## P value adjustment: scheffe method with rank 5Looking at the output, we can see that while the p-values differ slightly for each adjustment method, the results don’t really change: A-B, A-F, B-F, C-D, C-E, and D-E do not differ from each other in any of the pairwise comparisons. The output contains two tables. The first, and smaller, table provides the mean, pooled standard error (SE), degrees of freedom, and upper and lower confidence intervals for the mean for each of the sprays. The second table is the pairwise comparisons, with the mean difference between each pair (estimate), along with the associated p-value.
9.4.3 Running each adjustment method separately
Below is how you can run each of the adjustment methods discussed above individually, and outside the emmeans() package.
Bonferroni
The Bonferroni adjustment for a pairwise comparison is accomplished using the pairwise.t.test() function and specifying which p-value adjustment method to use (p.adj = "bonf"). In the function below, we first specify what our DV is (bugs$count) followed by our grouping variable (bugs$spray). This time we needed to include bugs$ since there is not a data definition option within the function. Running this will give us a table of p-values between each possible comparison. The upper diagonal will be filled with “-” since it is a repeat of the lower diagonal.
##
## Pairwise comparisons using t tests with pooled SD
##
## data: bugs$count and bugs$spray
##
## A B C D E
## B 1 - - - -
## C 1.1e-09 1.3e-10 - - -
## D 1.5e-06 1.8e-07 1 - -
## E 4.1e-08 4.9e-09 1 1 -
## F 1 1 4.2e-12 6.1e-09 1.6e-10
##
## P value adjustment method: bonferroniLooking at the output, we can see that spray combinations A-B, A-F, B-F, C-D, C-E, and D-E do not differ from each other. The other combinations differ from each other with p < 0.001.
Tukey’s HSD
We can perform Tukey’s HSD adjustment on pairwise comparisons using the TukeyHSD() function from base R, but it can only be used on an aov() object (ie, it will work on our model_b1 but will not work on model_b2). This is also a base R function, so no libraries to call. To run this, we feed our aov model to the TukeyHSD() function (remember this is model_b1), followed by our desired confidence level (conf.level = .95).
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = count ~ spray, data = bugs)
##
## $spray
## diff lwr upr p adj
## B-A 0.8333333 -3.866075 5.532742 0.9951810
## C-A -12.4166667 -17.116075 -7.717258 0.0000000
## D-A -9.5833333 -14.282742 -4.883925 0.0000014
## E-A -11.0000000 -15.699409 -6.300591 0.0000000
## F-A 2.1666667 -2.532742 6.866075 0.7542147
## C-B -13.2500000 -17.949409 -8.550591 0.0000000
## D-B -10.4166667 -15.116075 -5.717258 0.0000002
## E-B -11.8333333 -16.532742 -7.133925 0.0000000
## F-B 1.3333333 -3.366075 6.032742 0.9603075
## D-C 2.8333333 -1.866075 7.532742 0.4920707
## E-C 1.4166667 -3.282742 6.116075 0.9488669
## F-C 14.5833333 9.883925 19.282742 0.0000000
## E-D -1.4166667 -6.116075 3.282742 0.9488669
## F-D 11.7500000 7.050591 16.449409 0.0000000
## F-E 13.1666667 8.467258 17.866075 0.0000000Looking at the output, we see that it is a slightly different format from the Bonferroni adjustment, and some additional information. This is in a table, with the pairs along the far left, the mean difference between them in the diff column, and the p-value in the far right column (p adj). We see a similar pattern as before, where spray pairs A-B, A-F, B-F, C-D, C-E, and D-E are not significantly different from one another and all other pairs being significantly different. Also notice that it is the same six pairs that are not significantly different from each other as we saw in the Bonferroni adjustment.
Scheffe adjustment
The Scheffe adjustment can be performed using the ScheffeTest() function from the DescTools package. As with the Tukey’s HSD test, an aov() model object is fed into the function; we cannot use a lm() model object. We also specify our grouping variable (g = spray).
##
## Attaching package: 'DescTools'## The following objects are masked from 'package:Hmisc':
##
## %nin%, Label, Mean, Quantile## The following object is masked from 'package:car':
##
## Recode## The following objects are masked from 'package:psych':
##
## AUC, ICC, SD##
## Posthoc multiple comparisons of means: Scheffe Test
## 95% family-wise confidence level
##
## $spray
## diff lwr.ci upr.ci pval
## B-A 0.8333333 -4.659440 6.326107 0.9981
## C-A -12.4166667 -17.909440 -6.923893 2.7e-08 ***
## D-A -9.5833333 -15.076107 -4.090560 2.1e-05 ***
## E-A -11.0000000 -16.492773 -5.507227 8.0e-07 ***
## F-A 2.1666667 -3.326107 7.659440 0.8699
## C-B -13.2500000 -18.742773 -7.757227 3.6e-09 ***
## D-B -10.4166667 -15.909440 -4.923893 3.1e-06 ***
## E-B -11.8333333 -17.326107 -6.340560 1.1e-07 ***
## F-B 1.3333333 -4.159440 6.826107 0.9827
## D-C 2.8333333 -2.659440 8.326107 0.6802
## E-C 1.4166667 -4.076107 6.909440 0.9773
## F-C 14.5833333 9.090560 20.076107 1.4e-10 ***
## E-D -1.4166667 -6.909440 4.076107 0.9773
## F-D 11.7500000 6.257227 17.242773 1.3e-07 ***
## F-E 13.1666667 7.673893 18.659440 4.4e-09 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The output looks very similar to the Tukey’s HSD output in that it is a table with the mean difference, upper and lower confidence intervals, and a p-value (pval). As before, spray pairs A-B, A-F, B-F, C-D, C-E, and D-E are not significantly different from one another while all other pairs are.
9.4.4 Custom contrasts
We can also perform custom comparisons using the emmeans package and the contrast() function. Since we had previously specified to run pairwise comparisons in our emmeans model, we re-specify our model to just have group statistics (emmeans(model_b1, "spray", data = bugs). We are also saving this as an object, for later use. We then specify the contrasts we want to run. As a reminder, within any individual contrast, the values must add up to zero. The contrasts I have as examples are as follows:
- A vs. the average of C & D
- B vs. C (silly since we did pairwise, but maybe this is the only pair you wanted to test)
- The average of A & B vs. the average of E & F
We first assign these planned contrasts to an object (plan_con here). Using the contrast() function, we first give it our model from emmeans() (b1.emm here). Then, we list our contrasts. These will all fall within list(), and you can have as many or as few as you like. Each one has a name (eg, c1), and then a vector of numbers that add up to zero. Since we have six sprays, we need to have six numbers. You can think of it as “c1 = c(A, B, C, D, E, F)” where you are putting values for each of the sprays.
After we define our contrasts, we then test them with the test() function. This takes the object containing the contrasts as an argument, and we tell it we don’t want any adjustments made.
#Restate our emmeans model - get rid of pairwise comparisons
b1.emm <- emmeans(model_b1, "spray", data = bugs)
#State the contrasts
plan_con <- contrast(b1.emm, list(c1 = c(1, 0, -0.5, -0.5, 0, 0), c2 = c(0, 1, -1, 0, 0, 0), c3 = c(0.5, 0.5, 0, 0, -0.5, -0.5)))
#Test the contrasts
test(plan_con, adjust = "none")## contrast estimate SE df t.ratio p.value
## c1 11.00 1.39 66 7.933 <.0001
## c2 13.25 1.60 66 8.276 <.0001
## c3 4.83 1.13 66 4.269 0.0001Looking at the output, we can see that all of the planned contrasts we chose as examples are significant. We would interpret contrast 1 (c1) as the mean of A is 11 units higher than the average of C and D, or after using the A spray there were 11 more insects remaining when compared to the average of insects remaining after using spray C and spray D.