Chapter 13 Mixed ANOVA
Packages used: datarium, psych, tidyverse, ggplot2, qqplotr, viridis, car, emmeans, afex, rstatix
The data:
We will be using the “anxiety” data set from the datarium package, which has anxiety score (as a DV), measured at three time points (within-subjects IV) on individuals in three different physical activity groups. The physical activity groups are basal, moderate, and high; in the dataframe they are grp1, grp2, and grp3, respectively. This is the same dataset used in the mixed ANOVA, but we will be modifying it slightly to illustrate ANCOVA procedures. After modifying it, the t1 data point will now be a “Basal” anxiety level (ie, the covariate), and t3 will be the post anxiety level (ie, treatment effect).
First, we’ll load the data in:
#Call datarium package
library(datarium)
#Assign data set to an object
anx <- anxiety
#See what it looks like
head(anx)## # A tibble: 6 × 5
## id group t1 t2 t3
## <fct> <fct> <dbl> <dbl> <dbl>
## 1 1 grp1 14.1 14.4 14.1
## 2 2 grp1 14.5 14.6 14.3
## 3 3 grp1 15.7 15.2 14.9
## 4 4 grp1 16 15.5 15.3
## 5 5 grp1 16.5 15.8 15.7
## 6 6 grp1 16.9 16.5 16.2As in the one-way within subjects ANOVA, in order to test our assumptions and perform the ANOVA, we will need to convert to long format. Or, we will need to gather all the time points into one column. There will still be a treatment column, and multiple rows per ID. We first define a new dataframe, se2_long, and assign our se2 dataframe to it. Then %>% sends the anx dataframe to the next line. gather() is from the tidyverse package and “gathers” a value across columns. We specify the “key” column name with key = "time", and what value we want created with value = "score". We then specify what columns we want “gathered” : t1, t2, t3.
We then need to convert the time column from a character column (something that R interprets as words) to a factor column (something that R interprets as different levels of one variable). The as.factor() function will allow us to do that, and takes as an argument the column you want to change (se2_long$time). Since we want the time column to be changed, we need to reassign the change back to the time column.
After doing all that, we check our work before moving on.
#Load tidyverse for modifications
library(tidyverse)
#Gather columns t1, t2 and t3 into long format
anx_long <- anx %>%
gather(key = "time", value = "score", t1, t2, t3)
#Convert time column to a factor
anx_long$time <- as.factor(anx_long$time)
#Check work
head(anx_long)## # A tibble: 6 × 4
## id group time score
## <fct> <fct> <fct> <dbl>
## 1 1 grp1 t1 14.1
## 2 2 grp1 t1 14.5
## 3 3 grp1 t1 15.7
## 4 4 grp1 t1 16
## 5 5 grp1 t1 16.5
## 6 6 grp1 t1 16.913.1 Descriptive Statistics
We will get descriptive statistics for each time point as well as each treatment group combination (so, 3 time points x 3 exercise groups = 9 tables!), using the describeBy() function from the psych package. We start by telling the function what we want summarized (anx_long$score). Then, since we have two variables we want combinations of, we include them both, separated by a colon: (anx_long$group : anx_long$time).
#Load psych package
library(psych)
#Get descriptive statistics by group
describeBy(anx_long$score,
group = anx_long$group : anx_long$time)##
## Descriptive statistics by group
## group: grp1:t1
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 15 17.09 1.63 17 17.11 1.33 14.1 19.8 5.7 -0.1 -0.83 0.42
## ------------------------------------------------------------------------------------------------------------
## group: grp1:t2
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 15 16.93 1.7 16.9 16.88 1.63 14.4 20 5.6 0.25 -1.08 0.44
## ------------------------------------------------------------------------------------------------------------
## group: grp1:t3
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 15 16.51 1.56 16.5 16.47 1.19 14.1 19.4 5.3 0.3 -0.74 0.4
## ------------------------------------------------------------------------------------------------------------
## group: grp2:t1
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 15 16.65 1.57 16.9 16.67 1.63 13.7 19.3 5.6 -0.2 -1.07 0.4
## ------------------------------------------------------------------------------------------------------------
## group: grp2:t2
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 15 16.47 1.69 16.9 16.52 1.93 13.4 18.9 5.5 -0.26 -1.4 0.44
## ------------------------------------------------------------------------------------------------------------
## group: grp2:t3
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 15 15.53 1.7 16.1 15.58 1.78 12.7 17.7 5 -0.32 -1.54 0.44
## ------------------------------------------------------------------------------------------------------------
## group: grp3:t1
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 15 17.01 1.32 17.3 17.05 1.33 14.6 19 4.4 -0.37 -1.16 0.34
## ------------------------------------------------------------------------------------------------------------
## group: grp3:t2
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 15 15.01 1.39 15.4 15.02 1.48 12.7 17.2 4.5 -0.24 -1.23 0.36
## ------------------------------------------------------------------------------------------------------------
## group: grp3:t3
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 15 13.56 1.42 13.8 13.61 1.93 11 15.5 4.5 -0.32 -1.34 0.37In the output, we can see there are the expected nine sets of descriptive statistics - one for each time point and group combination (ie, time 1-grp1, time 1-grp2, etc.). We get the mean score for each combination, along with the other statistics we are accustomed to. We can also use these outputs to confirm that there are the same number of responses for each time point - if there were not, this would indicate we were missing data.
A boxplot can be used to visually identify if there are outliers in any of the combinations. We will make a boxplot using ggplot2 and using viridis for our color scale. In the code below, we first define our data (data = anx_long) and x (x = time) and y (y = score) values. Our x value is our grouping variable (time) that we want on the x-axis, and our y value is the one we are comparing (scores). The next line calls the boxplot function (geom_boxplot()). We added the argument aes(color = group) to allow different colors per exercise group. geom_jitter() prints each data point as a dot on the box plot, and the argument aes(color = group) again color-codes the dots by treatment. The next line, scale_color_viridis(discrete = TRUE) assigns the viridis color scale to the colors in the plot, which is a colorblind friendly scale. discrete = TRUE is used because we are not using all continuous variables. The last line is a theme line, and addresses details such as plot background color.
#Call ggplot
library(ggplot2)
#Also call viridis
library(viridis)
#Generate a boxplot
ggplot(data = anx_long, aes(x = time, y = score)) +
geom_boxplot(aes(color = group)) +
geom_jitter(aes(color = group), width = .25) +
scale_color_viridis(discrete = TRUE) +
theme_bw()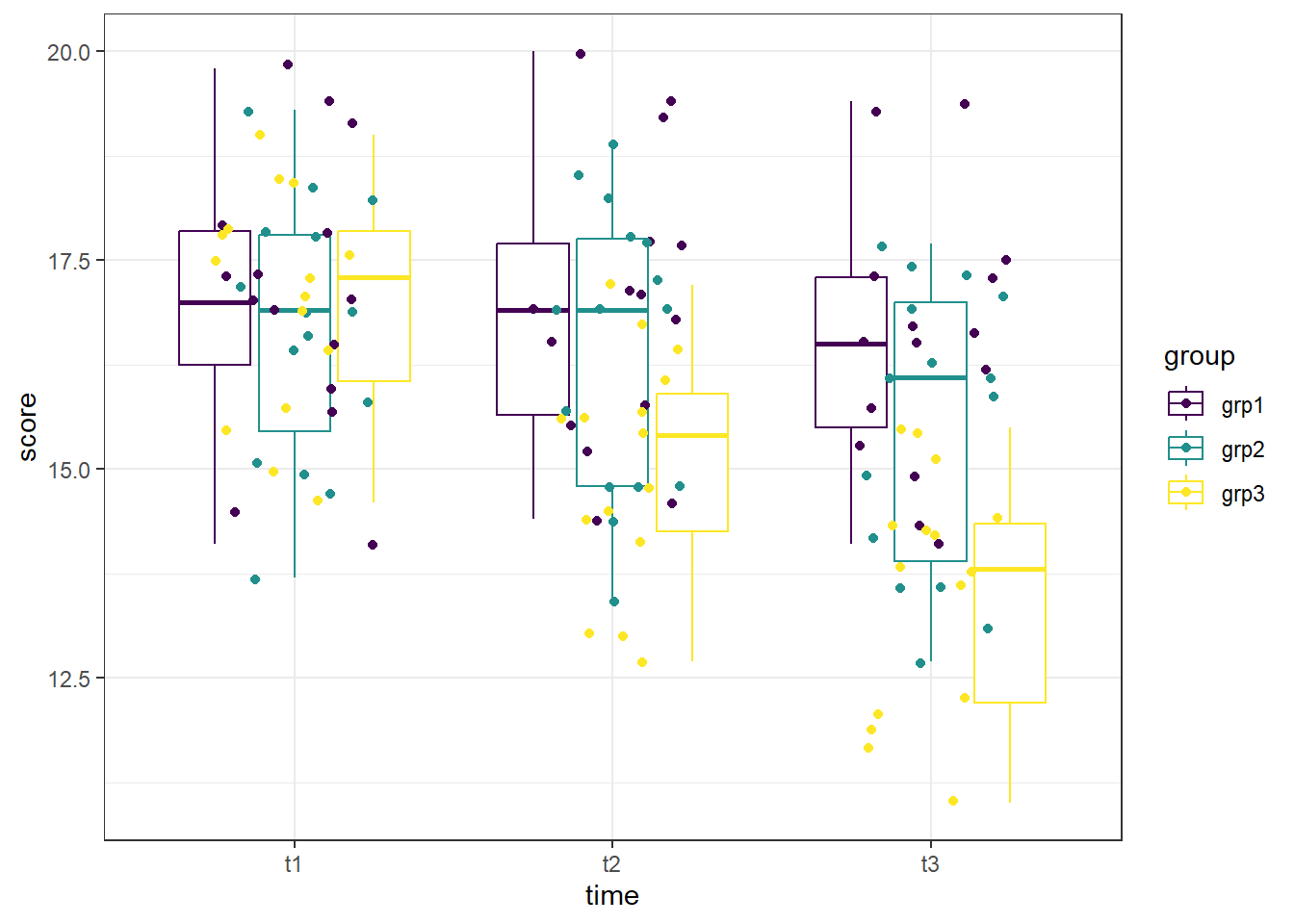
We can see that there does not appear to be any extreme outliers, as long as we are careful to color-match. This can get visually challenging, leading to errors in interpretation. Since each IV has three levels, switching which IV is the grouping variable and which is on the x-axis will not help in this case.
Another option for identifying outliers is to create the boxplot without the data points being shown, and instead use a function to determine if there are any extreme outliers, as we do below. The ggplot object is the same as above, except we removed the geom_point() line, which removed the individual data points. Next, we have a call to the rstatix package, which contains the identify_outliers() function. To get there, we first provide our data (anx_long), and send that (%>%) to the grouping function (group_by()) where we group by both time and exercise group. Then, we use the identify_outliers() function on the score to determine if there are any.
#Generate a boxplot - no dots this time
ggplot(data = anx_long, aes(x = time, y = score)) +
geom_boxplot(aes(color = group)) +
scale_color_viridis(discrete = TRUE) +
theme_bw()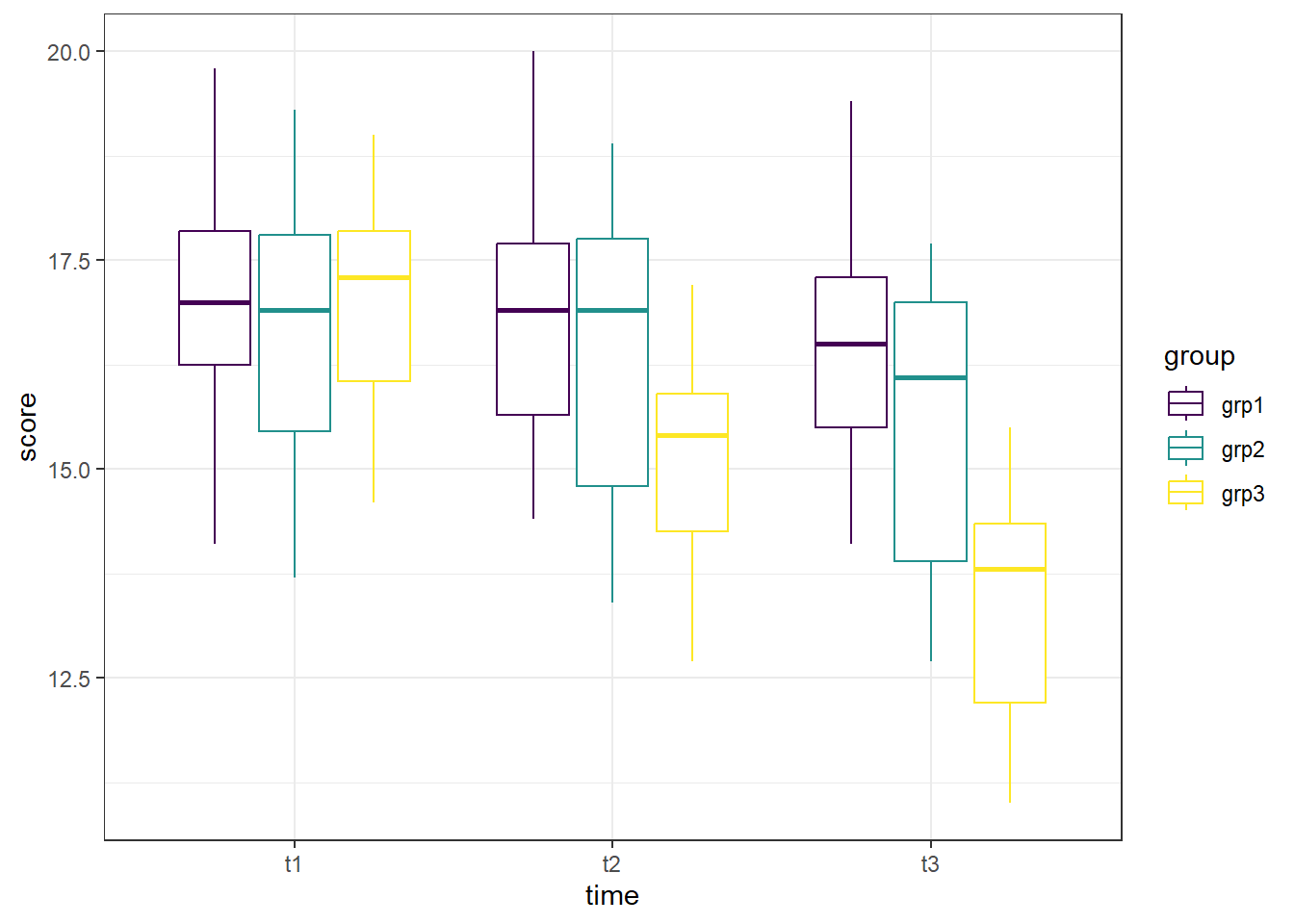
#Also test for extreme outliers
#Call rstatix package
library(rstatix)
#Test for outliers in each combination
anx_long %>%
group_by(time, group) %>%
identify_outliers(score)## [1] group time id score is.outlier is.extreme
## <0 rows> (or 0-length row.names)The graph is visually cleaner - no data points to compare to box plots. And the output for the identify_outliers() function is empty (<0 rows>). This means there are no extreme outliers in our data. If we compare that to what we could see in the first box plot, we can see they are in agreement.
13.2 Assumptions
We will be testing for meeting the assumption of normality, homogeneity of covariances, and sphericity.
Shapiro-Wilk
We will begin by running a Shapiro-Wilk test to test each combination of time and exercise group for normality. The shapiro.test() will allow us to get the test, though we will need to assign it to an object and ask for the information in a table. Specifically, we will be asking for the W statistic, or Shaprio-Wilk statistic, and the p-value from the test.
In the code below, we first call the tidyverse package to allow us to split by group before moving on to running the Shapiro-Wilk test. Then, we specify our data (anx_long) and send it on to the next line (%>%). The line group_by(time, group) takes our dataframe and groups it by both time and exercise group. Then, we send that on (%>%) to the Shapiro-Wilk test.
Running the Shapiro-Wilk test, we start with the summarise() function, and define what our columns will be. The first column is the Shapiro-Wilk statistic, named “S-W Statistic”, and we specify that the value in this column should be the statistic from the function: "S-W Statistic" = shapiro.test(score)$statistic. We see that we are calling the shapiro.test() function on the ‘score’ column (shapiro.test(score)), but then we are including $statistic because that’s the value from the Shapiro test we want in this column. In the second column we specify that the values should be the p-value from the shapiro.test() function: "p-value" = shapiro.test(score)$p.value.
#Call tidyverse
library(tidyverse)
#Run the Shapiro-Wilk test
anx_long %>%
group_by(time, group) %>%
summarise("S-W Statistic" = shapiro.test(score)$statistic,
"p-value" = shapiro.test(score)$p.value)## # A tibble: 9 × 4
## # Groups: time [3]
## time group `S-W Statistic` `p-value`
## <fct> <fct> <dbl> <dbl>
## 1 t1 grp1 0.964 0.769
## 2 t1 grp2 0.977 0.949
## 3 t1 grp3 0.954 0.588
## 4 t2 grp1 0.956 0.624
## 5 t2 grp2 0.935 0.328
## 6 t2 grp3 0.952 0.558
## 7 t3 grp1 0.949 0.506
## 8 t3 grp2 0.909 0.131
## 9 t3 grp3 0.925 0.232For each combination, p > 0.05, indicating that no distribution is significantly different than a normal distribution.
Histogram
We can also check the normality assumption visually, by generating histograms of each time-group combination. Given that we have nine possible combinations, we will be creating separate histograms for each.
We will use a stacked histogram, by adding the function facet_grid(time ~ group) to our ggplot object. This will generate one histogram per combination, in a grid layout rather than a truly “stacked” layout. This phrasing (time ~ group) is saying put the different times on the “y axis” of the overall grid, and different exercise groups along the “x axis” of the grid. If you’d like the grid to be inverted, with education level across the top and gender along the side, you would use gender ~ education_level. We also re-named the group labels to make them more human-readable; if we had not, we would need to rememeber what grp1, grp2, and grp3 represented. After reassigning names to an object with l <- c(grp1 = "basal", grp2 = "moderate", grp3 = "high"), we use the labeller argument to say what we would like renamed (labeller = labeller(group = l)). At the end, theme_minimal() is addressing how the graphs look - getting rid of the grey background, for example.
#Make more user-friendly labels
l <- c(grp1 = "basal", grp2 = "moderate", grp3 = "high")
#Generate side-by-side histograms
ggplot(data = anx_long, aes(x = score)) +
geom_histogram() +
facet_grid(time ~ group, labeller = labeller(group = l)) +
theme_minimal()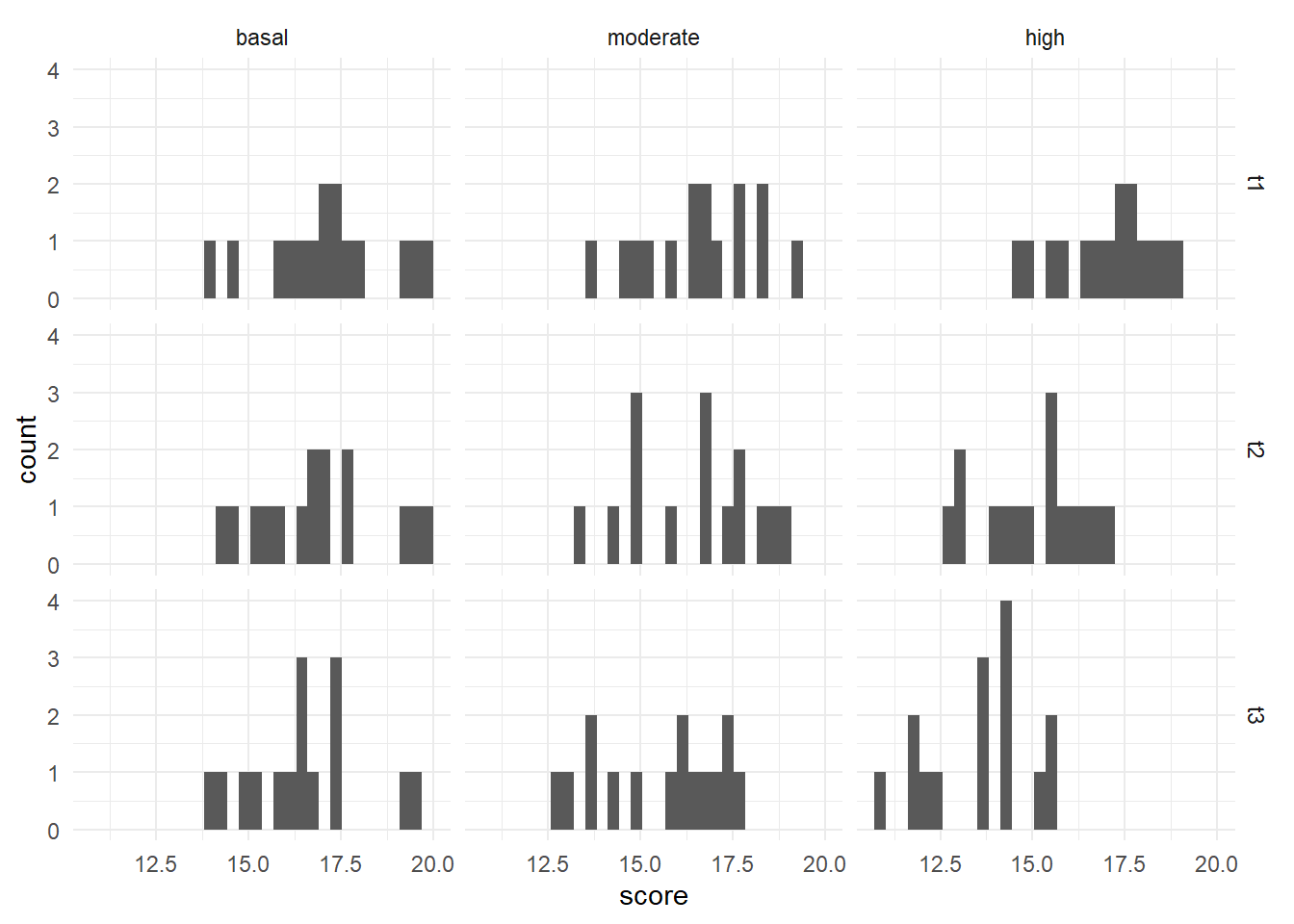
These histograms show that, visually, all the different combinations seem to be normally distributed.
QQ Plot
Another visual inspection for normality we can do is a Q-Q plot. We will use the package qqplotr to make these, as an addition to ggplot2.
Breaking down the code we will use to generate the plot:
1. ggplot(data = job, mapping = aes(sample = score, color = education_level, fill = education_level)) + is our call to ggplot. We are defining what data to use (data = job), and then giving some arguments to the aes() function. sample = score says to use the variable ‘score’, color = education_level is asking for each of the educational levels to be a different color, and fill = education_level corresponds to the filled in portion, again different colors for each educational level. To ensure colorblind friendliness, we will specify a particular color scale below.
2. stat_qq_band(alpha=0.5, conf=0.95, qtype=1, bandType = "ts") + is our first function using the qqploter package, and contains arguments about the confidence bands. This is defining the alpha level (alpha = 0.5) and the confidence interval (conf = 0.95) to use for the confidence bands. bandType = "pointwise" is saying to construct the confidence bands based on Normal confidence intervals.
3. stat_qq_line(identity = TRUE) + is another call to the qqplottr package and contains arguments about the line going through the qq plot. The argument identity = TRUE says to use the identity line as the reference to construct the confidence bands around.
4. stat_qq_point(col = "black") + is the last call to the qqplottr package and contains arguments about the data points. col = "black" means we’d like them to be black.
5. facet_grid((time ~ group), scales = "free", labeller = labeller(group = l)) + uses facet_grid rather than facet_wrap, as we have been, to better label our plots. This is sorting by time and exercise group combination (time ~ group), and creating a qq plot for each of the different combinations. The scales = "free" refers to the scales of the axes; by setting them to “free” we are allowing them to freely vary between each of the graphs. If you want the scale to be fixed, you would use scale = "fixed". We are again using the same labelling argument from the histograms for readability (labeller = labeller(group = l))). Since we have already set the labels above, we do not need to reset them here.
6. labs(x = "Theoretical Quantiles", y = "Sample Quantiles") + is a labeling function. Here, we are labeling the x and y axis (x = and y = respectively).
7. scale_fill_viridis(discrete = TRUE) is specifying a color fill that is colorblind friendly as well as grey-scale friendly. Since these are discrete groups, we add discrete = TRUE.
8. scale_color_viridis(discrete = TRUE) is again using a colorblind friendly scale for the outlines, to match the fill.
9. Lastly, theme_bw() is giving an overall preset theme to the graphs - this touches on things such as background, axis lines, grid lines, etc.
#Call qqplotr
library(qqplotr)
#Call viridis
library(viridis)
#Perform QQ plots for each combination
ggplot(data = anx_long, mapping = aes(sample = score, color = group, fill = group)) +
stat_qq_band(alpha = 0.5, conf = 0.95, bandType = "pointwise") +
stat_qq_line(identity = TRUE) +
stat_qq_point(col = "black") +
facet_grid((time ~ group), scales = "free", labeller = labeller(group = l)) +
labs(x = "Theoretical Quantiles", y = "Sample Quantiles") +
scale_fill_viridis(discrete = TRUE) +
scale_color_viridis(discrete = TRUE) +
theme_bw()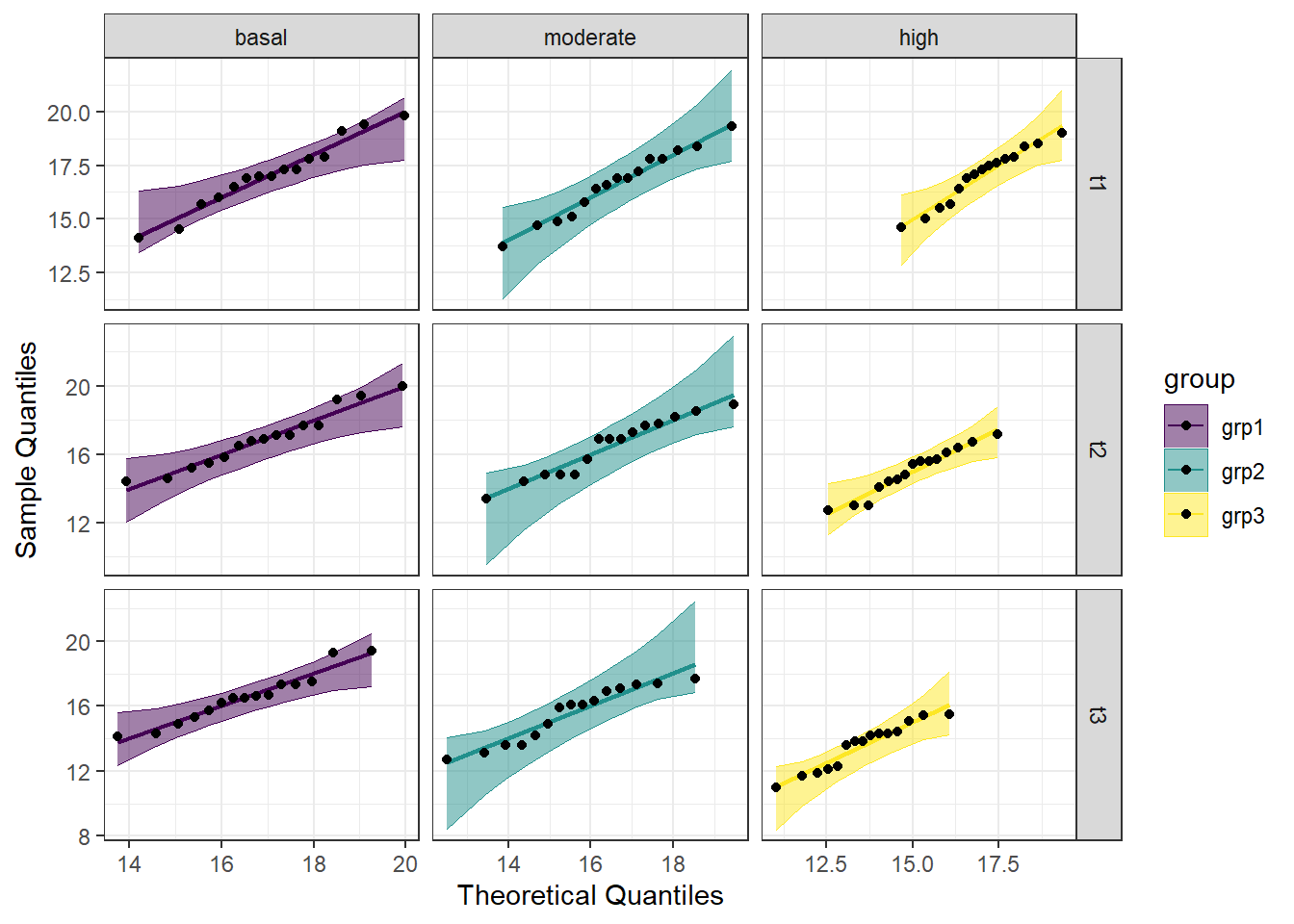
Looking at the Q-Q plot, we can see that all the data points fall within the 95% range, as well as falling pretty neatly along the trend line. The colors aren’t critical here, but it does make it nicer to look at.
Detrended QQ Plot
We can also make a detrended Q-Q plot using the same code but adding detrend = TRUE to all of the stat_qq_ functions.
#Perform detrended QQ plots for each combination
ggplot(data = anx_long, mapping = aes(sample = score, color = group, fill = group)) +
stat_qq_band(alpha = 0.5, conf = 0.95, bandType = "pointwise", detrend = TRUE) +
stat_qq_line(identity = TRUE, detrend = TRUE) +
stat_qq_point(col = "black", detrend = TRUE) +
facet_grid((time ~ group), scales = "free", labeller = labeller(group = l)) +
labs(x = "Theoretical Quantiles", y = "Sample Quantiles") +
scale_fill_viridis(discrete = TRUE) +
scale_color_viridis(discrete = TRUE) +
theme_bw()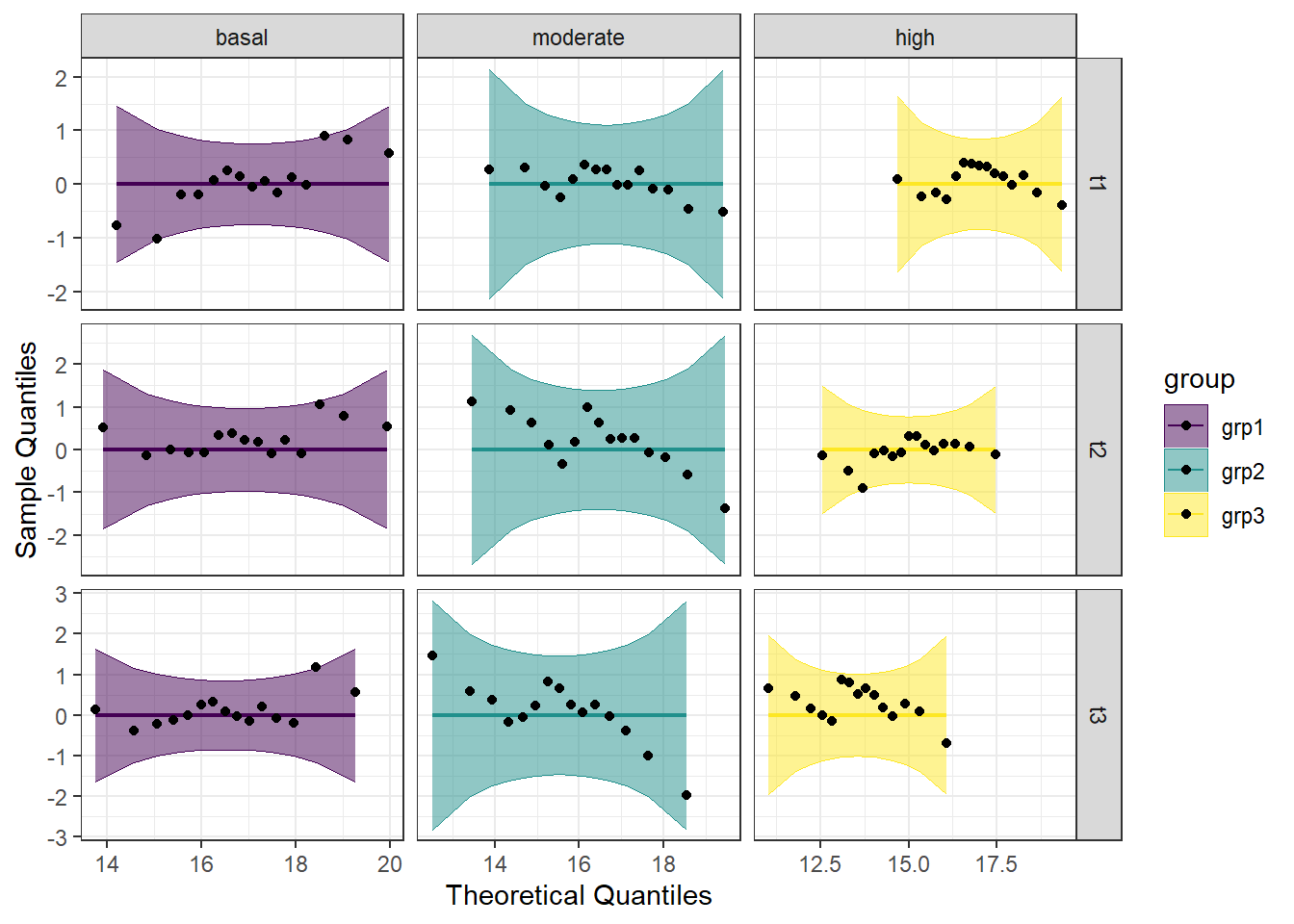
Looking at both the regular and detrended Q-Q plots, we can see that all of the educational level and gender combinations are normally distributed.
13.2.2 Homogeneity of Covariances
We will be testing homogeneity of covariances using Box’s M test, and it will require us to use our original data set (anx) in the wide format. The rstatix package has the box_m() function that will perform the test, and we only need to provide the data and the grouping variable. We only want to perform this on only the time columns of our data, so the data argument looks like anx[, 3:5]. This is saying we want the anx dataset, all rows (the empty bit before the “,”), but only the third through fifth columns ([, 3:5]). If you look back at our wide-format data, the time columns (t1 - t3) are columns 3-5.
## # A tibble: 1 × 4
## statistic p.value parameter method
## <dbl> <dbl> <dbl> <chr>
## 1 5.33 0.946 12 Box's M-test for Homogeneity of Covariance MatricesThe test is not significant, indicating that we do not reject the null hypothesis that the observed covariance matrices of the DV are equal across groups. In other words, the assumption of homogeneity of covariances has been met.
13.3 Run the Mixed ANOVA
We will use the aov_car() function from the afex package to run the omnibus test.
#Call the afex package
library(afex)
#Perform the ANOVA
model_anx <- aov_car(score ~ (time*group) + Error(id/time),
data = anx_long)
#Get the output
summary(model_anx)##
## Univariate Type III Repeated-Measures ANOVA Assuming Sphericity
##
## Sum Sq num Df Error SS den Df F value Pr(>F)
## (Intercept) 34919 1 299.146 42 4902.6660 < 2e-16 ***
## group 62 2 299.146 42 4.3518 0.01916 *
## time 67 2 7.081 84 394.9095 < 2e-16 ***
## group:time 37 4 7.081 84 110.1876 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Mauchly Tests for Sphericity
##
## Test statistic p-value
## time 0.88364 0.079193
## group:time 0.88364 0.079193
##
##
## Greenhouse-Geisser and Huynh-Feldt Corrections
## for Departure from Sphericity
##
## GG eps Pr(>F[GG])
## time 0.89577 < 2.2e-16 ***
## group:time 0.89577 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## HF eps Pr(>F[HF])
## time 0.9330916 1.037156e-40
## group:time 0.9330916 1.461019e-30We can first look at Mauchly tests for sphericity, and we see that it is not significant, satisfying the assumption of sphericity. Had we needed them, the Greenhouse-Geiser and Huynh_Feldt appear below the Mauchly tests of sphericity. If we needed an ANOVA table with the corrections, we could do anova(model_anx, correction = "GG").
Next, we can look at the ANVOA table. This provides the SS, df, F-value, and p-value for each of the main effects as well as the interaction. Looking first at the interaction (group:time), we can see that it is significant (p < .001).
13.3.1 Estimated Means
We can examine the estimated marginal means, using the emmeans() function from the emmeans package.
Even though we are only looking at the estimated means for now, we still run the emmeans() function, saving it as an object. The first argument is the ANOVA model object from the afex package (model_anx). We then specify on what variable we would like the means. Notice there are three different models we are making: one for means by time, one for means by group, and one for means for the interaction (each combination of time and group). We then call the models to visualize the means.
#Call emmeans
library(emmeans)
#Calculate estimated marginal means
anx_em_time <- emmeans(model_anx, specs = ~time)
anx_em_group <- emmeans(model_anx, specs = ~group)
anx_em_time_group <- emmeans(model_anx, specs = ~time*group)
#Look at the estimated means
anx_em_time## time emmean SE df lower.CL upper.CL
## t1 16.9 0.225 42 16.5 17.4
## t2 16.1 0.238 42 15.7 16.6
## t3 15.2 0.233 42 14.7 15.7
##
## Results are averaged over the levels of: group
## Confidence level used: 0.95## group emmean SE df lower.CL upper.CL
## grp1 16.8 0.398 42 16.0 17.6
## grp2 16.2 0.398 42 15.4 17.0
## grp3 15.2 0.398 42 14.4 16.0
##
## Results are averaged over the levels of: time
## Confidence level used: 0.95## time group emmean SE df lower.CL upper.CL
## t1 grp1 17.1 0.390 42 16.3 17.9
## t2 grp1 16.9 0.413 42 16.1 17.8
## t3 grp1 16.5 0.404 42 15.7 17.3
## t1 grp2 16.6 0.390 42 15.9 17.4
## t2 grp2 16.5 0.413 42 15.6 17.3
## t3 grp2 15.5 0.404 42 14.7 16.3
## t1 grp3 17.0 0.390 42 16.2 17.8
## t2 grp3 15.0 0.413 42 14.2 15.8
## t3 grp3 13.6 0.404 42 12.7 14.4
##
## Confidence level used: 0.95The output from the above code shows three tables with the estimated mean self esteem score for each time point, group, or combination (emmean column), as well as the standard error, degrees of freedom, and upper and lower confidence intervals.
13.3.2 Interaction Plot
We can also plot the interaction, to visually see how the estimated mean anxiety scores vary both at each time point, and to compare the different groups.
We will use ggplot() to plot. Breaking down the code below by line:
1. ggplot() is the main function, and gets fed what the data is (data = as.data.frame(model_anx_time_group)). You may notice the extra wrapper around our data this time, the as.data.frame(). This is because the estimated means table from the emmeans() function is not a dataframe, and ggplot only takes dataframes. This wrapper changes the object into a dataframe. The other argument on this line is defining our x and y values (aes(x = time, y = emmean)). 2. geom_line(aes(color = group, group = group)) is what allows our individual data points to be connected by a line. The aes(color = group, group = group) argument is telling the line graph how our data is grouped and what to connect. Since there are two different treatments, it is helpful to have each one a different color.
3. geom_point() is a scatterplot function, and creates the individual data points you will see on the graph. This needs no additional arguments.
4. scale_color_viridis(discrete = TRUE) calls the viridis color scale for accessibility. discrete = TRUE is needed, as we are not supplying a continuous set of data, but rather individual values from our emmeans object.
5. theme_bw() addresses the overall theme of the plot - removing the grey background, for example.
#Plot estimated marginal means
ggplot(data = as.data.frame(anx_em_time_group), aes(x = time, y = emmean)) +
geom_line(aes(color = group, group = group)) +
geom_point(aes(color = group)) +
scale_color_viridis(discrete = TRUE) +
theme_bw()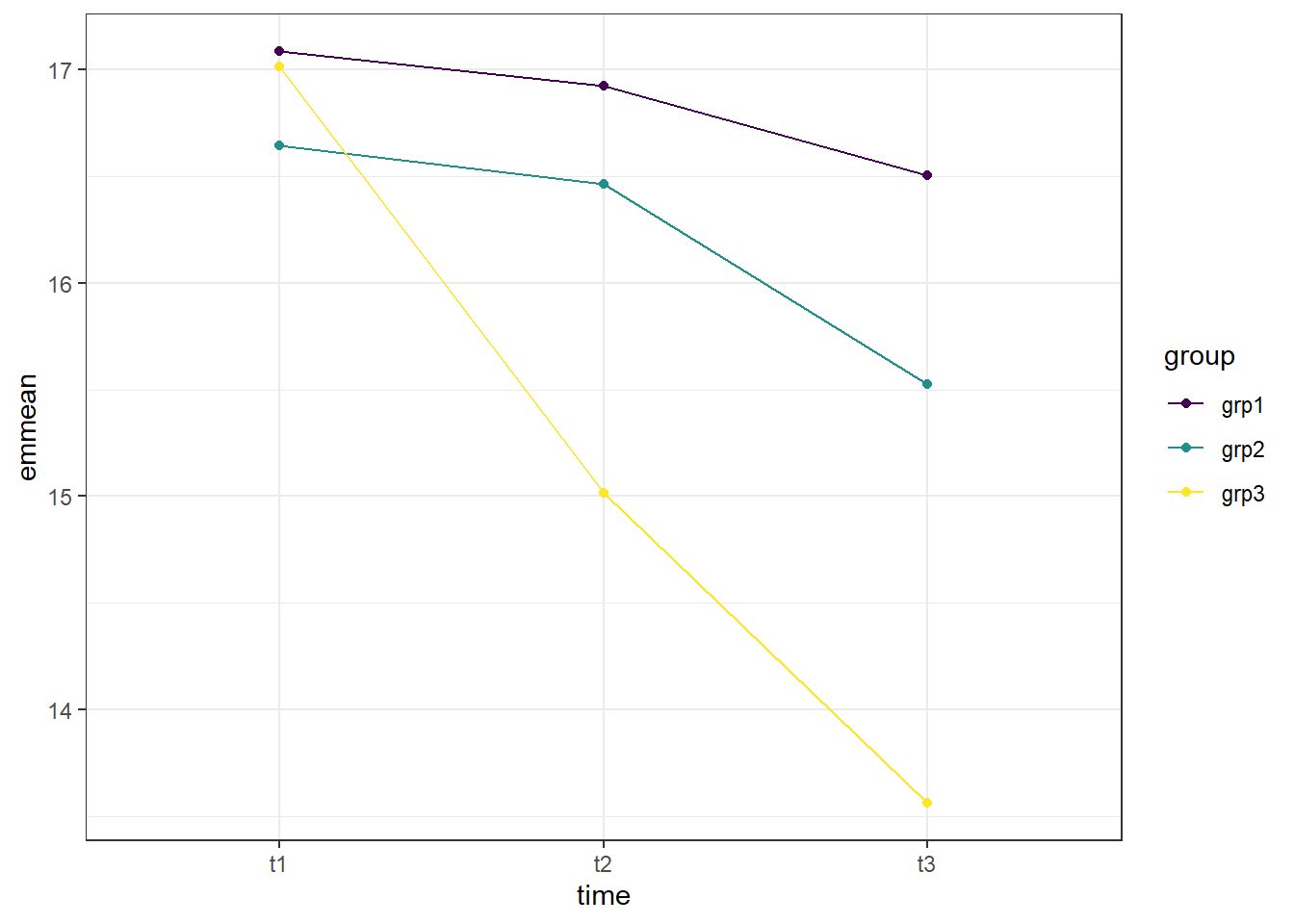
13.4 Post-hoc testing
The diagram below is a guide to which tests to pursue depending on what tests are significant. We always start with the interaction effect, and ask if it is significant or not. That will then guide our choices. The sections below are laid out with the same headings as the chart - pick the one(s) that suits your analysis, and proceed. The sections are laid out in such a way that the tests for an interaction effect are first (ie, simple main effects, and simple comparisons) followed by tests for a non-significant interaction. NOTE: I am using the same data for all the tests; this is for illustration purposes only! You would not run every test in “real life” - choose only the tests that are appropriate for your analysis.
Simple Main Effect of Group
We can determine the simple main effect of group on anxiety scores by seeing how it differs at each time point.
Breaking down the calculation line by line:
1. sme_treat_anx <- anx_long %>% to start, we are defining what data to use (se2_long), and assigning the whole thing to an object (sme_treat_se2). The %>% then sends it on to the next line.
2. group_by(time) %>% this is grouping by the different time points. So, gathering all the time 1 scores together, etc.
3. anova_test(score ~ group) %>% is the actual ANOVA test. As before, we supply it with the formula we want it to use: score ~ group. Since group is the between subjects IV, we do not need to specify Error(id/IV).
4. get_anova_table() %>% requests an ANOVA table from the anova_test() function above.
5. adjust_pvalue(method = "bonferroni") performs the adjustment to the p-values. The method chosen here is bonferroni; Tukey and Scheffe are not options with this function.
#Call Rstatix package
library(rstatix)
#Calculate simple main effect of group
sme_group_anx <- anx_long %>%
group_by(time) %>%
anova_test(score ~ group) %>%
get_anova_table() %>%
adjust_pvalue(method = "bonferroni")
#Call the output table
sme_group_anx## # A tibble: 3 × 9
## time Effect DFn DFd F p `p<.05` ges p.adj
## <fct> <chr> <dbl> <dbl> <dbl> <dbl> <chr> <dbl> <dbl>
## 1 t1 group 2 42 0.365 0.696 "" 0.017 1
## 2 t2 group 2 42 5.84 0.006 "*" 0.218 0.018
## 3 t3 group 2 42 13.8 0.0000248 "*" 0.396 0.0000744Looking at the table above, we can see that the effect of exercise group on anxiety score at time 1 is not significant (p = 0.69), but the effect of exercise group on anxiety score at time 2 and time 3 is significant. To determine between which exercise group levels the difference occurs, we would need to do simple comparisons.
Simple Main Effect of Time
We can also calculate the simple main effect of time, looking at the effect of time on the anxiety score by seeing how it differs at each exercise group level. Notice how since time is a within subjects IV, we need to add back in the + Error(id/time) component.
#Call Rstatix package (we just did above; for illustrative purposes here)
library(rstatix)
#Calculate simple main effect of treatment
sme_time_anx <- anx_long %>%
group_by(group) %>%
anova_test(score ~ time + Error(id/time)) %>%
get_anova_table() %>%
adjust_pvalue(method = "bonferroni")
#Call the output table
sme_time_anx## # A tibble: 3 × 9
## group Effect DFn DFd F p `p<.05` ges p.adj
## <fct> <chr> <dbl> <dbl> <dbl> <dbl> <chr> <dbl> <dbl>
## 1 grp1 time 2 28 14.8 4.05e- 5 * 0.024 1.21e- 4
## 2 grp2 time 2 28 77.5 3.88e-12 * 0.086 1.16e-11
## 3 grp3 time 2 28 490. 1.64e-22 * 0.531 4.92e-22Here, we can see that there is a significant effect of time on anxiety score on all three exercise groups. Since there is more than one level of time, we will proceed to simple comparisons to determine where the difference is in the control group.
13.4.2 Simple comparisons
Simple comparisons are performed just like pairwise comparisons were performed in a one-way within subjects ANOVA.
The code below is similar to the code above: we first call our data set, and assign it to an object. Then, we group by exercise group, before performing the pairwise t-test (pairwise_t_test()). The arguments for this function include the formula to use (score ~ time), paired = TRUE for the within subjects portion, and what adjustment method to use (p.adjust.method = "bonferroni").
#Simple comparisons for time
sc_anx <- anx_long %>%
group_by(group) %>%
pairwise_t_test(
score ~ time,
paired = TRUE,
p.adjust.method = "bonferroni"
)
#Call the summary
sc_anx## # A tibble: 9 × 11
## group .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif
## * <fct> <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <chr>
## 1 grp1 score t1 t2 15 15 2.01 14 6.5 e- 2 1.94e- 1 ns
## 2 grp1 score t1 t3 15 15 4.38 14 6.3 e- 4 2 e- 3 **
## 3 grp1 score t2 t3 15 15 3.77 14 2 e- 3 6 e- 3 **
## 4 grp2 score t1 t2 15 15 1.82 14 9 e- 2 2.68e- 1 ns
## 5 grp2 score t1 t3 15 15 10.5 14 5.02e- 8 1.51e- 7 ****
## 6 grp2 score t2 t3 15 15 11.3 14 2.04e- 8 6.12e- 8 ****
## 7 grp3 score t1 t2 15 15 19.1 14 1.99e-11 5.97e-11 ****
## 8 grp3 score t1 t3 15 15 27.1 14 1.72e-13 5.16e-13 ****
## 9 grp3 score t2 t3 15 15 14.8 14 5.93e-10 1.78e- 9 ****In the table above, we got a breakdown of each time by all three exercise groups options. We see that for exercise groups 1 and 2, the mean anxiety score was significantly different between time point 2 and 3, as well as for time point 1 and 3. The mean anxiety score was not significantly different between time point 1 and 2 for these exercise groups. For exercise group 3, the mean anxiety score was significantly different between all time point combinations.
13.4.3 Main Effects
If the interaction is not significant, we then look to the main effects. This is found in the main ANOVA table we ran above. As a reminder, it is reproduced below:
##
## Univariate Type III Repeated-Measures ANOVA Assuming Sphericity
##
## Sum Sq num Df Error SS den Df F value Pr(>F)
## (Intercept) 34919 1 299.146 42 4902.6660 < 2e-16 ***
## group 62 2 299.146 42 4.3518 0.01916 *
## time 67 2 7.081 84 394.9095 < 2e-16 ***
## group:time 37 4 7.081 84 110.1876 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Mauchly Tests for Sphericity
##
## Test statistic p-value
## time 0.88364 0.079193
## group:time 0.88364 0.079193
##
##
## Greenhouse-Geisser and Huynh-Feldt Corrections
## for Departure from Sphericity
##
## GG eps Pr(>F[GG])
## time 0.89577 < 2.2e-16 ***
## group:time 0.89577 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## HF eps Pr(>F[HF])
## time 0.9330916 1.037156e-40
## group:time 0.9330916 1.461019e-30As we have indicated, since the interaction is significant, we would perform other tests. However, had the interaction NOT been significant, we would then look at the main effect of time and the main effect for exercise group. Specifically, these rows:
We can see that both time and group have significant main effects, meaning we would then proceed to marginal comparisons.
13.4.4 Marginal Comparisons
To do marginal comparisons (used when the interaction is not significant, but the main effect(s) are), we will be using the pairwise_t_test(), which is in base R (ie, comes standard with R - no packages to declare). We define an object first, followed by our data (anx_long). Then we run the pairwise test (pairwie_t_test()) on the desired main effect. We set that with the formula: score ~ group will provide marginal comparisons for a significant main effect of treatment while score ~ time will provide marginal comparisons for a significant main effect of time. For time, we need indicate that this is a paired test (paired = TRUE); this is not necessary for group. Last, we define our desired p-value adjustment method (p.adjust.method = "bonferroni").
Treatment
#Do pairwise comparisons for group
mc_group <- anx_long %>%
pairwise_t_test(
score ~ group,
p.adjust.method = "bonferroni")
#Call the table
mc_group## # A tibble: 3 × 9
## .y. group1 group2 n1 n2 p p.signif p.adj p.adj.signif
## * <chr> <chr> <chr> <int> <int> <dbl> <chr> <dbl> <chr>
## 1 score grp1 grp2 45 45 0.094 ns 0.282 ns
## 2 score grp1 grp3 45 45 0.0000199 **** 0.0000597 ****
## 3 score grp2 grp3 45 45 0.00701 ** 0.021 *We see that the pairwise comparison between group 1 and 2 was not significant, but the comparisons between group 2 and 3, as well as between group 1 and 3, were significant.
Time
Since this is the within subjects IV, notice that we included paired = TRUE. This will also slightly change the look of the table produced.
#Do pairwise comparisons for time
mc_time <- anx_long %>%
pairwise_t_test(
score ~ time,
paired = TRUE,
p.adjust.method = "bonferroni")
#Call the table
mc_time## # A tibble: 3 × 10
## .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif
## * <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <chr>
## 1 score t1 t2 45 45 5.55 44 1.56e- 6 4.68e- 6 ****
## 2 score t1 t3 45 45 8.58 44 6.11e-11 1.83e-10 ****
## 3 score t2 t3 45 45 11.1 44 2.3 e-14 6.90e-14 ****Looking at the table, we can see that all pairwise comparisons are significant at p < .001.