4 Independence of Events

Example 4.1 Consider the following hypothetical data.

	Democrat ($D$)	Not Democrat ($D^c$)	Total
Loves puppies ($L$)	180	270	450
Does not love puppies ($L^c$)	20	30	50
Total	200	300	500

Suppose a person is randomly selected from this group. Consider the events \[\begin{align*} L & = \{\text{person loves puppies}\}\\ D & = \{\text{person is a Democrat}\} \end{align*}\]

Compute and interpret $\text{P}(L)$.
Compute and interpret $\text{P}(L|D)$.
Compute and interpret $\text{P}(L|D^c)$.
What do you notice about $\text{P}(L)$, $\text{P}(L|D)$, and $\text{P}(L|D^c)$?
Compute and interpret $\text{P}(D)$.
Compute and interpret $\text{P}(D|L)$.
Compute and interpret $\text{P}(D|L^c)$.
What do you notice about $\text{P}(D)$, $\text{P}(D|L)$, and $\text{P}(D|L^c)$?
Compute and interpret $\text{P}(D \cap L)$.
What is the relationship between $\text{P}(D \cap L$) and $\text{P}(D)$ and $\text{P}(L)$?
When randomly selecting a person from this particular group, would you say that events $D$ and $L$ are independent? Why?

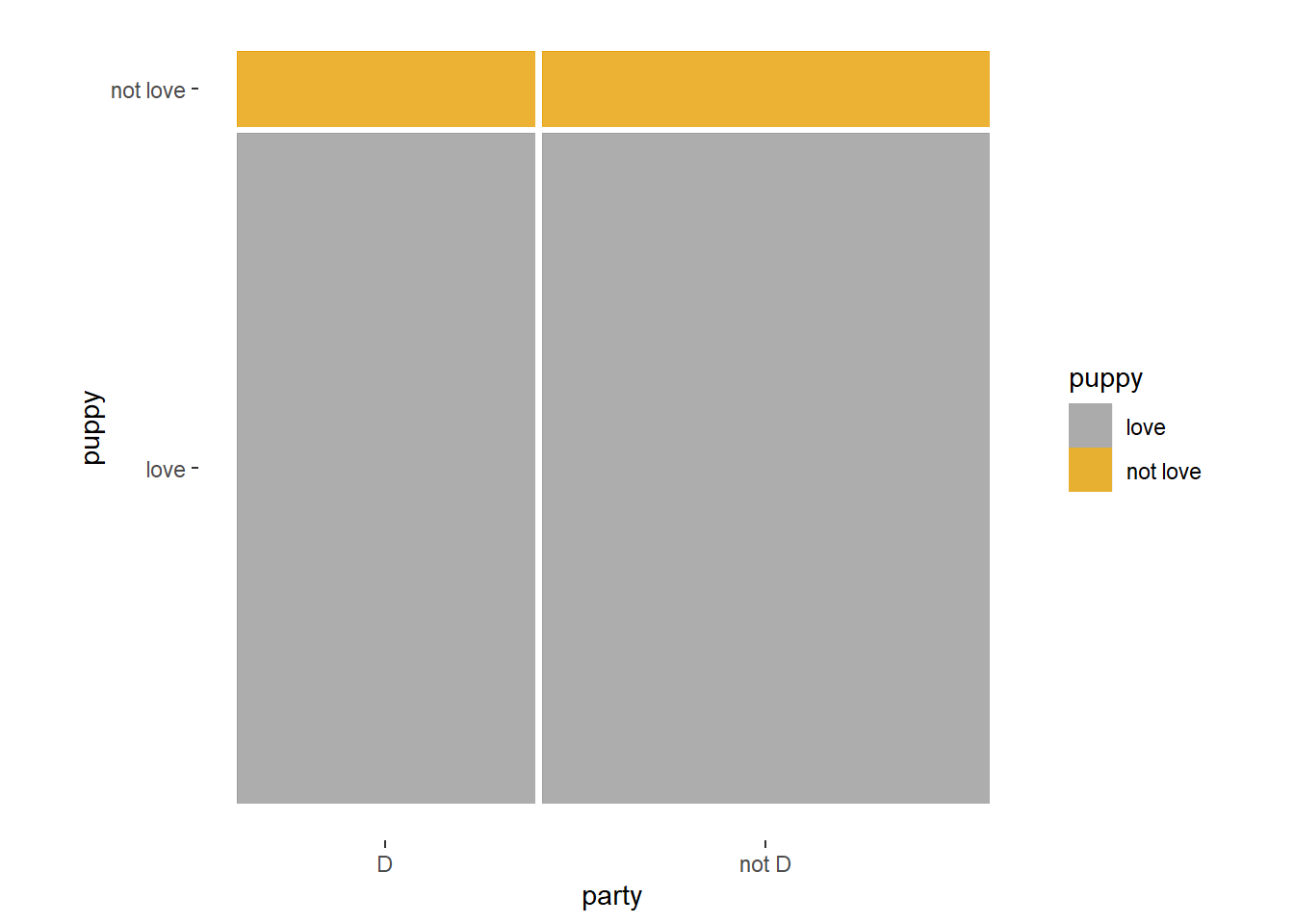
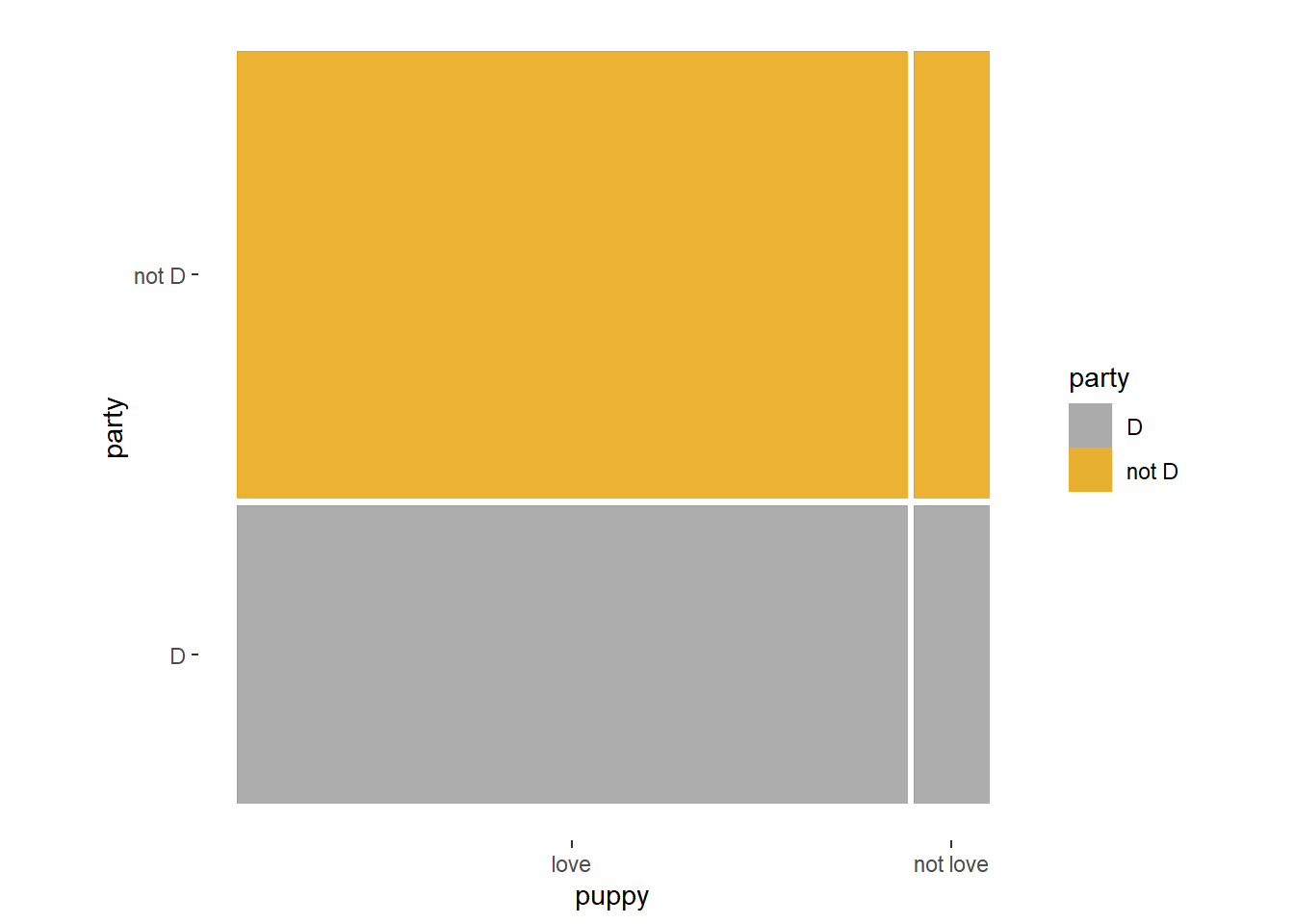
Events $A$ and $B$ are independent if the knowing whether or not one occurs does not change the probability of the other.
For events $A$ and $B$ (with $0<\text{P}(A)<1$ and $0<\text{P}(B)<1$) the following are equivalent. That is, if one is true then they all are true; if one is false, then they all are false.

\[\begin{align*} \text{$A$ and $B$} & \text{ are independent}\\ \text{P}(A \cap B) & = \text{P}(A)\text{P}(B)\\ \text{P}(A^c \cap B) & = \text{P}(A^c)\text{P}(B)\\ \text{P}(A \cap B^c) & = \text{P}(A)\text{P}(B^c)\\ \text{P}(A^c \cap B^c) & = \text{P}(A^c)\text{P}(B^c)\\ \text{P}(A|B) & = \text{P}(A)\\ \text{P}(A|B) & = \text{P}(A|B^c)\\ \text{P}(B|A) & = \text{P}(B)\\ \text{P}(B|A) & = \text{P}(B|A^c) \end{align*}\]

Example 4.2 A certain system consists of four identical components. Suppose that the probability that any particular component fails is 0.1, and failures of the components occur independently of each other. Find the probability that the system fails if:

The components are connected in parallel: the system fails only if all of the components fail.
The components are connected in series: the system fails whenever at least one of the components fails.
Donny Don’t says the answer to the previous part is $0.1 + 0.1 + 0.1 + 0.1 = 0.4$. Explain the error in Donny’s reasoning.

Events $A_1, A_2, A_3, \ldots$ are independent if:
- any pair of events $A_i, A_j, (i \neq j)$ satisfies $\text{P}(A_i\cap A_j)=\text{P}(A_i)\text{P}(A_j)$,
- and any triple of events $A_i, A_j, A_k$ (distinct $i,j,k$) satisfies $\text{P}(A_i\cap A_j\cap A_k)=\text{P}(A_i)\text{P}(A_j)\text{P}(A_k)$,
- and any quadruple of events satisfies $\text{P}(A_i\cap A_j\cap A_k \cap A_m)=\text{P}(A_i)\text{P}(A_j)\text{P}(A_k)\text{P}(A_m)$,
- and so on.
Intuitively, a collection of events is independent if knowing whether or not any combination of the events in the collection occur does not change the probability of any other event in the collection.
When events are independent, the multiplication rule simplifies greatly. \[ \text{P}(A_1 \cap A_2 \cap A_3 \cap \cdots \cap A_n) = \text{P}(A_1)\text{P}(A_2)\text{P}(A_3)\cdots\text{P}(A_n) \quad \text{if $A_1, A_2, A_3, \ldots, A_n$ are independent} \]
When a problem involves independence, you will want to take advantage of it. Work with “and” events whenever possible in order to use the multiplication rule. For example, for problems involving “at least one” (an “or” event) take the complement to obtain “none” (an “and” event).

Example 4.3 In the Powerball lottery, a player picks five different whole numbers between 1 and 69, and another whole number between 1 and 26 that is called the Powerball. In the drawing, the 5 numbers are drawn without replacement from a “hopper” with balls labeled 1 through 69, but the Powerball is drawn from a separate hopper with balls labeled 1 through 26. The player wins the jackpot if both the first 5 numbers match those drawn, in any order, and the Powerball is a match. Under this set up, there are 292,201,338 possible winning numbers.

What is the probability the next winning number is 6-7-16-23-26, plus the Powerball number, 4.
What is the probability the next winning number is 1-2-3-4-5, plus the Powerball number, 6.
The Powerball drawing happens twice a week. Suppose you play the same Powerball number, twice a week, every week for over 50 years. Let’s say you purchase a ticket for 6000 drawings in total. What is the probability that you win at least once?
Instead of playing for 50 years, you decide only to play one lottery, but you buy 6000 tickets, each with a different Powerball number. What is the probability that at least one of your tickets wins? How does this compare to the previous part? Why?
Each ticket costs 2 dollars, but the jackpot changes from drawing to drawing. Suppose you buy 6000 tickets for a single drawing. How large does the jackpot need to be for your “expected” profit to be positive? To be $100,000? (We’re ignoring inflation, taxes, transaction costs, and any changes in the rules.)