N_rep = 10000
x = runif(N_rep, 0, 60)
data.frame(1:N_rep, x) |>
head() |>
kbl(col.names = c("Repetition", "X")) |>
kable_styling(fixed_thead = TRUE)| Repetition | X |
|---|---|
| 1 | 8.242673 |
| 2 | 52.956114 |
| 3 | 41.968699 |
| 4 | 1.021410 |
| 5 | 23.001816 |
| 6 | 22.620659 |
hist).hist with freq = FALSE).Example 9.1 In the meeting problem assume that Regina’s arrival time \(X\) (minutes after noon) follows a Uniform(0, 60) distribution. Figure 9.1 displays a histogram of 10000 simulated values of \(X\).
N_rep = 10000
x = runif(N_rep, 0, 60)
data.frame(1:N_rep, x) |>
head() |>
kbl(col.names = c("Repetition", "X")) |>
kable_styling(fixed_thead = TRUE)| Repetition | X |
|---|---|
| 1 | 8.242673 |
| 2 | 52.956114 |
| 3 | 41.968699 |
| 4 | 1.021410 |
| 5 | 23.001816 |
| 6 | 22.620659 |
hist(x,
freq = FALSE,
main = "")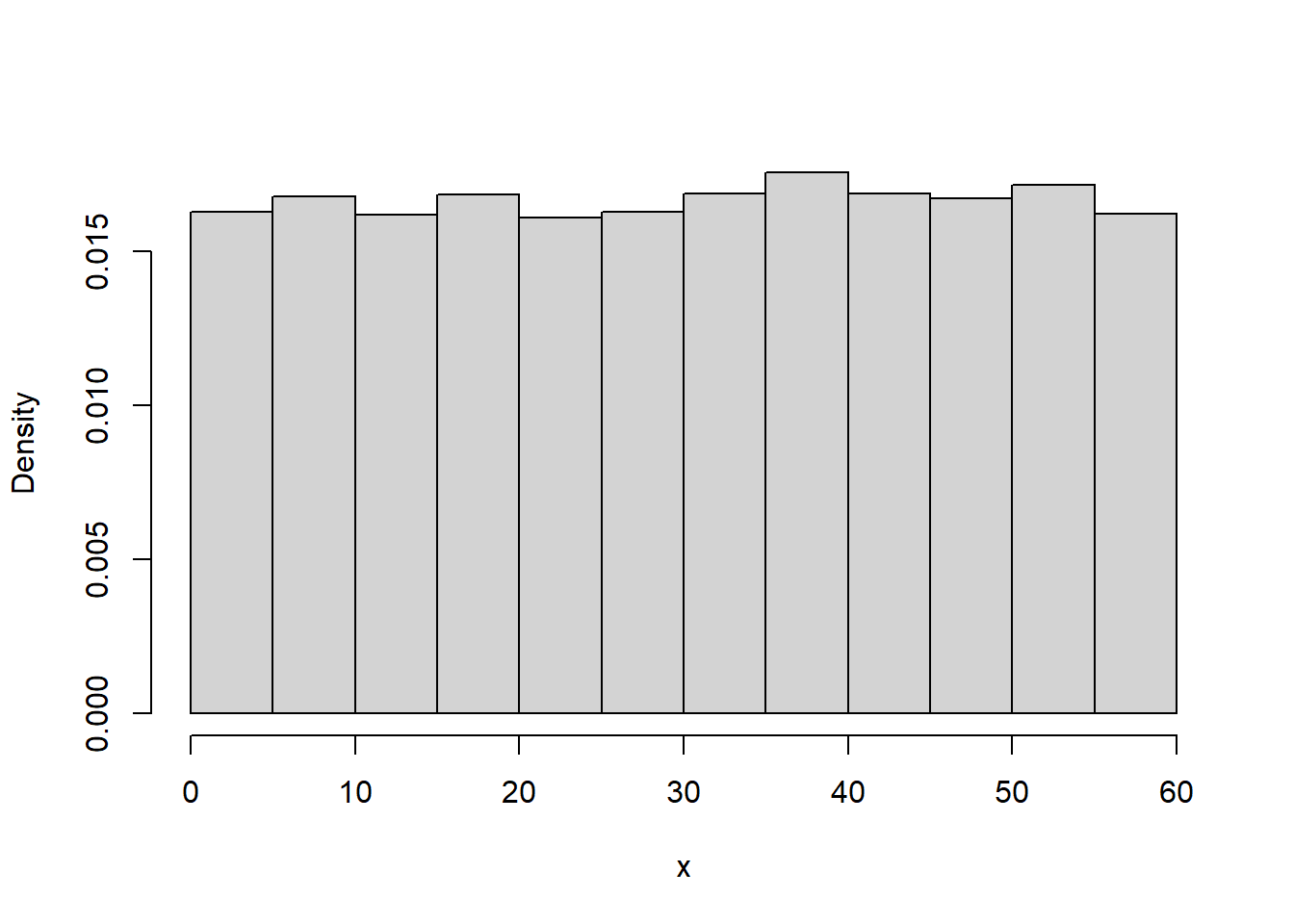
Example 9.2 Continuing Example 9.1, we will now we assume Regina’s arrival time has pdf
\[ f_X(x) = \begin{cases} cx, & 0\le x \le 60,\\ 0, & \text{otherwise.} \end{cases} \]
where \(c\) is an appropriate constant.
N_rep = 10000
u = runif(N_rep, 0, 1)
x = 60 * sqrt(u)
hist(x,
freq = FALSE,
main = "")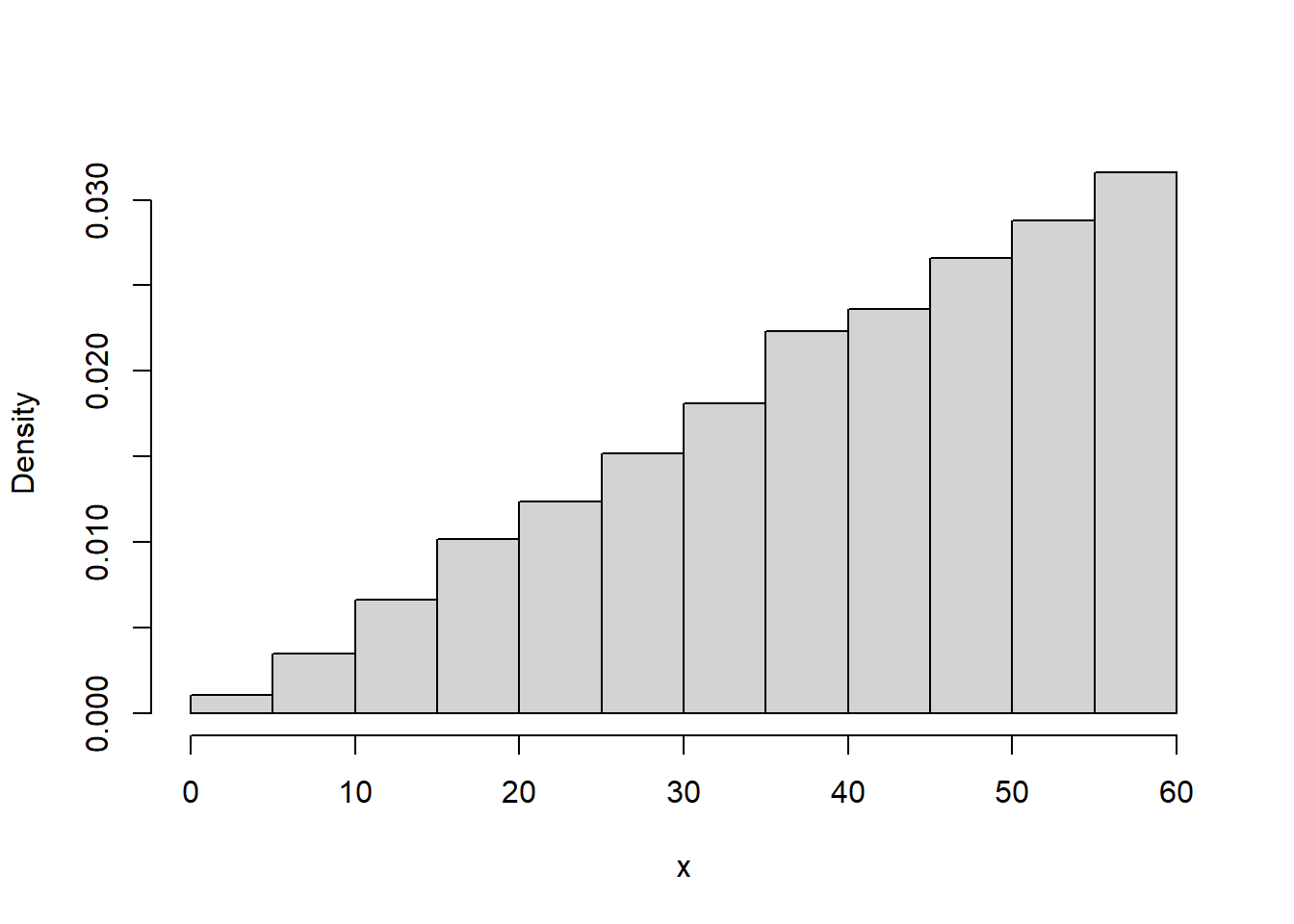
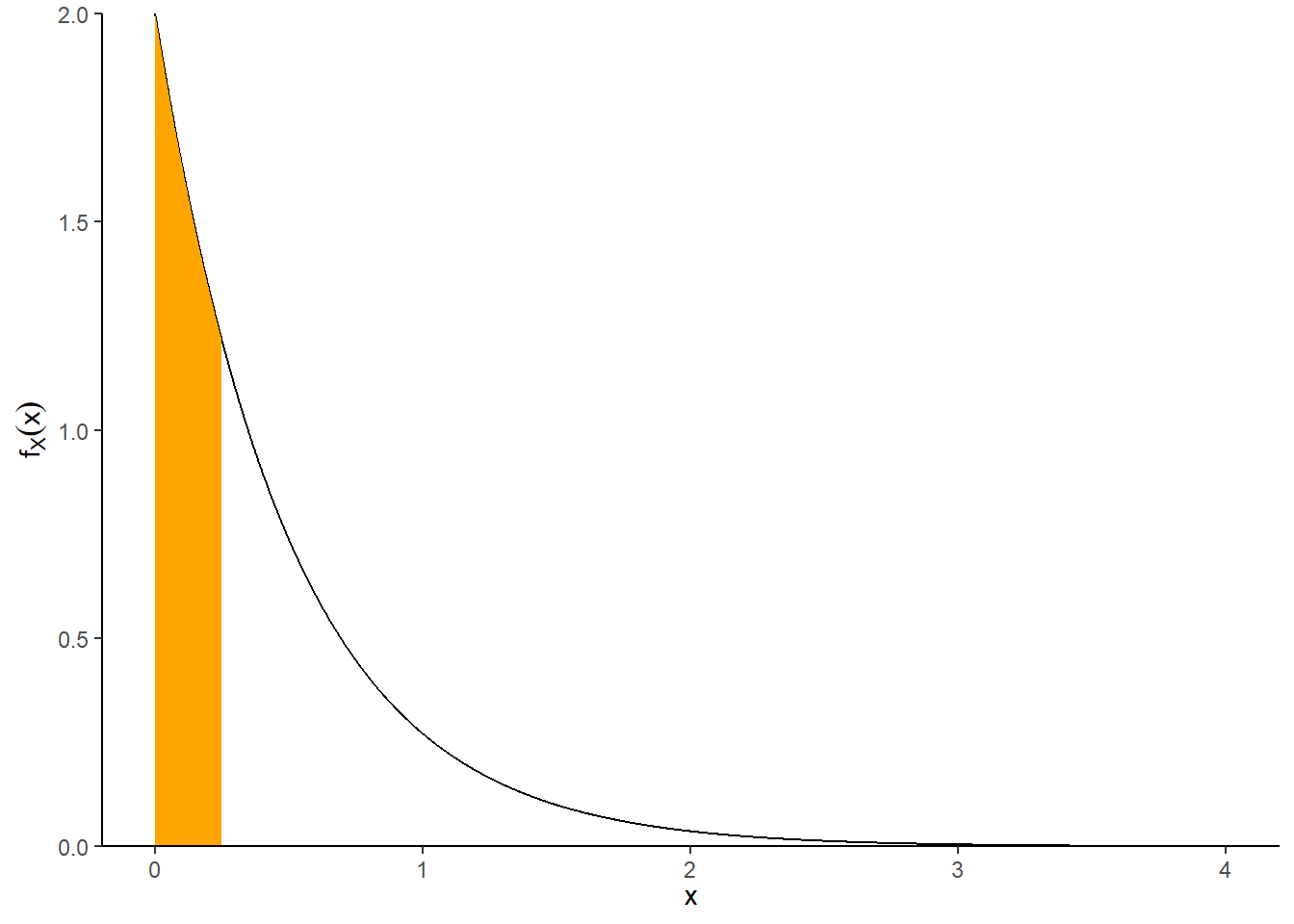
Example 9.3 Suppose that we model the waiting time, measured continuously in hours, from now until the next earthquake (of any magnitude) occurs in southern CA as a continuous random variable \(X\) with pdf \[ f_X(x) = 2 e^{-2x}, \qquad x \ge0 \] This is the pdf of the “Exponential(2)” distribution.
rexp(N_rep, rate) to simulate valuesdexp(x, rate) to compute the probability density functionpexp(x, rate) to compute the cumulative distribution function \(\text{P}(X \le x)\).qexp(p, rate) to compute the quantile function which returns \(x\) for which \(\text{P}(X\le x) = p\).N_rep = 10000
x = rexp(N_rep, rate = 2)
head(x) |>
kbl()| x |
|---|
| 0.8515704 |
| 1.7375826 |
| 0.2259141 |
| 2.1799714 |
| 0.4127839 |
| 0.0547144 |
sum(x <= 3) / N_rep[1] 0.9975pexp(3, 2)[1] 0.9975212sum(x > 0.25) / N_rep[1] 0.60521 - pexp(0.25, 2)[1] 0.6065307hist(x,
freq = FALSE,
main = "",
breaks = 20)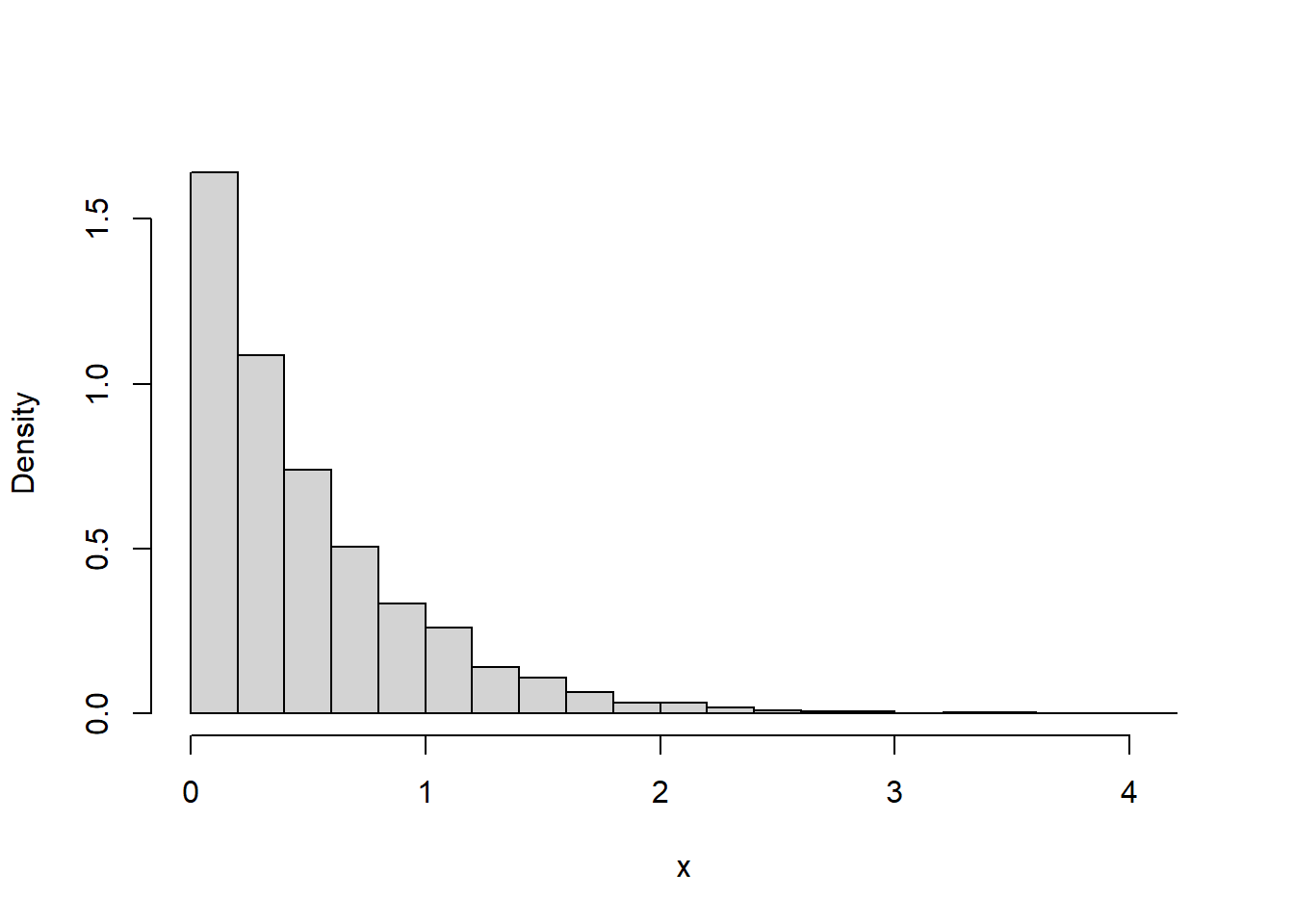
Warning: `qplot()` was deprecated in ggplot2 3.4.0.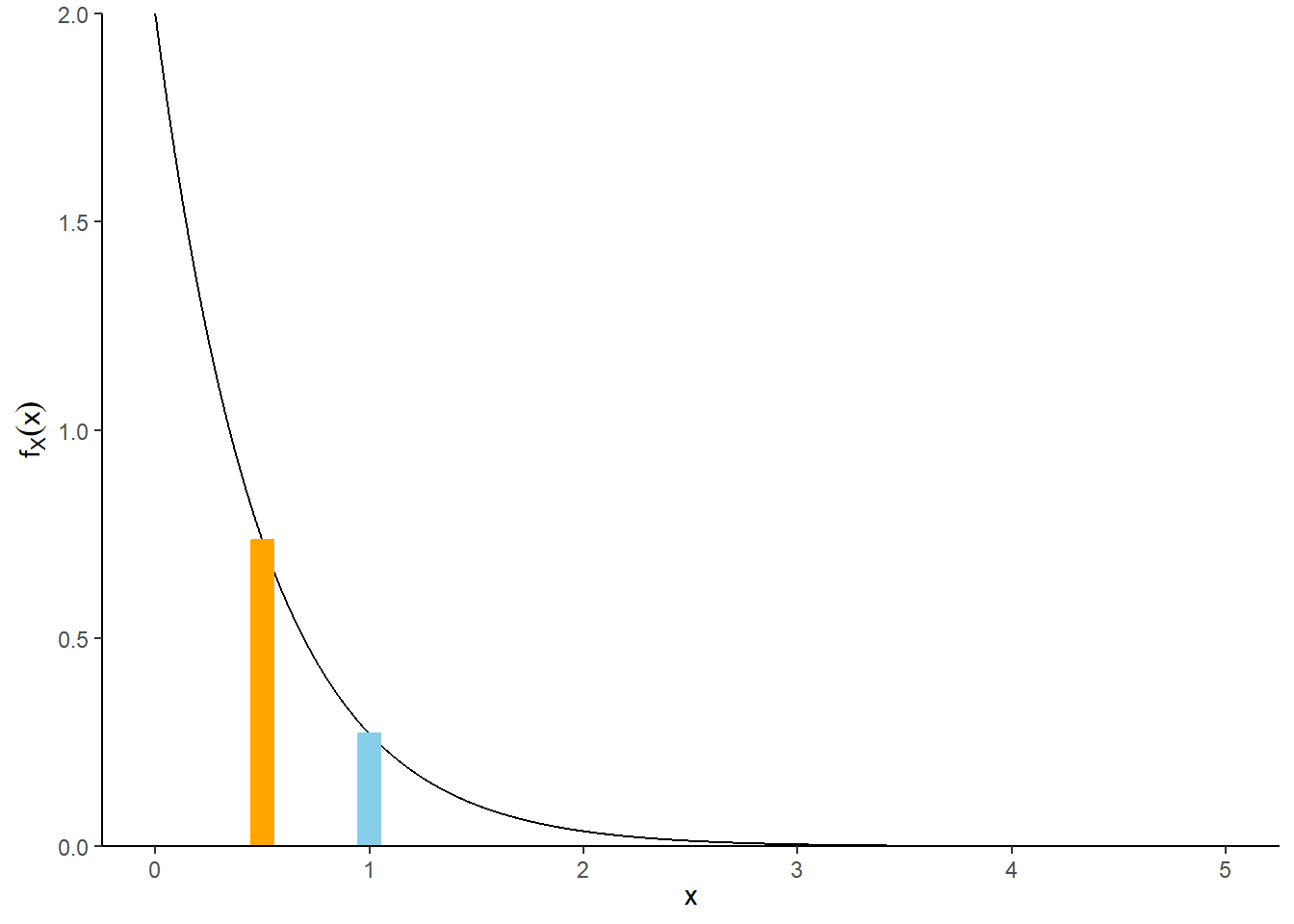
Example 9.4 Continuing Example 9.3, where \(X\), the waiting time (hours) from now until the next earthquake (of any magnitude) occurs in southern CA, has an Exponential distribution with rate 2.
sum(x) / N_rep[1] 0.5010452mean(x)[1] 0.5010452sum(x <= mean(x)) / N_rep[1] 0.6256pexp(0.5, 2)[1] 0.6321206Example 9.5 Continuing Example 9.3, where \(X\), the waiting time (hours) from now until the next earthquake (of any magnitude) occurs in southern CA, has an Exponential distribution with rate 2.
data.frame(x,
x - mean(x),
(x - mean(x)) ^ 2) |>
head() |>
kbl(col.names = c("Value", "Deviation from mean", "Squared deviation")) |>
kable_styling(fixed_thead = TRUE)| Value | Deviation from mean | Squared deviation |
|---|---|---|
| 0.8515704 | 0.3505251 | 0.1228679 |
| 1.7375826 | 1.2365374 | 1.5290247 |
| 0.2259141 | -0.2751311 | 0.0756971 |
| 2.1799714 | 1.6789262 | 2.8187930 |
| 0.4127839 | -0.0882614 | 0.0077901 |
| 0.0547144 | -0.4463309 | 0.1992113 |
mean(x)[1] 0.5010452mean((x - mean(x)) ^ 2)[1] 0.2447784var(x)[1] 0.2448029sqrt(var(x))[1] 0.4947756sd(x)[1] 0.4947756mean(x ^ 2)[1] 0.4958248