Capítulo 5 Transformación, Estandarización e Imputación de Datos
5.1 Transformación de datos
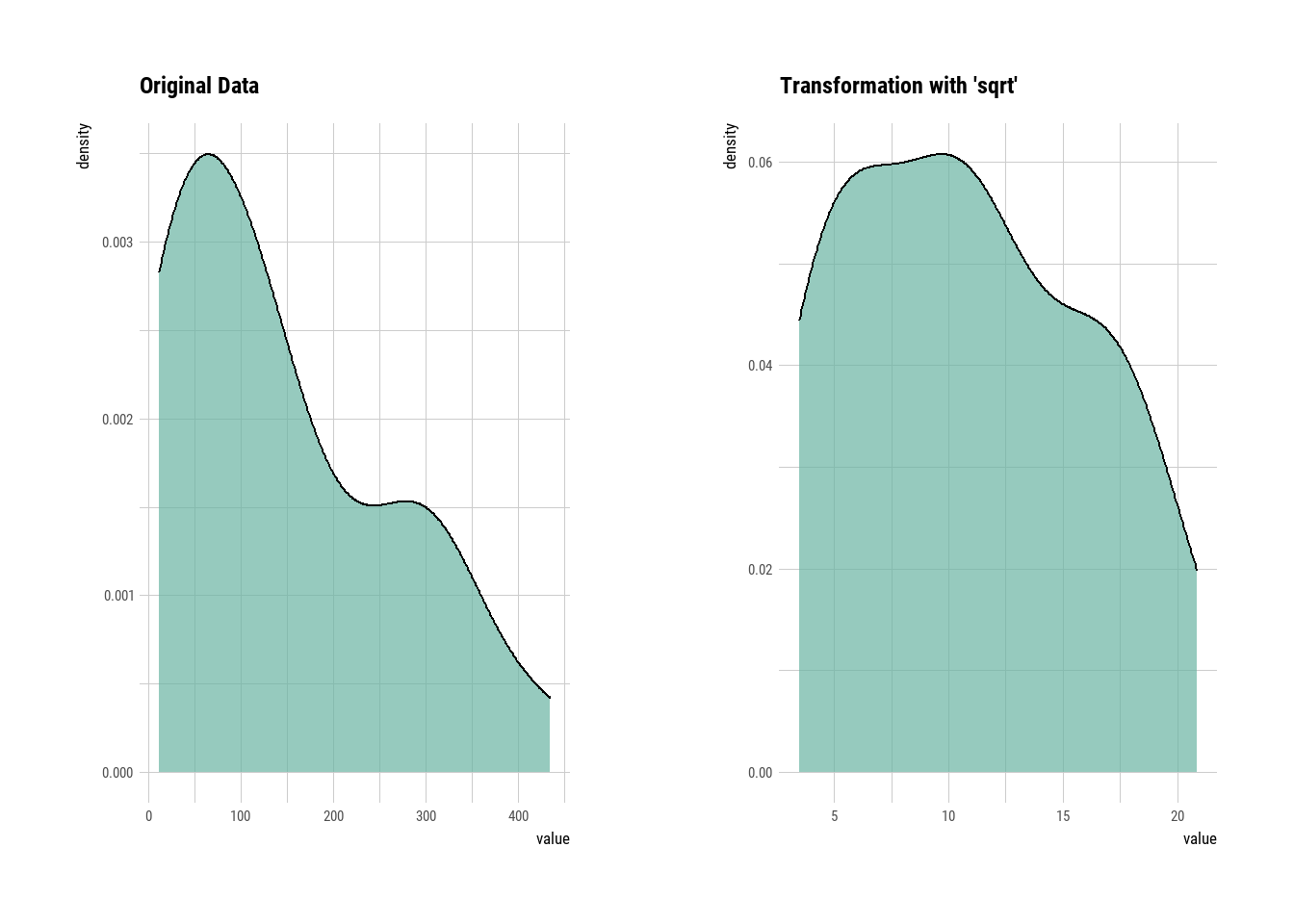
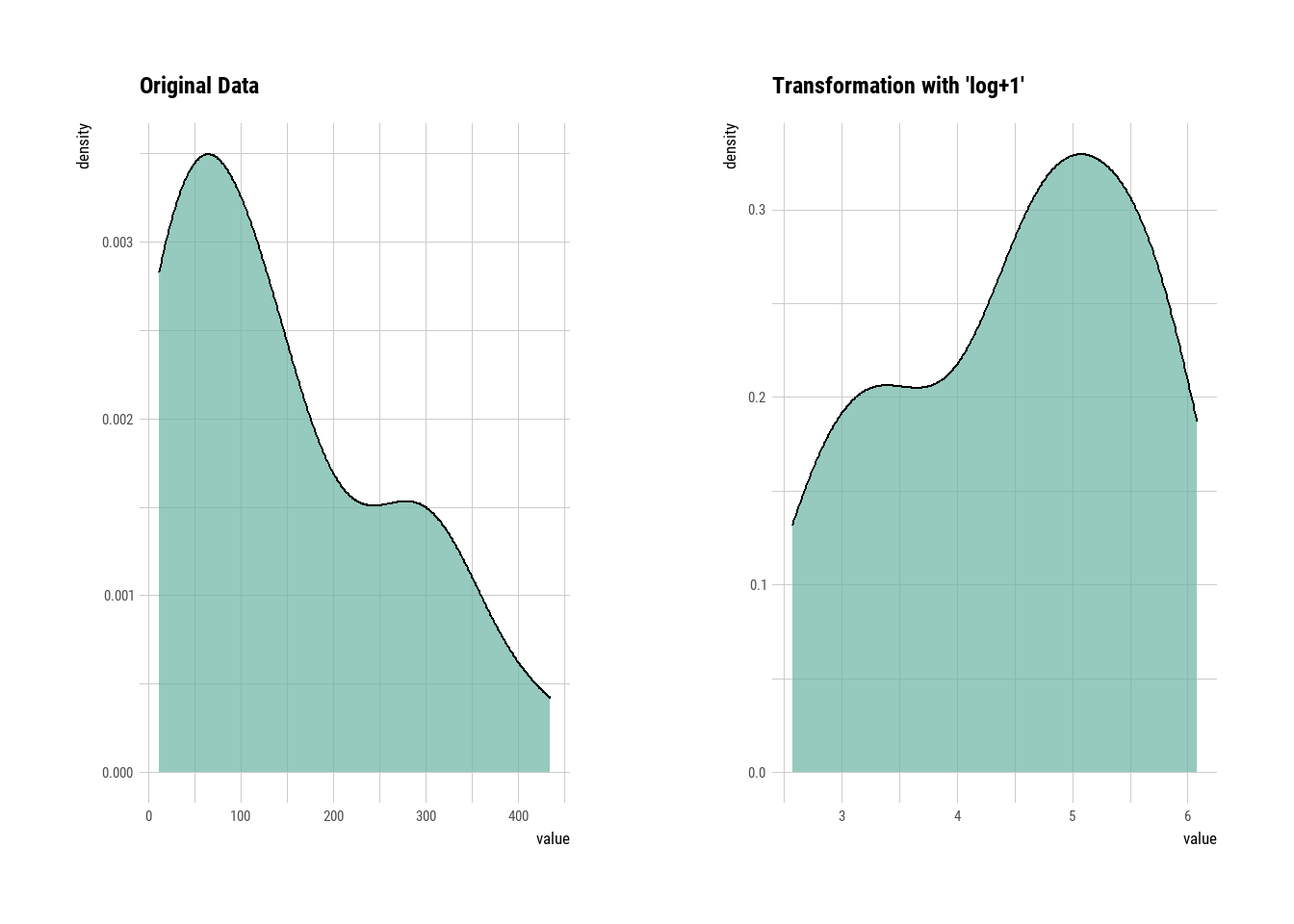
En estadística, la transformación de datos se utiliza para ajustar valores de una variable a una distribución normal. Los datos se pueden transformar usando por ejemplo la raíz cuadrada o el logaritmo para asegurarse que los datos se ajusten a los supuestos de los modelos. Con la transformación, los datos pueden utilizarse para análisis como regresión, t de student, correlación y análisis de varianza.
Recordar que los supuestos de los modelos lineales son los siguientes:
Independencia: Los residuos son independientes entre sí, es decir, los residuos constituyen una variable aleatoria. Cuando se trabaja con series tiempo, podemos hallar residuos autocorrelacionados entre sí.
Normalidad: Para cada valor de la variable independiente (o combinación de sus valores), los residuos se distribuyen normalmente con media cero.
Linealidad: La ecuación de regresión responde a una recta. A partir de esto,la variable dependiente constituye la suma de un conjunto de elementos que son: el origen de la recta, una combinación lineal de variables independientes o predictoras y los residuos. Este supuesto puede incumplirse por varias causas, como a) la no linealidad (la relación entre las variables independientes y la dependiente no es lineal), b) la no aditividad (el efecto de alguna variable independiente es sensible a los niveles de alguna otra variable independiente), c) la omisión de variables independientes, d) la inclusión de variables independientes irrelevantes, y e) parámetros cambiantes (los parámetros no permanecen constantes durante el tiempo).
Homocedasticidad: Para cada valor de la variable independiente (o combinación de sus valores), la varianza de los errores es constante a lo largo del tiempo. La palabra homocedasticidad se puede desglosar en dos partes, homo (igual) y cedasticidad (dispersión). De tal manera que, si unimos estas dos palabras de origen griego, obtendríamos algo así como igual dispersión.
A continuación una guía de las pruebas estadísticas sugeridas para los distintos tipos de datos:
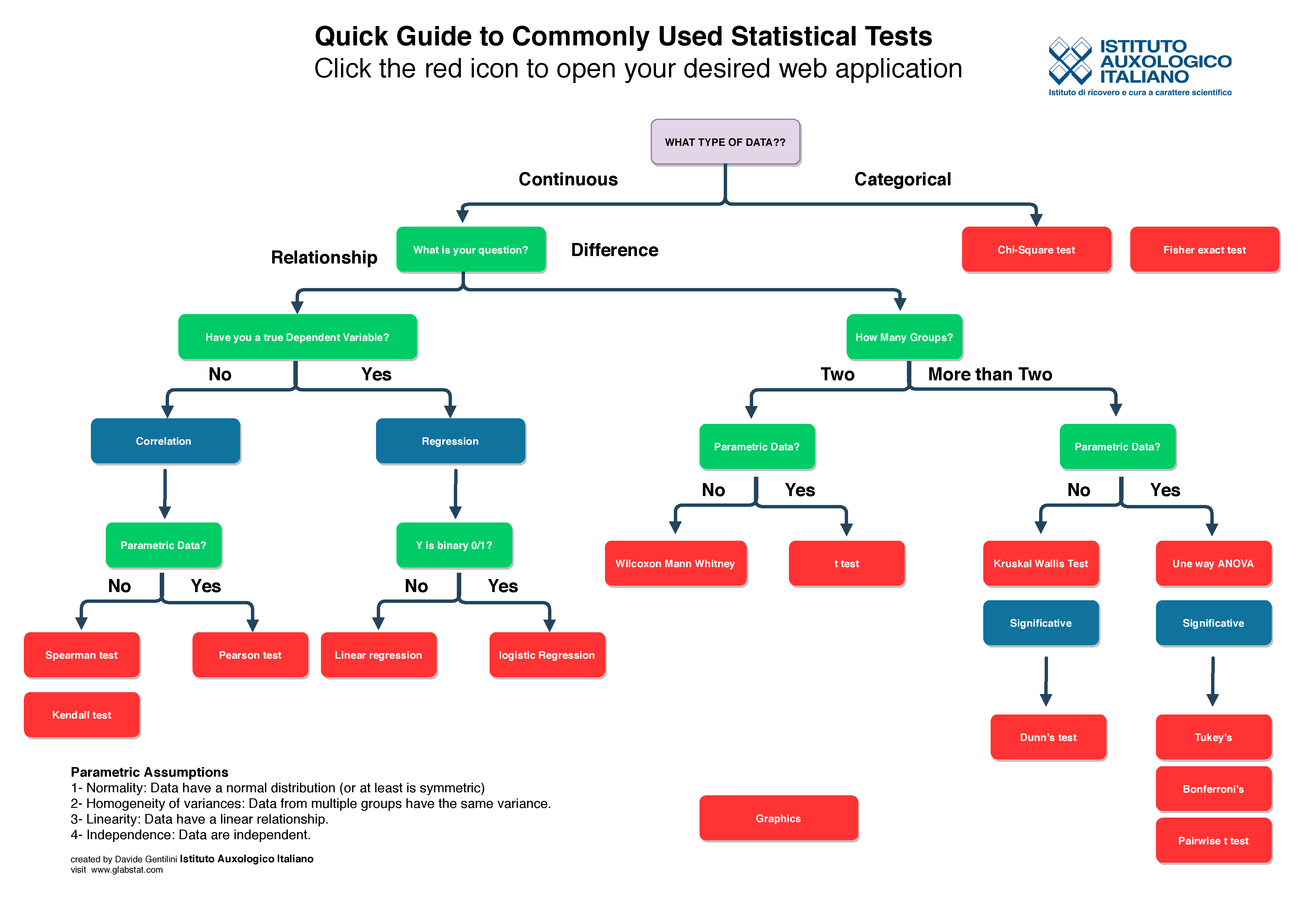
Guia para la selección de pruebas estadísticas. Imagen tomada de https://www.glabstat.com/test-flowchart
5.1.1 Determinación del sesgo o asimetría
Las medidas de skewness (sesgo o asimetría) son indicadores que permiten establecer el grado de sesgo que presenta una distribución de probabilidad de una variable aleatoria. Si una distribución es simétrica, existe el mismo número de valores a la derecha que a la izquierda de la media, por tanto, el mismo número de desviaciones con signo positivo que con signo negativo.
Para el ejemplo se utilizará el dataset varechem del programa vegan sobre mediciones químicas en suelos de varios ecosistemas.
library(vegan)
library(dlookr)
library(ggplot2)
library(vegan)
library(patchwork)
data("varechem")
str(varechem)
#> 'data.frame': 24 obs. of 14 variables:
#> $ N : num 19.8 13.4 20.2 20.6 23.8 22.8 26.6 24.2 29.8 28.1 ...
#> $ P : num 42.1 39.1 67.7 60.8 54.5 40.9 36.7 31 73.5 40.5 ...
#> $ K : num 140 167 207 234 181 ...
#> $ Ca : num 519 357 973 834 777 ...
#> $ Mg : num 90 70.7 209.1 127.2 125.8 ...
#> $ S : num 32.3 35.2 58.1 40.7 39.5 40.8 33.8 27.1 42.5 60.2 ...
#> $ Al : num 39 88.1 138 15.4 24.2 ...
#> $ Fe : num 40.9 39 35.4 4.4 3 ...
#> $ Mn : num 58.1 52.4 32.1 132 50.1 ...
#> $ Zn : num 4.5 5.4 16.8 10.7 6.6 9.1 7.4 5.2 9.3 9.1 ...
#> $ Mo : num 0.3 0.3 0.8 0.2 0.3 0.4 0.3 0.3 0.3 0.5 ...
#> $ Baresoil: num 43.9 23.6 21.2 18.7 46 40.5 23 29.8 17.6 29.9 ...
#> $ Humdepth: num 2.2 2.2 2 2.9 3 3.8 2.8 2 3 2.2 ...
#> $ pH : num 2.7 2.8 3 2.8 2.7 2.7 2.8 2.8 2.8 2.8 ...Para encontrar las variables asimétricas dentro de un set de datos se utiliza la función find_skewness() del programa dlookr.
find_skewness(varechem, index = FALSE)
#> [1] "Mg" "Al" "Fe" "Mn" "Zn"
#> [6] "Mo" "Baresoil" "pH"También, rápidamente se puede evaluar si los datos de una variable tienen una distribución normal
p1=ggplot(varechem, aes(Al)) +
geom_histogram(bins=30)+
theme_bw() +
ggtitle('Histogram')
p2=ggplot(varechem, aes(sample=Al)) +
stat_qq(aes(sample=Al))+
stat_qq_line(aes(sample=Al))+
theme_bw() +
ggtitle('Q-Q plot')
p1+p2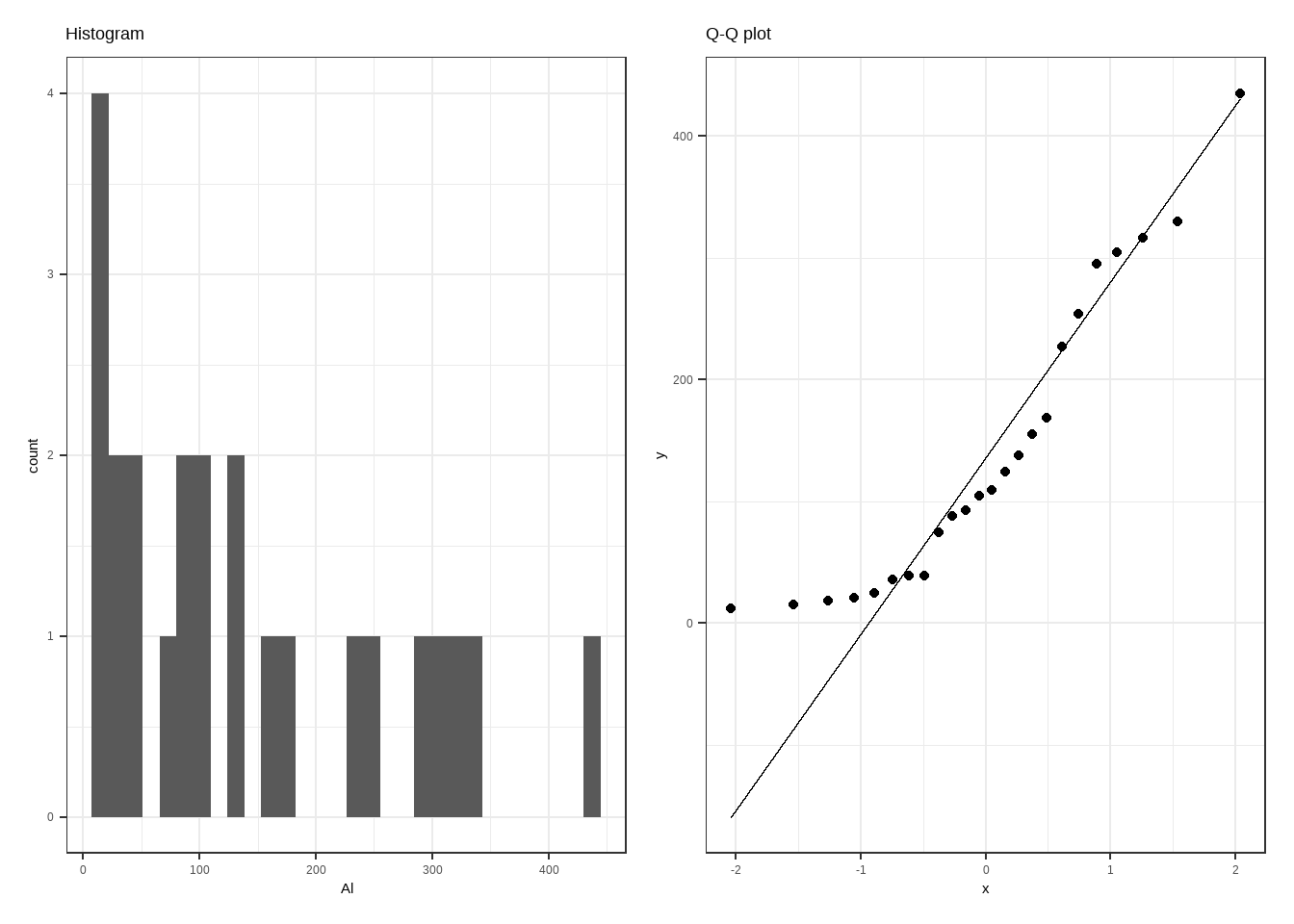
Figure 5.1: 5
Para comprobar la normalidad de una variable se puede utilizar la prueba de Shapiro-Wilk cuya hipótesis nula es que la variable presenta una distribución normal. En caso que esta hipótesis sea rechazada con una p < 0.05, la distribución no sería normal.
shapiro.test(varechem$Al)
#>
#> Shapiro-Wilk normality test
#>
#> data: varechem$Al
#> W = 0.88773, p-value = 0.01193Para calcular el valor del sesgo se utiliza la función skewness() del programa e1071. Si el valor resultante está por encima de +1 o por debajo de -1, los datos están muy sesgados. Si está entre +0.5 y -0.5, está sesgado moderadamente. Si el valor es 0, entonces los datos son simétricos.
5.1.2 Transformación simple
Para datos sesgados a la derecha (sesgo positivo) o sesgados a la izquierda (sesgo negativo), las transformaciones más comunes incluyen calcular la raíz cuadrada, raíz cúbica y logaritmo del valor de la variable. Notar que debido el \(\log (0)\) no está definido y por lo tanto se debe agregar una constante (+1) a todos los valores para que todos sean positivos antes de la transformación.
A menudo hay que intentar varias transformaciones hasta asegurarse de conseguir la normalidad de los datos. En este primer ejemplo utilizaremos la función transform() del programa dlookr para transformar de acuerdo a la raíz cuadrada y al log+1.
5.1.2.3 Raíz cúbica
Ahora se intentará con transformando con la raíz cúbica. Este cálculo se hace mediante operaciones de R. En este caso pareciera ser el mejor método de trasnformación
Al_cuberoot <- sign(varechem$Al)* abs(varechem$Al)^(1/3)
ggplot(varechem, aes(Al_cuberoot)) +geom_density()+
theme_bw()+ggtitle('Raíz Cúbica')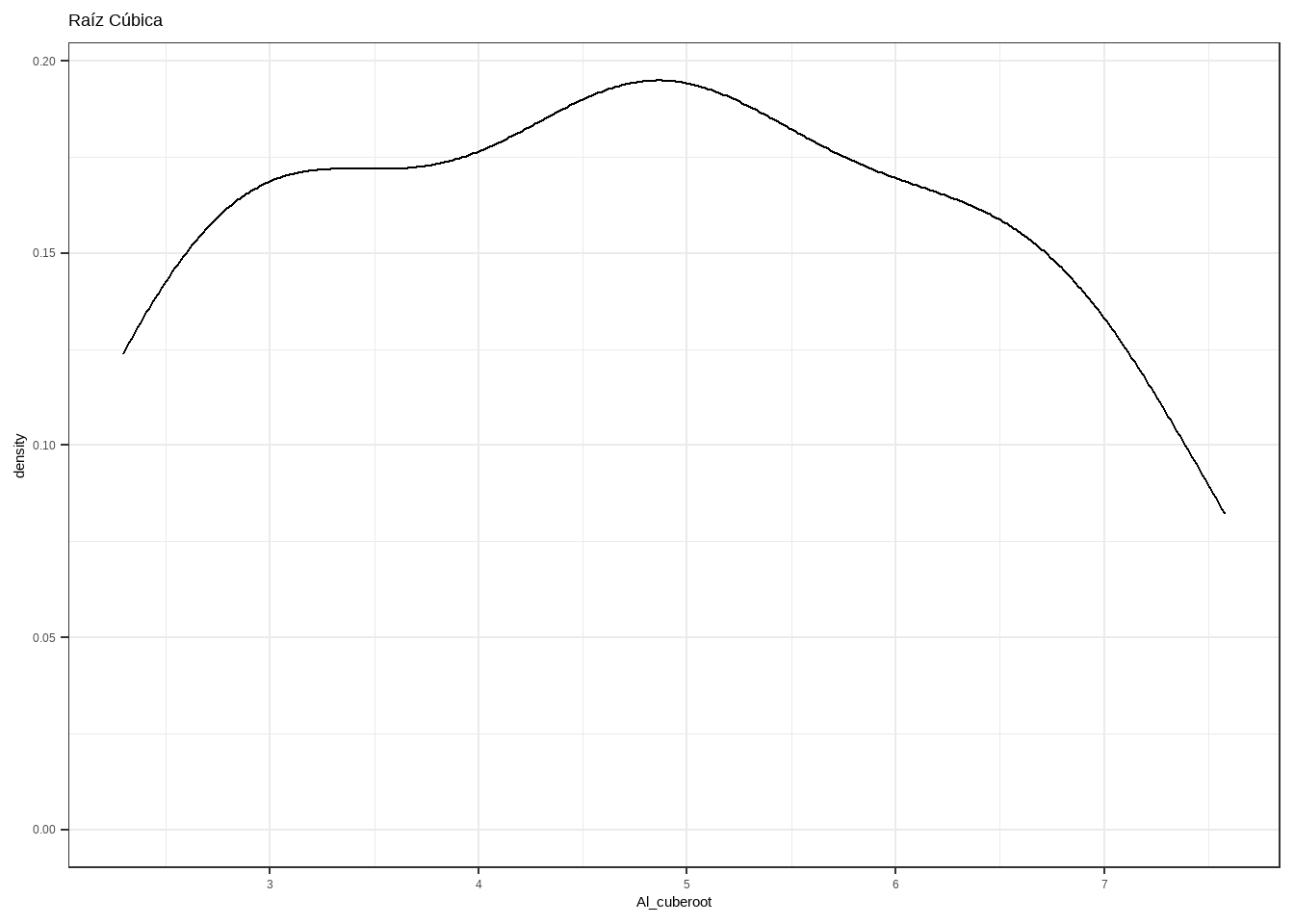
Figure 4.9: 5
Ahora, calculamos el valor de sesgo para comprobar. Como verán, este fue el método que funcionó mejor.
skewness(Al_cuberoot)
#> [1] 0.04935185.1.3 Manejo de outliers
Los valores atípicos se pueden encontrar utilizando la función de valores outliers() del paquete outliers. Esta función devuelve los valores a distancias extremas de la media. Una vez que se encuentran, podemos manejarlos en consecuencia para reducir la asimetría. Los valores atípicos pueden rectificar utilizando uno de los siguientes métodos:
A. Imputación: Esto significa reemplazar los valores atípicos por otros valores estimados a partir del conjunto de datos. Este tema lo analizaremos con más detalle en la siguiente sección.
B. Capado (Capping): Para los valores fuera de los límites de 1.5X del rango intercuartil, se reemplazan las observaciones fuera del límite inferior con el valor del percentil 5% y los que se encuentran por encima del límite superior, con el valor del percentil 95%.
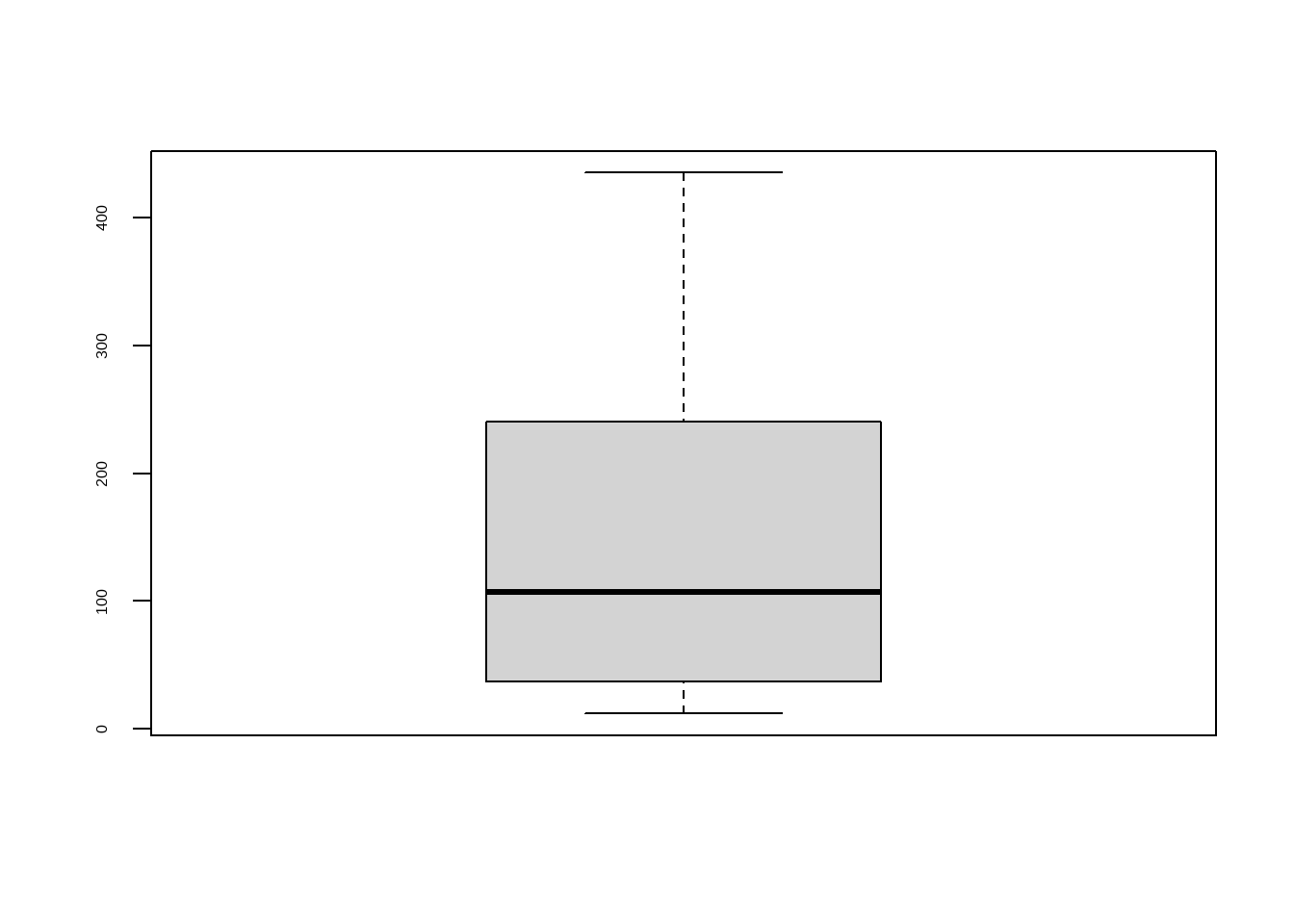
Figure 4.11: 5
outlier(varechem)
#> N P K Ca Mg S
#> 33.1 73.5 313.8 1169.7 209.1 60.2
#> Al Fe Mn Zn Mo Baresoil
#> 435.1 204.4 132.0 16.8 1.1 56.9
#> Humdepth pH
#> 3.8 3.6
outlier(varechem,opposite = TRUE )
#> N P K Ca Mg S
#> 13.40 22.70 43.60 188.50 25.70 14.90
#> Al Fe Mn Zn Mo Baresoil
#> 12.10 2.30 10.10 2.60 0.05 0.01
#> Humdepth pH
#> 1.00 2.70
x <- varechem$Al
range(x)
#> [1] 12.1 435.1
qnt <- quantile(x, probs=c(.25, .75))
caps <- quantile(x, probs=c(.05, .95))
x[x < qnt[1]] <- caps[1]
x[x > qnt[2]] <- caps[2]
range(x)
#> [1] 15.775 327.7205.1.4 Binning
Es una técnica transformación que permite agrupar en variables categóricas las variables numéricas. Normalmente se hace determinando rangos. Esto permite determinar patrones que no se observarían facilmente con datos continuos. Este método se utiliza a menudo para desarrollar indices. En el ejemplo utilizaremos la función binning() del paquete dlookr
library(dlookr)
library(vegan)
data(varechem)
bin1 <- binning(varechem$N, nbins = 3)
summary(bin1)
#> levels freq rate
#> 1 [13.4,19.97778] 8 0.3333333
#> 2 (19.97778,24.02222] 8 0.3333333
#> 3 (24.02222,33.1] 8 0.3333333
plot(bin1)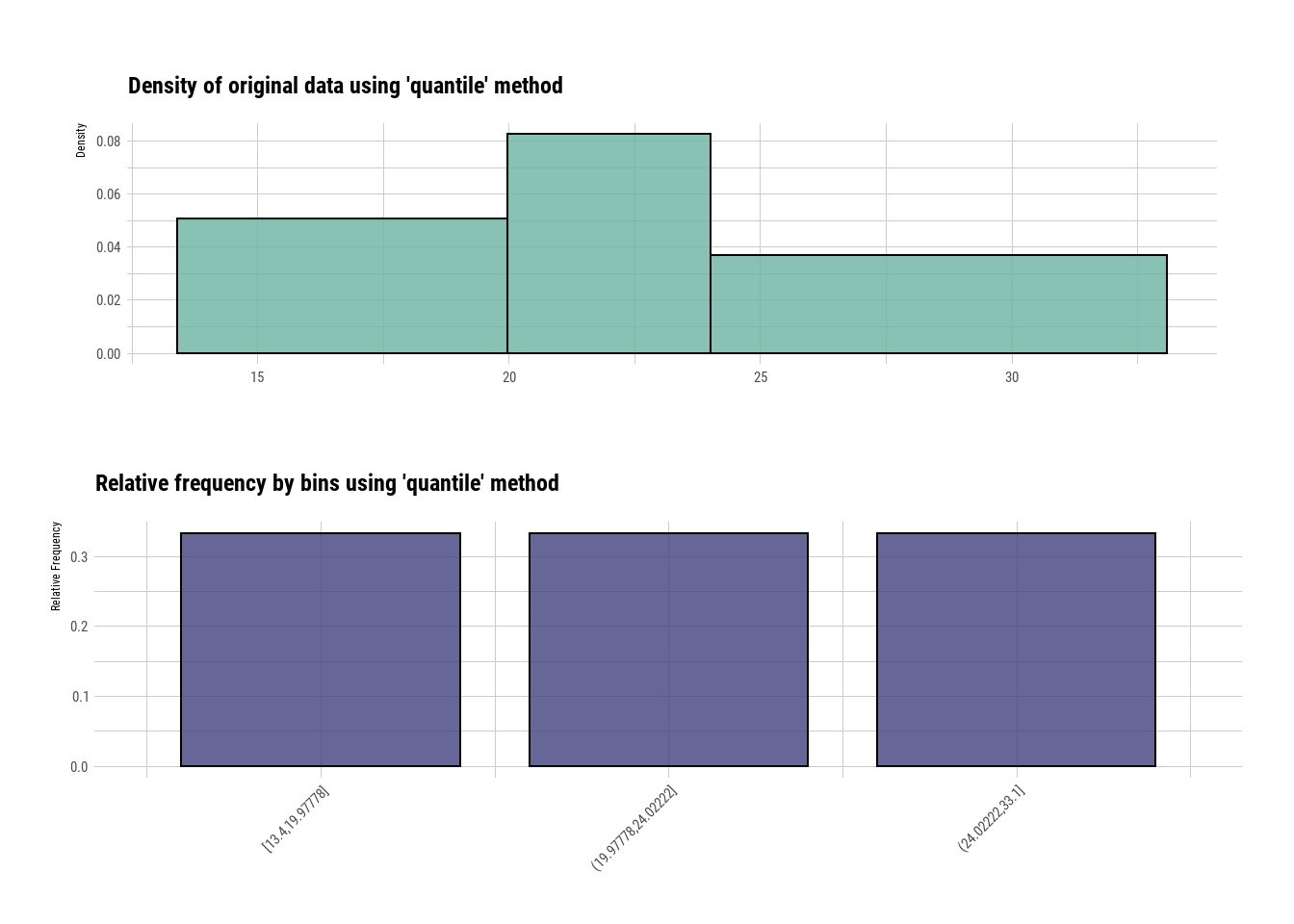
Figure 5.2: 5
También se puede ajustar para que las agrupaciones sea por números enteros
bin2 <- binning(varechem$N, nbins = 3, type="pretty")
summary(bin2)
#> levels freq rate
#> 1 [10,15] 3 0.1250000
#> 2 (15,20] 5 0.2083333
#> 3 (20,25] 9 0.3750000
#> 4 (25,30] 4 0.1666667
#> 5 (30,35] 3 0.1250000
plot(bin2)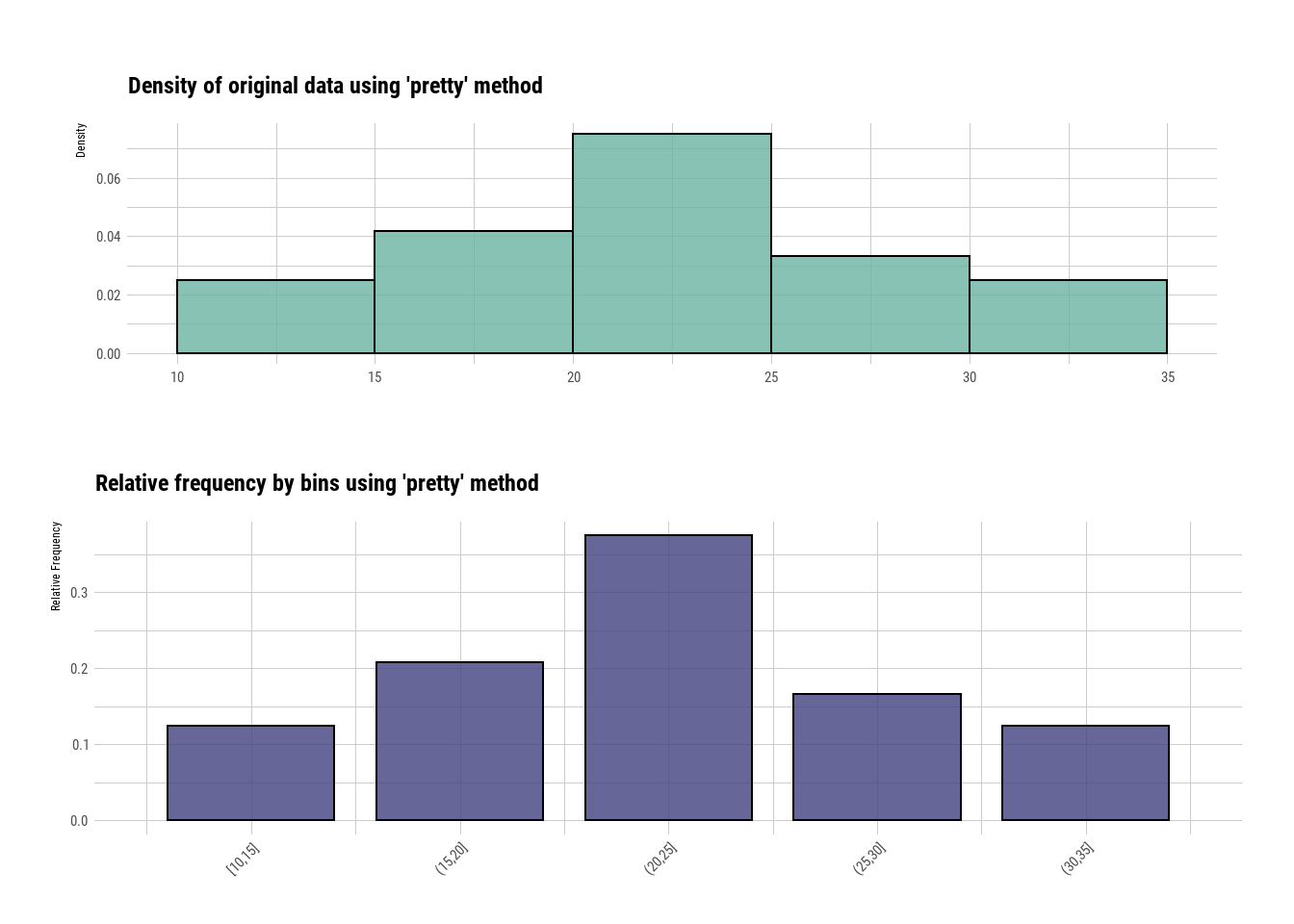
Figure 4.12: 5
Aunque lo más recomendado es utilizar un algoritmo especializado para definir los rangos de cada uno de los grupos, como el algoritmo de K means (K medias). Este método de agrupamiento tiene como objetivo la partición de un conjunto de n observaciones en k grupos en el que cada observación pertenece al grupo cuyo valor medio es más cercano. Esta técnica es muy utilizada en minería de datos.
bin3 <- binning(varechem$N, nbins = 3, type="kmeans")
summary(bin3)
#> levels freq rate
#> 1 [13.4,18.55] 6 0.2500000
#> 2 (18.55,25.2] 11 0.4583333
#> 3 (25.2,33.1] 7 0.2916667
plot(bin3)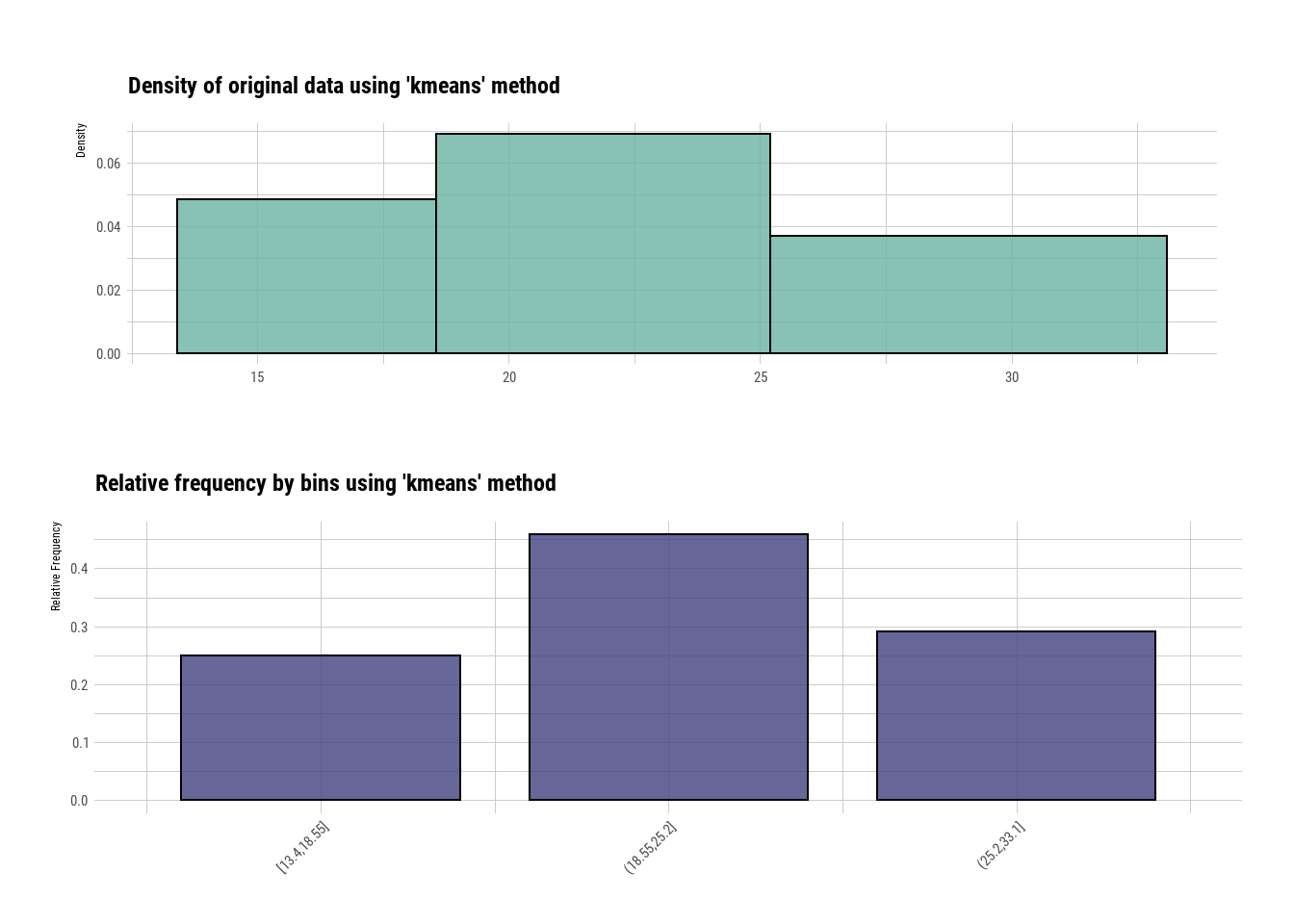
Figure 4.13: 5
5.2 Estandarización de datos
La estandarización (también llamada normalización o escalado) se refiere al ajuste de los valores medidos en diferentes escalas respecto a una escala común. Es decir, ajusta todas las columnas al mismo rango.
No hay nada ilícito en transformar o estandarizar los datos, pero debe mencionarse explícitamente el tipo de transformación que se le hizo a las variables cuando se muestran los resultados de los análisis.
Para poner todas las columnas en el mismo rango, se pueden utilizar las siguientes técnicas de normalización
5.3 Estandarización por variable
5.3.1 Min-Max:
Es una forma simple de escalar valores en una columna. Pero, trata de mover los valores hacia la media de la columna. Es el resultado de la resta del valor menos el valor mínimo entre la diferencia entre el valor máximo y el mínimo de la columna, según la siguiente fórmula
\(X_{new}=\frac{X_i-min(X)}{\max(X)-min(X)}\)
library(vegan)
library(dlookr)
data(varechem)
varechem_minmax_Al = transform(varechem$Al, method = "minmax")
plot(varechem_minmax_Al)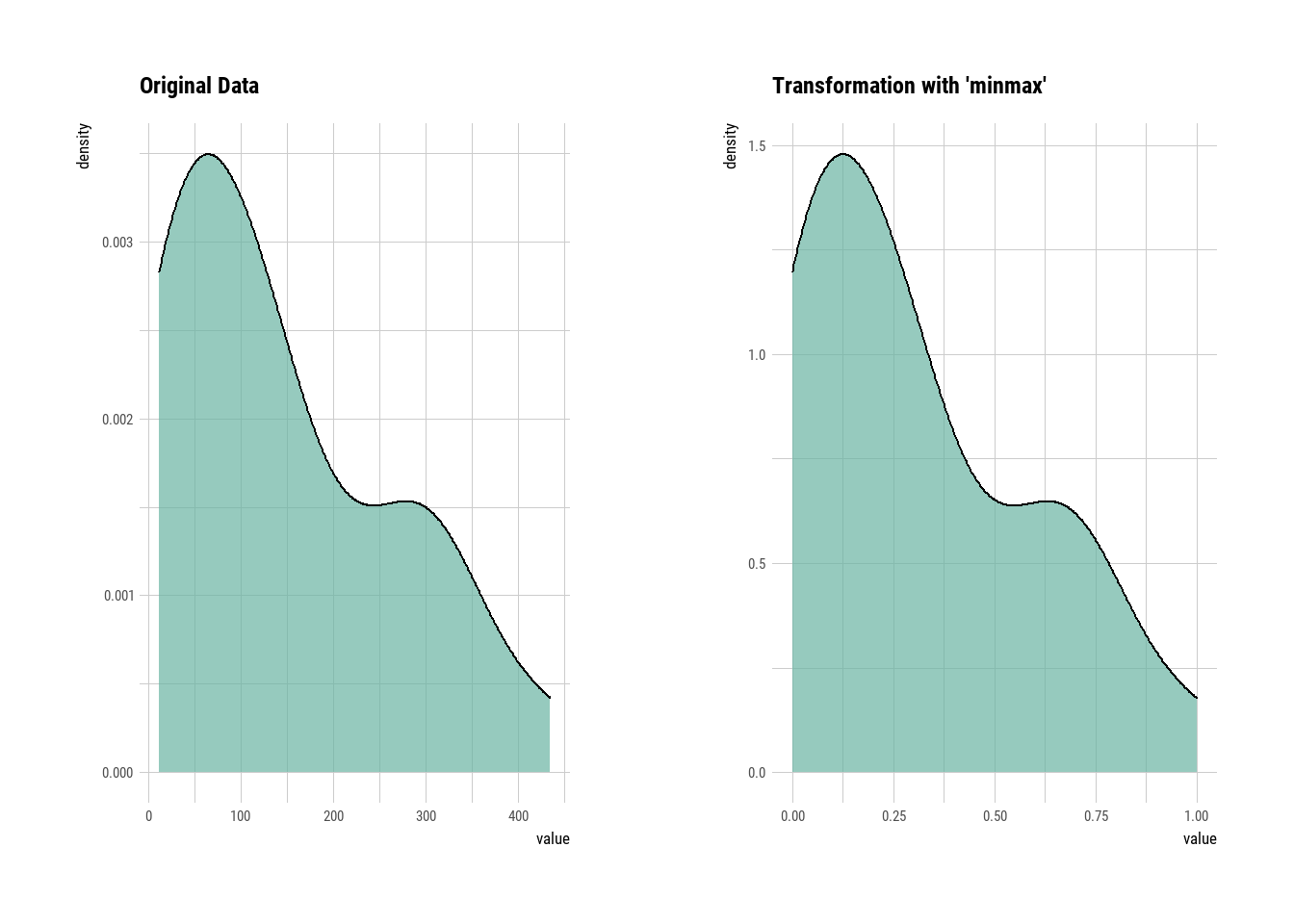
Figure 4.14: 5
skewness(varechem_minmax_Al)
#> [1] 0.74891795.3.1.1 Z score:
Es el resultado de la restar cada valor menos la media poblacional y luego dividirlo entre la desviación estándar, como se aprecia en la siguiente fórmula
\(Z =\frac{x_i-\mu}{\sigma}\)
Generalmente es preferible utilizar Min-Max cuando se realiza estandarización por variable, esto porque intenta acercar los valores a la media. Pero cuando hay datos atípicos (outliers) que son importantes y no se quiere perder su impacto, se opta por la normalización Z score. El inconveniente de esta técnica es la pérdida de interpretabilidad de los valores individuales.
library(vegan)
library(dlookr)
data(varechem)
varechem_zscore = transform(varechem$Al, method = "zscore")
plot(varechem_zscore)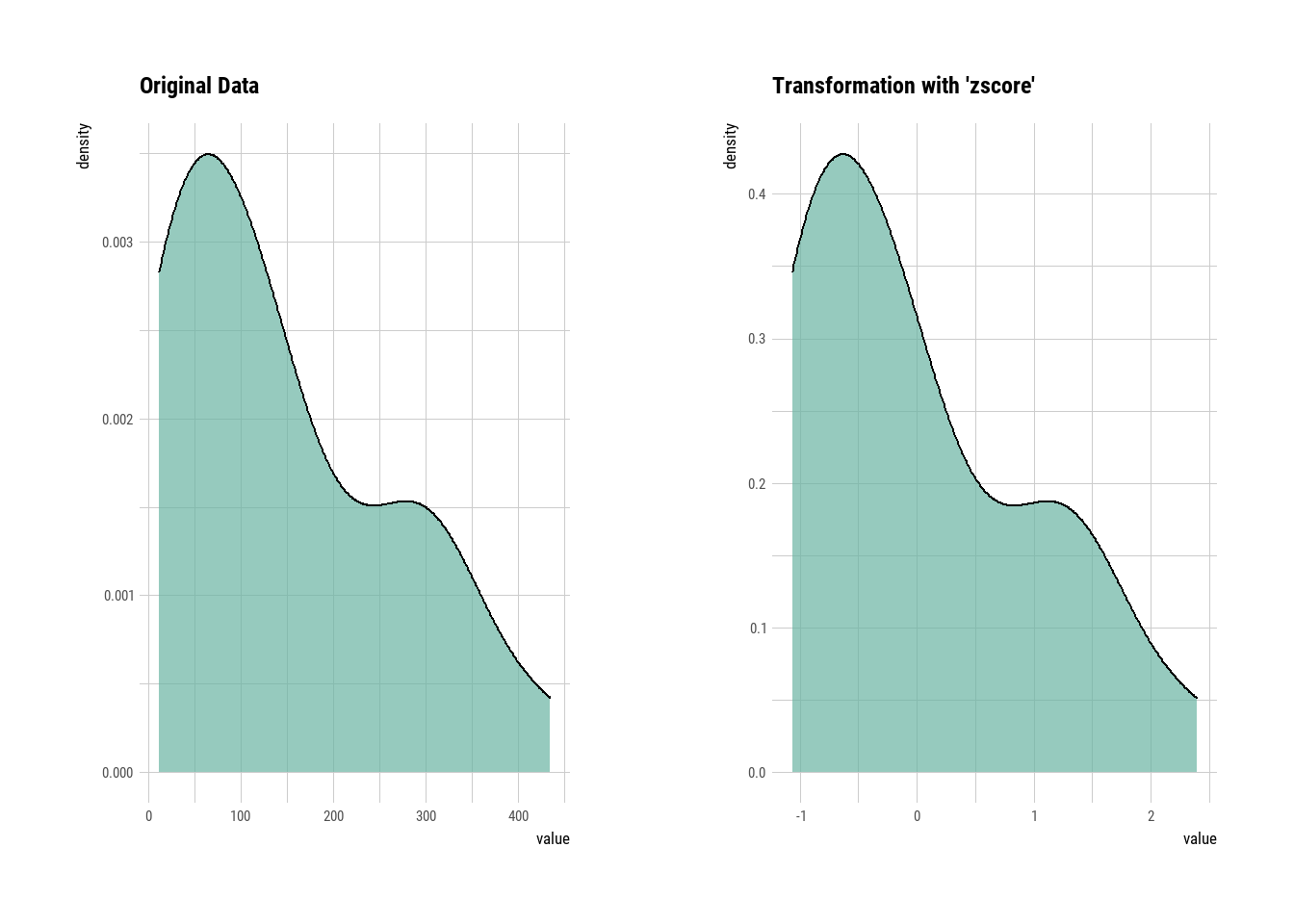
Figure 5.3: 5
skewness(varechem_zscore)
#> [1] 0.7489179Es importante hacer notar recordar que Min-Max y Z score son técnicas para estandarizar los datos respecto a los valores de otras variables en la base de datos. Por tanto, aunque no realicen ajustes en la normalidad (incumpliendo supuestos de modelos paramétricos) si podrían ser útiles en modelos no paramétricos.
5.3.2 Estandarización generalizada
Los valores no se transforman individualmente sino en relación con otros valores en la tabla de datos. En tablas de datos tipo especies por sitio o tipo gen versus tratamiento, la estandarización se puede hacer por fila, columna o ambos (perfiles dobles), dependiendo del enfoque del análisis.
En el siguiente ejemplo se usará la base de datos varespec del paquete vegan que contiene las abundancias de 44 especies de plantas en 24 sitios muestreados. La función decostand() se utiliza para realizar diferentes tipos de normalización de los datos. Con el parámetro hellinger se calculan las frecuencias relativas por perfiles de muestra y luego aplica la raíz cuadrada para reducir la importancia de valores muy altos
El parámetro method=pa se utiliza para transformar los datos en una matriz de presencia-ausencia
decostand(varespec, method="pa")El parámetro total se utiliza para transformar las abundancias en abundancias relativas (proporción) de cada una de las especies por sitio. En ecología por ejemplo, este es un tipo de normalización muy utilizado.
decostand(varespec, "total")Otra forma de normalizar los todos los datos de una tabla a una escala común es mediante dos funciones del programa caret.
La función preProcess() estima los parámetros requeridos para cada operación y la función predict.preProcess() se usa para aplicarlos a conjuntos de datos específicos. El parámetro center lo que hace es restar la media de los datos del predictor menos los valores del predictor, mientras que scale divide por la desviación estándar.
library(caret)
varechem_c <- preProcess(varechem, method = c("center","scale"))
varechem_c
#> Created from 24 samples and 14 variables
#>
#> Pre-processing:
#> - centered (14)
#> - ignored (0)
#> - scaled (14)
transformed <- predict(varechem_c, newdata = varechem)
str(transformed)
#> 'data.frame': 24 obs. of 14 variables:
#> $ N : num -0.467 -1.625 -0.395 -0.323 0.256 ...
#> $ P : num -0.199 -0.4 1.513 1.052 0.63 ...
#> $ K : num -0.3552 0.0674 0.6812 1.0914 0.2725 ...
#> $ Ca : num -0.206 -0.874 1.657 1.085 0.851 ...
#> $ Mg : num 0.062 -0.409 2.966 0.969 0.935 ...
#> $ S : num -0.419 -0.171 1.792 0.301 0.198 ...
#> $ Al : num -0.8459 -0.4445 -0.0366 -1.0389 -0.9669 ...
#> $ Fe : num -0.144 -0.176 -0.235 -0.748 -0.771 ...
#> $ Mn : num 0.2586 0.0906 -0.5081 2.4379 0.0227 ...
#> $ Zn : num -1.037 -0.736 3.085 1.04 -0.334 ...
#> $ Mo : num -0.399 -0.399 1.684 -0.816 -0.399 ...
#> $ Baresoil: num 1.2744 0.0396 -0.1064 -0.2585 1.4022 ...
#> $ Humdepth: num 0 0 -0.301 1.053 1.204 ...
#> $ pH : num -1.09 -0.623 0.312 -0.623 -1.09 ...5.4 Imputación de datos
Como parte del proceso de manipulación de bases de datos es muy común encontrar variables con datos faltantes. Esto es particularmente frecuente en datos científicos donde ocurren, por ejemplo, errores en procesamiento de algunas muestras, fallas en equipos de medición así como debido a la ocurrencia de problemas humanos de hardware o software.
Por eso, un paso importante antes de realizar análisis estadísticos o de aprendizaje automático es revisar la cantidad de datos faltantes. Luego, se puede decidir si se eliminan las muestras con los valores faltantes o, lo más recomendado, imputar los datos.
La imputación es el proceso de reemplazar los datos faltantes con valores sustituidos.
5.4.1 ¿Qué hacer con datos faltantes?
- Ignorar: Simplemente se eliminan los datos faltantes (poco recomendado)
- Imputación simple: Se sutituyen los valores faltantes por un valor único como la media o la mediana de la variable.
- Imputación por modelado: Se pueden utilizar modelo predictivos más sofisticados para sustituir valores individuales a partir de tendencias o relaciones con otras variables del set de datos.
- Imputación por machine learning: Se sustituye valor utilizando algoritmos de aprendiza automático
5.4.2 Visualización de datos faltantes
Para los ejemplos, modificaremos la base de datos iris introduciendo NAs. Para esto se utiliza la función prodNA() del programa missForest, que genera aleatoriamente NAs en un porcentaje de los datos.
library(missForest)
data(iris)
iris.mis <- prodNA(iris, noNA = 0.1)
summary(iris.mis)
#> Sepal.Length Sepal.Width Petal.Length
#> Min. :4.300 Min. :2.00 Min. :1.000
#> 1st Qu.:5.100 1st Qu.:2.80 1st Qu.:1.600
#> Median :5.800 Median :3.00 Median :4.400
#> Mean :5.841 Mean :3.07 Mean :3.792
#> 3rd Qu.:6.400 3rd Qu.:3.40 3rd Qu.:5.100
#> Max. :7.900 Max. :4.40 Max. :6.900
#> NA's :18 NA's :12 NA's :19
#> Petal.Width Species
#> Min. :0.100 setosa :46
#> 1st Qu.:0.300 versicolor:45
#> Median :1.400 virginica :49
#> Mean :1.228 NA's :10
#> 3rd Qu.:1.800
#> Max. :2.500
#> NA's :16Para visualizar los NAs utilizaremos la función vis_miss() del programa visdat

Figure 5.4: 5
También se puede hacer con la función aggr() del programa VIM
library(VIM)
aggr(iris.mis, col=c('navyblue','red'),
numbers=TRUE, sortVars=TRUE,
labels=names(iris.mis), cex.axis=.7,
gap=3, ylab=c("Missing data","Pattern"))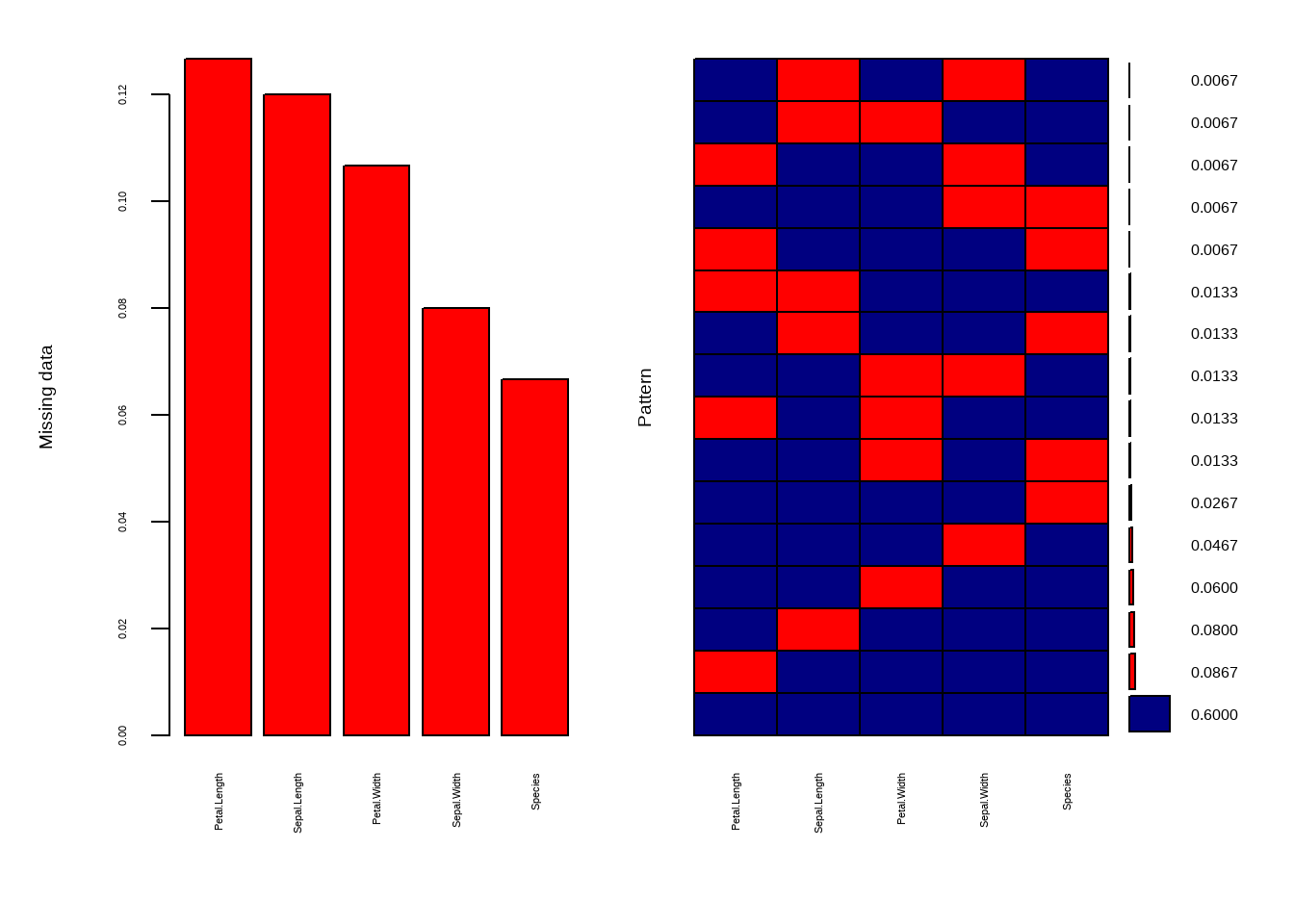
Figure 5.5: 5
#>
#> Variables sorted by number of missings:
#> Variable Count
#> Petal.Length 0.12666667
#> Sepal.Length 0.12000000
#> Petal.Width 0.10666667
#> Sepal.Width 0.08000000
#> Species 0.066666675.4.3 Identificación y eliminación datos faltantes
El método de eliminación se utiliza cuando la probabilidad de que falte una variable es la misma para todas las observaciones. La forma más común es la List Wise Deletion donde se eliminan las observaciones (filas) donde falta alguna de las variables. Este método reduce la potencia del modelo porque reduce el tamaño de la muestra.
También existe el Pairwise Deletion donde se elimina solo el valor particular resultando en diferentes tamaños de muestra para diferentes variables, por lo que no se recomienda. En R, los valores faltantes están codificados por el símbolo NA (not available). Se utilizará la función is.na() para identificarlos, la función complete.cases() para escoger las filas que tienen datos completos y na.omit() para eliminar las filas con NAs.
5.4.4 Imputación simple
La imputación es un método para completar los valores faltantes con valores estimados como por ejemplo la media, moda, mediana o al azar. El objetivo es emplear relaciones conocidas que puedan identificarse en los valores válidos del conjunto de datos para ayudar a estimar los valores faltantes.
Se reemplazan los datos faltantes para un atributo por la media o la mediana (atributo cuantitativo) o la moda (atributo cualitativo). La imputación puede ser general, es decir cuando se calcula la media o la mediana de todos los valores no faltantes y se aplica para todos los valores faltantes. La imputación también puede ser por caso, por ejemplo, cuando se calcula y remplaza la media de acuerdo a alguna de las variables factoriales p.e. año, sexo, región, etc.
5.4.4.1 Imputación simple con el programa Hmisc
Hmisc es un paquete de propósitos múltiples útil para el análisis de datos, gráficos de alto nivel, imputación de valores perdidos, creación avanzada de tablas, ajuste de modelos y diagnósticos (regresión lineal, regresión logística y regresión cox), etc.
La función impute() imputa el valor faltante mediante el método estadístico definido por el usuario (media, maximo, mediana). El valor predeterminado es la mediana.
5.4.4.2 Imputación simple con el programa mice
El paquete mice (Multivariate Imputation via Chained Equations) implementa un método para tratar los datos que faltan. El paquete crea imputaciones múltiples (valores de reemplazo) para datos faltantes multivariados. El método se basa en la especificación totalmente condicional, donde cada variable incompleta se imputa mediante un modelo separado. El algoritmo puede imputar mezclas de datos continuos, binarios, categóricos desordenados y ordenados. Es uno de los paquetes más utilizados en ciencia de datos para este propósito. La función mice() asume los datos faltantes al azar.
En el siguiente ejemplo se hará la imputación calculando la media. El argumento maxit se utiliza para definir el número de iteraciones sobre las cuales se realiza el cálculo. La función mice::complete()se utiliza para rellenar los datos faltantes con los valores calculados.
5.4.5 Imputación por modelado
Es uno de los métodos sofisticados para manejar los datos faltantes. Se crea un modelo predictivo para estimar valores que sustituirán los datos faltantes.
Pasos
Se divide el conjunto de datos en dos subconjuntos: un conjunto sin valores faltantes para la variable y otro con valores faltantes. El primer conjunto de datos se convierte en el conjunto de datos de entrenamiento del modelo, mientras que el segundo conjunto es el conjunto de datos de prueba y la variable con valores perdidos se trata como variable objetivo.
Creación de modelo: Se crea un modelo para predecir la variable de destino en función de otros atributos del conjunto de datos de entrenamiento y reemplazan los valores perdidos del conjunto de datos de prueba. Se puede usar regresión, ANOVA, regresión logística y varias técnicas de modelado.
Limitaciones:
- Los valores estimados del modelo suelen “comportarse” mejor que los valores reales.
- Debe existir alguna relación entre las variables, sino el modelo no será preciso para estimar los valores faltantes.
5.4.5.1 Imputación por modelado con Hmisc
La función aregImpute() del programa Hmisc permite la imputación de la media mediante el uso de modelos tipo additive regression, bootstrapping, y predictive mean matching(pmm). En bootstrapping, se utilizan diferentes muestras de bootstrap para cada una de las múltiples imputaciones. Luego, se ajusta un modelo aditivo (no paramétrico) en las muestras tomadas con reemplazos. Luego, utiliza predictive mean matching para imputar los valores perdidos. Además, esta técnica tiene la ventaja que identifica automaticamente tipo de variable. Inclusive, se puede calcular un valor de \(r^2\) de los valores predichos por variable.
Supuestos: a) Se asume linealidad en las variables que se están pronosticando. b) Utiliza el método de puntuación óptimo de Fisher para predecir variables categóricas.
library(Hmisc)
data(iris)
iris.mis <- prodNA(iris, noNA = 0.1)
impute_arg <- aregImpute(~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width+Species, data = iris.mis, n.impute = 5)
impute_arg
impute_arg$imp$Petal.WidthPara generar el set de datos resultante, con los valores imputados marcados con un asterisco se utiliza la función impute.transcan()
completeData2 <- impute.transcan(impute_arg, imputation=1, data=iris.mis, list.out=TRUE,pr=FALSE, check=FALSE) #dataset con datos imputados en asterisco
completeData25.4.5.2 Imputación por modelado con mice
La creación de múltiples imputaciones en comparación con una sola imputación (como la media) resuelve la incertidumbre en los valores faltantes. Algunos de los métodos múltiples del programa mice incluyen: PMM (Predictive Mean Matching) para variables numéricas (uno de los más robustos), logreg (Logistic regression) para variables binarias y polyreg (Bayesian polytomous regression) para variables factoriales.
A continuación una imputación múltiple utilizando la función mice() y un modelo bayesiano de regressión linear con el método norm
library(mice)
iris.mis <- prodNA(iris, noNA = 0.1)
iris.mis <- subset(iris.mis, select = -c(Species))
imputed_Data1 <- mice(iris.mis, m=5, maxit = 50, method = 'norm', seed = 123)
completeData1 <- mice::complete(imputed_Data1,2) #selecciona dataset2
completeData1Ejercicio 1. De la base de datos data(palmerpenguins) elimine la columna year y las filas con NAs en la variable sexo. Impute los datos faltantes utilizando una imputación por modelado con el método “pmm” y seleccionando para el relleno los datos del dataset 3.
5.4.6 Imputación usando Machine Learning con missForest
El paquete missForest (Nonparametric Missing Value Imputation using Random Forest) es una implementación de algoritmo de Random Forest para imputar datos. Es un método de imputación no paramétrica aplicable a varios tipos de variables.
El método no hace suposiciones explícitas sobre la forma funcional de f (cualquier función arbitraria). Construye un modelo de Random Forest para cada variable. Luego usa el modelo para predecir los valores faltantes en la variable con la ayuda de los valores observados. Estima el error de imputación OOB (out of Bag).
Además, proporciona un alto nivel de control en el proceso de imputación. Tiene opciones para calcular el OOB por separado (para cada variable) en lugar de agregarse a toda la matriz. Esto ayuda a observar más de cerca la precisión con la que el modelo ha imputado valores para cada variable. Además, funciona bien en variables categóricas, por lo no es necesario eliminarlas.
library(missForest)
iris.mis <- prodNA(iris, noNA = 0.1)
iris.imp <- missForest(iris.mis, ntree=500)
iris.imp$ximp # ver datos integradosUna fortaleza de este método es que permite evaluar el error de la predicción usando el NRMSE (normalized mean squared error) para las variables continuas, y el PFC (proportion of falsely classified) para las variables categóricas.
iris.imp$OOBerrorTambién se puede comparar la exactitud respecto a datos reales y el porcentaje de error de imputacion para variables continuas y categoricas
iris.err <- mixError(iris.imp$ximp, iris.mis, iris)
iris.err 5.5 Recursos Complementarios
- https://link.springer.com/content/pdf/10.1007/978-1-4419-9890-3.pdf
- https://topepo.github.io/caret/pre-processing.html
- https://bookdown.org/mwheymans/bookmi/multiple-imputation.html
- https://edisciplinas.usp.br/pluginfile.php/3518820/mod_resource/content/1/DataMiningWithR.pdf
- https://www.dcc.fc.up.pt/~ltorgo/DataMiningWithR/book.html
- https://medium.com/coinmonks/dealing-with-missing-data-using-r-3ae428da2d17
- https://rmisstastic.netlify.app/tutorials/josse_tierney_bookdown_user2018tutorial_2018
- https://doi.org/10.1007/s00357-017-9220-3
Solución a ejercicios
Ejercicio 1
library(palmerpenguins)
library(dplyr)
library(mice)
penguins_df <- penguins %>% select(-year)
penguins_df <- penguins_df %>% filter(!is.na(sex))
imputed_Data1 <- mice(penguins_df, m=5, maxit = 50, method = 'pmm', seed = 123)
completeData1 <- complete(imputed_Data1,3)
completeData1
# Elegante
imp_penguins <- complete(mice(data = penguins_df,
method = "pmm"), 3)
imp_penguins