Capítulo 9 Análisis de Redes

El principal objetivo del análisis de redes es describir los patrones de las relaciones entre los elementos que la forman. En el análisis de redes no interesa tanto él qué, sino el con quién.
En ciencias naturales este tipo de análisis es muy útil para establecer hipótesis de relaciones o asociaciones entre elementos pertenecientes a diferentes grupos.

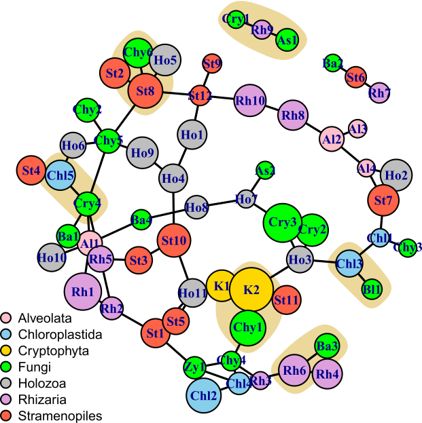
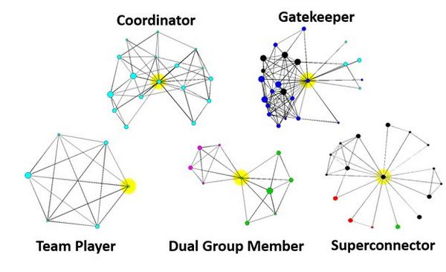
Otra utilidad importante de los análisis de redes es que permiten identificar elementos que desempeñan diferentes papeles clave para toda la red.

Los análisis de redes se basan en la teoría de grafos, la cual es una rama de las matemáticas que estudia las propiedades de los grafos (gráficos). Un grafo es conjunto de puntos (NODOS o VÉRTICES) unidos por líneas (ARCOS o ARISTAS). Permiten estudiar las interacciones entre los nodos y además ser modelados con diferentes algoritmos.

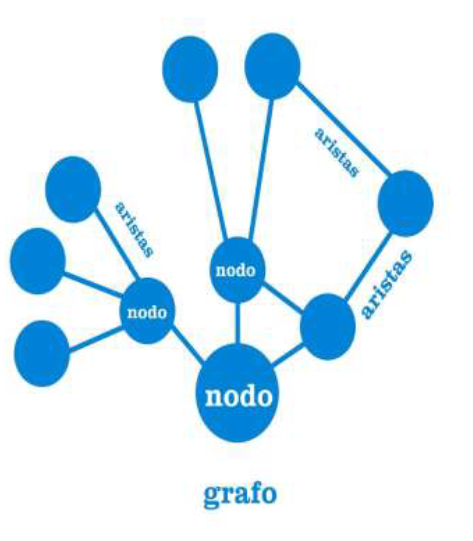
Elementos de un grafo. Imagen tomada de https://www.academia.edu/11309530/big_data_teoria_de_grafos

Grafo

Esquemáticamente un grafo se puede representar de la siguiente forma:

G = (V,E)

V es el conjunto de vértices o nodos

\(V=V_{1}, V_{2}, ..V_{n}\)
Representan los objetos concretos

E es el conjunto de arcos o aristas

\(E =V_{i}V_{j}, V_{m}V_{n}, ..\)
Representan las relaciones

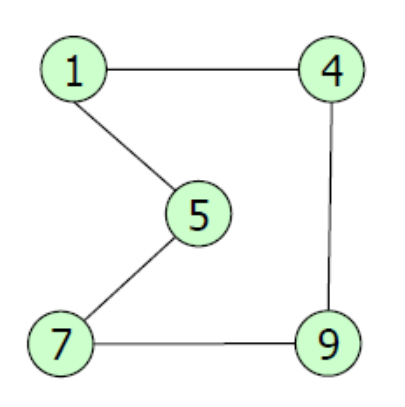
Imagen tomada de https://slideplayer.es/slide/11783363/

V = {1, 4, 5, 7, 9}
E= {(1,4), (4,9), (9,7), (7,5), (5,1), (4,1), (1,5), (5,7), (7, 9), (9,4)}

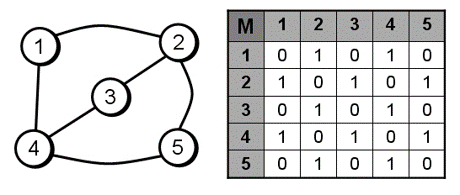
Matriz de adyacencia

Los análisis de redes de basan en matrices de adyacencia, la cual es una matriz booleana de dimensión n x n utilizada para representar un gráfico. Se crea una matriz cero, cuyas columnas y filas representan los nodos del grafo. Por cada arista que une a dos nodos, se suma 1 al valor que hay actualmente en la ubicación correspondiente de la matriz.

Métricas para análisis de redes

Métrica	Descripción
Grado	Es el número de conexiones asociadas a un vértice
Centralidad	Una medida de la importancia de un nodo en una red
Cercanía	Promedio de las distancias más cortas desde un nodo hacia todos los demás
Intermediación	El número de veces que un nodo actúa como un puente a lo largo del camino más corto entre otros dos nodos
Coeficiente de agrupamiento	Una medida de la probabilidad de que dos nodos vinculados a un nodo se asocien entre si

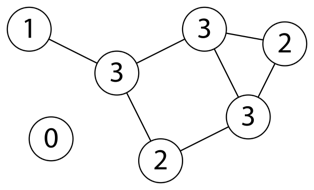
Grafo según grado

Topología de red

La topología de red es la disposición de los elementos (enlaces, nodos, etc.) de una red particular. La topología puede representarse física o lógicamente. La topología física se refiere a la ubicación de los diversos componentes, mientras que la topología lógica ilustra cómo fluyen los datos dentro de una red.

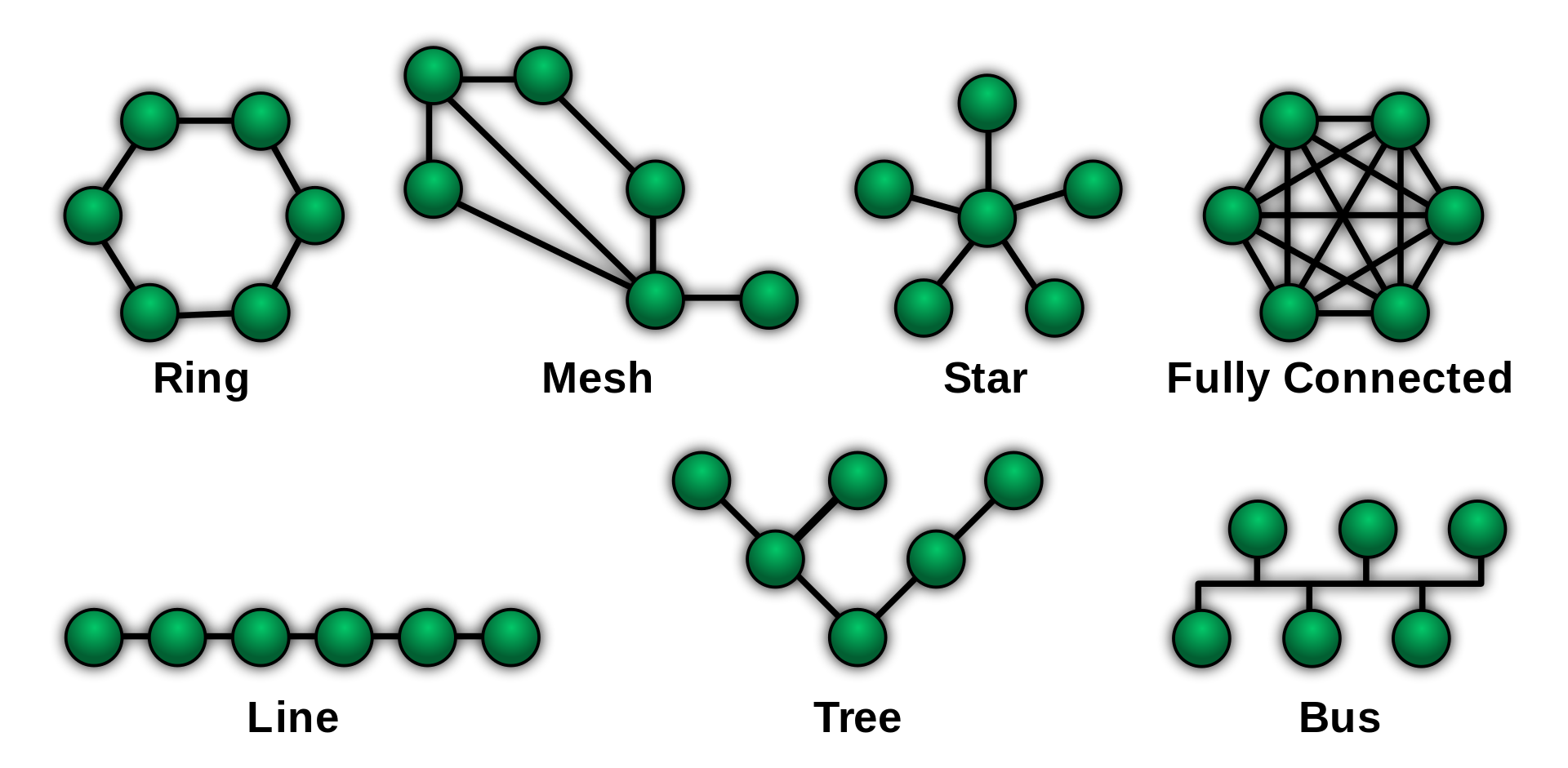
Diferentes tipos de topologías de red. Imagen tomada de https://en.wikipedia.org/wiki/Network_topology

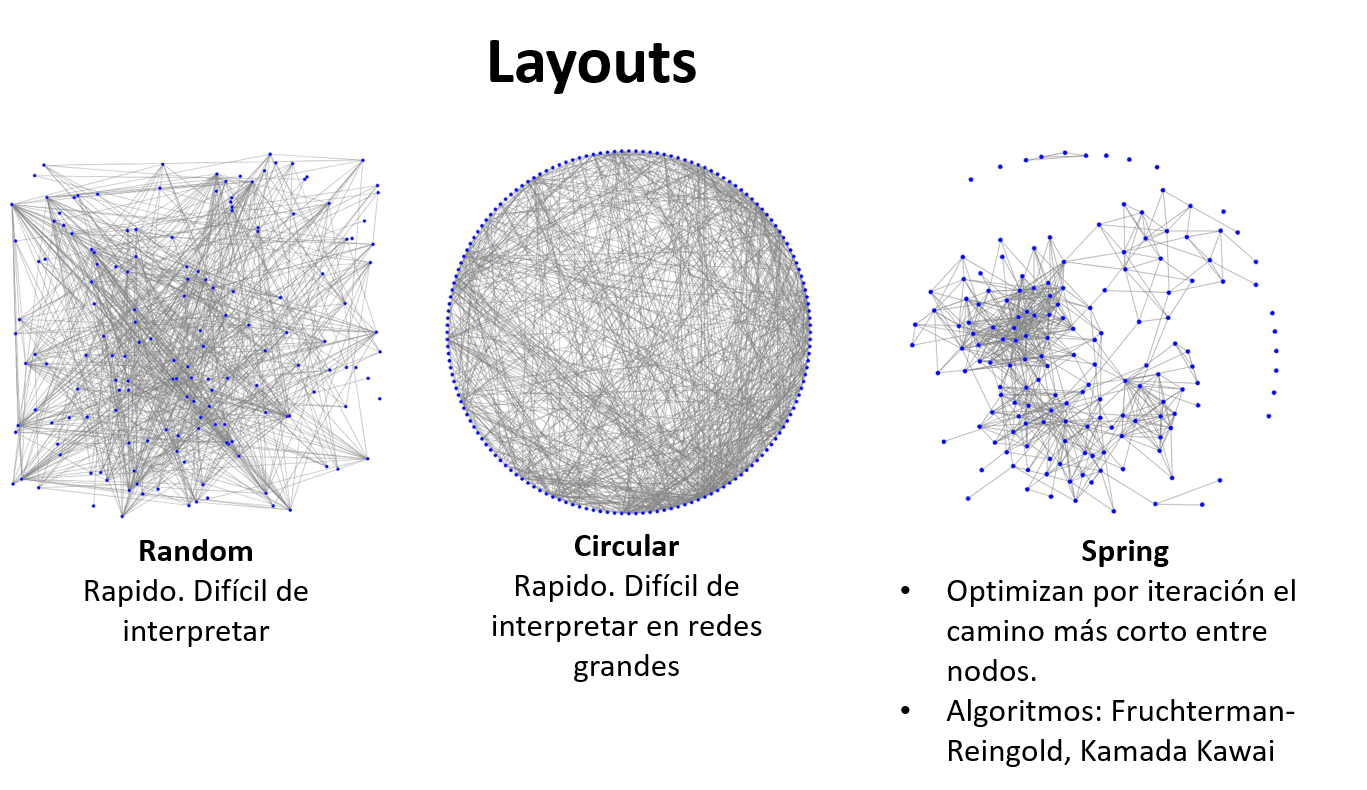
Además, dentro de algunas topologías pueden haber diferentes tipos de layouts (diseños), los cuales son estimados por diferentes algoritmos.

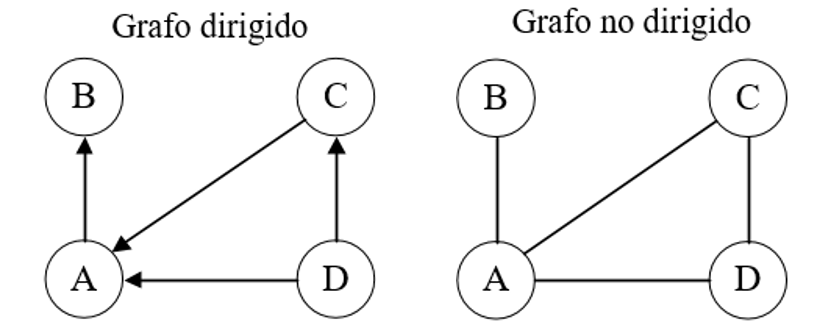
Redes dirigidas y no dirigidas

Una red dirigida es un grafo formado por un conjunto de vértices conectados por líneas con una orientación específica, de tal manera que el par ordenado \((a, b) \neq (b, a)\). Esta se diferencia de una red no dirigida, donde las lineas o aristas no tienen orientación, considerándose bidireccionales para efectos prácticos, lo que sería equivalente a decir que existen dos aristas orientadas entre los nodos, cada una en un sentido.

9.1 Creación de redes con igraph

igraph es un paquete R para el análisis de redes. Permite la implementación de algoritmos de grafos, así como el manejo rápido de grafos grandes, con millones de vértices y bordes. En el siguiente ejemplo crearemos un grafo no direccionado con la función graph().

library(igraph)
library(igraphdata)

g1 <- graph( edges=c(1,2, 2,3, 3,1), n=3, directed=F ) 
plot(g1,vertex.size=20,vertex.label.cex=.7)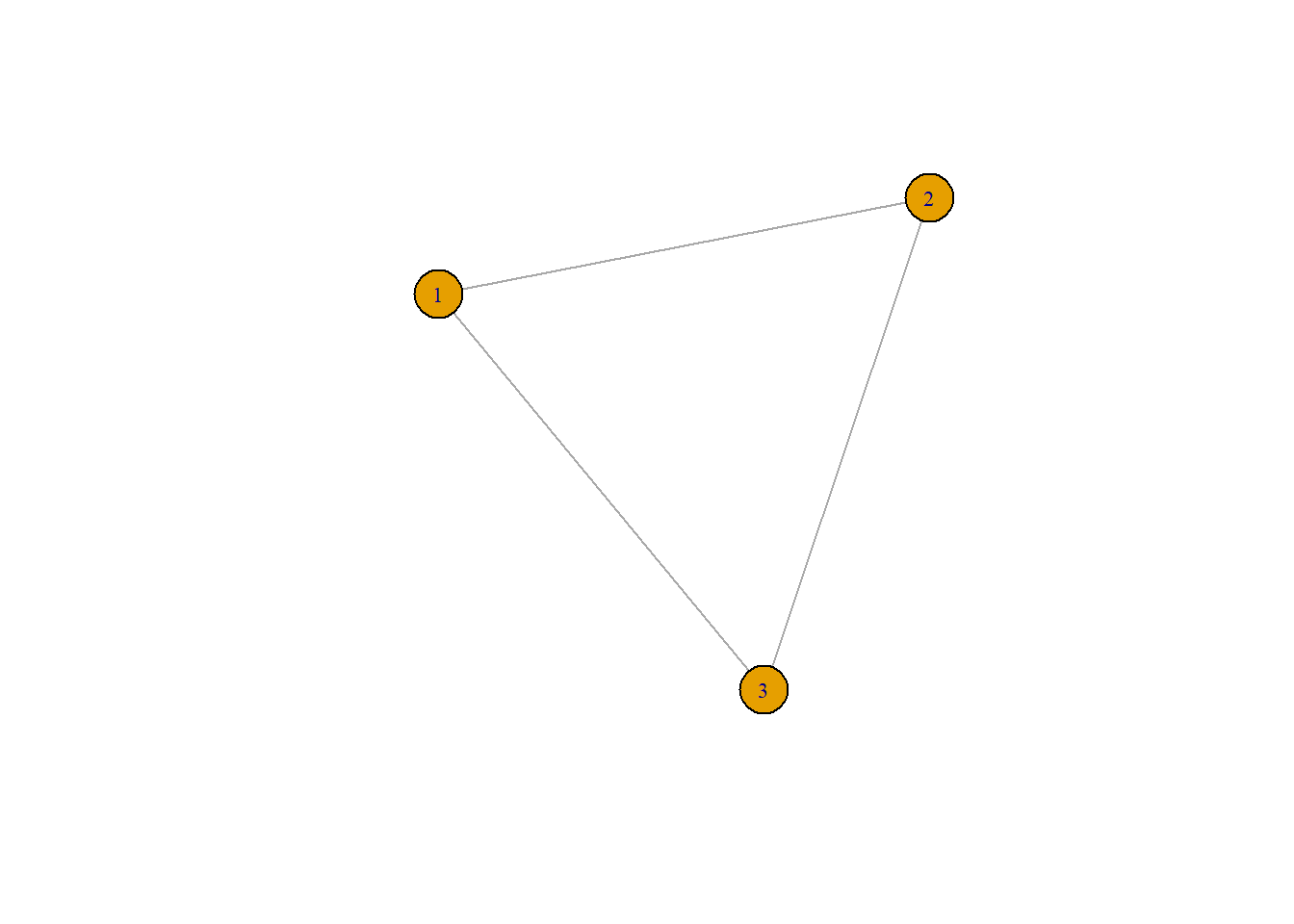

Figure 4.1: 9

tr <- make_tree(40, children = 3, mode = "undirected")
plot(tr, vertex.size=10, vertex.label=NA)

Figure 6.1: 9

kite <- make_empty_graph(directed = FALSE) + vertices(LETTERS[1:10]) +
edges('A','B', 'B','D', 'C','D', 'D','E', 'E','G', 'F','G', 'G','H', 'H','I', 'I','J')
plot(kite,vertex.label.cex=.5)

Figure 5.1: 9

data(karate)
head(as_data_frame(karate, what="edges"))
#>    from      to weight
#> 1 Mr Hi Actor 2      4
#> 2 Mr Hi Actor 3      5
#> 3 Mr Hi Actor 4      3
#> 4 Mr Hi Actor 5      3
#> 5 Mr Hi Actor 6      3
#> 6 Mr Hi Actor 7      3
head(as_data_frame(karate, what="vertices"))
#>         Faction    name label color
#> Mr Hi         1   Mr Hi     H     1
#> Actor 2       1 Actor 2     2     1
#> Actor 3       1 Actor 3     3     1
#> Actor 4       1 Actor 4     4     1
#> Actor 5       1 Actor 5     5     1
#> Actor 6       1 Actor 6     6     1

plot(karate,vertex.size=20,edge.color="orange",
     vertex.label.cex=.7)

Figure 4.6: 9

Se pueden detectar y visualizar cluster con la función cluster_label_prop()

clp <- cluster_label_prop(karate)
plot(clp, karate,vertex.label.cex=.5)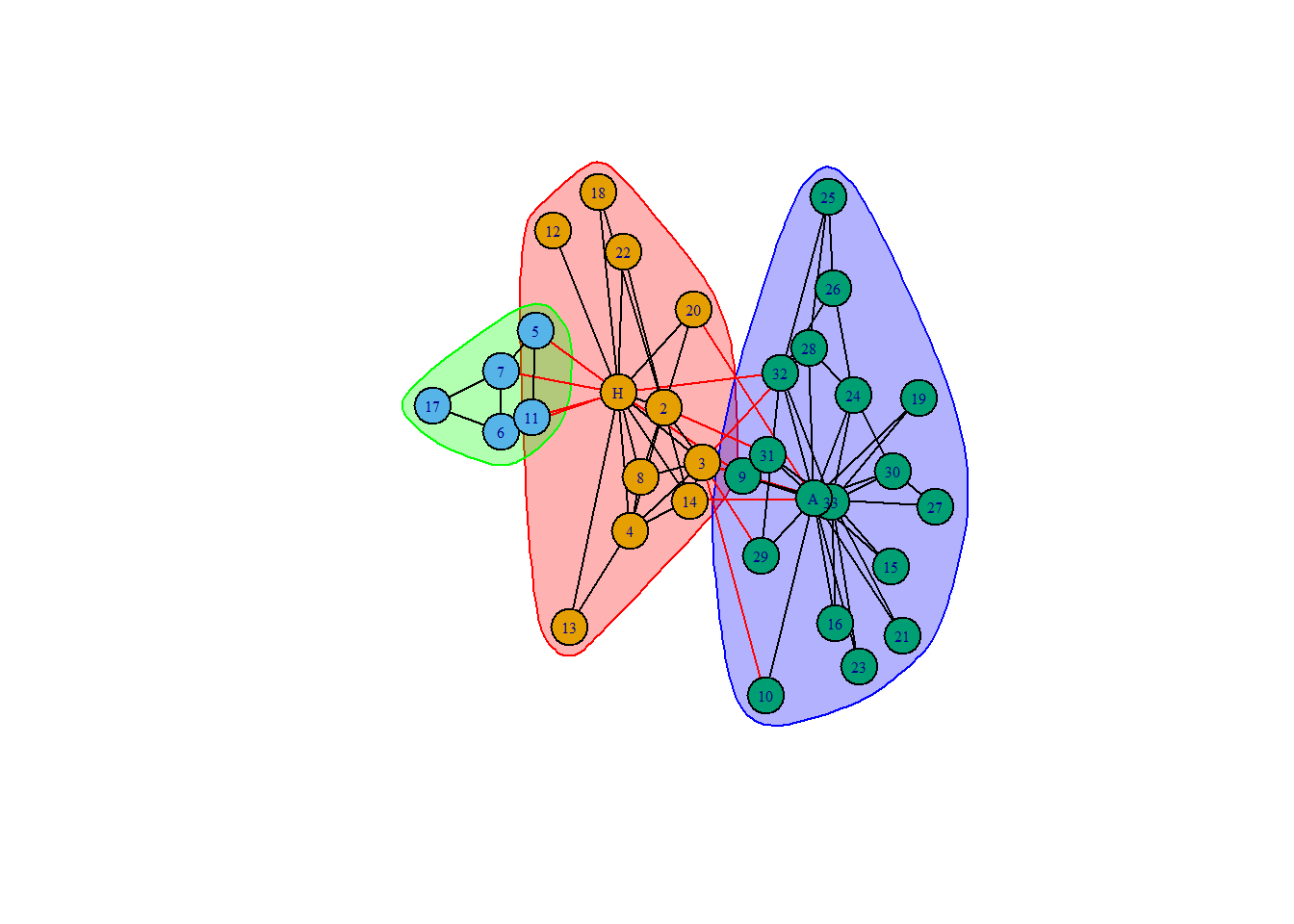

Figure 4.7: 9

Cálculo de métricas: grado, centralidad y cercanía

igraph::degree(karate, mode="in",loops = F)%>%sort(decreasing = TRUE)%>%.[1:5]
#>   John A    Mr Hi Actor 33  Actor 3  Actor 2 
#>       17       16       12       10        9
centr_degree(karate, mode="in", normalized=T,loops = F)$res%>%sort(decreasing = TRUE)%>%.[1:5]
#> [1] 17 16 12 10  9
igraph::closeness(karate, mode="all", weights=NA) %>%sort(decreasing = TRUE)%>%.[1:5]
#>      Mr Hi    Actor 3     John A   Actor 32    Actor 9 
#> 0.01724138 0.01694915 0.01666667 0.01639344 0.01562500

Tipos de layouts

net.bg <- sample_pa(80, 1.5) 
net.bg
#> IGRAPH d961133 D--- 80 79 -- Barabasi graph
#> + attr: name (g/c), power (g/n), m (g/n), zero.appeal
#> | (g/n), algorithm (g/c)
#> + edges from d961133:
#>  [1]  2-> 1  3-> 1  4-> 2  5-> 1  6-> 4  7-> 5  8-> 5  9-> 1
#>  [9] 10-> 1 11-> 5 12-> 5 13-> 1 14-> 1 15-> 1 16-> 5 17-> 1
#> [17] 18->16 19-> 1 20-> 5 21-> 1 22-> 5 23->15 24-> 5 25-> 3
#> [25] 26-> 5 27-> 1 28-> 1 29-> 1 30-> 1 31-> 1 32->18 33-> 1
#> [33] 34-> 1 35-> 1 36-> 1 37-> 1 38-> 7 39-> 1 40-> 1 41-> 1
#> [41] 42-> 1 43->17 44->13 45-> 1 46-> 1 47-> 1 48-> 1 49-> 1
#> [49] 50-> 1 51-> 5 52-> 1 53-> 5 54->25 55-> 1 56-> 1 57-> 1
#> + ... omitted several edges
V(net.bg)$size <- 8
V(net.bg)$frame.color <- "white"
V(net.bg)$color <- "orange"
V(net.bg)$label <- "" 
E(net.bg)$arrow.mode <- 0

plot(net.bg, layout=layout_randomly)#Random

Figure 4.9: 9

plot(net.bg, layout=layout_with_fr)#Fruchterman-Reingold

Figure 4.10: 9

plot(net.bg, layout=layout_in_circle)

Figure 4.11: 9

plot(net.bg, layout=layout_with_kk)#Kamada Kawai

Figure 5.2: 9

plot(net.bg, layout=layout_with_lgl)#LGL

Figure 4.12: 9

9.2 Redes interactivas con tkplot

La función tkplot() permite generar una red que se despliega en una nueva página del browser. En esa página se puede editar manualmente los nodos por ejemplo separando los que están muy juntos para tener una mejor visualización. La función tkplot.getcoords() permite registrar las nuevas coordenadas para posterior generar una versión final del gráfo de la red.

tkid <- tkplot(karate) 
l <- tkplot.getcoords(tkid) 
plot(karate, layout=l,vertex.size=20,vertex.label.cex=.7)

9.3 Redes generadas con ggraph

En ggplot2 se puede seleccionar entre una variedad de bloques de construcción visuales y agregarlos a sus gráficos uno por uno, una capa a la vez. tiempo. El paquete ggraph toma este principio y lo extiende a los datos de redes. Para el ejemplo se usa una base de datos de medios de comunicación en Estados Unidos. Cargamos el dataframe y lo transformamos en un objeto igraph con la función graph_from_data_frame()

library(ggraph)
library(igraph)
library(dplyr)
library(dplyr)
nodes=data.frame(id=c("s01","s02","s03","s04","s05","s06","s07","s08","s09","s10","s11","s12","s13","s14","s15","s16","s17"),
                    media=c("NY Times","Washington Post","Wall Street Journal","USA Today","LA Times","New York Post","CNN","MSNBC","FOX News","ABC","BBC","Yahoo News","Google News","Reuters.com","NYTimes.com","WashingtonPost.com","AOL.com"),
                    media.type=c("1","1","1","1","1","1","2","2","2","2","2","3","3","3","3","3","3"),
                    type.label=c("Newspaper","Newspaper","Newspaper","Newspaper","Newspaper","Newspaper","TV","TV","TV","TV","TV","Online","Online","Online","Online","Online","Online"),
                    audience.size=c(20,25,30,32,20,50,56,34,60,23,34,33,23,12,24,28,33))

links=data.frame(from=c("s01","s01","s01","s01","s02","s02","s02","s02","s03","s03","s03","s03","s03","s03","s03","s04","s04","s04","s04","s04","s05","s05","s05","s05","s06","s06","s06","s07","s07","s07","s07","s08","s08","s08","s09","s10","s12","s12","s12","s13","s13","s14","s14","s15","s15","s15","s16","s16","s17"),
                 to=c("s02","s03","s04","s15","s01","s03","s09","s10","s01","s04","s05","s08","s10","s11","s12","s03","s06","s11","s12","s17","s01","s02","s09","s15","s06","s16","s17","s03","s08","s10","s14","s03","s07","s09","s10","s03","s06","s13","s14","s12","s17","s11","s13","s01","s04","s06","s06","s17","s04"),
                 type=c("hyperlink","hyperlink","hyperlink","mention","hyperlink","hyperlink","hyperlink","hyperlink","hyperlink","hyperlink","hyperlink","hyperlink","mention","hyperlink","hyperlink","hyperlink","mention","mention","hyperlink","mention","mention","hyperlink","hyperlink","mention","hyperlink","hyperlink","mention","mention","mention","hyperlink","mention","hyperlink","mention","mention","mention","hyperlink","mention","hyperlink","mention","hyperlink","mention","mention","mention","hyperlink","hyperlink","hyperlink","hyperlink","mention","hyperlink"),
                 weight=c(22,22,21,20,23,21,1,5,21,22,1,4,2,1,1,23,1,22,3,2,1,21,2,21,1,21,21,1,22,21,4,2,21,23,21,2,2,22,22,21,1,1,21,22,1,4,23,21,4))
net <- graph_from_data_frame(d=links, vertices=nodes, directed=T) 
net
#> IGRAPH da1bb83 DNW- 17 49 -- 
#> + attr: name (v/c), media (v/c), media.type (v/c),
#> | type.label (v/c), audience.size (v/n), type (e/c),
#> | weight (e/n)
#> + edges from da1bb83 (vertex names):
#>  [1] s01->s02 s01->s03 s01->s04 s01->s15 s02->s01 s02->s03
#>  [7] s02->s09 s02->s10 s03->s01 s03->s04 s03->s05 s03->s08
#> [13] s03->s10 s03->s11 s03->s12 s04->s03 s04->s06 s04->s11
#> [19] s04->s12 s04->s17 s05->s01 s05->s02 s05->s09 s05->s15
#> [25] s06->s06 s06->s16 s06->s17 s07->s03 s07->s08 s07->s10
#> [31] s07->s14 s08->s03 s08->s07 s08->s09 s09->s10 s10->s03
#> + ... omitted several edges

Ahora generamos el gráfico de la red

ggraph(net, layout="lgl") +
  geom_edge_link() + 
  geom_node_point(aes(size = audience.size))+
  theme_void()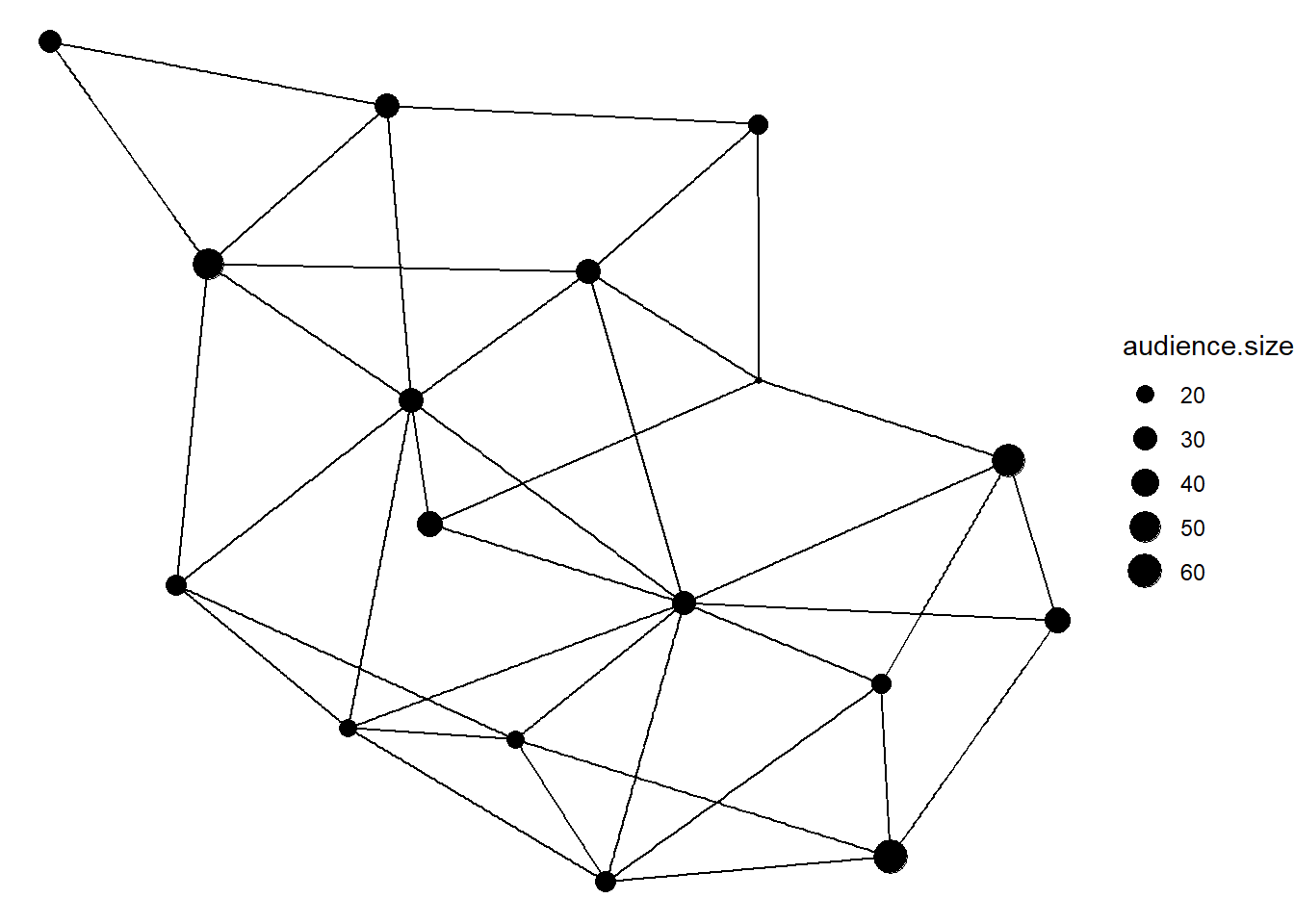

Figure 5.3: 9

9.4 Redes generadas con statnet

statnet es un conjunto de paquetes R para la gestión, exploración, análisis estadístico, simulación y visualización de datos de redes. El modelado estadístico se basa en modelos de gráficos aleatorios de familia exponencial (ERGM: Exponential-family Random Graph Models).

Incluye herramientas para estimación del modelo, simulación de redes, visualización de redes,evaluación del modelo. Desarrollado por el algoritmo Markov chain Monte Carlo (MCMC). Para el ejemplo usaremos un conjunto de datos de los lazos matrimoniales y comerciales entre las familias florentinas del Renacimiento.

library(statnet)
library(dplyr)
library(ergm) 
data(florentine) 

wealth=flomarriage %v% 'wealth' # %v% para vertex attributes
plot(flomarriage, vertex.cex=wealth/25,main="Florentine marriage by wealth", cex.main=0.8, label= "vertex.names",label.cex=0.5)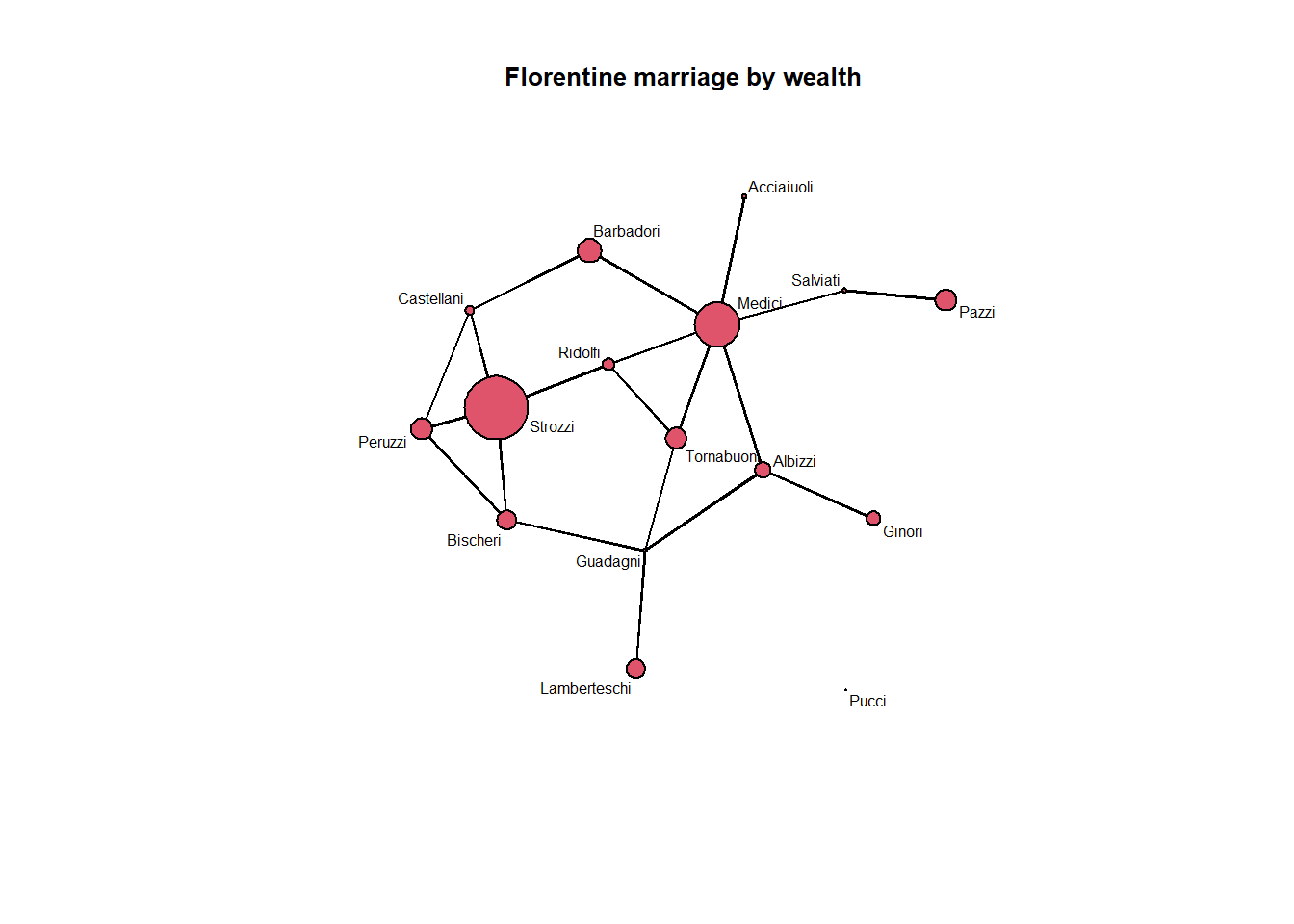

Figure 9.1: 9

summary(flomarriage~edges+triangle+kstar(1:3)+degree(0:5))
#>    edges triangle   kstar1   kstar2   kstar3  degree0 
#>       20        3       40       47       34        1 
#>  degree1  degree2  degree3  degree4  degree5 
#>        4        2        6        2        0

9.5 Redes interactivas generadas con visNetwork

Con el paquete visNetwork también se pueden generar grafos que se aprecian muy bien a la vista y a los cuales incluso se les puede mover los nodos de forma interactiva

library("visNetwork") 
visNetwork(nodes, links, height="600px", width="100%", main="Network!")

Figure 6.2: 9

Ahora, el mismo gráfico con un poco más de detalles

nodes$shape <- "dot"  
nodes$shadow <- TRUE 
nodes$title <- nodes$media 
nodes$label <- nodes$type.label
nodes$size <- nodes$audience.size 
nodes$borderWidth <- 2 

nodes$color.background <- c("slategrey", "tomato", "gold")[nodes$media.type]
nodes$color.border <- "black"
nodes$color.highlight.background <- "orange"
nodes$color.highlight.border <- "darkred"
visNetwork(nodes, links)

Figure 8.5: 9

9.6 Redes interactivas generadas con ndtv

El paquete ndtv permite producir animaciones digitales que se despliegan en una nueva página del browser. Para el ejemplo utilizamos la base de datos de redes de negocios de las principales familias de Florencia, Italia, durante el renacimiento.

library("ndtv")
data(short.stergm.sim)
short.stergm.sim 
head(as.data.frame(short.stergm.sim))
plot(short.stergm.sim)
plot( network.extract(short.stergm.sim, at=1) )#tiempo1
plot( network.extract(short.stergm.sim, onset=1, terminus=5, rule="all") )
plot( network.extract(short.stergm.sim, onset=1, terminus=10, rule="any") ) 
render.d3movie(short.stergm.sim,displaylabels=TRUE)

9.7 Recursos Complementarios

8 Análisis de Series de Tiempo

10 Redes Neuronales Artificiales y Aprendizaje Profundo