Skip to main content

Ciencia de Datos para Ciencias Naturales

Capítulo 10 Redes Neuronales Artificiales y Aprendizaje Profundo

El Aprendizaje Profundo (Deep Learning) consiste en un subconjunto de algoritmos de Machine Learning utilizados para modelar abstracciones de alto nivel, por medio de arquitecturas compuestas de transformaciones no lineales.

El aprendizaje profundo utiliza un enfoque iterativo para revisar los datos y llegar a conclusiones. Se utiliza para tareas de procesamiento más complejas que los sistemas de aprendizaje supervisado.

El aprendizaje profundo impulsó aún más el equilibrio entre complejidad e interpretabilidad. Aunque es un subconjunto de machine learning, comúnmente se trata como un campo completamente nuevo debido a sus principios específicos y las muchas arquitecturas que son específicas para tareas fuera del alcance del machine learning tradicional.

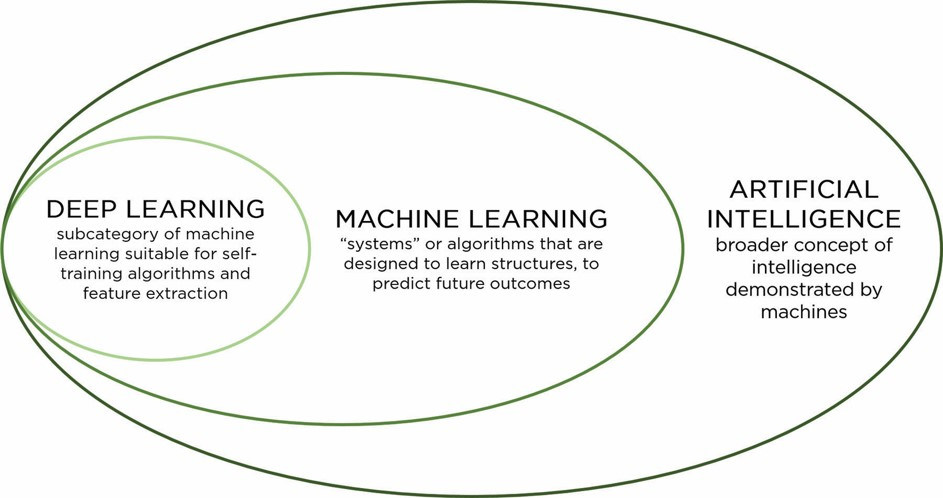
Contexto del aprendizaje profundo

Ventajas

  • Modelos son robustos y tolerantes a fallas
  • Tienen una altísima plasticidad y gran adaptabilidad
  • Pueden manejar información difusa, con ruido o inconsistente.
  • Procesan la información en paralelo
  • Poseen un alto nivel de tolerancia a fallas
  • Pueden trabajar en sistemas no lineales
  • Flexibles, se ajustan a nuevos ambientes de aprendizaje
  • Aprenden de ejemplos

Limitaciones

  • No se puede identificar claramente el mecanismo con el cual han resuelto un problema
  • No existe una metodología para establecer tipo de red, cantidad de neuronas de capa escondida y cantidad de capas escondidas.
  • Modelos pueden resultar difíciles de entender

10.1 Las neuronas: el modelo natural

Las neuronas son células especializadas del sistema nervioso cuya función principal es recibir, procesar y transmitir información a través de señales químicas y eléctricas. Están especializadas en la recepción de estímulos y conducción del impulso nervioso (en forma de potencial de acción) entre ellas mediante conexiones llamadas sinapsis.

Las neuronas están compuestas por las dendritas que reciben las señales que provienen de otras neuronas. El cuerpo celular integra las señales provenientes de dendritas. Produce señal eléctrica denominada potencial de acción y coordina las actividades metabólicas de la célula. El axón conduce potenciales de acción a largas distancias y las sinapsis trasmiten las señales de una célula a otras.

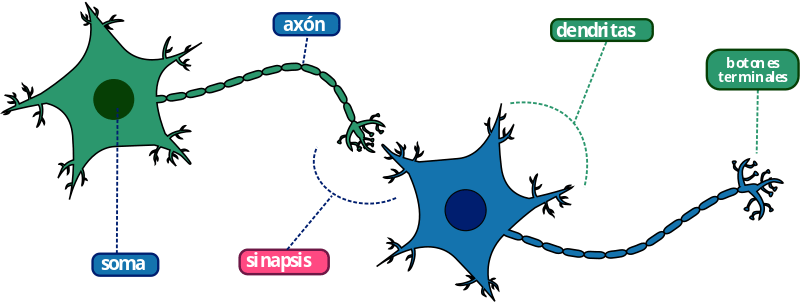
Estructura de las neuronas. Imagen tomada de https://genotipia.com/la-enfermedad-de-parkinson/neuronas-3/

Un potencial de acción es una onda de descarga eléctrica. Es un cambio muy rápido en la polaridad de la membrana de negativo a positivo y vuelta a negativo, en un ciclo que dura unos milisegundos. Se utilizan para enviar mensajes entre células nerviosas (sinapsis) o desde células nerviosas a otros tejidos. Los potenciales de acción son el camino fundamental de transmisión de códigos neurales. Los potenciales de acción se desencadenan cuando una despolarización inicial alcanza un umbral. Este potencial normalmente está en torno a –55 milivoltios sobre el potencial de reposo de la célula.

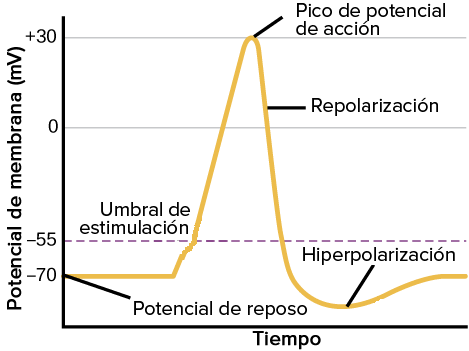
Potencial de acción de las neuronas. Imagen modificada de “Cómo se comunican las neuronas: figura 3”, de OpenStax College, Biología (CC BY 3.0)

Las redes neuronales naturales son, entonces, un sistema de neuronas que permite procesamiento cerebral de la información. Son altamente complejas, no lineales y con procesamiento paralelo.

10.2 Redes Neuronales Artificiales

Las redes neuronales artificiales son un modelo computacional inspirado en neuronas biológicas que contiene un conjunto de unidades conectadas entre sí para transmitir señales. Cada neurona está conectada con otras a través de enlaces. En los enlaces el valor de salida de la neurona anterior es multiplicado por un valor de peso. Sistemas aprenden y se forman a sí mismos, en lugar de ser programados.

Las redes neuronales funcionan combinando millones de ejemplos de datos de entrenamiento e identificando automáticamente correlaciones sutiles entre muchas variables. Una vez entrenado, el algoritmo puede usar su banco de asociaciones para interpretar nuevos datos.

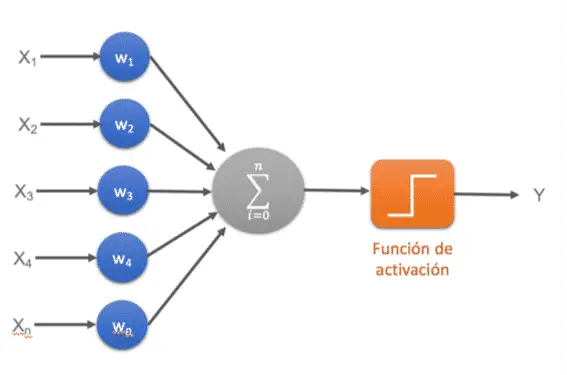
La neurona artificial es la unidad de procesamiento de la información. Es el dispositivo de cálculo con entradas, salida y memoria que puede ser realizada mediante software o hardware.

La neurona artificial posee varias entradas que son ponderadas, sumadas y comparadas con un umbral. La señal computada es tomada como argumento para una función de transferencia no lineal, la cual puede tener diferentes formas. Luego proporciona una única salida.

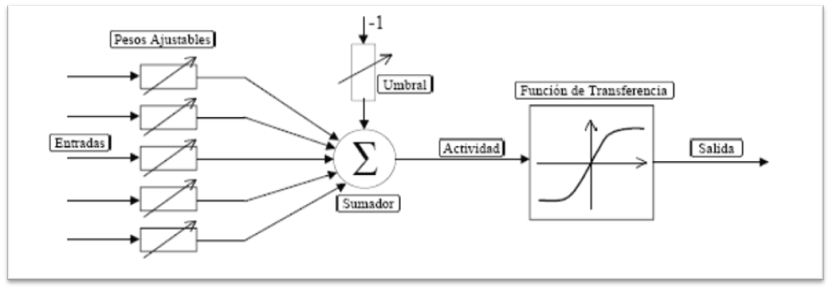
Las neuronas artificiales tienen los siguientes elementos:

  • Conjunto de entradas
  • Pesos sinápticos
  • Función de activación o transferencia
  • Sesgo o error

Las siguientes son algunas de las funciones de transferencia más utilizadas en redes neuronales

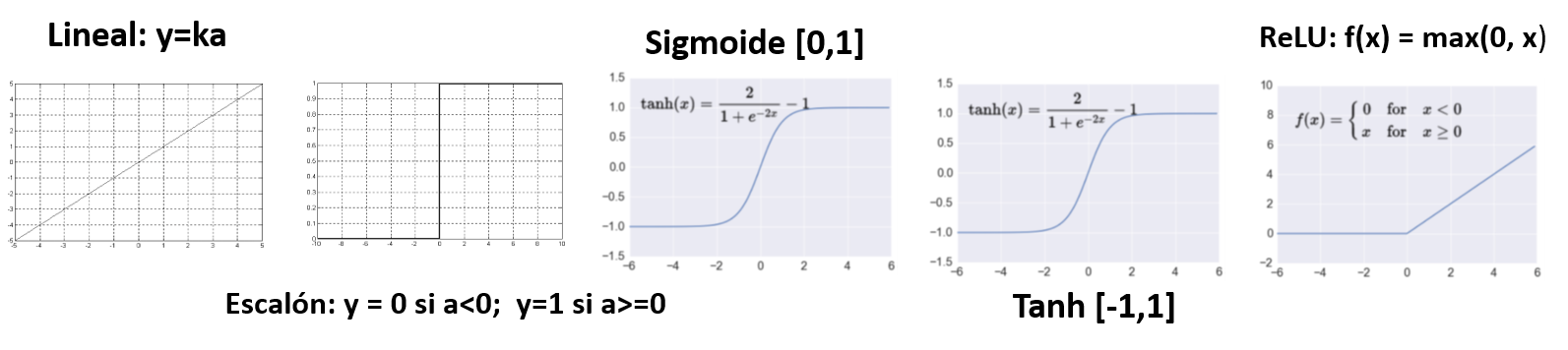
Mecanismo de Aprendizaje
En biología se acepta que la información memorizada en el cerebro se relaciona con los valores sinápticos de las conexiones. En las Redes Neuronales Artificiales se considera que el conocimiento se encuentra representado en los pesos de las conexiones. El proceso de aprendizaje se basa en cambios en estos pesos.

Los cambios en el proceso de aprendizaje se reducen a destrucción, modificación y creación de conexiones entre las neuronas. La creación de una conexión implica que el peso de la misma pasa a tener un valor distinto de cero. Una conexión se destruye cuando su valor pasa a ser cero.

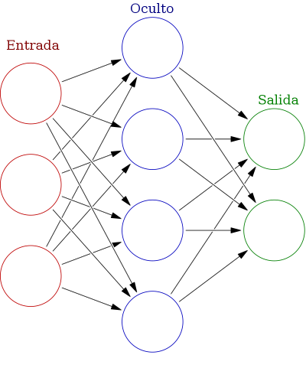
La red neuronal artificial aprende acerca de su ambiente a través de un proceso interactivo de ajustes de sus pesos sinápticos y niveles de sesgo (bias). El aprendizaje puede ser supervisado (set de entrenamiento) o no supervisado (no hay un set de entrenamiento pero se sabe donde se quiere llegar).

Las redes neuronales están compuestas por tres tipos capas sucesivas:

  • Entrada
  • Oculta
  • Salida

Regla Delta / Regla de Widrow-Hoff
El ajuste de un peso sináptico de una neurona es proporcional al producto de la señal de error y a la señal de entrada de la sinapsis en cuestión.

La propagación hacia atrás de errores (backpropagation)
Es un método de cálculo del gradiente utilizado para entrenar redes neuronales artificiales. El método emplea un ciclo propagación – adaptación de dos fases. Una vez que se ha aplicado un patrón a la entrada de la red como estímulo, este se propaga desde la primera capa a través de las capas siguientes de la red, hasta generar una salida. La señal de salida se compara con la salida deseada y se calcula una señal de error para cada una de las salidas. Luego, las salidas de error se propagan hacia atrás, partiendo de la capa de salida, hacia todas las neuronas de la capa oculta que contribuyen directamente a la salida.

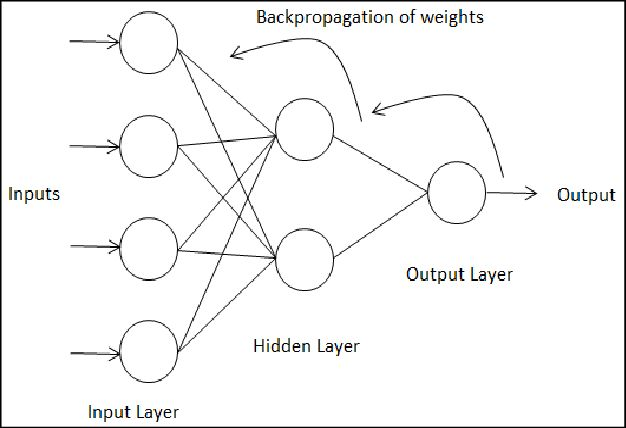
Este proceso se repite, capa por capa, hasta que todas las neuronas de la red hayan recibido una señal de error que describa su contribución relativa al error total. La importancia de este proceso consiste en que, a medida que se entrena la red, las neuronas de las capas intermedias se organizan a sí mismas de tal modo que las distintas neuronas aprenden a reconocer distintas características del espacio total de entrada.

10.3 Arquitecturas de Redes Neuronales

Durante la última década se han diversificado la cantidad, tipo y usos específicos de las redes neuronales, lo que ha resultado también en una gran cantidad de arquitecturas.

A continuación, se muestran algunos tipos más comunes de redes neuronales artificiales:

  • Red Neuronal Monocapa (Perceptrón simple): corresponde con la red neuronal más simple, está compuesta por una capa de neuronas que proyectan las entradas a una capa de neuronas de salida donde se realizan los diferentes cálculos.

Perceptrón simple. Imagen tomada de https://www.diegocalvo.es/clasificacion-de-redes-neuronales-artificiales/

  • Red Neuronal Multicapa (Perceptrón multicapa): Usadas para transformar un conjunto de datos especificado en otro también especificado. Su arquitectura típica dispone de un conjunto de capas intermedias (capas ocultas) entre la capa de entrada y la de salida. Salida depende de entradas y pesos.

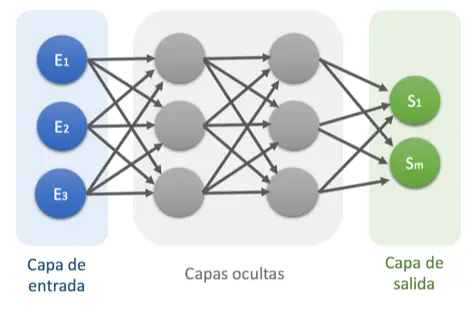
Perceptrón multicapa. Imagen tomada de https://www.diegocalvo.es/clasificacion-de-redes-neuronales-artificiales/

  • Red Neuronal Recurrente (RNN): Concebidas para almacenar eficientemente información. Salida depende de la historia pasada. No tienen una estructura de capas, sino que permiten conexiones arbitrarias entre las neuronas, incluso pudiendo crear ciclos, con esto se consigue crear la temporalidad, permitiendo que la red tenga memoria. Tienen capas especializadas para manejar series de tiempo.

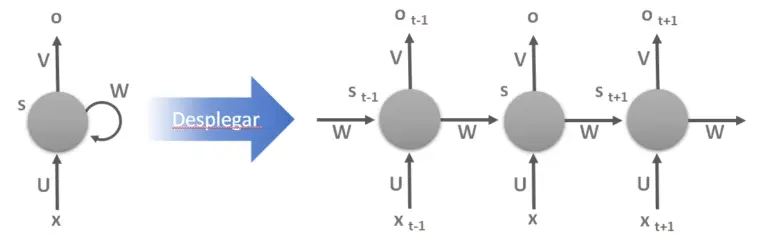
Red Neuronal Recurrente. Imagen tomada de https://www.diegocalvo.es/clasificacion-de-redes-neuronales-artificiales/

  • Redes de Base Radial (RBF): Se utilizan para estructurar la información en conjuntos de datos a priori desconocidos. Cada neurona tiene un cierto grado de conexión con neuronas colaterales. La salida es una combinación lineal de las funciones de activación radiales utilizadas por las neuronas individuales.
  • Red Neuronal Convolucional (CNN): Tipo de red neuronal donde las neuronas corresponden a campos receptivos de una manera muy similar a las neuronas en la corteza visual primaria. Son muy efectivas para tareas de visión artificial, como en la clasificación y segmentación de imágenes. La principal diferencia de la red neuronal convolucional con el perceptrón multicapa viene en que cada neurona no se une con todas y cada una de las capas siguientes sino que solo con un subgrupo de ellas (se especializa), con esto se consigue reducir el número de neuronas necesarias y la complejidad computacional necesaria para su ejecución.

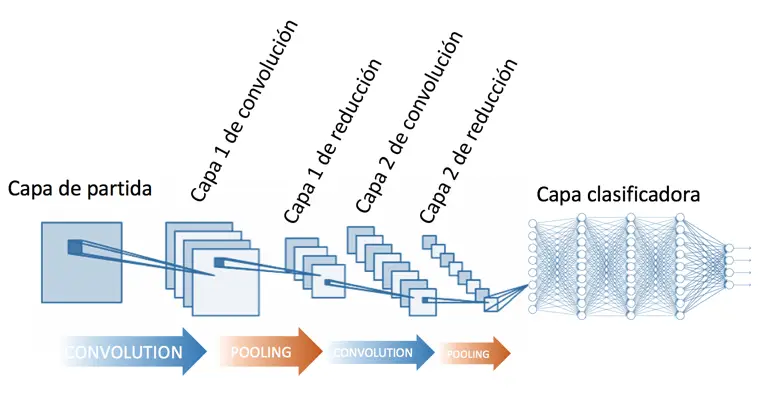
Red Neuronal Convolucional. Imagen tomada de https://www.diegocalvo.es/clasificacion-de-redes-neuronales-artificiales/

Red Neuronal Gráfica (GNN): Las redes neuronales gráficas (GNN) son un nuevo representante de la familia del aprendizaje profundo, pero están recibiendo cada vez más atención en los últimos años debido a su capacidad para procesar datos no euclidianos, como gráficos. Es una clase de red neuronal para procesar estructuras de datos representadas en gráficos. Se popularizaron por su uso en el aprendizaje supervisado de las propiedades de varias moléculas, también se aplican a dominios como redes sociales, redes de citas y comunidades en línea.

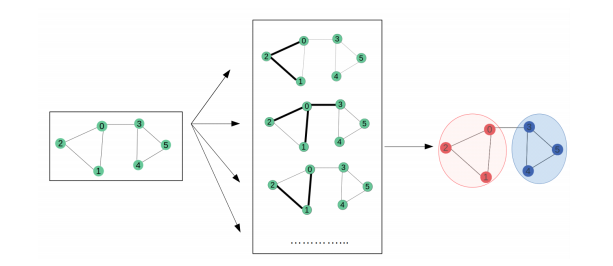
Red Neuronal Gráfica. Imagen tomada de https://medium.com/analytics-vidhya/a-review-of-graph-neural-networks-gnn-560be37b8bca

10.4 Red Neuronal Multicapa con neuralnet

Para el siguiente ejemplo haremos un analisis de redes neuronales con el programa neuralnet para realizar clasificaciones de especies con la base de datos iris.

library("neuralnet")
library("NeuralNetTools")
library("caret")
data(iris)

#Renombramos las variables de salida y hacemos partición de datos
iris$setosa <- iris$Species=="setosa"
iris$virginica <- iris$Species == "virginica"
iris$versicolor <- iris$Species == "versicolor"
iris.train.idx <- sample(x = nrow(iris), size = nrow(iris)*0.7)
iris.train <- iris[iris.train.idx,]
iris.valid <- iris[-iris.train.idx,]

Se utiliza la función neuralnet() para hacer el modelo, en este caso incluyendo dos capas ocultas con 10 neuronas cada una. Con la función plotnet() se grafica el modelo.

iris.net <- neuralnet(setosa+versicolor+virginica ~ 
                        Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, 
                      data=iris.train, hidden=c(10,10), rep = 5, err.fct = "ce", 
                      linear.output = F, lifesign = "minimal", stepmax = 1000000,
                      threshold = 0.001)
plotnet(iris.net, 
        alpha.val = 0.8, 
        circle_col = list('purple', 'white', 'white'), 
        bord_col = 'black')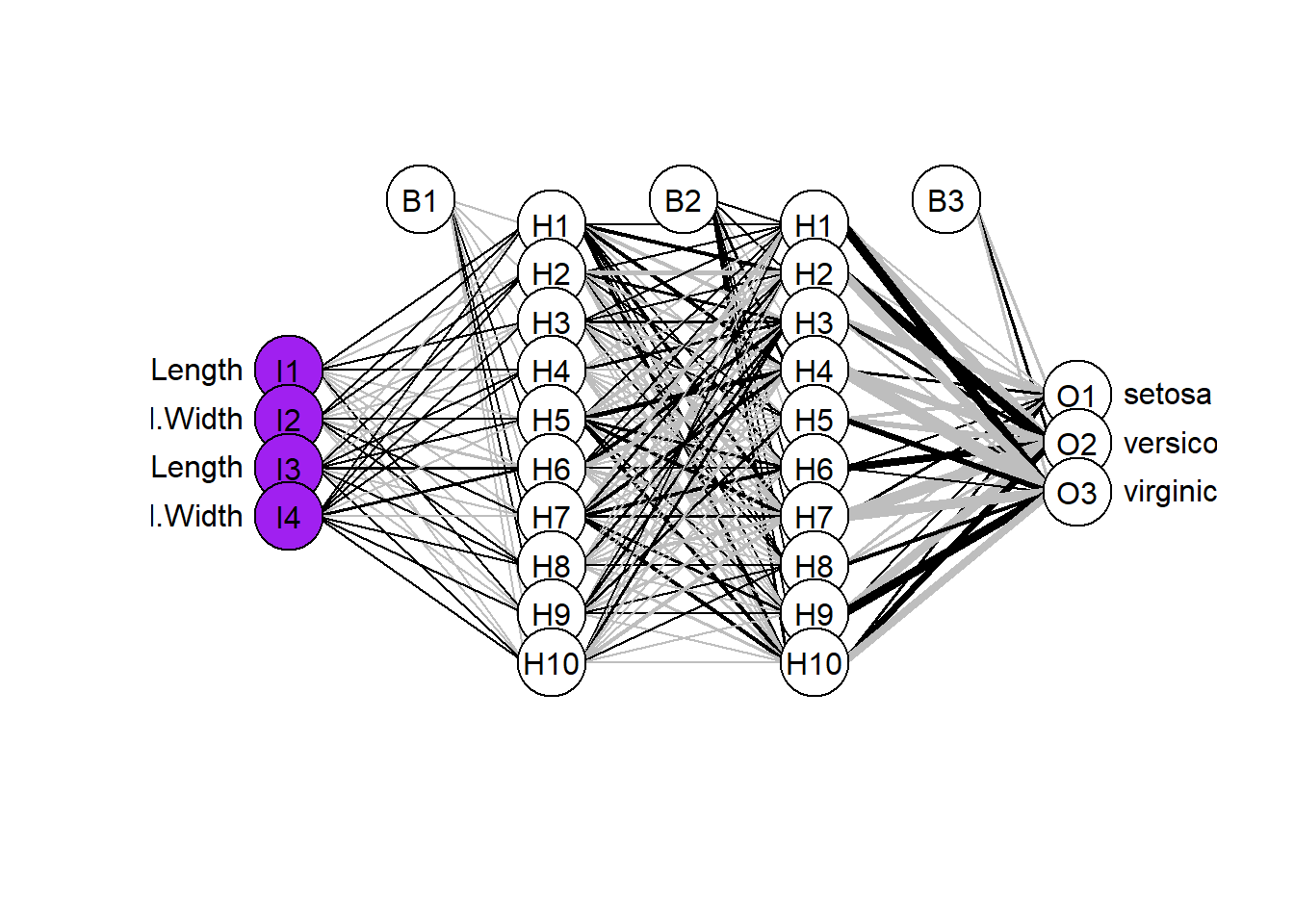

Hacemos la predicción y calculamos la matriz de confusión

iris.prediction <- compute(iris.net, iris.valid[-5:-8])
idx <- apply(iris.prediction$net.result, 1, which.max)
predicted <- c('setosa', 'versicolor', 'virginica')[idx]
table(predicted, iris.valid$Species)
#>             
#> predicted    setosa versicolor virginica
#>   setosa         16          0         0
#>   versicolor      0         16         1
#>   virginica       0          0        12

10.5 Red Neuronal Multicapa con Keras

Keras es una librería diseñada para trabajar en Python con redes neuronales. Es un sistema de código abierto capaz de correr en TensorFlow y diseñado para la experimentación rápida con redes neuronales profundas. TensorFlow por su parte es una librería diseñada para el cálculo numérico mediante gráficos de flujo de datos. Fue desarrollado por ingenieros de Google Brain para investigación en aprendizaje automático y redes neuronales profundas.

#devtools::install_github("rstudio/tensorflow")
library(tensorflow)
#install_tensorflow()
library(keras)
library(datasets)
library(tidyverse)
data(iris)
iris[,5] <- as.numeric(iris[,5]) -1
head(iris,3)
#>   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
#> 1          5.1         3.5          1.4         0.2       0
#> 2          4.9         3.0          1.4         0.2       0
#> 3          4.7         3.2          1.3         0.2       0
# asignación set entrenamiento y prueba
ind <- sample(2, nrow(iris), replace=TRUE, prob=c(0.7, 0.3))

# normalizar valores y separar sets
X.iris.training <- normalize(as.matrix(iris[ind==1, 1:4]))
X.iris.test <- normalize(as.matrix(iris[ind==2, 1:4]))

# separar set variable de respuesta
Y.iris.training <- iris[ind==1, 5]
Y.iris.test <- iris[ind==2, 5]

# transformar variable respuesta a valores (One hot encode)
YT.iris.training <- to_categorical(Y.iris.training)
YT.iris.test <- to_categorical(Y.iris.test)

# Establecer arquitectura modelo NN
DNN = keras_model_sequential() %>%
  layer_dense(units = 20, activation = 'relu', input_shape = c(4)) %>%  # primera capa
  layer_dense(units = 5, activation = 'relu', kernel_regularizer = regularizer_l1()) %>% # capa oculta
  layer_dense(units = 3, activation = 'softmax')# Capa salida con 3 neuronas y funcion activación prob. softmax 

# Compilación y optimización del modelo
DNN %>% compile(
  loss = 'categorical_crossentropy',
  optimizer = 'adam',
  metrics = 'accuracy')

# Ajuste y graficación de histórico para ver cambio en precisión y error de predicción (loss)
history <- DNN %>% fit(
  X.iris.training, 
  YT.iris.training, 
  epochs = 200,
  batch_size = 5, 
  validation_split = 0.2)
plot(history$metrics$acc, main="Model Accuracy", xlab = "epoch", ylab="accuracy", col="blue", type="l")

# Predicción y evaluación
head(predict(DNN, X.iris.test), n = 3)
evaluate(DNN, X.iris.test, YT.iris.test, verbose = 0)
#save_model_hdf5(DNN, "my_DNN.h5") #para salvar modelo

10.6 Red Neuronal Convolucional con Keras

Para el ejemplo se utilizará una Red neuronal convolucional (CNN) para clasificar imágenes del dataset CIFAR-10 El que consta de 60.000 imágenes en color de 32x32 en 10 clases, con 6000 imágenes por clase. Hay 50.000 imágenes para set de entrenamiento y 10.000 imágenes para set de prueba. Ejemplo tomado del siguiente link

Se verifican los datos

class_names <- c('airplane', 'automobile', 'bird', 'cat', 'deer',
                 'dog', 'frog', 'horse', 'ship', 'truck')
index <- 1:30

par(mfcol = c(5,6), mar = rep(1, 4), oma = rep(0.2, 4))
cifar$train$x[index,,,] %>% 
  purrr::array_tree(1) %>%
  purrr::set_names(class_names[cifar$train$y[index] + 1]) %>% 
  purrr::map(as.raster, max = 255) %>%
  purrr::iwalk(~{plot(.x); title(.y)})

Se define la base del modelo convolucional

model <- keras_model_sequential() %>% 
  layer_conv_2d(filters = 32, kernel_size = c(3,3), activation = "relu", 
                input_shape = c(32,32,3)) %>% 
  layer_max_pooling_2d(pool_size = c(2,2)) %>% 
  layer_conv_2d(filters = 64, kernel_size = c(3,3), activation = "relu") %>% 
  layer_max_pooling_2d(pool_size = c(2,2)) %>% 
  layer_conv_2d(filters = 64, kernel_size = c(3,3), activation = "relu")

Se agregan capas más densas que permiten aplanar hacer las clasificaciones

model %>% 
  layer_flatten() %>% 
  layer_dense(units = 64, activation = "relu") %>% 
  layer_dense(units = 10, activation = "softmax")

Se compila y entrena el modelo. Se desplegará una pantalla interactiva en la que se verán los cambios en los valores de loss y precisión en cada época (iteración de la corrida de todos los datos)

model %>% compile(
  optimizer = "adam",
  loss = "sparse_categorical_crossentropy",
  metrics = "accuracy")

history <- model %>% 
  fit(
    x = cifar$train$x, y = cifar$train$y,
    epochs = 10,
    validation_data = unname(cifar$test),
    verbose = 2)

Se evalúa el modelo

plot(history)
evaluate(model, cifar$test$x, cifar$test$y, verbose = 0)

10.7 Redes Neuronales recurrentes con Keras

Las redes neuronales recurrentes usan capas especializadas para manejar series de tiempo. Para el ejemplo se simula una serie de tiempo con un ARIMA simple, usando la función arima.sim(). Se pretende entrenar la red para predecir los próximos 10 puntos de tiempo en función de los 10 puntos de tiempo anteriores.

library(keras)

# Crear simulación de datos
data = as.matrix(arima.sim(n = 1000, list(ar = c(0.3, -0.7)) ))
data = matrix(data, ncol = 10L, byrow = TRUE)
X = array(data[seq(1, 100, by = 2), ], dim = c(50, 10, 1))
Y = data[seq(2, 100, by = 2), ]

# Establecer arquitectura
RNN =
  keras_model_sequential() %>%
  layer_gru(input_shape = list(10L, 1L),
            units = 50,
            activation = "relu") %>%
  layer_dense(units = 10)
# compilar y ajustar modelo
RNN %>%
  compile(loss = loss_mean_squared_error,
          optimizer = optimizer_adamax(0.01))
RNN %>%
  fit(X, Y, epochs = 50, verbose = 0)

# hacer predicción
head(predict(RNN, X), n = 3)
#>             [,1]      [,2]       [,3]       [,4]
#> [1,]  0.39035100 -1.006135 -0.5269412  0.1531326
#> [2,] -0.73223734 -1.069796  0.2831231  0.7221432
#> [3,] -0.06001849  1.272102  1.1481512 -0.7142213
#>             [,5]       [,6]       [,7]       [,8]
#> [1,]  0.41544086  0.2324742 -0.3812740 -0.9471649
#> [2,]  0.09829342 -0.2687518 -0.1069605 -0.3007618
#> [3,] -1.22208869  0.2052345  1.1249257  0.7955420
#>            [,9]      [,10]
#> [1,] -0.2273173  0.8001246
#> [2,] -0.1156124  0.4712369
#> [3,] -0.3441448 -0.8712916