Capítulo 6 Análisis de Cluster, Mapas de Calor y Análisis Multivariados

6.1 Matrices de distancia

Para determinar lo similares (o disimilares) que son dos muestras entre sí (cada muestra corresponde a una línea en un dataframe), el primer paso es calcular matrices de distancia. Estas matrices son la base para realizar otros cálculos que permiten hacer representaciones espaciales y el agrupamiento de las variables.

Cuando se analizan muchas muestras, el apreciar las diferencias entre cada par de comunidades sería complejo, por lo que interesa representar estas comunidades en un plano. La graficación de las comunidades en un plano es posible si disponemos de medidas de distancias entre las muestras.

Las distancias pueden ser estimadas a través de diferentes medidas como; distancias simétricas (por ejemplo Euclideana, Hellinger), o a través de medidas asimétricas (medidas de disimilitud, como Bray-Curtis).

Elegir una medida adecuada es esencial, ya que afectará en gran medida cómo se tratan sus datos durante el análisis y qué tipo de interpretaciones son significativas. Por ejemplo, el NMDS, el PCA y el análisis de conglomerados están fuertemente influenciados por la elección de la medida de (di)similitud utilizada.

6.1.1 Distancia euclidiana

La distancia euclidiana entre dos sitios es simplemente la longitud del vector que conecta los sitios y la podemos obtener como $\sqrt{x^2+y^2}$, donde “x” y “y” son las coordenadas (x, y) de distancia entre un par de sitios.

La distancia Euclidiana es fácil de interpretar, sin embargo, se usa poco en análisis biológicos. Normalmente los datos de la abundancia de especies en una comunidad están caracterizados por una gran cantidad de ceros (especies no encontradas) por lo que el cálculo incrementa la similitud entre comunidades que presentan ceros para la misma especie, cuando lo que vale son la especies presentes. A esto se le conoce como el efecto de doble-ceros.

6.1.2 Distancia Bray-Curtis

Una de las medidas de distancias más utilizada es la de Bray-Curtis, la cual es el opuesto del porcentaje de similitud. Se refiere a la diferencia total en la abundancia de especies entre dos sitios, dividido por la abundancia total en cada sitio.

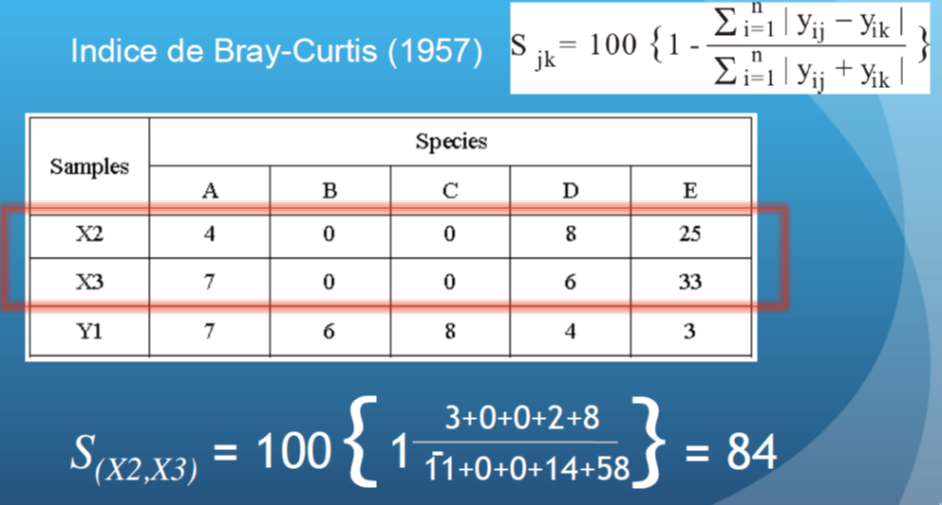
Imagen tomada de https://docplayer.es/93739615-Prof-dr-jose-jacobo-zubcoff-departamento-de-ciencias-del-mar-y-biologia-aplicada.html

Algunas ventajas de usar Bray-Curtis son las siguientes:

Dos muestras iguales toman el valor 100.
Cuando no hay especies en común el valor es 0.
No es afectado por los cambios en las unidades de medida.
No es afectado por las muestras (especies) ausentes.
No es afectado por el tamaño de muestras.
Detecta diferencias en abundancia total cuando las abundancias relativas son idénticas.

6.2 Análisis de cluster (Clustering)

La mayoría de los métodos de agrupamiento están basados en el emparejamiento de los grupos más similares con comportamiento homogéneo. Se basa en una matriz de similitud entre cada pareja de puntos. Permite representar de una manera visual la similitud (o disimilitud) entre las diferentes muestras. Cuando encuentra diferencias genera un nuevo clúster. El clustering jerárquico hace el agrupamiento por etapas e iterativamente utilizando el método de distancia mínima, máxima o media.

Limitaciones:

No funciona bien cuando los objetos están próximos.
Es sensible a los outliers.
Si un objeto se ha colocado erróneamente en un grupo al principio del proceso, ya no se puede arreglar en una etapa posterior.
El orden de representación no es único.

Para el ejemplo se utilizará la base de datos dune del programa vegan que contiene los registros de las abundancias de 30 especies de plantas en 20 sitios. Se calcula la matriz de distancia Bray-Curtis con la función vegdist() y se realiza la agrupación con la función hclust().

Procedemos a hacer una agrupación simple

library(vegan)
data(dune)
dist= vegdist((dune), "bray")
hc <- hclust(dist)
plot(hc)

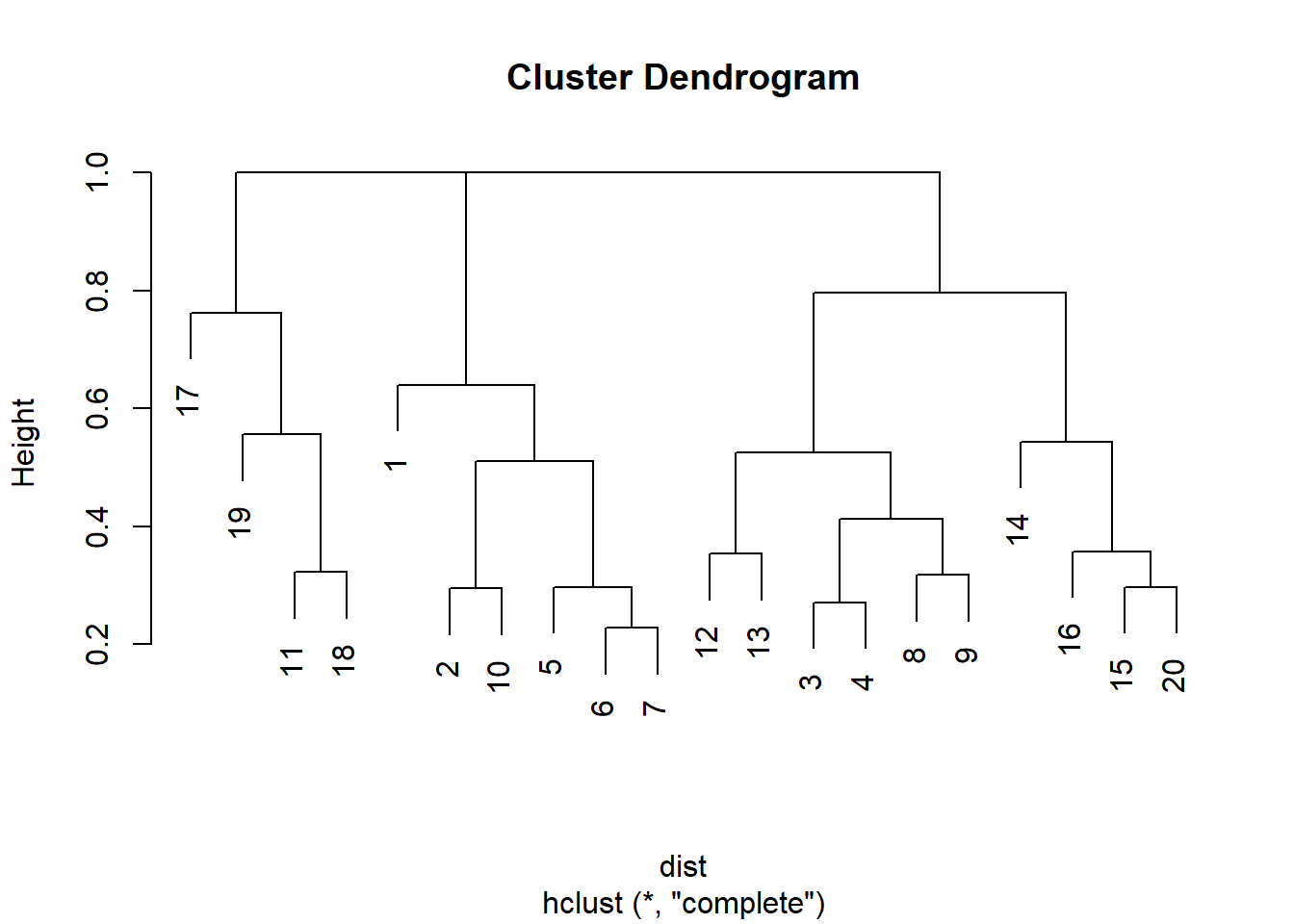
Figure 4.1: 6

También se puede hacer una agrupación un tanto más compleja agrupando por especie y por sitio

library(vegan)
data(dune, dune.taxon)
taxontree <- hclust(taxa2dist(dune.taxon))#calcula matriz de distancia a partir de sistemática de las plantas
plotree <- hclust(vegdist((dune), "bray"), "average") # vegdist para calcular matriz Bray-Curtis y la función hclust para agrupar con método promedio

tabasco(dune, plotree, sp.ind = taxontree)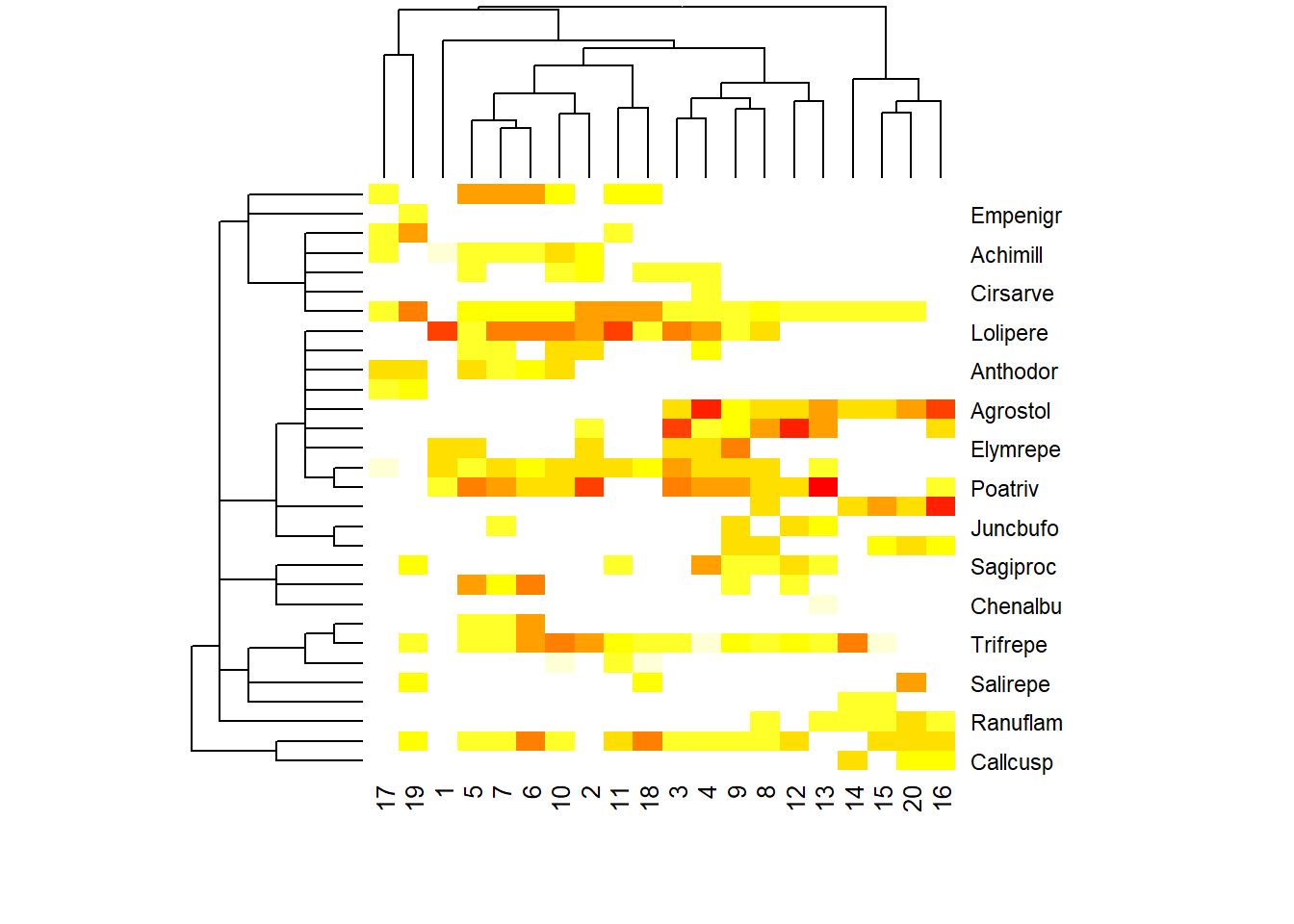

Figure 6.1: 6

6.3 Mapas de calor (Heatmaps)

Un mapa de calor es una representación gráfica de datos donde los valores individuales contenidos en una matriz se representan como colores. Es útil para mostrar un panorame general de datos numéricos. Para el ejemplo usaremos datos de un estudio de diversidad microbiana en un pozo inundado de una mina de asbesto abandonada.

Cargamos los datos

library(readr)
library(tidyr)
library("ggplot2")

url <- "https://tinyurl.com/mine-data-csv"
mine.data = read_csv(file = url)
head(mine.data)
#> # A tibble: 6 x 13
#>    Site Depth Sample.name Actinobacteria Cytophagia
#>   <dbl> <dbl> <chr>                <dbl>      <dbl>
#> 1     1   0.5 1-S                 373871       8052
#> 2     2   0.5 2-S                 332856      28561
#> 3     3   0.5 3-S                 326695      10468
#> 4     1   3.5 1-M                 409809       4481
#> 5     2   3.5 2-M                 319778      15885
#> 6     3   3.5 3-M                 445572       7302
#> # ... with 8 more variables: Flavobacteriia <dbl>,
#> #   Sphingobacteriia <dbl>, Nitrospira <dbl>,
#> #   Planctomycetia <dbl>, Alphaproteobacteria <dbl>,
#> #   Betaproteobacteria <dbl>, Deltaproteobacteria <dbl>,
#> #   Gammaproteobacteria <dbl>

Se transforma la tabla en formato ancho

mine.long <- pivot_longer(data = mine.data, 
                          cols = -c(Site, Depth, Sample.name), 
                          names_to = "Class", 
                          values_to = "Abundance")
head(mine.long)
#> # A tibble: 6 x 5
#>    Site Depth Sample.name Class            Abundance
#>   <dbl> <dbl> <chr>       <chr>                <dbl>
#> 1     1   0.5 1-S         Actinobacteria      373871
#> 2     1   0.5 1-S         Cytophagia            8052
#> 3     1   0.5 1-S         Flavobacteriia           0
#> 4     1   0.5 1-S         Sphingobacteriia         0
#> 5     1   0.5 1-S         Nitrospira               0
#> 6     1   0.5 1-S         Planctomycetia        4553

Se transforman los valores de abundancias totales y se grafica el mapa de calor con ggplot2

mine.long$Sqrt.abundance <- sqrt(mine.long$Abundance)
mine.heatmap <- ggplot(data = mine.long, 
                       mapping = aes(x = Sample.name,y = Class, 
                                     fill = Sqrt.abundance)) +
  geom_tile() +
  xlab(label = "Depth (m)") +
  facet_grid(~ Depth, switch = "x", scales = "free_x", space = "free_x") +
  scale_fill_gradient(name = "Sqrt(Abundance)",
                      low = "#FFFFFF",
                      high = "#012345") +
  theme_bw() +
  theme(strip.placement = "outside",
        plot.title = element_text(hjust = 0.5),
        axis.title.y = element_blank(),
        strip.background = element_rect(fill = "#EEEEEE", color = "#FFFFFF")) +
  ggtitle(label = "Microbe Class Abundance") +
  scale_y_discrete(limits = rev(levels(as.factor(mine.long$Class))))

mine.heatmap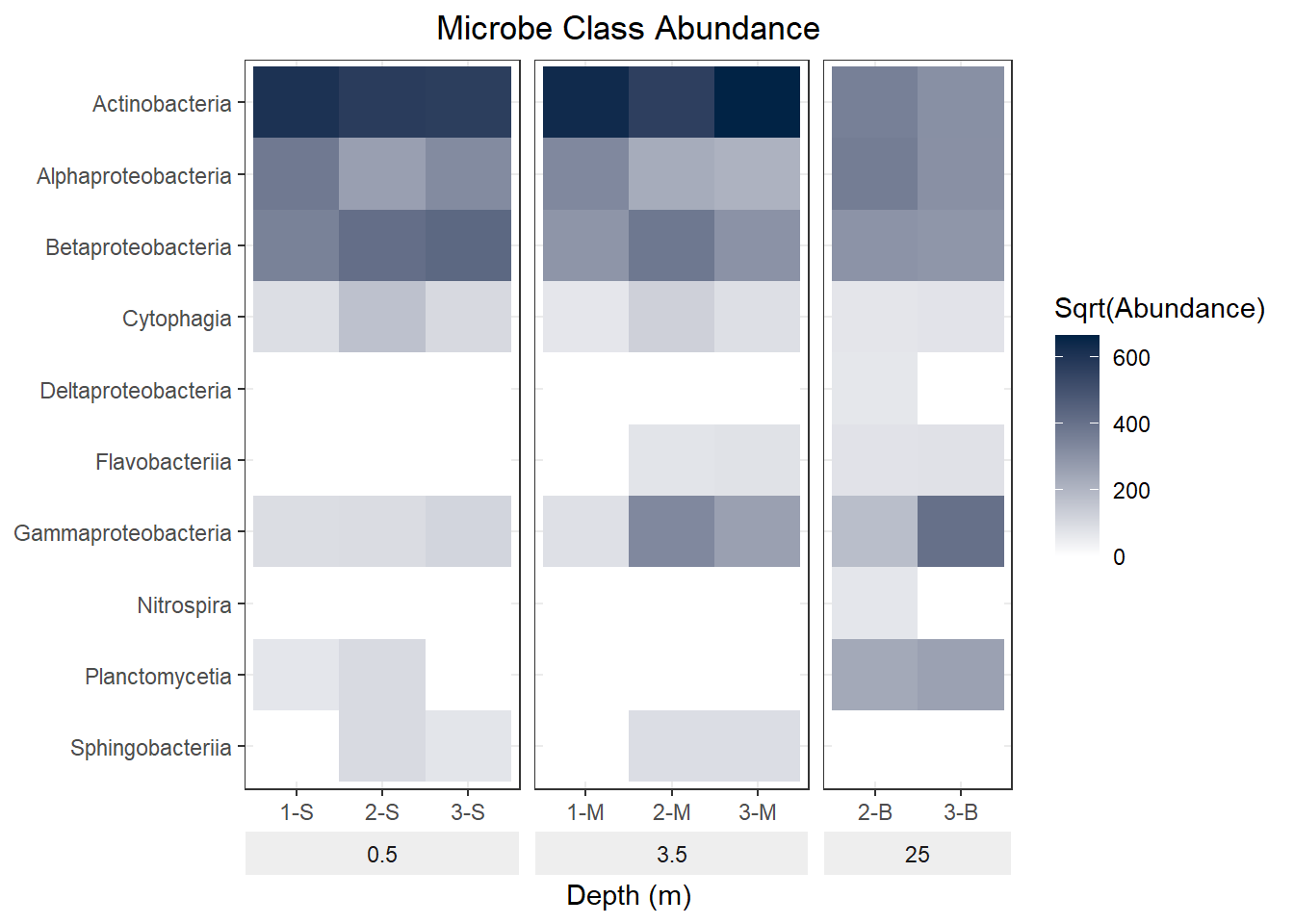

Figure 4.6: 6

6.4 Análisis multivariado

En ciencias naturales, la mayoría de fenómenos son inherentemente complejos. Por tanto, es raro que una sola variable de respuesta sea suficiente para describir un sistema, entidad o interacción.

Es común agregar múltiples variables explicativas a un análisis para explicar la variación en los datos de respuesta. En este sentido el análisis multivariado se define como el conjunto de técnicas estadísticas que permiten analizar simultáneamente más de dos variables en un grupo de muestras. Su uso en ciencias naturales ha ido en aumento. Las técnicas que se incluyen en esta categoría son diversas.

Los conjuntos de datos multivariantes incluyen múltiples variables de respuesta (R1…Rn). Los métodos de análisis multivariado permiten la evaluación de todas las variables de respuesta simultáneamente, en lugar de requerir múltiples ejecuciones de métodos univariados.

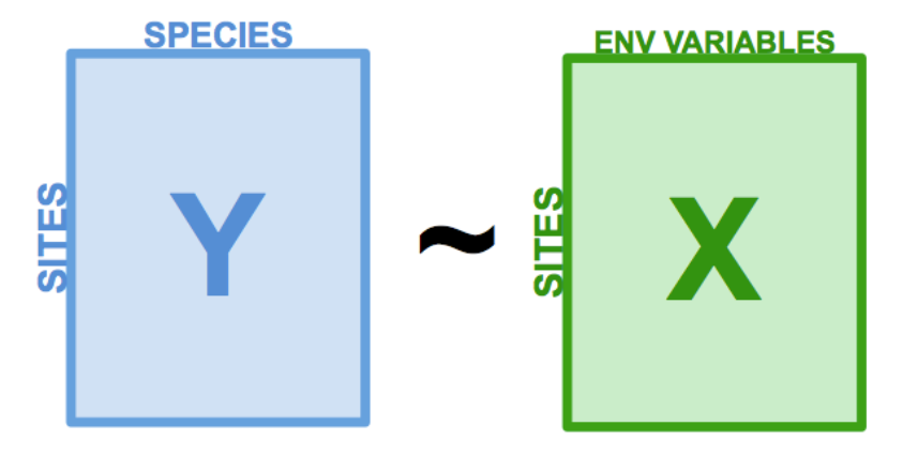
Ejemplo de la estructura de los set de datos en análisis multivariados

Tipos de investigación científica adecuados para la aplicación de métodos multivariados:

Reducción de datos o simplificación estructural. Varios métodos multivariados, como el análisis de componentes principales (PCA), permiten el resumen de múltiples variables a través de un conjunto comparativamente más pequeño de variables ‘sintéticas’ generadas por los propios análisis. Por lo tanto, los patrones de alta dimensión se presentan en un espacio de menor dimensión, lo que ayuda a la interpretación.
Ordenar y agrupar. Muchas preguntas están relacionadas con la similitud o disimilitud de una colección de entidades y su asignación a grupos. Varios métodos multivariados, como el escalado dimensional no métrico (NMDS), permiten la detección de grupos potenciales en los datos.
Investigación de la dependencia entre variables. La dependencia entre variables de respuesta es de interés clave. Los métodos que detectan la dependencia, como el análisis de redundancia (RDA), son valiosos para detectar la influencia o la covariación.
Predicción. Una vez detectada y caracterizada la dependencia entre variables, se pueden construir modelos multivariantes que permitan la predicción.
Construcción de hipótesis. Las técnicas exploratorias pueden revelar patrones en los datos a partir de los cuales se pueden construir hipótesis. Varios métodos, como el analisis de varianza permutacional (PERMANOVA), permiten probar hipótesis estadísticas sobre datos multivariados. De este modo, pueden someterse a prueba las aserciones construidas apropiadamente.

6.4.1 Análisis de componentes principales (PCA)

El análisis de componentes principales (PCA) es una técnica útil para visualizar la variación presente en un conjunto de datos con muchas variables. Es particularmente útil en el caso de conjuntos con muchas variables para cada muestra.

El PCA tiene como objetivo transformar un conjunto de variables, a las que se denominan variables originales, en un nuevo conjunto de variables denominadas componentes principales. Estas ultimas se caracterizan por estar no correlacionadas entre si.

El PCA permite resumir, en un espacio de baja dimensión, la varianza en una dispersión multivariante de puntos. Al hacerlo, proporciona una descripción general de las relaciones lineales entre sus objetos y variables. A menudo, actua como un buen punto de partida en el análisis de datos multivariados porque permite observar tendencias, agrupaciones, variables clave y posibles valores atípicos.

En el PCA, al igual que en otros análisis multivariados, los objetos similares se representan cerca unos de otros, mientras que los objetos diferentes se encuentran más separados. Algo importantes es que este análisis puede ayudar a revelar patrones pero no a explicarlos.

Normalmente el primer componente principal (PC1) captura la variación máxima en el conjunto de datos. Determina la dirección de mayor variabilidad. El segundo componente principal (PC2) captura la variación restante en los datos y no está correlacionado con PC1. En el ejemplo se utiliza la función prcomp() para calcular los componentes principales de la base de datos iris. Se genera una visualización con la función autoplot() de ggfortify.

library(ggfortify)
df <- iris[1:4]
pca_res <- prcomp(df, scale. = TRUE)
pca_res
#> Standard deviations (1, .., p=4):
#> [1] 1.7083611 0.9560494 0.3830886 0.1439265
#> 
#> Rotation (n x k) = (4 x 4):
#>                     PC1         PC2        PC3        PC4
#> Sepal.Length  0.5210659 -0.37741762  0.7195664  0.2612863
#> Sepal.Width  -0.2693474 -0.92329566 -0.2443818 -0.1235096
#> Petal.Length  0.5804131 -0.02449161 -0.1421264 -0.8014492
#> Petal.Width   0.5648565 -0.06694199 -0.6342727  0.5235971

autoplot(pca_res, data = iris, colour = 'Species',
         loadings = TRUE, loadings.colour = 'blue',
         loadings.label = TRUE, loadings.label.size = 3)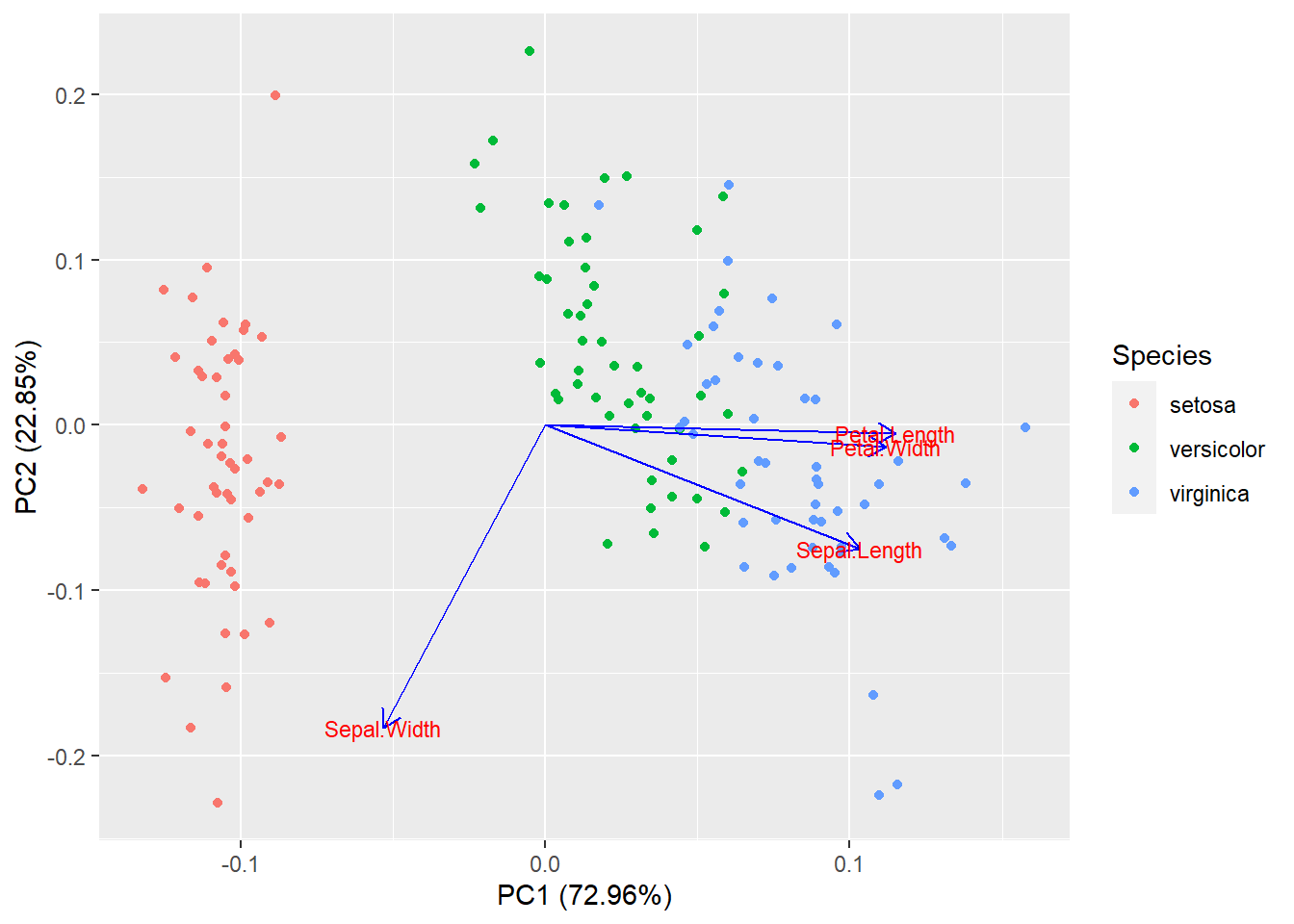

Figure 4.7: 6

6.4.2 Análisis de redundancia (RDA)

El análisis de redundancia (RDA) es un método para extraer y resumir la variación en un conjunto de variables de respuesta que puede explicarse mediante un conjunto de variables explicativas. En síntesis es una técnica de análisis de gradiente directo que resume las relaciones lineales entre los componentes de las variables de respuesta que son “redundantes”.

Para hacer esto, el RDA extiende la regresión lineal múltiple al permitir la regresión de múltiples variables de respuesta en múltiples variables explicativas. Luego, una matriz de los valores ajustados de todas las variables de respuesta generadas se somete a un análisis de componentes principales (PCA).

El RDA también puede considerarse una versión restringida del análisis de componentes principales (PCA), donde se genera una ordenación en el espacio definido por la matriz de variables de respuesta y otra en el espacio definido por la matriz de variables explicativas.

Este análisis se puede utilizar por ejemplo para comprender la influencia de diversos parámetros ambientales en la distribución de una o varias especies. Por ello, requiere un set de datos con las abundancias de especies (variables dependientes) y otro con las variables ambientales (variables independientes). Sin embargo,una limitación del RDA es que asume que existen relaciones lineales entre las variables.

Para el ejemplo utilizaremos es set de datos de especies de datos en dunas dune del programa vegan. La función rda() se utiliza para realizar el RDA. El modelo se puede refinar para escoger las variables más significativas usando la función ordistep().

library(vegan)
library(ggplot2)
library(ggvegan)

data("dune")
data("dune.env")

mod0 <- rda(dune ~ 1, dune.env)
mod1 <- rda(dune ~ ., dune.env)
mod2 <- ordistep(mod0, scope=formula(mod1))
#> 
#> Start: dune ~ 1 
#> 
#>              Df    AIC      F Pr(>F)   
#> + Management  3 87.082 2.8400  0.005 **
#> + Moisture    3 87.707 2.5883  0.010 **
#> + Manure      4 89.232 1.9539  0.015 * 
#> + A1          1 89.591 1.9217  0.030 * 
#> + Use         2 91.032 1.1741  0.270   
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Step: dune ~ Management 
#> 
#>              Df   AIC    F Pr(>F)   
#> - Management  3 89.62 2.84  0.005 **
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#>            Df    AIC      F Pr(>F)   
#> + Moisture  3 85.567 1.9764  0.005 **
#> + Manure    3 87.517 1.3902  0.110   
#> + A1        1 87.424 1.2965  0.190   
#> + Use       2 88.284 1.0510  0.405   
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Step: dune ~ Management + Moisture 
#> 
#>              Df    AIC      F Pr(>F)   
#> - Moisture    3 87.082 1.9764  0.015 * 
#> - Management  3 87.707 2.1769  0.005 **
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#>          Df    AIC      F Pr(>F)
#> + Manure  3 85.762 1.1225  0.275
#> + A1      1 86.220 0.8359  0.600
#> + Use     2 86.842 0.8027  0.730
mod2$call
#> rda(formula = dune ~ Management + Moisture, data = dune.env)
mod2
#> Call: rda(formula = dune ~ Management + Moisture,
#> data = dune.env)
#> 
#>               Inertia Proportion Rank
#> Total         84.1237     1.0000     
#> Constrained   46.4249     0.5519    6
#> Unconstrained 37.6988     0.4481   13
#> Inertia is variance 
#> 
#> Eigenvalues for constrained axes:
#>   RDA1   RDA2   RDA3   RDA4   RDA5   RDA6 
#> 21.588 14.075  4.123  3.163  2.369  1.107 
#> 
#> Eigenvalues for unconstrained axes:
#>   PC1   PC2   PC3   PC4   PC5   PC6   PC7   PC8   PC9  PC10 
#> 8.241 7.138 5.355 4.409 3.143 2.770 1.878 1.741 0.952 0.909 
#>  PC11  PC12  PC13 
#> 0.627 0.311 0.227

Se genera la visualización con la función autoplot()del programa ggvegan

autoplot(mod2, layers = c("sites", "centroids"))

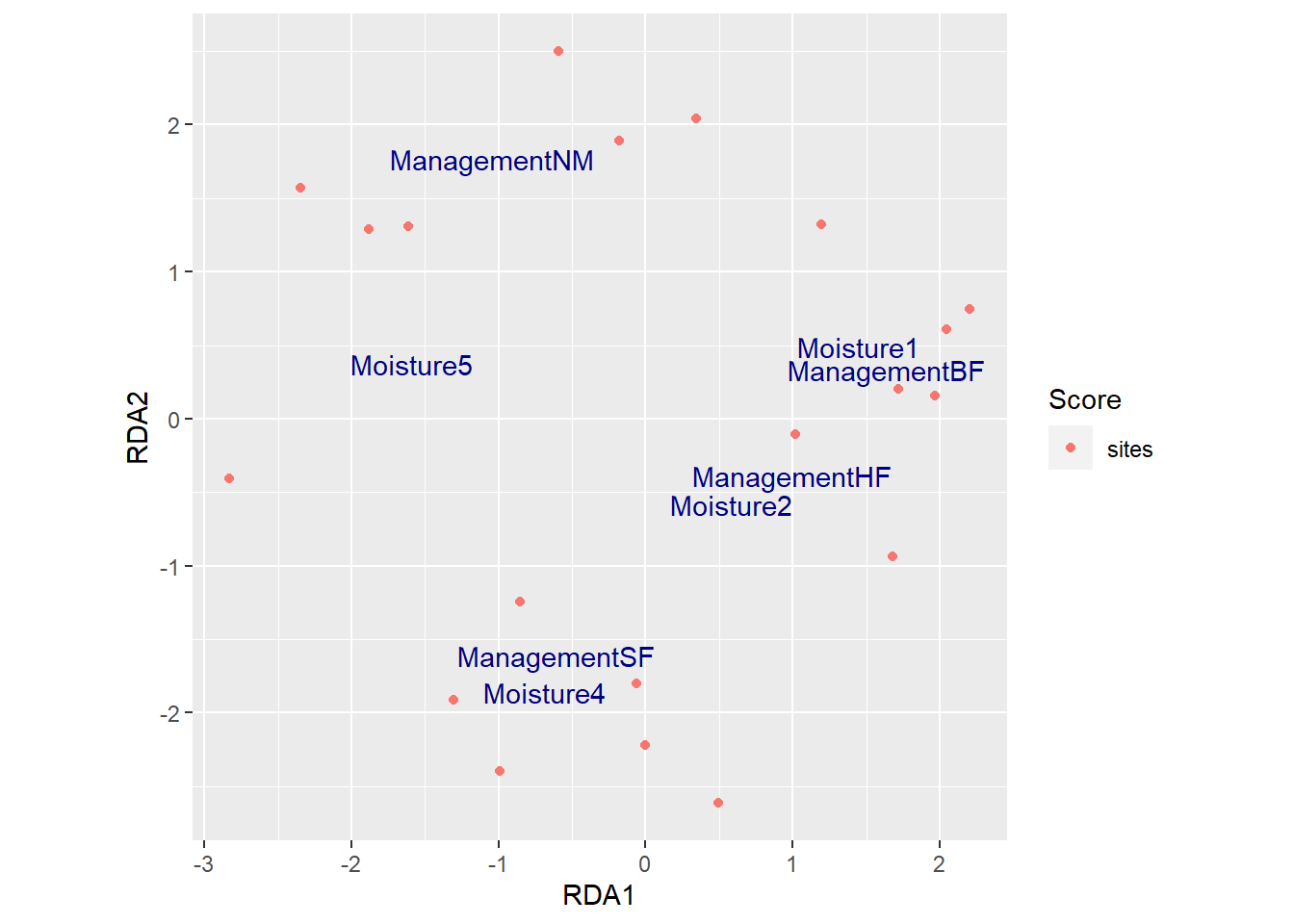
Figure 4.9: 6

Se utiliza la función adonis2()para realizar un análisis de varianza permutacional (Permanova), el cual permite determinar si hay diferencia significativa en la estructura de las comunidades de plantas de acuerdo a las variables analizadas.

adonis2(dune ~ Management + Moisture, dune.env)
#> Permutation test for adonis under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#> 
#> adonis2(formula = dune ~ Management + Moisture, data = dune.env)
#>            Df SumOfSqs      R2      F Pr(>F)    
#> Management  3   1.4686 0.34161 3.7907  0.001 ***
#> Moisture    3   1.1516 0.26788 2.9726  0.001 ***
#> Residual   13   1.6788 0.39051                  
#> Total      19   4.2990 1.00000                  
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

6.4.3 Análisis de correspondencia canónica (CCA)

El análisis restringido (constrained analysis) es una forma de análisis de gradiente directo, que intenta explicar la variación en una tabla de datos directamente a través de la variación en un conjunto de variables explicativas (p. ej., factores ambientales. La mayoría de los análisis restringidos requieren dos tablas o matrices como entrada: a) una tabla de objetos (como sitios o muestras) por un conjunto de variables de respuesta (p.ej. especies) y b) una tabla de los mismos objetos por un conjunto de variables explicativas (como los factores ambientales). Los factores explicativos se pueden visualizar en un bi- o triplot.

La elección de las variables explicativas que mide e introduce en estos análisis es crucial. Además, si el número de variables explicativas se acerca o supera el número de objetos de muestreo (sitios, muestras, observaciones), es posible que el análisis ya no esté restringido. Aumentar el número de variables explicativas generalmente aumenta la capacidad de los análisis restringidos para ajustar los datos observados a alguna combinación de estas variables. Esto rara vez es útil, ya que impide cualquier interpretación ecológicamente significativa de la relación de los datos de respuesta con las variables explicativas.

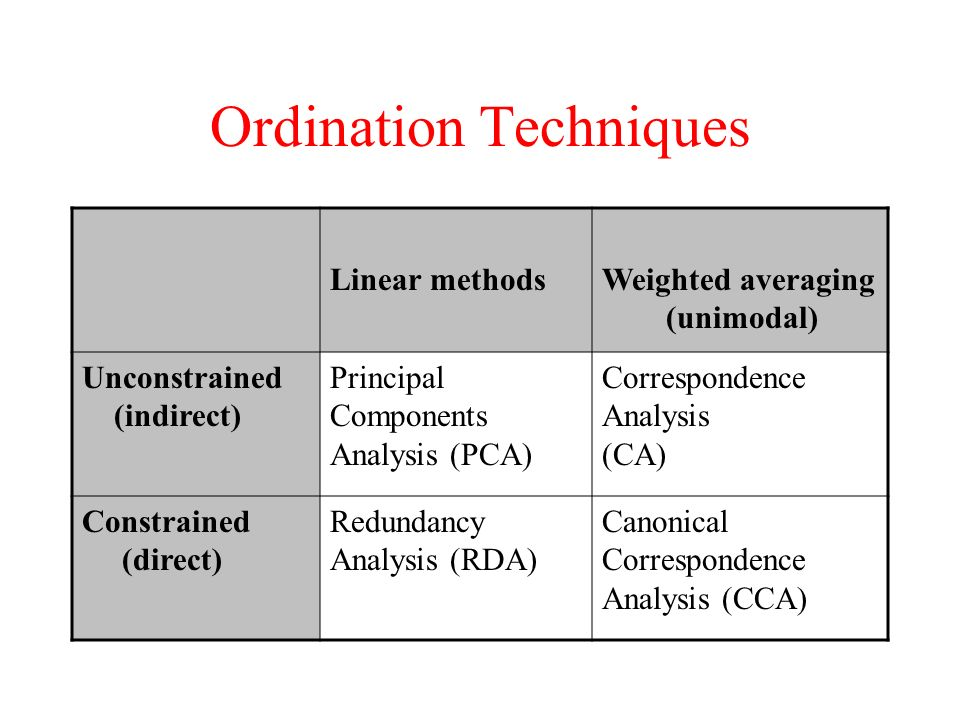
El análisis de correspondencias canónicas (CCA) es un tipo de análisis restrigido que se desarrolló para permitir a los ecólogos relacionar la abundancia de especies con variables ambientales por lo que permite dilucidar las relaciones entre los conjuntos biológicos de las especies y su entorno.

Es una excelente herramienta para analizar datos ecológicos que poseen una gran cantidad de especies y variabilidad inherente, donde hay especies que ocurren en sitios específicos y a su vez estos se relacionan a variables ambientales.

Es un análisis recomendado cuando las especies muestran relaciones unimodales con gradientes ambientales, pero también es robusto en rangos bimodales o desiguales. Esta técnica es adecuada para variables de respuesta que muestran distribuciones unimodales y conserva las distancias $X^2$ (chi-cuadrado) entre objetos. El CCA es sensible a especies raras que se encuentran en muestras pobres en especies.

Como en los casos anteriores, se necesitan dos conjuntos de datos (matriz de datos de la comunidad y matriz de datos ambientales). Los datos de las dos matrices deben organizarse en el mismo orden. Para el ejemplo, utilizaremos los set de datos varespec y varechem de vegan. Utilizamos la función cca()para hacer el análisis de correspondencia canónica.

library("vegan")
library("ggvegan")
data(varespec, varechem)
varechem <- decostand(varechem, "total")

mod0 <- cca(varespec ~ 1, varechem)
mod1 <- cca(varespec ~ ., varechem)
mod <- step(mod0, scope = formula(mod1), test = "perm")
#> Start:  AIC=130.31
#> varespec ~ 1
#> 
#>            Df    AIC      F Pr(>F)   
#> + Al        1 128.41 3.8838  0.005 **
#> + Mn        1 129.28 2.9605  0.005 **
#> + Baresoil  1 129.76 2.4724  0.010 **
#> + Ca        1 129.76 2.4699  0.010 **
#> + Fe        1 129.89 2.3373  0.010 **
#> + K         1 129.98 2.2436  0.015 * 
#> + N         1 130.16 2.0693  0.050 * 
#> + Mg        1 130.21 2.0209  0.060 . 
#> + pH        1 130.29 1.9367  0.035 * 
#> <none>        130.31                 
#> + Humdepth  1 130.78 1.4498  0.150   
#> + Mo        1 130.92 1.3158  0.225   
#> + P         1 131.10 1.1413  0.390   
#> + Zn        1 131.41 0.8491  0.600   
#> + S         1 131.52 0.7378  0.725   
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Step:  AIC=128.41
#> varespec ~ Al
#> 
#>            Df    AIC      F Pr(>F)   
#> + N         1 127.97 2.2469  0.020 * 
#> + Baresoil  1 128.17 2.0542  0.005 **
#> + pH        1 128.41 1.8312  0.060 . 
#> <none>        128.41                 
#> + K         1 128.78 1.4786  0.105   
#> + Zn        1 129.06 1.2191  0.360   
#> + Ca        1 129.14 1.1473  0.370   
#> + Mn        1 129.16 1.1282  0.335   
#> + P         1 129.20 1.0859  0.380   
#> + Humdepth  1 129.29 1.0007  0.410   
#> + Mo        1 129.51 0.8058  0.615   
#> + Mg        1 129.52 0.7937  0.670   
#> + S         1 129.74 0.5938  0.850   
#> + Fe        1 129.83 0.5196  0.920   
#> - Al        1 130.31 3.8838  0.005 **
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Step:  AIC=127.97
#> varespec ~ Al + N
#> 
#>            Df    AIC      F Pr(>F)   
#> + Baresoil  1 127.78 1.9127  0.055 . 
#> <none>        127.97                 
#> + K         1 128.24 1.4940  0.130   
#> + Zn        1 128.39 1.3614  0.225   
#> - N         1 128.41 2.2469  0.015 * 
#> + P         1 128.44 1.3175  0.220   
#> + Mn        1 128.61 1.1686  0.315   
#> + Ca        1 128.72 1.0750  0.410   
#> + pH        1 128.79 1.0134  0.490   
#> + Humdepth  1 128.89 0.9241  0.570   
#> + Mg        1 129.07 0.7705  0.675   
#> + Mo        1 129.11 0.7359  0.710   
#> + S         1 129.34 0.5357  0.850   
#> + Fe        1 129.41 0.4764  0.905   
#> - Al        1 130.16 3.9995  0.005 **
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Step:  AIC=127.78
#> varespec ~ Al + N + Baresoil
#> 
#>            Df    AIC      F Pr(>F)   
#> <none>        127.78                 
#> + K         1 127.85 1.5922  0.075 . 
#> - Baresoil  1 127.97 1.9127  0.075 . 
#> - N         1 128.17 2.0959  0.045 * 
#> + Ca        1 128.36 1.1574  0.340   
#> + Mn        1 128.38 1.1445  0.350   
#> + Zn        1 128.40 1.1254  0.325   
#> + pH        1 128.48 1.0605  0.385   
#> + P         1 128.72 0.8619  0.545   
#> + Mg        1 128.87 0.7376  0.720   
#> + Mo        1 128.91 0.7035  0.760   
#> + Humdepth  1 129.00 0.6284  0.840   
#> + S         1 129.02 0.6095  0.775   
#> + Fe        1 129.15 0.5071  0.930   
#> - Al        1 129.39 3.2424  0.005 **
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Se llama el mejor modelo con el parametro mod$call

mod$call
#> cca(formula = varespec ~ Al + N + Baresoil, data = varechem)

Visualizamos los sitios y las variables del mejor modelo.

autoplot(mod,layers = c("sites", "centroids","biplot"))

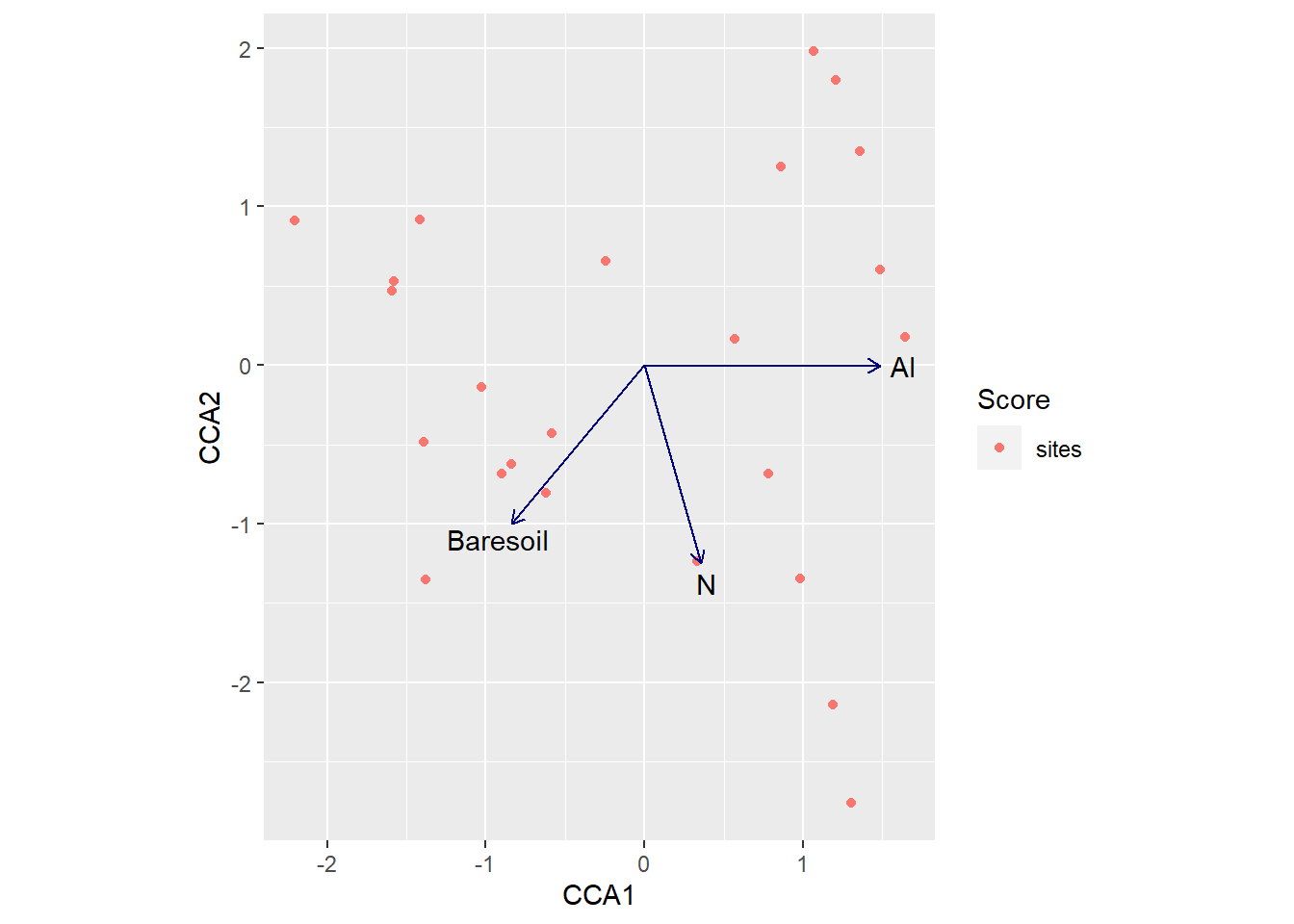
Figure 4.12: 6

Realizamos un test de significancia sobre el modelo.

anova(mod, perm.max = 1000)
#> Permutation test for cca under reduced model
#> Permutation: free
#> Number of permutations: 999
#> 
#> Model: cca(formula = varespec ~ Al + N + Baresoil, data = varechem)
#>          Df ChiSquare      F Pr(>F)    
#> Model     3   0.62334 2.8466  0.001 ***
#> Residual 20   1.45986                  
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

6.4.4 Análisis de coordenadas principales (PCoA)

El análisis de coordenadas principales (PCoA) también conocido como escalado multidimensional métrico, resume e intenta representar la (dis)similitud entre objetos en un espacio euclidiano de baja dimensión. En lugar de utilizar datos sin procesar, PCoA toma como entrada una matriz de (dis)similitud.

Es conceptualmente similar al análisis de componentes principales (PCA) al conservar las distancias euclidianas; sin embargo, puede preservar las distancias generadas a partir de cualquier medida de (dis)similitud, lo que permite un manejo más flexible de datos complejos.

El PCoA puede manejar matrices calculadas a partir de variables cuantitativas, semicuantitativas, cualitativas y mixtas. La elección de la medida de (dis)similitud es crítica y debe ser adecuada a los datos en cuestión. Tener en cuenta que PCoA solo puede representar completamente los componentes euclidianos de la matriz, incluso si la matriz contiene distancias no euclidianas.

Usaremos la base de datos mite de vegan. La función pcoa()del programa ape se utiliza para realizar el PCoA.

library(vegan)
library(ape)
data(mite)
mite.log <- log(mite[1:30, -35] + 1)# se transforman los datos al log+1
mite.D <- vegdist(mite.log, "bray")# se calcula matriz de Bray-Curtis

pcoa <- pcoa(mite.D)

Visualizamos el PCoA

library(ggplot2)
df.plot<-data.frame(pcoa$vectors)

x_label<-round(pcoa$values$Rel_corr_eig[1]*100,2)
y_label<-round(pcoa$values$Rel_corr_eig[2]*100,2)

ggplot(data=df.plot,aes(x=Axis.1,y=Axis.2))+
  geom_point()+
  theme_bw()+
  theme(panel.grid = element_blank())+
  geom_vline(xintercept = 0,lty="dashed")+
  geom_hline(yintercept = 0,lty="dashed")+
  labs(x=paste0("PCoA1 ",x_label,"%"),
       y=paste0("PCoA2 ",y_label,"%"))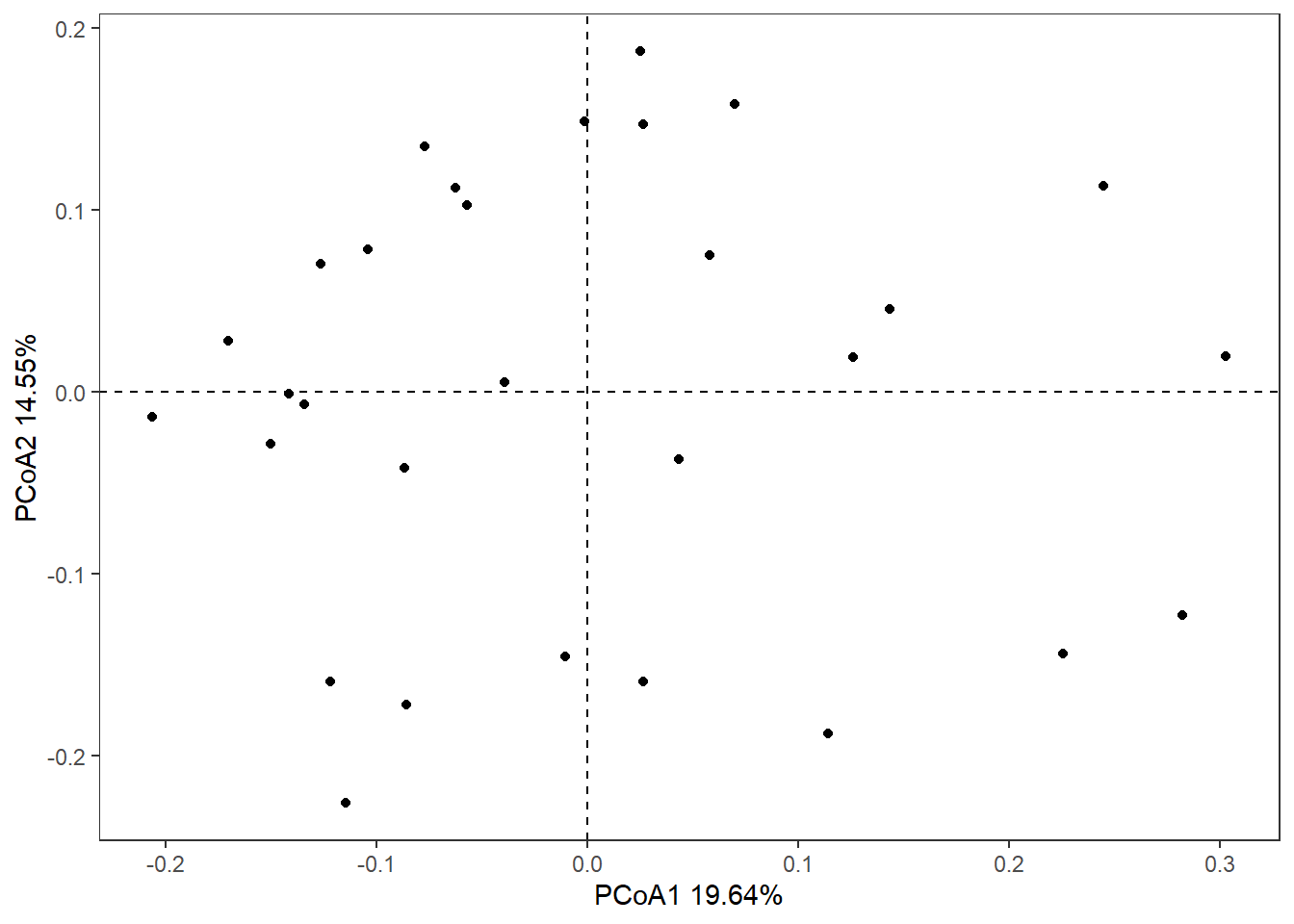

Figure 5.3: 6

6.4.5 Escalado multidimensional no métrico (NMDS)

El escalado multidimensional no métrico (NMDS) es un enfoque de análisis de gradiente indirecto que produce una ordenación basada en una matriz de distancia o disimilitud de variables cuantitativas, cualitativas o mixtas. Es uno de los métodos más utilizados en ciencias naturales por su robustez y versatilidad. A diferencia de los métodos que intentan maximizar la varianza o correspondencia entre objetos en una ordenación, NMDS intenta representar, lo más fielmente posible, la disimilitud por pares entre objetos en un espacio de baja dimensión.

Se puede utilizar cualquier coeficiente de disimilitud o medida de distancia para construir la matriz de distancia utilizada como entrada. Además, el NMDS es un enfoque basado en rangos, por lo que los datos de distancia originales se sustituyen por rangos. Los métodos basados en rangos son generalmente más robustos para los datos que no tienen una distribución identificable.

Dado que NMDS es un algoritmo iterativo, puede volverse computacionalmente exigente. se necesitan varias ejecuciones del algoritmo NMDS para garantizar que se haya alcanzado una solución estable.

Se utiliza la función metaMDS() del paquete vegan para realizar el NMDS. El valor de estrés resultante indica cuán diferentes son los rangos en la configuración de ordenación de los rangos en la matriz de distancia original. Un valor alrededor de 0,2 o superior se considera sospechoso. Los valores iguales o inferiores a 0,1 se consideran justos, mientras que los valores iguales o inferiores a 0,05 indican un buen ajuste.

library(vegan)
library(ggplot2)

data(dune, dune.env)

nmds = decostand(dune, method = "total")
nmds = metaMDS(nmds, distance = "bray")
#> Run 0 stress 0.1071832 
#> Run 1 stress 0.1071832 
#> ... Procrustes: rmse 6.05281e-06  max resid 2.073657e-05 
#> ... Similar to previous best
#> Run 2 stress 0.1071832 
#> ... New best solution
#> ... Procrustes: rmse 4.363579e-06  max resid 1.448276e-05 
#> ... Similar to previous best
#> Run 3 stress 0.2004106 
#> Run 4 stress 0.1071832 
#> ... Procrustes: rmse 6.47579e-06  max resid 2.210283e-05 
#> ... Similar to previous best
#> Run 5 stress 0.1071833 
#> ... Procrustes: rmse 1.795309e-05  max resid 5.92939e-05 
#> ... Similar to previous best
#> Run 6 stress 0.1071832 
#> ... Procrustes: rmse 1.138372e-05  max resid 4.115913e-05 
#> ... Similar to previous best
#> Run 7 stress 0.1824724 
#> Run 8 stress 0.106197 
#> ... New best solution
#> ... Procrustes: rmse 0.01725468  max resid 0.05476313 
#> Run 9 stress 0.1071832 
#> Run 10 stress 0.1071832 
#> Run 11 stress 0.106197 
#> ... Procrustes: rmse 6.610747e-06  max resid 2.510252e-05 
#> ... Similar to previous best
#> Run 12 stress 0.106197 
#> ... Procrustes: rmse 3.455367e-06  max resid 1.080297e-05 
#> ... Similar to previous best
#> Run 13 stress 0.1071832 
#> Run 14 stress 0.106197 
#> ... New best solution
#> ... Procrustes: rmse 1.11985e-06  max resid 3.832621e-06 
#> ... Similar to previous best
#> Run 15 stress 0.106197 
#> ... Procrustes: rmse 2.274271e-06  max resid 8.564958e-06 
#> ... Similar to previous best
#> Run 16 stress 0.1930314 
#> Run 17 stress 0.1071832 
#> Run 18 stress 0.106197 
#> ... Procrustes: rmse 3.436971e-07  max resid 1.11567e-06 
#> ... Similar to previous best
#> Run 19 stress 0.106197 
#> ... Procrustes: rmse 2.908405e-06  max resid 1.079623e-05 
#> ... Similar to previous best
#> Run 20 stress 0.1071832 
#> *** Solution reached
nmds
#> 
#> Call:
#> metaMDS(comm = nmds, distance = "bray") 
#> 
#> global Multidimensional Scaling using monoMDS
#> 
#> Data:     nmds 
#> Distance: bray 
#> 
#> Dimensions: 2 
#> Stress:     0.106197 
#> Stress type 1, weak ties
#> Two convergent solutions found after 20 tries
#> Scaling: centring, PC rotation, halfchange scaling 
#> Species: expanded scores based on 'nmds'

en = envfit(nmds, dune.env, permutations = 999, na.rm = TRUE)#ajusta factores ambientales en una ordenación.

data.scores = as.data.frame(nmds$points)
data.scores$Management = dune.env$Management
data.scores
#>           MDS1        MDS2 Management
#> 1  -0.97605157 -0.65794112         SF
#> 2  -0.49079077 -0.32839024         BF
#> 3  -0.13560304 -0.41454646         SF
#> 4  -0.12805257 -0.48668981         SF
#> 5  -0.59642428 -0.04175432         HF
#> 6  -0.42204424  0.16865879         HF
#> 7  -0.49803979 -0.03151564         HF
#> 8   0.25861373 -0.19684308         HF
#> 9   0.02987032 -0.45039012         HF
#> 10 -0.51914440  0.06647694         BF
#> 11 -0.30744058  0.41122680         BF
#> 12  0.37593766 -0.48426208         SF
#> 13  0.34018161 -0.61123682         SF
#> 14  1.02646493  0.38492376         NM
#> 15  0.91117089  0.17938131         NM
#> 16  1.01230616 -0.19542641         SF
#> 17 -0.82443667  0.92701070         NM
#> 18 -0.16427771  0.56546759         NM
#> 19  0.03385014  1.02285752         NM
#> 20  1.07391019  0.17299270         NM

gg = ggplot(data = data.scores, aes(x = MDS1, y = MDS2)) + 
  geom_point(data = data.scores, aes(colour = Management), size = 3, alpha = 0.5) + 
  theme(axis.title = element_text(size = 10, face = "bold", colour = "grey30"), 
        panel.background = element_blank(), panel.border = element_rect(fill = NA, colour = "grey30"), 
        axis.ticks = element_blank(), axis.text = element_blank(), legend.key = element_blank(), 
        legend.title = element_text(size = 10, face = "bold", colour = "grey30"), 
        legend.text = element_text(size = 9, colour = "grey30")) +
  labs(colour = "Use")
gg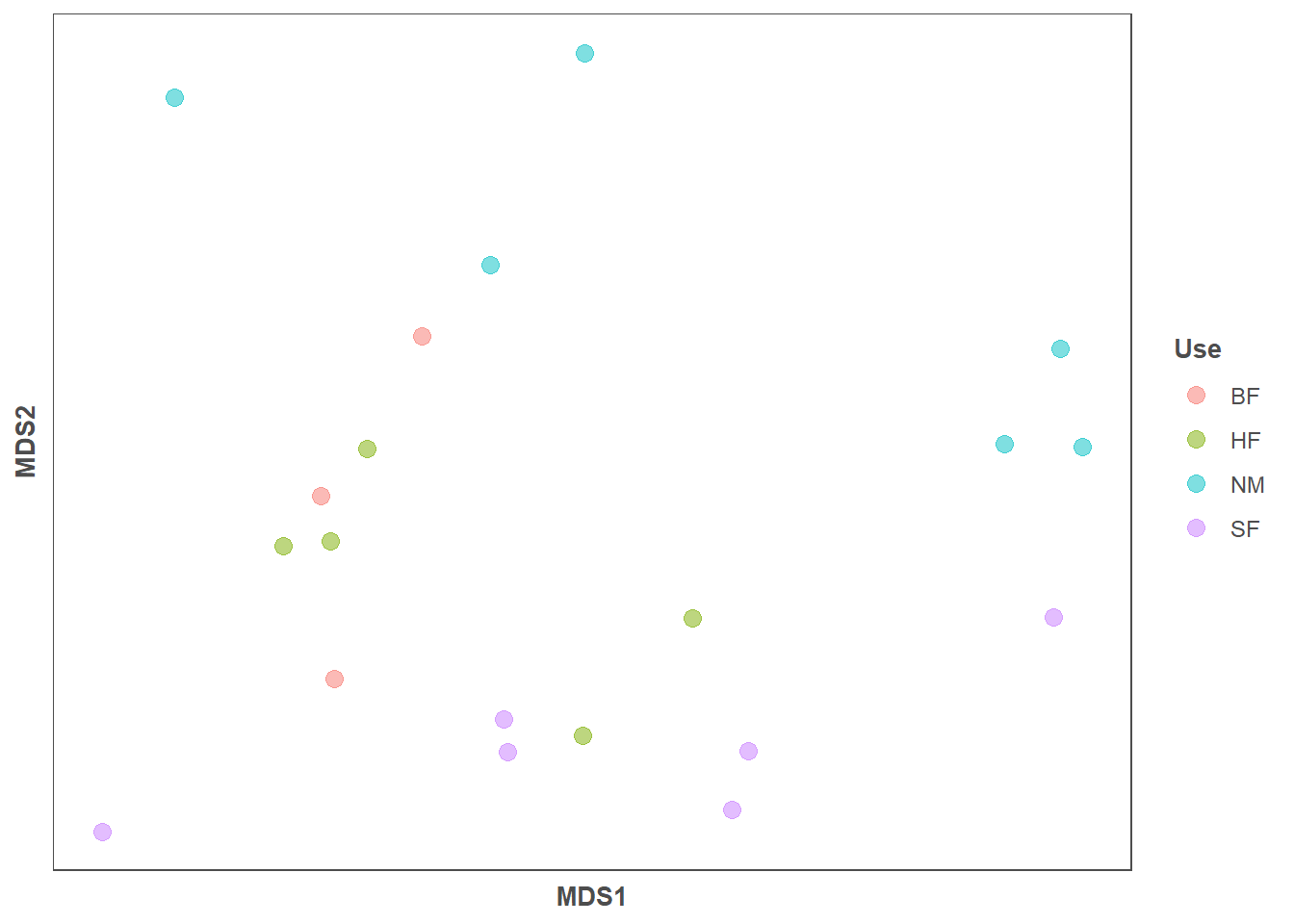

Figure 6.2: 6

6.5 Recursos complementarios

5 Transformación, Estandarización e Imputación de Datos

7 Aprendizaje Automático (Machine Learning)