Capítulo 3 Análisis de Componentes Principales
3.1 Marco Téorico
El Análisis de Componentes Principales (ACP) tiene como objetivo transformar un conjunto de variables, a las que se denominan variables originales, en un nuevo conjunto de variables denominadas componentes principales. Estas ultimas se caracterizan por estar no correlacionadas entre si.
En muchas ocasiones el investigador se enfrenta a situaciones en las que para analizar un fenómeno, dispone de información de muchas variables que están correlacionadas entre si en mayor o menor grado. Estas correlaciones son como un velo que impiden evaluar adecuadamente el papel que juega cada variable en el fenómeno estudiado. El ACP permite pasar a un nuevo conjunto de variables -las componentes principales- que gozan de la ventaja de estar no correlacionadas entre si y que, además, pueden ordenarse de acuerdo con la información que llevan incorporada.
Como medida de la cantidad de información incorporada en una componente se utiliza su variancia. Es decir, cuanto mayor sea su variancia mayor es la información que lleva incorporada dicha componente. Por esta razón se selecciona como primera componente aquella que tenga mayor variancia, mientras que, por el contrario, la ultima es la de menor variancia
En el caso de no correlación entre las variables originales, el ACP no tiene mucho que hacer, pues las componentes se corresponderían con cada variable por orden de magnitud en la varianza; es decir, la primera componente coincide con la variable de mayor varianza, la segunda componente con la variable de segunda mayor varianza, y así sucesivamente.
3.2 Ejemplos
# Otras opciones
options(scipen=999) # Eliminar la notación científica
options(digits = 4) # Número de decimales
# Paquetes
library(pacman)
p_load("ade4", "psych", "car","matrixcalc","FactoMineR",
"factoextra","PerformanceAnalytics","GGally",
"corrplot","corrr","funModeling","apaTables")Este ejemplo fue tomado del libro de Hair
Hair, J. Anderson, R. Tatham, R. Black, W. (1999). Análisis Multivariante Prentice Hall
Ingreso de datos
Estos datos corresponden a 100 observaciones de 7 variables influyentes en la elección de distribuidor, en un ejemplo de un estudio de segmentación de la situación empresa a empresa,específicamente un informe sobre los clientes actuales de HATCO.
datos.acp <- read.delim("hatco-acp.txt")
library(readr)
str(datos.acp)'data.frame': 100 obs. of 7 variables:
$ id: int 1 2 3 4 5 6 7 8 9 10 ...
$ x1: num 4.1 1.8 3.4 2.7 6 1.9 4.6 1.3 5.5 4 ...
$ x2: num 0.6 3 5.2 1 0.9 3.3 2.4 4.2 1.6 3.5 ...
$ x3: num 6.9 6.3 5.7 7.1 9.6 7.9 9.5 6.2 9.4 6.5 ...
$ x4: num 4.7 6.6 6 5.9 7.8 4.8 6.6 5.1 4.7 6 ...
$ x5: num 2.35 4 2.7 2.3 4.6 1.9 4.5 2.2 3 3.2 ...
$ x6: num 5.2 8.4 8.2 7.8 4.5 9.7 7.6 6.9 7.6 8.7 ...datos.acp$id <- NULLAnálisis Descriptivo
summary(datos.acp) x1 x2 x3 x4 x5
Min. :0.00 Min. :0.20 Min. : 5.00 Min. :2.50 Min. :1.10
1st Qu.:2.50 1st Qu.:1.48 1st Qu.: 6.70 1st Qu.:4.58 1st Qu.:2.20
Median :3.40 Median :2.15 Median : 8.05 Median :5.00 Median :2.60
Mean :3.52 Mean :2.36 Mean : 7.89 Mean :5.25 Mean :2.67
3rd Qu.:4.60 3rd Qu.:3.23 3rd Qu.: 9.10 3rd Qu.:6.00 3rd Qu.:3.00
Max. :6.10 Max. :5.40 Max. :10.00 Max. :8.20 Max. :4.60
x6
Min. : 3.70
1st Qu.: 5.80
Median : 7.15
Mean : 6.97
3rd Qu.: 8.32
Max. :10.00 library(psych)
psych::describe(datos.acp) vars n mean sd median trimmed mad min max range skew kurtosis se
x1 1 100 3.52 1.32 3.40 3.53 1.48 0.0 6.1 6.1 -0.08 -0.59 0.13
x2 2 100 2.36 1.20 2.15 2.30 1.19 0.2 5.4 5.2 0.46 -0.59 0.12
x3 3 100 7.89 1.39 8.05 7.95 1.70 5.0 10.0 5.0 -0.28 -1.12 0.14
x4 4 100 5.25 1.13 5.00 5.23 1.04 2.5 8.2 5.7 0.21 -0.04 0.11
x5 5 100 2.67 0.77 2.60 2.63 0.59 1.1 4.6 3.5 0.48 -0.02 0.08
x6 6 100 6.97 1.59 7.15 7.01 1.85 3.7 10.0 6.3 -0.22 -0.91 0.16# Otras Formas
library(funModeling)
# Descripción de los datos
df_status(datos.acp) variable q_zeros p_zeros q_na p_na q_inf p_inf type unique
1 x1 1 1 0 0 0 0 numeric 47
2 x2 0 0 0 0 0 0 numeric 45
3 x3 0 0 0 0 0 0 numeric 47
4 x4 0 0 0 0 0 0 numeric 40
5 x5 0 0 0 0 0 0 numeric 30
6 x6 0 0 0 0 0 0 numeric 46# Descripción de las variables numéricas
profiling_num(datos.acp) variable mean std_dev variation_coef p_01 p_05 p_25 p_50 p_75 p_95
1 x1 3.515 1.3207 0.3757 0.594 1.585 2.500 3.40 4.600 5.505
2 x2 2.364 1.1957 0.5058 0.398 0.695 1.475 2.15 3.225 4.500
3 x3 7.894 1.3865 0.1756 5.099 5.595 6.700 8.05 9.100 9.900
4 x4 5.248 1.1314 0.2156 2.896 3.395 4.575 5.00 6.000 7.100
5 x5 2.666 0.7706 0.2891 1.298 1.400 2.200 2.60 3.000 4.000
6 x6 6.971 1.5852 0.2274 3.799 4.495 5.800 7.15 8.325 9.205
p_99 skewness kurtosis iqr range_98 range_80
1 6.001 -0.08394 2.455 2.100 [0.594, 6.001] [1.9, 5.3]
2 5.202 0.46220 2.456 1.750 [0.398, 5.202] [0.9, 4.1]
3 9.901 -0.28472 1.920 2.400 [5.099, 9.901] [5.9, 9.61]
4 7.804 0.21464 3.021 1.425 [2.896, 7.804] [3.8, 6.71]
5 4.600 0.48480 3.044 0.800 [1.298, 4.6] [1.7, 3.9]
6 9.901 -0.22552 2.133 2.525 [3.799, 9.901] [4.79, 8.91]library(pastecs)
stat.desc(datos.acp) x1 x2 x3 x4 x5 x6
nbr.val 100.0000 100.0000 100.0000 100.0000 100.00000 100.0000
nbr.null 1.0000 0.0000 0.0000 0.0000 0.00000 0.0000
nbr.na 0.0000 0.0000 0.0000 0.0000 0.00000 0.0000
min 0.0000 0.2000 5.0000 2.5000 1.10000 3.7000
max 6.1000 5.4000 10.0000 8.2000 4.60000 10.0000
range 6.1000 5.2000 5.0000 5.7000 3.50000 6.3000
sum 351.5000 236.4000 789.4000 524.8000 266.55000 697.1000
median 3.4000 2.1500 8.0500 5.0000 2.60000 7.1500
mean 3.5150 2.3640 7.8940 5.2480 2.66550 6.9710
SE.mean 0.1321 0.1196 0.1387 0.1131 0.07706 0.1585
CI.mean.0.95 0.2621 0.2372 0.2751 0.2245 0.15291 0.3145
var 1.7443 1.4296 1.9224 1.2801 0.59387 2.5130
std.dev 1.3207 1.1957 1.3865 1.1314 0.77063 1.5852
coef.var 0.3757 0.5058 0.1756 0.2156 0.28911 0.2274Análisis de Correlación
# matriz de variancia-covariancia
(cov1 <- cov(datos.acp)) x1 x2 x3 x4 x5 x6
x1 1.74432 -0.5515 0.93262 0.07533 0.07881 -1.0105
x2 -0.55147 1.4296 -0.80769 0.36821 0.17077 0.8904
x3 0.93262 -0.8077 1.92239 -0.18213 -0.03718 -0.9849
x4 0.07533 0.3682 -0.18213 1.28010 0.68718 0.3587
x5 0.07881 0.1708 -0.03718 0.68718 0.59387 0.2158
x6 -1.01047 0.8904 -0.98492 0.35868 0.21576 2.5130cov1 <- as.matrix(cov1)
diag(cov(datos.acp)) x1 x2 x3 x4 x5 x6
1.7443 1.4296 1.9224 1.2801 0.5939 2.5130 sum(diag(cov(datos.acp))) #traza[1] 9.483# Otra forma
library(matrixcalc)
matrix.trace(cov(datos.acp))[1] 9.483Coeficientes de Correlación
cor(datos.acp) x1 x2 x3 x4 x5 x6
x1 1.00000 -0.3492 0.5093 0.05041 0.07743 -0.4826
x2 -0.34923 1.0000 -0.4872 0.27219 0.18533 0.4697
x3 0.50930 -0.4872 1.0000 -0.11610 -0.03480 -0.4481
x4 0.05041 0.2722 -0.1161 1.00000 0.78814 0.2000
x5 0.07743 0.1853 -0.0348 0.78814 1.00000 0.1766
x6 -0.48263 0.4697 -0.4481 0.19998 0.17661 1.0000# Prueba estadística
library(psych)
corr.test(datos.acp)Call:corr.test(x = datos.acp)
Correlation matrix
x1 x2 x3 x4 x5 x6
x1 1.00 -0.35 0.51 0.05 0.08 -0.48
x2 -0.35 1.00 -0.49 0.27 0.19 0.47
x3 0.51 -0.49 1.00 -0.12 -0.03 -0.45
x4 0.05 0.27 -0.12 1.00 0.79 0.20
x5 0.08 0.19 -0.03 0.79 1.00 0.18
x6 -0.48 0.47 -0.45 0.20 0.18 1.00
Sample Size
[1] 100
Probability values (Entries above the diagonal are adjusted for multiple tests.)
x1 x2 x3 x4 x5 x6
x1 0.00 0.00 0.00 1.00 1.00 0.00
x2 0.00 0.00 0.00 0.05 0.39 0.00
x3 0.00 0.00 0.00 1.00 1.00 0.00
x4 0.62 0.01 0.25 0.00 0.00 0.32
x5 0.44 0.06 0.73 0.00 0.00 0.39
x6 0.00 0.00 0.00 0.05 0.08 0.00
To see confidence intervals of the correlations, print with the short=FALSE optionGráficos de correlación
Evaluamos la correlacipon entre todas las variables con diferentes paquetes
pairs(datos.acp)
# Otras Formas
library(car)
scatterplotMatrix(datos.acp, diagonal = "density")
library(PerformanceAnalytics)
chart.Correlation(datos.acp, histogram=T, pch=20)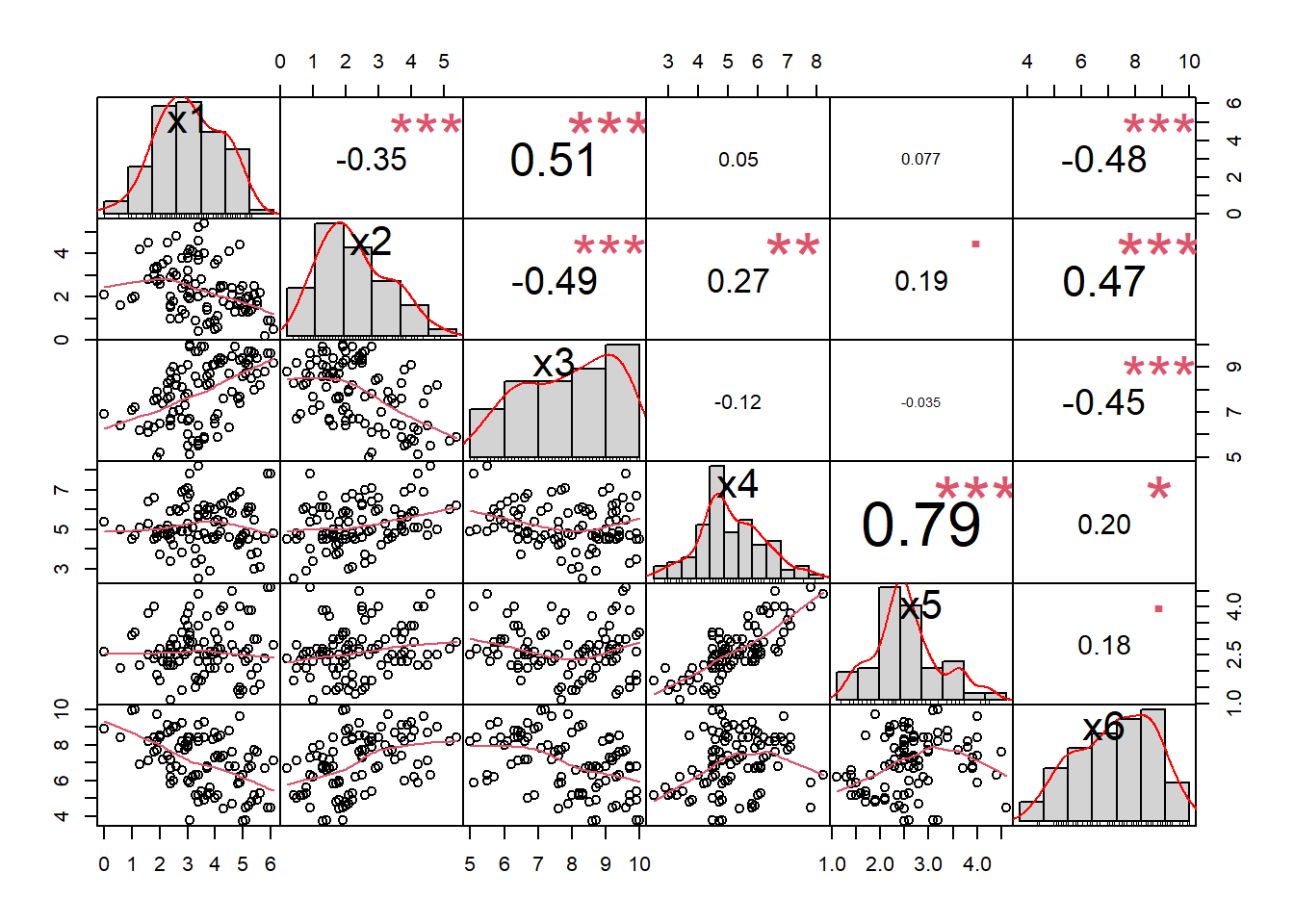
library(psych)
pairs.panels(datos.acp,
pch=20,
stars=T,
main="Gráfico de Correlación")
library(GGally)
ggpairs(datos.acp)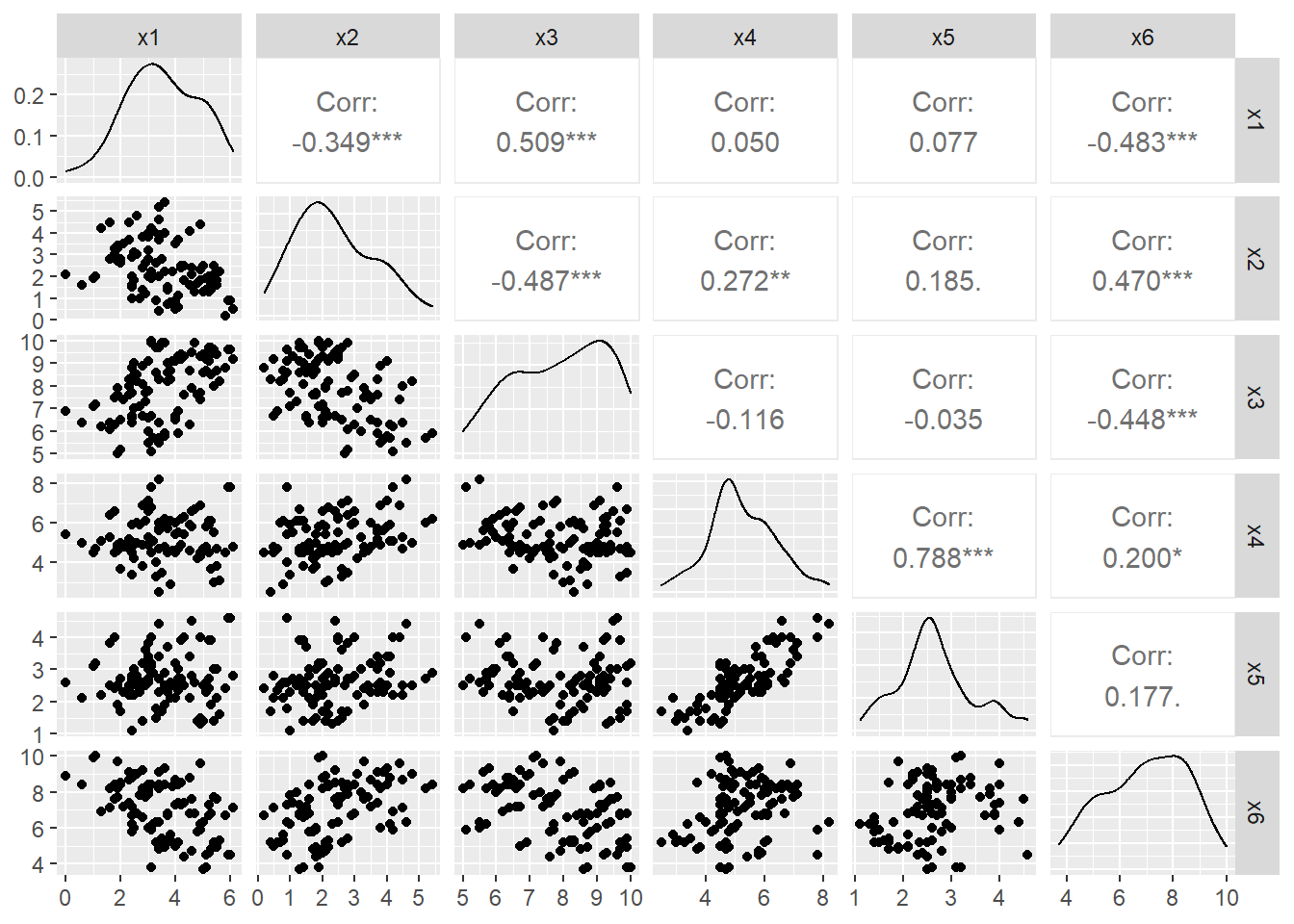
# Mapa de Calor
library(psych)
cor.plot(cor(datos.acp),
main="Mapa de Calor",
diag=T,
show.legend = T,numbers=F,upper=F) 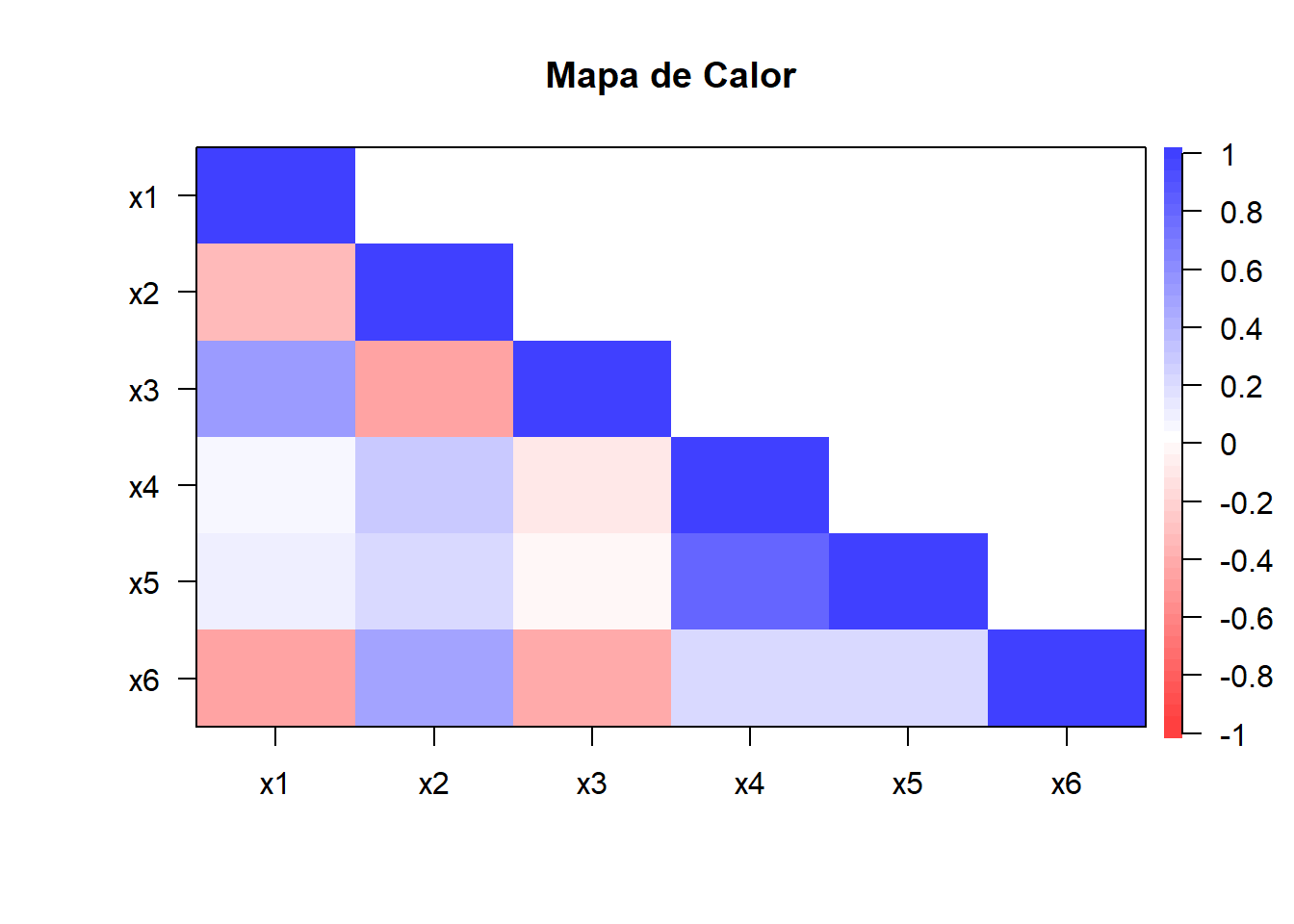
library(GGally)
ggcorr(datos.acp)
# Red de correlaciones
library(corrr)
cor <- correlate(datos.acp) ; cor # A tibble: 6 x 7
term x1 x2 x3 x4 x5 x6
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 x1 NA -0.349 0.509 0.0504 0.0774 -0.483
2 x2 -0.349 NA -0.487 0.272 0.185 0.470
3 x3 0.509 -0.487 NA -0.116 -0.0348 -0.448
4 x4 0.0504 0.272 -0.116 NA 0.788 0.200
5 x5 0.0774 0.185 -0.0348 0.788 NA 0.177
6 x6 -0.483 0.470 -0.448 0.200 0.177 NA network_plot(cor)
Identificando predictores correlacionados
descrCor <- cor(datos.acp)
summary(descrCor[upper.tri(descrCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.4872 -0.2327 0.0774 0.0541 0.2361 0.7881 library(caret)
altaCorr <- findCorrelation(descrCor, cutoff = .50, names=TRUE)
altaCorr[1] "x3" "x4"descrCor2 <- cor(datos.acp[,-c(3,4)])
summary(descrCor2[upper.tri(descrCor2)]) Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.4826 -0.2426 0.1270 0.0129 0.1832 0.4697 altaCorr2 <- findCorrelation(descrCor2, cutoff = .50, names=TRUE)
altaCorr2character(0)Análisis de Componentes Principales usando el paquete ade4
Seleccionamos aquellas componentes cuyo autovalor excede de la media de los autovalores
# Matriz de correlaciones
str(datos.acp)'data.frame': 100 obs. of 6 variables:
$ x1: num 4.1 1.8 3.4 2.7 6 1.9 4.6 1.3 5.5 4 ...
$ x2: num 0.6 3 5.2 1 0.9 3.3 2.4 4.2 1.6 3.5 ...
$ x3: num 6.9 6.3 5.7 7.1 9.6 7.9 9.5 6.2 9.4 6.5 ...
$ x4: num 4.7 6.6 6 5.9 7.8 4.8 6.6 5.1 4.7 6 ...
$ x5: num 2.35 4 2.7 2.3 4.6 1.9 4.5 2.2 3 3.2 ...
$ x6: num 5.2 8.4 8.2 7.8 4.5 9.7 7.6 6.9 7.6 8.7 ...library(ade4)
acp <- dudi.pca(datos.acp,
scannf=FALSE,
scale=TRUE, #Matriz de correlación
nf=2)
summary(acp)Class: pca dudi
Call: dudi.pca(df = datos.acp, scale = TRUE, scannf = FALSE, nf = 2)
Total inertia: 6
Eigenvalues:
Ax1 Ax2 Ax3 Ax4 Ax5
2.5131 1.7396 0.5975 0.5298 0.4157
Projected inertia (%):
Ax1 Ax2 Ax3 Ax4 Ax5
41.885 28.994 9.959 8.830 6.928
Cumulative projected inertia (%):
Ax1 Ax1:2 Ax1:3 Ax1:4 Ax1:5
41.89 70.88 80.84 89.67 96.59
(Only 5 dimensions (out of 6) are shown)print(acp)Duality diagramm
class: pca dudi
$call: dudi.pca(df = datos.acp, scale = TRUE, scannf = FALSE, nf = 2)
$nf: 2 axis-components saved
$rank: 6
eigen values: 2.513 1.74 0.5975 0.5298 0.4157 ...
vector length mode content
1 $cw 6 numeric column weights
2 $lw 100 numeric row weights
3 $eig 6 numeric eigen values
data.frame nrow ncol content
1 $tab 100 6 modified array
2 $li 100 2 row coordinates
3 $l1 100 2 row normed scores
4 $co 6 2 column coordinates
5 $c1 6 2 column normed scores
other elements: cent norm # Valores propios
acp$eig[1] 2.5131 1.7396 0.5975 0.5298 0.4157 0.2043inertia.dudi(acp)Inertia information:
Call: inertia.dudi(x = acp)
Decomposition of total inertia:
inertia cum cum(%)
Ax1 2.5131 2.513 41.89
Ax2 1.7396 4.253 70.88
Ax3 0.5975 4.850 80.84
Ax4 0.5298 5.380 89.67
Ax5 0.4157 5.796 96.59
Ax6 0.2043 6.000 100.00# Vectores propios
acp$c1 CS1 CS2
x1 0.3956 -0.38980
x2 -0.4785 0.05153
x3 0.4605 -0.25457
x4 -0.3116 -0.60547
x5 -0.2677 -0.63078
x6 -0.4835 0.12699Gráfica de Valores propios
# Primera forma
plot(acp$eig,type="b",pch=20,col="blue")
abline(h=1,lty=3,col="red")
# Segunda forma
screeplot(acp, main ="Screeplot - Valores Propios")
# Tercera forma
library(factoextra)
eig.val <- get_eigenvalue(acp)
eig.val eigenvalue variance.percent cumulative.variance.percent
Dim.1 2.5131 41.885 41.89
Dim.2 1.7396 28.994 70.88
Dim.3 0.5975 9.959 80.84
Dim.4 0.5298 8.830 89.67
Dim.5 0.4157 6.928 96.59
Dim.6 0.2043 3.405 100.00barplot(eig.val[, 2], names.arg=1:nrow(eig.val),
main = "Autovalores",
xlab = "Componentes Principales",
ylab = "Porcentaje de variancias",
col ="steelblue")
lines(x = 1:nrow(eig.val), eig.val[, 2],
type="b", pch=19, col = "red")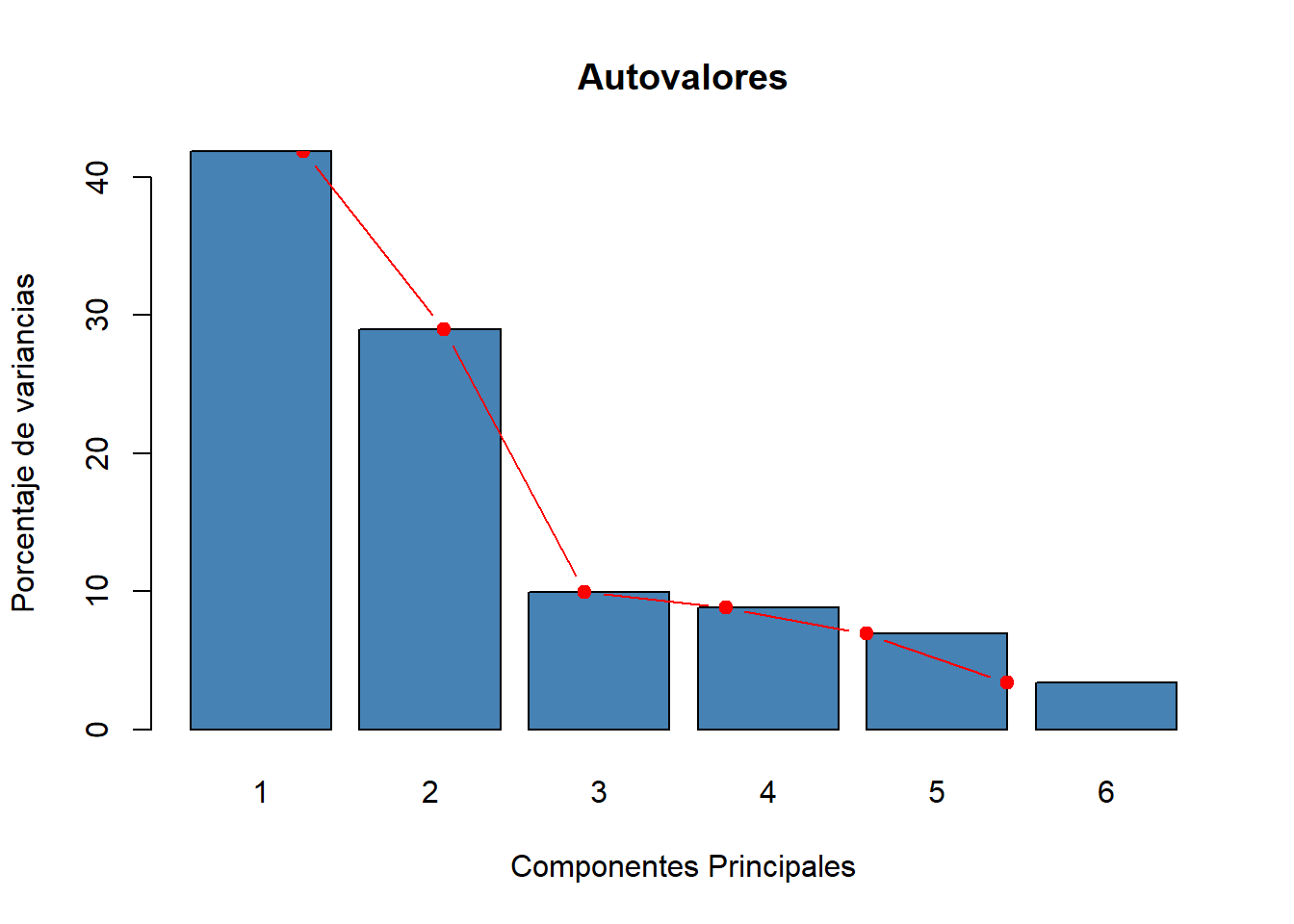
# Cuarta forma
library(factoextra)
fviz_screeplot(acp, ncp=6)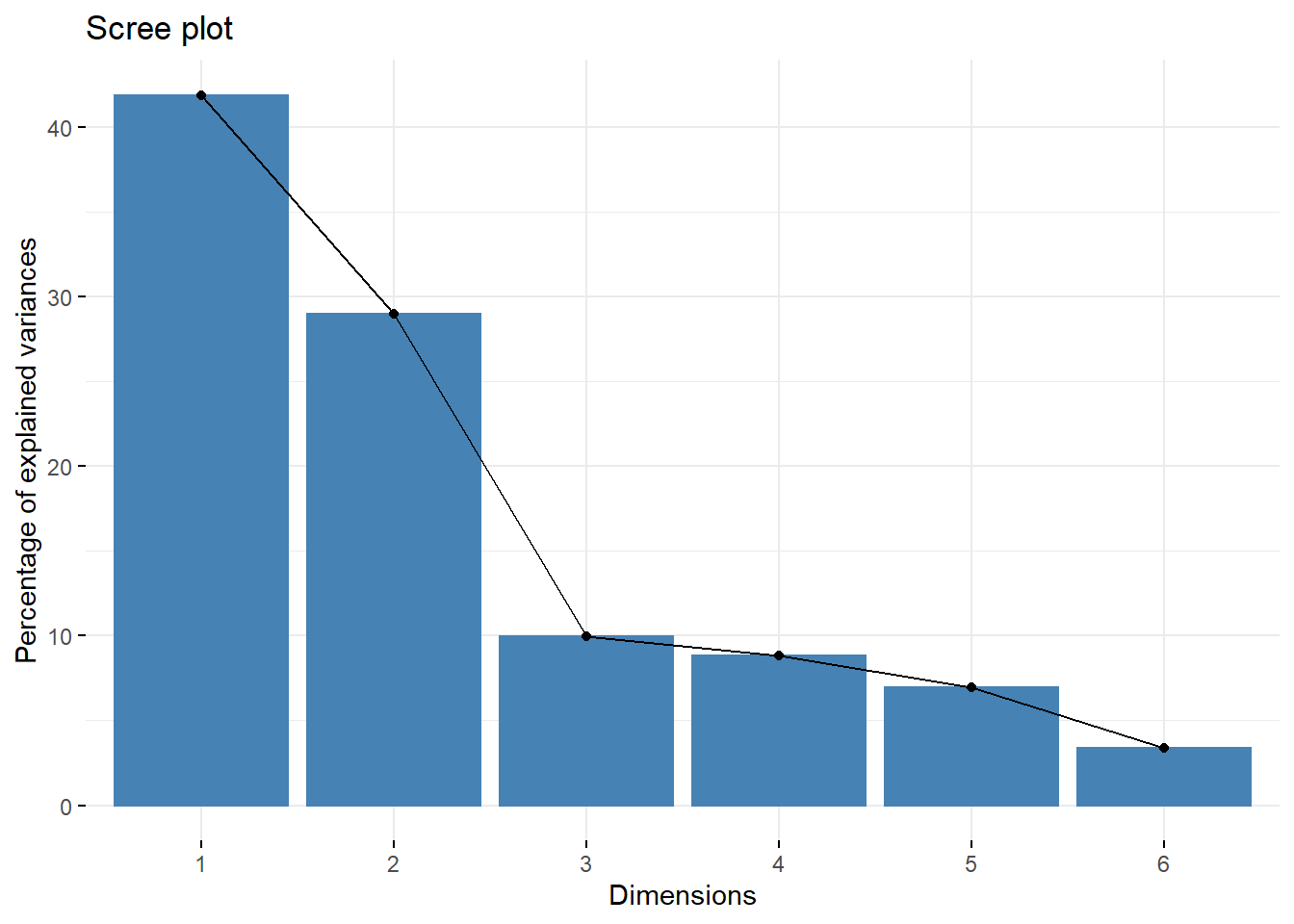
fviz_eig(acp, addlabels=TRUE, hjust = -0.3)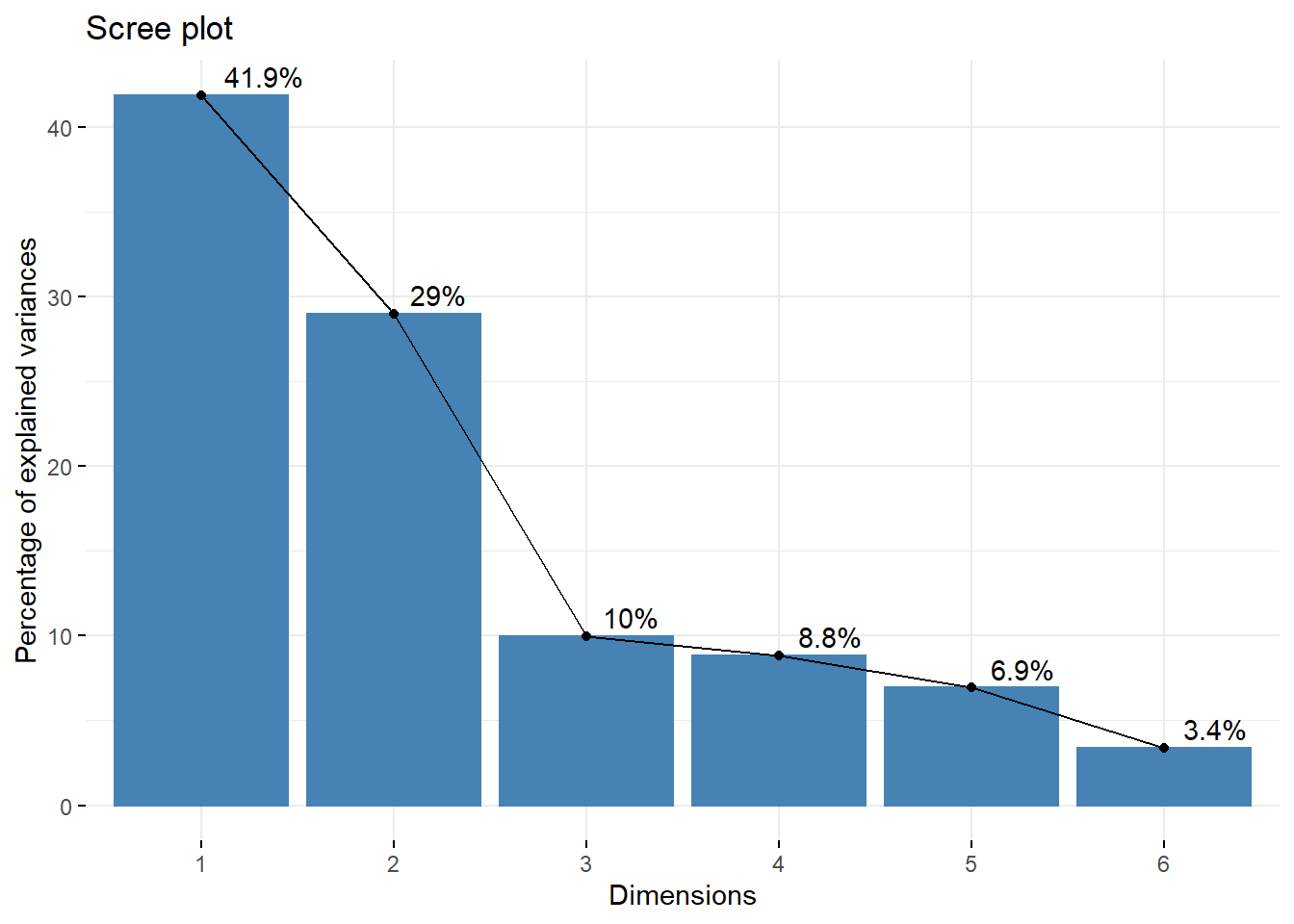
fviz_eig(acp, addlabels=TRUE, hjust = -0.3,
barfill="white", barcolor ="darkblue",
linecolor ="red") + ylim(0,50) + theme_minimal()
Gráfica de Variables sobre el círculo de correlaciones
# Correlaciones entre las variables y los componentes
acp$co Comp1 Comp2
x1 0.6271 -0.51412
x2 -0.7586 0.06796
x3 0.7300 -0.33577
x4 -0.4939 -0.79858
x5 -0.4243 -0.83196
x6 -0.7665 0.16749# Primera forma
s.corcircle(acp$co,grid=FALSE)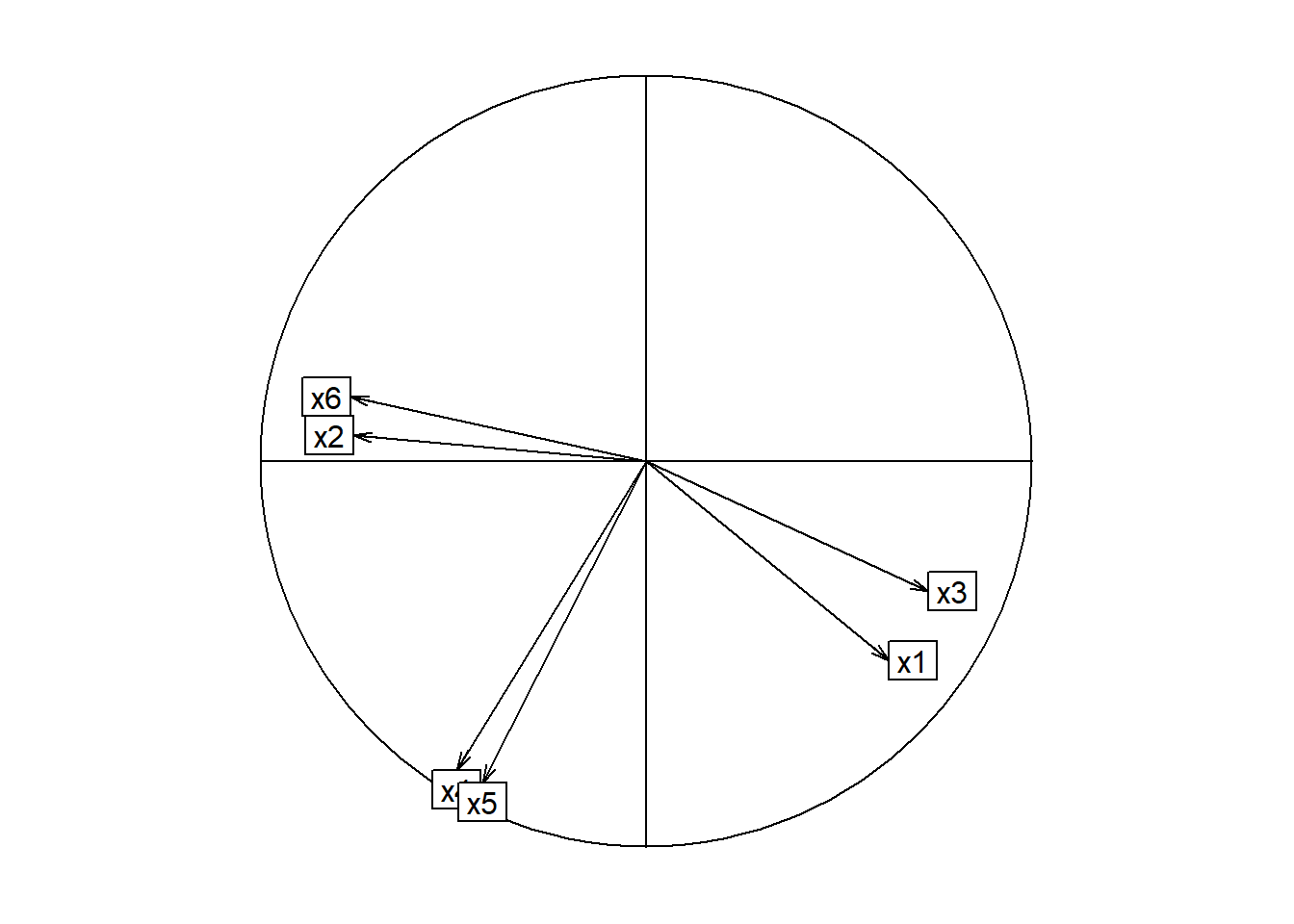
# Segunda forma
fviz_pca_var(acp)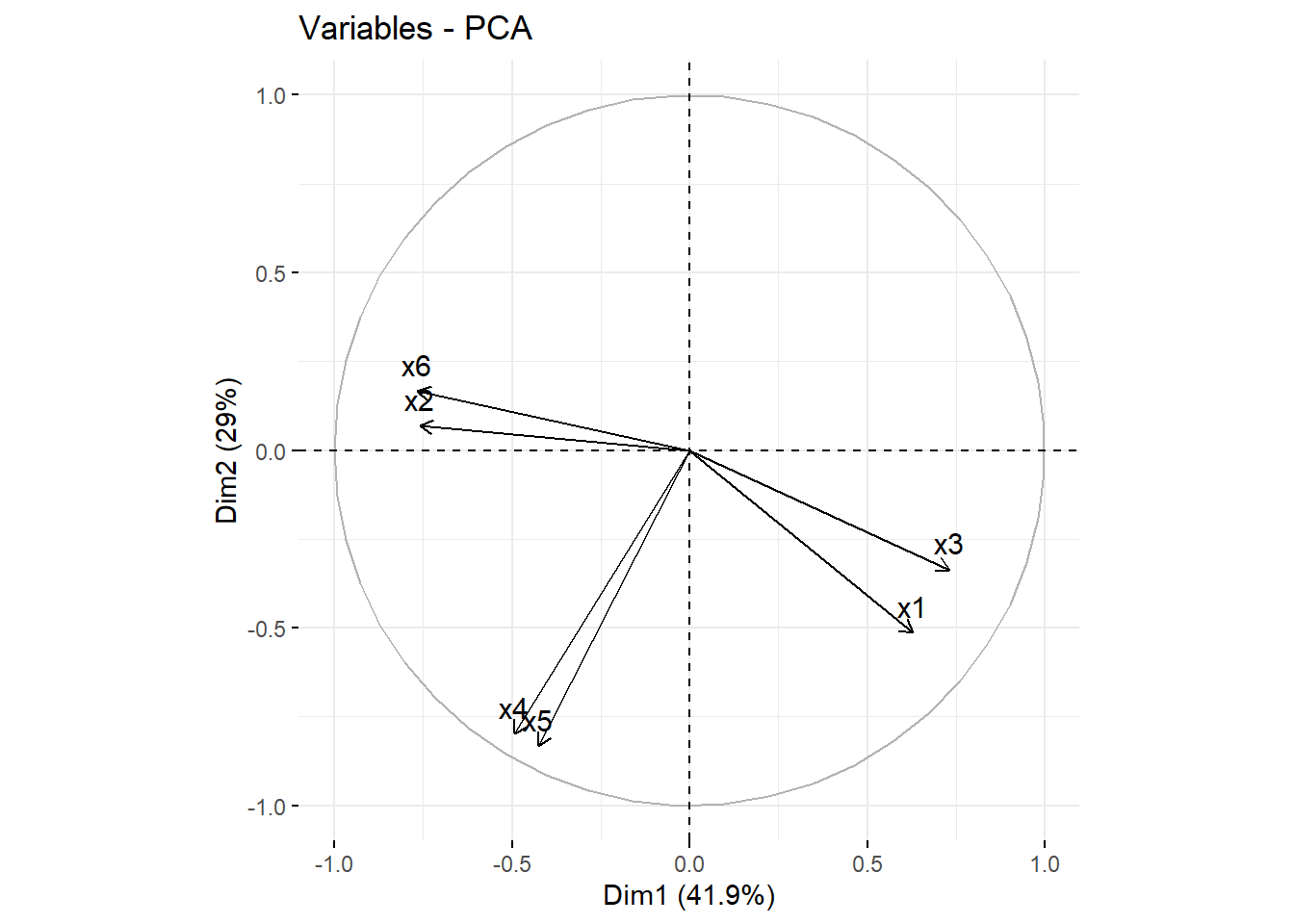
fviz_pca_var(acp, col.var="steelblue")+theme_minimal()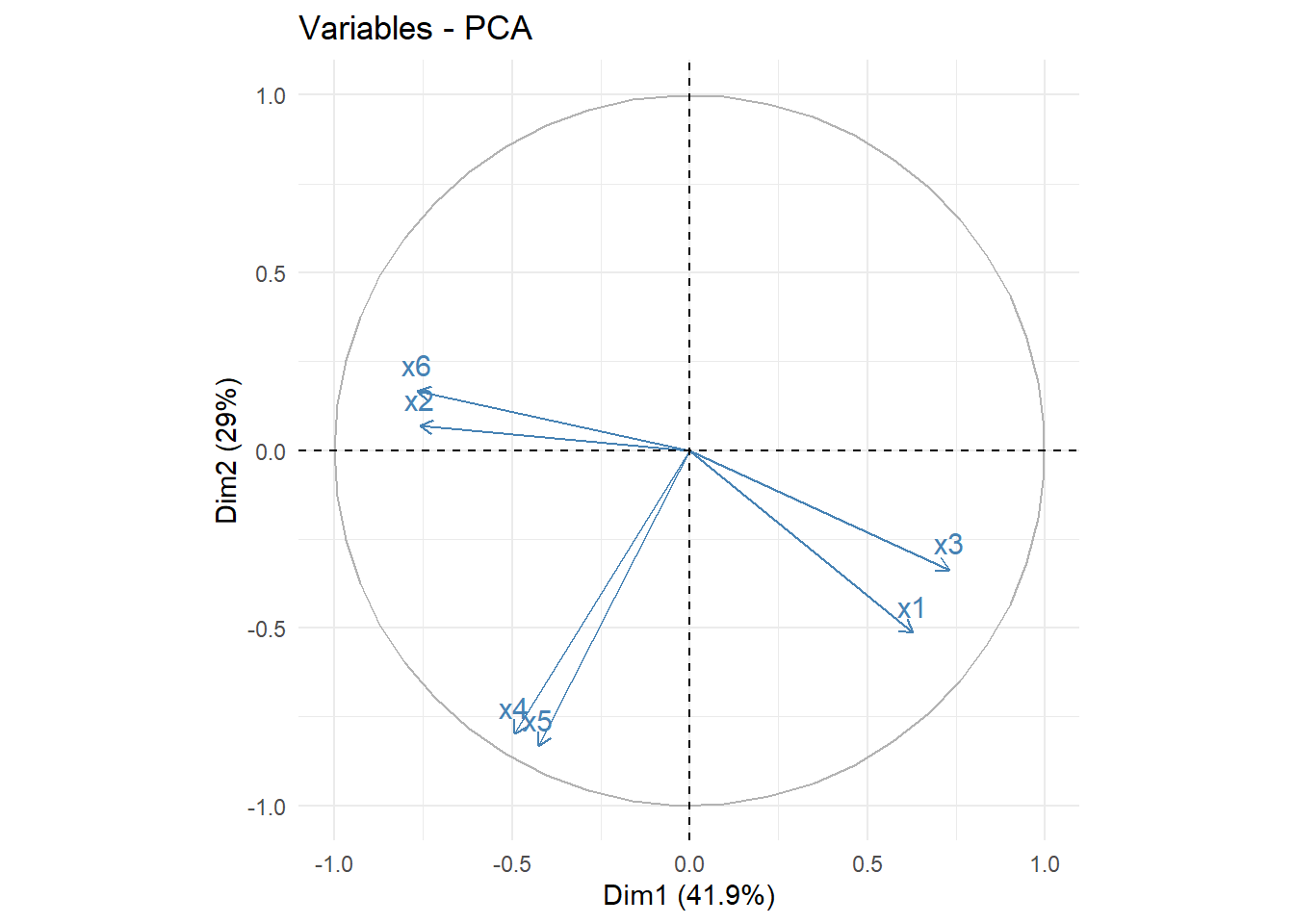
Contribución de las variables a los componentes principaes
(contrib <- acp$co*acp$co) Comp1 Comp2
x1 0.3933 0.264321
x2 0.5754 0.004619
x3 0.5329 0.112740
x4 0.2439 0.637723
x5 0.1801 0.692160
x6 0.5875 0.028054contrib <- as.matrix(contrib)
library(corrplot)
corrplot(contrib,is.corr=FALSE)
# Scores o Puntuaciones de cada individuo
acp$li[1:10,] Axis1 Axis2
1 1.3585 0.3452
2 -2.5822 -0.8795
3 -2.5046 0.2279
4 -0.2687 0.3459
5 1.2822 -4.2782
6 -1.3060 1.6089
7 -0.3592 -2.8023
8 -1.7455 1.5060
9 1.2496 -0.8296
10 -1.7010 -0.5424Análisis descriptivo de los scores
options(scipen=999)
cov(acp$li)## Axis1 Axis2
## Axis1 2.5385017425976257321 0.0000000000000004252
## Axis2 0.0000000000000004252 1.7571886001840355540cor(acp$li)## Axis1 Axis2
## Axis1 1.0000000000000000000 0.0000000000000002013
## Axis2 0.0000000000000002013 1.0000000000000000000describe(acp$li)## acp$li
##
## 2 Variables 100 Observations
## --------------------------------------------------------------------------------
## Axis1
## n missing distinct
## 100 0 99
## Info Mean Gmd
## 1 0.0000000000000000297 1.832
## .05 .10 .25
## -2.4454 -1.9305 -1.4246
## .50 .75 .90
## -0.2227 1.4345 1.9390
## .95
## 2.2765
##
## lowest : -2.950 -2.645 -2.640 -2.582 -2.505, highest: 2.316 2.323 2.326 2.368 2.531
## --------------------------------------------------------------------------------
## Axis2
## n missing distinct
## 100 0 99
## Info Mean Gmd
## 1 0.0000000000000003615 1.474
## .05 .10 .25
## -2.3756 -1.6829 -0.7394
## .50 .75 .90
## 0.2379 1.0009 1.5071
## .95
## 1.6195
##
## lowest : -4.278 -4.249 -2.802 -2.496 -2.392, highest: 1.821 1.922 2.004 2.467 2.527
## --------------------------------------------------------------------------------# Gráfica de individuos sobre el primer plano de componentes
# Primera forma
s.label(acp$li,xax=1,yax=2,clabel=0.7,grid=FALSE,boxes=FALSE)
# Segunda forma
fviz_pca_ind(acp)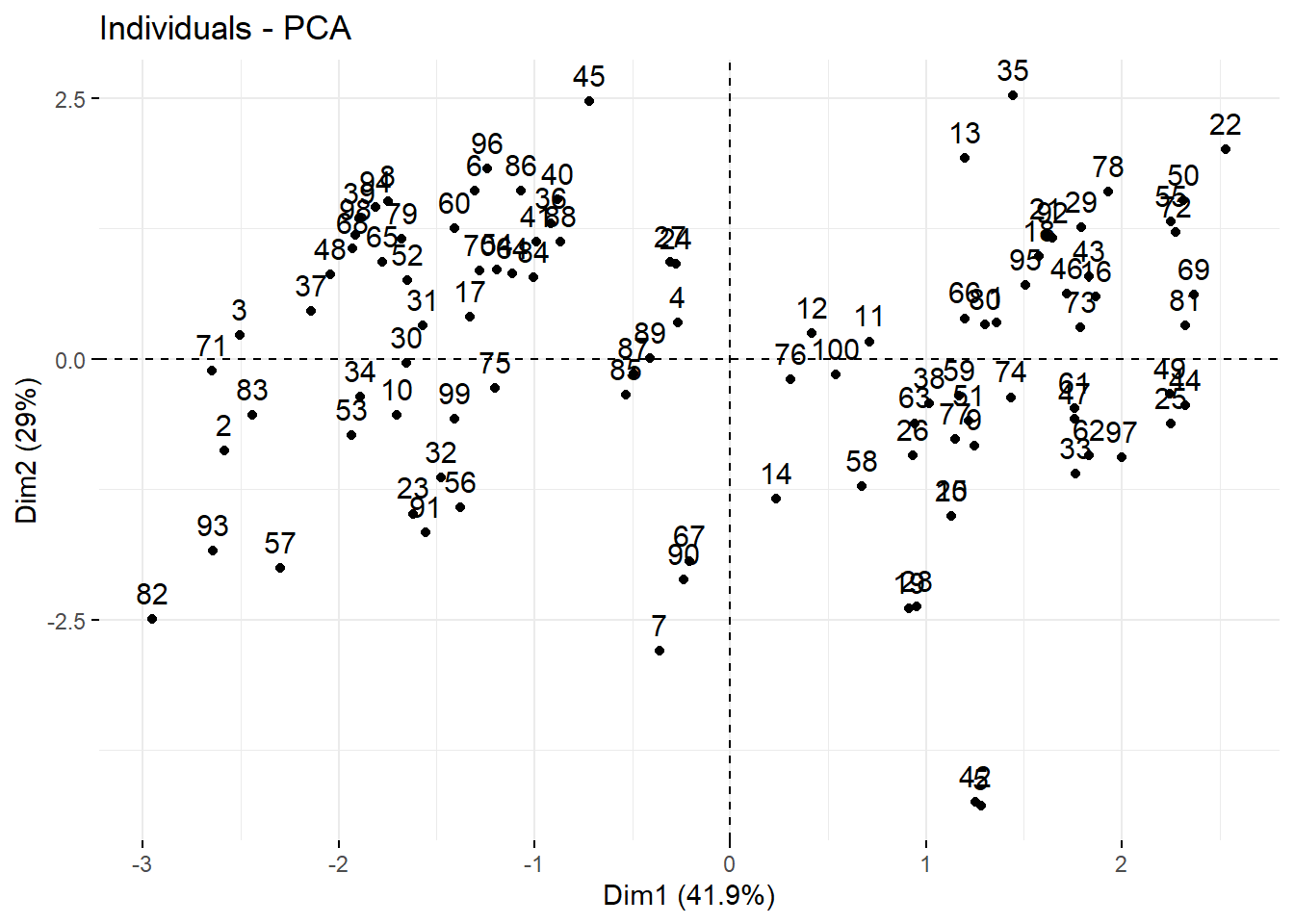
# Gráfica de individuos sobre los componentes 2 y 3. Para realizar este gráfico se tiene que cambiar el número de factores en la función dudi.pca
# s.label(acp$li,xax=2,yax=3,clabel=0.7,grid=FALSE,boxes=FALSE)
# Gráfica de individuos sobre el primer plano con biplot
# Primera forma
s.label(acp$li,clabel=0.7,grid=FALSE,boxes=FALSE)
s.corcircle(acp$co,grid=FALSE,add=TRUE,clabel=0.7)
# Segunda forma
fviz_pca_biplot(acp, repel = FALSE,
col.var = "steelblue",
col.ind = "black" )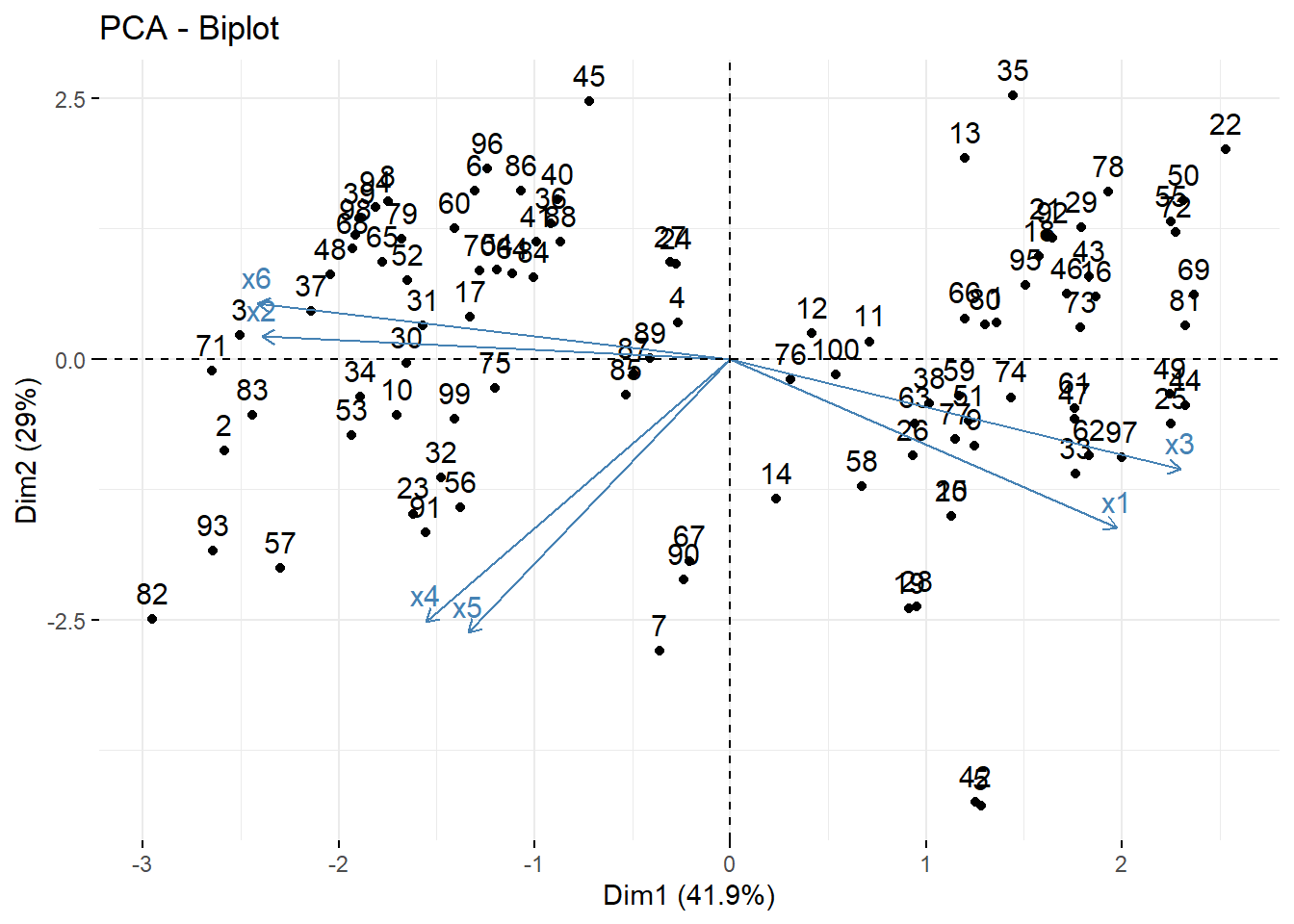
Grabar los datos y los resultados de los scores en un archivo CSV
salida.acp <- cbind(datos.acp,acp$li[,c(1,2)])
head(salida.acp) x1 x2 x3 x4 x5 x6 Axis1 Axis2
1 4.1 0.6 6.9 4.7 2.35 5.2 1.3585 0.3452
2 1.8 3.0 6.3 6.6 4.00 8.4 -2.5822 -0.8795
3 3.4 5.2 5.7 6.0 2.70 8.2 -2.5046 0.2279
4 2.7 1.0 7.1 5.9 2.30 7.8 -0.2687 0.3459
5 6.0 0.9 9.6 7.8 4.60 4.5 1.2822 -4.2782
6 1.9 3.3 7.9 4.8 1.90 9.7 -1.3060 1.6089str(salida.acp)'data.frame': 100 obs. of 8 variables:
$ x1 : num 4.1 1.8 3.4 2.7 6 1.9 4.6 1.3 5.5 4 ...
$ x2 : num 0.6 3 5.2 1 0.9 3.3 2.4 4.2 1.6 3.5 ...
$ x3 : num 6.9 6.3 5.7 7.1 9.6 7.9 9.5 6.2 9.4 6.5 ...
$ x4 : num 4.7 6.6 6 5.9 7.8 4.8 6.6 5.1 4.7 6 ...
$ x5 : num 2.35 4 2.7 2.3 4.6 1.9 4.5 2.2 3 3.2 ...
$ x6 : num 5.2 8.4 8.2 7.8 4.5 9.7 7.6 6.9 7.6 8.7 ...
$ Axis1: num 1.359 -2.582 -2.505 -0.269 1.282 ...
$ Axis2: num 0.345 -0.88 0.228 0.346 -4.278 ...write.csv(salida.acp,"hatco-acp-resultados.csv")Generar un índice para cada individuo
y <- (acp$li$Axis1*acp$eig[1] + acp$li$Axis2*acp$eig[2])/(2.5131+1.7396)
head(y)[1] 0.94402 -1.88573 -1.38683 -0.01729 -0.99234 -0.11364y <- as.data.frame(y)
y y
1 0.94402
2 -1.88573
3 -1.38683
4 -0.01729
5 -0.99234
6 -0.11364
7 -1.35858
8 -0.41544
9 0.39908
10 -1.22704
11 0.48772
12 0.34609
13 1.49401
14 -0.40825
15 0.04930
16 1.34953
17 -0.62309
18 1.33376
19 -0.43863
20 0.04930
21 1.44378
22 2.31555
23 -1.56300
24 0.20934
25 1.07722
26 0.17204
27 0.19716
28 -0.40747
29 1.57490
30 -0.99363
31 -0.79768
32 -1.33975
33 0.59203
34 -1.26617
35 1.88622
36 -0.01307
37 -1.07714
38 0.42481
39 -0.57040
40 0.10358
41 -0.12470
42 -0.99800
43 1.40599
44 1.18885
45 0.58387
46 1.27236
47 0.80181
48 -0.87589
49 1.18675
50 1.98923
51 0.47766
52 -0.66612
53 -1.44013
54 -0.35509
55 1.86906
56 -1.39761
57 -2.17738
58 -0.10186
59 0.54527
60 -0.31907
61 0.84392
62 0.70365
63 0.30336
64 -0.32356
65 -0.66991
66 0.86783
67 -0.91616
68 -0.70931
69 1.65185
70 -0.41191
71 -1.61007
72 1.84116
73 1.17946
74 0.69560
75 -0.82608
76 0.10232
77 0.36603
78 1.79814
79 -0.51993
80 0.90275
81 1.50377
82 -2.76417
83 -1.66249
84 -0.27702
85 -0.45395
86 0.02575
87 -0.34798
88 -0.05378
89 -0.24053
90 -1.00578
91 -1.60034
92 1.44539
93 -2.31202
94 -0.47648
95 1.17807
96 0.01157
97 0.79495
98 -0.64503
99 -1.06716
100 0.25881