Capítulo 5 Análisis de Correspondencia Simple
5.1 Marco Téorico
El objetivo de algunas técnicas multivariadas consiste en explicar con un menor número de dimensiones (factores o componentes), la información inicial. Cuando las variables son continuas o medidas en escala de intervalo o de razón, la técnica de Análisis de Componentes Principales o el modelo de Análisis Factorial son los procedimientos apropiados para analizar la interdependencia de un conjunto de variables o features. En cambio, cuando las variables estudiadas son cualitativas, es necesario acudir al Análisis de Correspondencia Simple (si se trabajan con dos variables) o al Análisis de Correspondencia Múltiple (si se trabajan con tres o más variables) para obtener estas dimensiones subyacentes que permitirán interpretar de forma rápida las relaciones de interdependencia del conjunto de variables originales. En esta técnica lo que se busca es encontrar la relación que exista entre las categorías de una variable con las categorías de otra(s) variable(s).
5.2 Ejemplos
5.2.1 Ejemplo 1. Renta vs Opinión
Este ejemplo fue tomado del libro de Luque
Luque, T. (2000). Técnicas de Análisis de Datos en Investigación de Mercados. Ediciones Pirámide.
Ingreso de datos
Estos datos corresponden a una encuesta que se realizó a 500 personas con relación a su opinión del sistema sanitario público. Se registró adicionalmente, el tipo de renta percibido por cada encuestado.
| Opinión | |||
|---|---|---|---|
| Renta | Bueno | Malo | Regular |
| Bajo | 75 | 40 | 35 |
| Medio | 60 | 50 | 70 |
| Alto | 20 | 40 | 30 |
| Muy alto | 15 | 40 | 25 |
datos.acs <- matrix(c(75,40,35,
60,50,70,
20,40,30,
15,40,25),nrow=4,byrow=T) #ncol=3
datos.acs [,1] [,2] [,3]
[1,] 75 40 35
[2,] 60 50 70
[3,] 20 40 30
[4,] 15 40 25dimnames(datos.acs)<- list(renta=c("Bajo","Medio","Alto",
"Muy Alto"),
opinion=c("Bueno","Malo","Regular"))
datos.acs opinion
renta Bueno Malo Regular
Bajo 75 40 35
Medio 60 50 70
Alto 20 40 30
Muy Alto 15 40 25datos.acs[2,1][1] 60addmargins(datos.acs) opinion
renta Bueno Malo Regular Sum
Bajo 75 40 35 150
Medio 60 50 70 180
Alto 20 40 30 90
Muy Alto 15 40 25 80
Sum 170 170 160 500Visualización de una Tabla de Contingencia usando una matriz gráfica
Con las gráficas se analizará la asociación entre las variables
Primera forma - Balloonplots
library(gplots)
# Convertir los datos en una tabla
dt <- as.table(datos.acs)
dt opinion
renta Bueno Malo Regular
Bajo 75 40 35
Medio 60 50 70
Alto 20 40 30
Muy Alto 15 40 25str(dt) 'table' num [1:4, 1:3] 75 60 20 15 40 50 40 40 35 70 ...
- attr(*, "dimnames")=List of 2
..$ renta : chr [1:4] "Bajo" "Medio" "Alto" "Muy Alto"
..$ opinion: chr [1:3] "Bueno" "Malo" "Regular"# Para graficarlo con % fila (perifles fila)
dt <- prop.table(dt,margin=1)
dt opinion
renta Bueno Malo Regular
Bajo 0.5000000 0.2666667 0.2333333
Medio 0.3333333 0.2777778 0.3888889
Alto 0.2222222 0.4444444 0.3333333
Muy Alto 0.1875000 0.5000000 0.3125000balloonplot(t(dt),
main ="Gráfico Opinión Renta",
xlab ="Opinión",
ylab="Renta",
label = F, cum.margins=F,
label.lines=F, show.margins = FALSE)
Segunda forma - Mosaicos
library(graphics)
mosaicplot(t(dt),shade=F)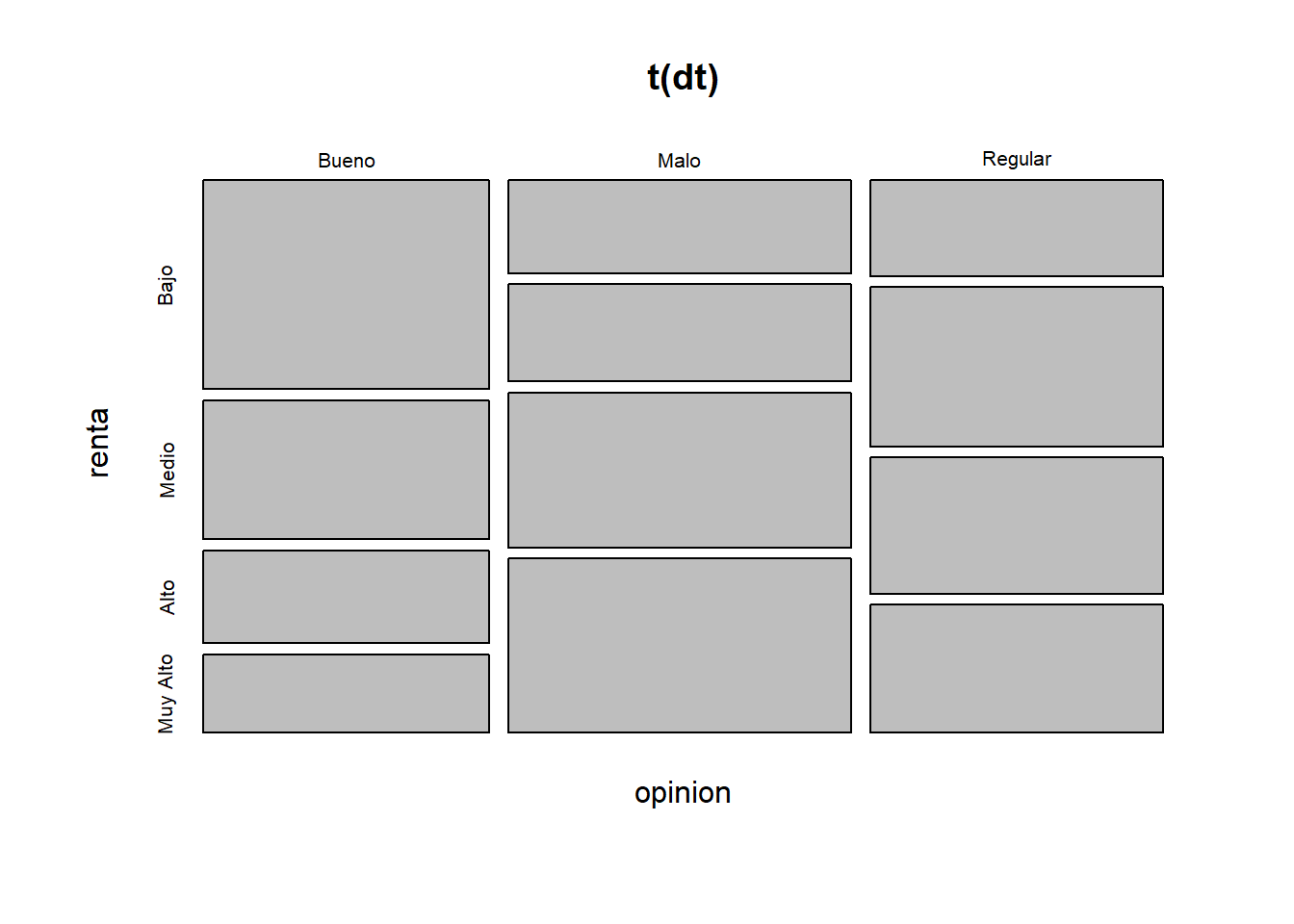
Prueba de Independencia Chi-Cuadrado
Contrastamos la hipótesis nula de independencia entre las dos variables que conforman la tabla de contingencia.
\(H_{o}\): Las variables son independientes
\(H_{1}\): Las variables son dependientes
prueba <- chisq.test(datos.acs)
prueba
Pearson's Chi-squared test
data: datos.acs
X-squared = 40.049, df = 6, p-value = 4.455e-07Tabla de perfiles fila y perfiles columnas
# Frecuencia Relativa (fij)
prop.table(datos.acs) opinion
renta Bueno Malo Regular
Bajo 0.15 0.08 0.07
Medio 0.12 0.10 0.14
Alto 0.04 0.08 0.06
Muy Alto 0.03 0.08 0.05# Perfiles Fila
prop.table(datos.acs, 1) opinion
renta Bueno Malo Regular
Bajo 0.5000000 0.2666667 0.2333333
Medio 0.3333333 0.2777778 0.3888889
Alto 0.2222222 0.4444444 0.3333333
Muy Alto 0.1875000 0.5000000 0.3125000# Perfiles Columna
prop.table(datos.acs, 2) opinion
renta Bueno Malo Regular
Bajo 0.44117647 0.2352941 0.21875
Medio 0.35294118 0.2941176 0.43750
Alto 0.11764706 0.2352941 0.18750
Muy Alto 0.08823529 0.2352941 0.15625# Tabla con el paquete gmodels y función CrossTable()
library(gmodels)Registered S3 method overwritten by 'gdata':
method from
reorder.factor gplotsCrossTable(datos.acs,
prop.t=F, # Frecuencia Relativa
prop.r=F, # Perfil Fila
prop.c=F, #Perfil Columna
prop.chisq=FALSE)
Cell Contents
|-------------------------|
| N |
|-------------------------|
Total Observations in Table: 500
| opinion
renta | Bueno | Malo | Regular | Row Total |
-------------|-----------|-----------|-----------|-----------|
Bajo | 75 | 40 | 35 | 150 |
-------------|-----------|-----------|-----------|-----------|
Medio | 60 | 50 | 70 | 180 |
-------------|-----------|-----------|-----------|-----------|
Alto | 20 | 40 | 30 | 90 |
-------------|-----------|-----------|-----------|-----------|
Muy Alto | 15 | 40 | 25 | 80 |
-------------|-----------|-----------|-----------|-----------|
Column Total | 170 | 170 | 160 | 500 |
-------------|-----------|-----------|-----------|-----------|
Análisis de Correspondencias Simple con el paquete FactoMineR
Con la función CA de FactoMineR se obtienen los autovalores y la prueba de independencia de Chi Cuadrado
library(FactoMineR)
#3 filas y 4 columnas min(3,4)-1 -> ncp=2
res.ca <- CA(datos.acs,ncp=2,graph=F)
res.ca **Results of the Correspondence Analysis (CA)**
The row variable has 4 categories; the column variable has 3 categories
The chi square of independence between the two variables is equal to 40.04927 (p-value = 4.454704e-07 ).
*The results are available in the following objects:
name description
1 "$eig" "eigenvalues"
2 "$col" "results for the columns"
3 "$col$coord" "coord. for the columns"
4 "$col$cos2" "cos2 for the columns"
5 "$col$contrib" "contributions of the columns"
6 "$row" "results for the rows"
7 "$row$coord" "coord. for the rows"
8 "$row$cos2" "cos2 for the rows"
9 "$row$contrib" "contributions of the rows"
10 "$call" "summary called parameters"
11 "$call$marge.col" "weights of the columns"
12 "$call$marge.row" "weights of the rows" # Scree Plot de los Autovalores
res.ca$eig eigenvalue percentage of variance cumulative percentage of variance
dim 1 0.06510303 81.27866 81.27866
dim 2 0.01499552 18.72134 100.00000# Otra forma
library(factoextra)
eig.val <- get_eigenvalue(res.ca)
eig.val eigenvalue variance.percent cumulative.variance.percent
Dim.1 0.06510303 81.27866 81.27866
Dim.2 0.01499552 18.72134 100.00000fviz_screeplot(res.ca)
fviz_screeplot(res.ca, addlabels = TRUE, ylim = c(0, 90))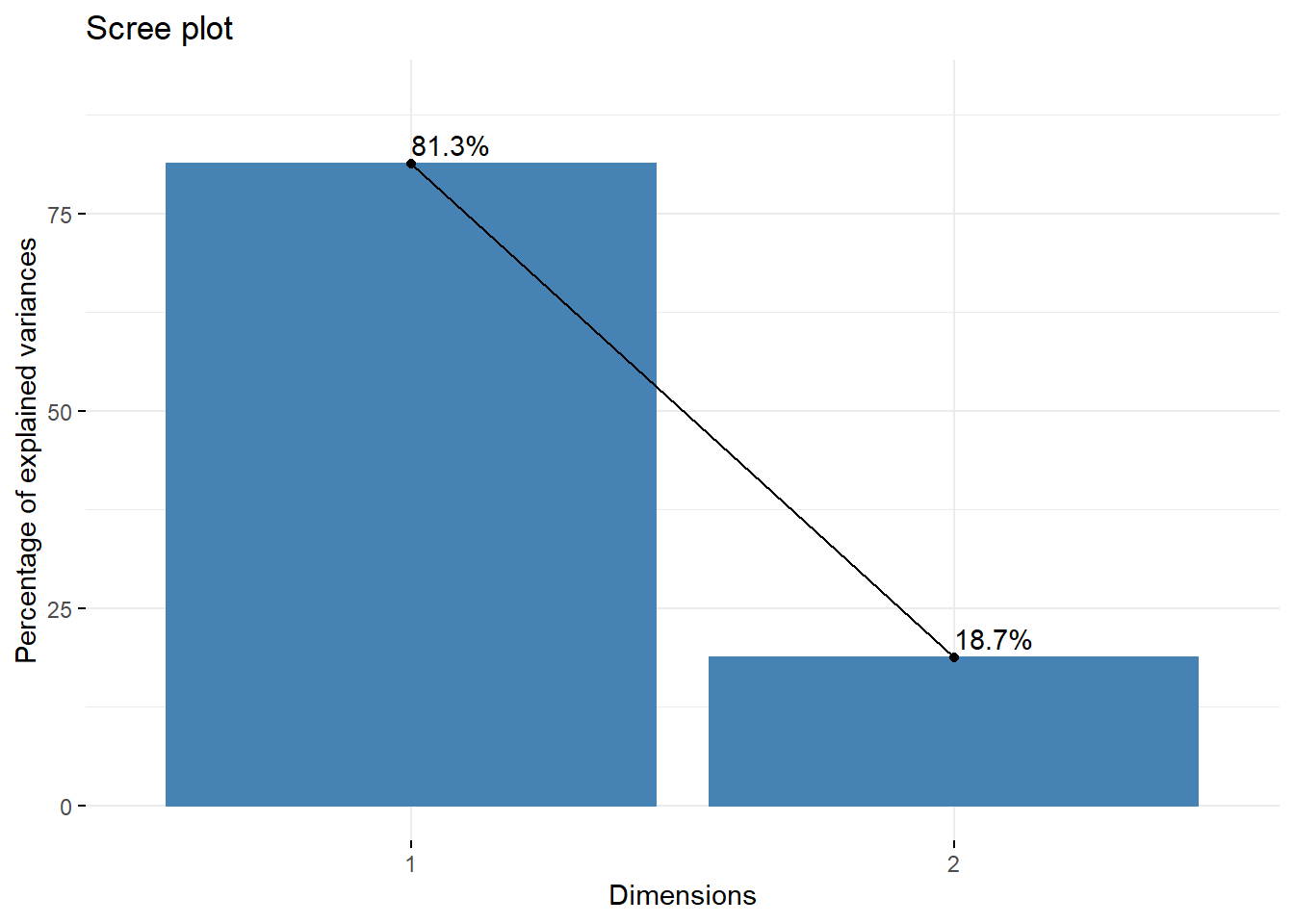
Gráficos- Biplot
Representación gráfica de los datos en las dos dimensiones
# Primera forma - usando plot.CA de FactoMineR
plot.CA(res.ca) # Mapa Simétrico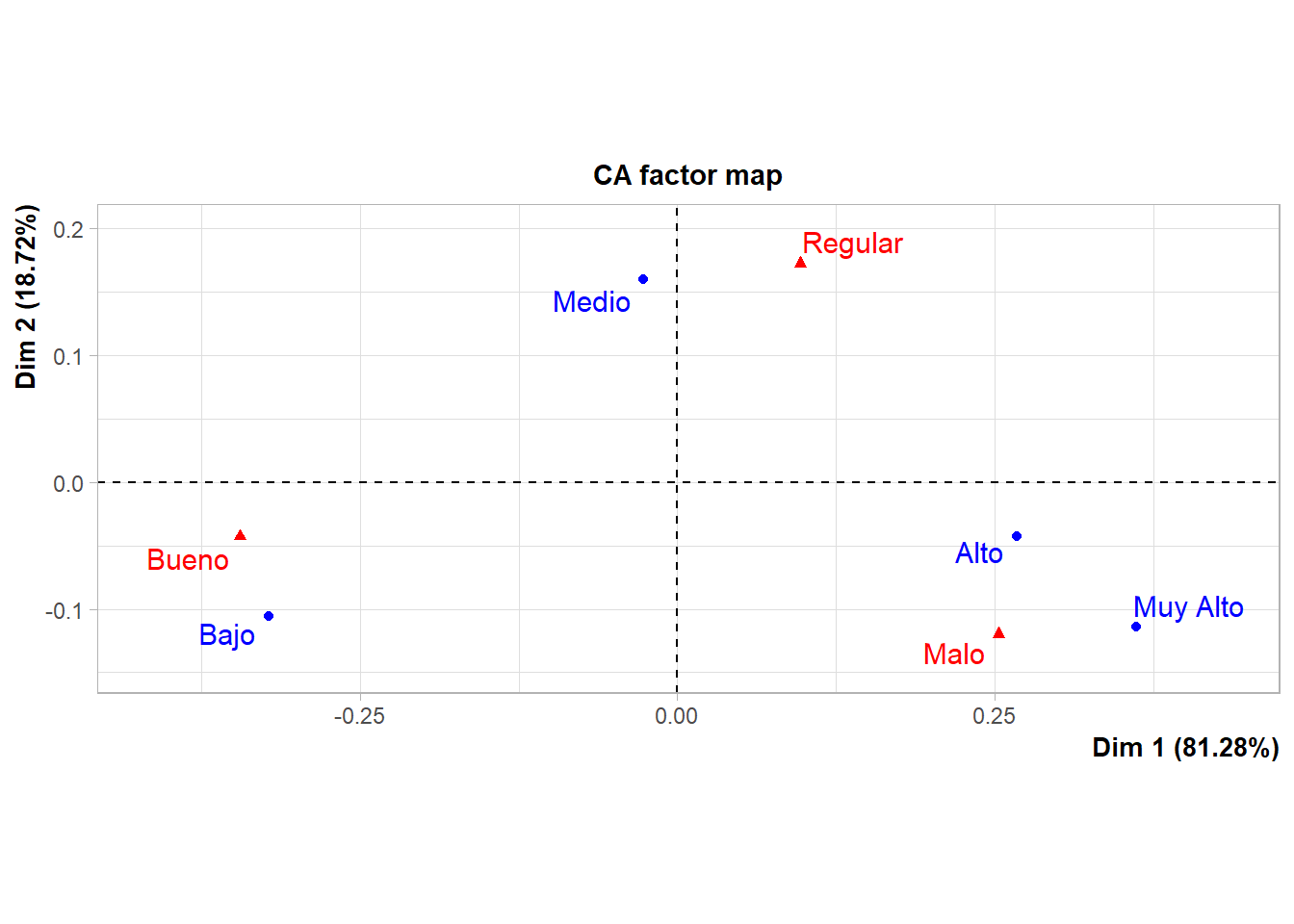
plot.CA(res.ca, axes = c(1,2), col.row = "blue", col.col = "red")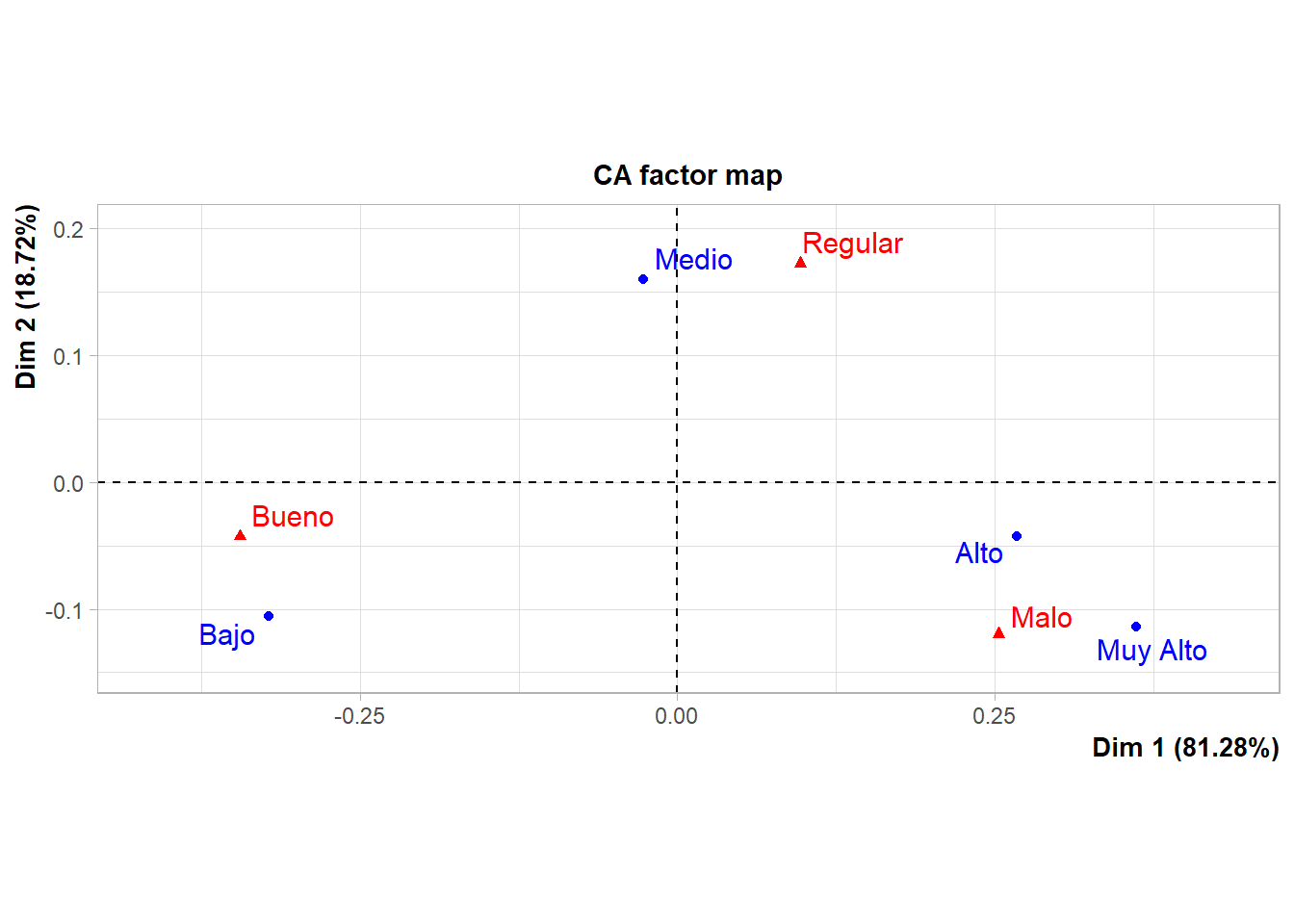
plot.CA(res.ca,mass=c(T,T))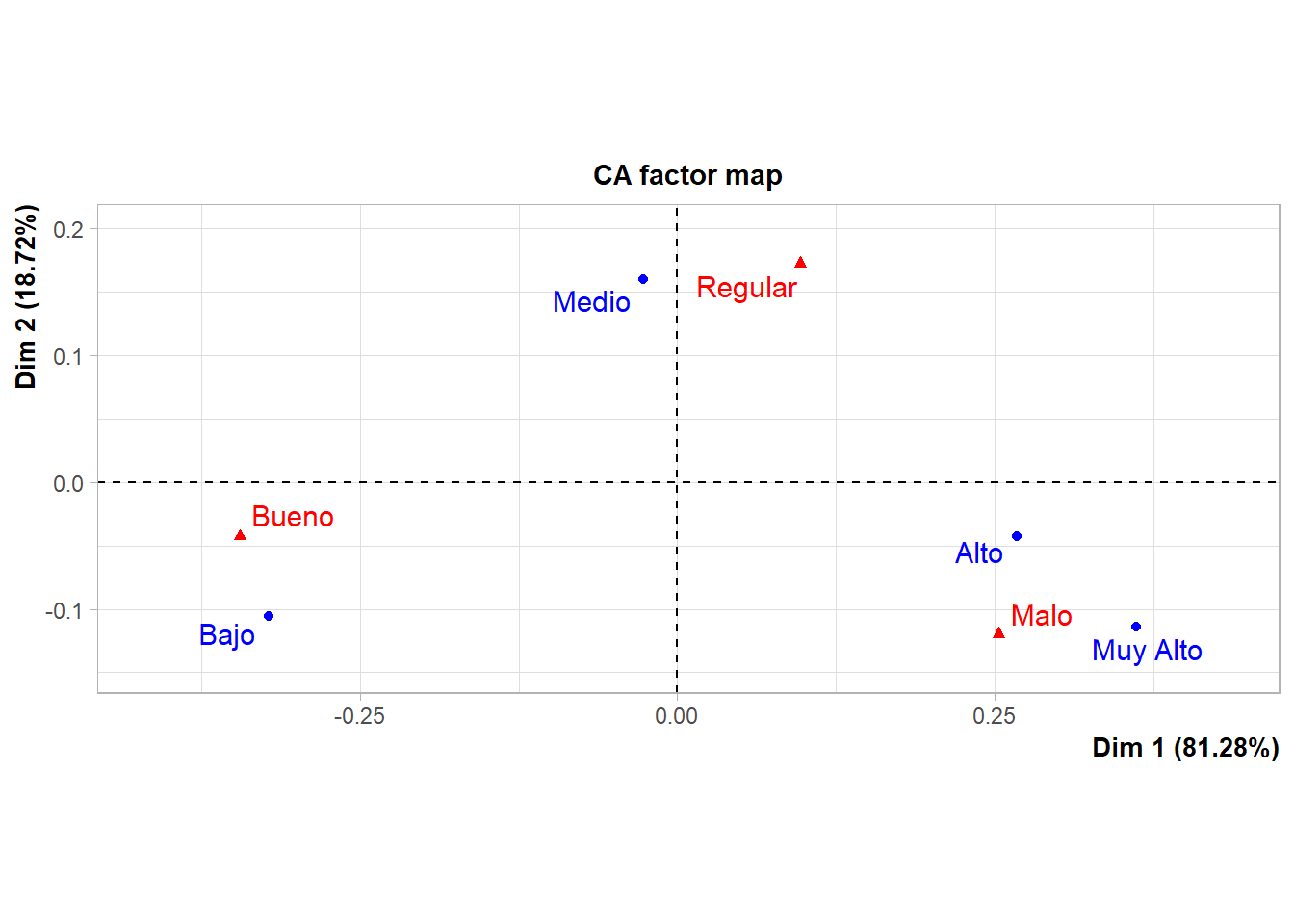
# Segunda forma - usando fviz_ca_biplot de factoextra
fviz_ca_biplot(res.ca, repel = T)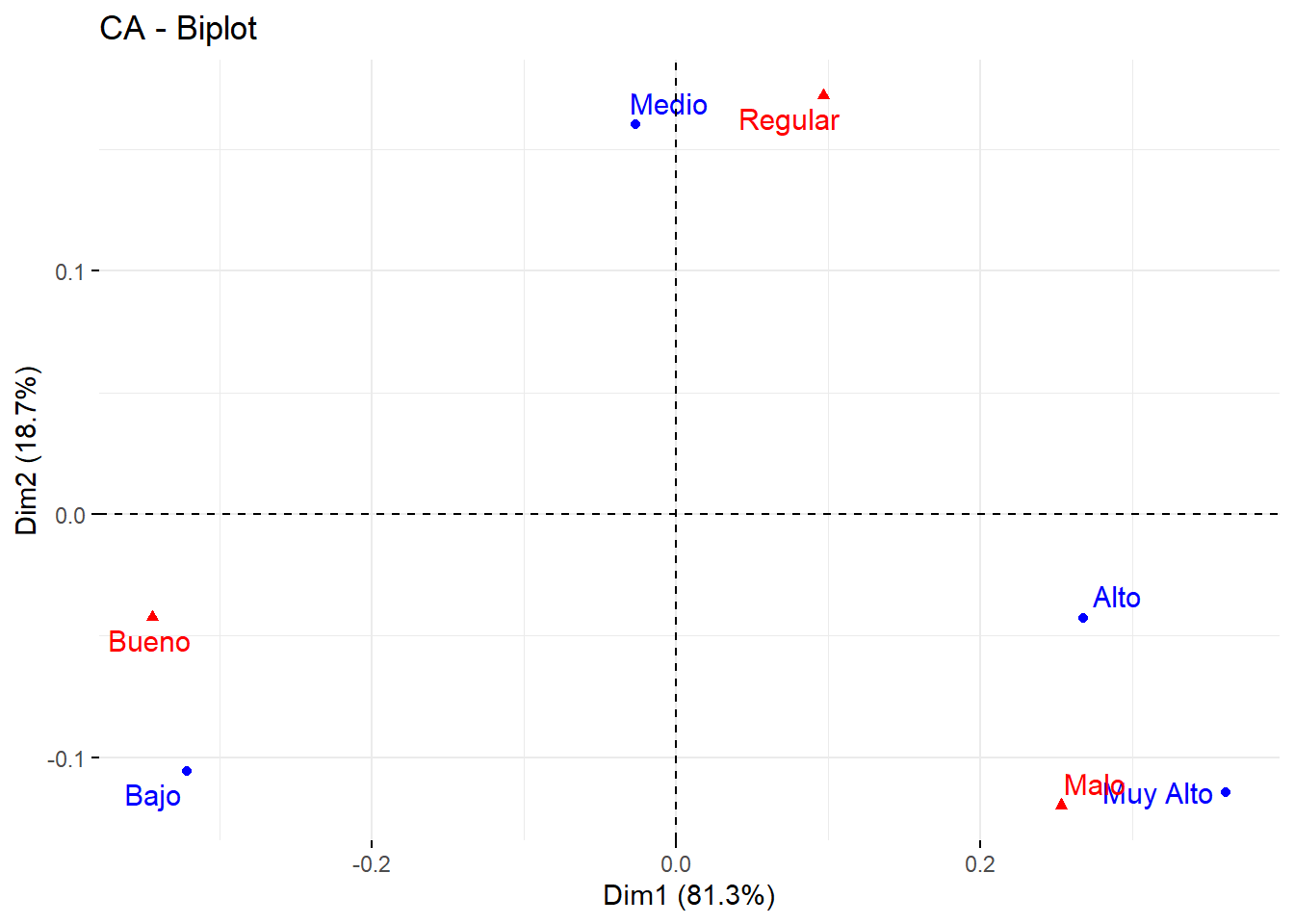
# Elegir distintos temas
library(ggthemes)
library(tvthemes)
fviz_ca_biplot(res.ca, repel = T) + theme_minimal()
fviz_ca_biplot(res.ca, repel = T) + theme_light()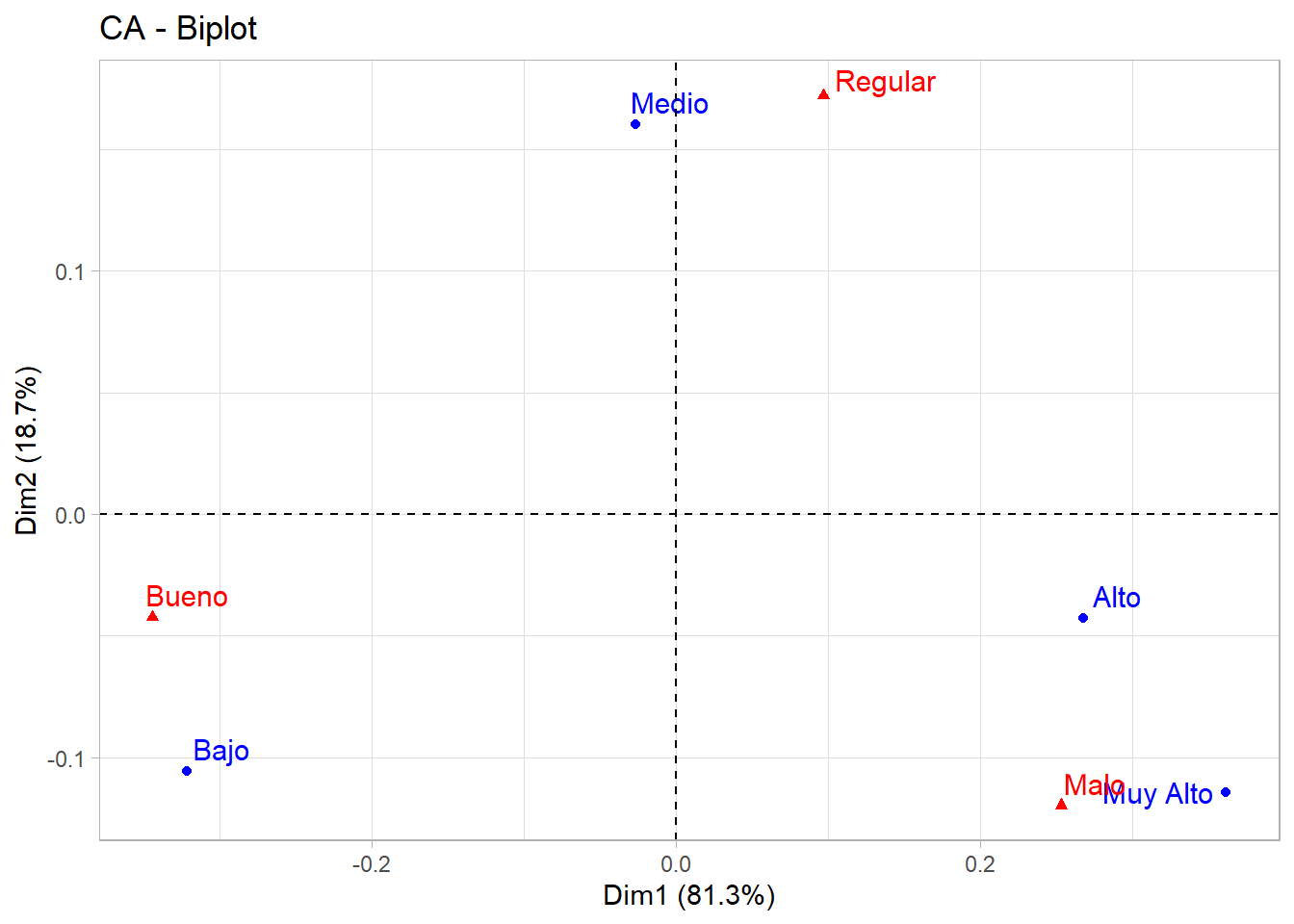
fviz_ca_biplot(res.ca, repel = T) + theme_void()
fviz_ca_biplot(res.ca, repel = T) + theme_gray()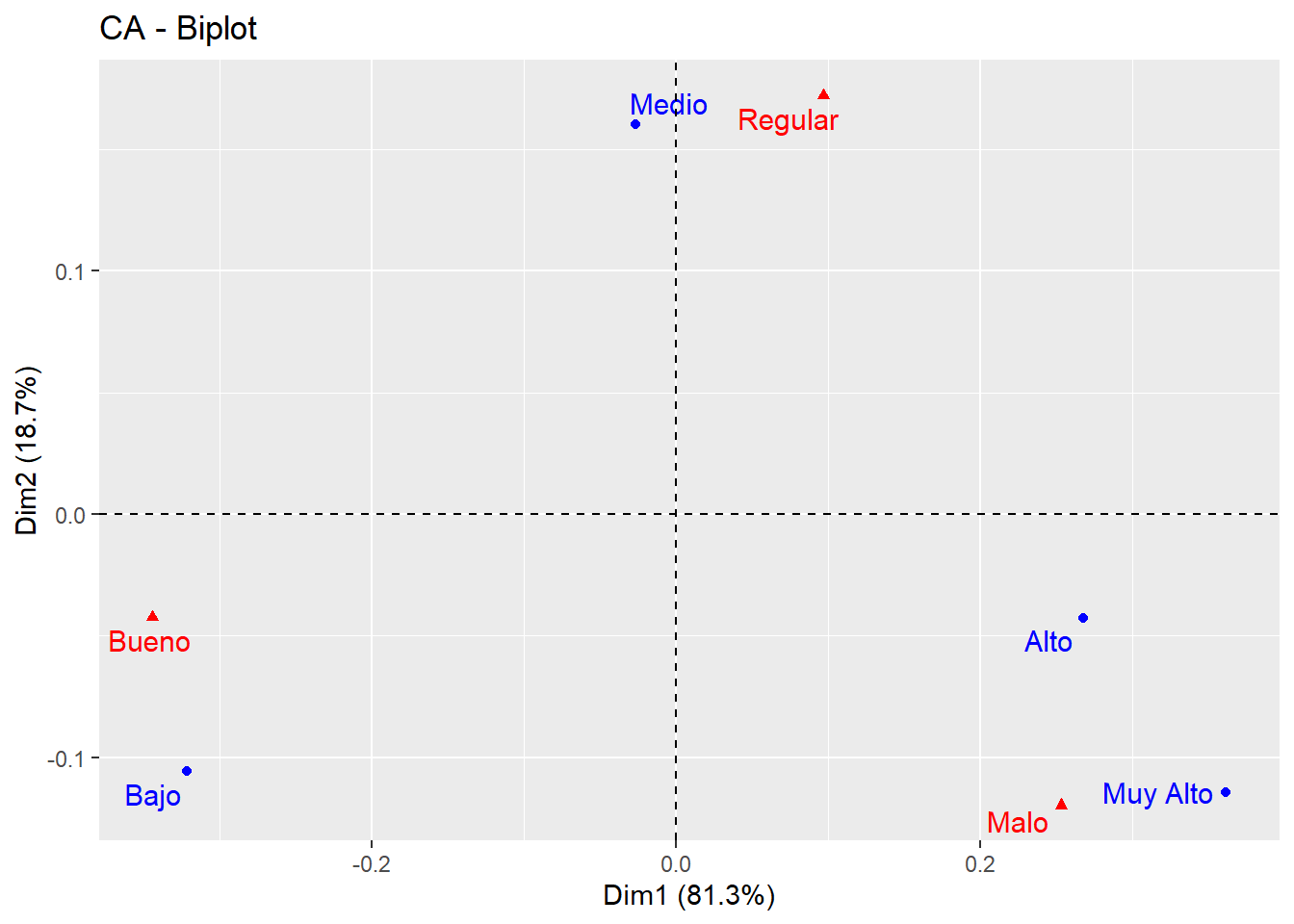
fviz_ca_biplot(res.ca, repel = T) + theme_bw()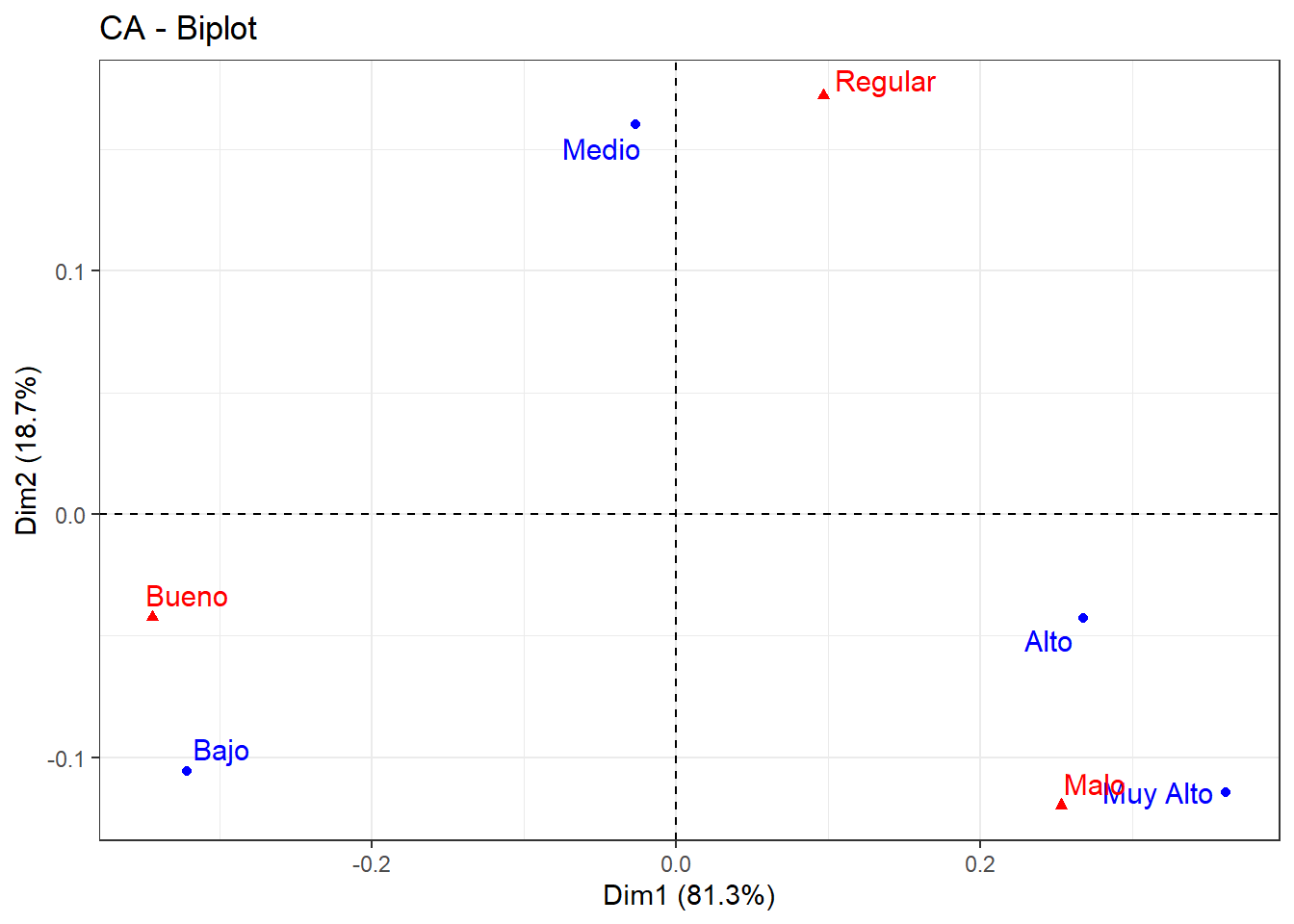
fviz_ca_biplot(res.ca, repel = T) + theme_stata()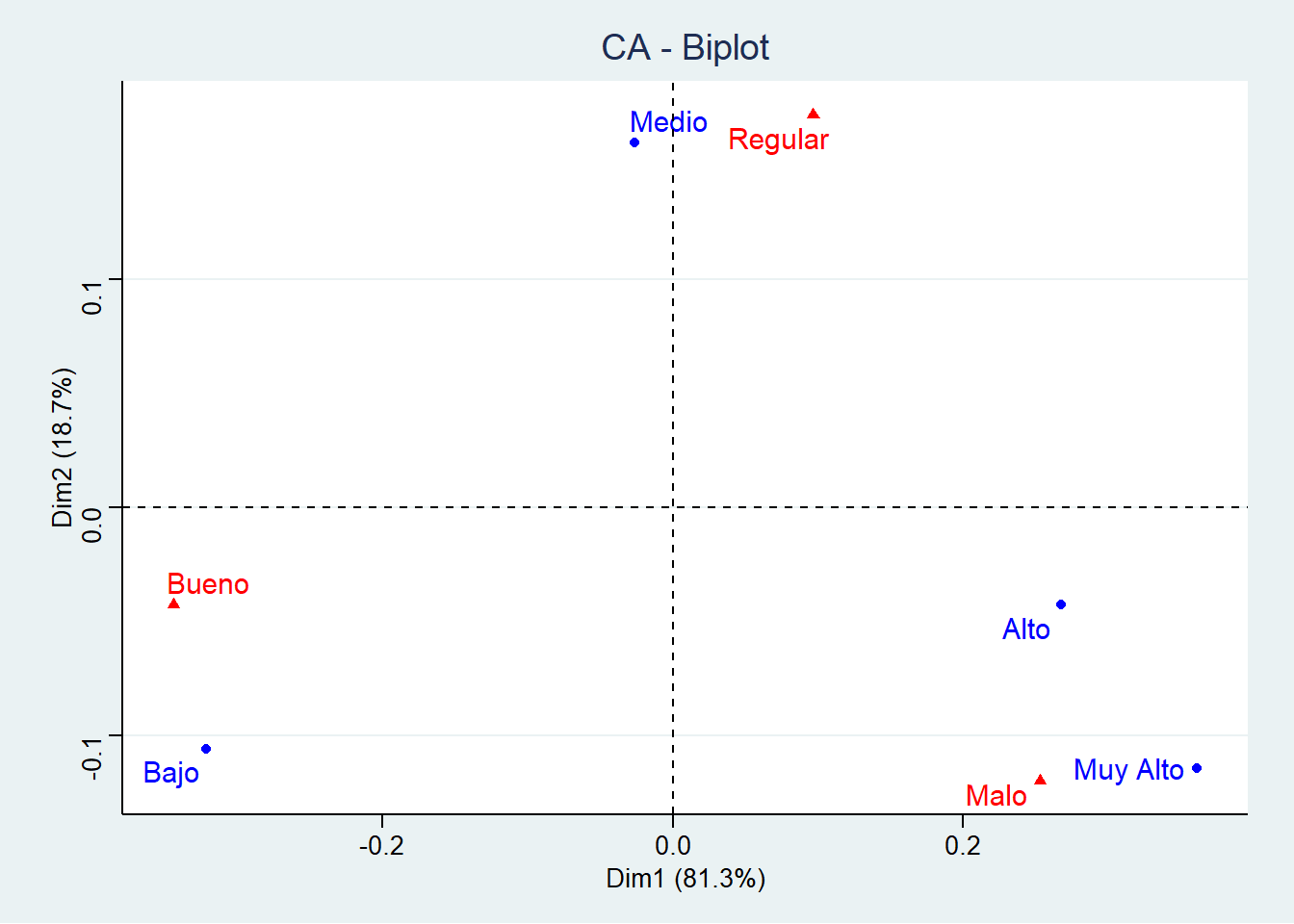
fviz_ca_biplot(res.ca, repel = T) + theme_simpsons()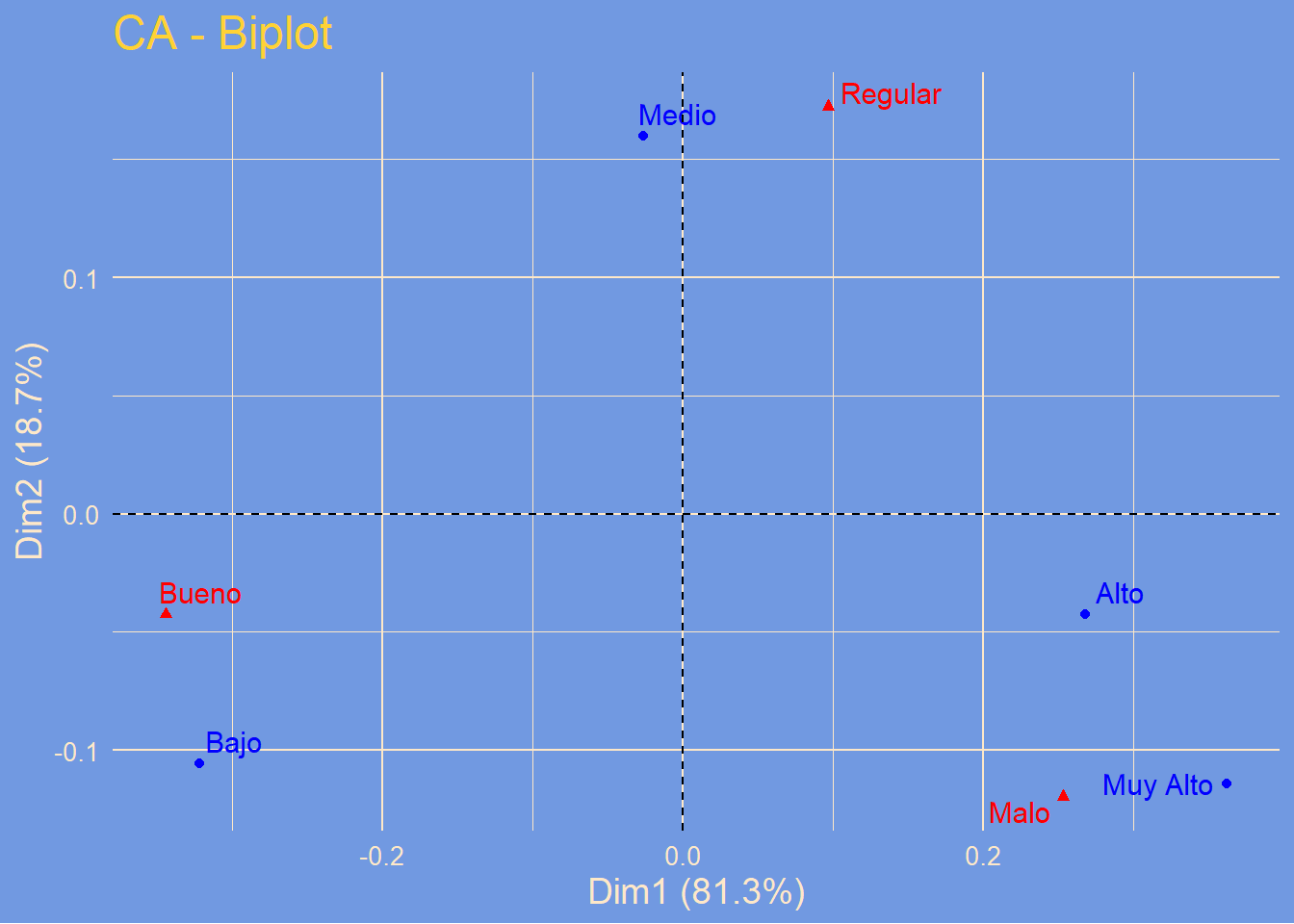
Interpretación de los Indicadores del ACS
summary(res.ca,nb.dec = 3, ncp = 2)
Call:
CA(X = datos.acs, ncp = 2, graph = F)
The chi square of independence between the two variables is equal to 40.04927 (p-value = 4.454704e-07 ).
Eigenvalues
Dim.1 Dim.2
Variance 0.065 0.015
% of var. 81.279 18.721
Cumulative % of var. 81.279 100.000
Rows
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2
Bajo | 34.375 | -0.322 47.655 0.903 | -0.106 22.341 0.097 |
Medio | 9.485 | -0.027 0.391 0.027 | 0.160 61.558 0.973 |
Alto | 13.219 | 0.268 19.803 0.975 | -0.043 2.178 0.025 |
Muy Alto | 23.019 | 0.362 32.151 0.909 | -0.114 13.923 0.091 |
Columns
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2
Bueno | 40.923 | -0.344 61.919 0.985 | -0.042 4.081 0.015 |
Malo | 26.667 | 0.253 33.467 0.817 | -0.120 32.533 0.183 |
Regular | 12.509 | 0.097 4.614 0.240 | 0.172 63.386 0.760 |# Coordenadas de las Dimensiones para filas y columnas
row <- get_ca_row(res.ca)
col <- get_ca_col(res.ca)
head(row$coord) Dim 1 Dim 2
Bajo -0.32158412 -0.10567395
Medio -0.02657899 0.16012994
Alto 0.26762688 -0.04259682
Muy Alto 0.36169272 -0.11423227head(col$coord) Dim 1 Dim 2
Bueno -0.34432911 -0.04242433
Malo 0.25314619 -0.11978473
Regular 0.09688186 0.17234713# Gráficos de las contribuciones absolutas de las filas y columnas a cada dimensión
head(row$contrib) Dim 1 Dim 2
Bajo 47.6550858 22.340641
Medio 0.3906413 61.558217
Alto 19.8029896 2.178037
Muy Alto 32.1512832 13.923105head(col$contrib) Dim 1 Dim 2
Bueno 61.919181 4.080819
Malo 33.467286 32.532714
Regular 4.613534 63.386466fviz_contrib(res.ca, choice = "row", axes = 1)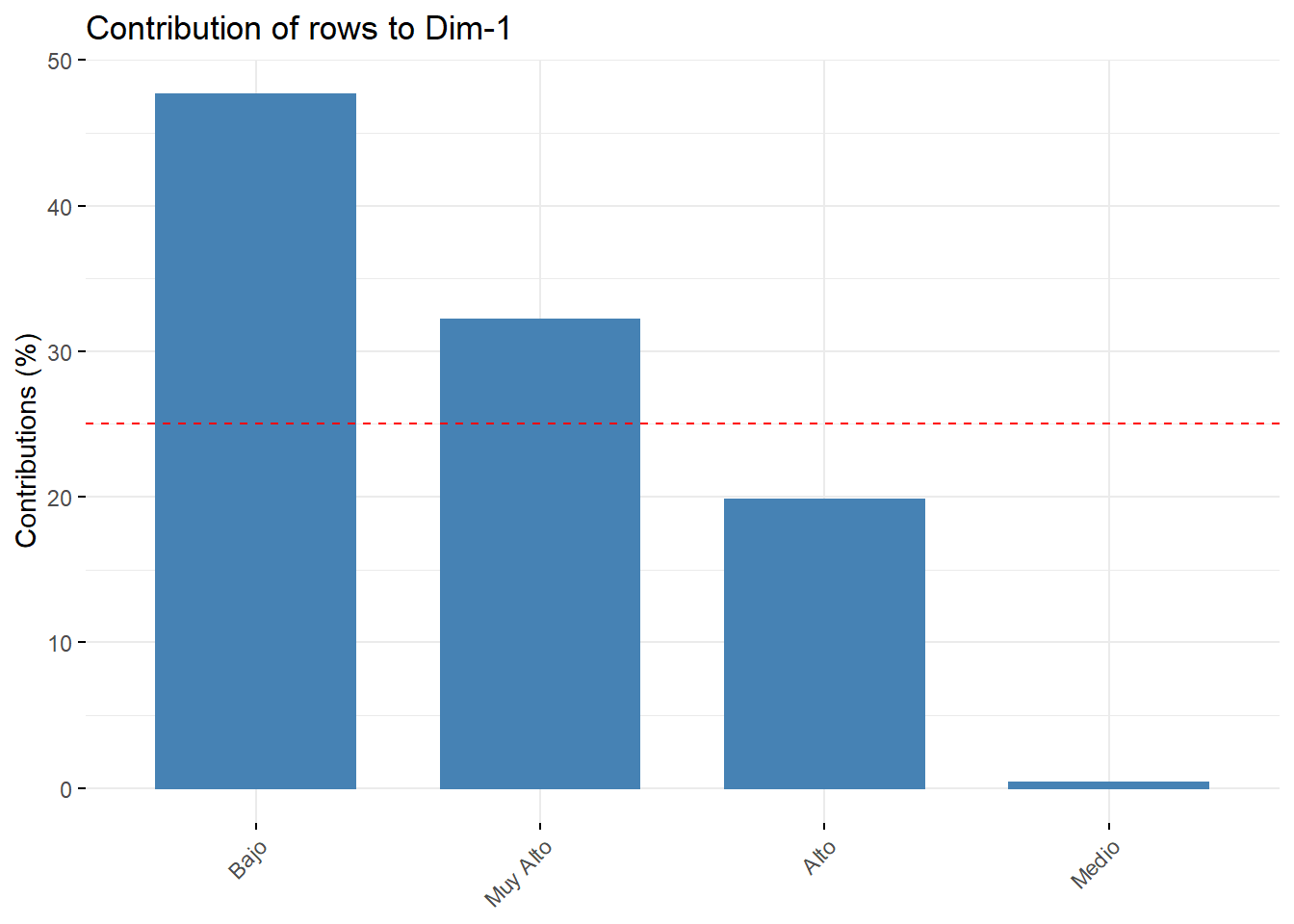
fviz_contrib(res.ca, choice = "row", axes = 2)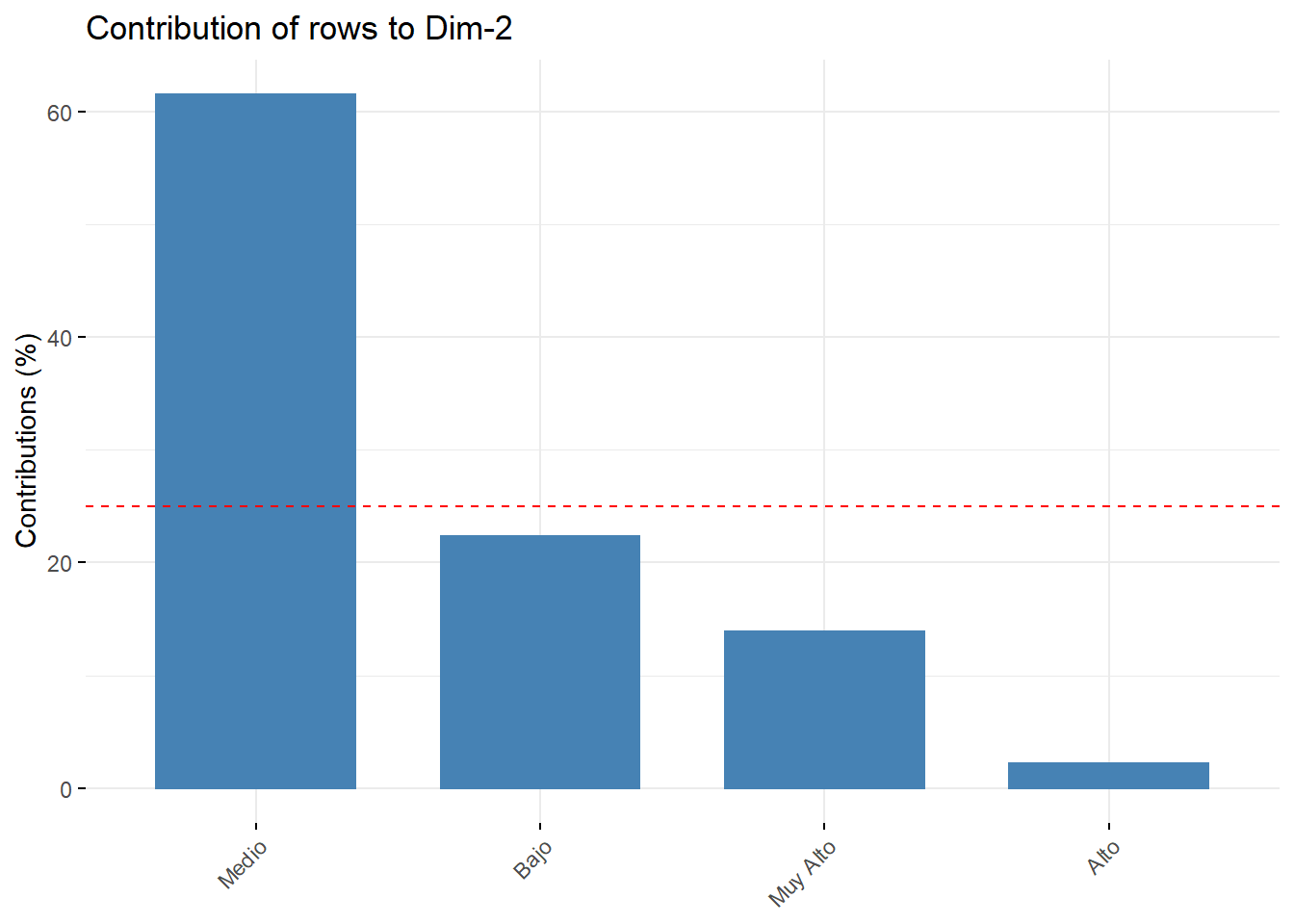
fviz_contrib(res.ca, choice = "col", axes = 1)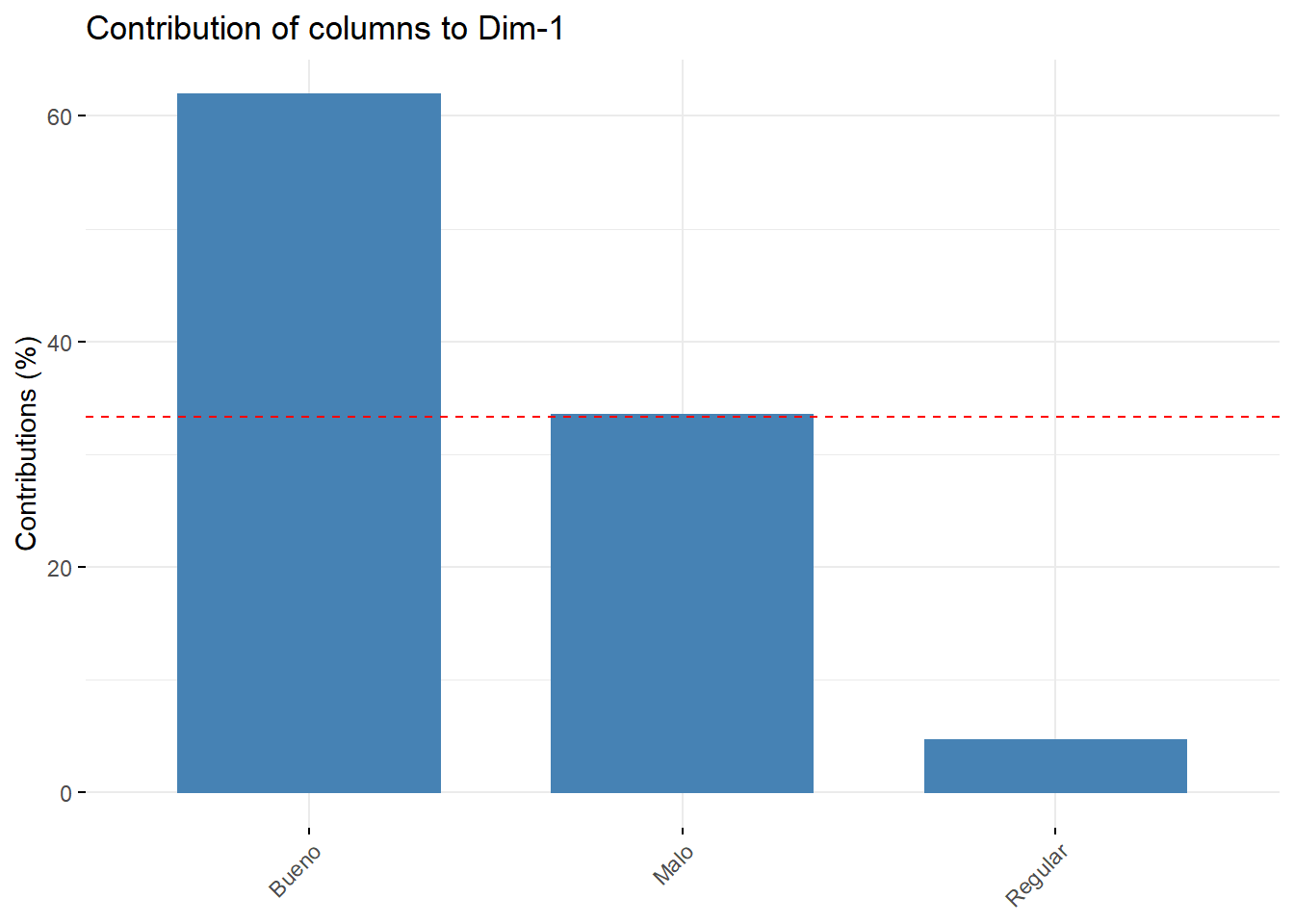
fviz_contrib(res.ca, choice = "col", axes = 2)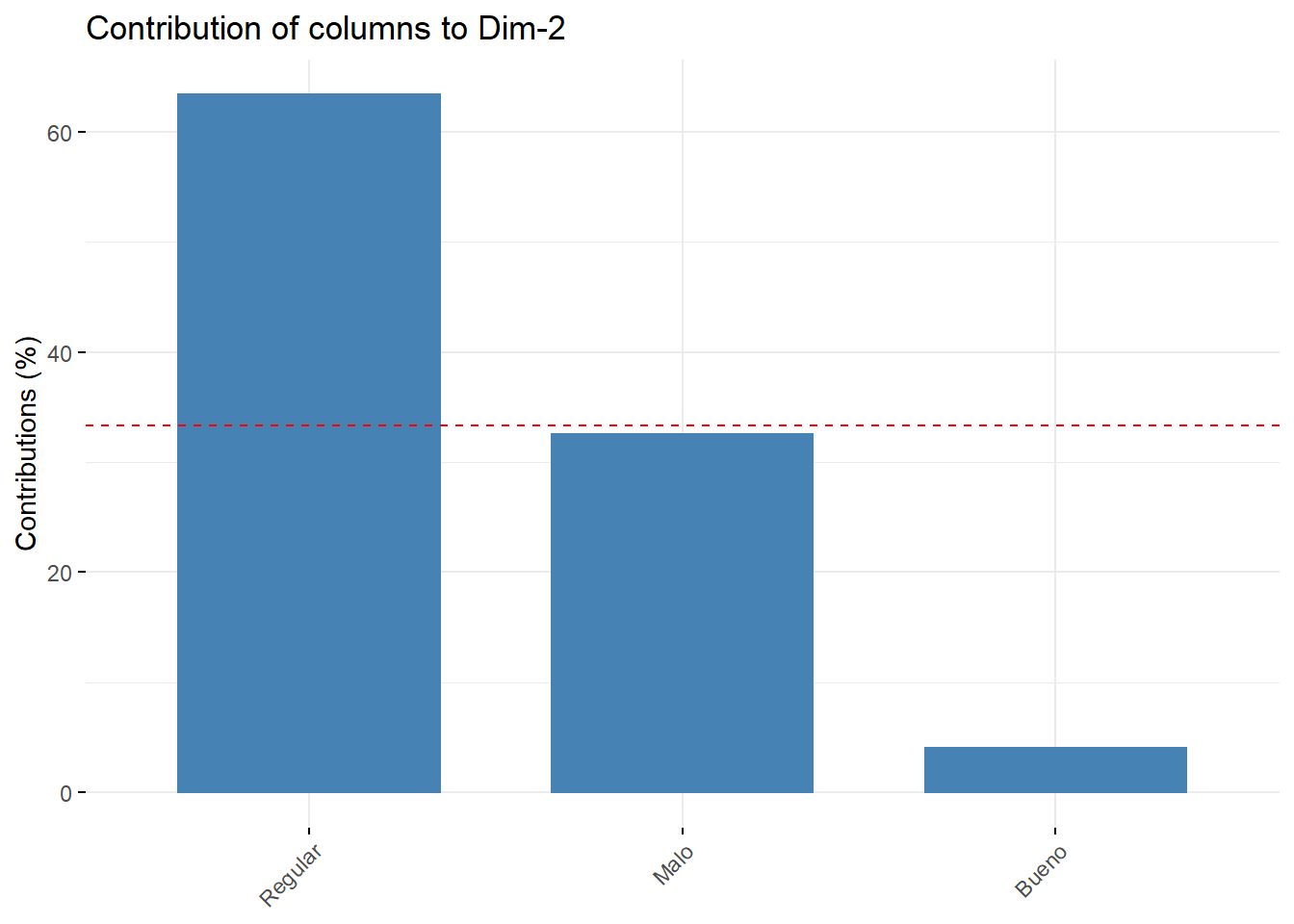
# Gráficos de las contribuciones relativas de cada dimensión
head(row$cos2) Dim 1 Dim 2
Bajo 0.90254268 0.09745732
Medio 0.02681196 0.97318804
Alto 0.97529245 0.02470755
Muy Alto 0.90930038 0.09069962head(col$cos2) Dim 1 Dim 2
Bueno 0.9850466 0.01495338
Malo 0.8170581 0.18294186
Regular 0.2401173 0.75988273fviz_cos2(res.ca, choice = "row", axes = 1)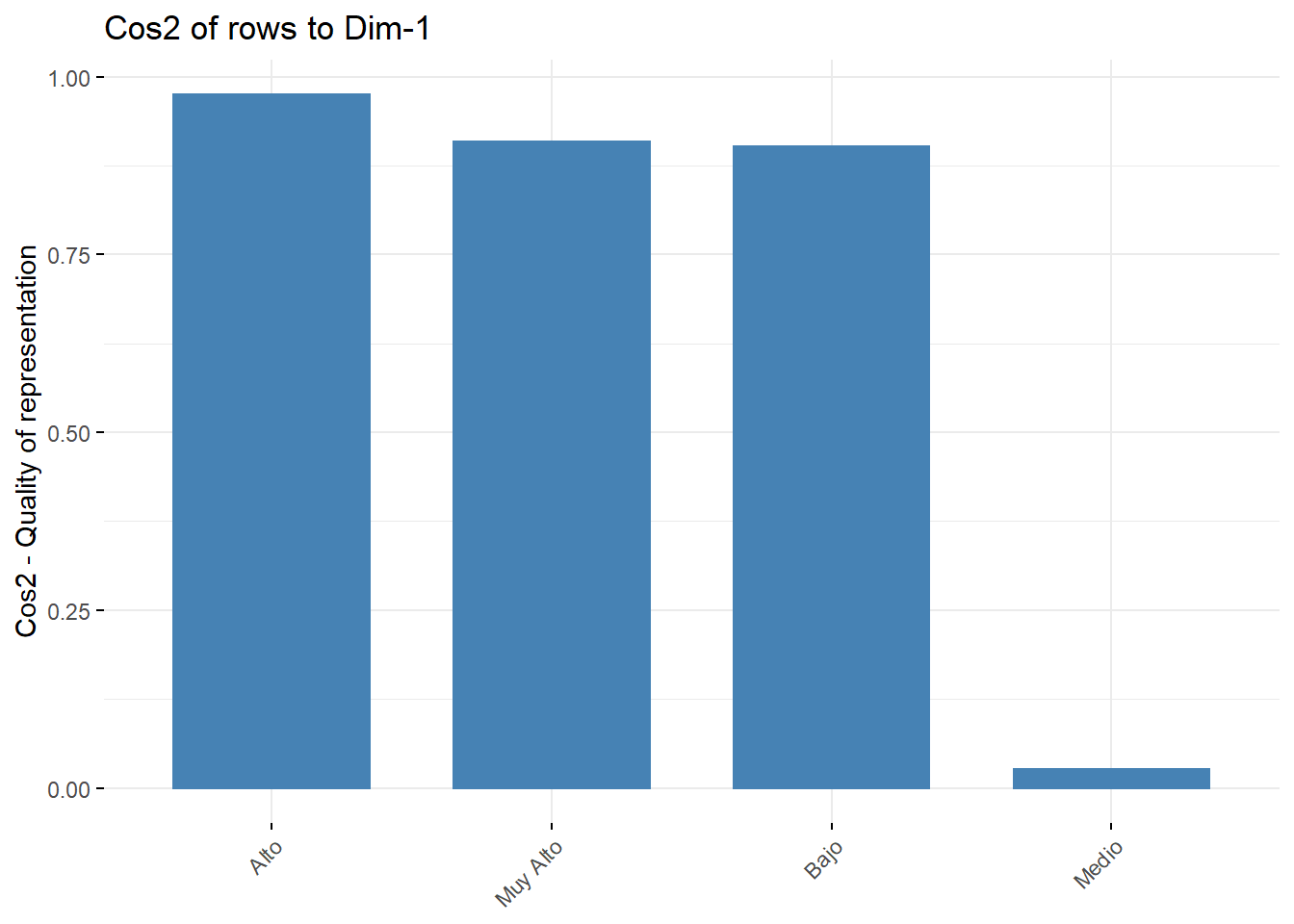
fviz_cos2(res.ca, choice = "row", axes = 2)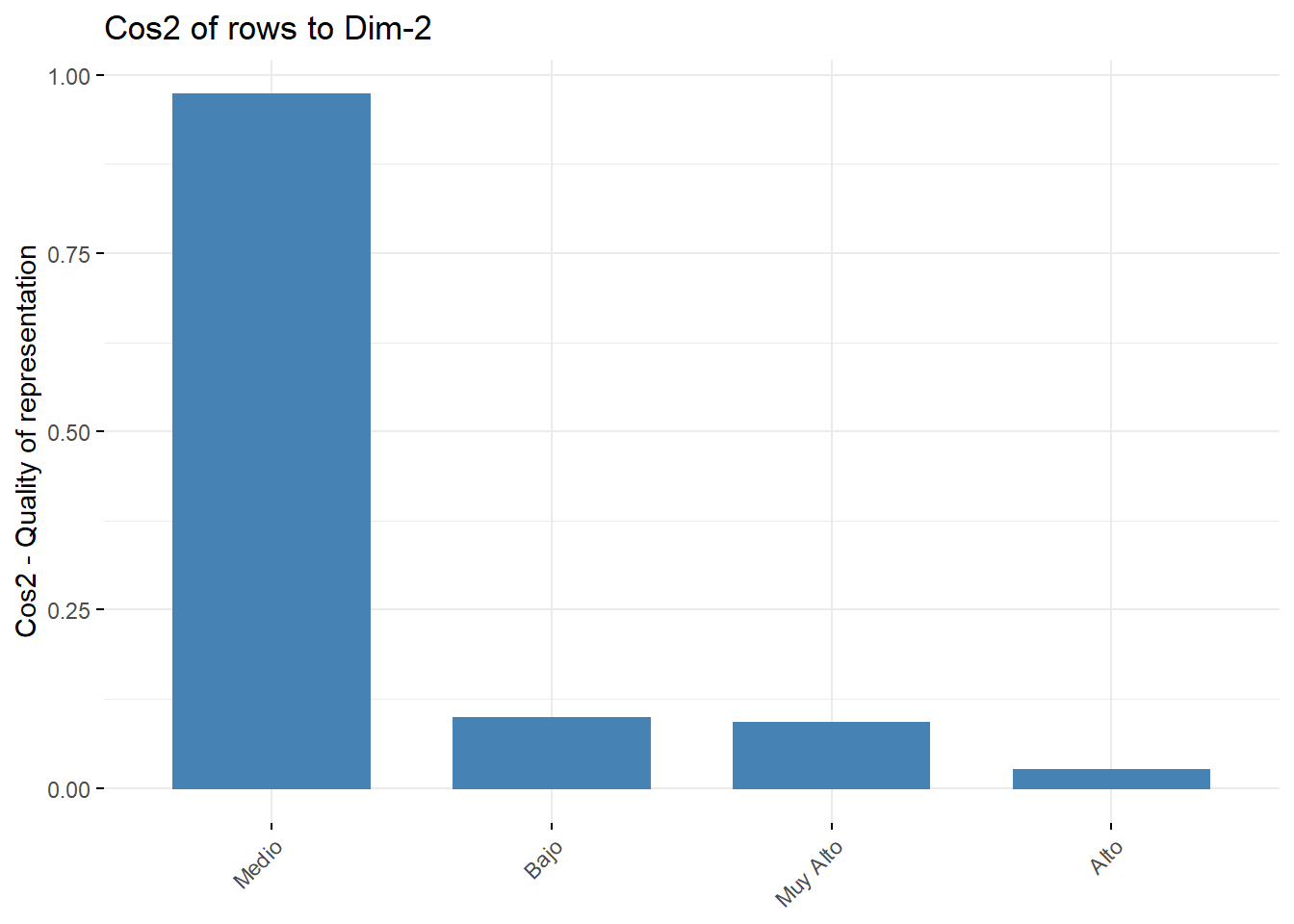
ACS con el paquete anacor
library(anacor)
fit2 <- anacor(datos.acs)
str(fit2)List of 25
$ datname : chr [1:3] "structure(c(75, 60, 20, 15, 40, 50, 40, 40, 35, 70, 30, 25), .Dim = 4:3, .Dimnames = list(" " renta = c(\"Bajo\", \"Medio\", \"Alto\", \"Muy Alto\"), opinion = c(\"Bueno\", " " \"Malo\", \"Regular\")))"
$ tab : num [1:4, 1:3] 75 60 20 15 40 50 40 40 35 70 ...
..- attr(*, "dimnames")=List of 2
.. ..$ renta : chr [1:4] "Bajo" "Medio" "Alto" "Muy Alto"
.. ..$ opinion: chr [1:3] "Bueno" "Malo" "Regular"
$ ndim : num 2
$ row.covariates : NULL
$ col.covariates : NULL
$ row.scores : num [1:4, 1:2] 0.3216 0.0266 -0.2676 -0.3617 -0.1057 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:4] "Bajo" "Medio" "Alto" "Muy Alto"
.. ..$ : chr [1:2] "D1" "D2"
$ col.scores : num [1:3, 1:2] 0.3443 -0.2531 -0.0969 -0.0424 -0.1198 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:3] "Bueno" "Malo" "Regular"
.. ..$ : chr [1:2] "D1" "D2"
$ chisq.decomp : num [1:2, 1:3] 32.552 7.498 0.813 0.187 0.813 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:2] "Dimension 1" "Dimension 2"
.. ..$ : chr [1:3] "Chisq" "Proportion" "Cumulative Proportion"
$ chisq : num 40
$ singular.values : num [1:2] 0.255 0.122
$ se.singular.values: NULL
$ stestmat : NULL
$ left.singvec : num [1:4, 1:2] 0.6903 0.0625 -0.445 -0.567 -0.4727 ...
$ right.singvec : num [1:3, 1:2] 0.787 -0.579 -0.215 -0.202 -0.57 ...
$ eigen.values : num [1:2] 0.0651 0.015
$ eigenall : num [1:2] 0.0651 0.015
$ scaling : chr [1:2] "Benzecri" "Benzecri"
$ bdmat :List of 4
..$ bdobs.row: num [1:4, 1:4] 0 0.000315 0.000702 0.000934 0.000315 ...
.. ..- attr(*, "dimnames")=List of 2
.. .. ..$ : chr [1:4] "Bajo" "Medio" "Alto" "Muy Alto"
.. .. ..$ : chr [1:4] "Bajo" "Medio" "Alto" "Muy Alto"
..$ bdfit.row: num [1:4, 1:4] 0 0.000315 0.000702 0.000934 0.000315 ...
.. ..- attr(*, "dimnames")=List of 2
.. .. ..$ : chr [1:4] "Bajo" "Medio" "Alto" "Muy Alto"
.. .. ..$ : chr [1:4] "Bajo" "Medio" "Alto" "Muy Alto"
..$ bdobs.col: num [1:3, 1:3] 0 0.000726 0.000482 0.000726 0 ...
.. ..- attr(*, "dimnames")=List of 2
.. .. ..$ : chr [1:3] "Bueno" "Malo" "Regular"
.. .. ..$ : chr [1:3] "Bueno" "Malo" "Regular"
..$ bdfit.col: num [1:3, 1:3] 0 0.000726 0.000482 0.000726 0 ...
.. ..- attr(*, "dimnames")=List of 2
.. .. ..$ : chr [1:3] "Bueno" "Malo" "Regular"
.. .. ..$ : chr [1:3] "Bueno" "Malo" "Regular"
$ rmse :List of 2
..$ rmse.row: num 4.97e-19
..$ rmse.col: num 1.36e-18
$ row.acov : NULL
$ col.acov : NULL
$ cancoef :List of 2
..$ rows : NULL
..$ columns: NULL
$ sitescores :List of 2
..$ rows : NULL
..$ columns: NULL
$ isetcor :List of 2
..$ rows : NULL
..$ columns: NULL
$ call : language anacor(tab = datos.acs)
- attr(*, "class")= chr "anacor"summary(fit2) Length Class Mode
datname 3 -none- character
tab 12 -none- numeric
ndim 1 -none- numeric
row.covariates 0 -none- NULL
col.covariates 0 -none- NULL
row.scores 8 -none- numeric
col.scores 6 -none- numeric
chisq.decomp 6 -none- numeric
chisq 1 -none- numeric
singular.values 2 -none- numeric
se.singular.values 0 -none- NULL
stestmat 0 -none- NULL
left.singvec 8 -none- numeric
right.singvec 6 -none- numeric
eigen.values 2 -none- numeric
eigenall 2 -none- numeric
scaling 2 -none- character
bdmat 4 -none- list
rmse 2 -none- list
row.acov 0 -none- NULL
col.acov 0 -none- NULL
cancoef 2 -none- list
sitescores 2 -none- list
isetcor 2 -none- list
call 2 -none- call plot(fit2,plot.type="jointplot")
plot(fit2)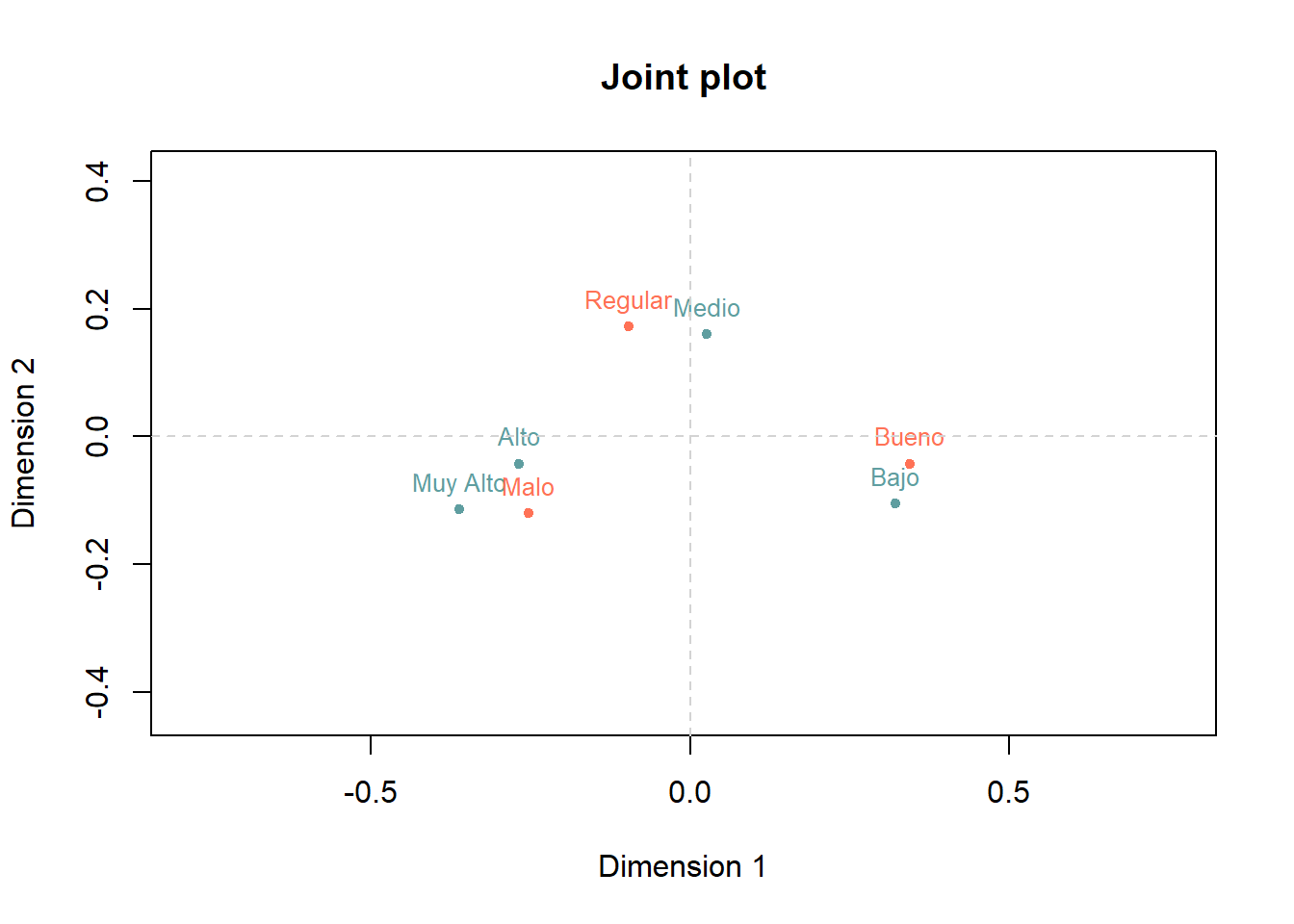
ACS con el paquete vegan
library(vegan)
corres2 <- cca(datos.acs)
summary(corres2)
Call:
cca(X = datos.acs)
Partitioning of scaled Chi-square:
Inertia Proportion
Total 0.0801 1
Unconstrained 0.0801 1
Eigenvalues, and their contribution to the scaled Chi-square
Importance of components:
CA1 CA2
Eigenvalue 0.0651 0.0150
Proportion Explained 0.8128 0.1872
Cumulative Proportion 0.8128 1.0000
Scaling 2 for species and site scores
* Species are scaled proportional to eigenvalues
* Sites are unscaled: weighted dispersion equal on all dimensions
Species scores
CA1 CA2
Bueno -0.34433 0.04242
Malo 0.25315 0.11978
Regular 0.09688 -0.17235
Site scores (weighted averages of species scores)
CA1 CA2
Bajo -1.2604 0.8630
Medio -0.1042 -1.3077
Alto 1.0489 0.3479
Muy Alto 1.4176 0.9328fviz_cos2(res.ca, choice = "col", axes = 2)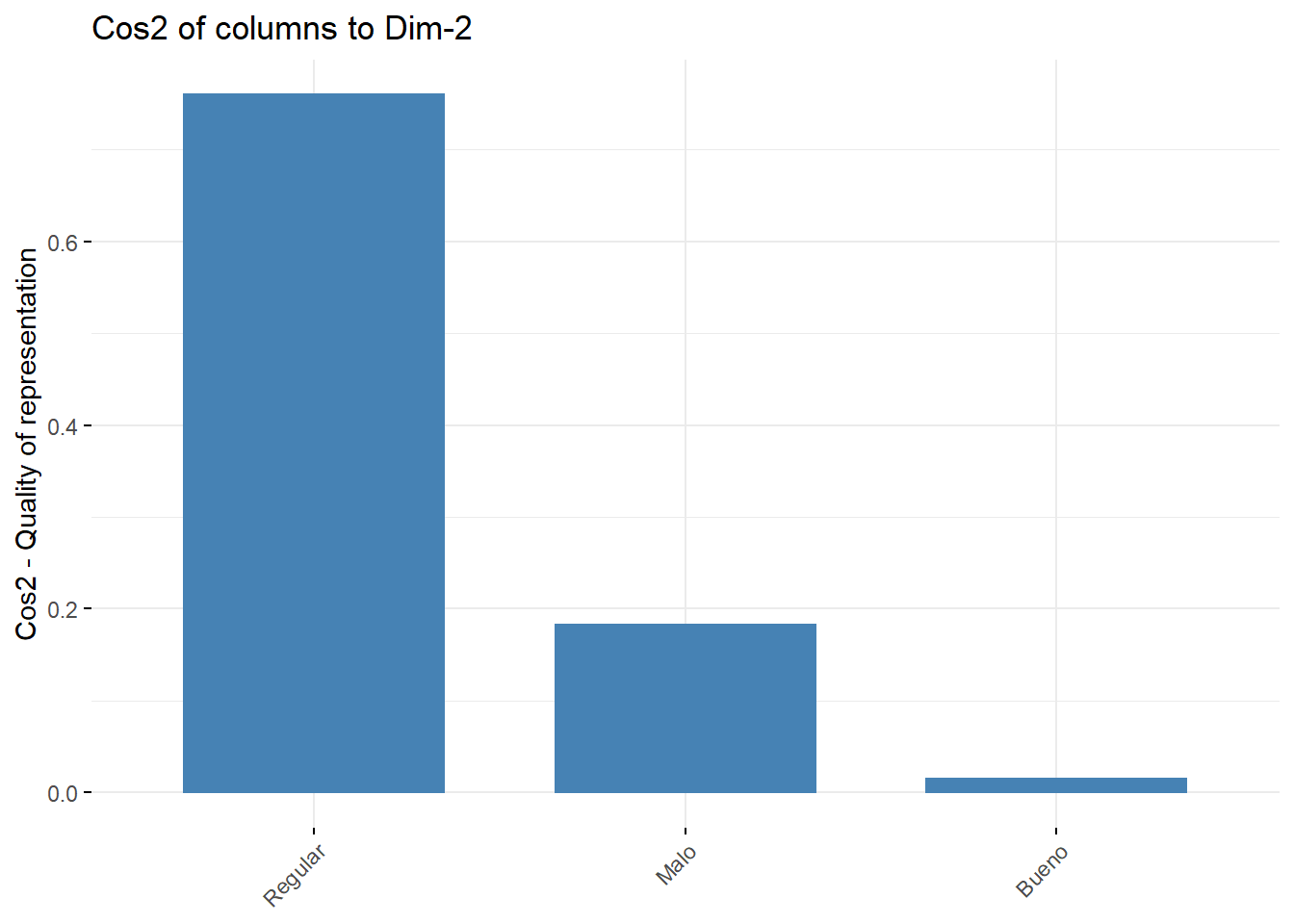
5.2.2 Ejemplo 2. ACS de una base de datos
Los datos corresponden a la información de 8471 personas afiliadas a una entidad bancaria.
Para realizar el Análisis de Componentes Simples se emplearan las varaibles Número de dependientes y Departamento.
library(foreign)
datos <- read.spss("Riesgo_morosidad.sav",
use.value.labels = T,
to.data.frame=TRUE)re-encoding from CP1252attach(datos)
table(nrodepen)nrodepen
0 1 2 3 4 5
1472 1554 1602 728 1437 1678 table(dpto)dpto
Lima Trujillo Arequipa Cusco Ica Piura
5000 1000 1000 500 500 471 addmargins(table(dpto,nrodepen)) nrodepen
dpto 0 1 2 3 4 5 Sum
Lima 768 747 756 361 1064 1304 5000
Trujillo 209 236 301 146 61 47 1000
Arequipa 227 291 263 120 50 49 1000
Cusco 107 119 114 37 68 55 500
Ica 86 77 80 30 109 118 500
Piura 75 84 88 34 85 105 471
Sum 1472 1554 1602 728 1437 1678 8471datos.acs1 <- as.matrix(table(dpto,nrodepen))
datos.acs1 nrodepen
dpto 0 1 2 3 4 5
Lima 768 747 756 361 1064 1304
Trujillo 209 236 301 146 61 47
Arequipa 227 291 263 120 50 49
Cusco 107 119 114 37 68 55
Ica 86 77 80 30 109 118
Piura 75 84 88 34 85 105library(FactoMineR)
res.ca1 <- CA(datos.acs1,ncp=5,graph=FALSE)
res.ca1$eig eigenvalue percentage of variance cumulative percentage of variance
dim 1 1.076264e-01 96.680369773 96.68037
dim 2 2.810881e-03 2.525003950 99.20537
dim 3 7.565388e-04 0.679595992 99.88497
dim 4 1.252623e-04 0.112522648 99.99749
dim 5 2.791548e-06 0.002507637 100.00000fviz_screeplot(res.ca1)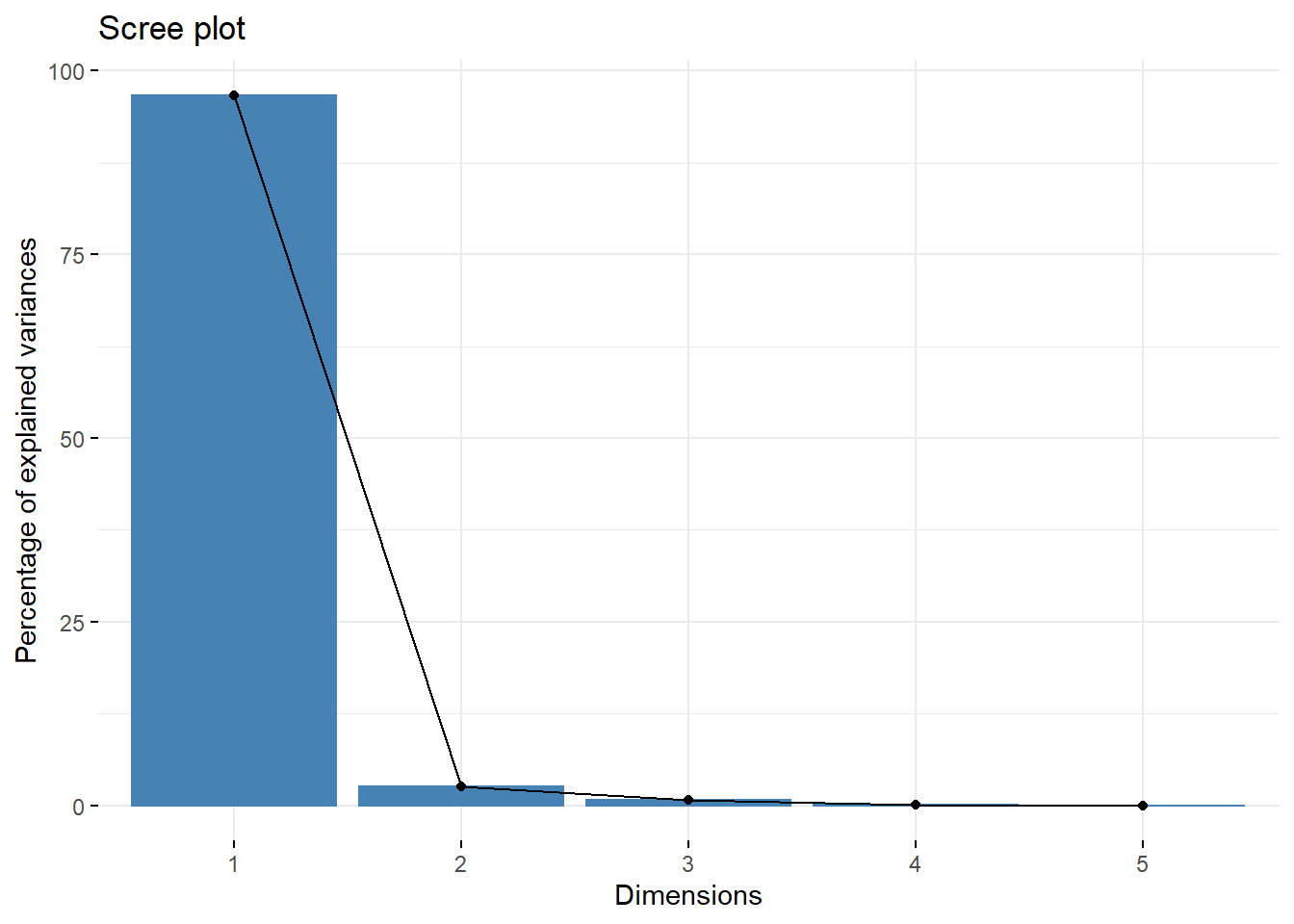
#según el gráfico 2 variables son suficientes
res.ca1 <- CA(datos.acs,ncp=2,graph=FALSE)
summary(res.ca1,nb.dec=3,ncp=2)
Call:
CA(X = datos.acs, ncp = 2, graph = FALSE)
The chi square of independence between the two variables is equal to 40.04927 (p-value = 4.454704e-07 ).
Eigenvalues
Dim.1 Dim.2
Variance 0.065 0.015
% of var. 81.279 18.721
Cumulative % of var. 81.279 100.000
Rows
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2
Bajo | 34.375 | -0.322 47.655 0.903 | -0.106 22.341 0.097 |
Medio | 9.485 | -0.027 0.391 0.027 | 0.160 61.558 0.973 |
Alto | 13.219 | 0.268 19.803 0.975 | -0.043 2.178 0.025 |
Muy Alto | 23.019 | 0.362 32.151 0.909 | -0.114 13.923 0.091 |
Columns
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2
Bueno | 40.923 | -0.344 61.919 0.985 | -0.042 4.081 0.015 |
Malo | 26.667 | 0.253 33.467 0.817 | -0.120 32.533 0.183 |
Regular | 12.509 | 0.097 4.614 0.240 | 0.172 63.386 0.760 |# Analizar las que estan por encima del promedio
fviz_ca_biplot(res.ca1, repel = T)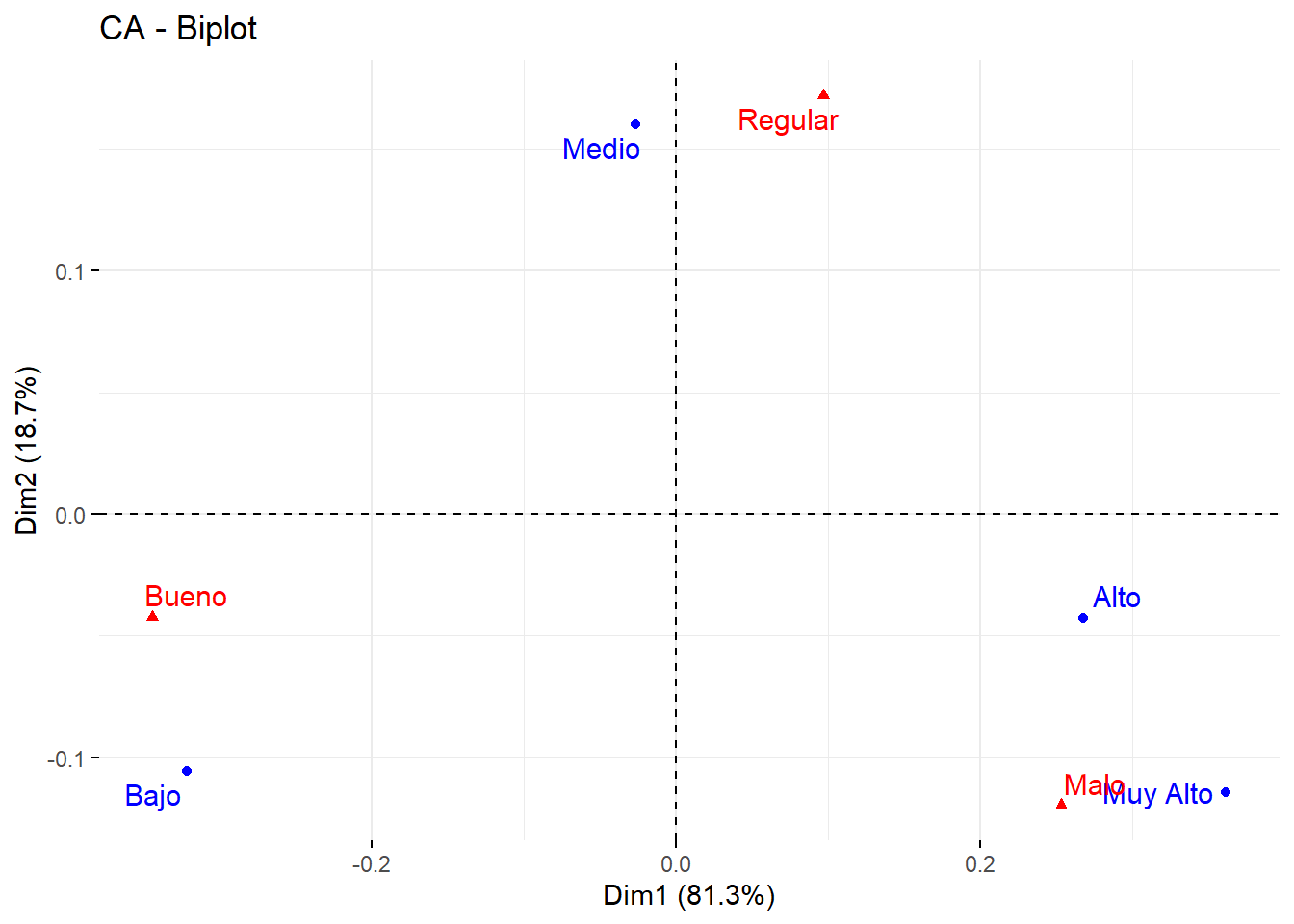
5.2.3 Ejemplo 3. ACS con filas y columnas suplementarias
Los datos presentados en la tabla corresponden a una encuesta en relación a la opinión de 9 empresas. Se añade una nueva columna (ideal) y una nueva fila (acceso)
| E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | E9 | Ideal | |
|---|---|---|---|---|---|---|---|---|---|---|
| Precios | 16 | 17 | 18 | 19 | 16 | 45 | 15 | 19 | 18 | 45 |
| Variedad | 8 | 15 | 18 | 17 | 27 | 20 | 2 | 14 | 53 | 53 |
| Rapidez | 20 | 20 | 23 | 21 | 29 | 20 | 19 | 18 | 25 | 29 |
| Información | 11 | 13 | 12 | 17 | 20 | 16 | 15 | 10 | 44 | 44 |
| Trato | 28 | 25 | 25 | 22 | 30 | 26 | 24 | 22 | 26 | 30 |
| Condiciones | 21 | 21 | 20 | 24 | 27 | 22 | 18 | 21 | 24 | 27 |
| Acceso | 21 | 21 | 21 | 23 | 26 | 15 | 16 | 18 | 21 | 26 |
datos_s.acs <- matrix(c(16,17,18,19,16,45,15,19,18,45,
8,15,18,17,27,20, 2,14,53,53,
20,20,23,21,29,20,18,19,25,29,
11,13,12,17,20,16,15,10,44,44,
28,25,25,22,30,26,24,22,26,30,
21,21,20,24,27,22,18,21,24,27,
21,21,21,23,26,15,16,18,21,26),
nrow=7,byrow=T)
datos_s.acs [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 16 17 18 19 16 45 15 19 18 45
[2,] 8 15 18 17 27 20 2 14 53 53
[3,] 20 20 23 21 29 20 18 19 25 29
[4,] 11 13 12 17 20 16 15 10 44 44
[5,] 28 25 25 22 30 26 24 22 26 30
[6,] 21 21 20 24 27 22 18 21 24 27
[7,] 21 21 21 23 26 15 16 18 21 26# Asignación de nombres a las filas y columnas de la tabla
dimnames(datos_s.acs)<-list(Atributos=c("Precios", "Variedad",
"Rapidez", "Información",
"Trato","Condiciones",
"Acceso")
,Empresa=c("Empresa 1","Empresa 2",
"Empresa 3","Empresa 4",
"Empresa 5","Empresa 6",
"Empresa 7","Empresa 8",
"Empresa 9","Ideal"))
datos_s.acs Empresa
Atributos Empresa 1 Empresa 2 Empresa 3 Empresa 4 Empresa 5 Empresa 6
Precios 16 17 18 19 16 45
Variedad 8 15 18 17 27 20
Rapidez 20 20 23 21 29 20
Información 11 13 12 17 20 16
Trato 28 25 25 22 30 26
Condiciones 21 21 20 24 27 22
Acceso 21 21 21 23 26 15
Empresa
Atributos Empresa 7 Empresa 8 Empresa 9 Ideal
Precios 15 19 18 45
Variedad 2 14 53 53
Rapidez 18 19 25 29
Información 15 10 44 44
Trato 24 22 26 30
Condiciones 18 21 24 27
Acceso 16 18 21 26addmargins(datos_s.acs) Empresa
Atributos Empresa 1 Empresa 2 Empresa 3 Empresa 4 Empresa 5 Empresa 6
Precios 16 17 18 19 16 45
Variedad 8 15 18 17 27 20
Rapidez 20 20 23 21 29 20
Información 11 13 12 17 20 16
Trato 28 25 25 22 30 26
Condiciones 21 21 20 24 27 22
Acceso 21 21 21 23 26 15
Sum 125 132 137 143 175 164
Empresa
Atributos Empresa 7 Empresa 8 Empresa 9 Ideal Sum
Precios 15 19 18 45 228
Variedad 2 14 53 53 227
Rapidez 18 19 25 29 224
Información 15 10 44 44 202
Trato 24 22 26 30 258
Condiciones 18 21 24 27 225
Acceso 16 18 21 26 208
Sum 108 123 211 254 1572# Prueba de Independencia Chi-Cuadrado
prueba <- chisq.test(datos_s.acs[,-10])
prueba
Pearson's Chi-squared test
data: datos_s.acs[, -10]
X-squared = 108.66, df = 48, p-value = 1.344e-06# ACS con el paquete FactoMiner
library(FactoMineR)
res.ca.s <- CA(datos_s.acs,
ncp=2,
graph=FALSE,
col.sup = 10) #Indica la columna suplementaria [10]
# Scree Plot de los Autovalores
library(ggplot2)
library(factoextra)
get_eigenvalue(res.ca.s) eigenvalue variance.percent cumulative.variance.percent
Dim.1 0.0520284322 63.1093169 63.10932
Dim.2 0.0230835951 27.9998812 91.10920
Dim.3 0.0058650195 7.1141366 98.22333
Dim.4 0.0010003264 1.2133734 99.43671
Dim.5 0.0003101078 0.3761537 99.81286
Dim.6 0.0001542801 0.1871383 100.00000fviz_screeplot(res.ca.s, addlabels = TRUE, ylim = c(0, 80))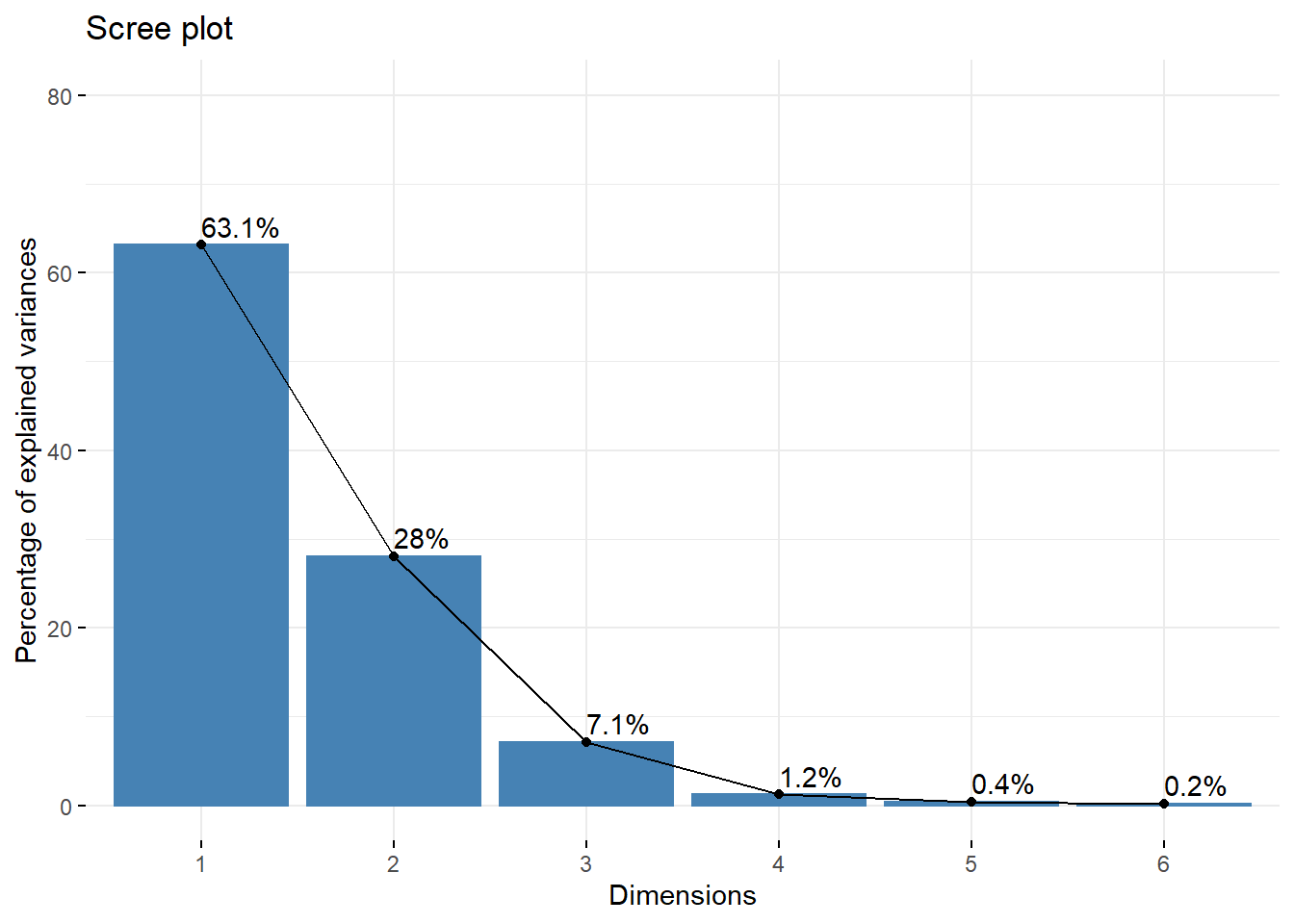
# Interpretación de los Indicadores del ACS
summary(res.ca.s,nb.dec = 3, ncp = 2)
Call:
CA(X = datos_s.acs, ncp = 2, col.sup = 10, graph = FALSE)
The chi square of independence between the two variables is equal to 108.6582 (p-value = 1.343894e-06 ).
Eigenvalues
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6
Variance 0.052 0.023 0.006 0.001 0.000 0.000
% of var. 63.109 28.000 7.114 1.213 0.376 0.187
Cumulative % of var. 63.109 91.109 98.223 99.437 99.813 100.000
Rows
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2
Precios | 22.307 | 0.202 10.837 0.253 | -0.346 72.147 0.747 |
Variedad | 29.767 | -0.457 52.879 0.924 | -0.069 2.721 0.021 |
Rapidez | 2.394 | 0.076 1.661 0.361 | 0.089 5.037 0.486 |
Información | 14.544 | -0.300 20.719 0.741 | 0.015 0.123 0.002 |
Trato | 5.477 | 0.151 7.557 0.718 | 0.070 3.720 0.157 |
Condiciones | 2.544 | 0.105 3.163 0.647 | 0.060 2.320 0.211 |
Acceso | 5.410 | 0.110 3.183 0.306 | 0.153 13.931 0.594 |
Columns
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2
Empresa 1 | 6.542 | 0.229 9.536 0.758 | 0.120 5.925 0.209 |
Empresa 2 | 1.248 | 0.082 1.301 0.542 | 0.063 1.742 0.322 |
Empresa 3 | 1.465 | 0.055 0.614 0.218 | 0.044 0.858 0.135 |
Empresa 4 | 1.032 | 0.028 0.167 0.084 | 0.040 0.743 0.166 |
Empresa 5 | 3.089 | -0.067 1.155 0.195 | 0.119 8.170 0.611 |
Empresa 6 | 19.969 | 0.121 3.513 0.092 | -0.382 78.531 0.908 |
Empresa 7 | 9.792 | 0.253 10.112 0.537 | 0.104 3.816 0.090 |
Empresa 8 | 1.909 | 0.120 2.599 0.708 | -0.008 0.028 0.003 |
Empresa 9 | 37.395 | -0.480 71.002 0.988 | -0.016 0.187 0.001 |
Supplementary column
Dim.1 cos2 Dim.2 cos2
Ideal | -0.275 0.598 | -0.215 0.367 |# Biplot filas, columnas y columna suplementaria
fviz_ca_biplot(res.ca.s, repel = T) + theme_light()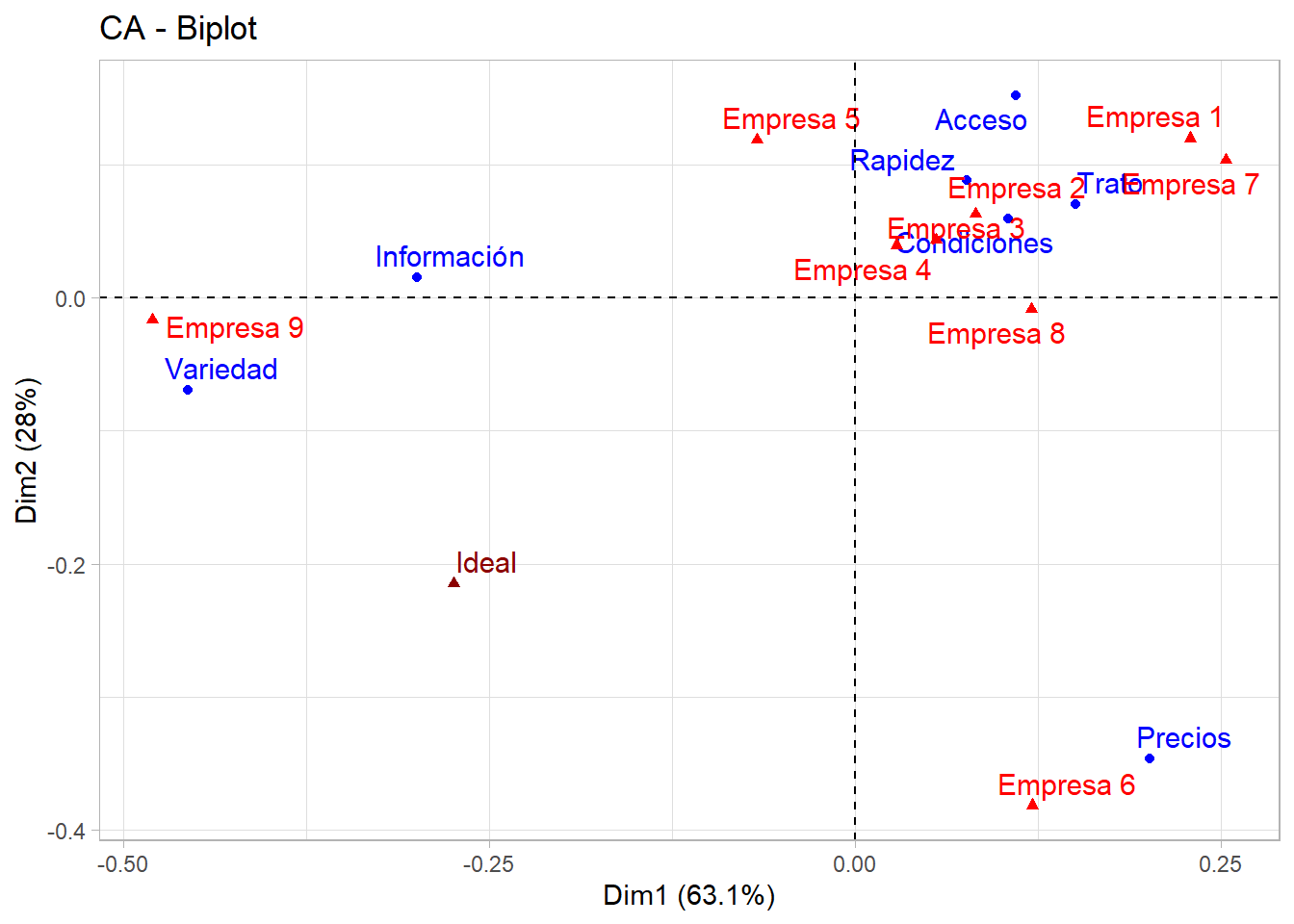
5.2.4 Ejemplo 4. Malas prácticas en ACS
Estos datos corresponden a la cantidad de personas con ciertas caracteristicas de acuerdo a la marca de su preferencia.
datos.acs.c <- matrix(c(25,30,10,
30,30,5,
35,20,15,
40,15,20,
25,10,15),nrow=5,byrow=T)
datos.acs.c [,1] [,2] [,3]
[1,] 25 30 10
[2,] 30 30 5
[3,] 35 20 15
[4,] 40 15 20
[5,] 25 10 15dimnames(datos.acs.c) <- list(marca=c("Marca 1", "Marca 2",
"Marca 3", "Marca 4",
"Marca 5")
,opinion=c("Adulto","NSE A/B",
"Auto"))
datos.acs.c opinion
marca Adulto NSE A/B Auto
Marca 1 25 30 10
Marca 2 30 30 5
Marca 3 35 20 15
Marca 4 40 15 20
Marca 5 25 10 15prueba <- chisq.test(datos.acs.c)
prueba
Pearson's Chi-squared test
data: datos.acs.c
X-squared = 25.559, df = 8, p-value = 0.001249res.ca.c <- CA(datos.acs.c,ncp=2,graph=FALSE)
eig.val <- get_eigenvalue(res.ca.c)
eig.val eigenvalue variance.percent cumulative.variance.percent
Dim.1 0.074324354 94.508496 94.5085
Dim.2 0.004318686 5.491504 100.0000fviz_screeplot(res.ca.c)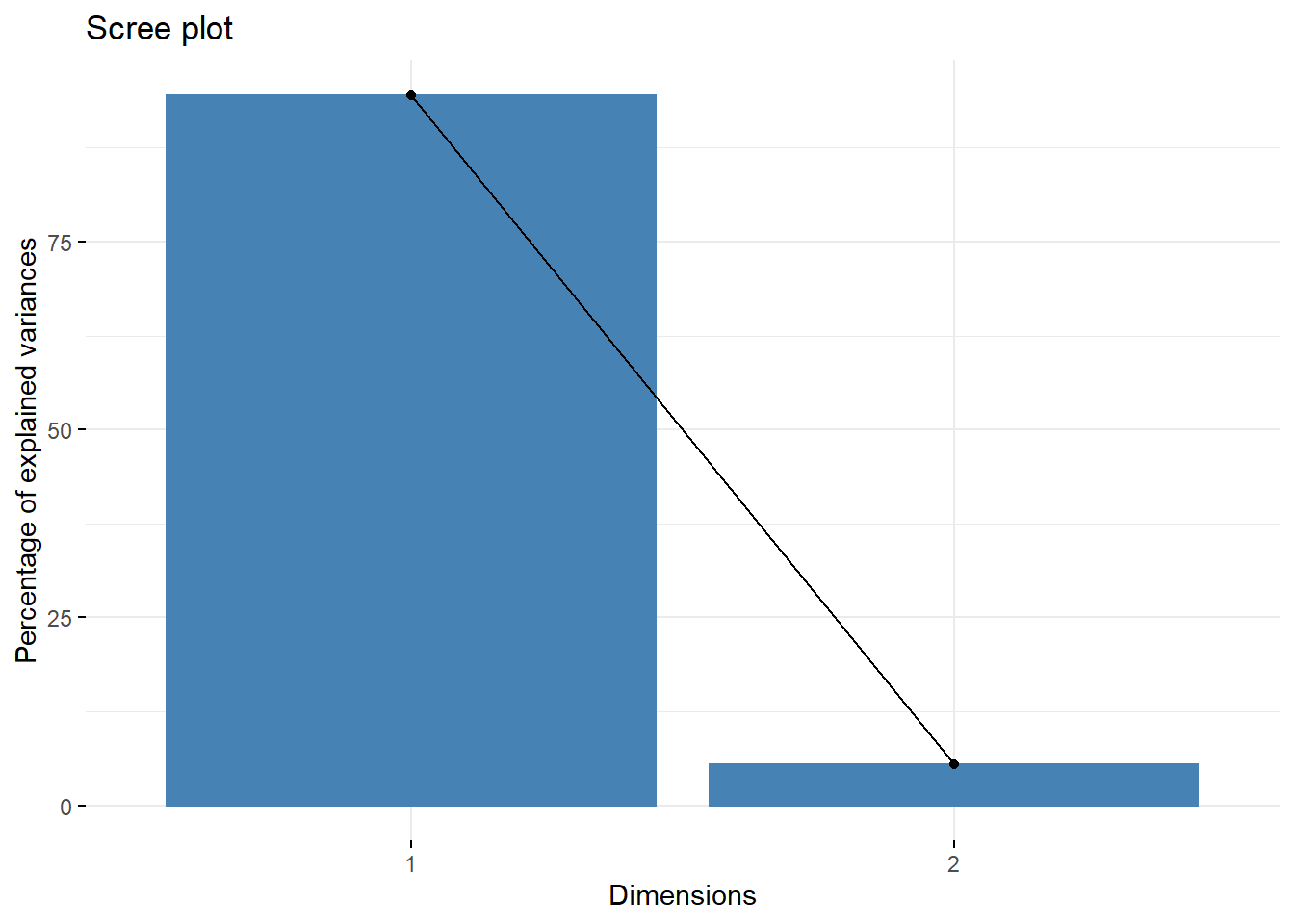
# Gráficos- Biplot
# Usando fviz_ca_biplot de factoextra
fviz_ca_biplot(res.ca.c, repel = T)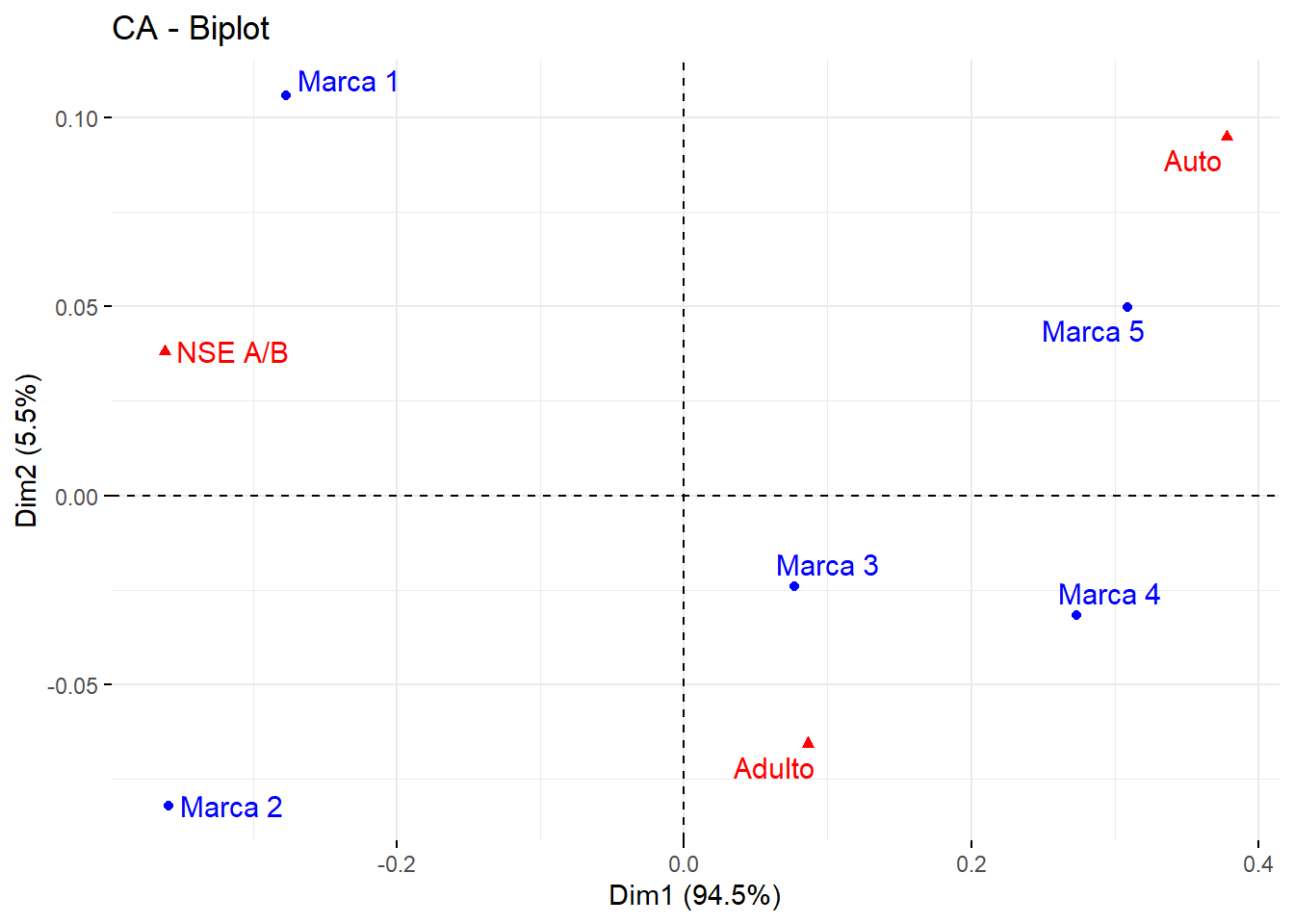
# Interpretación de los Indicadores del ACS
summary(res.ca.c,nb.dec = 3, ncp = 2)
Call:
CA(X = datos.acs.c, ncp = 2, graph = FALSE)
The chi square of independence between the two variables is equal to 25.55899 (p-value = 0.001249165 ).
Eigenvalues
Dim.1 Dim.2
Variance 0.074 0.004
% of var. 94.508 5.492
Cumulative % of var. 94.508 100.000
Rows
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2
Marca 1 | 17.572 | -0.277 20.626 0.872 | 0.106 51.898 0.128 |
Marca 2 | 27.115 | -0.359 34.678 0.951 | -0.082 31.050 0.049 |
Marca 3 | 1.391 | 0.077 1.703 0.910 | -0.024 2.896 0.090 |
Marca 4 | 17.488 | 0.273 23.221 0.987 | -0.032 5.308 0.013 |
Marca 5 | 15.077 | 0.309 19.772 0.975 | 0.050 8.848 0.025 |
Columns
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2
Adulto | 5.624 | 0.087 4.807 0.635 | -0.066 47.500 0.365 |
NSE A/B | 42.700 | -0.362 56.819 0.989 | 0.038 10.873 0.011 |
Auto | 30.318 | 0.378 38.373 0.941 | 0.095 41.627 0.059 |