Capítulo 7 Análisis Discriminante
7.1 Marco Téorico
Las técnicas discriminantes o de clasificación se utilizan para clasificar a distintos individuos en grupos o poblaciones ya conocidos a partir de los valores de un conjunto de variables sobre los individuos a los que se pretende clasificar.
Se plantea un modelo de dependencia del tipo: Y = f(X1, X2,…, Xp) , donde la variable dependiente Y (categórica) se denomina variable objetivo, target, dependiente o a predecir y las variables X1, X2,…, Xp se denominan variables independientes, predictoras o clasificadoras y pueden ser cuantitativas y/o categóricas.
El Análisis Discriminante Lineal se caracteriza por que las variables predictoras son numéricas.
7.2 Ejemplos
7.2.1 Ejemplo 1. Préstamos Fallidos del Banco Ademuz
options(scipen=999) # Eliminar la notación científica
options(digits = 3) # Número de decimales
library(pacman)
p_load(MASS, dplyr, ggplot2, klaR, psych, gains, caret, Boruta, gmodels,vegan, MLmetrics, vcd, Epi, InformationValue,ROCit)Este ejemplo fue tomado del libro de Uriel
Uriel, E. y Aldas, J. (2017). Análisis multivariante aplicado con R. Ediciones Paraninfo
Ingreso de Datos
En el Banco Ademuz se tiene información acerca de 16 clientes a los que se les concedió un préstamo instantáneo por un importe de 12.000 euros cada uno. Una vez pasados tres años desde la concesión de los préstamos había 8 clientes, de ese grupo de 16, que fueron clasificados como fallidos, mientras que los otros 8 clientes son cumplidores, ya que reintegraron el préstamo. Para cada uno de los clientes se dispone de información sobre su patrimonio neto y deudas pendientes correspondientes al momento de la solicitud. Con la información sobre las variabes de patrimonio neto y deudas pendientes se desea construir una función discriminante que clasifique con los menores errores posibles a los clientes en dos grupos: fallidos y no fallidos.
Patrimonio <- c(1.3,3.7,5,5.9,7.1,4,7.9,5.1,5.2,9.8,9,12,6.3,8.7,11.1,9.9)
Deuda <- c(4.1,6.9,3,6.5,5.4,2.7,7.6,3.8,1,4.2,4.8,2,5.2,1.1,4.1,1.6)
Grupo <- c(1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0)
datosd <- data.frame(Patrimonio,Deuda,Grupo)
str(datosd)'data.frame': 16 obs. of 3 variables:
$ Patrimonio: num 1.3 3.7 5 5.9 7.1 4 7.9 5.1 5.2 9.8 ...
$ Deuda : num 4.1 6.9 3 6.5 5.4 2.7 7.6 3.8 1 4.2 ...
$ Grupo : num 1 1 1 1 1 1 1 1 0 0 ...datosd$Grupo <- factor(datosd$Grupo,levels=c(0,1),
labels=c("No Fallido","Fallido"))
Patrimonio <- c(1.3,3.7,5,5.9,7.1,4,7.9,5.1,5.2,9.8,9,12,6.3,8.7,11.1,9.9)
Deuda <- c(4.1,6.9,3,6.5,5.4,2.7,7.6,3.8,1,4.2,4.8,2,5.2,1.1,4.1,1.6)
Grupo <- c(1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0)
datosd <- data.frame(Patrimonio,Deuda,Grupo)
str(datosd)'data.frame': 16 obs. of 3 variables:
$ Patrimonio: num 1.3 3.7 5 5.9 7.1 4 7.9 5.1 5.2 9.8 ...
$ Deuda : num 4.1 6.9 3 6.5 5.4 2.7 7.6 3.8 1 4.2 ...
$ Grupo : num 1 1 1 1 1 1 1 1 0 0 ...datosd$Grupo <- factor(datosd$Grupo,levels=c(0,1),
labels=c("No Fallido","Fallido"))
# No Fallido: no moroso (0)
# Fallido: deudor (1)
# write.csv(datosd,"data fallidos.csv",row.names = F)
contrasts(datosd$Grupo) Fallido
No Fallido 0
Fallido 1str(datosd)'data.frame': 16 obs. of 3 variables:
$ Patrimonio: num 1.3 3.7 5 5.9 7.1 4 7.9 5.1 5.2 9.8 ...
$ Deuda : num 4.1 6.9 3 6.5 5.4 2.7 7.6 3.8 1 4.2 ...
$ Grupo : Factor w/ 2 levels "No Fallido","Fallido": 2 2 2 2 2 2 2 2 1 1 ...prop.table(table(datosd$Grupo)) # Data Balanceada
No Fallido Fallido
0.5 0.5 library(ggplot2)
ggplot(datosd) + aes(x=Patrimonio,y=Deuda,color=Grupo) +
geom_point() +
scale_x_continuous(breaks=seq(0,12,2)) +
scale_y_continuous(breaks=seq(0,8,1)) +
theme_bw() +
theme(panel.grid = element_blank())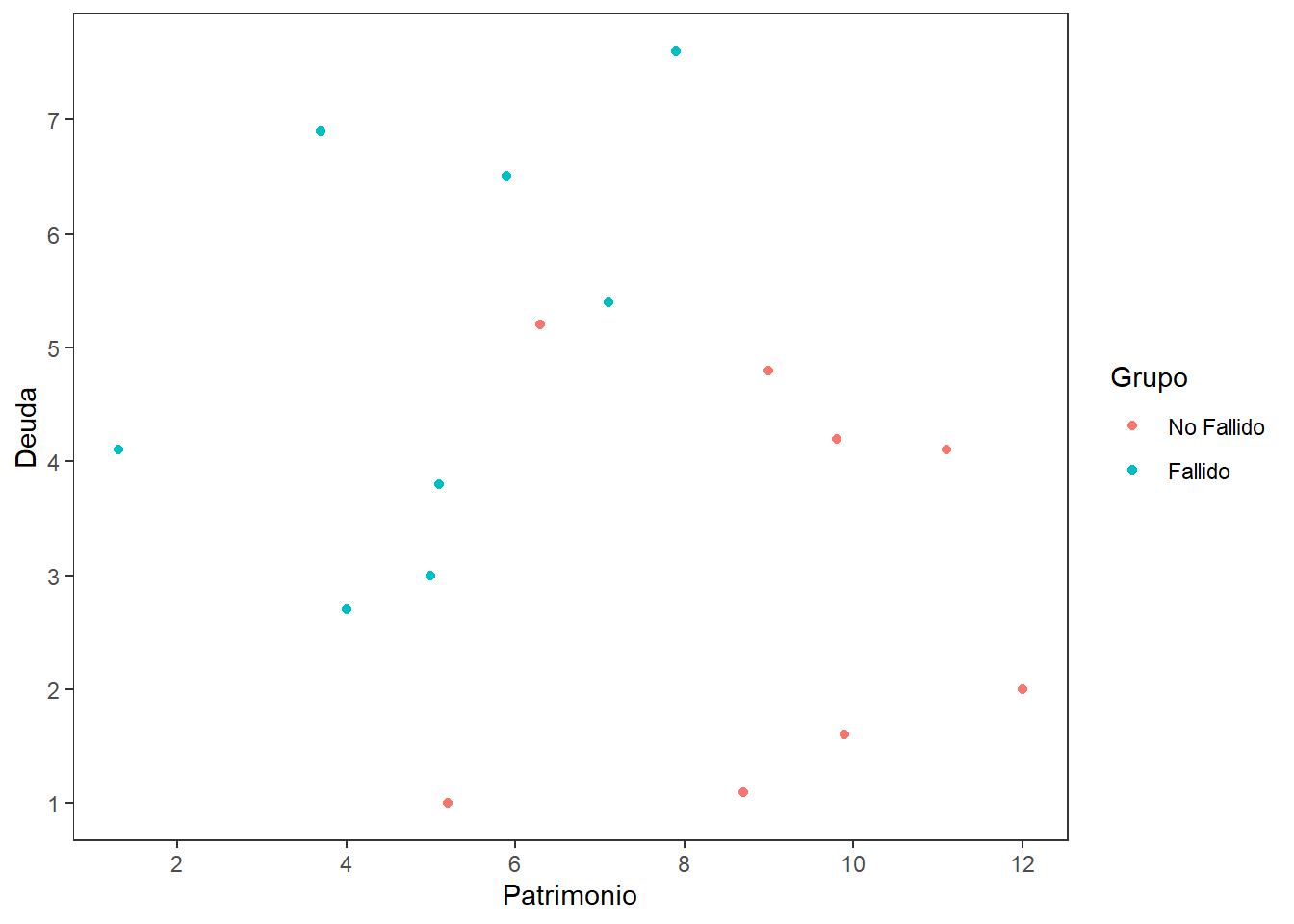
Clasificación con dos grupos y una variable predictora
Usando X1: Patrimonio
tapply(datosd$Patrimonio,datosd$Grupo,mean)No Fallido Fallido
9 5 C1 <- (5+9)/2 ; C1[1] 7datosd$clase.pred1 <- ifelse(datosd$Patrimonio < C1, 1, 0)
datosd$clase.pred1 <- factor(datosd$clase.pred1,levels = c(0, 1),
labels = c("No Fallido","Fallido"))
table(Clase_Real=datosd$Grupo,
Clase_Predicha=datosd$clase.pred1) Clase_Predicha
Clase_Real No Fallido Fallido
No Fallido 6 2
Fallido 2 6mean(datosd$Grupo==datosd$clase.pred1) # Accuracy: porcentaje de acierto[1] 0.75mean(datosd$Grupo!=datosd$clase.pred1) # Tasa de error del modelo[1] 0.25Graficando Patrimonio vs Grupo y el punto de corte
ggplot(datosd) + aes(x=Patrimonio,fill=Grupo) +
geom_histogram(alpha = 0.25, position="identity") +
theme_bw() +
geom_vline(xintercept = C1, linetype = "longdash") +
scale_x_continuous(breaks = seq(0,13,1))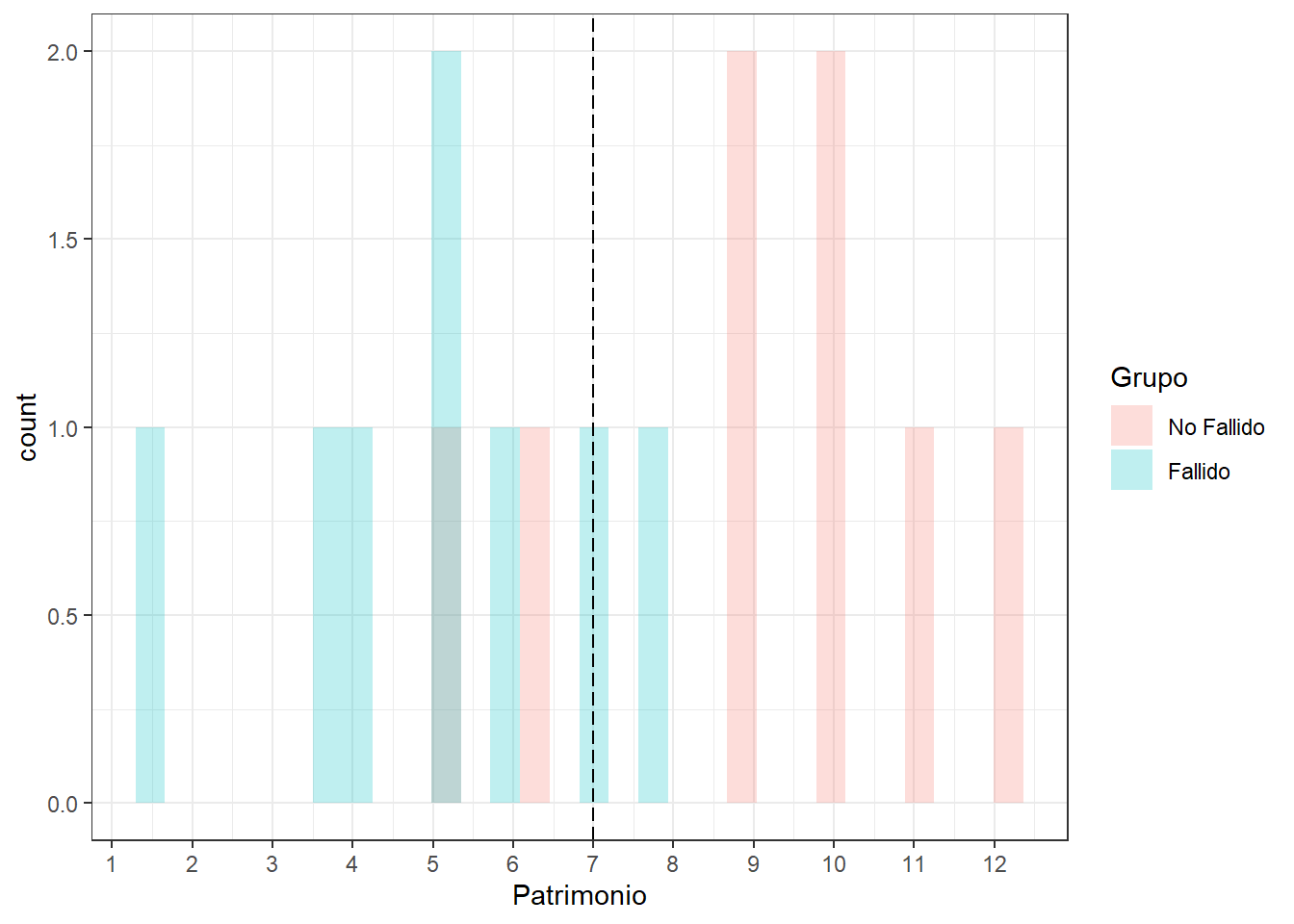
Usando X2: Deudas pendientes
tapply(datosd$Deuda,datosd$Grupo,mean)No Fallido Fallido
3 5 C2 <- (3+5)/2 ; C2[1] 4datosd$clase.pred2 <- ifelse(datosd$Deuda>C2,1,0)
datosd$clase.pred2 <- factor(datosd$clase.pred2,levels=c(0,1),
labels=c("No Fallido","Fallido"))
table(Clase_Real=datosd$Grupo,
Clase_Predicha=datosd$clase.pred2) Clase_Predicha
Clase_Real No Fallido Fallido
No Fallido 4 4
Fallido 3 5mean(datosd$Grupo==datosd$clase.pred2) # Accuracy[1] 0.562mean(datosd$Grupo!=datosd$clase.pred2) # Tasa de error[1] 0.438Graficando Patrimonio vs Grupo y el punto de corte
ggplot(datosd) + aes(x=Deuda,fill=Grupo) +
geom_histogram(alpha = 0.25, position="identity") +
theme_bw() +
geom_vline(xintercept = C2, linetype = "longdash") +
scale_x_continuous(breaks = seq(0,8,1))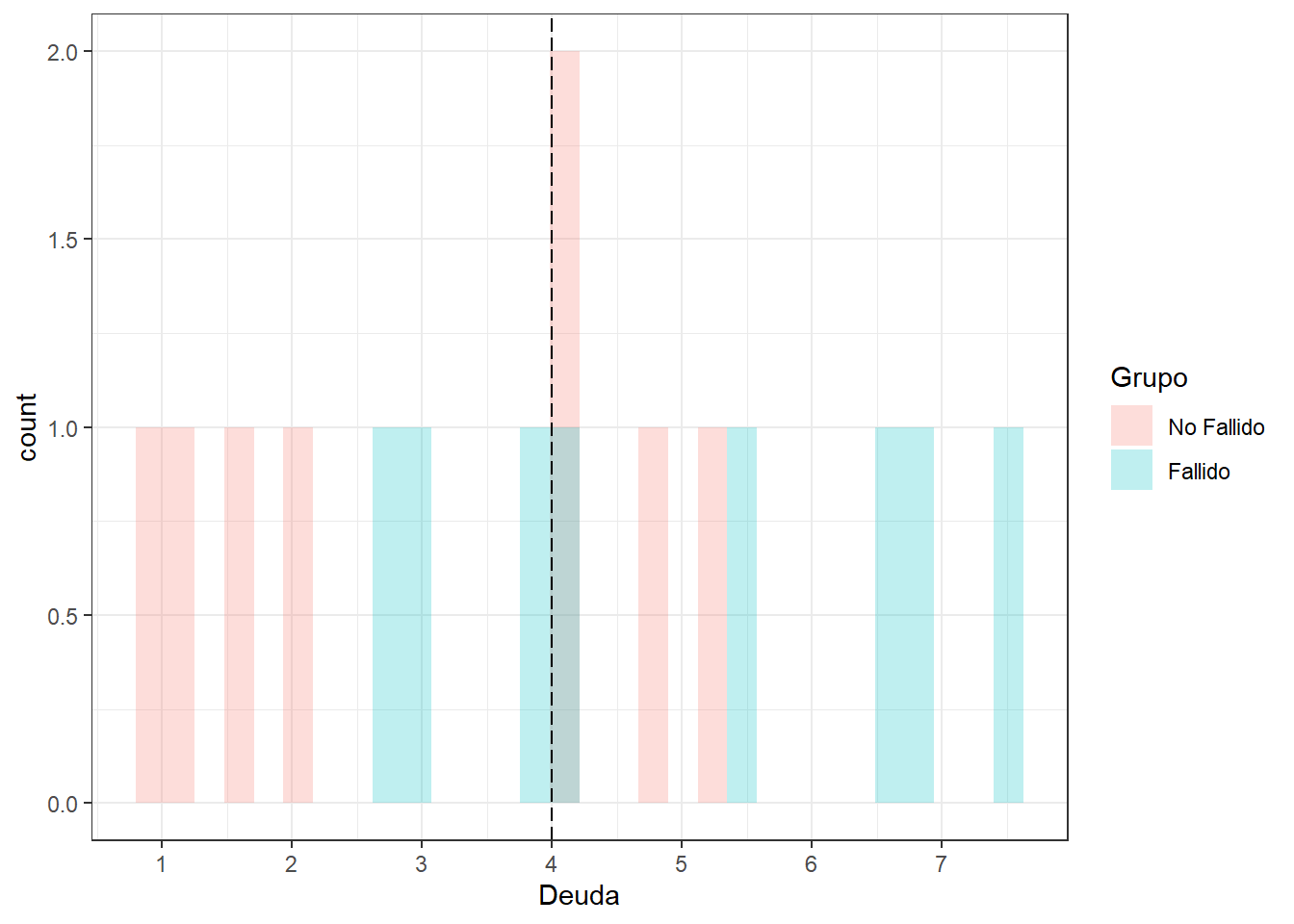
Clasificación con dos grupos y dos variable predictoras
library(MASS)
modelo <- lda(Grupo ~ Patrimonio + Deuda,datosd)
str(modelo)List of 10
$ prior : Named num [1:2] 0.5 0.5
..- attr(*, "names")= chr [1:2] "No Fallido" "Fallido"
$ counts : Named int [1:2] 8 8
..- attr(*, "names")= chr [1:2] "No Fallido" "Fallido"
$ means : num [1:2, 1:2] 9 5 3 5
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:2] "No Fallido" "Fallido"
.. ..$ : chr [1:2] "Patrimonio" "Deuda"
$ scaling: num [1:2, 1] -0.422 0.38
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:2] "Patrimonio" "Deuda"
.. ..$ : chr "LD1"
$ lev : chr [1:2] "No Fallido" "Fallido"
$ svd : num 4.9
$ N : int 16
$ call : language lda(formula = Grupo ~ Patrimonio + Deuda, data = datosd)
$ terms :Classes 'terms', 'formula' language Grupo ~ Patrimonio + Deuda
.. ..- attr(*, "variables")= language list(Grupo, Patrimonio, Deuda)
.. ..- attr(*, "factors")= int [1:3, 1:2] 0 1 0 0 0 1
.. .. ..- attr(*, "dimnames")=List of 2
.. .. .. ..$ : chr [1:3] "Grupo" "Patrimonio" "Deuda"
.. .. .. ..$ : chr [1:2] "Patrimonio" "Deuda"
.. ..- attr(*, "term.labels")= chr [1:2] "Patrimonio" "Deuda"
.. ..- attr(*, "order")= int [1:2] 1 1
.. ..- attr(*, "intercept")= int 1
.. ..- attr(*, "response")= int 1
.. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
.. ..- attr(*, "predvars")= language list(Grupo, Patrimonio, Deuda)
.. ..- attr(*, "dataClasses")= Named chr [1:3] "factor" "numeric" "numeric"
.. .. ..- attr(*, "names")= chr [1:3] "Grupo" "Patrimonio" "Deuda"
$ xlevels: Named list()
- attr(*, "class")= chr "lda"modeloCall:
lda(Grupo ~ Patrimonio + Deuda, data = datosd)
Prior probabilities of groups:
No Fallido Fallido
0.5 0.5
Group means:
Patrimonio Deuda
No Fallido 9 3
Fallido 5 5
Coefficients of linear discriminants:
LD1
Patrimonio -0.422
Deuda 0.380modelo$means Patrimonio Deuda
No Fallido 9 3
Fallido 5 5# Usando el modelo
datosd$D <- -0.422*datosd$Patrimonio + 0.380*datosd$Deuda
mean(datosd$D)[1] -1.43tapply(datosd$D,datosd$Grupo,mean)No Fallido Fallido
-2.66 -0.21 C3 <- (-2.66-0.21)/2 ; C3[1] -1.44datosd$clase.pred3 <- ifelse(datosd$D>C3,1,0)
datosd$clase.pred3 <- factor(datosd$clase.pred3,levels=c(0,1),
labels=c("No Fallido","Fallido"))
table(Clase_Real=datosd$Grupo,
Clase_Predicha=datosd$clase.pred3) Clase_Predicha
Clase_Real No Fallido Fallido
No Fallido 7 1
Fallido 0 8mean(datosd$Grupo==datosd$clase.pred3)[1] 0.938mean(datosd$Grupo!=datosd$clase.pred3)[1] 0.0625Graficando d vs Grupo y el punto de corte
ggplot(datosd) + aes(x=D,fill=Grupo) +
geom_histogram(alpha = 0.25, position="identity") +
theme_bw() +
geom_vline(xintercept = C3, linetype = "longdash") +
scale_x_continuous(breaks = seq(-5,5,1))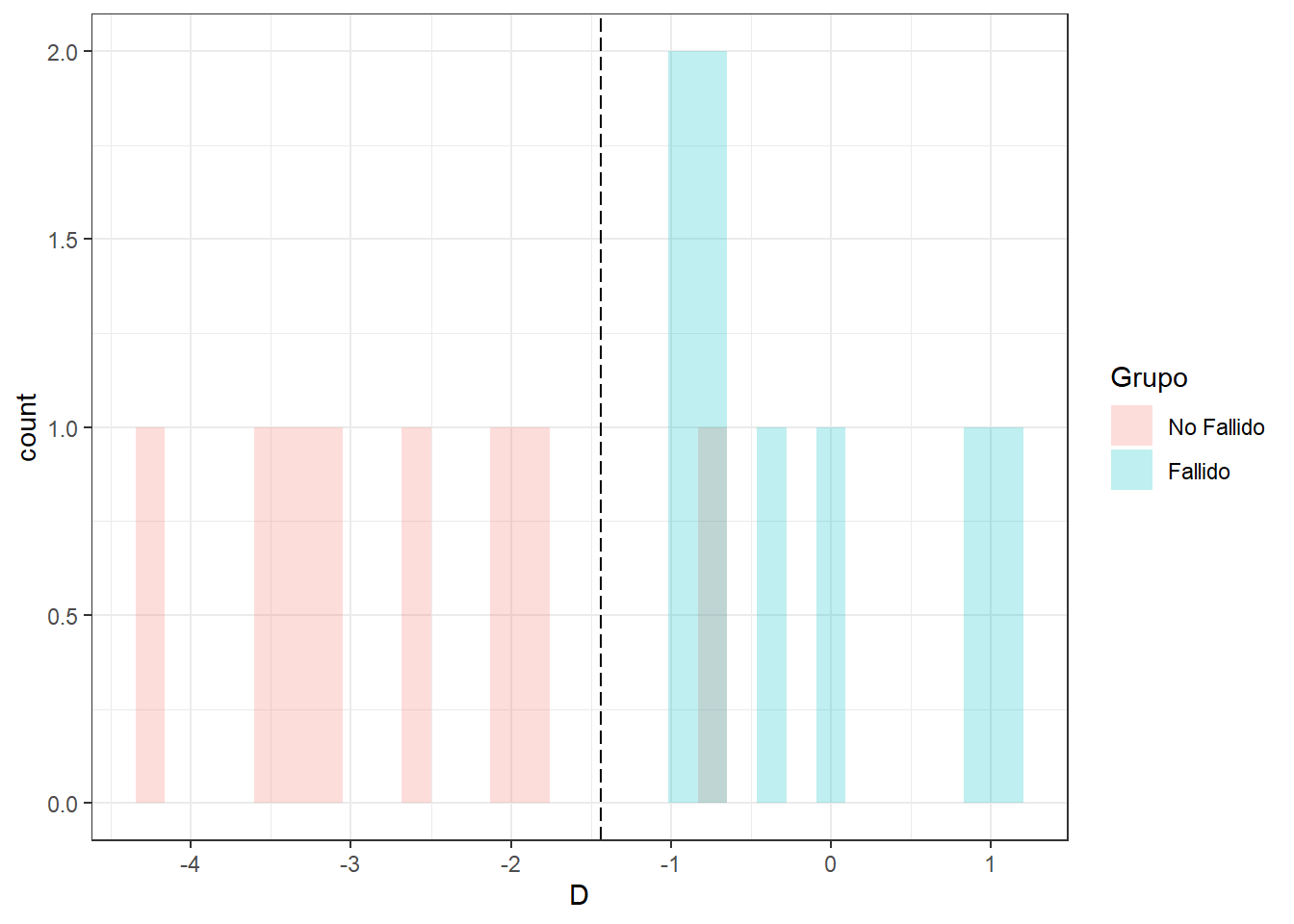
datosd$dif <- datosd$D - C3
datosd$dif [1] 2.444 2.496 0.465 1.415 0.491 0.773 0.989 0.727 -0.379 -1.105
[11] -0.539 -2.869 0.752 -1.818 -1.691 -2.135predicciones <- predict(modelo)
str(predicciones)List of 3
$ class : Factor w/ 2 levels "No Fallido","Fallido": 2 2 2 2 2 2 2 2 1 1 ...
$ posterior: num [1:16, 1:2] 0.00249 0.0022 0.24253 0.03023 0.23132 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:16] "1" "2" "3" "4" ...
.. ..$ : chr [1:2] "No Fallido" "Fallido"
$ x : num [1:16, 1] 2.446 2.497 0.465 1.415 0.49 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:16] "1" "2" "3" "4" ...
.. ..$ : chr "LD1"# Igual a la diferencia de D y C3
predicciones$x LD1
1 2.446
2 2.497
3 0.465
4 1.415
5 0.490
6 0.773
7 0.989
8 0.727
9 -0.380
10 -1.107
11 -0.541
12 -2.873
13 0.752
14 -1.821
15 -1.694
16 -2.138plot(modelo)
# Otra forma
ldahist(data = predicciones$x, g = datosd$Grupo)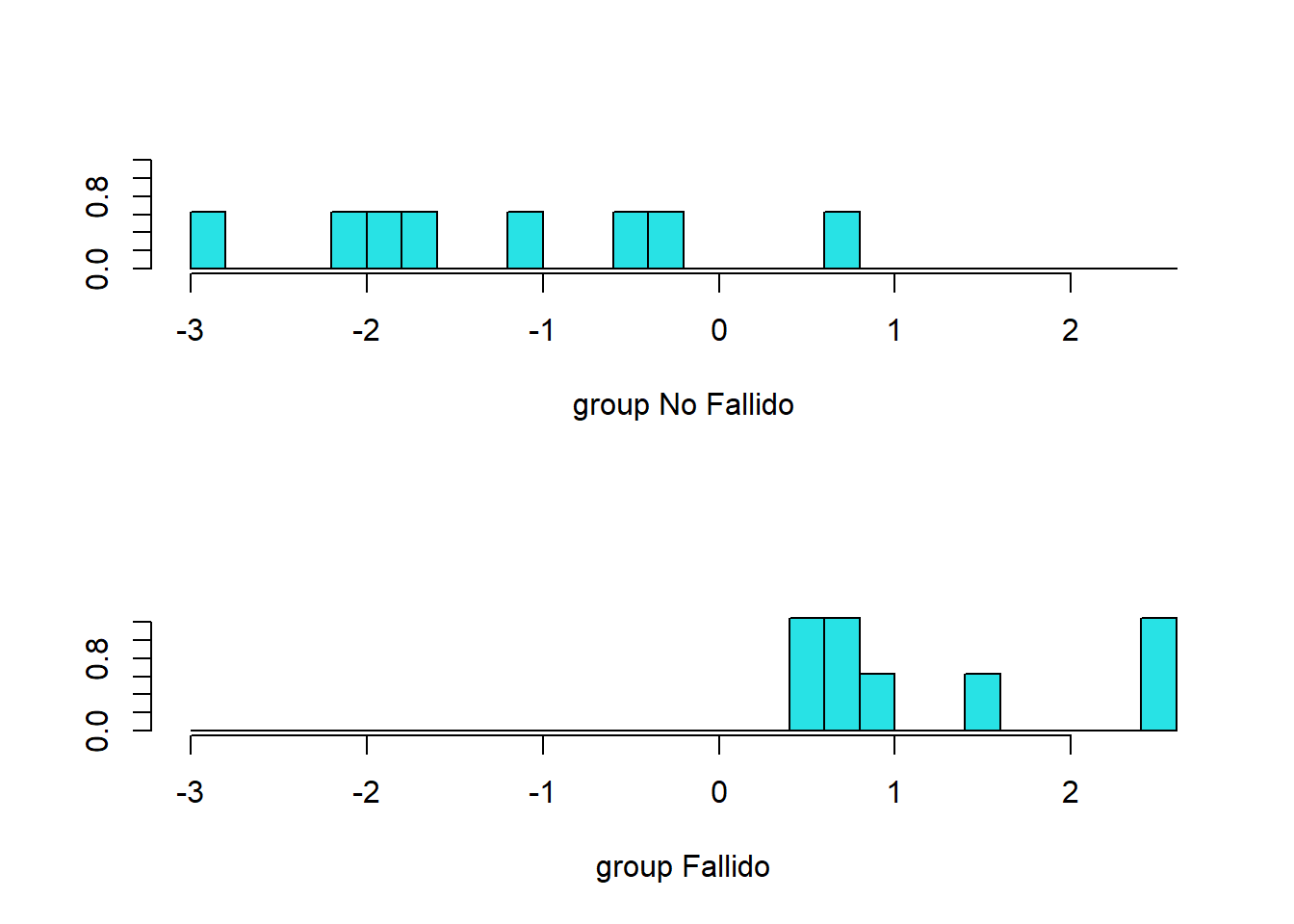
Graficando regla (dif,x) vs Grupo y el punto de corte
ggplot(datosd) + aes(x=dif,fill=Grupo) +
geom_histogram(alpha = 0.25, position="identity") +
theme_bw() +
geom_vline(xintercept = 0, linetype = "longdash") +
scale_x_continuous(breaks = seq(-5,5,1))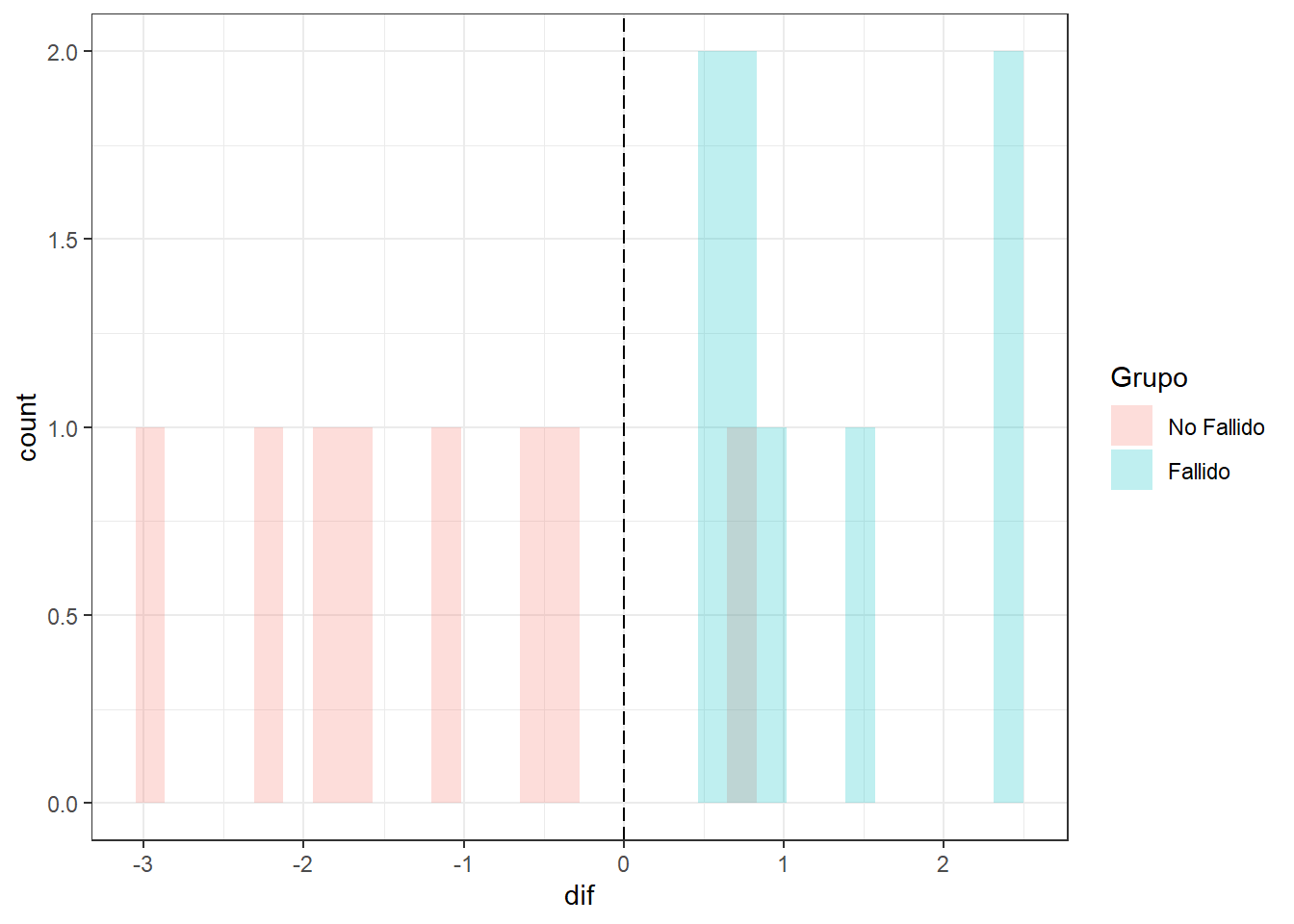
Prediciendo la probabilidad
predicciones$posterior No Fallido Fallido
1 0.00249 0.997513
2 0.00220 0.997803
3 0.24253 0.757470
4 0.03023 0.969765
5 0.23132 0.768677
6 0.13072 0.869282
7 0.08148 0.918518
8 0.14422 0.855782
9 0.71740 0.282599
10 0.93776 0.062243
11 0.79005 0.209955
12 0.99912 0.000876
13 0.13673 0.863272
14 0.98859 0.011409
15 0.98450 0.015497
16 0.99472 0.005281datosd$proba <- predicciones$posterior[,2]
predicciones$class # Punto de corte por defecto= 0.5 (umbral) [1] Fallido Fallido Fallido Fallido Fallido Fallido
[7] Fallido Fallido No Fallido No Fallido No Fallido No Fallido
[13] Fallido No Fallido No Fallido No Fallido
Levels: No Fallido FallidoGraficando la probabilidad predicha y la clase real
Con función de densidad
ggplot(datosd) + aes(x=proba,color= Grupo,fill=Grupo) +
geom_density(alpha = 0.25) + theme_bw() +
geom_vline(xintercept = 0.5, linetype = "longdash") + theme_bw()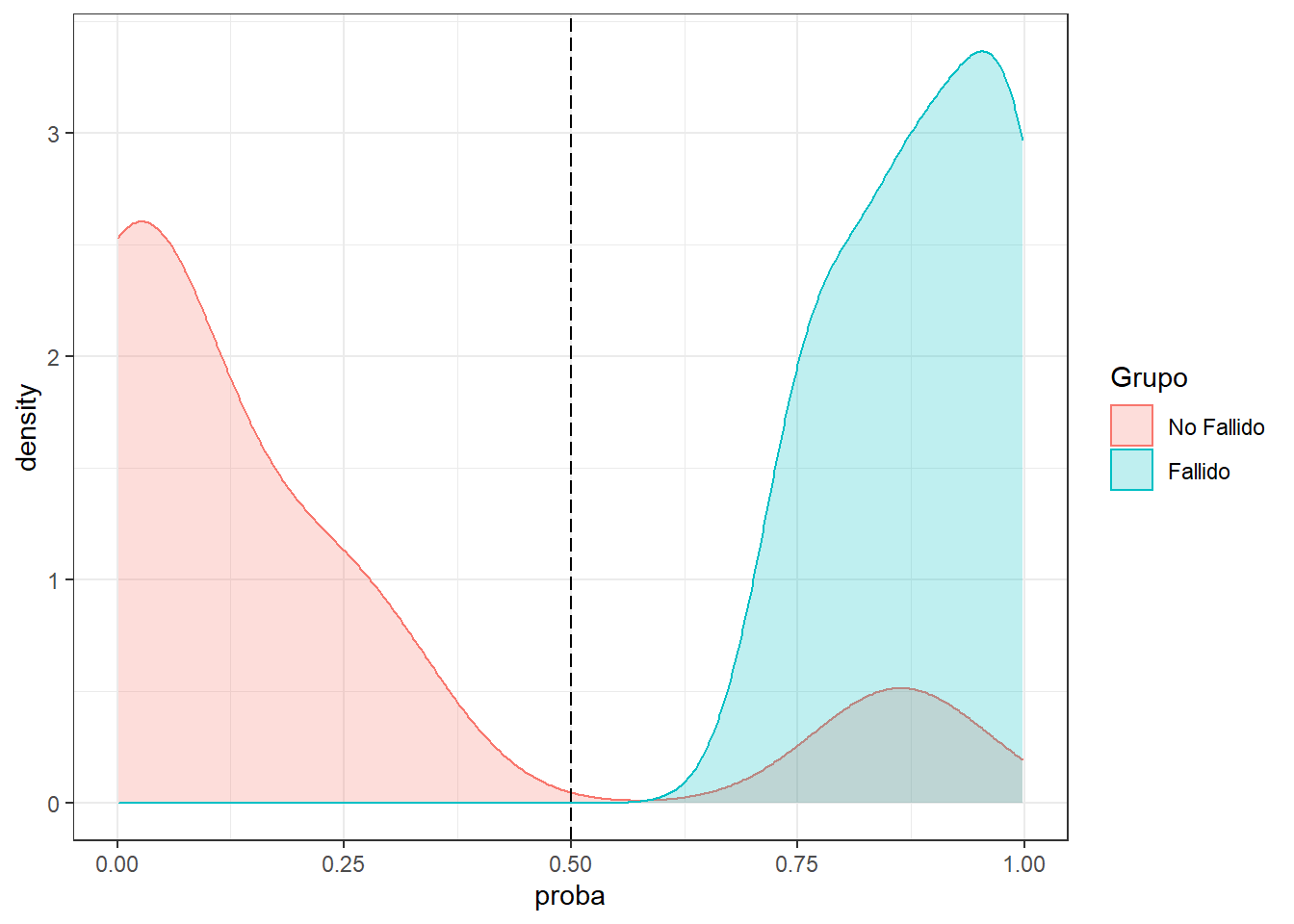
Con histograma
ggplot(datosd) + aes(x=proba,color= Grupo,fill=Grupo) +
geom_histogram(alpha = 0.25) + theme_bw() +
geom_vline(xintercept = 0.5, linetype = "longdash") + theme_bw()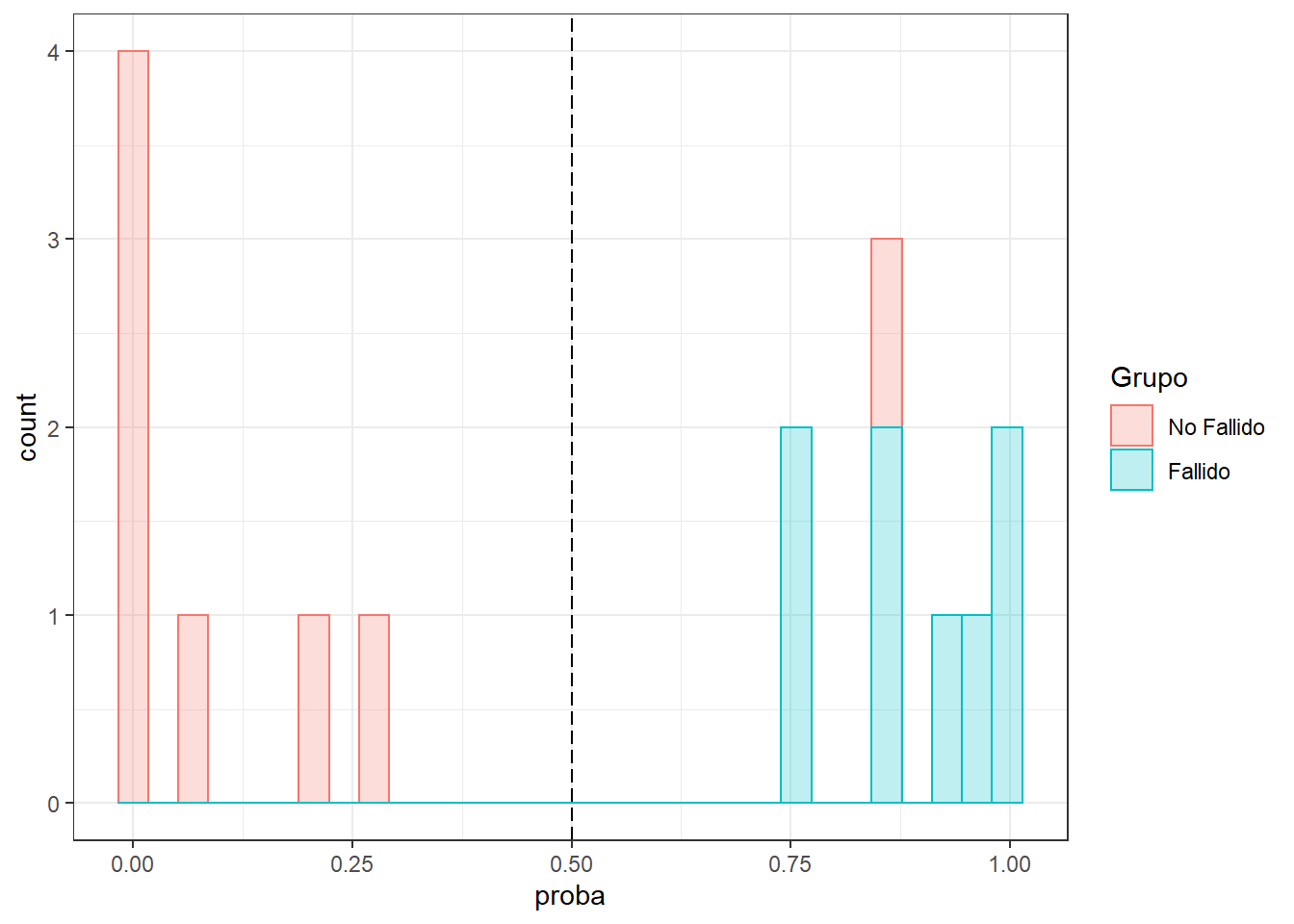
Usando el paquete klaR
Usar solo para 2 variables
library(klaR)
# Análisis discriminante lineal
partimat(Grupo ~ Deuda + Patrimonio, data = datosd, method = "lda")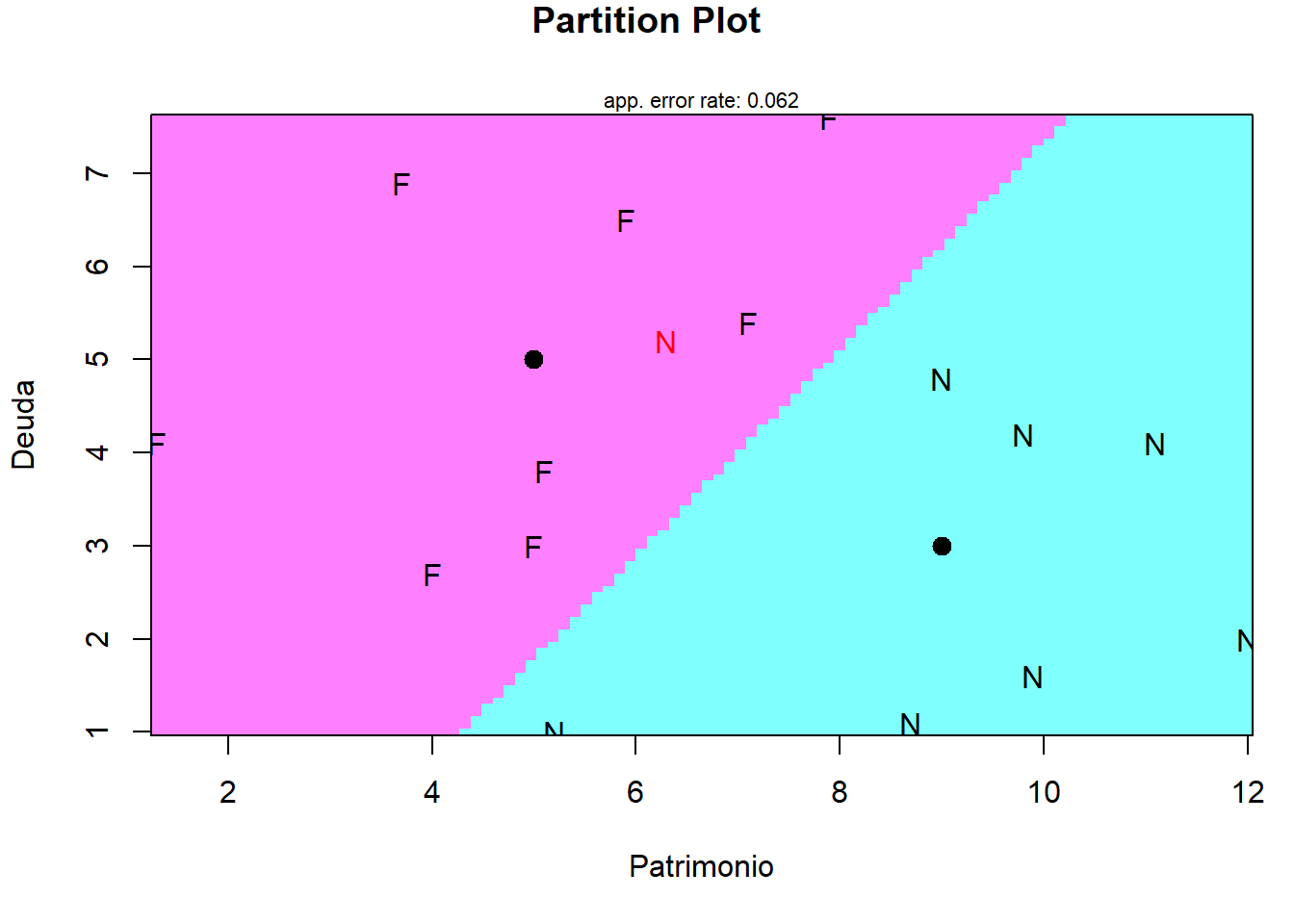
# Análisis discriminante cuadratico
partimat(Grupo ~ Deuda + Patrimonio, data = datosd, method = "qda")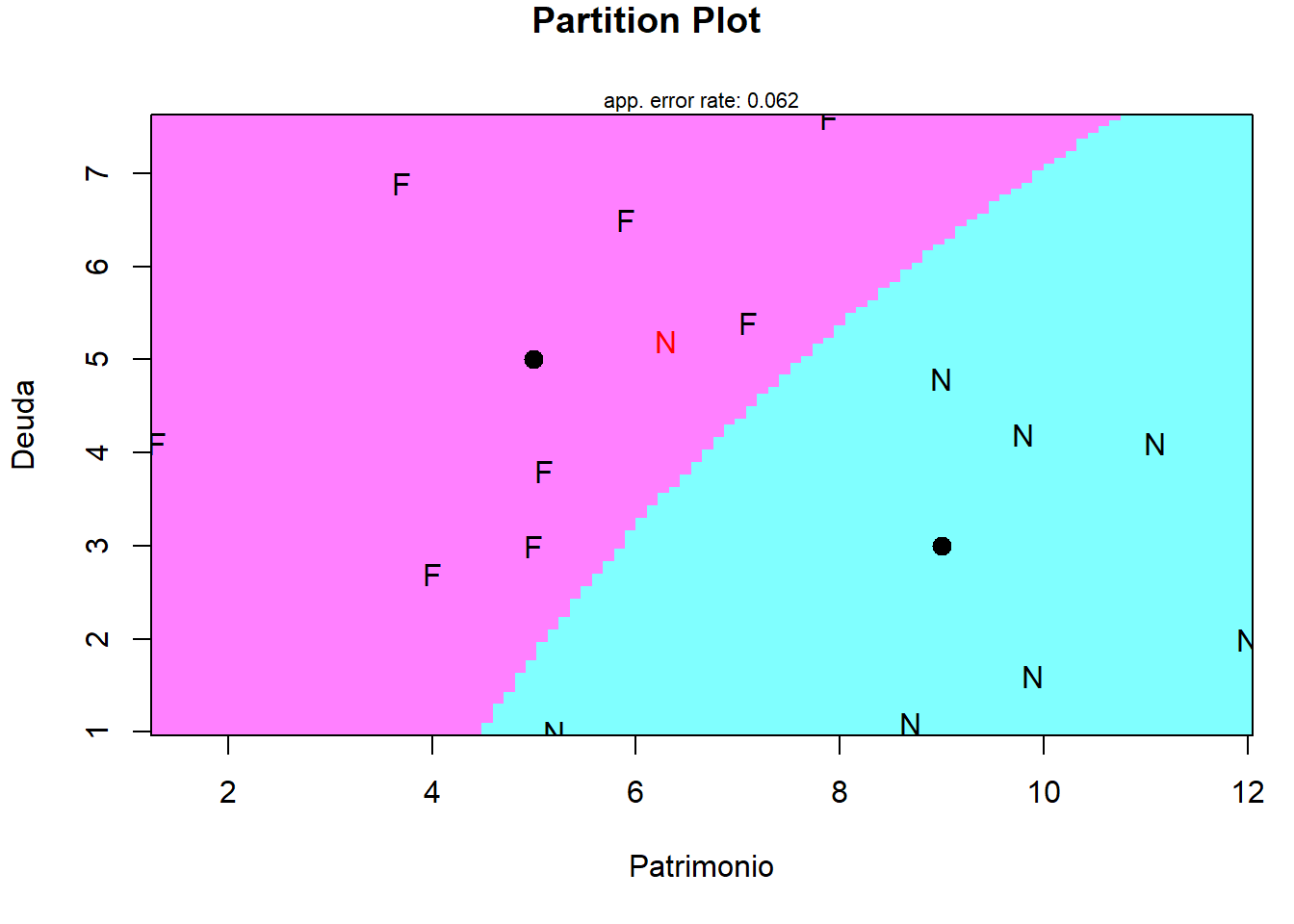
Predicción para nuevos individuos
Patrimonio <- c(10.1,9.7)
Deuda <- c(6.8,2.2)
nuevos.casos <- data.frame(Patrimonio,Deuda)
nuevas.predicciones <- predict(modelo,nuevos.casos)
nuevas.predicciones$posterior No Fallido Fallido
1 0.646 0.3542
2 0.989 0.0113nuevas.predicciones$class[1] No Fallido No Fallido
Levels: No Fallido FallidoUsando el Criterio de la Distancia de Mahalanobis
Caso general
nuevos.casos <- data.frame(Patrimonio=1,Deuda=4)
nuevos.casos Patrimonio Deuda
1 1 4cov_nf <- by(datosd[,c(1,2)],datosd$Grupo,cov)[[1]]
cov_nf # matriz varianza-covarianza de los no fallidos Patrimonio Deuda
Patrimonio 5.240 0.177
Deuda 0.177 3.043cov_f <- by(datosd[,c(1,2)],datosd$Grupo,cov)[[2]]
cov_f # matriz varianza-covarianza de los fallidos Patrimonio Deuda
Patrimonio 4.29 1.82
Deuda 1.82 3.47cov <- (7*cov_nf + 7*cov_f)/(14)
cov Patrimonio Deuda
Patrimonio 4.76 1.00
Deuda 1.00 3.26library(dplyr)
datosd %>% select(Patrimonio,Deuda,Grupo) %>%
group_by(Grupo) %>%
summarise_if(is.numeric,mean) %>% as.data.frame-> centroides
centroides Grupo Patrimonio Deuda
1 No Fallido 9 3
2 Fallido 5 5Distancia del individuo a los No Fallidos
centroides_nf <- as.matrix(centroides[1,-1]); centroides_nf Patrimonio Deuda
1 9 3solve(cov) Patrimonio Deuda
Patrimonio 0.2244 -0.0689
Deuda -0.0689 0.3280as.matrix(nuevos.casos-centroides_nf)%*%solve(cov)%*%
t(as.matrix(nuevos.casos-centroides_nf)) [,1]
[1,] 15.8# De Otra Forma
mahalanobis(nuevos.casos, centroides_nf, cov) [1] 15.8Distancia del individuo a los Fallidos
centroides_f <- as.matrix(centroides[2,-1]); centroides_f Patrimonio Deuda
2 5 5as.matrix(nuevos.casos-centroides_f)%*%solve(cov)%*%
t(as.matrix(nuevos.casos-centroides_f)) [,1]
[1,] 3.37# Otra Forma
mahalanobis(nuevos.casos, centroides_f, cov)[1] 3.377.2.2 Ejemplo 2. Ejemplo Suscripción
Este ejemplo fue tomado del libro de Uriel.
Uriel,E. y Aldas, J. (2002). Análisis Multivariante Aplicado. Aplicaciones al marketing, investigación de mercados, economía, dirección de empresas y turismo. Ediciones Paraninfo
Ingreso de Datos
La compañía de cable edita y promociona una revista de cine (de edición mensual) a un grupo (442) de sus suscriptores durante 6 meses. Al cabo de dicho periodo le ofrece la posibilidad de suscribirse a dicha revista. De los 442 clientes a los que se ofreció la promoción, se suscribieron a la revista 329 y no se suscribieron 113.
library(foreign)
datosd <- read.spss("suscripcion-discriminante.sav",
use.value.labels = TRUE,
max.value.labels = TRUE,
to.data.frame = TRUE)
attr(datosd, "variable.labels") <- NULL # para quitar las variables names
str(datosd)'data.frame': 442 obs. of 6 variables:
$ Educacion : num 12 12 11 12 12 11 10 12 13 12 ...
$ Edad : num 18 19 20 20 20 20 20 20 21 21 ...
$ Tvdiario : num 3 2 1 3 4 4 5 5 1 1 ...
$ Organizaciones: num 0 0 0 1 0 2 0 2 0 4 ...
$ Hijos : num 0 0 0 1 1 1 0 0 0 0 ...
$ Suscripcion : num 0 0 0 0 1 1 1 1 0 0 ...
..- attr(*, "value.labels")= Named chr [1:2] "1" "0"
.. ..- attr(*, "names")= chr [1:2] "Si" "No"
- attr(*, "codepage")= int 1252datosd$Suscripcion <- factor(datosd$Suscripcion)
datosd$Suscripcion <- factor(datosd$Suscripcion,
levels = c(0, 1),
labels = c("No", "Si"))
contrasts(datosd$Suscripcion) Si
No 0
Si 1str(datosd)'data.frame': 442 obs. of 6 variables:
$ Educacion : num 12 12 11 12 12 11 10 12 13 12 ...
$ Edad : num 18 19 20 20 20 20 20 20 21 21 ...
$ Tvdiario : num 3 2 1 3 4 4 5 5 1 1 ...
$ Organizaciones: num 0 0 0 1 0 2 0 2 0 4 ...
$ Hijos : num 0 0 0 1 1 1 0 0 0 0 ...
$ Suscripcion : Factor w/ 2 levels "No","Si": 1 1 1 1 2 2 2 2 1 1 ...
- attr(*, "codepage")= int 1252attach(datosd)Para cambiar la categoría de referencia (v predictoras)
datosd$Suscripcion <- relevel(datosd$Suscripcion, ref="No") # El 0 es para NO
contrasts(datosd$Suscripcion) Si
No 0
Si 1Explorando las variables predictoras
library(funModeling) # Pablo Casas Udemy
# Reduciendo el código
predictores <- setdiff(names(datosd), "Suscripcion")
predictores[1] "Educacion" "Edad" "Tvdiario" "Organizaciones"
[5] "Hijos" # Boxplot por cada variable predictora vs target
plotar(datosd, target = "Suscripcion", input = predictores,
plot_type = "boxplot")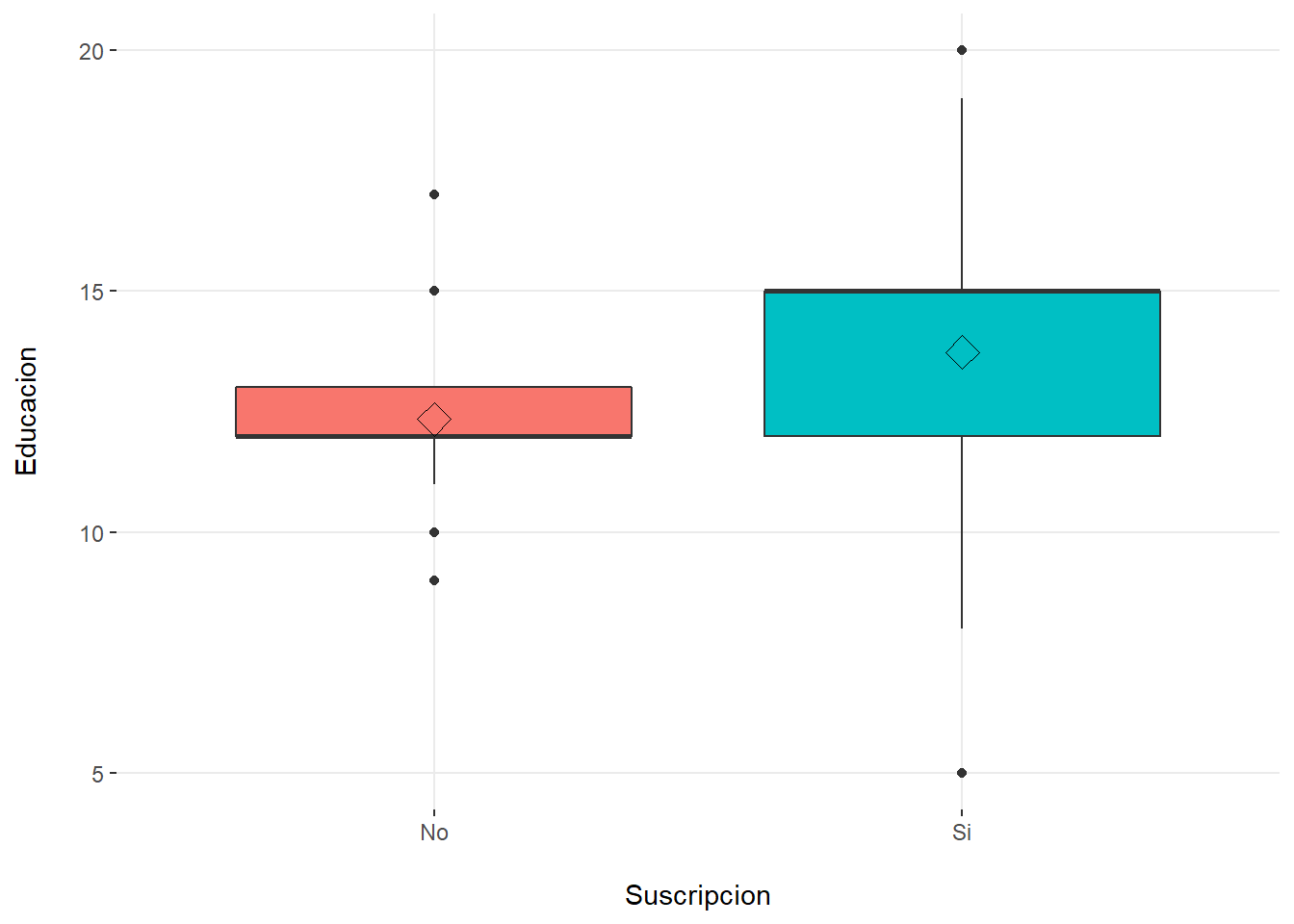
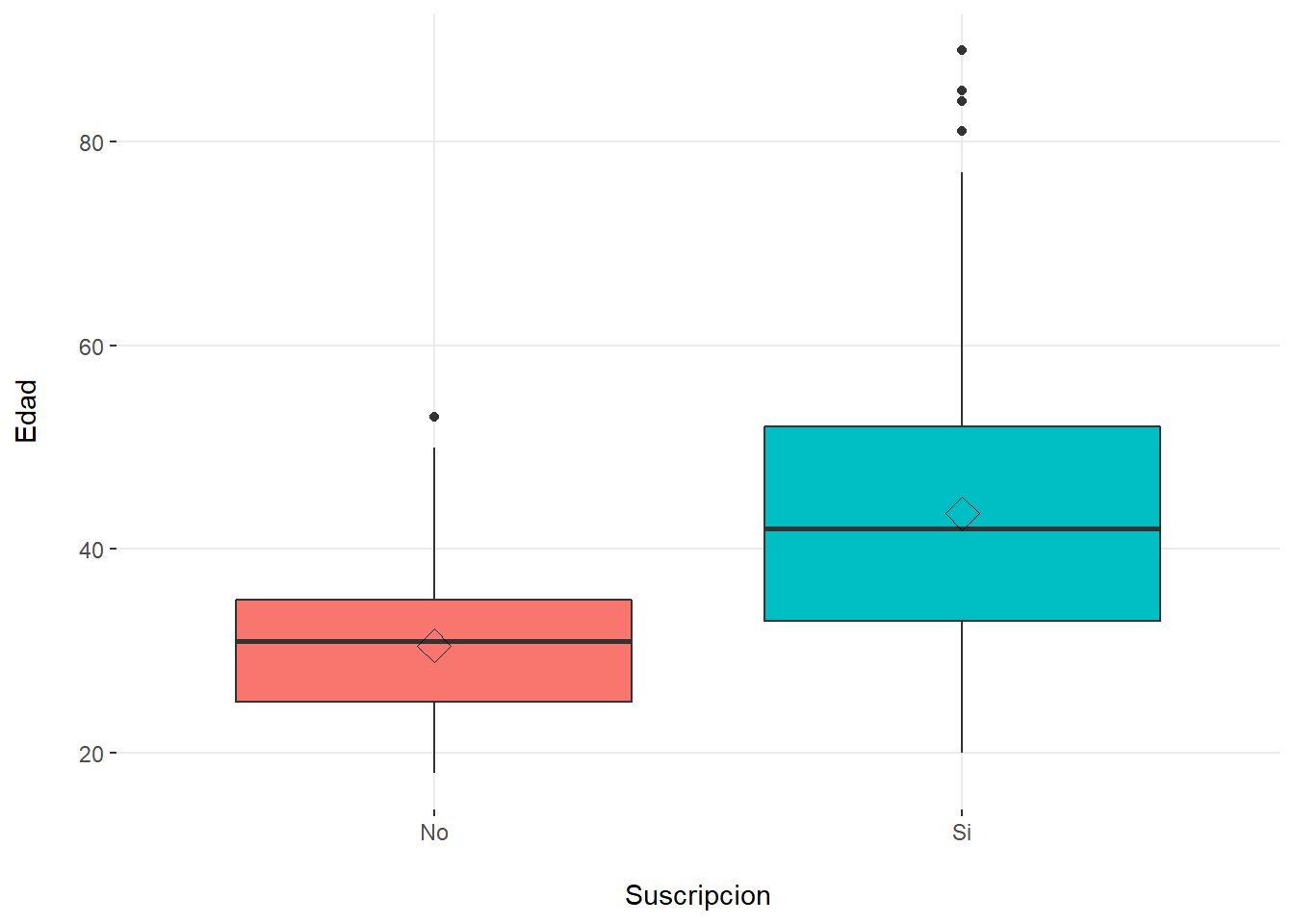
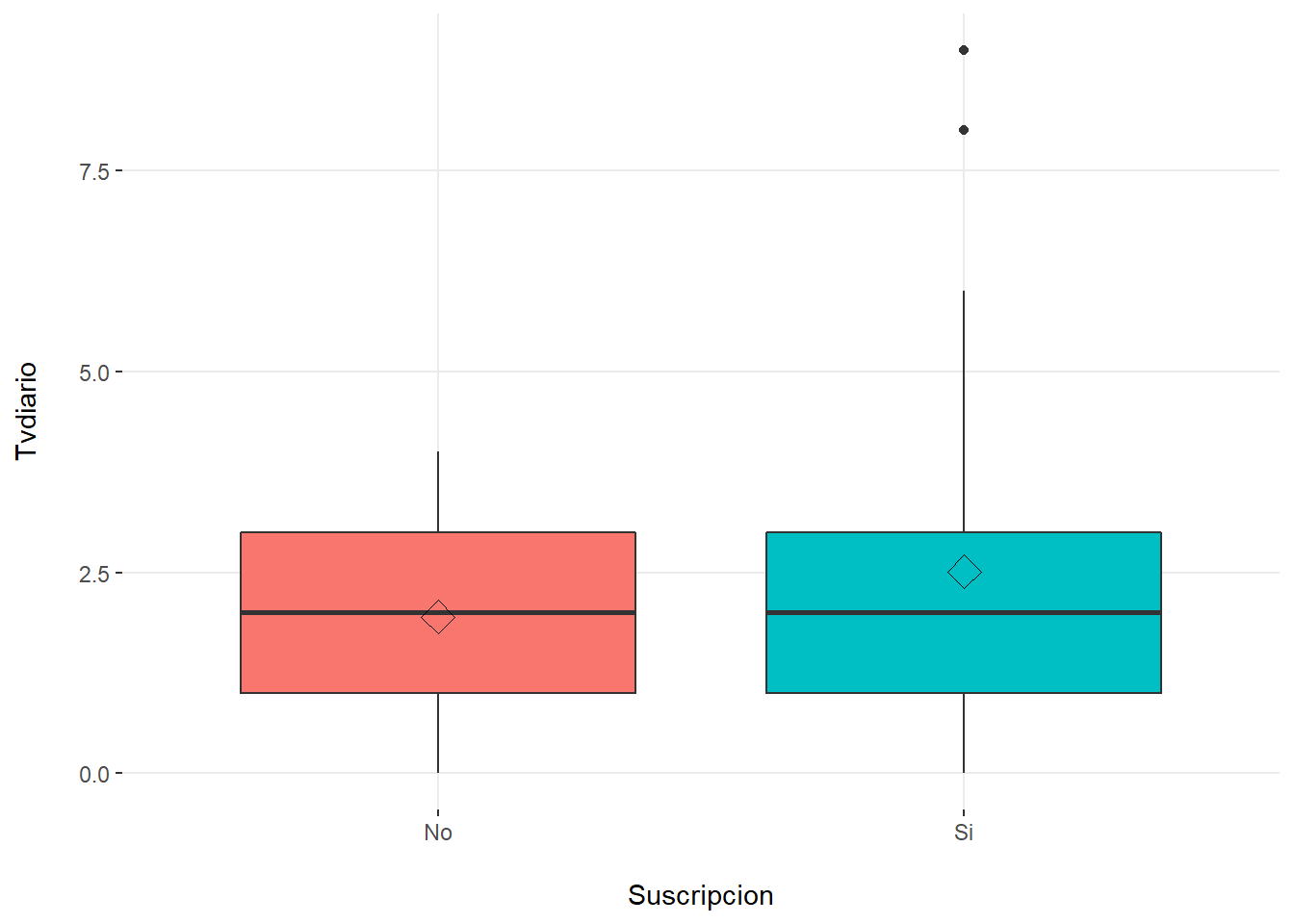
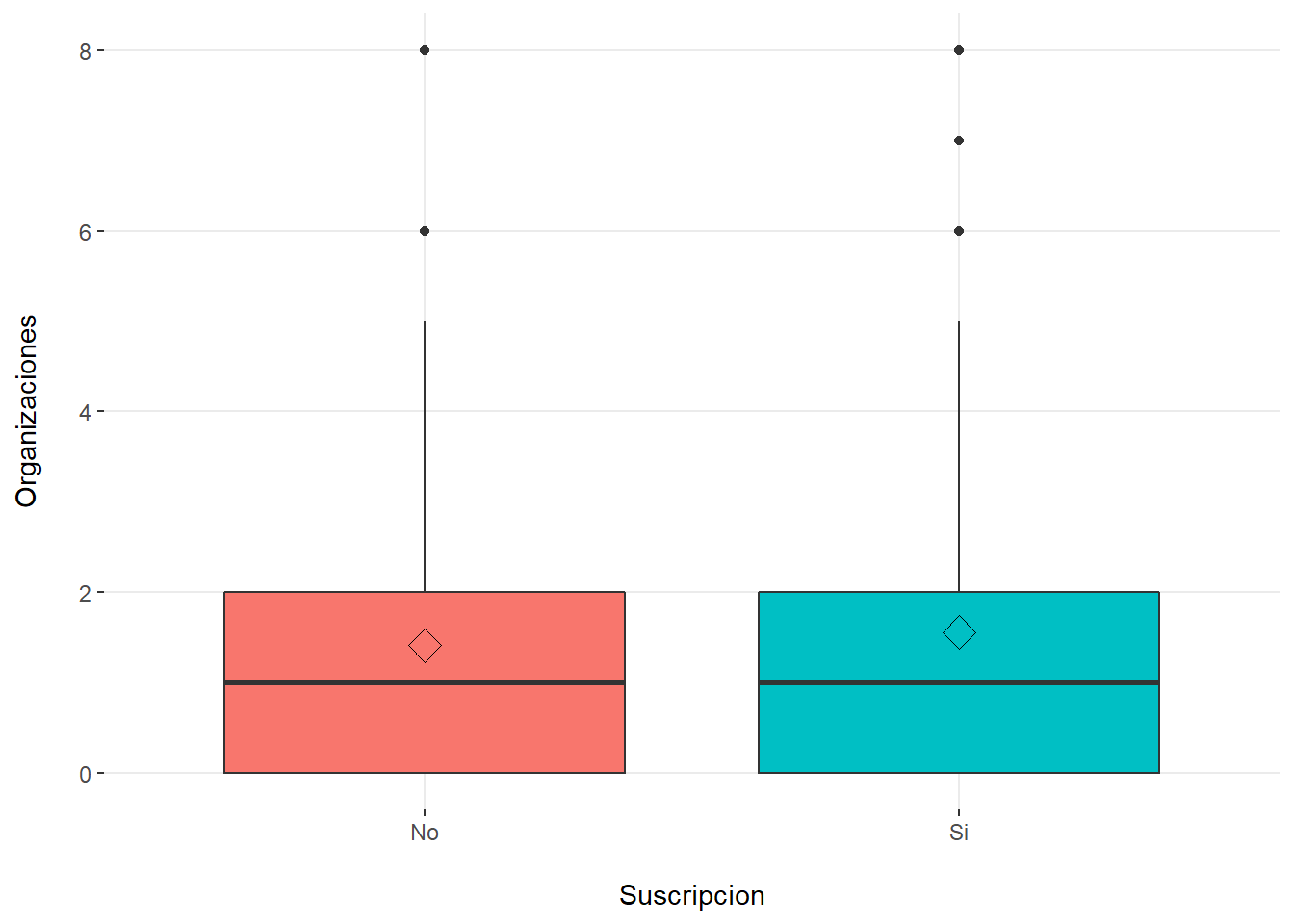
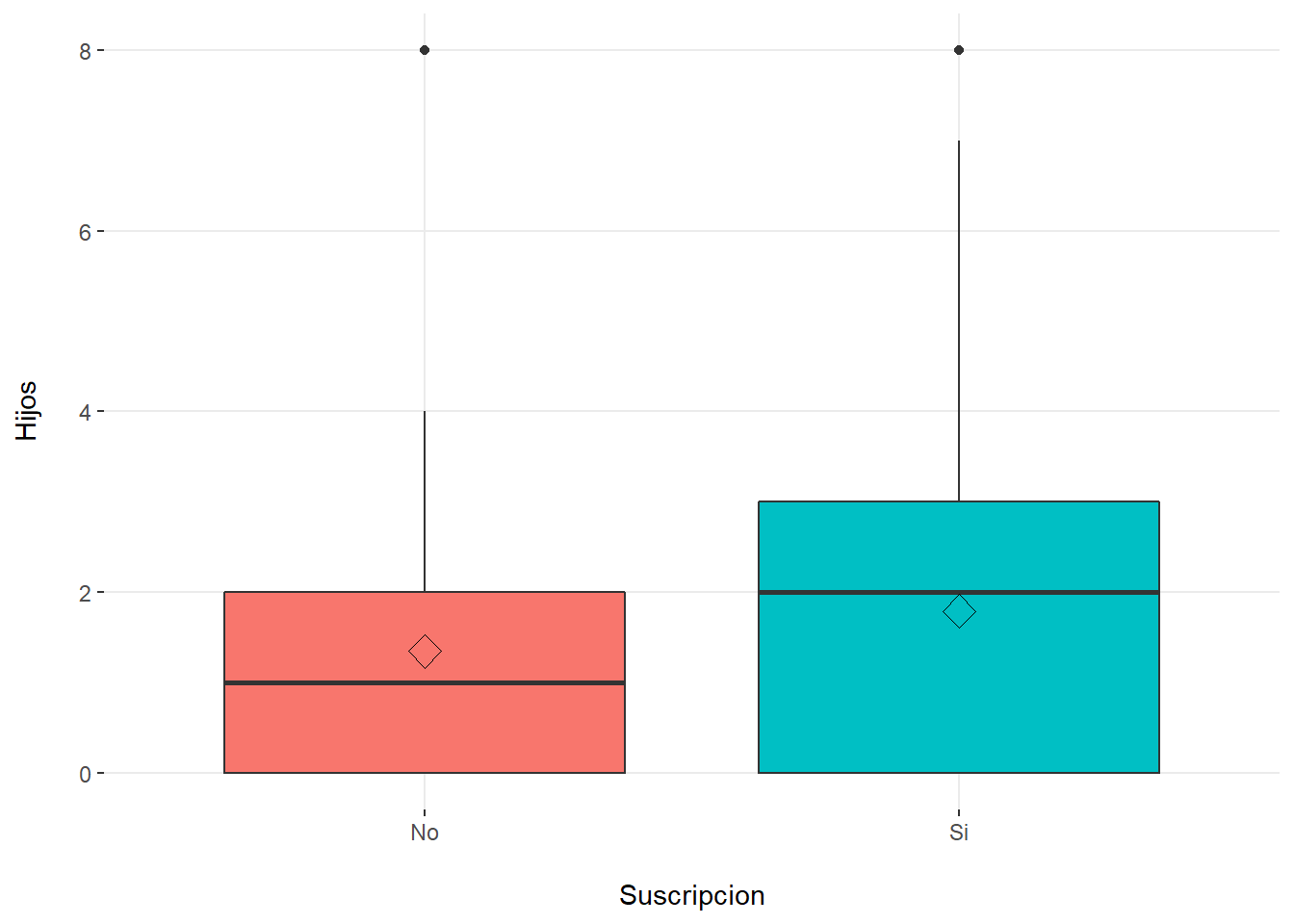
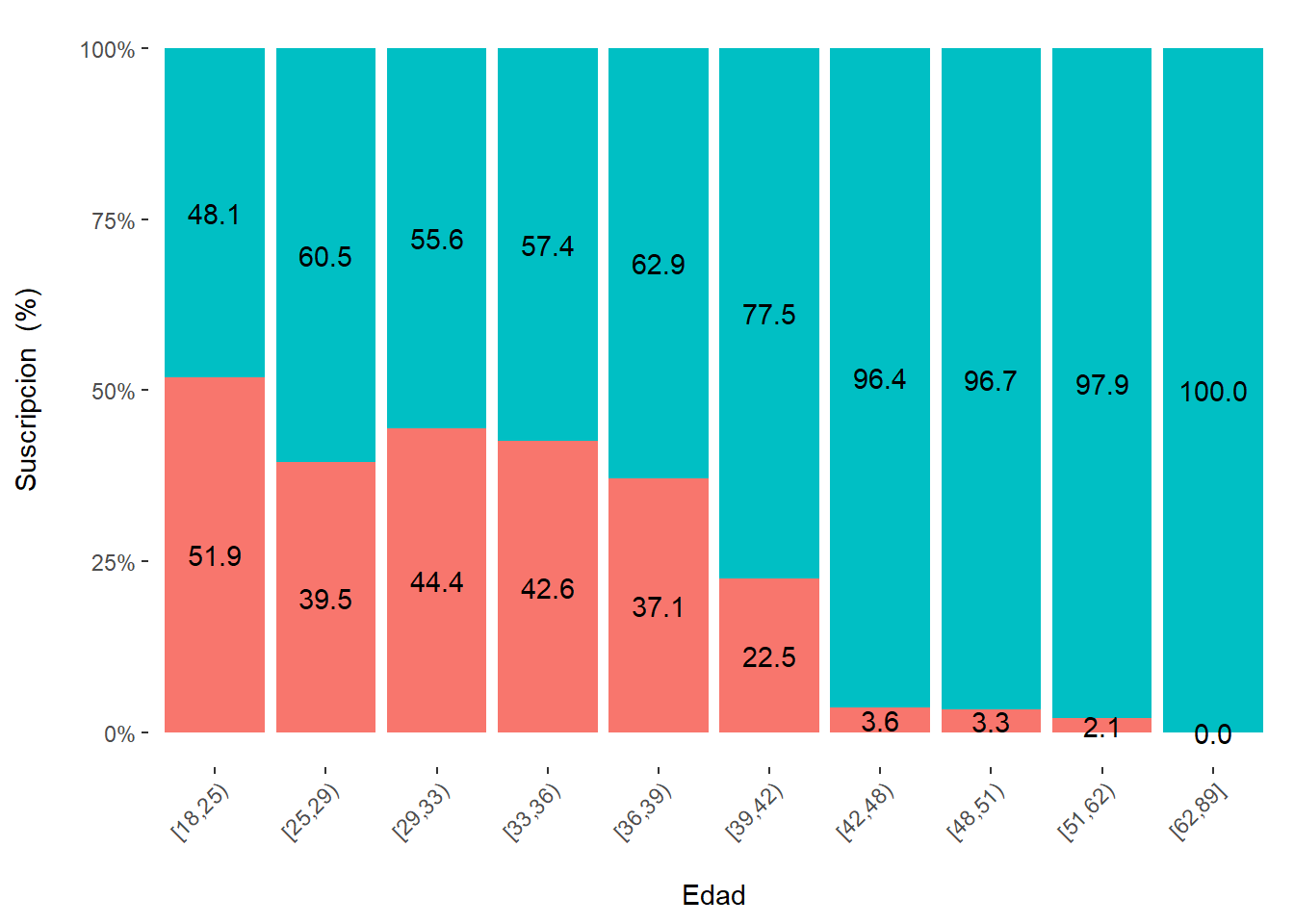
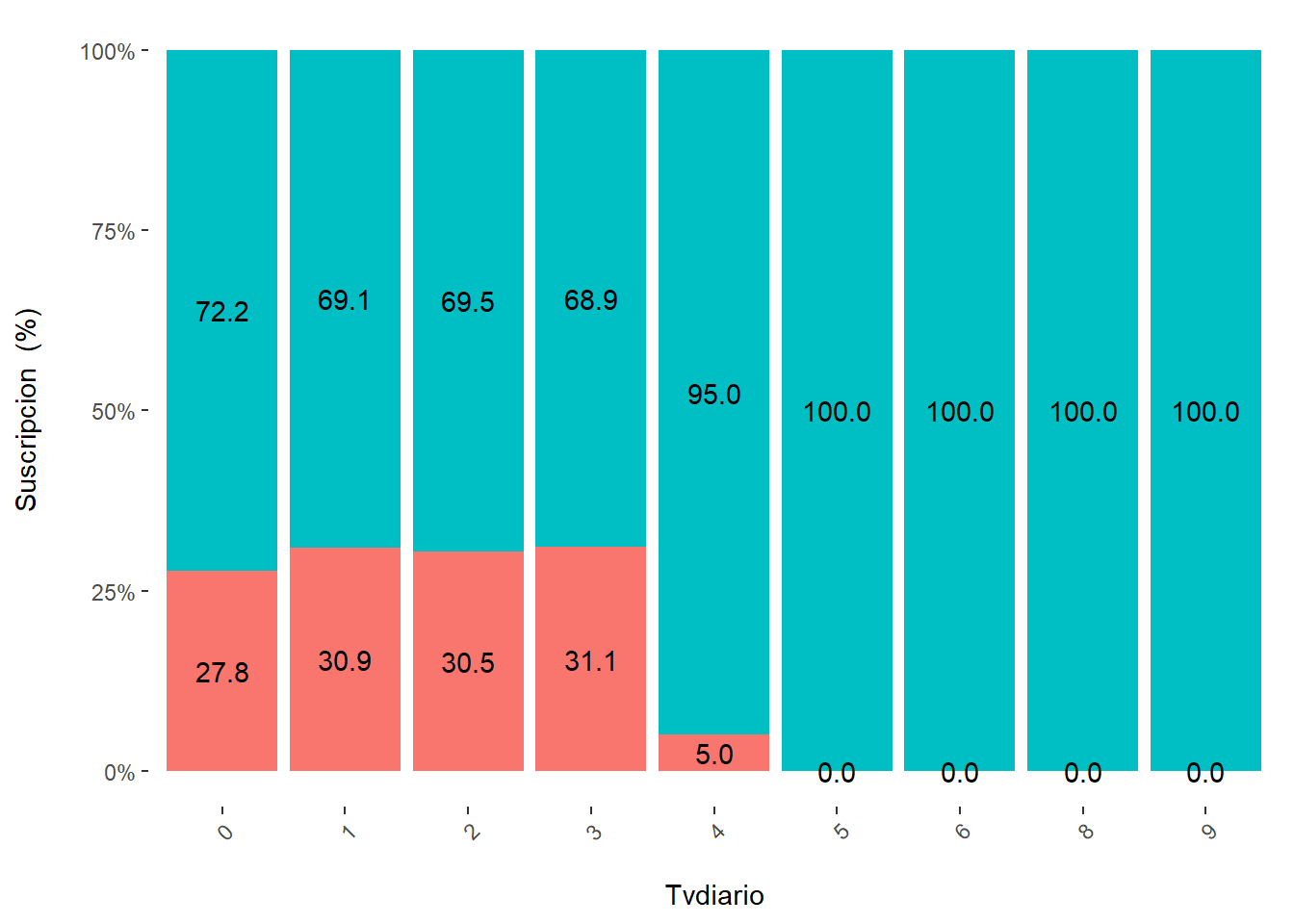
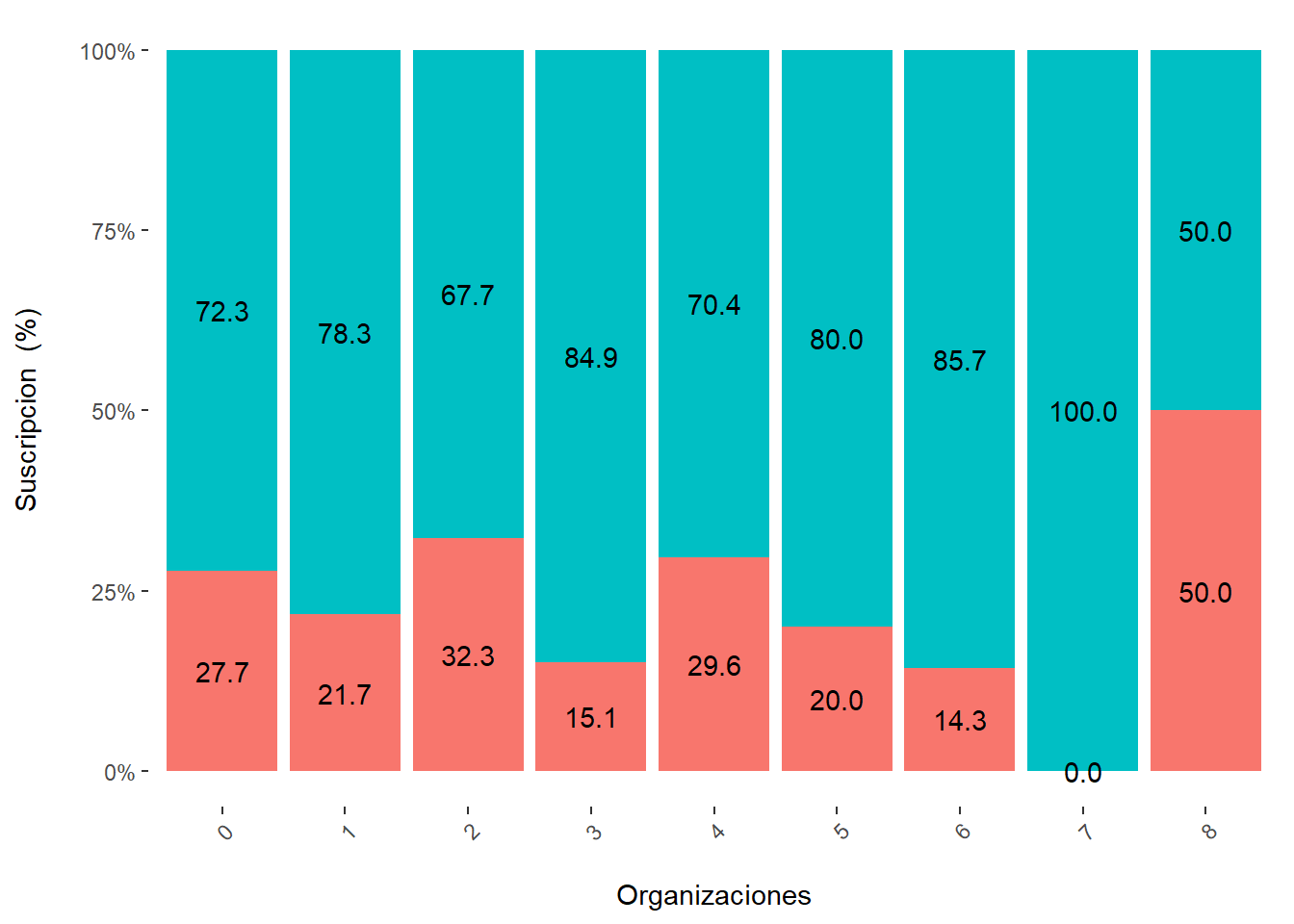
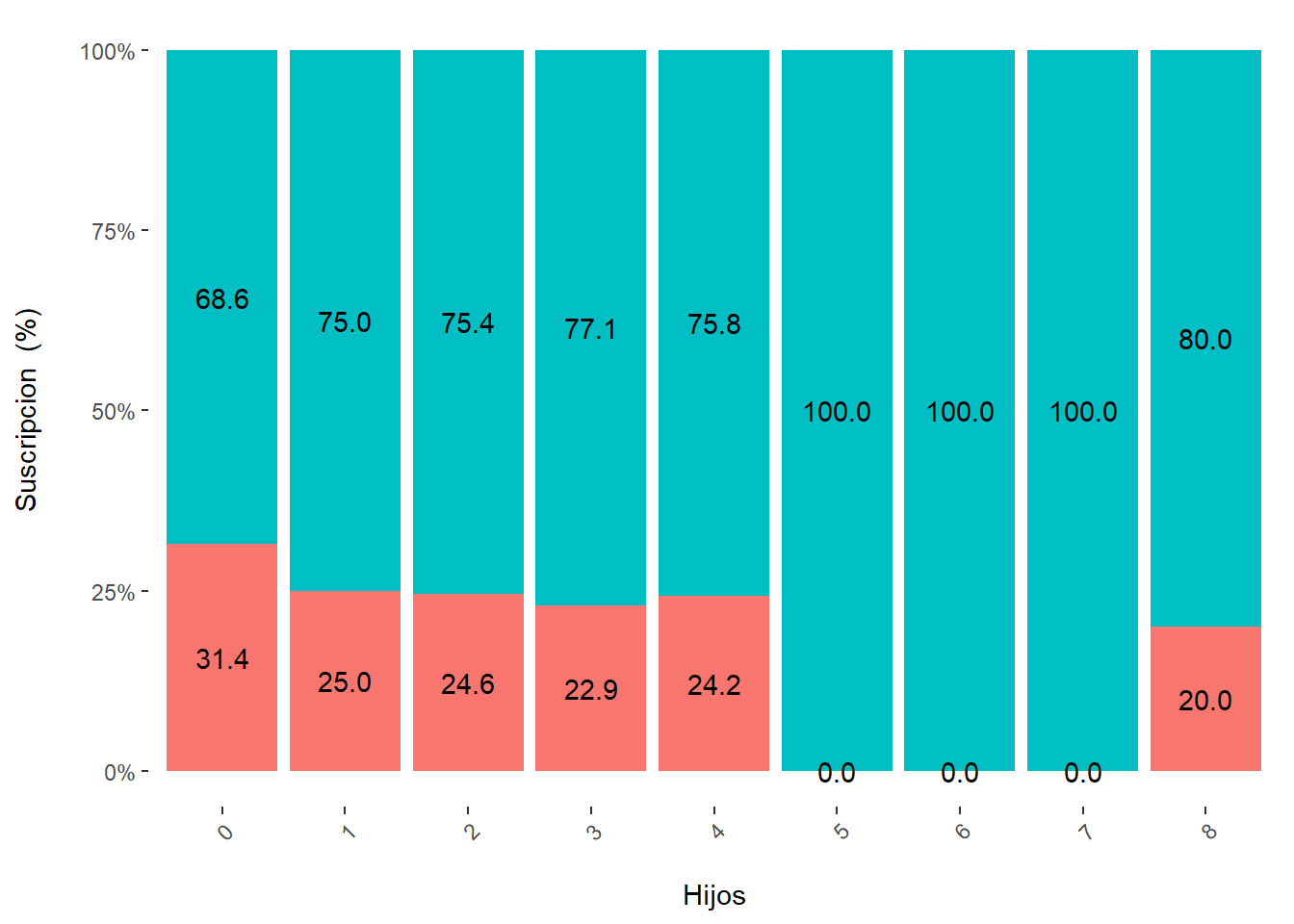
# Gráfico de Barras Apilado en proporción por cada variable predictora vs target
cross_plot(datosd,
input=predictores,
target="Suscripcion",
plot_type = "percentual")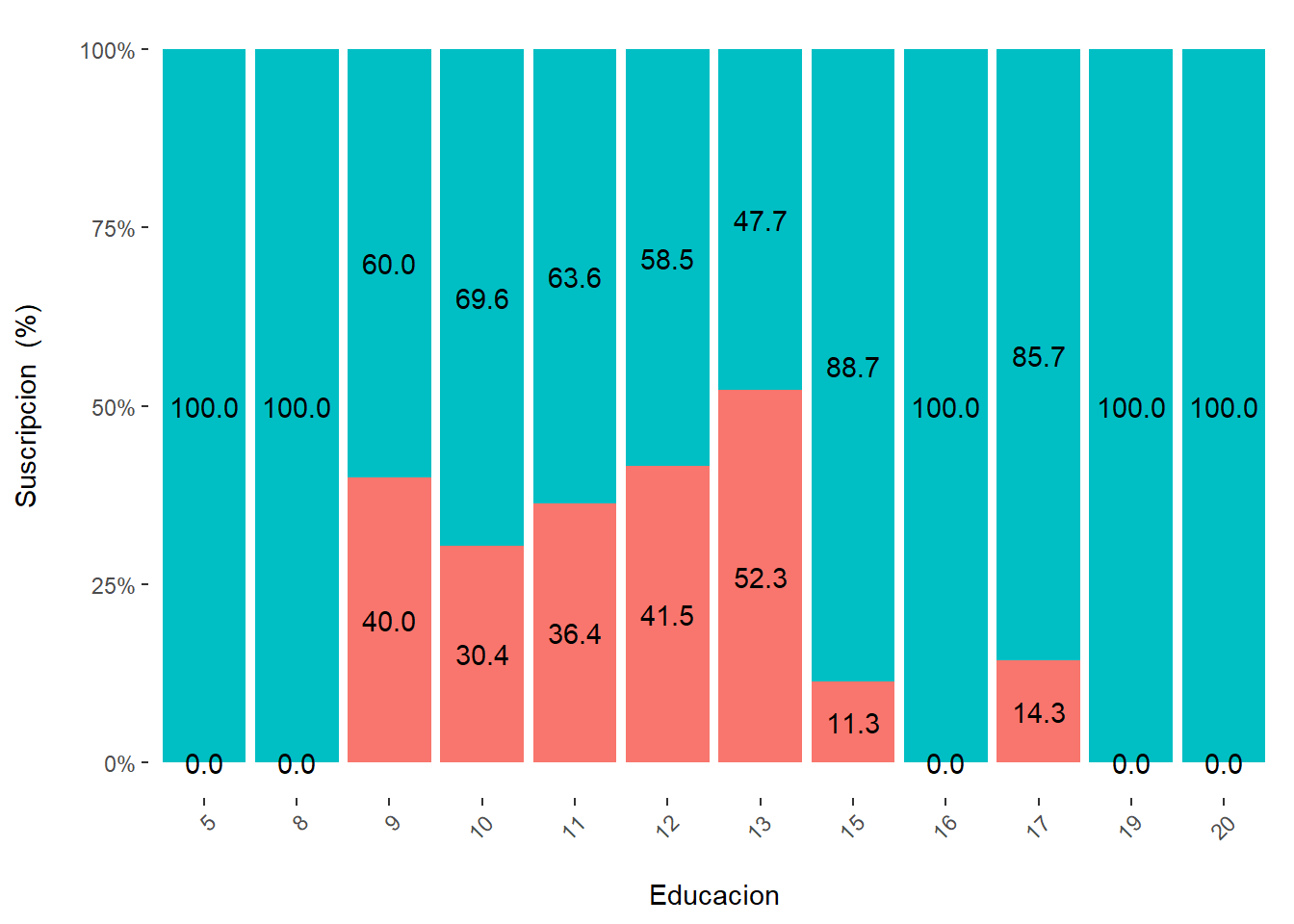
# Media por cada variable predictora vs. target
tapply(Educacion,Suscripcion,mean) No Si
12.3 13.7 tapply(Edad,Suscripcion,mean) No Si
30.5 43.5 tapply(Tvdiario,Suscripcion,mean) No Si
1.95 2.51 tapply(Organizaciones,Suscripcion,mean) No Si
1.42 1.56 tapply(Hijos,Suscripcion,mean) No Si
1.35 1.80 Selección de variables
# Criterio de lambda de Wilks para selección de variables
library(klaR)
greedy.wilks(Suscripcion ~ .,data=datosd)Formula containing included variables:
Suscripcion ~ Edad + Educacion + Tvdiario
<environment: 0x000001f449871a98>
Values calculated in each step of the selection procedure:
vars Wilks.lambda F.statistics.overall
1 Edad 0.830 90.1
2 Educacion 0.700 93.9
3 Tvdiario 0.657 76.3
p.value.overall F.statistics.diff
1 0.00000000000000000014310293096217724937488 90.1
2 0.00000000000000000000000000000000011024379 81.3
3 0.00000000000000000000000000000000000000102 29.0
p.value.diff
1 0.000000000000000000143
2 0.000000000000000000000
3 0.000000116182738985060División de la Muestra y Modelamiento
# Distribución de individuos en el target
prop.table(table(datosd$Suscripcion))
No Si
0.256 0.744 # Selección de muestra de entrenamiento (80%)
library(ggplot2)
library(caret)
set.seed(123)
index <- createDataPartition(datosd$Suscripcion,
p=0.8,
list=FALSE)
tail(index) Resample1
[350,] 437
[351,] 438
[352,] 439
[353,] 440
[354,] 441
[355,] 442training <- datosd[ index, ] # 355 datos
testing <- datosd[-index, ] # 87 datos
# Verificando la estructura de los datos particionados
prop.table(table(datosd$Suscripcion))
No Si
0.256 0.744 prop.table(table(training$Suscripcion)) #en la data de entrenamiento
No Si
0.256 0.744 prop.table(table(testing$Suscripcion))
No Si
0.253 0.747 Estimación de la Función Discriminante Lineal
modelo.training <- lda(Suscripcion ~ Educacion + Edad + Tvdiario,
training)
str(modelo.training)List of 10
$ prior : Named num [1:2] 0.256 0.744
..- attr(*, "names")= chr [1:2] "No" "Si"
$ counts : Named int [1:2] 91 264
..- attr(*, "names")= chr [1:2] "No" "Si"
$ means : num [1:2, 1:3] 12.35 13.66 31.13 44.34 1.92 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:2] "No" "Si"
.. ..$ : chr [1:3] "Educacion" "Edad" "Tvdiario"
$ scaling: num [1:3, 1] 0.3921 0.0656 0.3568
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:3] "Educacion" "Edad" "Tvdiario"
.. ..$ : chr "LD1"
$ lev : chr [1:2] "No" "Si"
$ svd : num 13.2
$ N : int 355
$ call : language lda(formula = Suscripcion ~ Educacion + Edad + Tvdiario, data = training)
$ terms :Classes 'terms', 'formula' language Suscripcion ~ Educacion + Edad + Tvdiario
.. ..- attr(*, "variables")= language list(Suscripcion, Educacion, Edad, Tvdiario)
.. ..- attr(*, "factors")= int [1:4, 1:3] 0 1 0 0 0 0 1 0 0 0 ...
.. .. ..- attr(*, "dimnames")=List of 2
.. .. .. ..$ : chr [1:4] "Suscripcion" "Educacion" "Edad" "Tvdiario"
.. .. .. ..$ : chr [1:3] "Educacion" "Edad" "Tvdiario"
.. ..- attr(*, "term.labels")= chr [1:3] "Educacion" "Edad" "Tvdiario"
.. ..- attr(*, "order")= int [1:3] 1 1 1
.. ..- attr(*, "intercept")= int 1
.. ..- attr(*, "response")= int 1
.. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
.. ..- attr(*, "predvars")= language list(Suscripcion, Educacion, Edad, Tvdiario)
.. ..- attr(*, "dataClasses")= Named chr [1:4] "factor" "numeric" "numeric" "numeric"
.. .. ..- attr(*, "names")= chr [1:4] "Suscripcion" "Educacion" "Edad" "Tvdiario"
$ xlevels: Named list()
- attr(*, "class")= chr "lda"modelo.trainingCall:
lda(Suscripcion ~ Educacion + Edad + Tvdiario, data = training)
Prior probabilities of groups:
No Si
0.256 0.744
Group means:
Educacion Edad Tvdiario
No 12.4 31.1 1.92
Si 13.7 44.3 2.56
Coefficients of linear discriminants:
LD1
Educacion 0.3921
Edad 0.0656
Tvdiario 0.3568# valor de la función discriminante menos el punto de corte
modelo.values <- predict(modelo.training)
modelo.values$x LD1
3 -2.78446
4 -1.67882
6 -1.71412
7 -1.74941
8 -0.96526
9 -1.93470
10 -2.32678
11 -2.32678
12 -1.57792
13 -1.57792
16 -1.57792
17 -2.04059
18 -1.25643
19 -2.65325
20 -2.26117
21 -1.08494
22 -1.08494
24 -1.90439
25 -1.90439
26 -1.51231
28 -0.72816
29 -0.72816
30 -0.01459
33 -1.80349
34 -1.01933
35 -1.01933
36 -1.83879
37 -1.44671
38 -0.27047
39 -0.30577
43 -1.90939
44 -2.12997
45 -0.20487
46 -0.20487
47 -1.41641
48 -0.24017
49 -1.84378
50 -1.05963
51 -1.05963
52 -0.66755
53 -1.24491
54 -0.88813
55 -0.49605
56 -0.88813
57 -0.13927
58 -0.13927
60 -2.13496
62 -0.99402
64 -1.17931
65 -0.82253
68 -1.64198
69 -1.24990
70 -1.64198
71 -0.46574
72 -2.06936
73 -0.10896
74 -1.28520
75 -0.10896
76 -2.32524
77 -1.93316
78 -0.40014
79 -0.40014
80 -1.21960
82 -1.86756
83 -0.29924
85 -1.51078
86 -1.51078
87 -0.33454
88 -1.51078
89 -1.15400
90 -0.76192
91 0.02224
92 0.41432
94 -0.79722
95 0.37902
98 -2.58611
99 -1.44517
100 -0.26894
101 -1.44517
102 -1.48047
103 0.47992
104 0.47992
105 -1.12369
107 0.83670
108 -1.73635
109 -0.20333
111 -1.02279
112 0.90231
114 -0.49451
117 -1.31397
119 -0.95719
120 0.21905
122 0.21905
124 -0.20833
125 -1.60515
126 -0.42891
128 -0.03683
132 -1.24837
134 -0.89158
135 -0.89158
136 0.67673
137 0.67673
140 0.28465
141 -1.89632
142 -1.93162
143 -1.53954
144 -1.53954
145 -1.14746
146 -0.36331
147 -0.36331
150 -0.79068
151 -0.00653
152 -0.00653
155 -0.00653
156 -2.35900
157 -0.82598
158 0.35025
159 -1.25336
160 -0.86128
161 -0.46920
162 -0.07712
163 0.70704
164 0.48645
165 0.09438
166 -0.29770
167 -0.29770
168 0.09438
169 0.09438
171 -0.76038
172 -0.76038
173 0.41586
174 -0.04682
175 0.34526
176 -0.58888
178 -1.40834
179 -1.40834
180 -1.40834
181 -0.23210
183 0.15998
185 0.51676
186 0.51676
187 0.51676
188 -1.05156
190 0.48146
191 -0.69478
192 0.48146
193 1.23032
194 0.01878
196 -1.73481
197 -1.34273
199 -0.16650
200 -1.77011
201 -0.98595
202 0.58236
203 0.54706
204 0.54706
206 1.29592
207 -1.63391
208 -0.06560
209 -0.10089
210 0.29118
211 0.25589
212 0.64796
215 -0.17149
216 -0.17149
217 -0.56357
218 -0.20679
219 -1.21153
220 -0.03529
221 -0.03529
222 0.74887
223 0.35679
224 0.32149
225 0.32149
227 -0.10589
228 -0.49797
229 -0.14119
230 -0.75385
231 -0.75385
232 0.42239
234 0.42239
235 -0.75385
236 -0.39707
237 -0.82444
238 1.13595
239 1.13595
240 -0.04029
241 1.45743
243 0.88007
244 -0.68824
245 0.45269
246 -0.72354
248 0.45269
250 -1.15092
251 -0.36676
253 -0.43736
254 1.87982
255 0.16152
256 0.55360
257 -0.65794
258 -0.65794
259 -0.26586
260 -0.26586
261 0.51830
262 0.51830
263 0.51830
264 -0.30116
265 -0.30116
266 0.87508
267 0.41240
268 1.94542
269 1.83952
270 0.61920
272 -0.59234
273 -0.59234
274 -0.20026
275 0.97598
276 -0.23556
277 -0.23556
278 0.12122
279 0.12122
280 1.68954
281 -0.88352
282 -0.49144
283 0.29272
284 0.29272
285 0.64950
286 -0.91881
287 -0.13466
288 0.64950
289 1.00628
290 1.00628
291 1.00628
292 0.18683
295 0.35832
296 0.75040
297 -2.02945
298 -0.85321
299 -0.46113
303 1.07189
304 1.17279
305 -0.03875
306 -0.03875
307 -0.32993
309 0.59043
311 0.59043
312 0.55513
313 0.94721
314 0.94721
315 -0.26432
316 0.91191
317 1.30399
318 2.87231
323 0.41394
325 0.62074
326 -0.19872
328 1.36959
331 0.51484
332 1.69108
334 -0.48990
336 -0.09782
337 -0.09782
338 0.68634
339 1.47050
340 -0.13312
341 0.22366
343 0.22366
345 0.75194
347 0.75194
348 1.10872
349 1.10872
350 1.50080
351 1.50080
352 1.89288
354 0.64605
355 -0.71547
356 1.53110
358 1.92318
359 0.91845
360 1.27523
361 0.06369
362 1.63201
363 1.63201
364 -2.32408
365 0.42047
367 -0.79106
368 0.77725
369 -0.58427
370 -0.65487
371 0.84285
373 1.72791
374 2.08469
375 -1.23722
376 0.61728
378 0.35641
379 0.74848
380 1.10526
381 1.49734
382 0.45731
383 0.02993
384 0.42201
385 2.38240
386 -1.04541
387 0.52291
388 2.41271
389 3.16157
390 3.83983
391 1.40797
392 -0.19565
393 0.58851
395 0.94529
396 0.51792
397 0.65411
398 0.65411
399 1.83035
400 0.61882
401 2.18713
402 2.47332
403 1.93125
404 -0.84860
405 0.32764
406 0.71972
407 2.25273
408 3.00159
409 -0.13504
410 0.42854
411 -0.03414
413 1.49888
414 0.88622
415 0.06677
417 1.24300
418 2.02716
419 1.17241
420 1.27331
421 1.98687
422 1.04773
423 1.76129
424 1.57102
425 1.53572
426 2.42078
427 1.31014
428 1.27484
429 2.02370
430 2.58728
431 0.19951
432 0.87777
433 2.97437
434 2.57729
435 0.82369
437 1.24108
438 3.84444
439 1.11142
440 1.30822
441 3.65570
442 3.31045ldahist(data = modelo.values$x[,1], g=training$Suscripcion)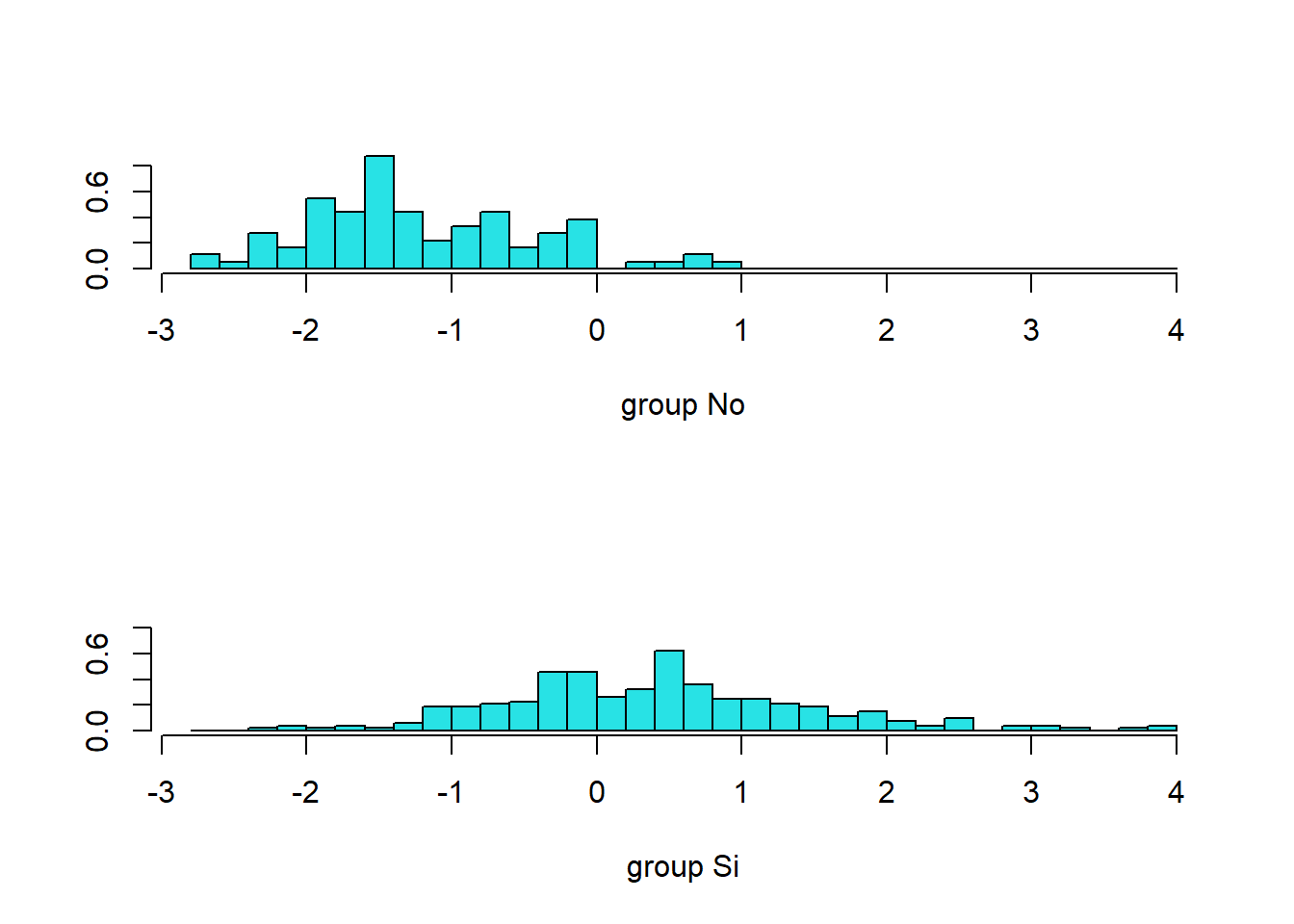
modelo.values$posterior # predicción de la probabilidad No Si
3 0.941575 0.0584
4 0.731709 0.2683
6 0.742696 0.2573
7 0.753384 0.2466
8 0.464259 0.5357
9 0.804467 0.1955
10 0.885383 0.1146
11 0.885383 0.1146
12 0.698715 0.3013
13 0.698715 0.3013
16 0.698715 0.3013
17 0.829855 0.1701
18 0.580455 0.4195
19 0.928839 0.0712
20 0.874244 0.1258
21 0.512269 0.4877
22 0.512269 0.4877
24 0.796694 0.2033
25 0.796694 0.2033
26 0.676072 0.3239
28 0.371877 0.6281
29 0.371877 0.6281
30 0.158331 0.8417
33 0.769171 0.2308
34 0.485923 0.5141
35 0.485923 0.5141
36 0.779086 0.2209
37 0.652574 0.3474
38 0.221050 0.7790
39 0.230970 0.7690
43 0.797991 0.2020
44 0.849182 0.1508
45 0.203434 0.7966
46 0.203434 0.7966
47 0.641454 0.3585
48 0.212780 0.7872
49 0.780464 0.2195
50 0.502105 0.4979
51 0.502105 0.4979
52 0.349427 0.6506
53 0.575939 0.4241
54 0.433610 0.5664
55 0.289644 0.7104
56 0.433610 0.5664
57 0.186885 0.8131
58 0.186885 0.8131
60 0.850207 0.1498
62 0.475772 0.5242
64 0.550011 0.4500
65 0.407926 0.5921
68 0.719932 0.2801
69 0.577897 0.4221
70 0.719932 0.2801
71 0.279729 0.7203
72 0.836282 0.1637
73 0.179599 0.8204
74 0.591668 0.4083
75 0.179599 0.8204
76 0.885132 0.1149
77 0.804078 0.1959
78 0.258992 0.7410
79 0.258992 0.7410
80 0.565977 0.4340
82 0.786939 0.2131
83 0.229111 0.7709
85 0.675531 0.3245
86 0.675531 0.3245
87 0.239281 0.7607
88 0.675531 0.3245
89 0.539927 0.4601
90 0.384633 0.6154
91 0.150602 0.8494
92 0.086285 0.9137
94 0.398142 0.6019
95 0.090863 0.9091
98 0.921371 0.0786
99 0.652014 0.3480
100 0.220625 0.7794
101 0.652014 0.3480
102 0.664769 0.3352
103 0.078329 0.9217
104 0.078329 0.9217
105 0.527810 0.4722
107 0.045715 0.9543
108 0.749464 0.2505
109 0.203034 0.7970
111 0.487311 0.5127
112 0.041331 0.9587
114 0.289136 0.7109
117 0.602786 0.3972
119 0.461035 0.5390
120 0.114446 0.8856
122 0.114446 0.8856
124 0.204336 0.7957
125 0.707845 0.2922
126 0.267961 0.7320
128 0.163151 0.8368
132 0.577295 0.4227
134 0.434974 0.5650
135 0.434974 0.5650
136 0.058332 0.9417
137 0.058332 0.9417
140 0.104190 0.8958
141 0.794586 0.2054
142 0.803688 0.1963
143 0.685579 0.3144
144 0.685579 0.3144
145 0.537319 0.4627
146 0.247796 0.7522
147 0.247796 0.7522
150 0.395630 0.6044
151 0.156611 0.8434
152 0.156611 0.8434
155 0.156611 0.8434
156 0.890533 0.1095
157 0.409268 0.5907
158 0.094754 0.9052
159 0.579252 0.4207
160 0.423048 0.5770
161 0.280849 0.7192
162 0.172184 0.8278
163 0.055715 0.9443
164 0.077575 0.9224
165 0.136368 0.8636
166 0.228675 0.7713
167 0.228675 0.7713
168 0.136368 0.8636
169 0.136368 0.8636
171 0.384048 0.6160
172 0.384048 0.6160
173 0.086091 0.9139
174 0.165354 0.8346
175 0.095444 0.9046
176 0.321267 0.6787
178 0.638467 0.3615
179 0.638467 0.3615
180 0.638467 0.3615
181 0.210616 0.7894
183 0.124423 0.8756
185 0.074161 0.9258
186 0.074161 0.9258
187 0.074161 0.9258
188 0.498863 0.5011
190 0.078151 0.9218
191 0.359437 0.6406
192 0.078151 0.9218
193 0.024820 0.9752
194 0.151314 0.8487
196 0.749000 0.2510
197 0.613798 0.3862
199 0.193625 0.8064
200 0.759511 0.2405
201 0.472539 0.5275
202 0.067241 0.9328
203 0.070887 0.9291
204 0.070887 0.9291
206 0.022392 0.9776
207 0.717311 0.2827
208 0.169560 0.8304
209 0.177696 0.8223
210 0.103214 0.8968
211 0.108583 0.8914
212 0.060924 0.9391
215 0.194881 0.8051
216 0.194881 0.8051
217 0.312464 0.6875
218 0.203934 0.7961
219 0.562789 0.4372
220 0.162813 0.8372
221 0.162813 0.8372
222 0.052282 0.9477
223 0.093857 0.9061
224 0.098793 0.9012
225 0.098793 0.9012
227 0.178872 0.8211
228 0.290279 0.7097
229 0.187354 0.8126
230 0.381569 0.6184
231 0.381569 0.6184
232 0.085268 0.9147
234 0.085268 0.9147
235 0.381569 0.6184
236 0.258045 0.7420
237 0.408671 0.5913
238 0.028767 0.9712
239 0.028767 0.9712
240 0.163910 0.8361
241 0.017363 0.9826
243 0.042770 0.9572
244 0.357024 0.6430
245 0.081546 0.9185
246 0.370147 0.6299
248 0.081546 0.9185
250 0.538699 0.4613
251 0.248833 0.7512
253 0.270633 0.7294
254 0.008884 0.9911
255 0.124154 0.8758
256 0.070199 0.9298
257 0.345926 0.6541
258 0.345926 0.6541
259 0.219776 0.7802
260 0.219776 0.7802
261 0.073992 0.9260
262 0.073992 0.9260
263 0.073992 0.9260
264 0.229656 0.7703
265 0.229656 0.7703
266 0.043100 0.9569
267 0.086529 0.9135
268 0.008002 0.9920
269 0.009473 0.9905
270 0.063623 0.9364
272 0.322479 0.6775
273 0.322479 0.6775
274 0.202236 0.7978
275 0.036887 0.9631
276 0.211541 0.7885
277 0.211541 0.7885
278 0.131367 0.8686
279 0.131367 0.8686
280 0.012023 0.9880
281 0.431791 0.5682
282 0.288121 0.7119
283 0.102986 0.8970
284 0.102986 0.8970
285 0.060783 0.9392
286 0.445756 0.5542
287 0.185762 0.8142
288 0.060783 0.9392
289 0.035196 0.9648
290 0.035196 0.9648
291 0.035196 0.9648
292 0.119799 0.8802
295 0.093648 0.9064
296 0.052160 0.9478
297 0.827311 0.1727
298 0.419886 0.5801
299 0.278238 0.7218
303 0.031786 0.9682
304 0.027158 0.9728
305 0.163572 0.8364
306 0.163572 0.8364
307 0.237935 0.7621
309 0.066432 0.9336
311 0.066432 0.9336
312 0.070037 0.9300
313 0.038565 0.9614
314 0.038565 0.9614
315 0.219353 0.7806
316 0.040723 0.9593
317 0.022110 0.9779
318 0.001816 0.9982
323 0.086333 0.9137
325 0.063475 0.9365
326 0.201837 0.7982
328 0.019942 0.9801
331 0.074373 0.9256
332 0.011994 0.9880
334 0.287615 0.7124
336 0.176975 0.8230
337 0.176975 0.8230
338 0.057490 0.9425
339 0.017009 0.9830
340 0.185388 0.8146
341 0.113697 0.8863
343 0.113697 0.8863
345 0.052038 0.9480
347 0.052038 0.9480
348 0.030015 0.9700
349 0.030015 0.9700
350 0.016213 0.9838
351 0.016213 0.9838
352 0.008701 0.9913
354 0.061100 0.9389
355 0.367129 0.6329
356 0.015455 0.9845
358 0.008291 0.9917
359 0.040315 0.9597
360 0.023132 0.9769
361 0.142280 0.8577
362 0.013172 0.9868
363 0.013172 0.9868
364 0.884943 0.1151
365 0.085509 0.9145
367 0.395776 0.6042
368 0.050068 0.9499
369 0.319653 0.6803
370 0.344809 0.6552
371 0.045286 0.9547
373 0.011312 0.9887
374 0.006408 0.9936
375 0.572919 0.4271
376 0.063806 0.9362
378 0.093910 0.9061
379 0.052313 0.9477
380 0.030177 0.9698
381 0.016302 0.9837
382 0.080993 0.9190
383 0.149029 0.8510
384 0.085316 0.9147
385 0.003982 0.9960
386 0.496393 0.5036
387 0.073486 0.9265
388 0.003793 0.9962
389 0.001142 0.9989
390 0.000384 0.9996
391 0.018772 0.9812
392 0.201042 0.7990
393 0.066624 0.9334
395 0.038679 0.9613
396 0.074034 0.9260
397 0.060361 0.9396
398 0.060361 0.9396
399 0.009612 0.9904
400 0.063659 0.9363
401 0.005441 0.9946
402 0.003442 0.9966
403 0.008185 0.9918
404 0.418082 0.5819
405 0.097917 0.9021
406 0.054652 0.9453
407 0.004899 0.9951
408 0.001476 0.9985
409 0.185855 0.8141
410 0.084501 0.9155
411 0.162560 0.8374
413 0.016263 0.9837
414 0.042367 0.9576
415 0.141678 0.8583
417 0.024331 0.9757
418 0.007024 0.9930
419 0.027175 0.9728
420 0.023202 0.9768
421 0.007491 0.9925
422 0.033003 0.9670
423 0.010728 0.9893
424 0.014509 0.9855
425 0.015342 0.9847
426 0.003744 0.9963
427 0.021898 0.9781
428 0.023146 0.9769
429 0.007063 0.9929
430 0.002868 0.9971
431 0.117667 0.8823
432 0.042921 0.9571
433 0.001542 0.9985
434 0.002914 0.9971
435 0.046636 0.9534
437 0.024405 0.9756
438 0.000381 0.9996
439 0.029889 0.9701
440 0.021964 0.9780
441 0.000516 0.9995
442 0.000899 0.9991modelo.values$class # predicción de la clase [1] No No No No Si No No No No No No No No No No No No No No No Si Si Si No Si
[26] Si No No Si Si No No Si Si No Si No No No Si No Si Si Si Si Si No Si No Si
[51] No No No Si No Si No Si No No Si Si No No Si No No Si No No Si Si Si Si Si
[76] No No Si No No Si Si No Si No Si Si Si Si No Si Si Si Si No Si Si No Si Si
[101] Si Si Si No No No No No Si Si Si Si Si Si No Si Si No Si Si Si Si Si Si Si
[126] Si Si Si Si Si Si Si Si Si No No No Si Si Si Si Si Si Si Si Si Si Si No No
[151] Si No Si Si Si Si Si No Si Si Si Si Si Si Si Si Si No Si Si Si Si Si Si Si
[176] Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si No Si Si Si Si Si Si
[201] Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si
[226] Si Si Si Si Si Si Si Si Si Si Si No Si Si Si Si Si Si Si Si Si Si Si Si Si
[251] Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si
[276] Si Si Si Si Si Si Si Si No Si Si Si Si Si Si Si Si No Si Si Si Si Si Si Si
[301] Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si
[326] Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si Si
[351] Si Si Si Si Si
Levels: No SiClasificación y probabilidades de las observaciones
Probabilidad predicha
proba.pred <- predict(modelo.training,testing[,-6])$posterior
# Se está retirando la columna suscripcion
head(proba.pred,10) No Si
1 0.771 0.2290
2 0.843 0.1568
5 0.606 0.3941
14 0.699 0.3013
15 0.813 0.1868
23 0.359 0.6413
27 0.372 0.6281
31 0.917 0.0827
32 0.862 0.1378
40 0.231 0.7690testing$proba.pred <- proba.pred[,2]
head(testing$proba.pred,10) [1] 0.2290 0.1568 0.3941 0.3013 0.1868 0.6413 0.6281 0.0827 0.1378 0.7690Clase predicha (punto de corte, umbral es 0.5)
testing$clase.pred <- predict(modelo.training, testing[, -6])$class
head(testing$clase.pred, 10) [1] No No No No No Si Si No No Si
Levels: No Si# Almacenamiento de datos con clase y probabilidad predecida
# write.csv(testing,"testing-suscripcion-adl-scores.csv")
ggplot(testing) + aes(x = proba.pred,
color = Suscripcion,
fill = Suscripcion) +
geom_histogram(alpha = 0.25)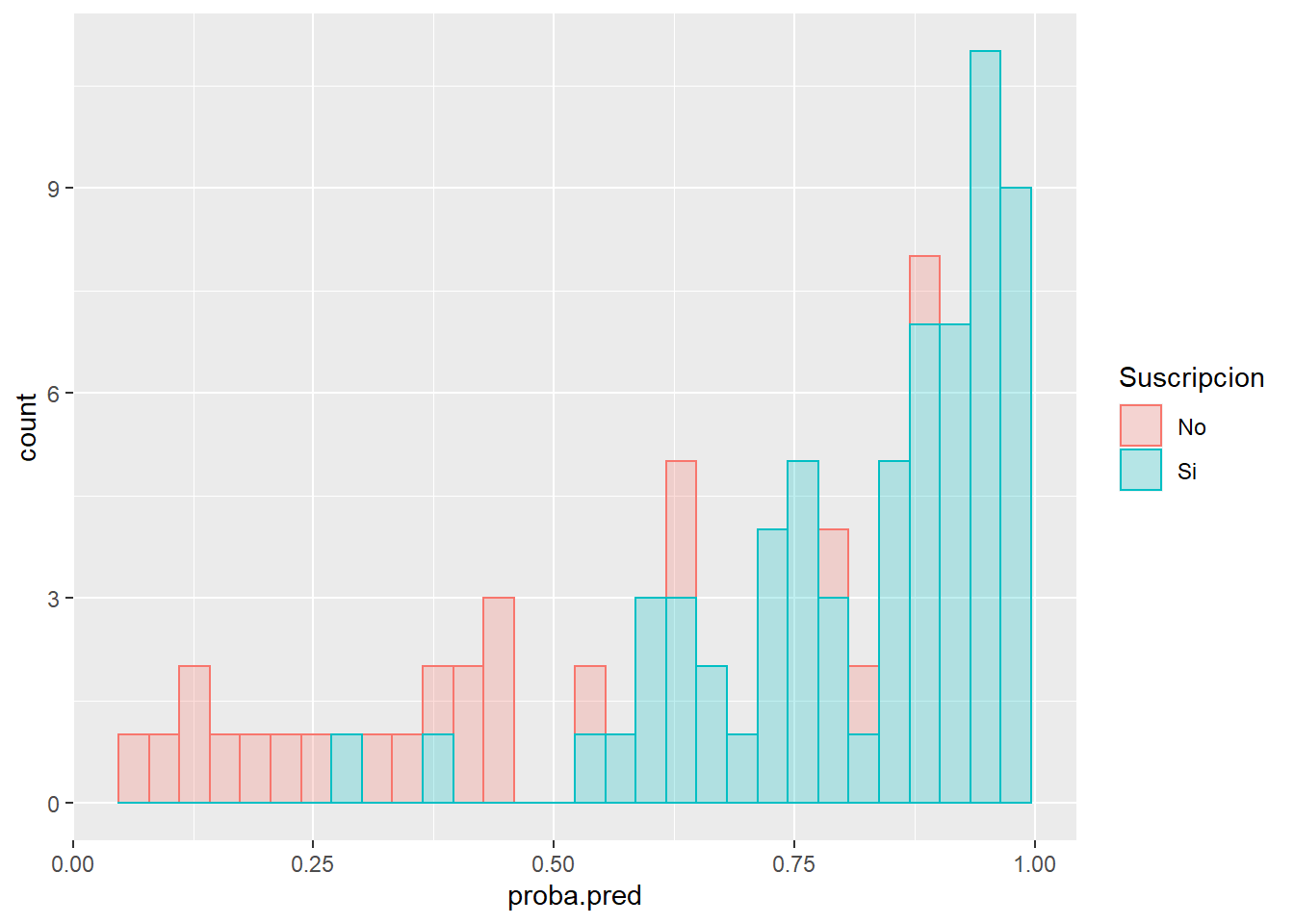
ggplot(testing) + aes(x = proba.pred,
color = Suscripcion,
fill = Suscripcion) +
geom_density(alpha = 0.25)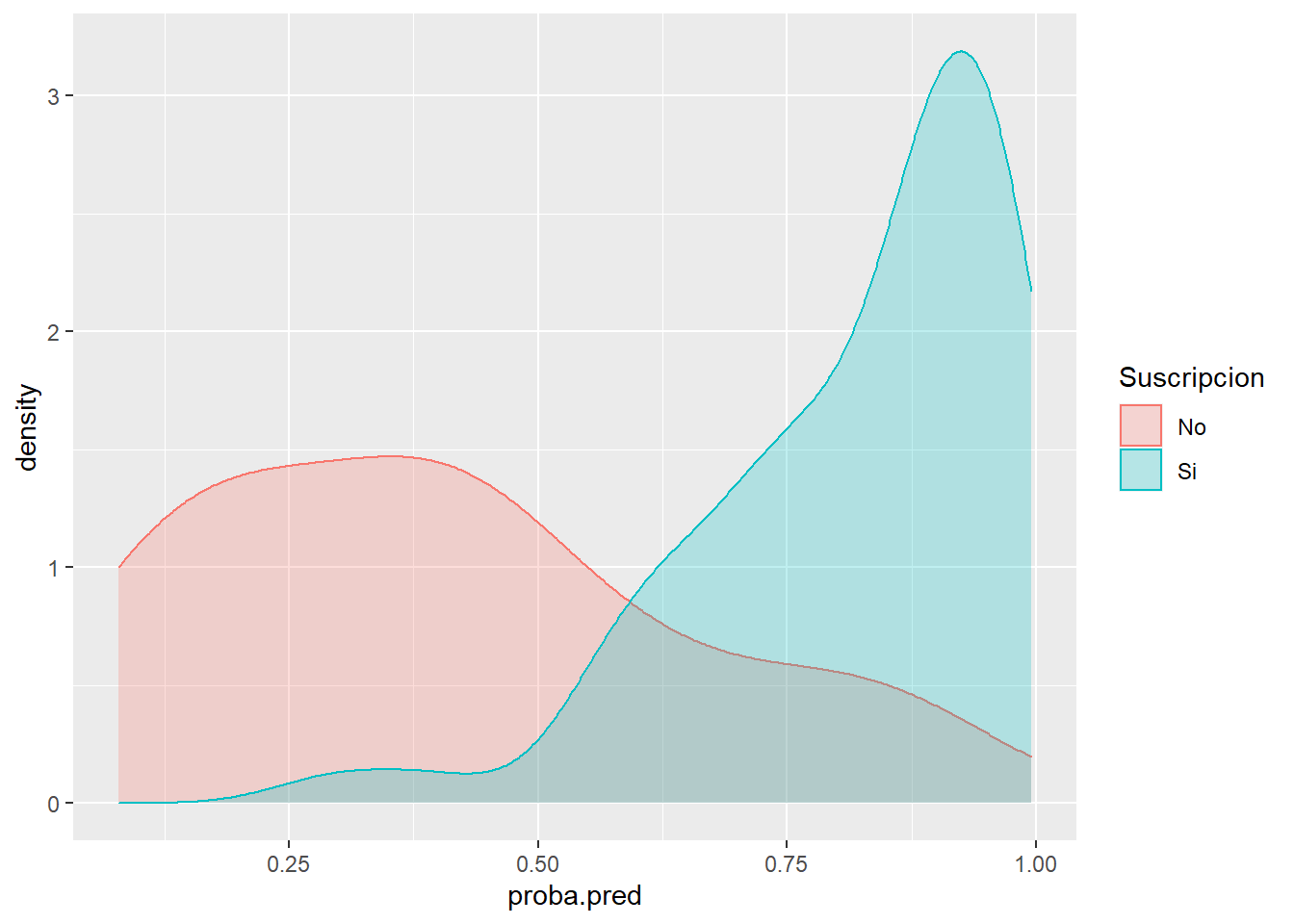
Modelamiento con el paquete caret
# Relación de modelos en caret
library(caret) #Classification and Regression Training
names(getModelInfo()) [1] "ada" "AdaBag" "AdaBoost.M1"
[4] "adaboost" "amdai" "ANFIS"
[7] "avNNet" "awnb" "awtan"
[10] "bag" "bagEarth" "bagEarthGCV"
[13] "bagFDA" "bagFDAGCV" "bam"
[16] "bartMachine" "bayesglm" "binda"
[19] "blackboost" "blasso" "blassoAveraged"
[22] "bridge" "brnn" "BstLm"
[25] "bstSm" "bstTree" "C5.0"
[28] "C5.0Cost" "C5.0Rules" "C5.0Tree"
[31] "cforest" "chaid" "CSimca"
[34] "ctree" "ctree2" "cubist"
[37] "dda" "deepboost" "DENFIS"
[40] "dnn" "dwdLinear" "dwdPoly"
[43] "dwdRadial" "earth" "elm"
[46] "enet" "evtree" "extraTrees"
[49] "fda" "FH.GBML" "FIR.DM"
[52] "foba" "FRBCS.CHI" "FRBCS.W"
[55] "FS.HGD" "gam" "gamboost"
[58] "gamLoess" "gamSpline" "gaussprLinear"
[61] "gaussprPoly" "gaussprRadial" "gbm_h2o"
[64] "gbm" "gcvEarth" "GFS.FR.MOGUL"
[67] "GFS.LT.RS" "GFS.THRIFT" "glm.nb"
[70] "glm" "glmboost" "glmnet_h2o"
[73] "glmnet" "glmStepAIC" "gpls"
[76] "hda" "hdda" "hdrda"
[79] "HYFIS" "icr" "J48"
[82] "JRip" "kernelpls" "kknn"
[85] "knn" "krlsPoly" "krlsRadial"
[88] "lars" "lars2" "lasso"
[91] "lda" "lda2" "leapBackward"
[94] "leapForward" "leapSeq" "Linda"
[97] "lm" "lmStepAIC" "LMT"
[100] "loclda" "logicBag" "LogitBoost"
[103] "logreg" "lssvmLinear" "lssvmPoly"
[106] "lssvmRadial" "lvq" "M5"
[109] "M5Rules" "manb" "mda"
[112] "Mlda" "mlp" "mlpKerasDecay"
[115] "mlpKerasDecayCost" "mlpKerasDropout" "mlpKerasDropoutCost"
[118] "mlpML" "mlpSGD" "mlpWeightDecay"
[121] "mlpWeightDecayML" "monmlp" "msaenet"
[124] "multinom" "mxnet" "mxnetAdam"
[127] "naive_bayes" "nb" "nbDiscrete"
[130] "nbSearch" "neuralnet" "nnet"
[133] "nnls" "nodeHarvest" "null"
[136] "OneR" "ordinalNet" "ordinalRF"
[139] "ORFlog" "ORFpls" "ORFridge"
[142] "ORFsvm" "ownn" "pam"
[145] "parRF" "PART" "partDSA"
[148] "pcaNNet" "pcr" "pda"
[151] "pda2" "penalized" "PenalizedLDA"
[154] "plr" "pls" "plsRglm"
[157] "polr" "ppr" "pre"
[160] "PRIM" "protoclass" "qda"
[163] "QdaCov" "qrf" "qrnn"
[166] "randomGLM" "ranger" "rbf"
[169] "rbfDDA" "Rborist" "rda"
[172] "regLogistic" "relaxo" "rf"
[175] "rFerns" "RFlda" "rfRules"
[178] "ridge" "rlda" "rlm"
[181] "rmda" "rocc" "rotationForest"
[184] "rotationForestCp" "rpart" "rpart1SE"
[187] "rpart2" "rpartCost" "rpartScore"
[190] "rqlasso" "rqnc" "RRF"
[193] "RRFglobal" "rrlda" "RSimca"
[196] "rvmLinear" "rvmPoly" "rvmRadial"
[199] "SBC" "sda" "sdwd"
[202] "simpls" "SLAVE" "slda"
[205] "smda" "snn" "sparseLDA"
[208] "spikeslab" "spls" "stepLDA"
[211] "stepQDA" "superpc" "svmBoundrangeString"
[214] "svmExpoString" "svmLinear" "svmLinear2"
[217] "svmLinear3" "svmLinearWeights" "svmLinearWeights2"
[220] "svmPoly" "svmRadial" "svmRadialCost"
[223] "svmRadialSigma" "svmRadialWeights" "svmSpectrumString"
[226] "tan" "tanSearch" "treebag"
[229] "vbmpRadial" "vglmAdjCat" "vglmContRatio"
[232] "vglmCumulative" "widekernelpls" "WM"
[235] "wsrf" "xgbDART" "xgbLinear"
[238] "xgbTree" "xyf" # Relación de hiperparámetros a ajustar de un modelo
modelLookup(model="rpart") model parameter label forReg forClass probModel
1 rpart cp Complexity Parameter TRUE TRUE TRUEmodelLookup(model="xgbTree") model parameter label forReg forClass
1 xgbTree nrounds # Boosting Iterations TRUE TRUE
2 xgbTree max_depth Max Tree Depth TRUE TRUE
3 xgbTree eta Shrinkage TRUE TRUE
4 xgbTree gamma Minimum Loss Reduction TRUE TRUE
5 xgbTree colsample_bytree Subsample Ratio of Columns TRUE TRUE
6 xgbTree min_child_weight Minimum Sum of Instance Weight TRUE TRUE
7 xgbTree subsample Subsample Percentage TRUE TRUE
probModel
1 TRUE
2 TRUE
3 TRUE
4 TRUE
5 TRUE
6 TRUE
7 TRUEmodelLookup(model='lda') model parameter label forReg forClass probModel
1 lda parameter parameter FALSE TRUE TRUE# Aplicando el modelo con Validación Cruzada
RNGkind(sample.kind = "Rounding")
set.seed(123)
ctrl <- trainControl(method="cv", number = 10)
# Contruye 11 modelos: 10 para validación cruzada y un modelo para todos los datos
modelo_lda <- train(Suscripcion ~ Educacion + Edad + Tvdiario,
data = training,
method = "lda",
trControl = ctrl,
tuneLength = 5,
metric="Accuracy")
modelo_ldaLinear Discriminant Analysis
355 samples
3 predictor
2 classes: 'No', 'Si'
No pre-processing
Resampling: Cross-Validated (10 fold)
Summary of sample sizes: 320, 319, 320, 320, 319, 320, ...
Resampling results:
Accuracy Kappa
0.843 0.569# Se probó con el 90% de la data de entrenamiento
355*0.9[1] 320modelo_lda$finalModelCall:
lda(x, grouping = y)
Prior probabilities of groups:
No Si
0.256 0.744
Group means:
Educacion Edad Tvdiario
No 12.4 31.1 1.92
Si 13.7 44.3 2.56
Coefficients of linear discriminants:
LD1
Educacion 0.3921
Edad 0.0656
Tvdiario 0.3568# Importancia de las variables
varImp(modelo_lda)ROC curve variable importance
Importance
Edad 100.0
Educacion 38.6
Tvdiario 0.0plot(varImp(modelo_lda))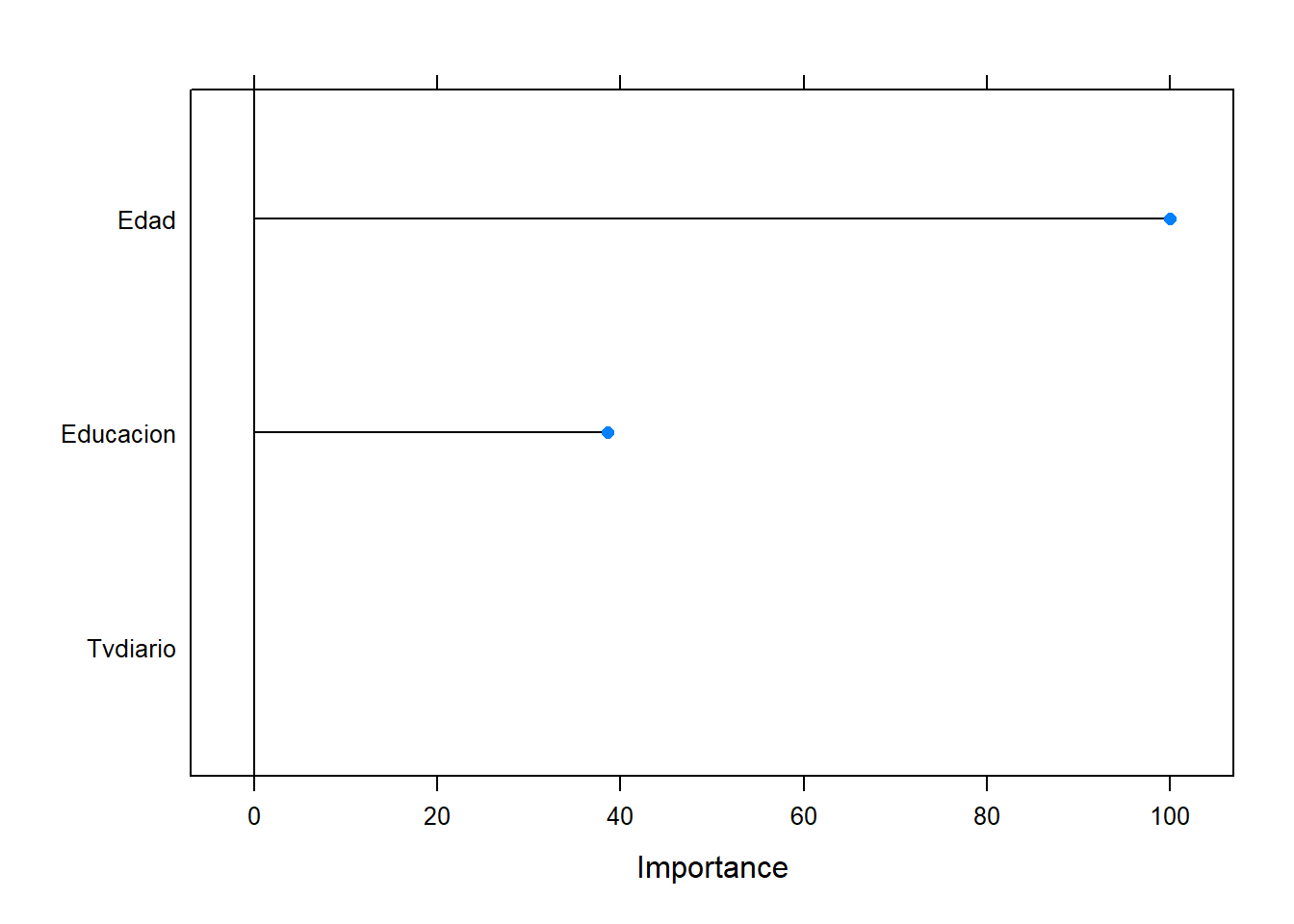
modelo_lda$resample Accuracy Kappa Resample
1 0.914 0.767 Fold01
2 0.917 0.750 Fold02
3 0.857 0.580 Fold03
4 0.829 0.551 Fold04
5 0.889 0.652 Fold05
6 0.829 0.551 Fold06
7 0.676 0.178 Fold07
8 0.800 0.457 Fold08
9 0.829 0.551 Fold09
10 0.889 0.652 Fold10# Gráfico de puntos para los valores de accuracy
dotplot(modelo_lda$resample$Accuracy)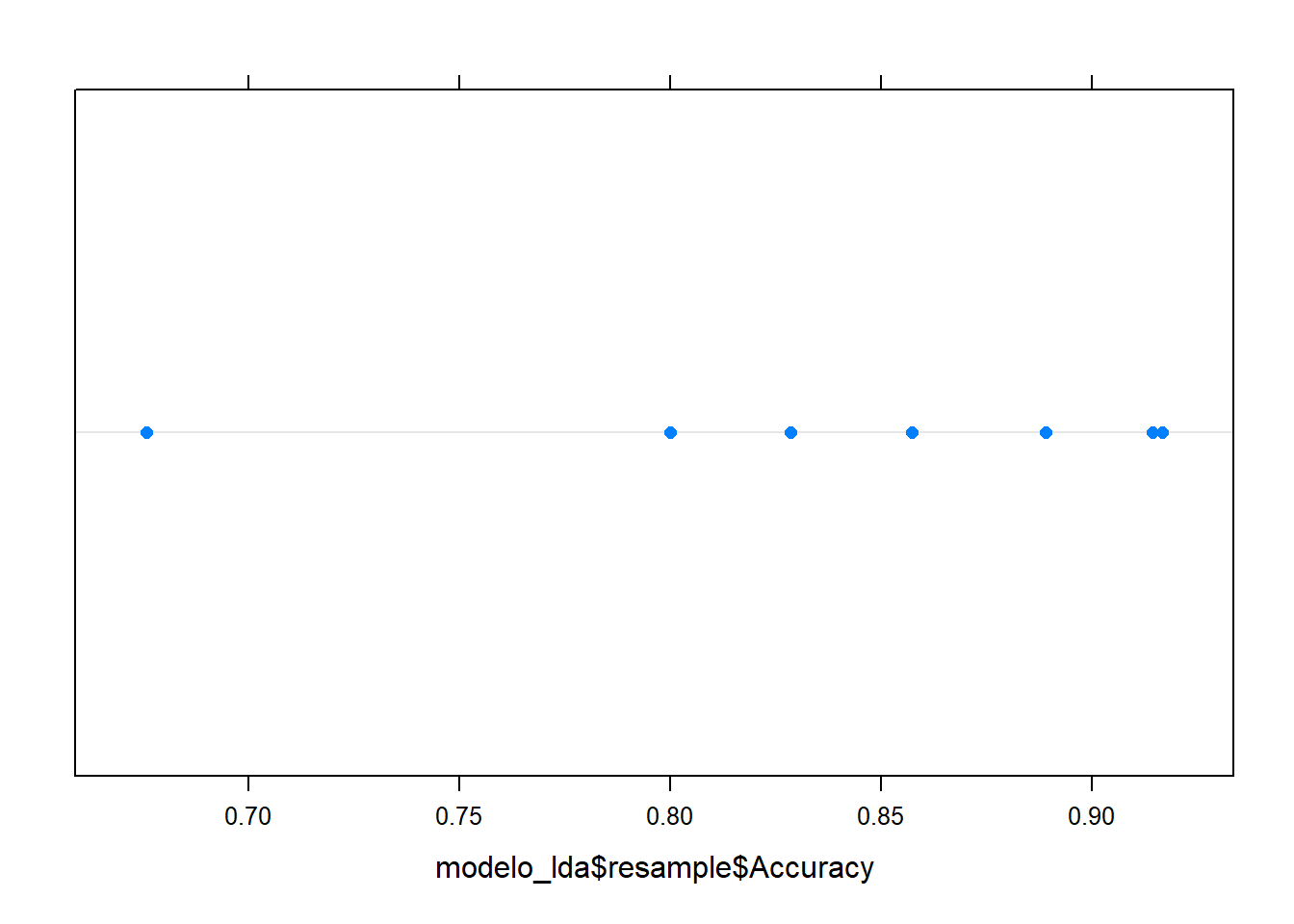
# Diagrama de cajas
bwplot(modelo_lda$resample$Accuracy)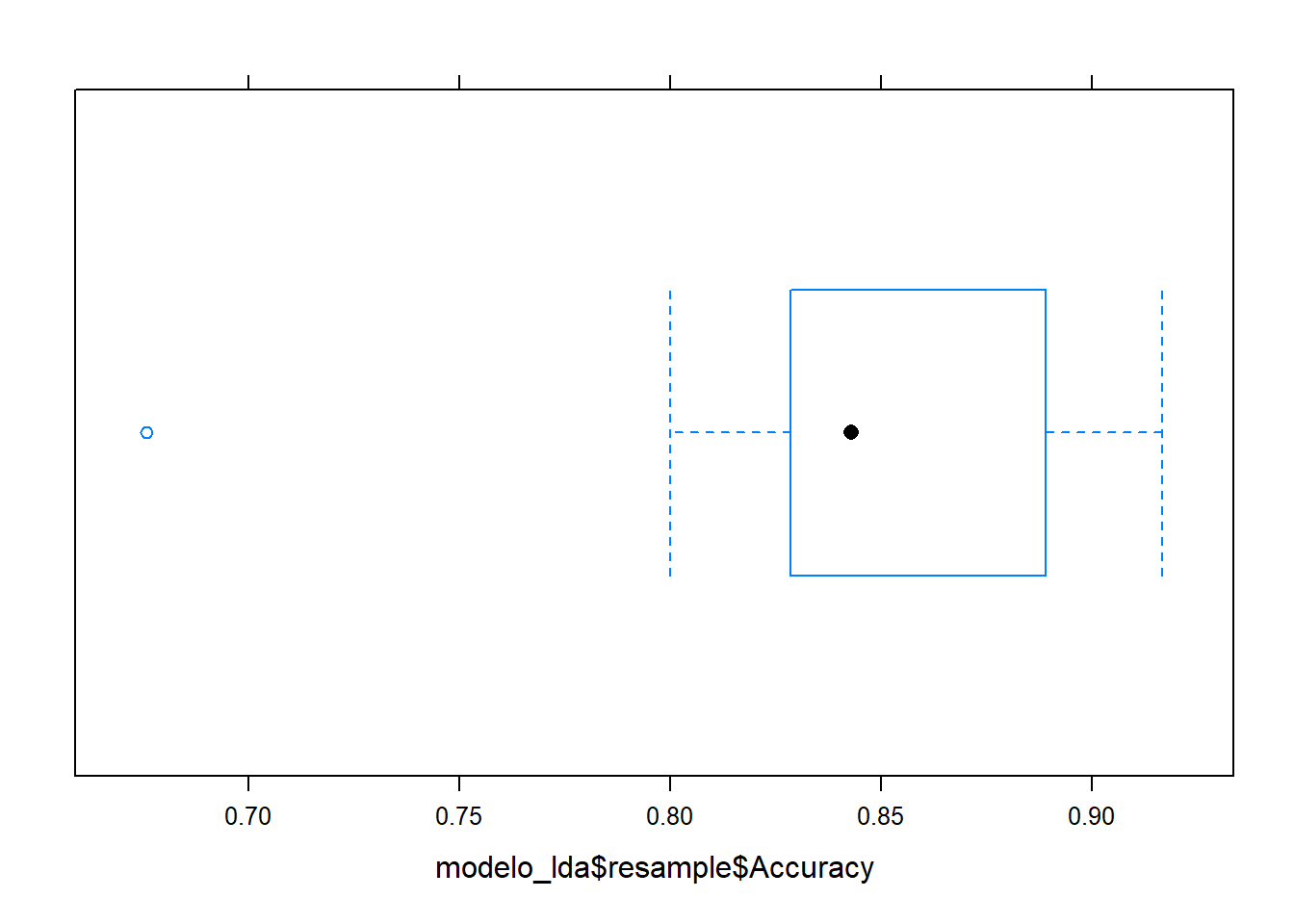
summary(modelo_lda$resample$Accuracy) Min. 1st Qu. Median Mean 3rd Qu. Max.
0.676 0.829 0.843 0.843 0.889 0.917 # También se puede analizar el Kappa
summary(modelo_lda$resample$Kappa) Min. 1st Qu. Median Mean 3rd Qu. Max.
0.178 0.551 0.566 0.569 0.652 0.767 Indicadores para Evaluación de Modelos
1. Tabla de Clasificación / Matriz de Confusión
library(gmodels)
CrossTable(x = testing$Suscripcion,
y = testing$clase.pred,
prop.t=FALSE,
prop.c=FALSE,
prop.r=FALSE,
prop.chisq = FALSE)
Cell Contents
|-------------------------|
| N |
|-------------------------|
Total Observations in Table: 87
| testing$clase.pred
testing$Suscripcion | No | Si | Row Total |
--------------------|-----------|-----------|-----------|
No | 16 | 6 | 22 |
--------------------|-----------|-----------|-----------|
Si | 2 | 63 | 65 |
--------------------|-----------|-----------|-----------|
Column Total | 18 | 69 | 87 |
--------------------|-----------|-----------|-----------|
# Otra Forma
addmargins(table(Clase_Real=testing$Suscripcion,
Clase_Predicha=testing$clase.pred)) Clase_Predicha
Clase_Real No Si Sum
No 16 6 22
Si 2 63 65
Sum 18 69 87prop.table(table(Clase_Real=testing$Suscripcion,
Clase_Predicha=testing$clase.pred),1) Clase_Predicha
Clase_Real No Si
No 0.7273 0.2727
Si 0.0308 0.9692vcd::mosaic(testing$clase.pred~testing$Suscripcion)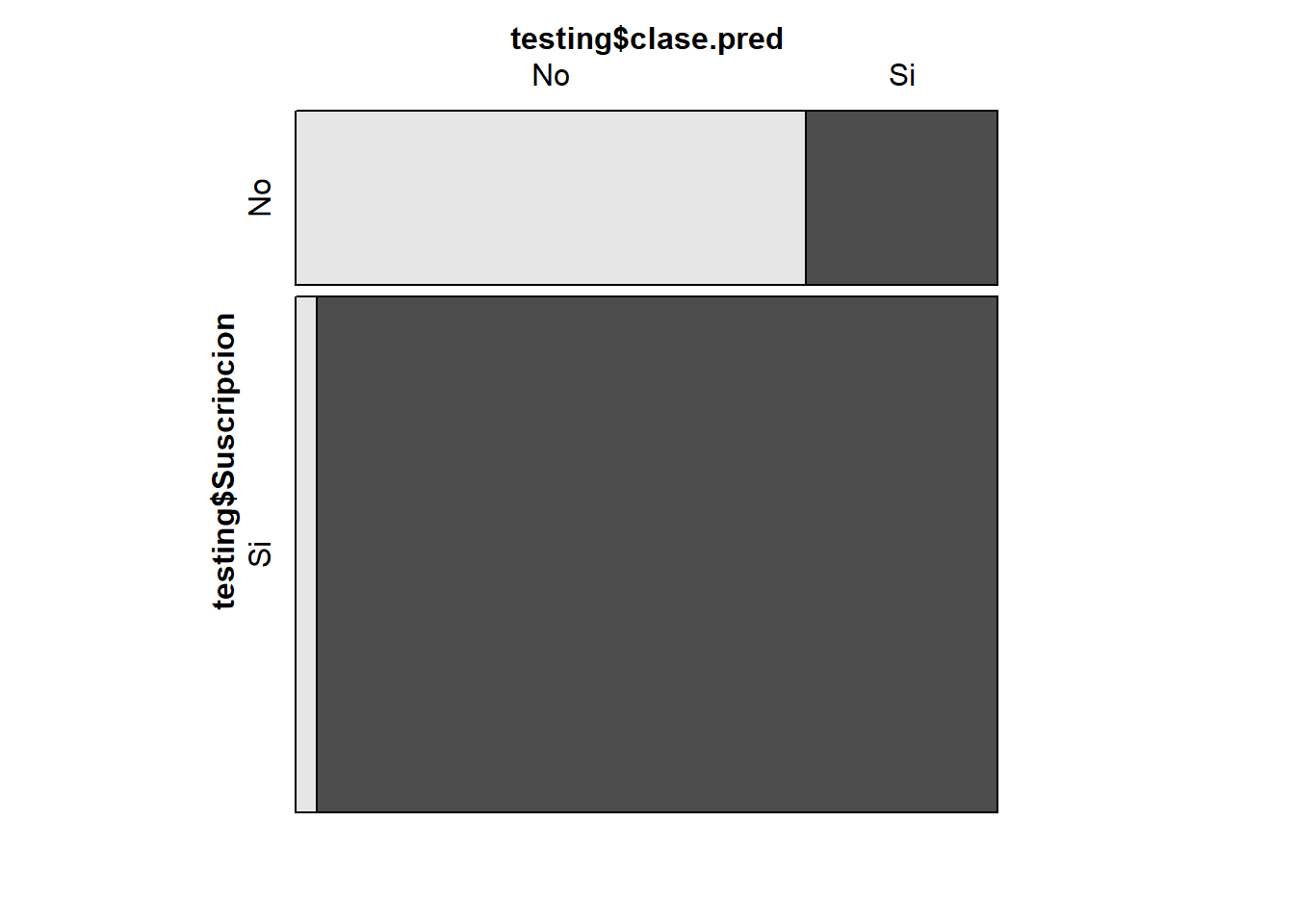
# Calcular el accuracy
accuracy <- mean(testing$Suscripcion==testing$clase.pred)
accuracy[1] 0.908# Calcular el error de mala clasificación (Tasa de error)
error <- mean(testing$Suscripcion!=testing$clase.pred)
error[1] 0.092# Usando el paquete caret
library(caret)
cm <- caret::confusionMatrix(testing$clase.pred,
testing$Suscripcion,
positive="Si")
cmConfusion Matrix and Statistics
Reference
Prediction No Si
No 16 2
Si 6 63
Accuracy : 0.908
95% CI : (0.827, 0.959)
No Information Rate : 0.747
P-Value [Acc > NIR] : 0.000135
Kappa : 0.741
Mcnemar's Test P-Value : 0.288844
Sensitivity : 0.969
Specificity : 0.727
Pos Pred Value : 0.913
Neg Pred Value : 0.889
Prevalence : 0.747
Detection Rate : 0.724
Detection Prevalence : 0.793
Balanced Accuracy : 0.848
'Positive' Class : Si
cm$table Reference
Prediction No Si
No 16 2
Si 6 63cm$byClass["Sensitivity"] Sensitivity
0.969 cm$byClass["Specificity"] Specificity
0.727 cm$overall["Accuracy"]Accuracy
0.908 precision <- cm$byClass['Pos Pred Value'] ; precisionPos Pred Value
0.913 # Sensibilidad
recall <- cm$byClass['Sensitivity'] ; recallSensitivity
0.969 # F1 score
# De Forma Manual
f_measure <- 2*((precision*recall)/(precision+recall));f_measurePos Pred Value
0.94 library(MLmetrics)
Precision(testing$Suscripcion,testing$clase.pred,positive="Si")[1] 0.913Recall(testing$Suscripcion,testing$clase.pred,positive="Si")[1] 0.969F1_Score(testing$Suscripcion,testing$clase.pred,positive="Si")[1] 0.942. Estadístico de Kappa
# Tabla de Clasificación
addmargins(table(Clase_Real=testing$Suscripcion,
Clase_Predicha=testing$clase.pred)) Clase_Predicha
Clase_Real No Si Sum
No 16 6 22
Si 2 63 65
Sum 18 69 87# Accuracy o Probabilidad observada
pr_o <- (16+63)/87 ; pr_o[1] 0.908# Probabilidad esperada
pr_e <- (22/87)*(18/87) + (65/87)*(69/87) ; pr_e[1] 0.645k <- (pr_o - pr_e)/(1 - pr_e) ; k[1] 0.741# Estadístico de Kappa
k <- cm$overall['Kappa'] ; kKappa
0.741 3. Estadístico Kolmogorov - Smirnov
library(InformationValue)
ks_stat(testing$Suscripcion,testing$proba.pred, returnKSTable = T) rank total_pop non_responders responders expected_responders_by_random
1 1 9 0 9 6.72
2 2 9 0 9 6.72
3 3 9 0 9 6.72
4 4 9 1 8 6.72
5 5 9 2 7 6.72
6 6 9 0 9 6.72
7 7 9 2 7 6.72
8 8 9 4 5 6.72
9 9 9 7 2 6.72
10 10 6 6 0 4.48
perc_responders perc_non_responders cum_perc_responders
1 0.1385 0.0000 0.138
2 0.1385 0.0000 0.277
3 0.1385 0.0000 0.415
4 0.1231 0.0455 0.538
5 0.1077 0.0909 0.646
6 0.1385 0.0000 0.785
7 0.1077 0.0909 0.892
8 0.0769 0.1818 0.969
9 0.0308 0.3182 1.000
10 0.0000 0.2727 1.000
cum_perc_non_responders difference
1 0.0000 0.138
2 0.0000 0.277
3 0.0000 0.415
4 0.0455 0.493
5 0.1364 0.510
6 0.1364 0.648
7 0.2273 0.665
8 0.4091 0.560
9 0.7273 0.273
10 1.0000 0.000ks_stat(testing$Suscripcion,testing$proba.pred)[1] 0.665# Graficando el estadístico K-S
ks_plot(testing$Suscripcion,testing$proba.pred)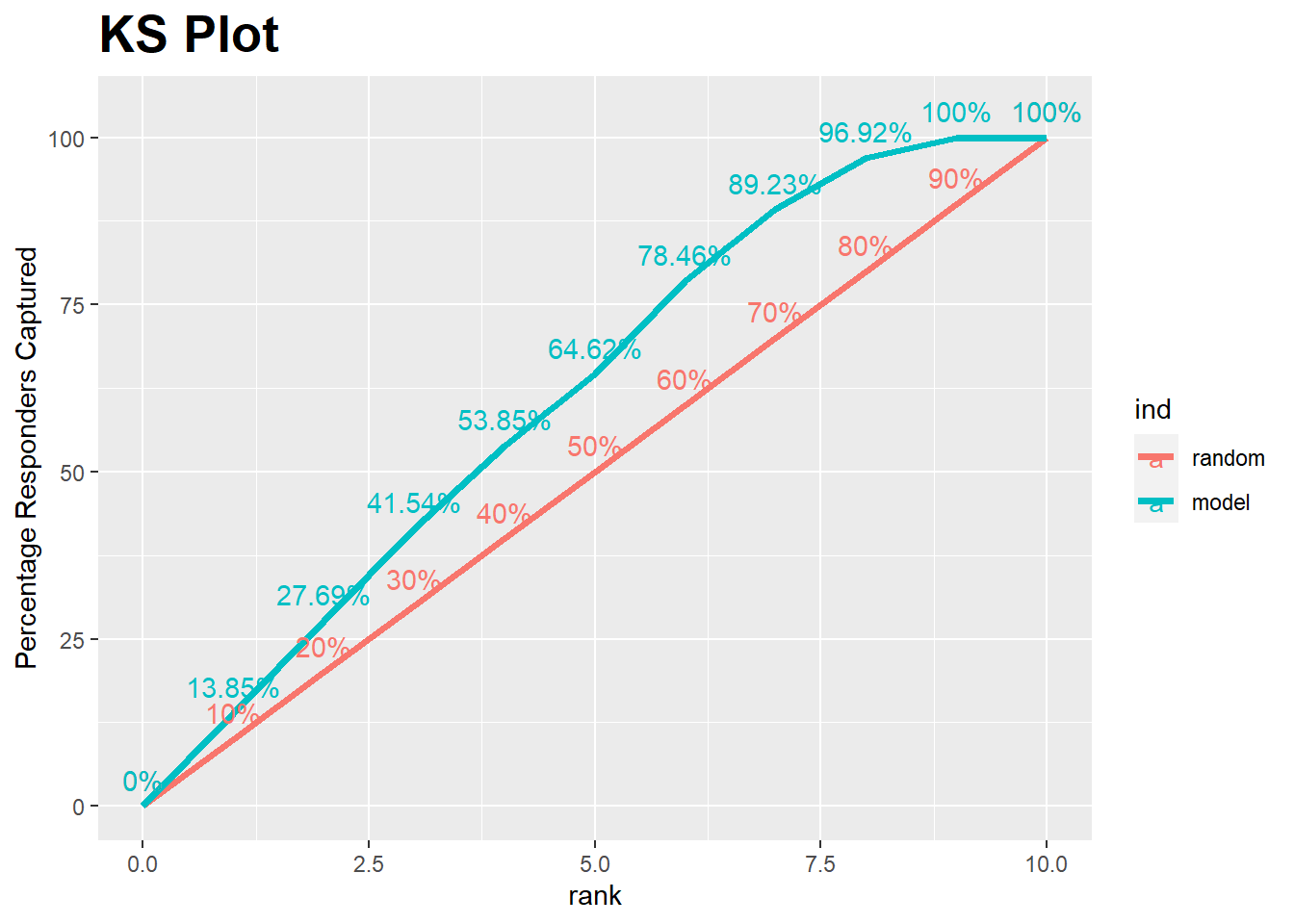
library(ROCit)
ROCit_obj <- rocit(score=testing$proba.pred,
class=testing$Suscripcion)
ksplot(ROCit_obj,legend=T,values=T)
ksplot1 <- ksplot(ROCit_obj,legend=T,values=T)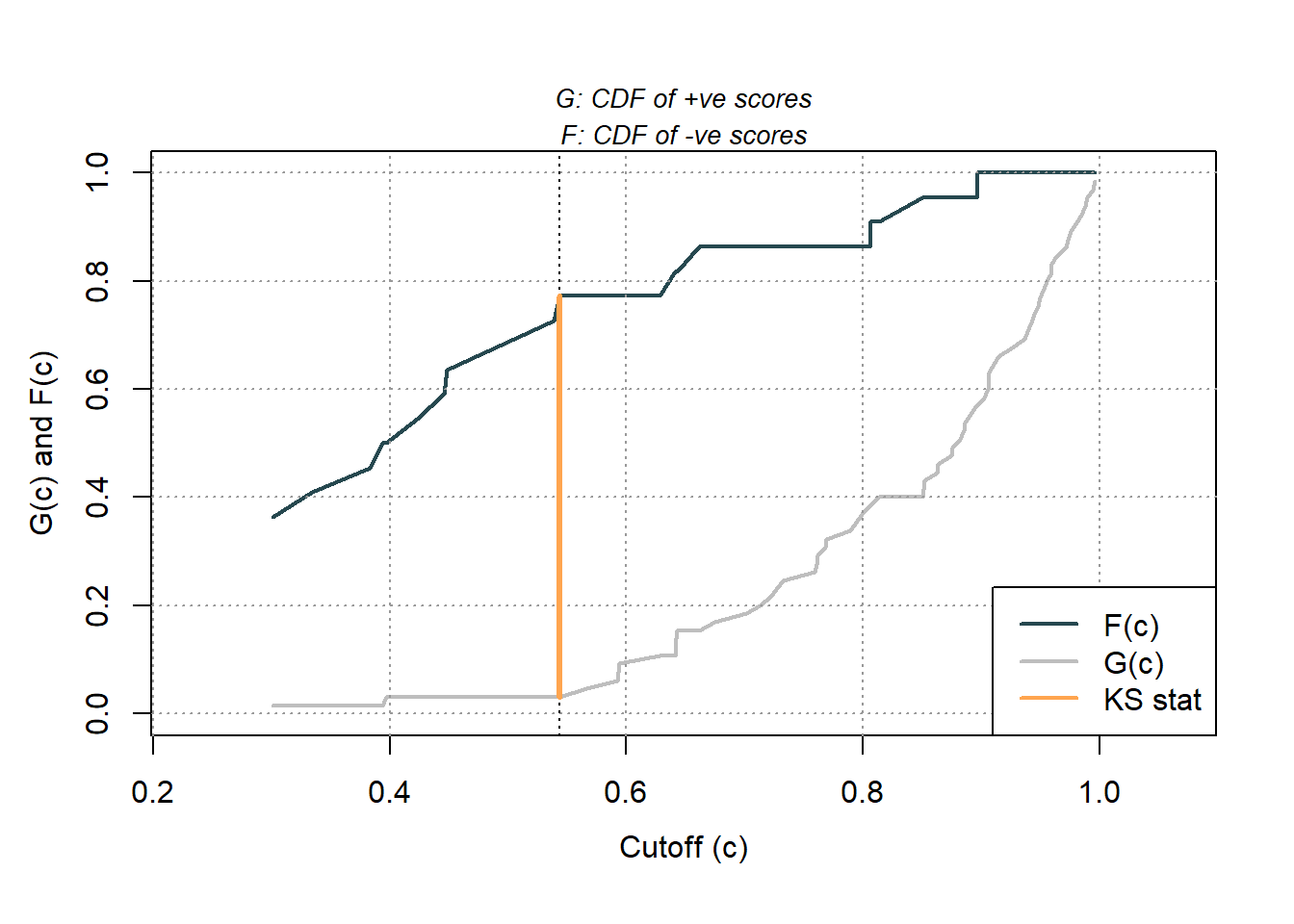
ksplot1$`KS Cutoff` # punto de corte óptimo con el mayor K-S[1] 0.543ksplot1$`KS stat` # K-S al punto de corte óptimo[1] 0.7424. Curva ROC y Área bajo la Curva
# 1. Usando el paquete caTools
library(caTools)
AUC <- colAUC(testing$proba.pred,testing$Suscripcion,plotROC = TRUE)
abline(0, 1,col="red",lty=3)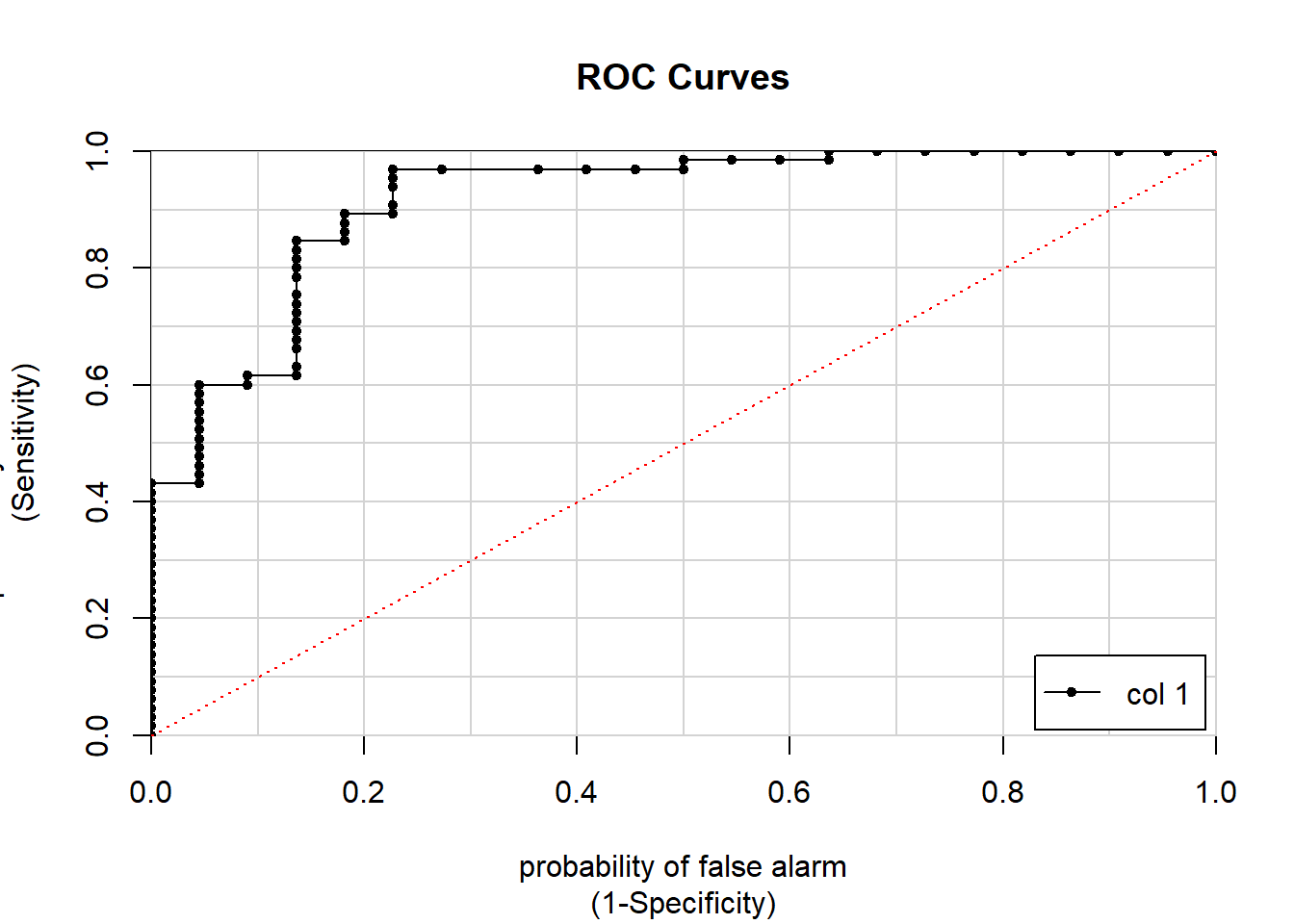
AUC [,1]
No vs. Si 0.916# 2. Usando el paquete pROC
library(pROC)
# Área bajo la curva
roc <- roc(testing$Suscripcion,testing$proba.pred)
roc
Call:
roc.default(response = testing$Suscripcion, predictor = testing$proba.pred)
Data: testing$proba.pred in 22 controls (testing$Suscripcion No) < 65 cases (testing$Suscripcion Si).
Area under the curve: 0.916roc$thresholds # puntos de corte que ha probado el modelo [1] -Inf 0.0806 0.1014 0.1290 0.1473 0.1718 0.2079 0.2352 0.2668 0.2967
[11] 0.3180 0.3589 0.3886 0.3957 0.4100 0.4344 0.4473 0.4938 0.5412 0.5548
[21] 0.5792 0.5930 0.6110 0.6347 0.6415 0.6418 0.6424 0.6523 0.6681 0.6880
[31] 0.7068 0.7171 0.7269 0.7456 0.7599 0.7611 0.7648 0.7685 0.7792 0.7940
[41] 0.8019 0.8057 0.8099 0.8319 0.8505 0.8514 0.8570 0.8627 0.8688 0.8748
[51] 0.8787 0.8837 0.8858 0.8887 0.8935 0.8962 0.8994 0.9037 0.9055 0.9061
[61] 0.9082 0.9124 0.9202 0.9310 0.9377 0.9404 0.9433 0.9464 0.9487 0.9510
[71] 0.9537 0.9568 0.9589 0.9611 0.9673 0.9720 0.9741 0.9778 0.9822 0.9860
[81] 0.9884 0.9918 0.9948 Inf# Sensitividad para cada punto de corte
roc$sensitivities [1] 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.9846
[11] 0.9846 0.9846 0.9846 0.9692 0.9692 0.9692 0.9692 0.9692 0.9692 0.9538
[21] 0.9385 0.9077 0.8923 0.8923 0.8769 0.8615 0.8462 0.8462 0.8308 0.8154
[31] 0.8000 0.7846 0.7538 0.7385 0.7231 0.7077 0.6923 0.6769 0.6615 0.6308
[41] 0.6154 0.6154 0.6000 0.6000 0.5846 0.5692 0.5538 0.5385 0.5231 0.5077
[51] 0.4923 0.4769 0.4615 0.4462 0.4308 0.4308 0.4154 0.4000 0.3846 0.3692
[61] 0.3538 0.3385 0.3231 0.3077 0.2923 0.2769 0.2615 0.2462 0.2308 0.2154
[71] 0.2000 0.1846 0.1692 0.1538 0.1385 0.1231 0.1077 0.0923 0.0769 0.0615
[81] 0.0462 0.0308 0.0154 0.0000# Especifidad para cada punto de corte
roc$specificities [1] 0.0000 0.0455 0.0909 0.1364 0.1818 0.2273 0.2727 0.3182 0.3636 0.3636
[11] 0.4091 0.4545 0.5000 0.5000 0.5455 0.5909 0.6364 0.7273 0.7727 0.7727
[21] 0.7727 0.7727 0.7727 0.8182 0.8182 0.8182 0.8182 0.8636 0.8636 0.8636
[31] 0.8636 0.8636 0.8636 0.8636 0.8636 0.8636 0.8636 0.8636 0.8636 0.8636
[41] 0.8636 0.9091 0.9091 0.9545 0.9545 0.9545 0.9545 0.9545 0.9545 0.9545
[51] 0.9545 0.9545 0.9545 0.9545 0.9545 1.0000 1.0000 1.0000 1.0000 1.0000
[61] 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
[71] 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
[81] 1.0000 1.0000 1.0000 1.0000# 2da Forma
areaROC <- auc(roc(testing$Suscripcion,testing$proba.pred))
areaROCArea under the curve: 0.916# 3era forma
roc$aucArea under the curve: 0.916# Gráfica curva ROC
plot.roc(testing$Suscripcion,testing$proba.pred,
xlab="1- Especificidad", legacy.axes=TRUE,
ylab="Sensibilidad",
main = paste('Área bajo la curva =',round(areaROC,4)),
col="blue")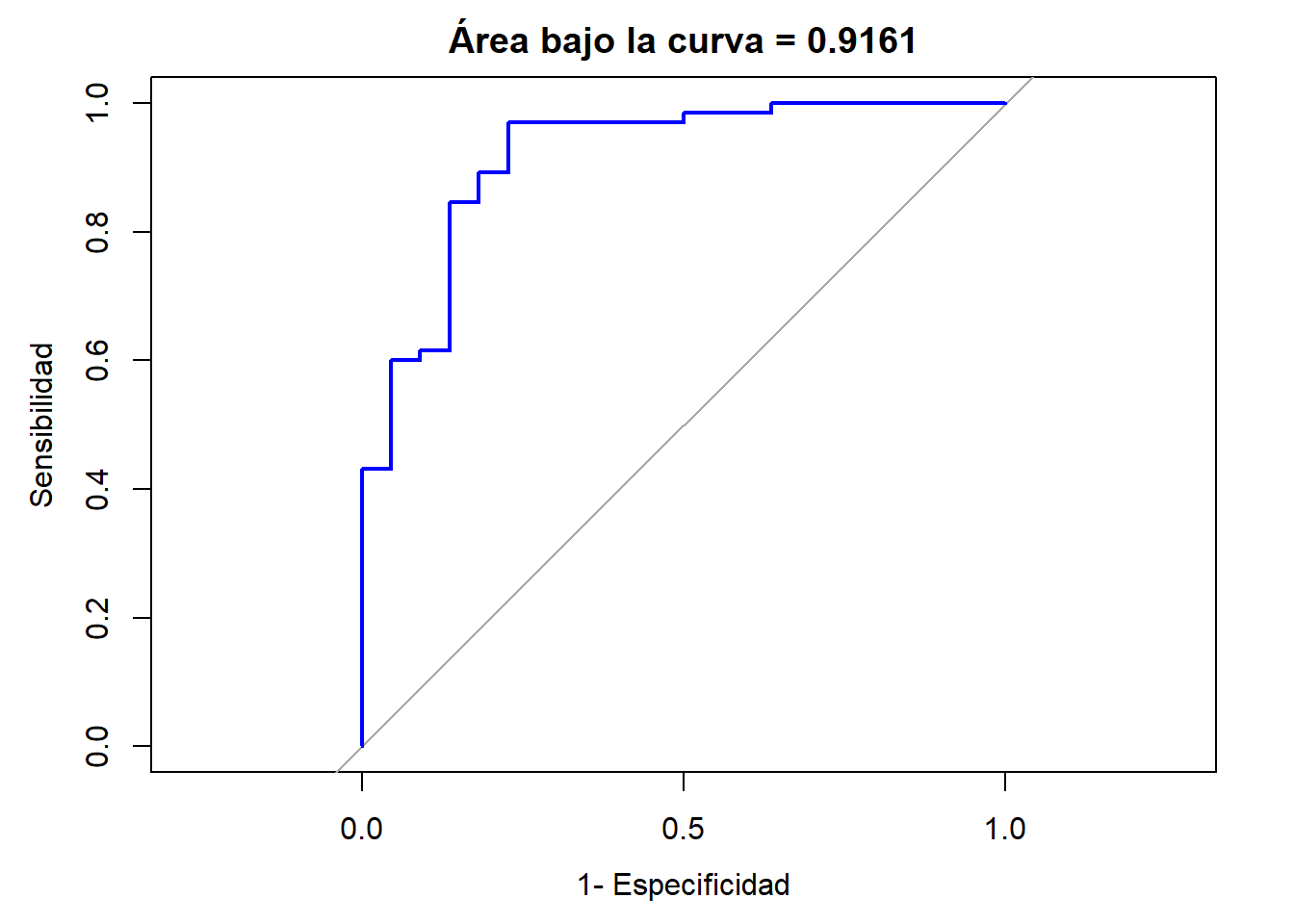
puntos.corte <- data.frame(prob=roc$thresholds,
sen=roc$sensitivities,
esp=roc$specificities,
s_e=roc$sensitivities+roc$specificities)
head(puntos.corte) prob sen esp s_e
1 -Inf 1 0.0000 1.00
2 0.0806 1 0.0455 1.05
3 0.1014 1 0.0909 1.09
4 0.1290 1 0.1364 1.14
5 0.1473 1 0.1818 1.18
6 0.1718 1 0.2273 1.23# Punto de corte óptimo (mayor sensibilidad y especificidad)
coords(roc, "best",ret=c("threshold","specificity", "sensitivity","accuracy")) threshold specificity sensitivity accuracy
threshold 0.541 0.773 0.969 0.92coords(roc, "best") threshold specificity sensitivity
1 0.541 0.773 0.969plot(roc,print.thres=T) # punto de corte, especificidad, sensibilidad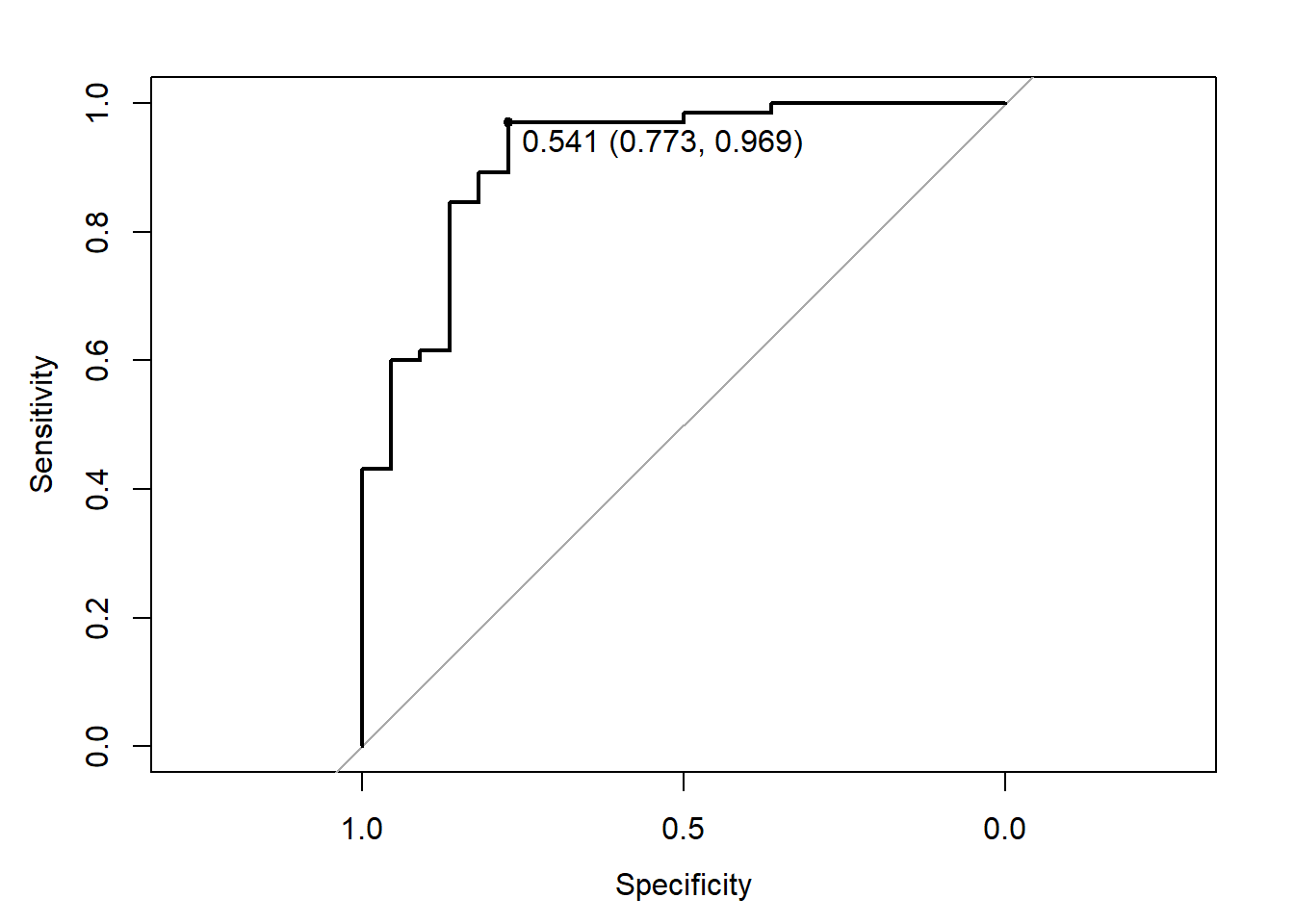
# Graficando la Sensibilidad y Especificidad
ggplot(puntos.corte, aes(x=prob)) +
geom_line(aes(y=sen, color="Sensibilidad")) +
geom_line(aes(y=esp, color="Especificidad")) +
labs(title ="Sensibilidad vs Especificidad",
x="Probabilidad") +
scale_color_discrete(name="Indicador") +
geom_vline(aes(xintercept=0.541), # punto de corte obtenido en coords
color="black", linetype="dashed", size=0.5) +
theme_bw() + theme(line = element_blank())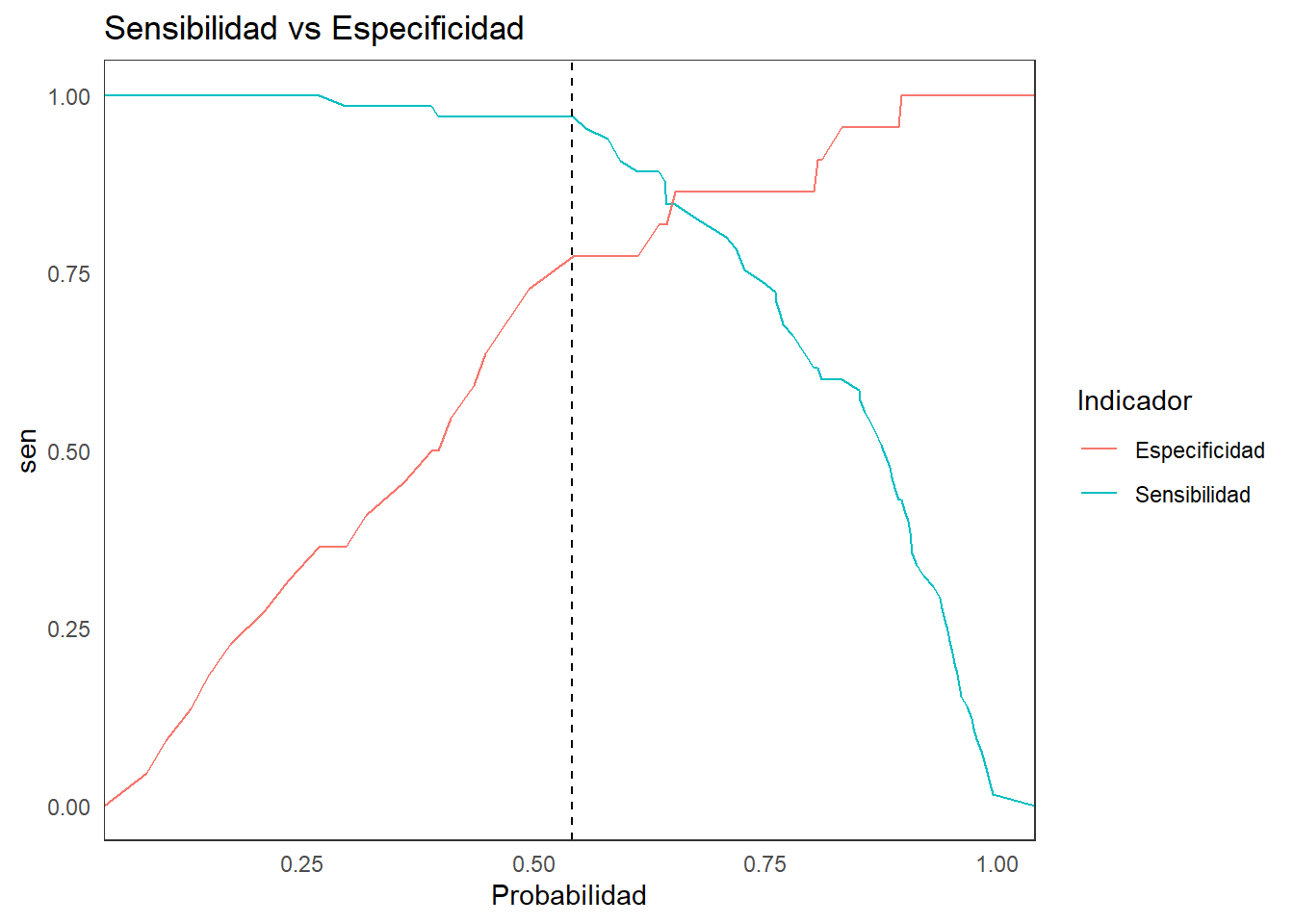
coords(roc, "best") threshold specificity sensitivity
1 0.541 0.773 0.969# Gráficando la Sensibilidad más la Especificidad
puntos.corte$suma <- puntos.corte$esp+puntos.corte$sen
optimo <- which.max(puntos.corte$suma)
optimo [1] 19# indica en orden en que se encuentra el punto optimo
puntos.corte[optimo,] prob sen esp s_e suma
19 0.541 0.969 0.773 1.74 1.745. Coeficiente de Gini
# Calculando manualmente
library(caTools)
AUC <- colAUC(testing$proba.pred,
testing$Suscripcio,
plotROC=T)
abline(0,1,col="red",lty=2)
gini <- 2*AUC -1 ; gini [,1]
No vs. Si 0.8326. Log Loss
# Usando el paquete MLmetrics
library(MLmetrics)
# Transformar la variable CHURN a numérica
real <- as.numeric(testing$Suscripcion)
head(real)[1] 1 1 2 1 1 2# Recodificar los 1 y 2 como 0 y 1 respectivamente
real <- ifelse(real==2,1,0)
head(real)[1] 0 0 1 0 0 1LogLoss(testing$proba.pred,real)[1] 0.32Predicción para Nuevos Individuos
Para datos de manera individual
Educacion Edad Tvdiario 12 18 3
nuevo1 <- data.frame(Educacion=12,Edad=18,Tvdiario=3)
predict(modelo_lda,nuevo1,type="prob") No Si
1 0.771 0.229predict(modelo_lda,nuevo1)[1] No
Levels: No Sinuevo2<-data.frame(Educacion=16,Edad=22,Tvdiario=1)
predict(modelo_lda,nuevo2,type="prob") No Si
1 0.359 0.641predict(modelo_lda,nuevo2)[1] Si
Levels: No SiPara un conjunto de datos
library(foreign)
datosn <- read.spss("suscripcion-nuevos-discriminante.sav",
use.value.labels=TRUE,
max.value.labels=TRUE,
to.data.frame=TRUE)
attr(datosn,"variable.labels") <- NULL
str(datosn)## 'data.frame': 20 obs. of 5 variables:
## $ Educacion : num 12 16 12 15 12 15 12 13 16 15 ...
## $ Edad : num 18 31 20 43 20 22 23 23 23 23 ...
## $ Tvdiario : num 3 2 4 2 4 4 0 2 2 3 ...
## $ Organizaciones: num 0 0 0 1 0 3 0 1 2 1 ...
## $ Hijos : num 0 0 0 1 1 0 1 0 0 0 ...
## - attr(*, "codepage")= int 1252clase <- predict(modelo_lda,datosn,type="prob")
proba <- predict(modelo_lda,datosn)
datonsdp <- cbind(datosn,clase,proba)