Capítulo 8 Análisis de Series de Tiempo
Una serie de tiempo es una secuencia de datos u observaciones medidos en determinados momentos, en intervalos iguales o desiguales, y ordenados cronológicamente.
El análisis de series de tiempo se refiere al proceso de analizar los datos disponibles para descubrir el patrón o la tendencia en los datos. Permite extraer y modelar las relaciones entre datos a lo largo del tiempo, sea extrapolando (hacia futuro) o interpolando (hacia el pasado) el comportamiento de datos no observados.
En general los análisis de series de tiempo tienen los siguientes tres pasos:
- Análisis exploratorio
- Escogencia y ajuste del modelo
- Diagnóstico
Además, existen dos técnicas de modelado principales para hacer análisis de series de tiempo:
- Holt Winters
- ARIMA models
8.1 Análisis exploratorio
Dentro del análisis exploratorio de series de tiempo se pueden realizar los siguientes procedimientos:
- Estimación de tendencias y descomposición: Se utiliza para el ajuste estacional. Busca construir, a partir de una serie temporal observada, una serie de subcomponentes con diferentes características.
- Análisis de autocorrelación: permite estimar qué valor en el pasado tiene una correlación con el valor actual. Proporciona la estimación de los factores p, d, q para los modelos ARIMA.
- Análisis espectral: Describe cómo la variación en una serie de tiempo puede ser explicada por componentes cíclicos. Permite separar los componentes periódicos en un ambiente ruidoso.
El primer paso del análisis exploratorio consiste en la lectura y transformación de datos. Se utiliza la función ts() para transformar los datos a formato series de tiempo. La función plot.ts() se utiliza para graficar. La función window() se usa para extraer información de una ventana de tiempo particular.
La base de datos del ejemplo es de nacimientos registrados por mes en la ciudad de Nueva York entre 1946 y 1959, tomados de https://a-little-book-of-r-for-time-series.readthedocs.io/en/latest/src/timeseries.html
births <- scan("http://robjhyndman.com/tsdldata/data/nybirths.dat")
birthstimeseries <- ts(births, frequency=12, start=c(1946,1))
plot.ts(birthstimeseries)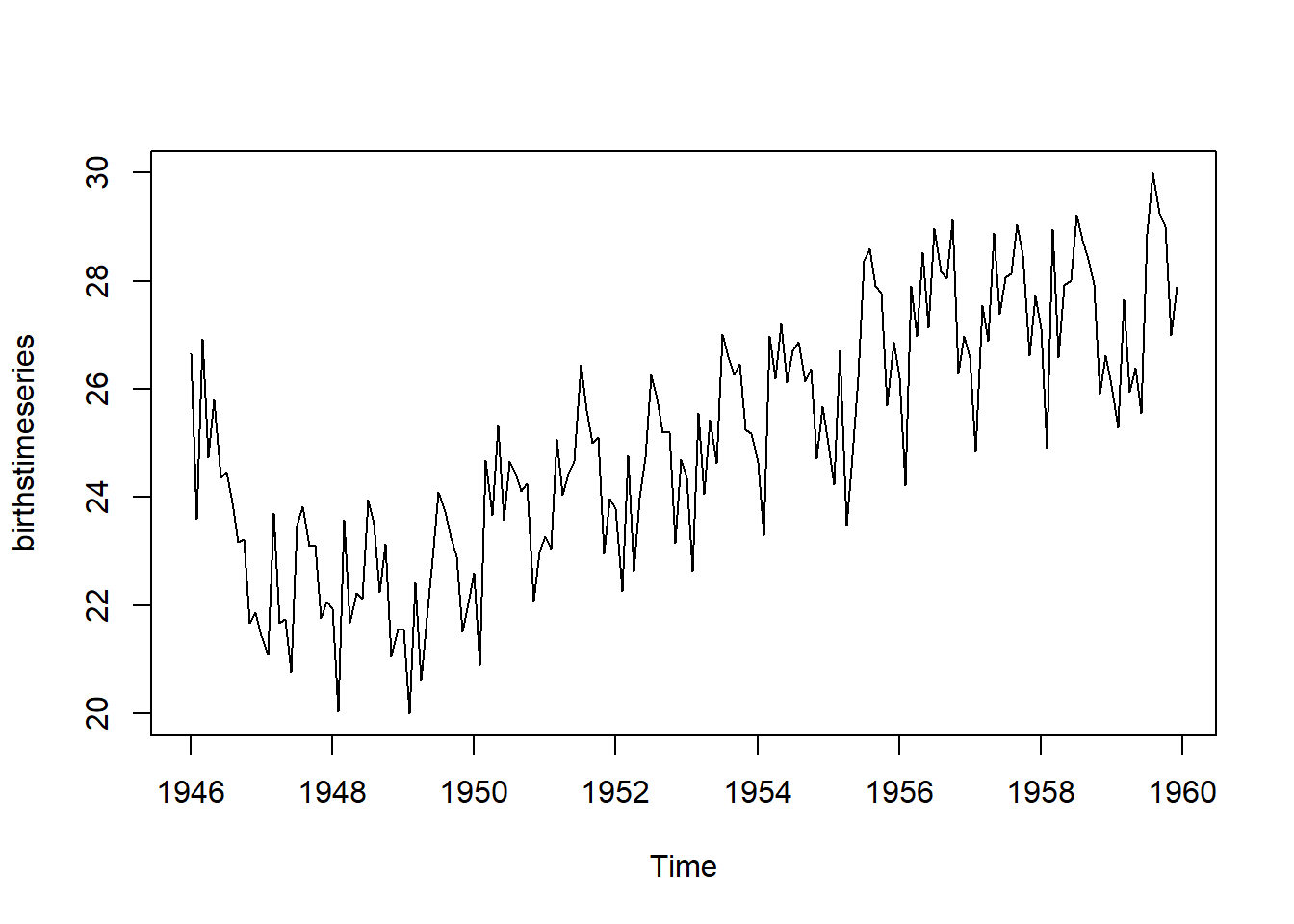
Figure 4.1: 8
Figure 6.1: 8
jul1956<-window(birthstimeseries, start=c(1956,6))
jul1956
#> Jan Feb Mar Apr May Jun Jul
#> 1956 27.139 28.982
#> 1957 26.589 24.848 27.543 26.896 28.878 27.390 28.065
#> 1958 27.132 24.924 28.963 26.589 27.931 28.009 29.229
#> 1959 26.076 25.286 27.660 25.951 26.398 25.565 28.865
#> Aug Sep Oct Nov Dec
#> 1956 28.169 28.056 29.136 26.291 26.987
#> 1957 28.141 29.048 28.484 26.634 27.735
#> 1958 28.759 28.405 27.945 25.912 26.619
#> 1959 30.000 29.261 29.012 26.992 27.8978.1.1 Componentes de las series de tiempo
- Tendencia: Es el patrón subyacente en los datos a lo largo del tiempo. No es necesariamente lineal.
- Estacionalidad: Cuando una serie está influenciada por factores estacionales de periodo fijo como el dia, mes, trimestre.
- Cíclicidad: Cuando los datos muestran subidas y caídas que no son del período fijo. Las fluctuaciones suelen ser de al menos 2 años.
- Aleatoriedad: parte inexplicable de los datos
Otras definiciones incluyen el ruido blanco (White noise) referente a la suposición de que los valores en una serie de tiempo son aleatorios, independientes entre sí (no están correlacionados), tienen una media de cero y varianza constante. Cuando estos supuestos no se cumplen se deben aplicar modelos autorregresivos (AR) y de media móvil (MA) para corrigir las infracciones de esta suposición.
Los time Lags se refieren a que los valores de \(y_{t}\) en una serie de tiempo se ven afectados por los valores de \(y\) en el pasado. Las regresiones que no contabilizan estos lags fallan en establecer (sobreestiman) las relaciones entre las variables dependientes e independientes.
La descomposición de la serie de tiempo se realiza con la función decompose() la cual desagrega la serie de tiempo en los componentes: tendencia, estacional, cíclico y aleatorio.
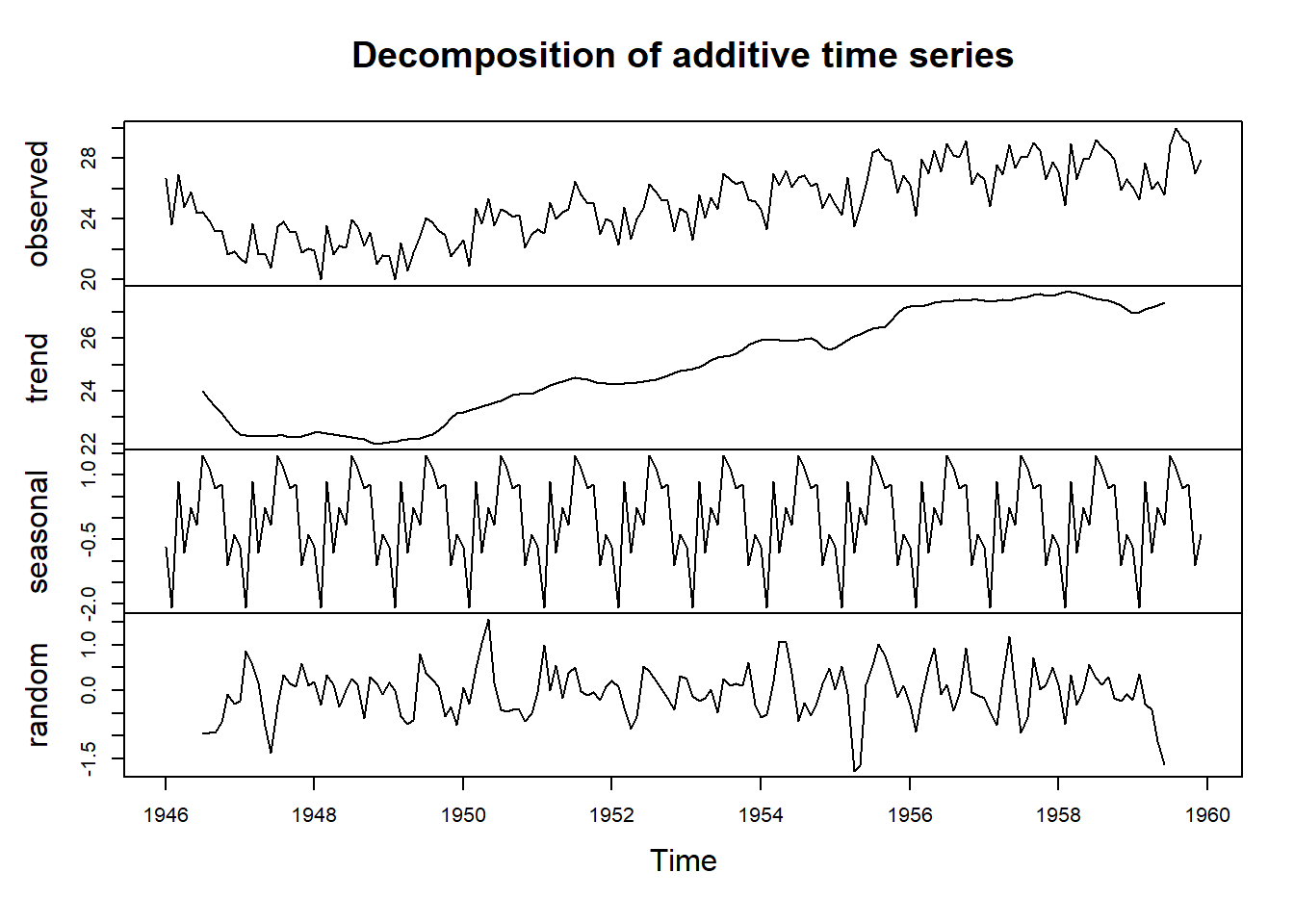
Figure 5.1: 8
También se pueden graficar algunos componentes por separado
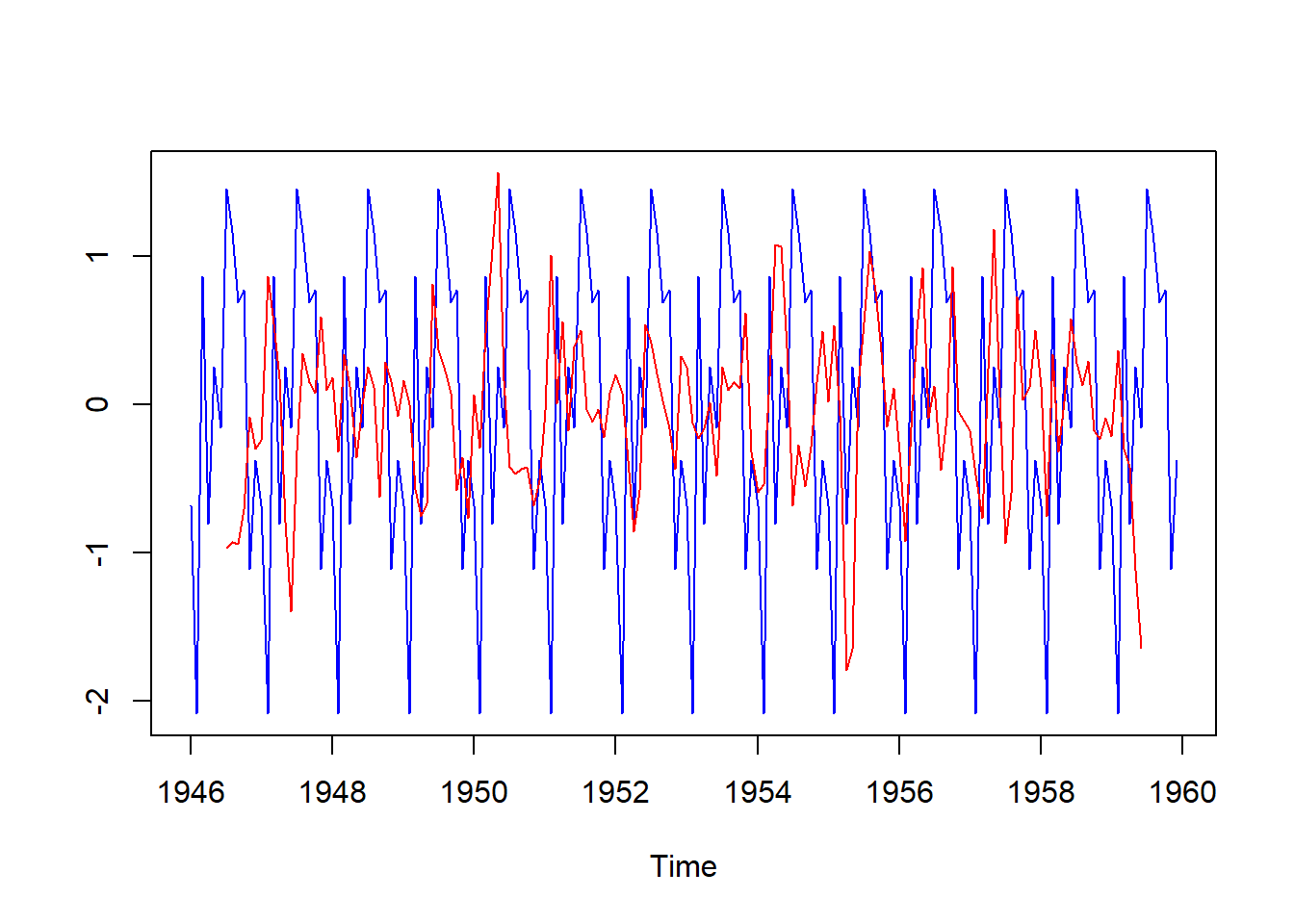
Figure 4.5: 8
8.1.2 Corrección de la estacionariedad (stationarity) y estacionalidad (seasonality)
Algunas técnicas para corregir la no estacionariedad (stationarity) son las siguientes:
- Ajuste por diferencial: calcula las diferencias entre observaciones consecutivas
- Cálculo de log o raíz cuadrada: para estabilizar la varianza no constante
- Unit root test (Prueba de raíz unitaria): esta prueba se usa para descubrir la primera diferencia o regresión que se debe usar para hacerla estacionaria. En la prueba Kwiatkowski-Phillips-Schmidt-Shin (KPSS), los valores pequeños de p sugieren que se requiere una diferenciación.
Por ejemplo, la fórmula para calcular el diferencial de primer orden sería así:
\(\Delta y_{t}=y_{t}-y_{t-1}\).
Se utiliza la función urkpssTest() del paquete fUnitRoots para descubrir el primer diferencial que se debe usar para alcanzar estacionariedad. La función diff() permite calcular los diferenciales para diferentes lags.
library("fUnitRoots")
urkpssTest(birthstimeseries, type = c("tau"), lags = c("long"),use.lag = NULL, doplot = TRUE)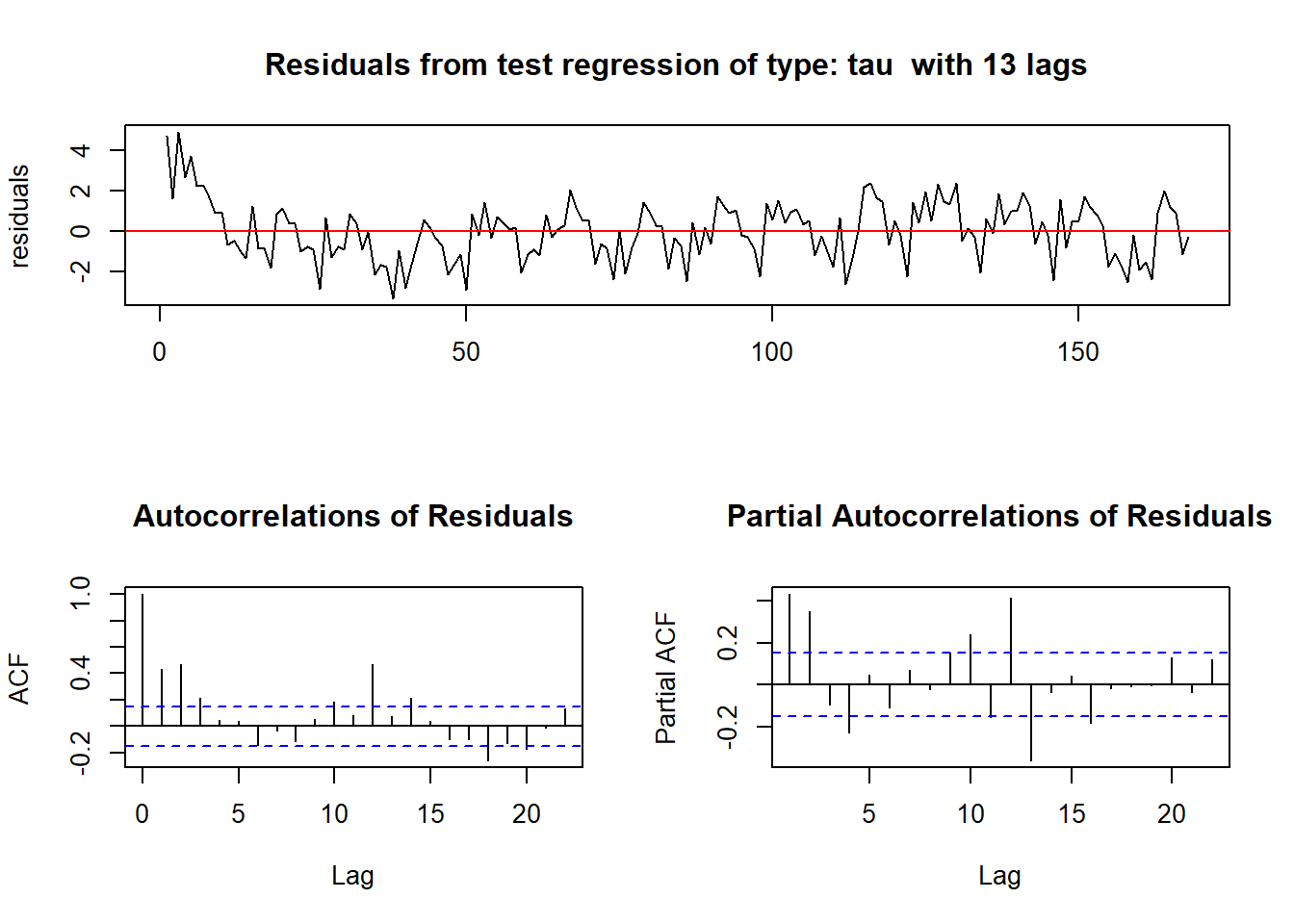
Figure 8.1: 8
#>
#> Title:
#> KPSS Unit Root Test
#>
#> Test Results:
#> NA
#>
#> Description:
#> Mon Sep 26 20:19:38 2022 by user: koroj
stationary = diff(birthstimeseries, differences=1)
plot(stationary)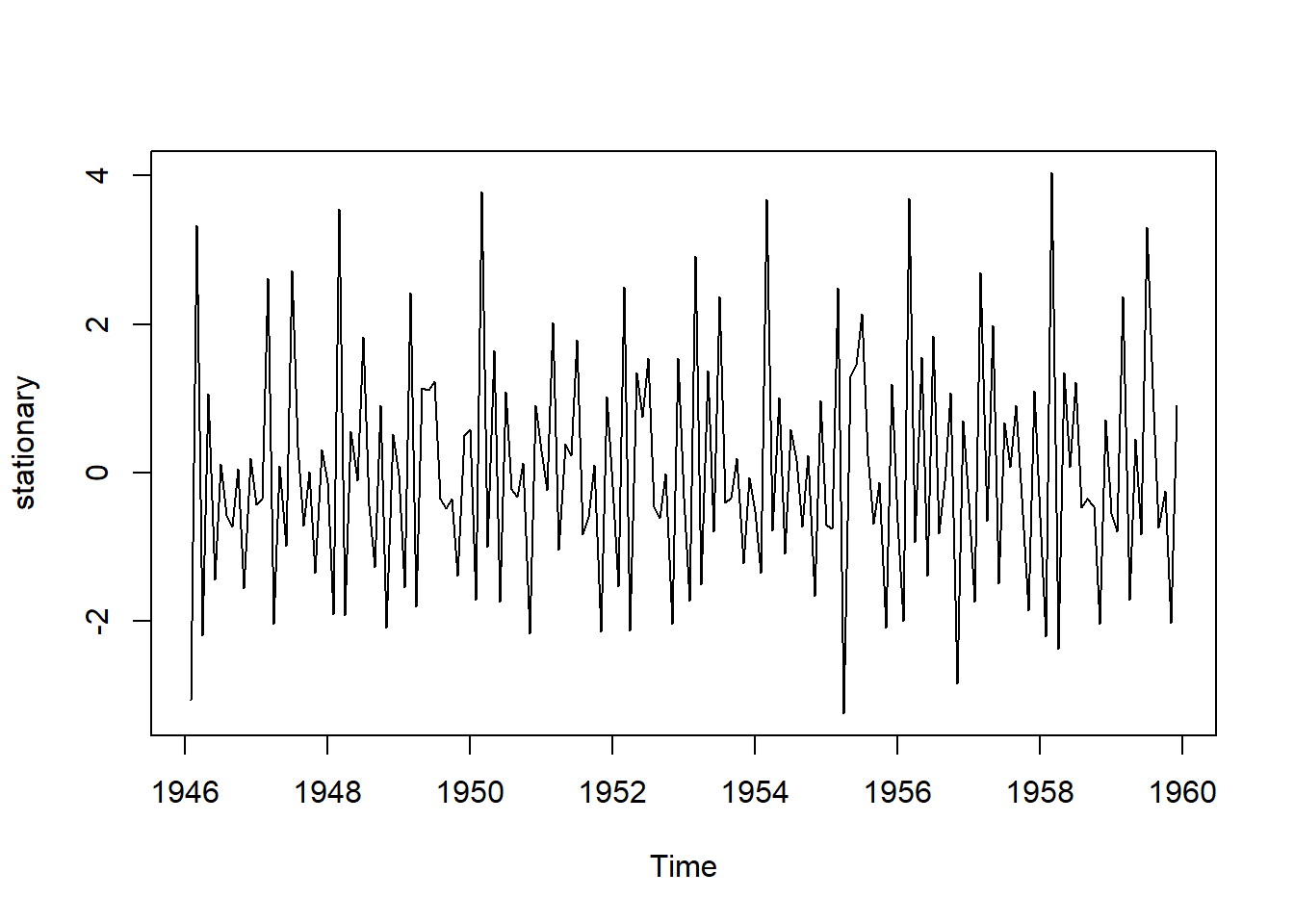
Figure 8.2: 8
Para detectar la seasonality (estacionalidad), se utilizan los auto correlation plot con la función acf(). El lag 0 siempre toma el valor 1, ya que representa la correlación entre los datos y ellos mismos, pero generalmente disminuye a medida que aumenta el numero de lag.
acf(birthstimeseries,lag.max=20) 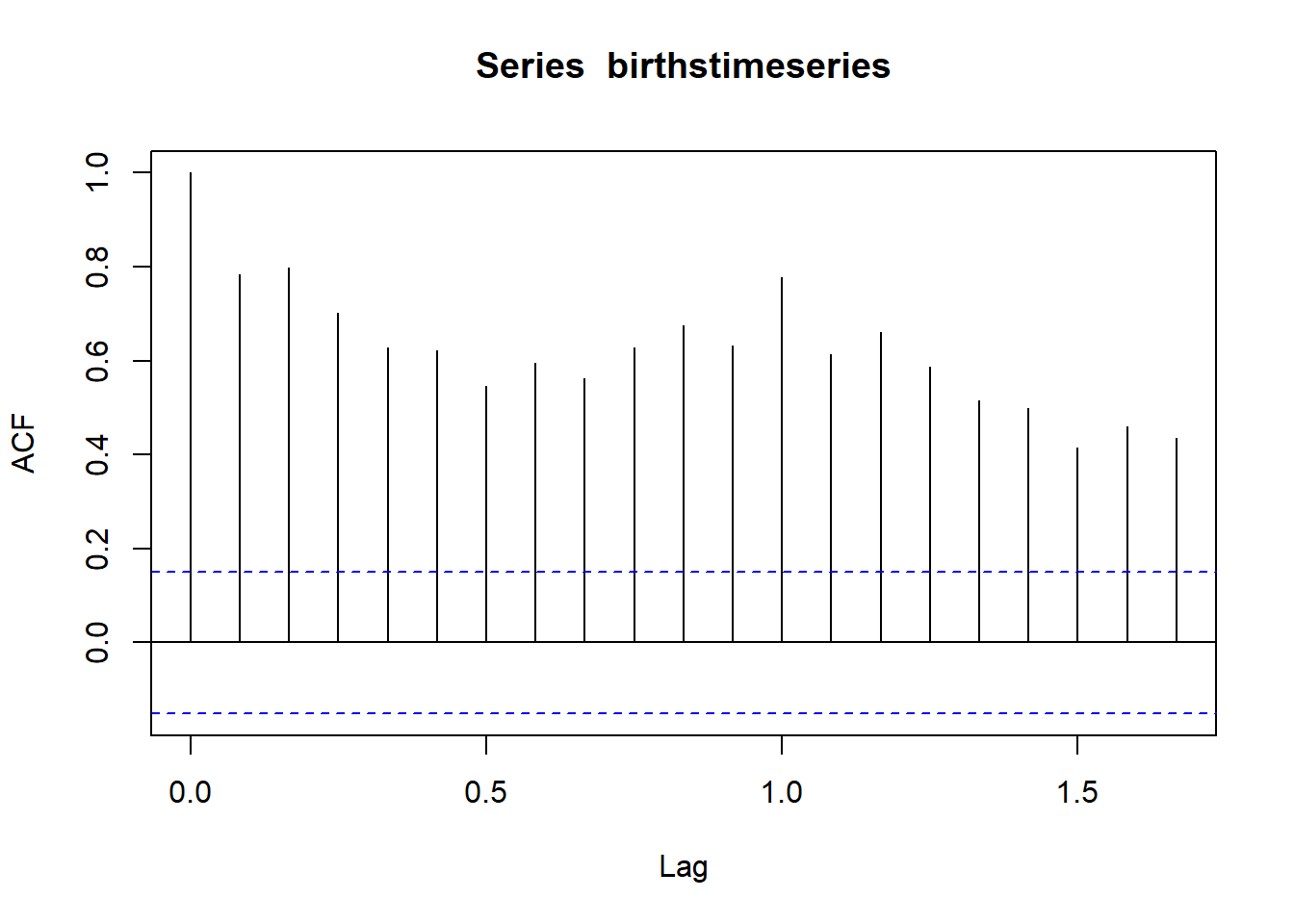
Figure 4.7: 8
Para ajustar la serie de tiempo por el componente de estacionalidad, se resta el componente estacional de la serie original y luego se le calcula el diferencial para hacerlo estacionario. Una vez se han corregido la seasonality y stationarity se puede proceder a hacer predicciones con diferentes modelos.
birthstimeseriesseasonallyadjusted <- birthstimeseries- birthstimeseriescomponents$seasonal
tsstationary <- diff(birthstimeseriesseasonallyadjusted, differences=1)
plot(tsstationary)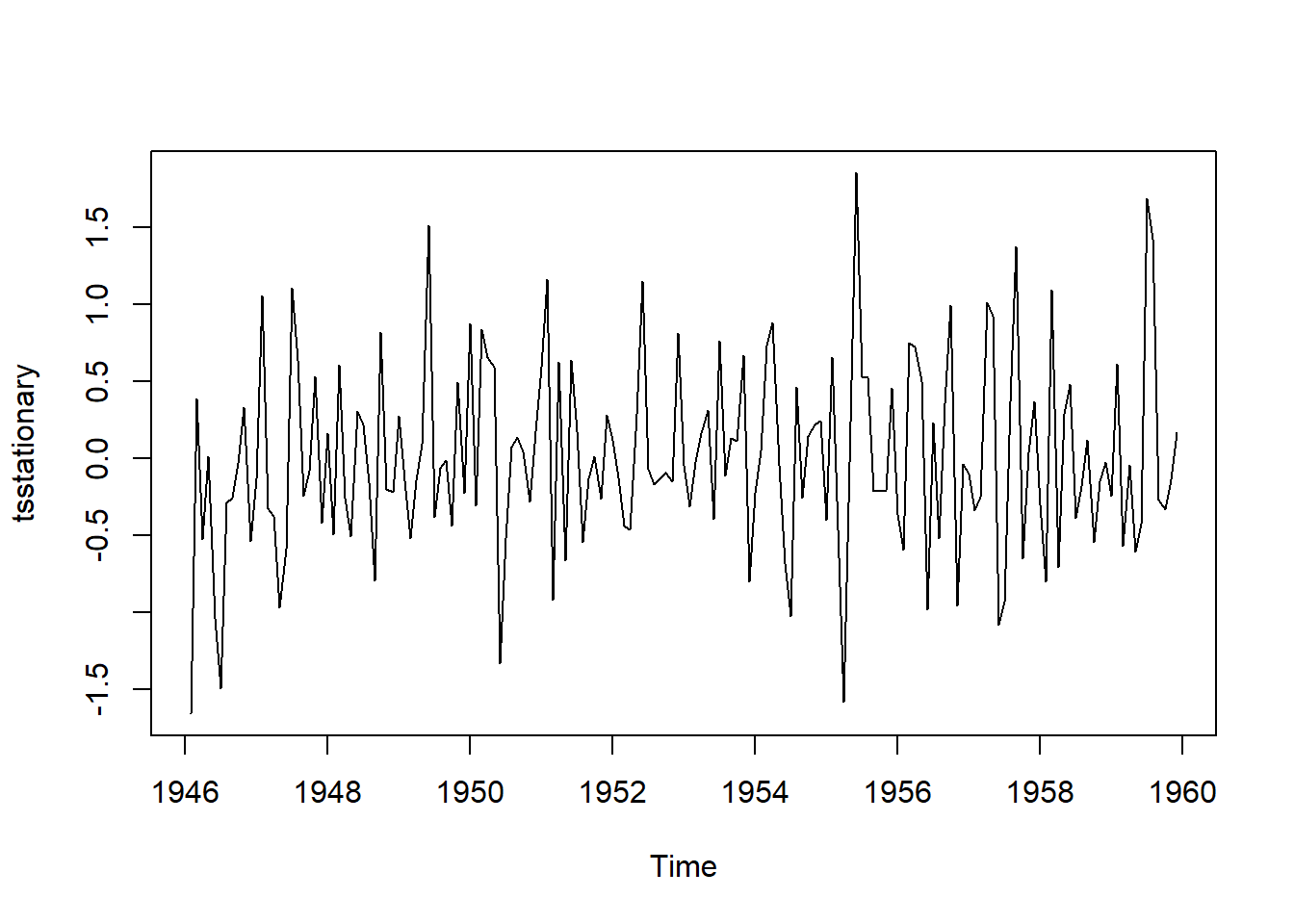
Figure 4.8: 8
8.1.3 Suavizado de tendencia (Smoothing)
El smoothing ayuda a ver mejor los patrones y las tendencias en las series de tiempo. Suaviza las irregularidades para ver la señal más clara. También suaviza la estacionalidad para que identificar mejor la tendencia. El suavizado no nos proporciona un modelo, pero puede ser un buen primer paso para describir varios componentes de la serie.
Se puede estimar el componente de tendencia de esta serie de tiempo alisando con una media móvil simple. por ejemplo de orden 3 o de orden 8 para mayor suavizado. Se utiliza la función SMA() del programa TTR.
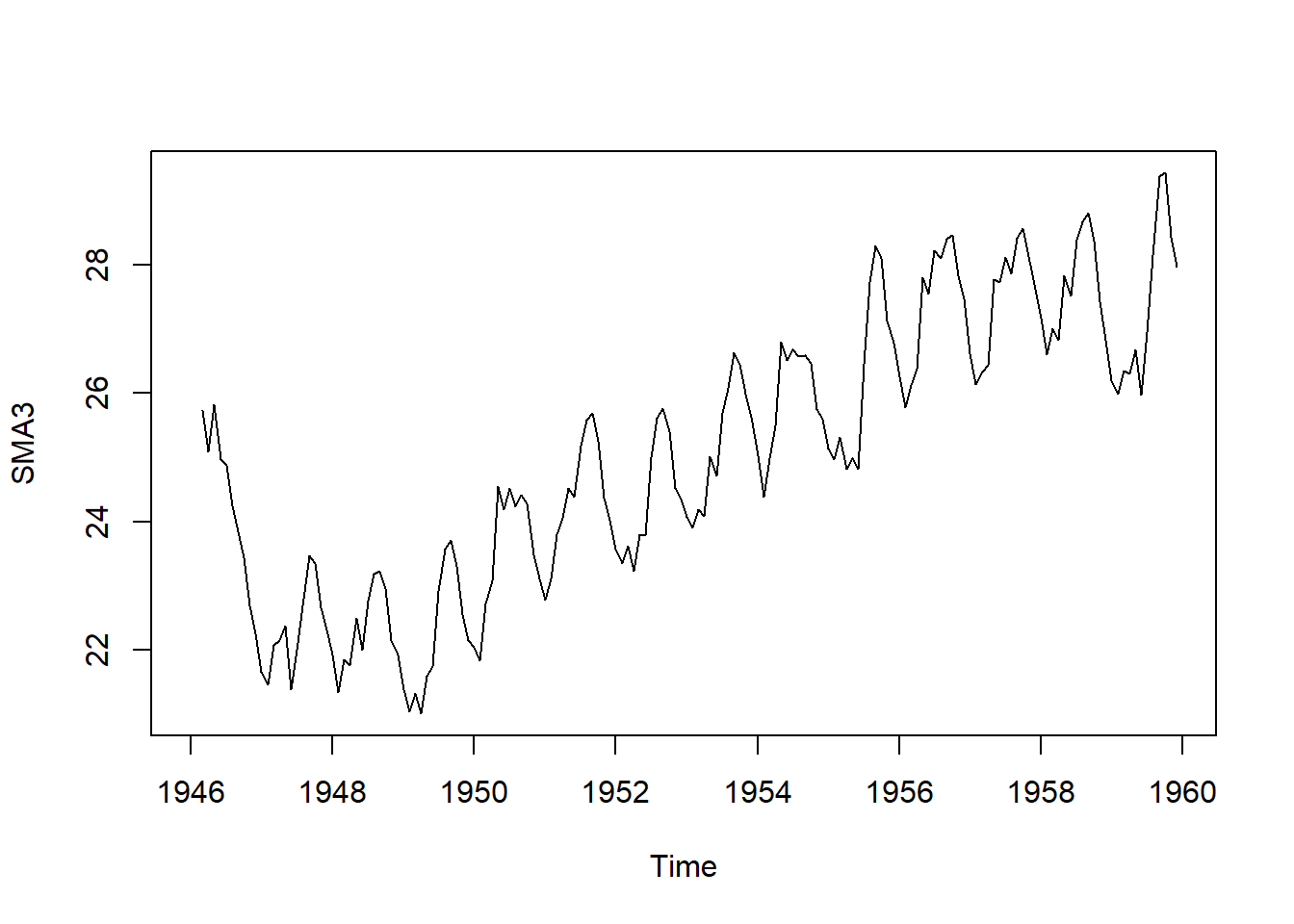
Figure 4.9: 8
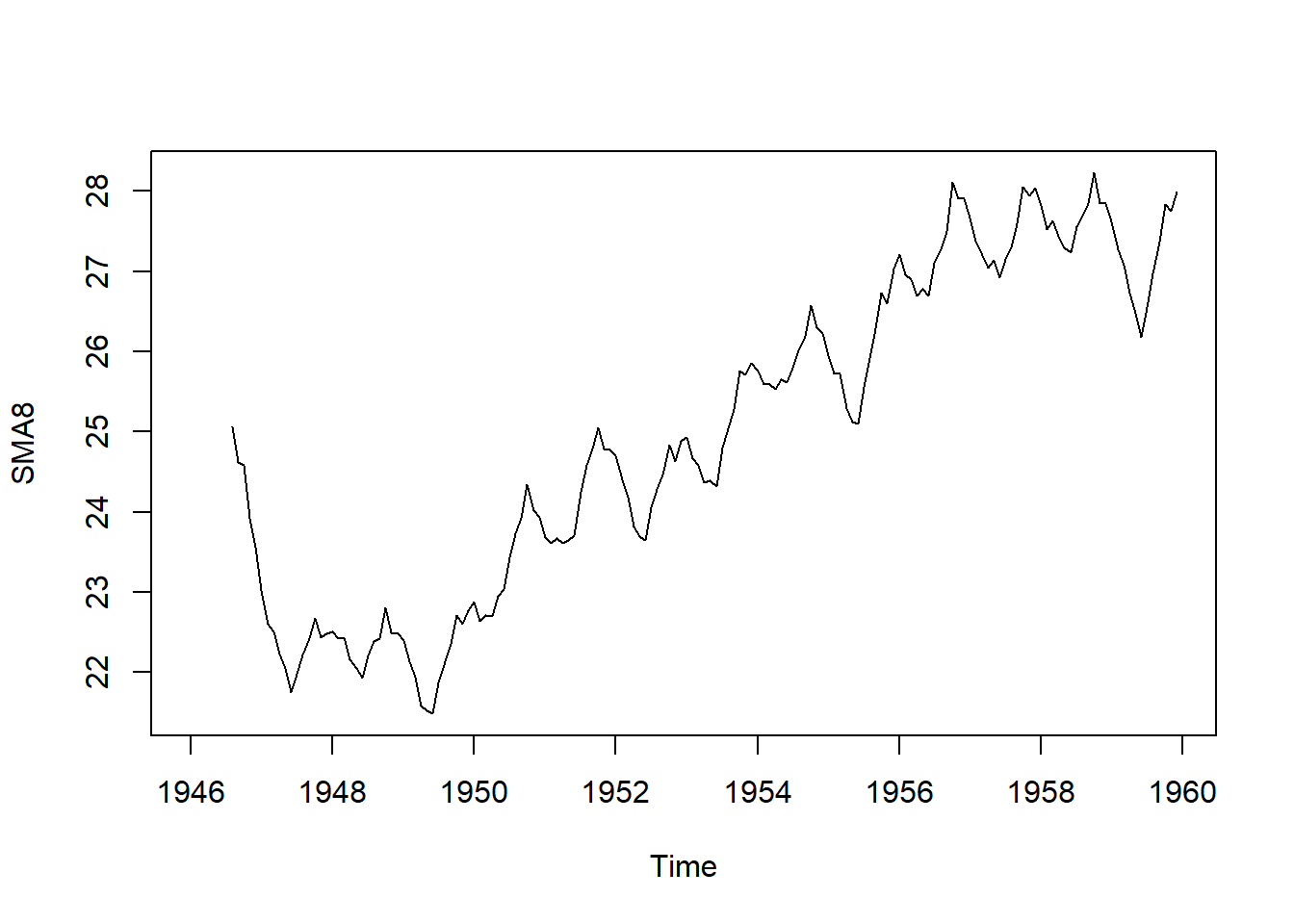
Figure 4.10: 8
8.2 Escogencia y ajuste del modelo
8.2.1 HoltWinters
Es una de las técnicas para hacer suavizado y predicción en series de tiempo. Se puede usar la función HoltWinters() del programa forecasts si la serie de tiempo puede describirse utilizando un modelo aditivo con tendencia creciente o decreciente y sin estacionalidad.
Se controla mediante el parámetro alfa, para la estimación del nivel en el punto de tiempo actual; beta para la estimación de la pendiente b del componente de tendencia en el punto de tiempo actual y gamma para el componente estacional en el momento actual.
Los parámetros tienen valores entre 0 y 1 donde los valores cercanos a 0 significan que se coloca poco peso en las observaciones más recientes.
library(forecast)
birthstimeseriesforecasts <- HoltWinters(birthstimeseriesseasonallyadjusted, beta=FALSE, gamma=FALSE)
birthstimeseriesforecasts
#> Holt-Winters exponential smoothing without trend and without seasonal component.
#>
#> Call:
#> HoltWinters(x = birthstimeseriesseasonallyadjusted, beta = FALSE, gamma = FALSE)
#>
#> Smoothing parameters:
#> alpha: 0.9418836
#> beta : FALSE
#> gamma: FALSE
#>
#> Coefficients:
#> [,1]
#> a 28.26434
plot(birthstimeseriesforecasts) # grafico de observados vs fitted 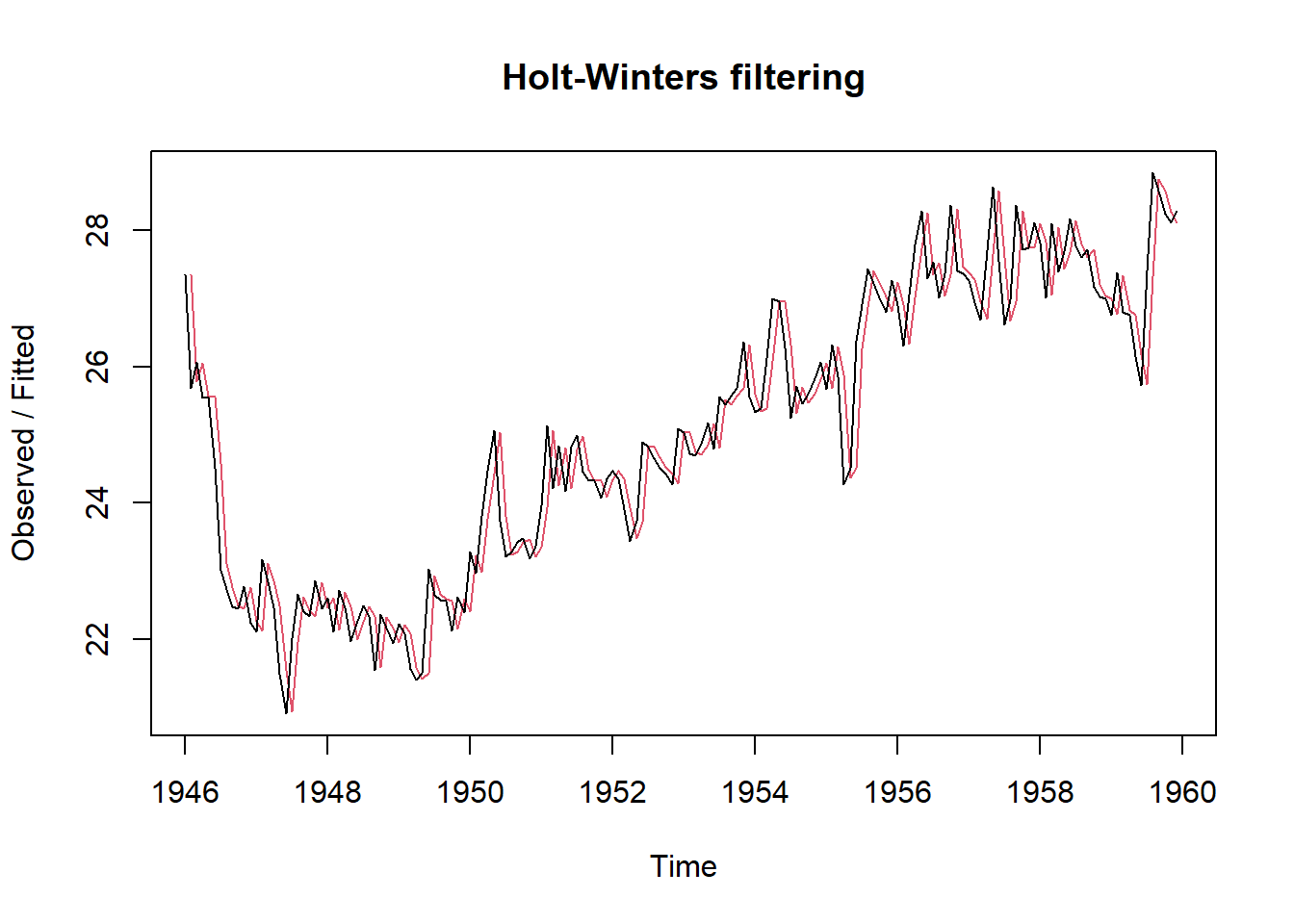
Figure 4.11: 8
Se usa la función forecast() para hacer predicción.
birthstimeseriesforecasts2 <- forecast(birthstimeseriesforecasts, h=12)
plot(birthstimeseriesforecasts2)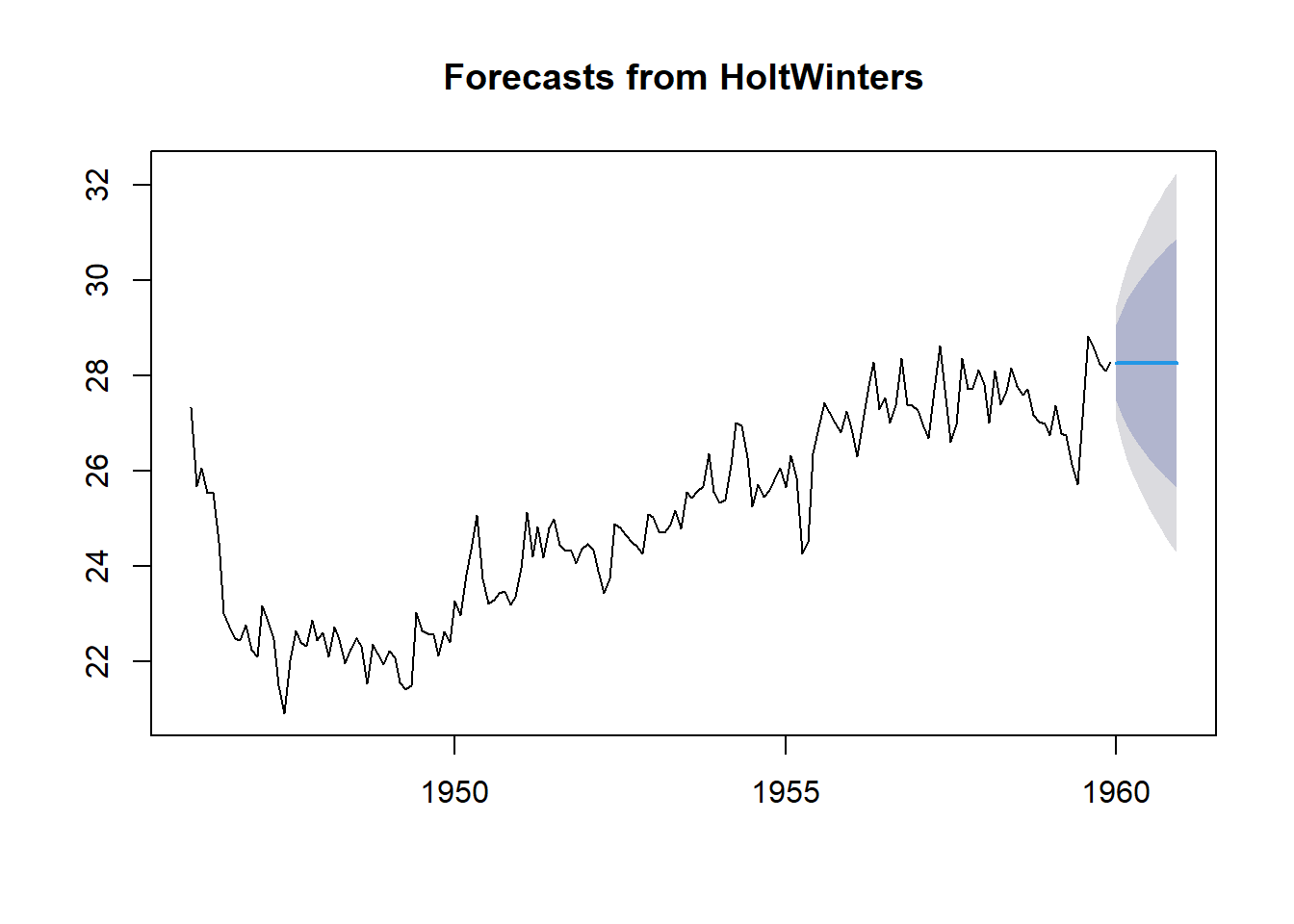
Figure 5.2: 8
Se grafican los residuales para verificar si los errores se distribuyen normalmente con media cero y variación constante
plot.ts(birthstimeseriesforecasts2$residuals) 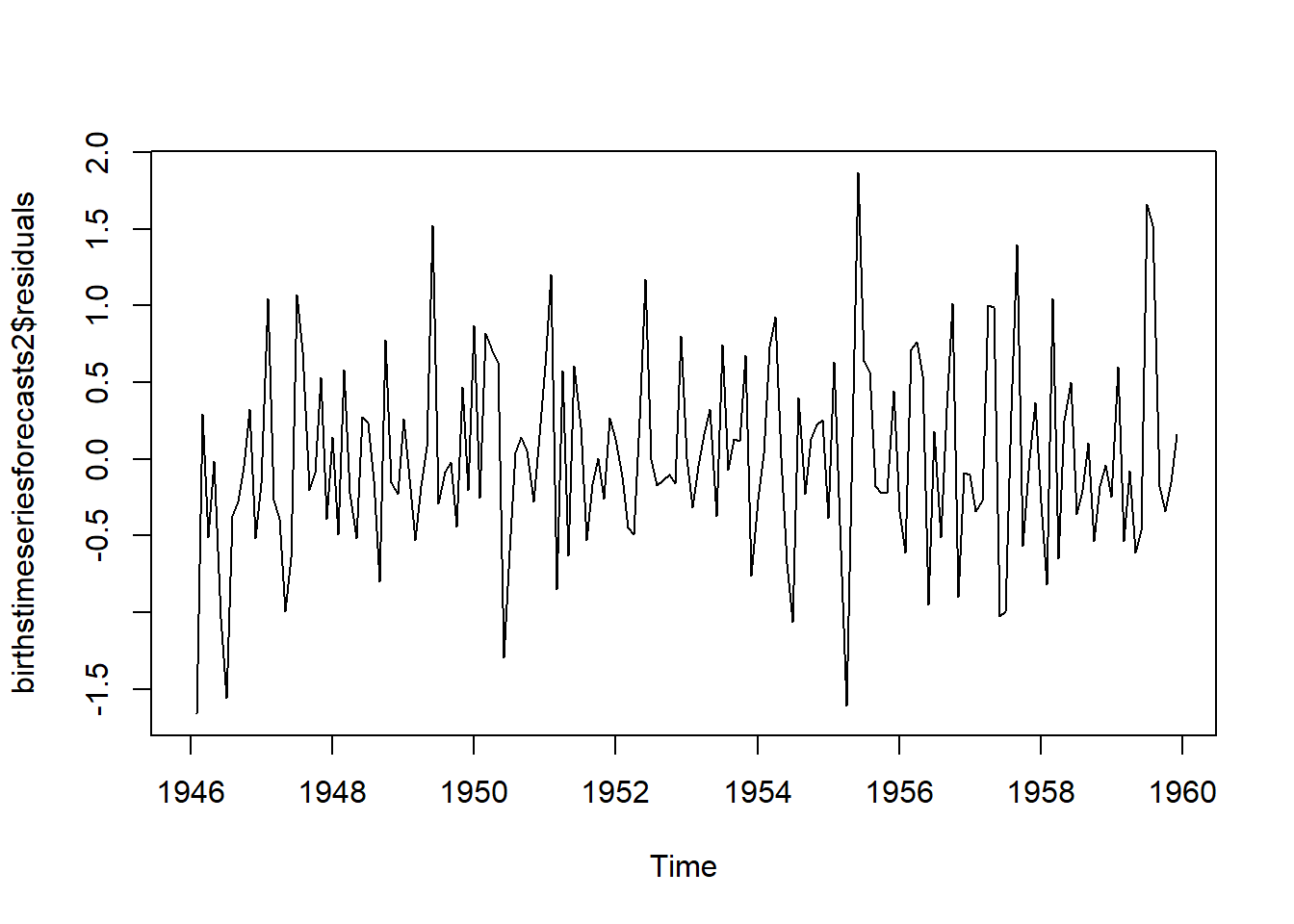
Figure 4.12: 8
En este ejemplo se ajusta la no estacionariedad calculando el logaritmo.
logbirthstimeseries <- log(birthstimeseries)
birthstimeseriesforecasts3 <- HoltWinters(logbirthstimeseries, beta=FALSE, gamma=TRUE)
plot(birthstimeseriesforecasts3)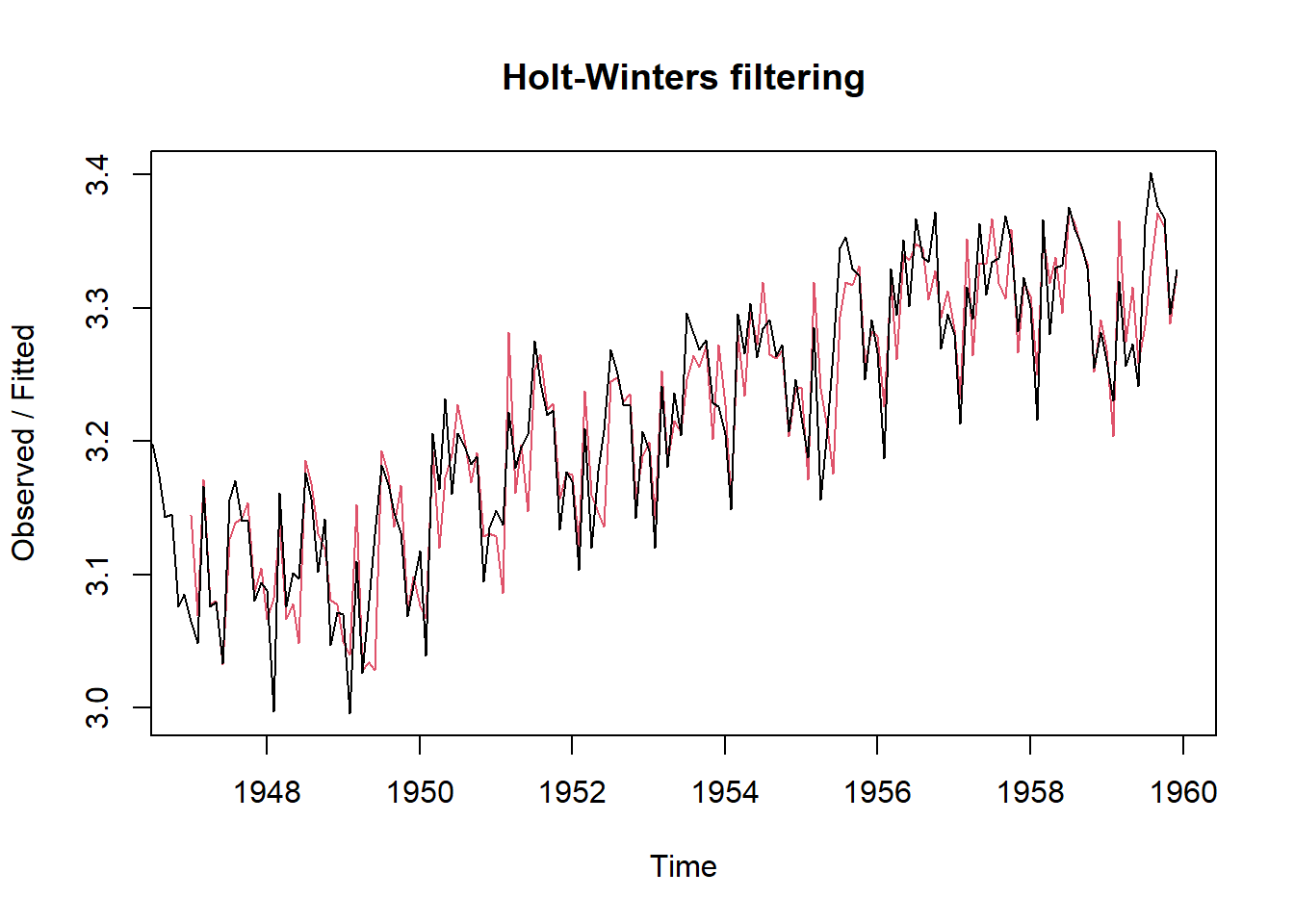
Figure 4.13: 8
birthstimeseriesforecasts3 <- forecast(birthstimeseriesforecasts, h=12)
plot(birthstimeseriesforecasts3)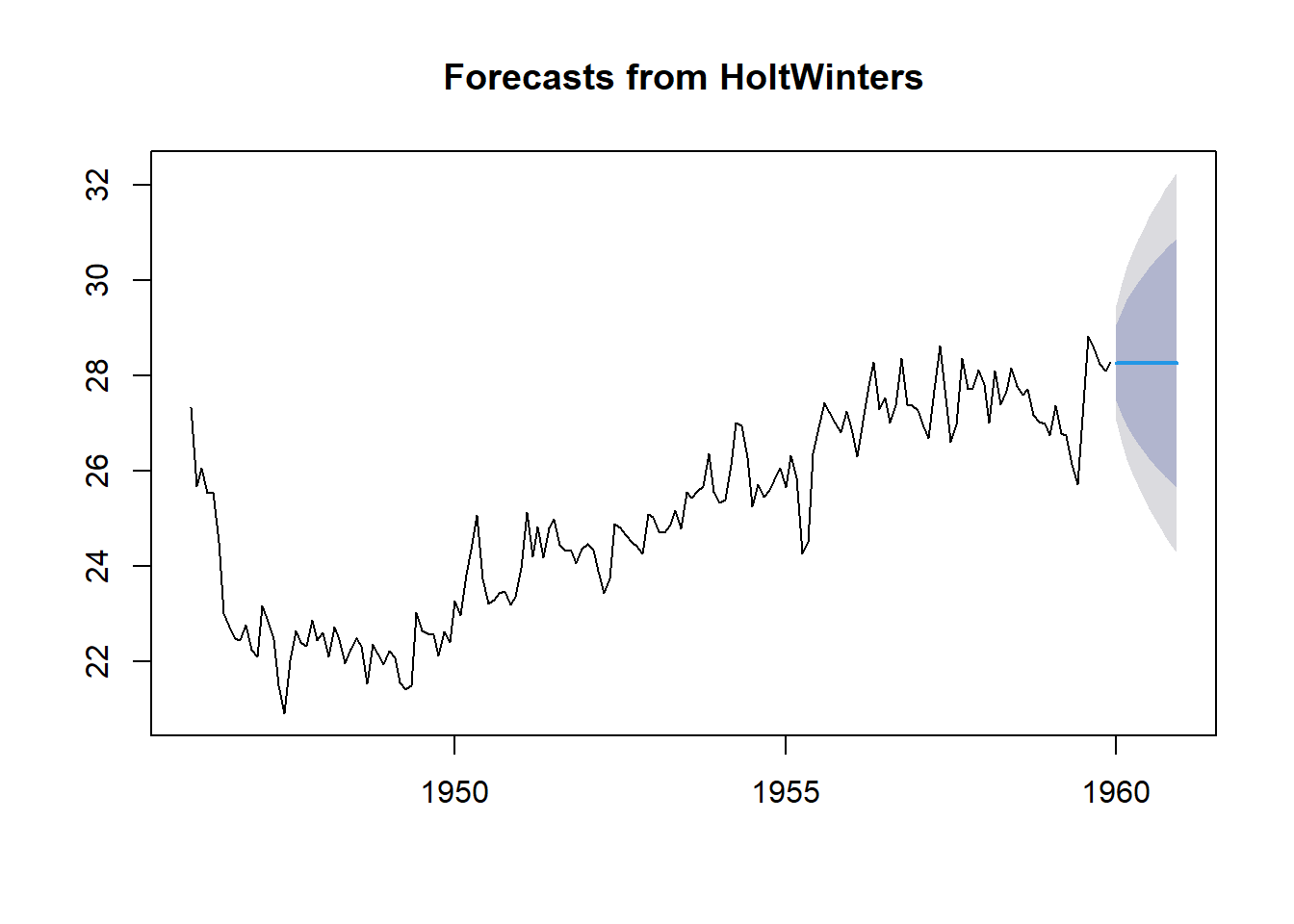
Figure 4.14: 8
8.2.2 ARIMA
ARIMA es una abreviación de AutoRegressive Integrated Moving Average. En sí, es una combinación de las propiedades de diferentes tipos de modelos:
(AR) Auto Regressive Son modelos donde el valor de una variable en un periodo se relaciona con los valores de periodos previos. Se refiere a los lags p de las diferencias de los valores entre las series.
(I) se refiere al orden del número diferencial que se usan para hacer las series de tiempo estacionarias.
(MA) Moving Average Consideran la posibilidad de una relación entre la variable y los residuales de periodos previos. Se refiere a los lags q de los errores,
Supuestos del ARIMA
- Los datos deben ser estacionarios: las propiedades de la serie no dependen del momento en que se capturan. Un proceso estacionario tiene una media y una variación que no cambian con el tiempo y no tiene una tendencia.
- Los datos deben ser univariados: ARIMA trabaja con una sola variable. La regresión automática tiene que ver con la regresión con los valores pasados.
La función acf() proporciona la autocorrelación en todos los lags posibles. La función pacf() describe la correlación entre todos los puntos de datos que están exactamente k pasos atrás.
acf(tsstationary, lag.max=34) # ajustar el modelo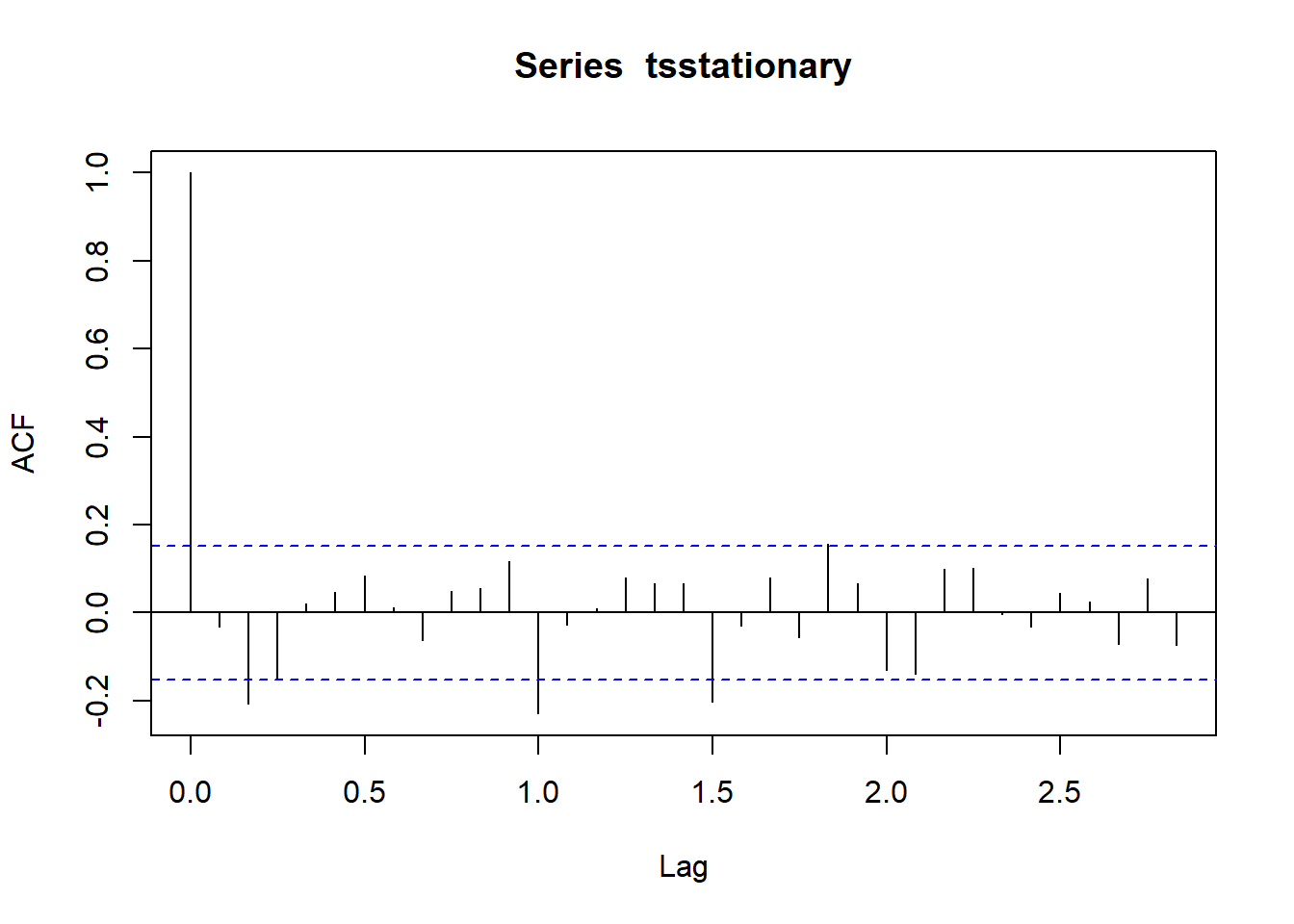
Figure 8.3: 8
pacf(tsstationary, lag.max=34)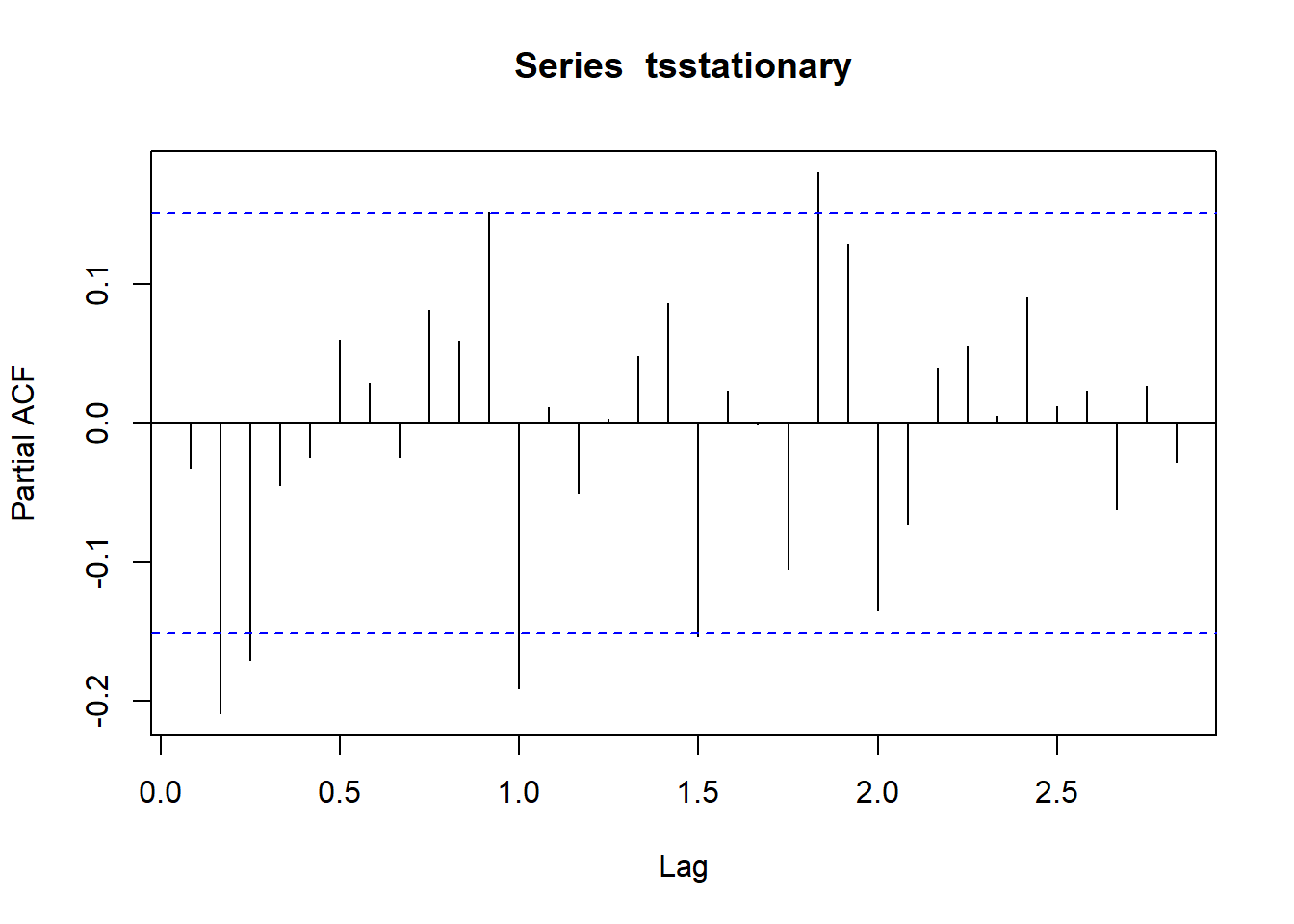
Figure 8.4: 8
El modelo ARIMA se corre una vez que los datos están listos y satisfacen todos los supuestos. Se ajustan tres variables: p, d y q con números enteros no negativos que se refieren a las partes AR, I, MA, respectivamente.
Para la escogencia del modelo se utiliza máxima verosimilitud (ML). Se maximiza el log-likelihood para valores de p, d y q respecto a los datos observados. Se calcula el Criterio de Información de Akaike (AIC) y el Criterio de Información Bayesiano (BIC). Se escoge el que tiene valores más bajos. Se verifican los valores de los coeficientes.
8.3 Diagnóstico del modelo
El diagnósitcos se realiza para determinar el patrón en los residuos del modelo elegido en el ACF de los residuos.
Si el modelo predictivo no se puede mejorar, no debería haber correlaciones entre los errores de pronóstico para las predicciones sucesivas. Para averiguarlo se realiza un correlograma de los residuales en la muestra utilizando la función acf().
acf(fitARIMA$residuals)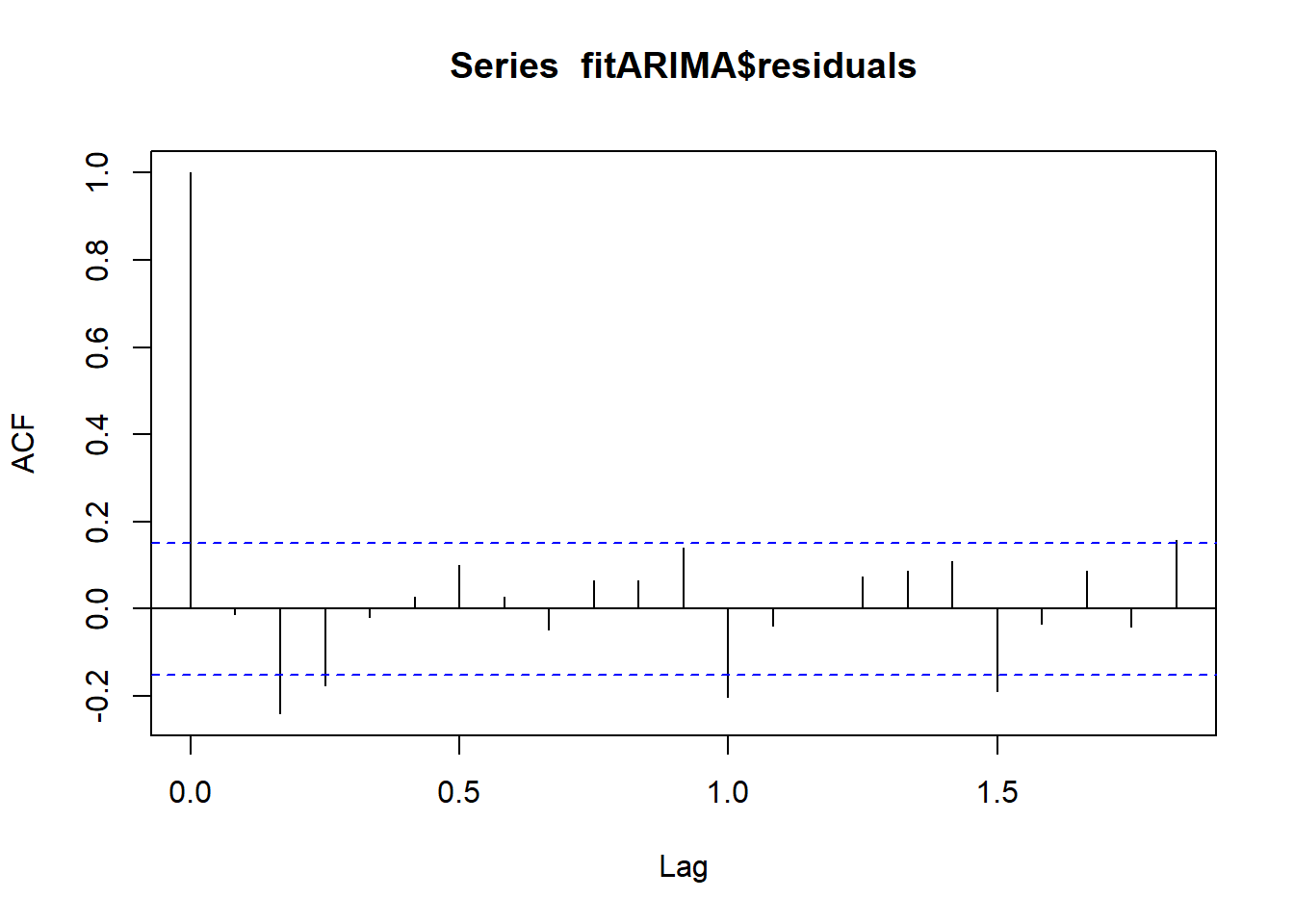
Figure 6.2: 8
Para probar si existe evidencia significativa de la no autocorrelación en los residuales se realiza la prueba Box-Ljung con la función Box.test(). Esta prueba evalua aleatoriedad general (independencia) basada en un número de lags. Se aplica a los residuos de un modelo ARIMA ajustado, no a la serie original. La hipótesis es que los residuos del modelo ARIMA no tienen autocorrelación.
Box.test(fitARIMA$residuals, lag=20, type="Ljung-Box")
#>
#> Box-Ljung test
#>
#> data: fitARIMA$residuals
#> X-squared = 43.672, df = 20, p-value = 0.001665
plot.ts(fitARIMA$residuals) 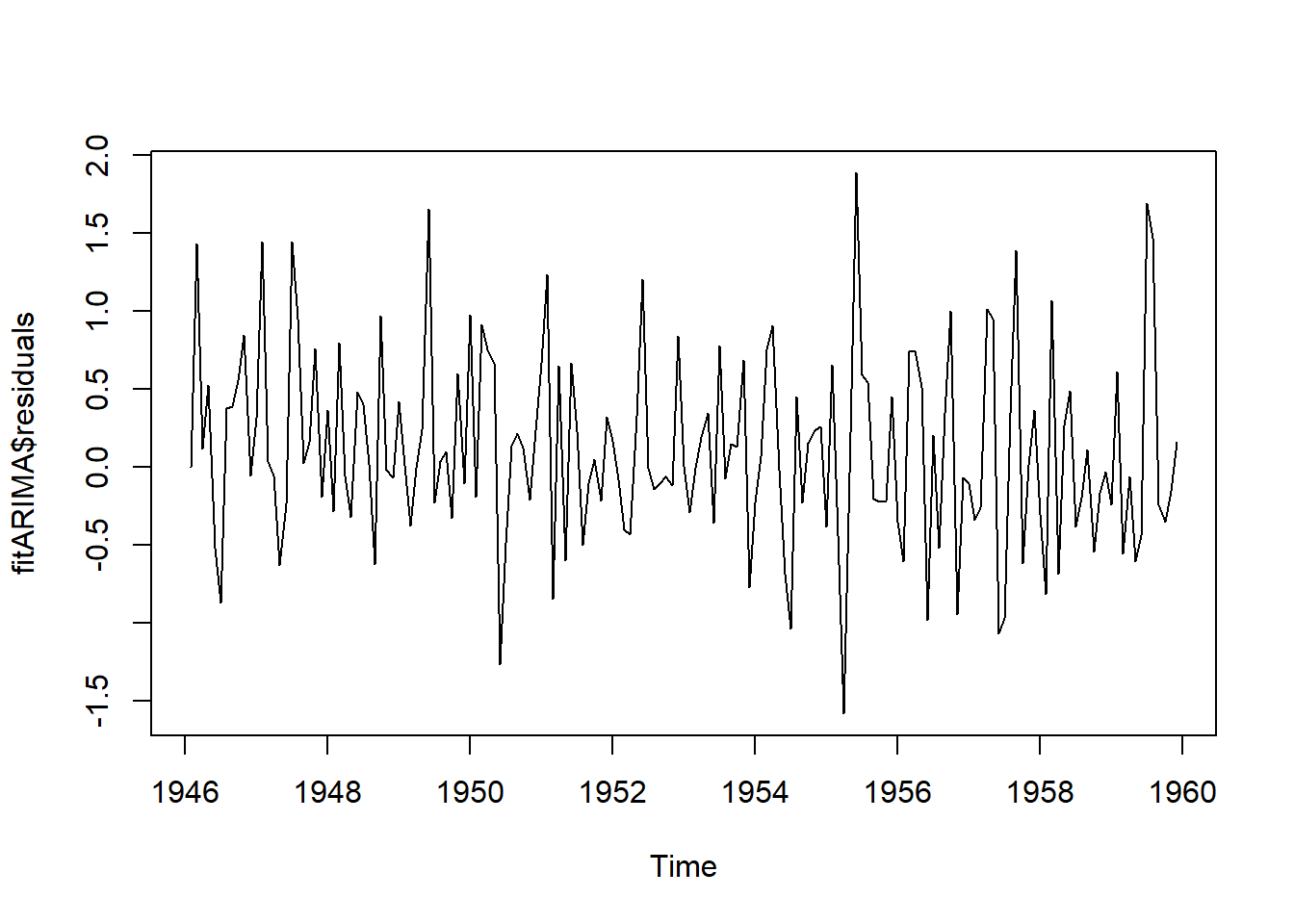
Figure 8.5: 8
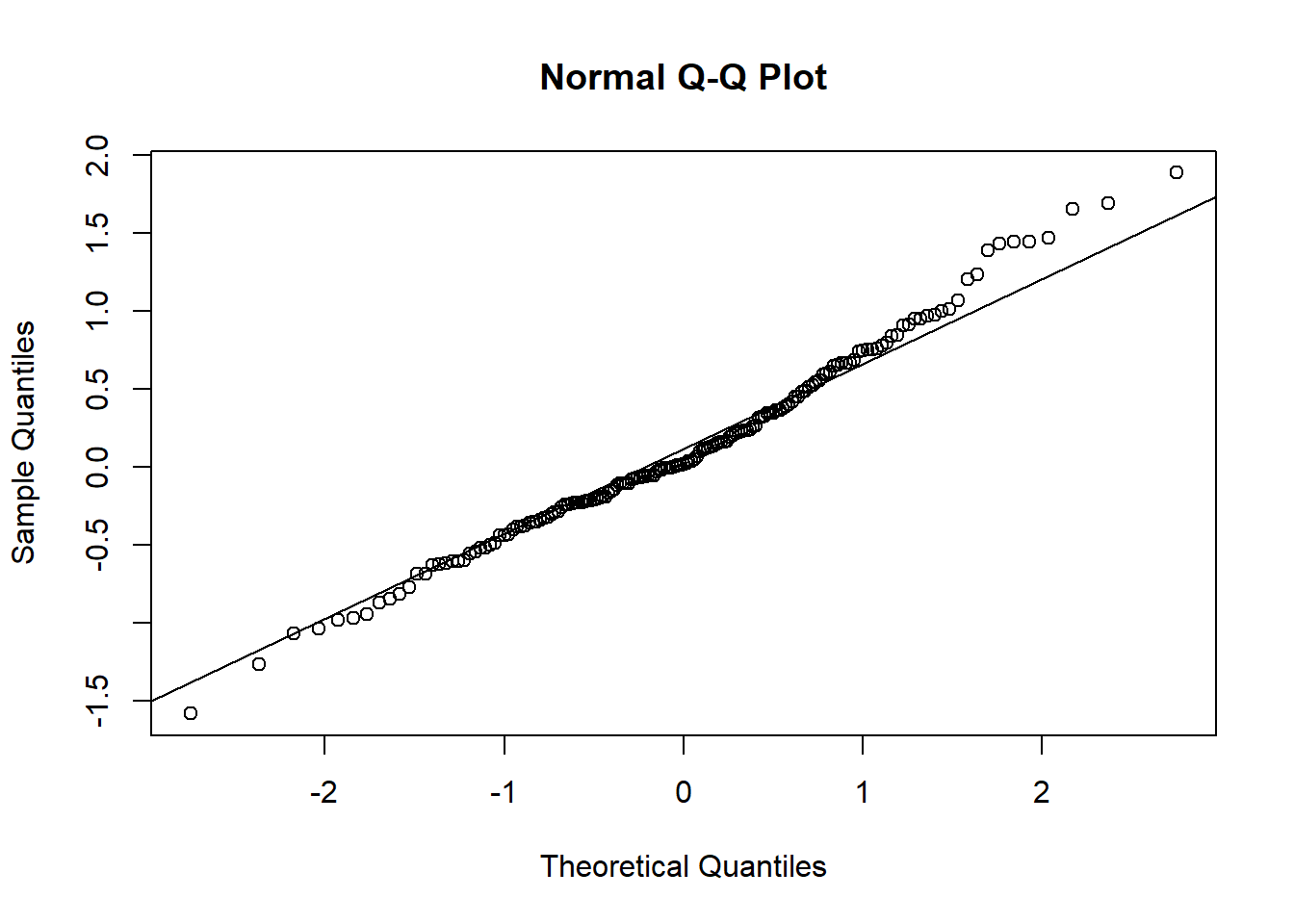
Figure 8.6: 8
8.4 La función auto.arima().
Se utiliza para la selección automática de modelos ARIMA además permite evaluarlos utilizando el Criterio de Información de Akaike (AIC) y el Criterio de Información Bayesiano (BIC)
library(forecast)
auto.arima(birthstimeseries, trace=TRUE)
#>
#> Fitting models using approximations to speed things up...
#>
#> ARIMA(2,1,2)(1,1,1)[12] : 298.0772
#> ARIMA(0,1,0)(0,1,0)[12] : 430.8611
#> ARIMA(1,1,0)(1,1,0)[12] : 379.9178
#> ARIMA(0,1,1)(0,1,1)[12] : 359.51
#> ARIMA(2,1,2)(0,1,1)[12] : Inf
#> ARIMA(2,1,2)(1,1,0)[12] : 353.8013
#> ARIMA(2,1,2)(2,1,1)[12] : 314.3744
#> ARIMA(2,1,2)(1,1,2)[12] : 300.1112
#> ARIMA(2,1,2)(0,1,0)[12] : 410.4715
#> ARIMA(2,1,2)(0,1,2)[12] : Inf
#> ARIMA(2,1,2)(2,1,0)[12] : 335.9213
#> ARIMA(2,1,2)(2,1,2)[12] : 315.1246
#> ARIMA(1,1,2)(1,1,1)[12] : 320.4393
#> ARIMA(2,1,1)(1,1,1)[12] : 301.0456
#> ARIMA(3,1,2)(1,1,1)[12] : 313.9098
#> ARIMA(2,1,3)(1,1,1)[12] : 298.7452
#> ARIMA(1,1,1)(1,1,1)[12] : 332.9843
#> ARIMA(1,1,3)(1,1,1)[12] : 316.3476
#> ARIMA(3,1,1)(1,1,1)[12] : 314.7169
#> ARIMA(3,1,3)(1,1,1)[12] : 312.7039
#>
#> Now re-fitting the best model(s) without approximations...
#>
#> ARIMA(2,1,2)(1,1,1)[12] : 329.6692
#>
#> Best model: ARIMA(2,1,2)(1,1,1)[12]
#> Series: birthstimeseries
#> ARIMA(2,1,2)(1,1,1)[12]
#>
#> Coefficients:
#> ar1 ar2 ma1 ma2 sar1 sma1
#> 0.6539 -0.4540 -0.7255 0.2532 -0.2427 -0.8451
#> s.e. 0.3004 0.2429 0.3228 0.2879 0.0985 0.0995
#>
#> sigma^2 = 0.4076: log likelihood = -157.45
#> AIC=328.91 AICc=329.67 BIC=350.21
fitARIMA2 <- arima(tsstationary, order=c(2,1,2),seasonal = list(order = c(1,0,0),period = 12),method="ML")
fitARIMA2
#>
#> Call:
#> arima(x = tsstationary, order = c(2, 1, 2), seasonal = list(order = c(1, 0,
#> 0), period = 12), method = "ML")
#>
#> Coefficients:
#> ar1 ar2 ma1 ma2 sar1
#> 0.5617 -0.2501 -1.6129 0.6504 -0.2834
#> s.e. 0.1685 0.0870 0.1684 0.1655 0.0823
#>
#> sigma^2 estimated as 0.3299: log likelihood = -145.64, aic = 303.27Notar que el mejor modelo fue c(2,1,2). Este modelo se compone de 2 períodos anteriores de tsstationary, un diferencial de primer orden y 2 períodos anteriores de ruido blanco.
Y ahora realizamos el diagnóstico del mejor modelo
acf(fitARIMA2$residuals)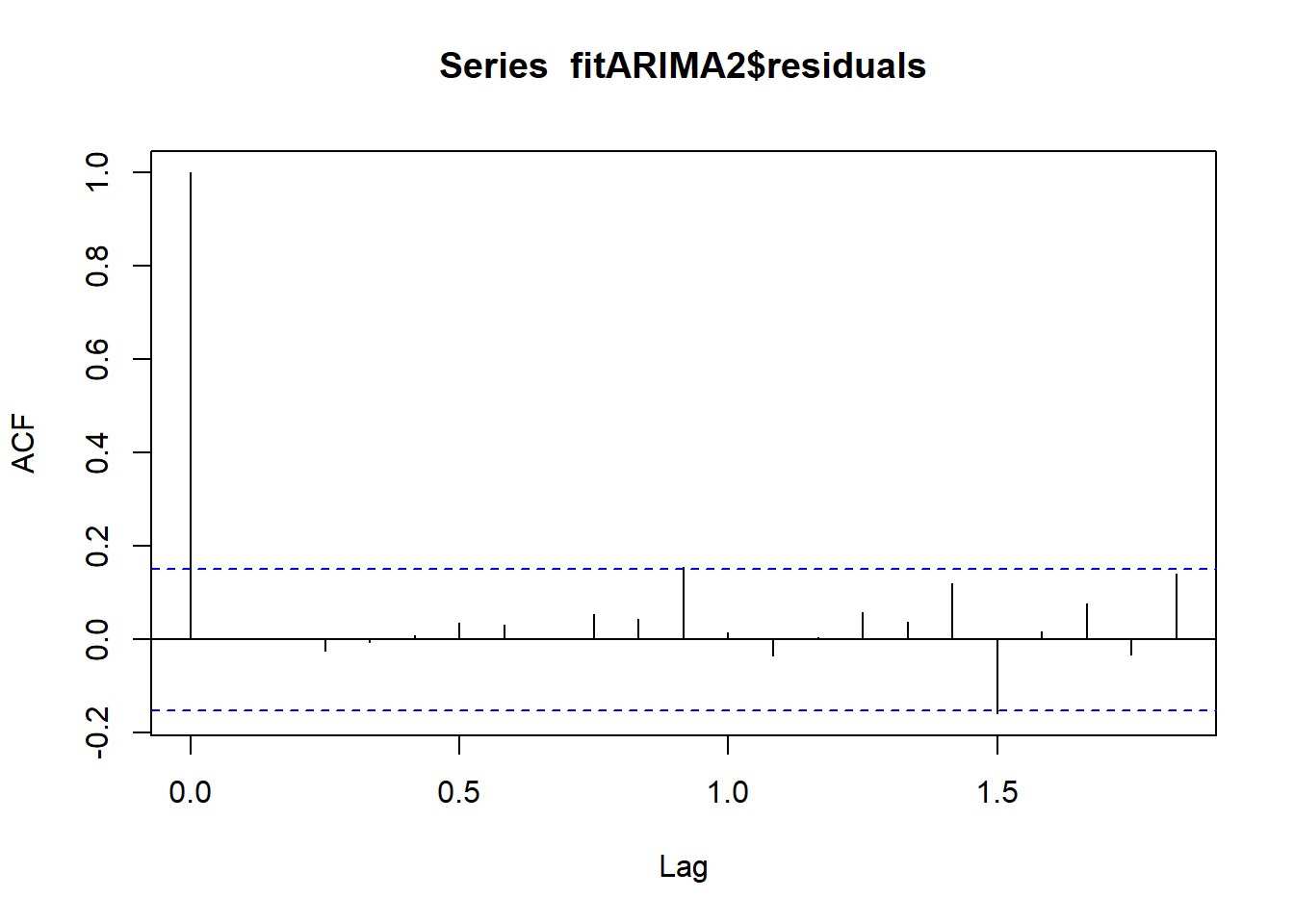
Figure 8.7: 8
Box.test(fitARIMA2$residuals, lag=20, type="Ljung-Box")
#>
#> Box-Ljung test
#>
#> data: fitARIMA2$residuals
#> X-squared = 15.5, df = 20, p-value = 0.7471
plot.ts(fitARIMA2$residuals) 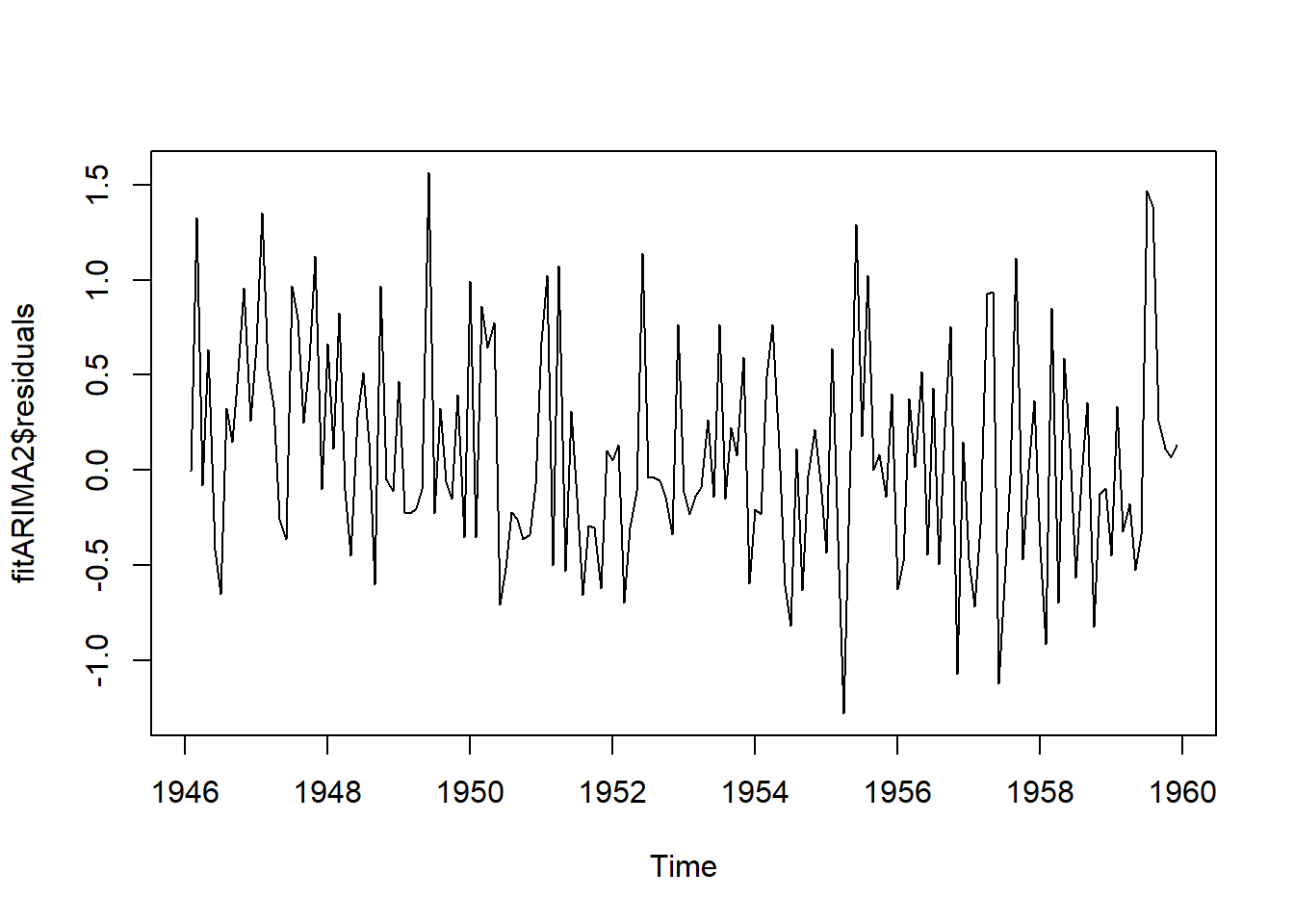
Figure 8.8: 8
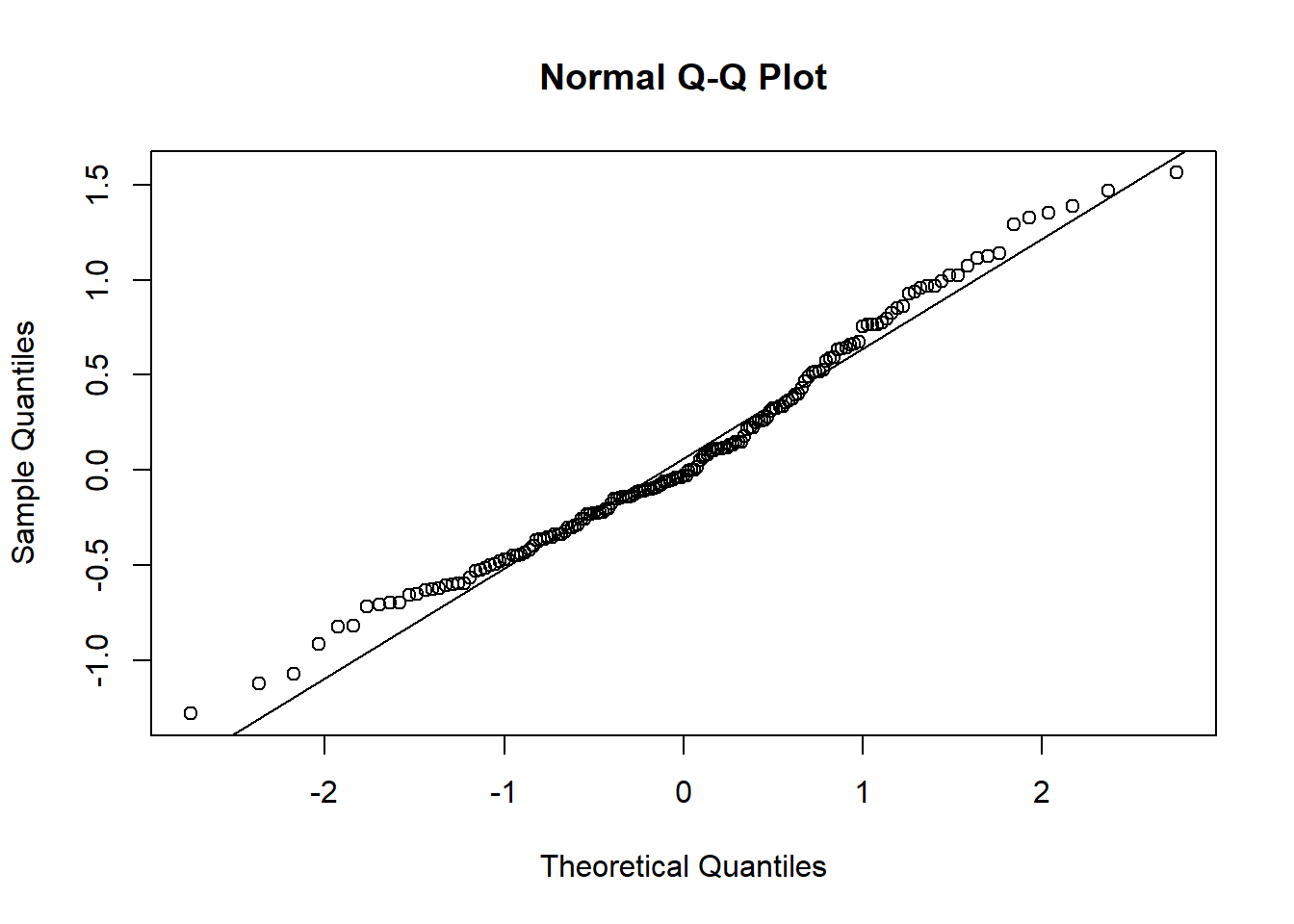
Figure 8.9: 8
8.5 Forecasting
La función predict() que se usa para predicciones a partir de los resultados de varias funciones de ajuste. El argumento n.ahead() especifica la cantidad de tiempo a predecir.
predict(fitARIMA2,n.ahead = 5)
#> $pred
#> Jan Feb Mar Apr
#> 1960 0.17230696 -0.10290049 0.23100115 0.08822442
#> May
#> 1960 0.25169868
#>
#> $se
#> Jan Feb Mar Apr May
#> 1960 0.5743664 0.5751196 0.5916049 0.5936322 0.5943244
futurVal <- forecast(fitARIMA2,h=5, level=c(99.5))
futurVal
#> Point Forecast Lo 99.5 Hi 99.5
#> Jan 1960 0.17230696 -1.439959 1.784573
#> Feb 1960 -0.10290049 -1.717281 1.511480
#> Mar 1960 0.23100115 -1.429654 1.891656
#> Apr 1960 0.08822442 -1.578121 1.754570
#> May 1960 0.25169868 -1.416590 1.919987
plot(futurVal)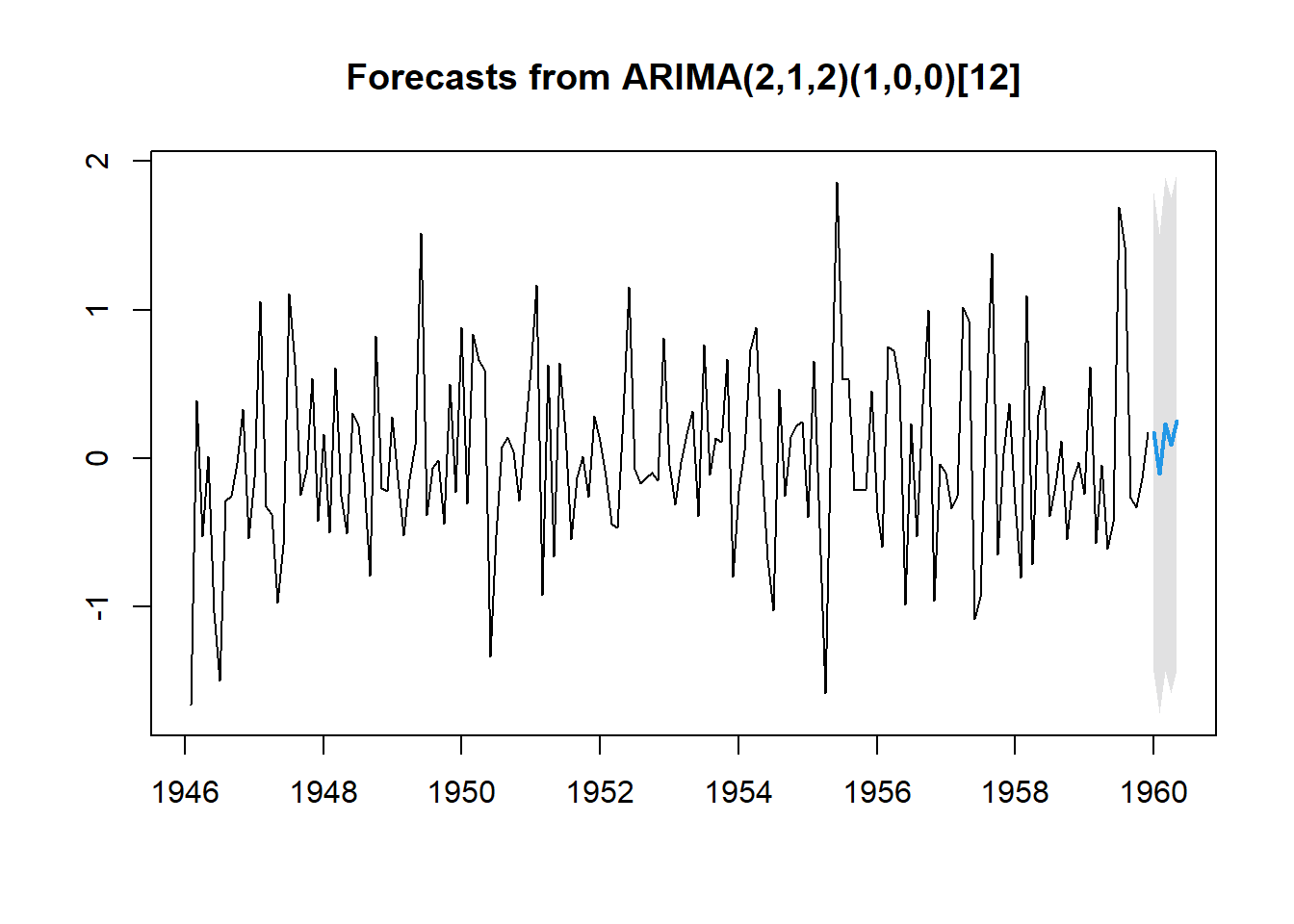
Figure 8.10: 8