Capítulo 7 Aprendizaje Automático (Machine Learning)

Desde hace algunos años, el aprendizaje automático (ML), junto con la inteligencia artificial (IA) y el aprendizaje profundo (Dl) están revolucionado prácticamente todas las áreas del conocimiento.

Este campo ha experimentado un enorme crecimiento gracias al desarrollo de nuevos conceptos teóricos y algoritmos como boosting, bagging, y random forest que hoy desafían, por primera vez, la supremacía de los enfoques estadísticos clásicos basados en probabilidad.

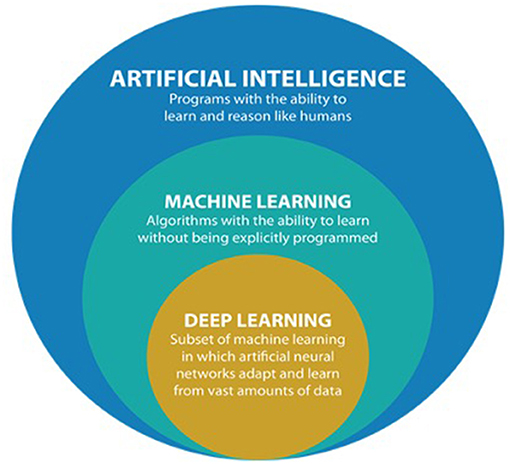
Imagen tomada de https://doi.org/10.3389/fmed.2021.710329

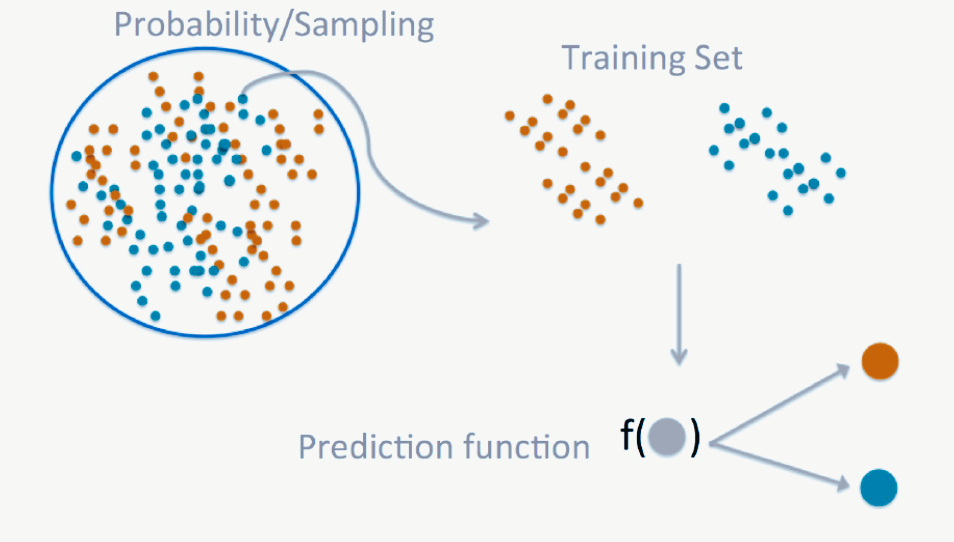
El aprendizaje automático se refiere a una subárea de la IA enfocada en proveer a los sistemas computacionales (programas y algoritmos) la habilidad para aprender y mejorar automáticamente a partir de set de datos específicos. En síntesis, el objetivo del aprendizaje automático es hacer “buenos” modelos predictivos para “nuevos” datos.

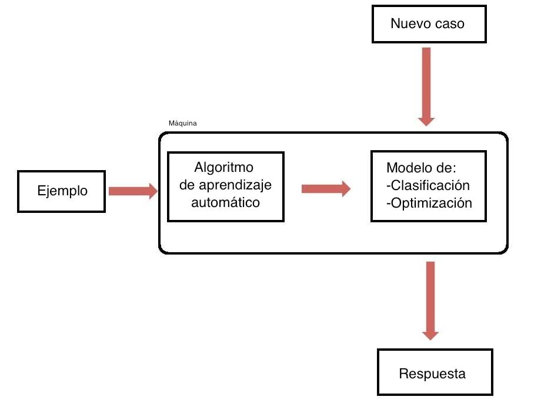
Imagen tomada del siguiente link

En el aprendizaje automático, los diferentes casos de uso de los algoritmos se denominan tareas. Las principales tareas según el objetivo de predicción son:
1) regresiones (predicción de una variable numérica) 2) clasificaciones (por ejemplo el etiquetado de una imagen) 3) agrupamiento (basados en métodos de distancia).

Las tareas son desarrolladas en diferentes ambientes de aprendizaje:
a) supervisado, b) no supervisado c) por reforzamiento

En el entorno de ML las variables independientes son denominadas entradas, features o predictores. Por otro lado, a las variables dependientes se les conoce como salidas, tags o variables de respuesta.

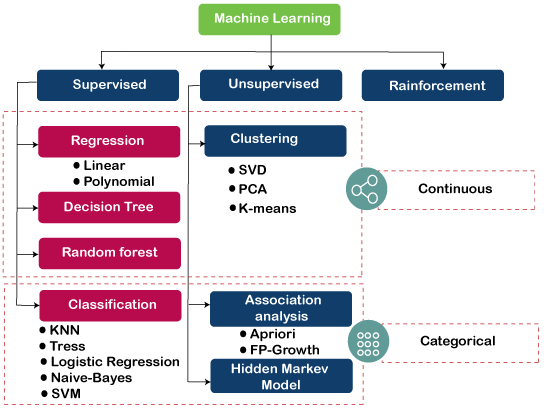
Imagen tomada de https://www.javatpoint.com/machine-learning-algorithms

7.1 Tipos de aprendizaje automático supervisado

7.1.1 Aprendizaje automático supervisado

En el aprendizaje supervisado, se desarrollan algoritmos que requieren de ejemplos de entrenamiento para los cuales se conoce de antemano la salida correcta (tag). Se tienen generalmente varias variables de entrada (x) y una variable de salida (Y). Se utiliza un algoritmo para aprender la función de mapeo de la entrada a la salida.

El científico de datos determina qué variables debe usar el modelo para desarrollar predicciones. Una vez que se completa el entrenamiento, el algoritmo aplicará lo aprendido a los nuevos datos.

Dos tipos:

Clasificación: cuando la variable de salida es una categoría, como “rojo” o “azul” o “sano” y “enfermo”.
Regresión: cuando la variable de salida es un valor real, como “dólares” o “peso”.

Ejemplos de algoritmos:

Linear regression (regresiones)
Clasificación de Naïve Bayes (clasificación)
Random forest (clasificación y regresiones)
Support vector machines (clasificación)

7.1.2 Aprendizaje automático no supervisado

En el aprendizaje no supervisado, se desarrollan algoritmos que tratan de encontrar la estructura subyacente o patrones presentes en datos no etiquetados. Solamente se tienen datos de entrada (x) y no se tienen variables de salida. No hay interferencia del científico de datos. Los algoritmos descubren por si mismos el patrón subyacente.

Se utlizan principalmente para hacer clustering o asociaciones, es decir, cuando se desea descubrir las agrupaciones inherentes en los datos, como por ejemplo agrupar clientes por comportamiento de compra.

Ejemplos de algoritmos:

K-means (K-medias)
Análisis de componentes principales

7.1.3 Aprendizaje automático por refuerzo

También existe un tipo particular denominado aprendizaje automático por refuerzo, donde los algoritmos se desarrollan para optimizar las acciones en función una recompensa.

El algoritmo se entrena interactuando con un entorno (virtual). El aprendizaje por refuerzo se utiliza en tareas en las que el aprendizaje depende de acciones ejecutadas y sus consecuencias producidas, por ejemplo, jugar juegos de computadora de estrategia.

7.2 Aplicaciones

Procesamiento del lenguaje natural (NLP): estudia la interacción entre las computadoras y los lenguajes humanos naturales. Algunos de los retos de esta área involucran el reconocimiento del habla, reconocimiento de la escritura, entendimiento del lenguaje natural y generación de lenguaje natural. Ejemplos: Cortana, Alexa y Grammarly
Visión por computador (CV): estudia cómo las computadoras pueden obtener un entendimiento de alto nivel a partir de imágenes digitales y videos. Utilizada para detección de objetos, rastreo en videos, detección de eventos, reconstrucción de escenas y restauración de imágenes. Ejemplos: Vehículos autónomos, reconocimiento facial.
Sistemas de recomendación (RS): son sistemas de filtrado de información que permiten predecir el nivel de preferencia que un usuario daría a un artículo. Ejemplos: Spotify, Netflix, Facebook, Youtube
Servicios financieros (FS): Se utiliza para identificar oportunidades de inversión y comercio y predecir movimientos en la bolsa de valores.
Otros ejemplos: Motores de búsqueda, diagnósticos médicos, predicción del estado del tiempo, clasificación secuencias ADN, predición de estructuras de proteinas.

Imagen tomada de https://futurism.com/

7.3 Consideraciones para realizar predicciones usando Aprendizaje Automático

La pregunta
El tipo de datos
Selección de características
Algoritmos
Parámetros
Evaluación

“La combinación de algunos datos y el deseo de una respuesta no garantiza que se pueda extraer una respuesta razonable de un set de datos determinado” John Tuckey

Propiedades deseables de las variables predictoras

Permiten una buena comprensión de los datos
Contienen información relevante
Han sido filtradas por criterio experto

Errores comunes al escoger variables predictoras

Hacer la selección automática
Omitir particularidades del set de datos
Descartar innecesariamente información

7.4 Etapas del aprendizaje automático

Adquisición de datos
Análisis exploratorio de datos (EDA) (resumen de estadísticas, visualizaciones, buscar correlaciones, tendencias generales)
Manipulación de datos (Limpieza y ordenación de datos, seleccionar atributos)
Ingeniería de características (Imputación de valores faltantes, manejo de datos duplicados, datos inconsistentes, ruido, valores atípicos, estandarización)
Selección del algoritmo

Determinar el tipo de problema (clasificación, regresión, análisis de conglomerados, análisis asociativo).
Seleccionar la técnica adecuada (árbol de decisión, regresión lineal, k-means, etc)

Construcción del modelo (training set y test set, ajustar para minimizar el error, refinado)
Evaluar el rendimiento (Accuracy, Confussion matrix, curva ROC)
Comunicación y actualización (Resumen los hallazgos, monitoreo, actualización del modelo)

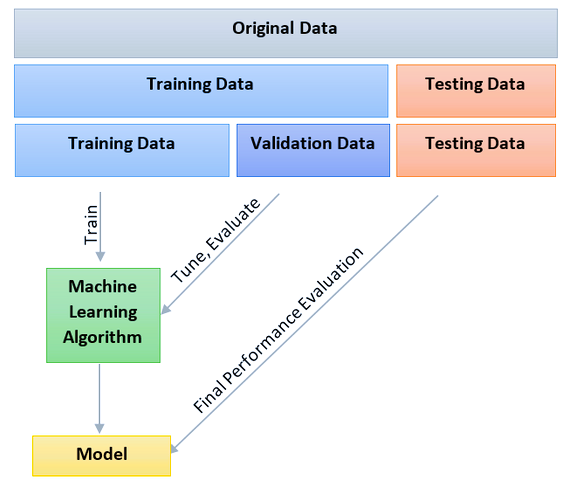
7.5 Ejecución del modelo

Divida los datos en un set para entrenamiento y otro para prueba (p.e. 60% entrenamiento, 20% test, 20% validación)
Escoja algunas variables dentro del training y use cross-validation
En el set de training escoja funciones de predicción
Aplique funciones en testing set y refine modelo
Aplique al menos un tipo de evaluación del error
Evite pequeños tamaños de muestra
Training set debe contener al menos 60% de los datos
El test set no se toca

7.6 Métricas de evaluación

7.6.1 Tipos de error

Verdadero positivo: correctamente identificado
Falso positivo: incorrectamente identificado (sano incorrectamente identificado como enfermo). Falsas alarmas o Error tipo I.
Verdadero negativo: rechazos correctos (enfermo correctamente identificado)
Falso negativo: incorrectamente rechazado (enfermo incorrectamente identificado como sano). Error de tipo II

7.6.2 Metricas del error

Precisión (Accuracy): Una de las métricas más utilizada en aprendizaje automático. Probabilidad de que resultados sean correctos. El porcentaje de ejemplos correctamente estimados del total de predicciones hechas
Error cuadrático medio (MSE): mide el promedio de los errores al cuadrado. Sensible a los outliers.
Raíz cuadrada del error medio (RMSE): es la raíz cuadrada del MSE.
Desviación absoluta del promedio o desviación media. Es la media de las desviaciones absolutas y es un resumen de la dispersión. Medida robusta.
Sensibilidad: Razón de verdaderos positivos. La probabilidad de que para un sujeto enfermo se obtenga en una prueba diagnóstica un resultado positivo.
Especificidad: la capacidad de la prueba para detectar la enfermedad. Razón de Verdaderos Negativos.
Kappa: Similar a la exactitud pero normalizada

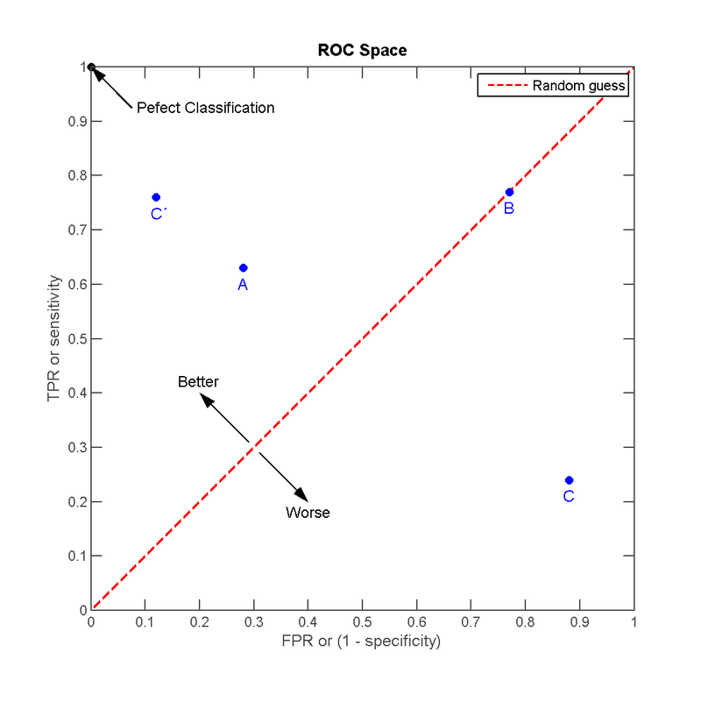
7.6.3 Curva ROC (Receiver Operator Characteristic)

Representación gráfica de la sensibilidad frente a la especificidad para un clasificador. Una representación de la razón de verdaderos positivos frente a la razón de falsos positivos. Usado evaluar el desempeño de modelos en problemas de clasificación.

El mejor método posible: la esquina superior izquierda del espacio ROC, representando un 100% de sensibilidad y un 100% también de especificidad. Los valores de AUC (Area under de curve) por arriba de 0.8 son considerados buenos.

7.6.4 Validación cruzada (Cross-Validation)

Técnica utilizada para evaluar los resultados de un análisis y garantizar que son independientes de la partición entre datos de entrenamiento y prueba. Consiste en repetir y calcular la media de las medidas de evaluación sobre diferentes particiones.

Se utiliza para estimar la precisión de un modelo que se llevará a cabo a la práctica. Permite escoger mejores variables, mejores modelos de predición, parámetros de las funciones, comparar diferentes métodos.

Pasos:

Se dividen datos en set de entrenamiento y prueba
Se construye modelo en el set de entrenamiento
Se evalúa en el set de prueba
Se repite el proceso y promedian errores estimados

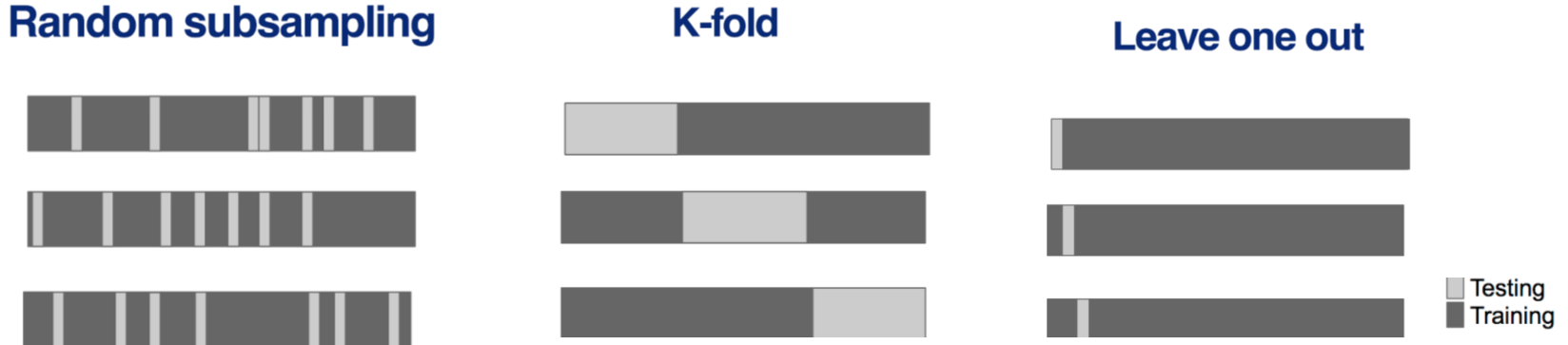
Consideraciones:

El Random sampling de ser sin remplazo
El Random sampling con remplazo es un bootstrap
Entre mayor k el K-fold, menor desviación, pero mayor será la varianza
Para datos de series de tiempo, los datos deben usarse en trozos.
El método Leave-one-out cross-validation (LOOCV) implica tener una sola muestra para prueba y todo el resto para entrenamiento. El error obtenido es muy bajo, pero es computacionalmente costoso.

7.6.5 Matriz de Confusión (Confusion matrix)

Es una herramienta que permite visualizar el desempeño de un algoritmo. Cada columna representa el número de predicciones y cada fila representa a las instancias en la clase real. Facilitan ver si el sistema está confundiendo dos clases.

7.7 Principales algoritmos

En el ambiente de aprendizaje automático se han desarrollado una gran variedad de familias de algoritmos de acuerdo a las tareas a realizar. Dentro de cada familia, también hay diferentes tipos de algoritmos.

Fuente: AI SCIENCES

A continuación, presentaremos algunos de los más utilizados en ciencias naturales y principalmente con datos tabulares.

7.7.1 Árboles de decisión

Supervisado. Clasificación y regresión
Modelo no lineal de predicción basado en construcciones lógicas en forma de árbol.
Sirven para representar una serie de condiciones que ocurren de forma sucesiva
Iterativamente dividen las variables en grupos
Evalúan la homogeneidad dentro de los grupos
Separan de nuevo los grupos de ser necesario

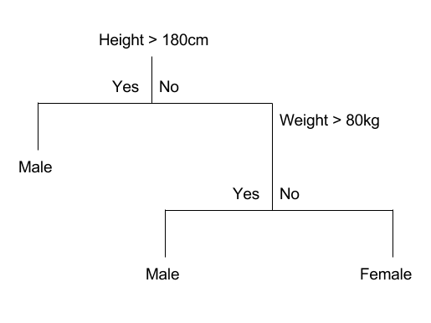
Pros

Fáciles de interpretar
Variables continuas y categóricas

Contras

Difícil de estimar la incertidumbre
Resultados pueden variar

7.7.2 Random Forest (Bosques Aleatorios)

Supervisado. Clasificación y regresión
Funciona mediante la construcción de una multitud de árboles de decisión en el momento del entrenamiento.
El resultado es la moda de las clases (clasificación) o la predicción media (regresión) de los árboles individuales

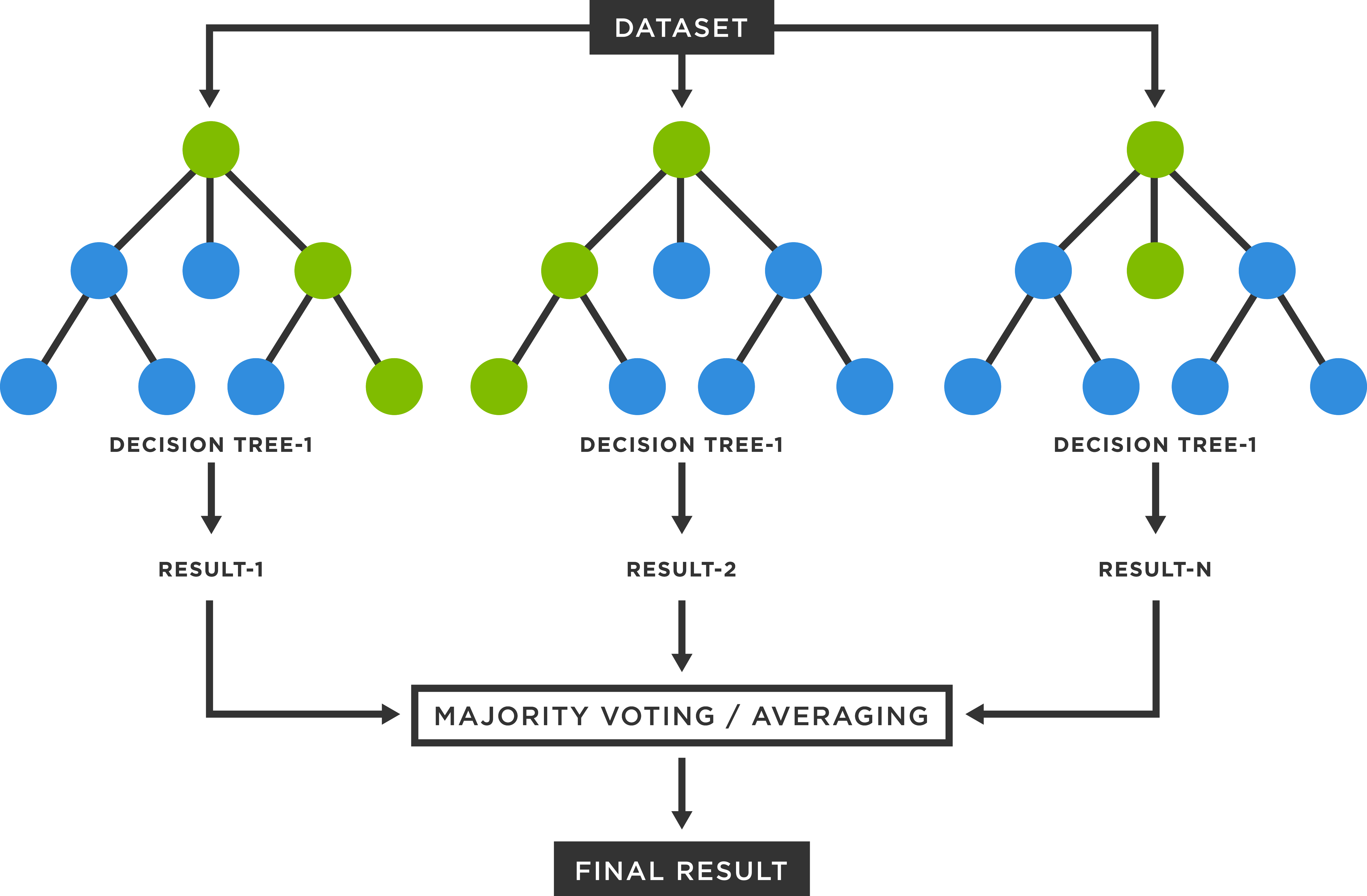
Imagen tomada de https://www.tibco.com/reference-center/what-is-a-random-forest

Pros

Exactitud
Popular y ampliamente utilizado
Calcula el valor de importancia de variables predictoras

Contras

Velocidad
Interpretabilidad
Overfitting

7.7.3 Boosted Regression Tree (BRT)

Supervisado. Clasificación y regresión
El modelo Boosted Regression Tree (arbol de regresión potenciado) resultan de la combinación de dos técnicas: algoritmos de árboles de decisión y metodos de boosting.
Al igual que los modelos Random Forest, los BRT ajustan repetidamente muchos árboles de decisión.
Los BRT utilizan el método de boosting en el que los datos de entrada se ponderan en árboles posteriores de manera sucesiva, de manera que el modelo intenta mejorar continuamente su precisión.

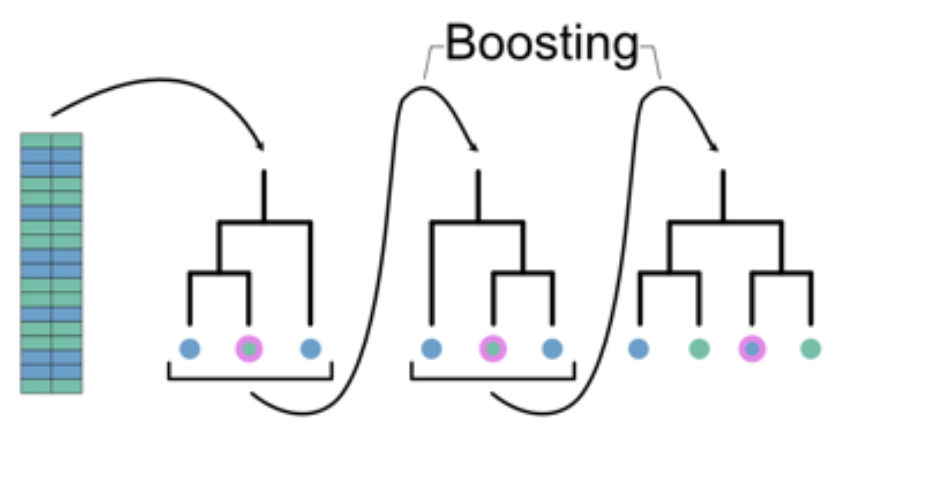
Pros

Permite calcular el valor de importancia de predictores
El mejor ajuste es detectado automáticamente por el algoritmo
El modelo representa el efecto de cada predictor después de tener en cuenta los efectos de otros predictores
Robusto a valores perdidos y atípicos

Contras

Requiere de al menos 2 variables predictoras para correr
Modelo de alta complejidad

7.7.4 Clasificador Bayesiano (Naive Bayes Classifier)

Supervisado. Clasificación y regresión
Usa teorema de Bayes para encontrar clasificación óptima
Asume que los datos siguen modelo probabilístico condicional
Estima parámetros de datos históricos y calcula la probabilidad posterior de cada clase en set de prueba.
Robusto para atributos irrelevantes
Razonablemente exacto en problemas reales
Asume independencia entre los atributos

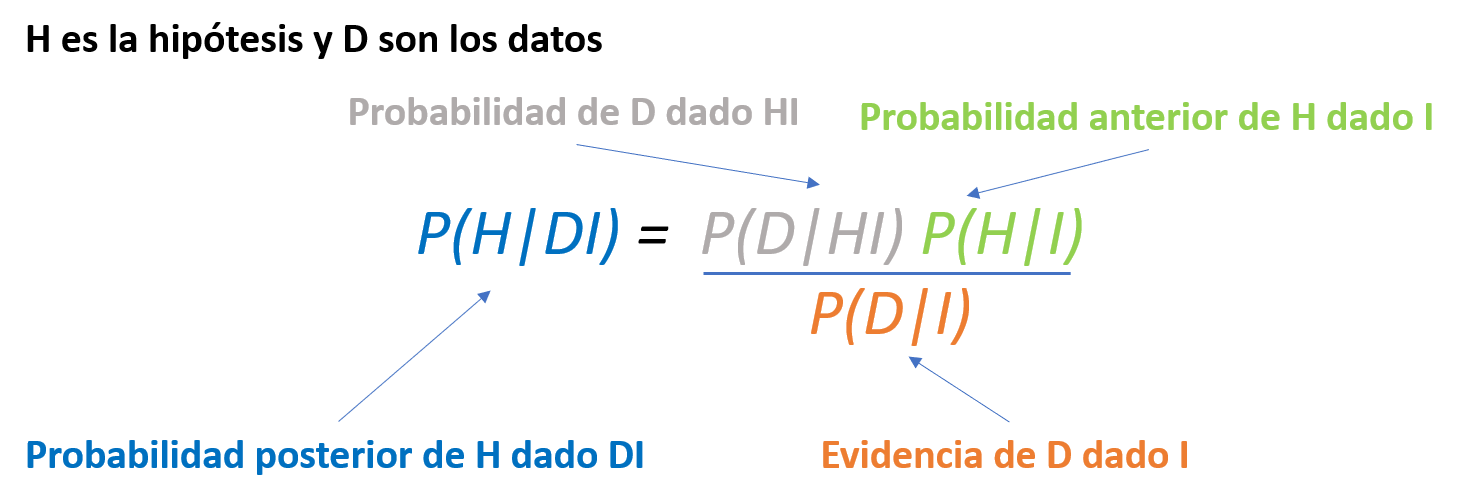
7.7.5 Support Vector Machine

Supervisado. Clasificación y regresión
Conjunto de algoritmos de aprendizaje supervisado relacionados con problemas de clasificación y regresión.
Se etiquetan clases y se entrena la SVM para construir un modelo que prediga la clase de una nueva muestra.
La SVM es un modelo que representa a los puntos de muestra en el espacio, separando las clases a 2 espacios lo más amplios posibles mediante un hiperplano de separación definido.

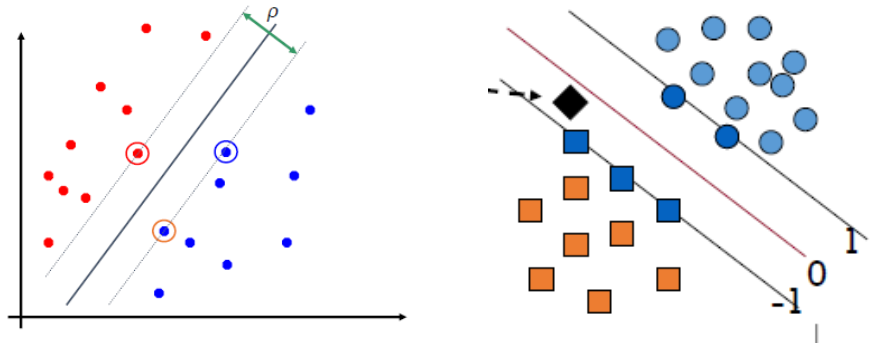
SVM no lineal

Se utiliza una función Kernel cuando algoritmo SVM debe tratar con más de dos variables predictoras, líneas curvas y clasificaciones en más de dos categorías.
La función supera esas limitaciones mapeando espacio de la característica original a un espacio de la característica de dimensión superior donde el conjunto de entrenamiento es separable.

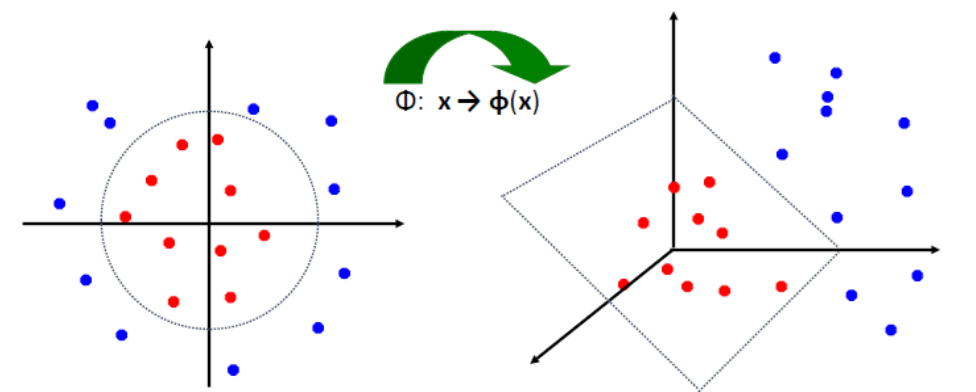
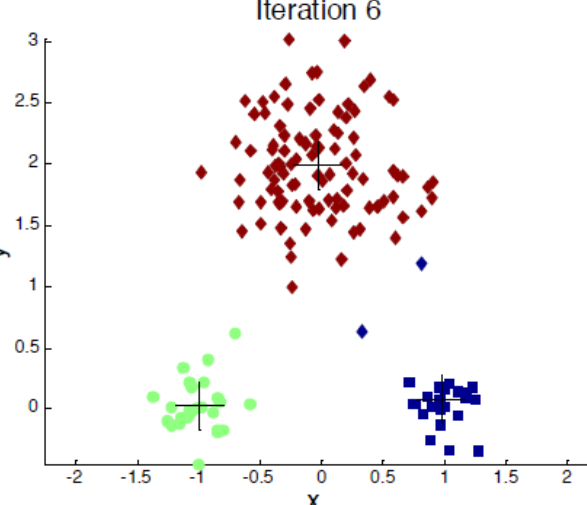
7.7.6 K-medias (K-Means Clustering)

No supervisado. Agrupamiento
K-medias es un método de agrupamiento que tiene como objetivo la partición de un conjunto de n observaciones en k grupos en el que cada observación pertenece al grupo cuyo valor medio es más cercano
Se utiliza cuando no hay etiquetas para hacer las predicciones
Crea clusters con un centroide. Cada punto es asignado al cluster con centroide más cercano.
Construye el predictor y evalúa los clusters de predicción en nuevo set de datos
El número de clusters K, debe especificarse

## Ejemplos prácticos ### Partición de datos Se utiliza la función createDataPartition() del programa caret para dividir los datos en un set para entrenamiento que generalmente debe tener más del 60% de los datos y otro de prueba. Para los siguientes ejemplos estaremos trabajando con el set de datos iris.

data(iris); library(caret);

inTrain <- createDataPartition(y=iris$Species, p=0.70, list=FALSE)
training <- iris[inTrain,]
testing <- iris[-inTrain,]
dim(training); dim(testing)
#> [1] 105   5
#> [1] 45  5

La función createFolds() divide los datos en k grupos

k10 <- createFolds(y=iris$Species,k=10,list=TRUE,returnTrain=TRUE)
head(k10, n=2)
#> $Fold01
#>   [1]   1   2   3   4   5   6   7   8   9  10  11  12  13
#>  [14]  14  15  16  17  18  19  20  21  22  23  24  25  26
#>  [27]  28  29  31  32  33  34  35  36  38  39  40  41  43
#>  [40]  45  46  47  48  49  50  51  52  54  55  57  58  59
#>  [53]  60  61  62  63  64  65  66  67  68  69  70  71  72
#>  [66]  73  74  75  76  77  78  79  80  81  82  84  85  86
#>  [79]  87  88  89  90  91  92  93  94  95  97  98 100 101
#>  [92] 102 103 104 105 106 107 108 109 110 111 112 113 114
#> [105] 115 116 117 118 119 121 124 125 126 127 128 129 130
#> [118] 132 133 134 135 136 137 138 139 140 142 143 144 145
#> [131] 146 147 148 149 150
#> 
#> $Fold02
#>   [1]   1   2   3   4   5   6   7   8   9  10  11  13  14
#>  [14]  15  16  17  19  20  21  22  23  24  25  26  27  28
#>  [27]  30  31  32  34  35  36  37  38  39  40  41  42  43
#>  [40]  44  45  46  47  48  50  52  53  54  55  56  57  58
#>  [53]  60  61  62  63  64  65  66  68  69  70  71  72  74
#>  [66]  75  76  77  78  79  80  81  82  83  84  85  86  87
#>  [79]  88  89  90  91  92  93  95  96  97  98  99 100 101
#>  [92] 102 103 104 105 106 107 108 109 110 111 112 113 114
#> [105] 115 116 117 118 119 120 122 123 124 125 127 128 129
#> [118] 130 131 132 133 134 135 136 137 140 141 143 144 145
#> [131] 146 147 148 149 150

La función createResample() crea una o más muestras para hacer Bootstrap

t10 <- createResample(y=iris$Species,times=10,list=TRUE)
head(t10, n=1)
#> $Resample01
#>   [1]   3   3   5   5   6   6   8   8   9  10  11  11  15
#>  [14]  15  15  17  17  18  20  20  22  22  23  23  24  25
#>  [27]  26  26  27  27  27  27  28  29  29  29  31  32  33
#>  [40]  34  36  36  38  39  41  41  41  42  45  45  48  50
#>  [53]  50  51  51  51  52  52  54  54  55  55  56  56  56
#>  [66]  57  58  58  63  64  65  66  66  66  68  68  69  70
#>  [79]  73  74  74  77  77  77  78  78  79  79  80  82  84
#>  [92]  88  89  89  90  90  91  92  93  94  99 100 101 102
#> [105] 102 104 106 108 109 110 112 112 112 113 114 114 116
#> [118] 116 118 119 119 119 119 119 120 120 121 122 123 126
#> [131] 126 127 130 132 137 138 139 139 141 141 142 145 146
#> [144] 147 148 148 148 150 150 150

La función createTimeSlices() crea una división para validación cruzada util en series de tiempo.

time <- 1:1000
w20 <- createTimeSlices(y=time,initialWindow=20,horizon=10)
w20$train[[1]]
#>  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
#> [19] 19 20

7.8 Determinación de la precisión (Accuracy)

Para el ejemplo se utiliza un set de datos del Instituto Nacional de Diabetes de EEUU. Notar que primero se define el método de validación cruzada por resampling con la función trainControl(). Luego se ejecuta un modelo lineal generalizado usando como parámetro de evaluación la precisión y el tipo de validación cruzada definido anteriormente. En el programa caret existen una gran cantidad de métodos que se pueden implementar que se pueden observar en este link Se obtiene el cuadro con los valores de precisión y Kappa para el algoritmo de aprendizaje automático evaluado.

library(caret); library(mlbench);data(PimaIndiansDiabetes)

control <- trainControl(method="cv", number=5)

modelfit <- train(diabetes~., data=PimaIndiansDiabetes, method="glm", metric="Accuracy", trControl=control)
modelfit
#> Generalized Linear Model 
#> 
#> 768 samples
#>   8 predictor
#>   2 classes: 'neg', 'pos' 
#> 
#> No pre-processing
#> Resampling: Cross-Validated (5 fold) 
#> Summary of sample sizes: 614, 614, 614, 615, 615 
#> Resampling results:
#> 
#>   Accuracy   Kappa    
#>   0.7708599  0.4695115

7.8.1 Decision Tree (Arbol de decisión):

Modelo no lineal de predicción basado en construcciones lógicas en forma de árbol. Sirve para representar una serie de condiciones que ocurren de forma sucesiva.

Se utiliza la función train()para establecer el modelo de predición de la variable Species utilizando el set de entrenamiento

data(iris); library(caret); library(rpart.plot)

inTrain <- createDataPartition(y=iris$Species,p=0.75, list=FALSE)
training <- iris[inTrain,]
testing <- iris[-inTrain,]

modFit <- train(Species ~ .,method="rpart",data=training)
modFit$finalModel
#> n= 114 
#> 
#> node), split, n, loss, yval, (yprob)
#>       * denotes terminal node
#> 
#> 1) root 114 76 setosa (0.3333333 0.3333333 0.3333333)  
#>   2) Petal.Length< 2.45 38  0 setosa (1.0000000 0.0000000 0.0000000) *
#>   3) Petal.Length>=2.45 76 38 versicolor (0.0000000 0.5000000 0.5000000)  
#>     6) Petal.Width< 1.75 40  2 versicolor (0.0000000 0.9500000 0.0500000) *
#>     7) Petal.Width>=1.75 36  0 virginica (0.0000000 0.0000000 1.0000000) *
modFit
#> CART 
#> 
#> 114 samples
#>   4 predictor
#>   3 classes: 'setosa', 'versicolor', 'virginica' 
#> 
#> No pre-processing
#> Resampling: Bootstrapped (25 reps) 
#> Summary of sample sizes: 114, 114, 114, 114, 114, 114, ... 
#> Resampling results across tuning parameters:
#> 
#>   cp         Accuracy   Kappa    
#>   0.0000000  0.9623064  0.9426832
#>   0.4736842  0.6734041  0.5292975
#>   0.5000000  0.5710356  0.3823566
#> 
#> Accuracy was used to select the optimal model using
#>  the largest value.
#> The final value used for the model was cp = 0.

Lo graficamos para entenderlo mejor

rpart.plot(modFit$finalModel)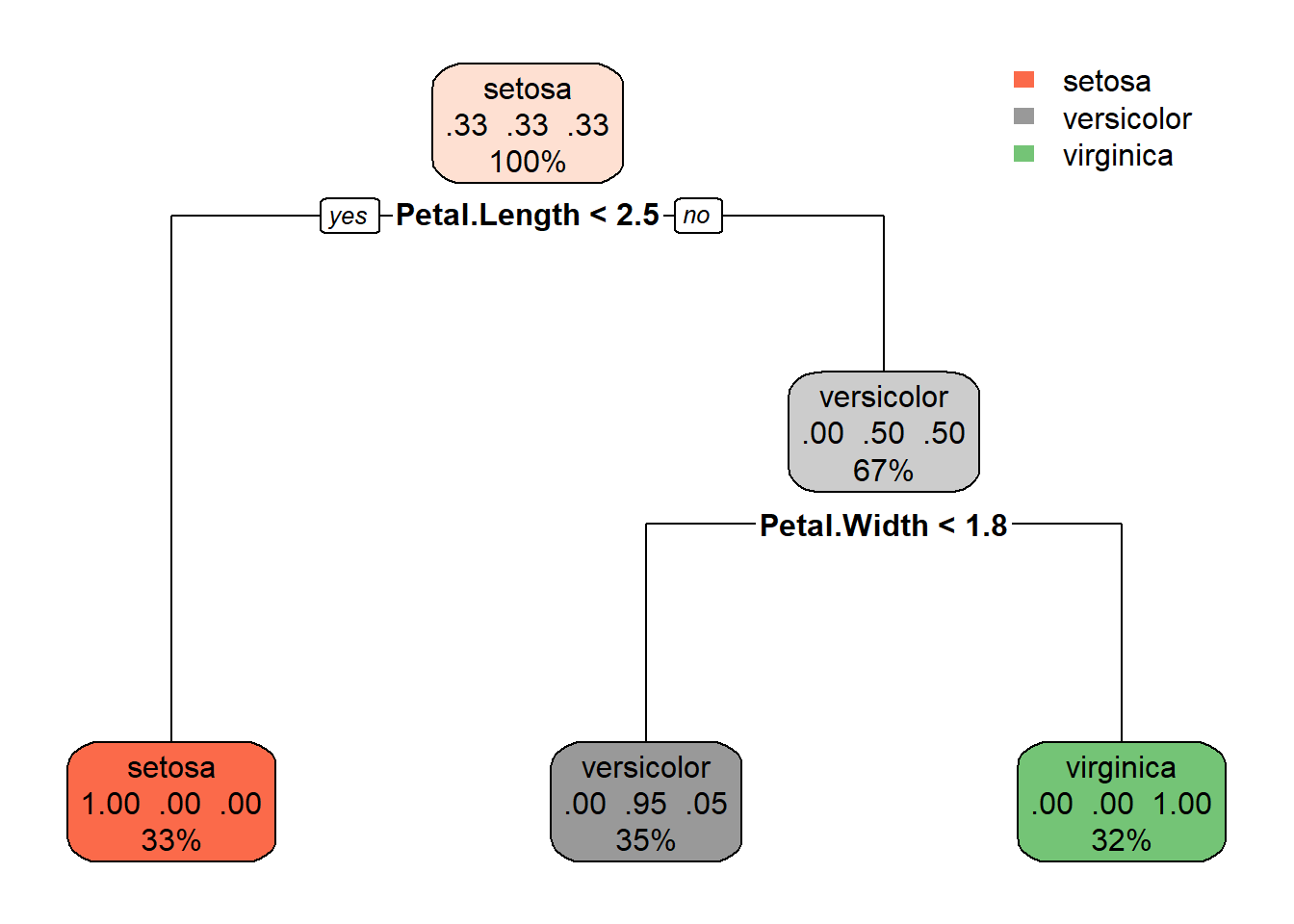

Figure 4.8: 7

Se utiliza la función predict()para realizar las prediciones sobre el set de datos de prueba.

predict(modFit,newdata=testing)
#>  [1] setosa     setosa     setosa     setosa     setosa    
#>  [6] setosa     setosa     setosa     setosa     setosa    
#> [11] setosa     setosa     versicolor virginica  versicolor
#> [16] versicolor versicolor versicolor versicolor versicolor
#> [21] versicolor versicolor versicolor versicolor versicolor
#> [26] virginica  virginica  versicolor virginica  virginica 
#> [31] versicolor virginica  virginica  virginica  virginica 
#> [36] virginica 
#> Levels: setosa versicolor virginica

7.8.2 Random Forest

Funciona mediante la construcción de una multitud de árboles de decisión en el momento del entrenamiento. El resultado es la moda de las clases (clasificación) o la predicción media (regresión) de los árboles individuales.

El algoritmo de RF es probablemente uno de los algoritmos de ML más famosos. En comparación con otros algoritmos de buen rendimiento, RF tiene solo unos pocos hiperparámetros y, debido al bagging y al muestreo aleatorio de las variables disponibles, tiene una adaptación de complejidad interna que funciona bien.

Utilizaremos el algoritmo de RF implementado en paquete el ranger sobre el set de datos de entrenamiento.

data(iris);library(caret);library(ranger)

index <- createDataPartition(iris$Species, p = 0.75, list = FALSE)
training <- iris[index, ]
testing  <- iris[-index, ]

rf <- train(Species ~ ., data = training, method = "ranger", importance = "impurity")
rf
#> Random Forest 
#> 
#> 114 samples
#>   4 predictor
#>   3 classes: 'setosa', 'versicolor', 'virginica' 
#> 
#> No pre-processing
#> Resampling: Bootstrapped (25 reps) 
#> Summary of sample sizes: 114, 114, 114, 114, 114, 114, ... 
#> Resampling results across tuning parameters:
#> 
#>   mtry  splitrule   Accuracy   Kappa    
#>   2     gini        0.9679514  0.9509847
#>   2     extratrees  0.9653142  0.9468732
#>   3     gini        0.9688816  0.9523829
#>   3     extratrees  0.9662031  0.9482955
#>   4     gini        0.9688816  0.9523829
#>   4     extratrees  0.9662031  0.9482955
#> 
#> Tuning parameter 'min.node.size' was held constant at
#>  a value of 1
#> Accuracy was used to select the optimal model using
#>  the largest value.
#> The final values used for the model were mtry =
#>  3, splitrule = gini and min.node.size = 1.

Luego se realiza la predicción sobre el set de datos de prueba con la función predict(). También se puede hacer una matriz de confusión con la función confusionMatrix() para visualizar el desempeño del algoritmo.

Predict <- predict(rf, testing)
confusionMatrix(Predict, testing$Species)
#> Confusion Matrix and Statistics
#> 
#>             Reference
#> Prediction   setosa versicolor virginica
#>   setosa         12          0         0
#>   versicolor      0         10         1
#>   virginica       0          2        11
#> 
#> Overall Statistics
#>                                           
#>                Accuracy : 0.9167          
#>                  95% CI : (0.7753, 0.9825)
#>     No Information Rate : 0.3333          
#>     P-Value [Acc > NIR] : 3.978e-13       
#>                                           
#>                   Kappa : 0.875           
#>                                           
#>  Mcnemar's Test P-Value : NA              
#> 
#> Statistics by Class:
#> 
#>                      Class: setosa Class: versicolor
#> Sensitivity                 1.0000            0.8333
#> Specificity                 1.0000            0.9583
#> Pos Pred Value              1.0000            0.9091
#> Neg Pred Value              1.0000            0.9200
#> Prevalence                  0.3333            0.3333
#> Detection Rate              0.3333            0.2778
#> Detection Prevalence        0.3333            0.3056
#> Balanced Accuracy           1.0000            0.8958
#>                      Class: virginica
#> Sensitivity                    0.9167
#> Specificity                    0.9167
#> Pos Pred Value                 0.8462
#> Neg Pred Value                 0.9565
#> Prevalence                     0.3333
#> Detection Rate                 0.3056
#> Detection Prevalence           0.3611
#> Balanced Accuracy              0.9167

Podemos ver otras métricas de evaluación del modelo como por ejemplo el error OOB.

rf$finalModel
#> Ranger result
#> 
#> Call:
#>  ranger::ranger(dependent.variable.name = ".outcome", data = x,      mtry = min(param$mtry, ncol(x)), min.node.size = param$min.node.size,      splitrule = as.character(param$splitrule), write.forest = TRUE,      probability = classProbs, ...) 
#> 
#> Type:                             Classification 
#> Number of trees:                  500 
#> Sample size:                      114 
#> Number of independent variables:  4 
#> Mtry:                             3 
#> Target node size:                 1 
#> Variable importance mode:         impurity 
#> Splitrule:                        gini 
#> OOB prediction error:             3.51 %

Calculamos el valor de importancia de las variables predictoras con la función varImp()

varImp(rf)
#> ranger variable importance
#> 
#>               Overall
#> Petal.Width  100.0000
#> Petal.Length  69.4297
#> Sepal.Length   0.6255
#> Sepal.Width    0.0000

7.8.3 Boosted Regression Trees (BRT)

Este algoritmo logra un rendimiento de última generación para datos estructurados (tabulares), lo que lo convierte probablemente en uno de los algoritmos más importantes para las ciencias naturales donde los datos estructurados dominan el campo.

Para este ejemplo utilizaremos el paquete XGBoost. En este programa la variable independiente debe ser transformada a un número entero empezando por cero. La función para correr el algoritmo es xgboost(). Notar que el parámetro nrounds corresponde la número de arboles que se utilizan para el ensamblado.

data(iris); library(xgboost)
X = as.matrix(iris[,1:4])
Y = as.integer(iris[,5]) - 1 

xgdata = xgb.DMatrix(X, label = Y)


brt = xgboost(data = xgdata,
              objective="multi:softprob",
              nrounds = 50,
              num_class = 3,
              verbose = 0)

Se calcula el valor de importancia de las variables predictoras

xgb.importance(model = brt)
#>         Feature        Gain      Cover Frequency
#> 1: Petal.Length 0.671879438 0.57441039 0.3792049
#> 2:  Petal.Width 0.311535837 0.29261084 0.3088685
#> 3:  Sepal.Width 0.010177107 0.04910115 0.1162080
#> 4: Sepal.Length 0.006407618 0.08387763 0.1957187

Se realiza la predicción de la probabilidad de asignación de cada individuo a una especie

head(matrix(predict(brt, newdata = xgb.DMatrix(X)), ncol =3), n = 3)
#>             [,1]        [,2]        [,3]
#> [1,] 0.995287061 0.002195822 0.001027058
#> [2,] 0.003323558 0.995396435 0.001592265
#> [3,] 0.001389398 0.002407764 0.997380674

7.8.4 Naive Bayes

Usa teorema de Bayes para encontrar clasificación óptima. Asume que los datos siguen modelo probabilístico condicional. Estima parámetros de datos históricos y calcula la probabilidad posterior de cada clase en el set de prueba. Algunas veces se puede optimizar el modelo haciendo algunas variaciones en el número de validaciones cruzadas.

data(iris); library(caret)

inTrain <- createDataPartition(y=iris$Species,p=0.75, list=FALSE)
training <- iris[inTrain,]
testing <- iris[-inTrain,]

modnb = train(Species ~ ., data=training,method="nb",
              trControl=trainControl(method='cv',number=5))
modnb$results
#>   usekernel fL adjust  Accuracy     Kappa AccuracySD
#> 1     FALSE  0      1 0.9568511 0.9351563 0.02950487
#> 2      TRUE  0      1 0.9647892 0.9470545 0.01974651
#>      KappaSD
#> 1 0.04426534
#> 2 0.02970573

Se realiza la predicción y la matriz de confusión

pred=predict(modnb$finalModel,testing)$class
confusionMatrix(pred, testing$Species)
#> Confusion Matrix and Statistics
#> 
#>             Reference
#> Prediction   setosa versicolor virginica
#>   setosa         12          0         0
#>   versicolor      0         12         2
#>   virginica       0          0        10
#> 
#> Overall Statistics
#>                                           
#>                Accuracy : 0.9444          
#>                  95% CI : (0.8134, 0.9932)
#>     No Information Rate : 0.3333          
#>     P-Value [Acc > NIR] : 1.728e-14       
#>                                           
#>                   Kappa : 0.9167          
#>                                           
#>  Mcnemar's Test P-Value : NA              
#> 
#> Statistics by Class:
#> 
#>                      Class: setosa Class: versicolor
#> Sensitivity                 1.0000            1.0000
#> Specificity                 1.0000            0.9167
#> Pos Pred Value              1.0000            0.8571
#> Neg Pred Value              1.0000            1.0000
#> Prevalence                  0.3333            0.3333
#> Detection Rate              0.3333            0.3333
#> Detection Prevalence        0.3333            0.3889
#> Balanced Accuracy           1.0000            0.9583
#>                      Class: virginica
#> Sensitivity                    0.8333
#> Specificity                    1.0000
#> Pos Pred Value                 1.0000
#> Neg Pred Value                 0.9231
#> Prevalence                     0.3333
#> Detection Rate                 0.2778
#> Detection Prevalence           0.2778
#> Balanced Accuracy              0.9167

7.8.5 Support Vector Machines

El algoritmo de la máquina de vectores de soporte (SVM) estima hiperplanos para separar nuestras especies de respuesta. La mejor implementación de SVM en R proviene del paquete e1071.

data(iris); library(e1071);library(caret)

inTrain <- createDataPartition(y=iris$Species,p=0.75, list=FALSE)
training <- iris[inTrain,]
testing <- iris[-inTrain,]

SVMFit <- svm(Species ~ ., data = training)

La predicción y la matriz de confusión para evaluar el modelo

SVMPredict <- predict(SVMFit, newdata = testing)
confusionMatrix(SVMPredict, testing$Species)
#> Confusion Matrix and Statistics
#> 
#>             Reference
#> Prediction   setosa versicolor virginica
#>   setosa         12          0         0
#>   versicolor      0         12         0
#>   virginica       0          0        12
#> 
#> Overall Statistics
#>                                      
#>                Accuracy : 1          
#>                  95% CI : (0.9026, 1)
#>     No Information Rate : 0.3333     
#>     P-Value [Acc > NIR] : < 2.2e-16  
#>                                      
#>                   Kappa : 1          
#>                                      
#>  Mcnemar's Test P-Value : NA         
#> 
#> Statistics by Class:
#> 
#>                      Class: setosa Class: versicolor
#> Sensitivity                 1.0000            1.0000
#> Specificity                 1.0000            1.0000
#> Pos Pred Value              1.0000            1.0000
#> Neg Pred Value              1.0000            1.0000
#> Prevalence                  0.3333            0.3333
#> Detection Rate              0.3333            0.3333
#> Detection Prevalence        0.3333            0.3333
#> Balanced Accuracy           1.0000            1.0000
#>                      Class: virginica
#> Sensitivity                    1.0000
#> Specificity                    1.0000
#> Pos Pred Value                 1.0000
#> Neg Pred Value                 1.0000
#> Prevalence                     0.3333
#> Detection Rate                 0.3333
#> Detection Prevalence           0.3333
#> Balanced Accuracy              1.0000

7.8.6 K-Means Clustering

K-medias es un método de agrupamiento que tiene como objetivo la partición de un conjunto de n observaciones en k grupos en el que cada observación pertenece al grupo cuyo valor medio es más cercano. Crea clusters con un centroide. Cada punto es asignado al cluster con centroide más cercano. Construye el predictor. Evalúa los clusters de predicción en nuevo set de datos.

En primer lugar, cuando se desconoce el set de datos y se debe determinar un número de grupos (k), se puede utilizar el método del codo, donde se elige el valor donde la curva cambia drásticamente.

data(iris);library(ggplot2);library(cluster)

wcss <- vector()
for (i in 1:10) wcss[i] <- sum(kmeans(iris[, -5], i)$withinss)

plot(1:10,
     wcss,
     type = "b",
     main = paste("The Elbow Method"),
     xlab = "Number of Clusters",
     ylab = "WCSS")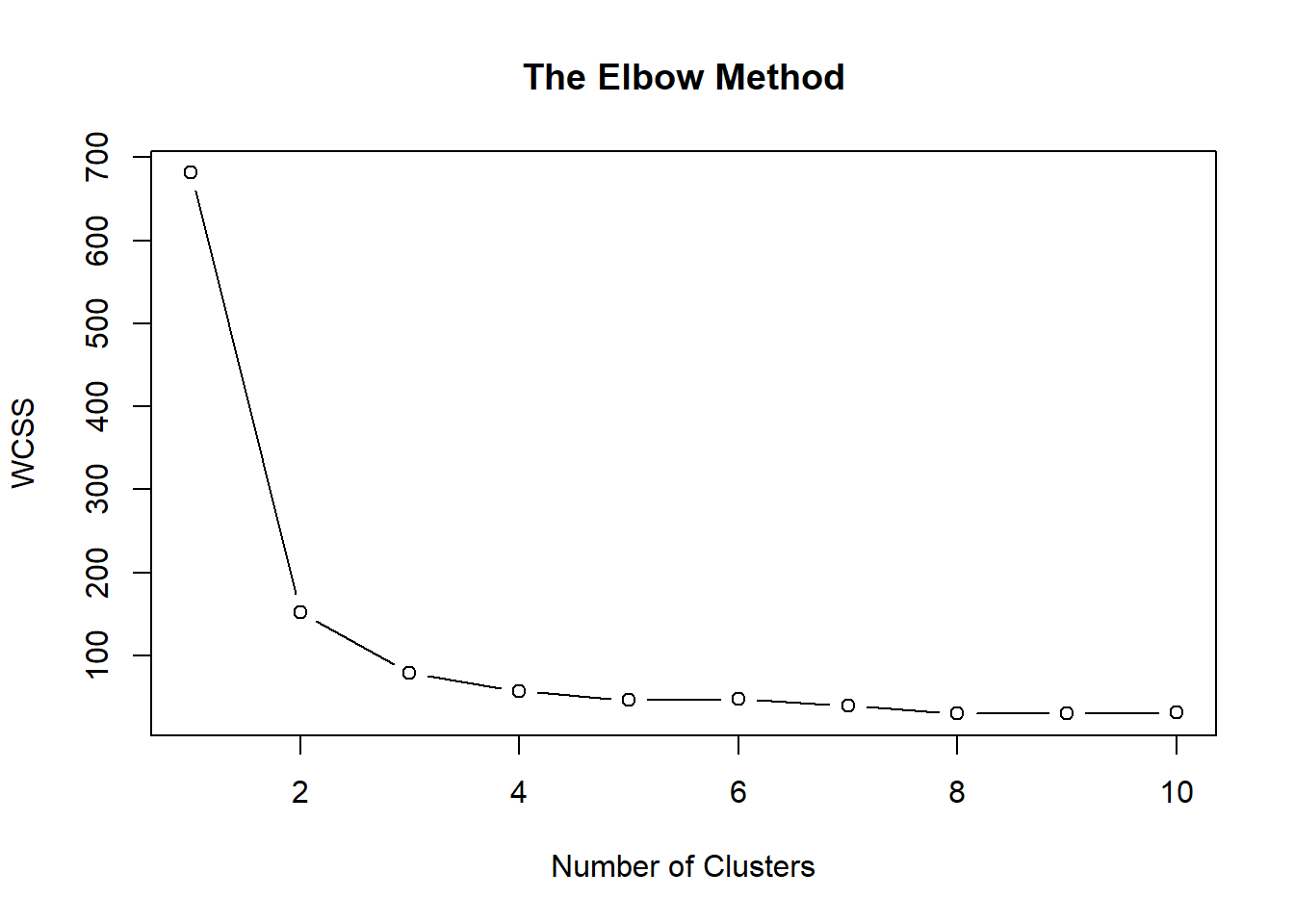

Figure 7.1: 7

Se generan los clusters con la función kmeans()

inTrain <- createDataPartition(y=iris$Species,p=0.75, list=FALSE)
training <- iris[inTrain,]
testing <- iris[-inTrain,]

kMeans <- kmeans(training[, -5] , centers = 3,iter.max = 100)
training$clusters <- as.factor(kMeans$cluster)
table(kMeans$cluster,training$Species)
#>    
#>     setosa versicolor virginica
#>   1     12          3         0
#>   2      0         35        38
#>   3     26          0         0

Se visualizan los cluster

clusplot(training[, -5],
         training$clusters,
         lines = 0,
         shade = TRUE,
         color = TRUE,
         labels = 0,
         plotchar = FALSE,
         span = TRUE,
         main = paste("Clusters"))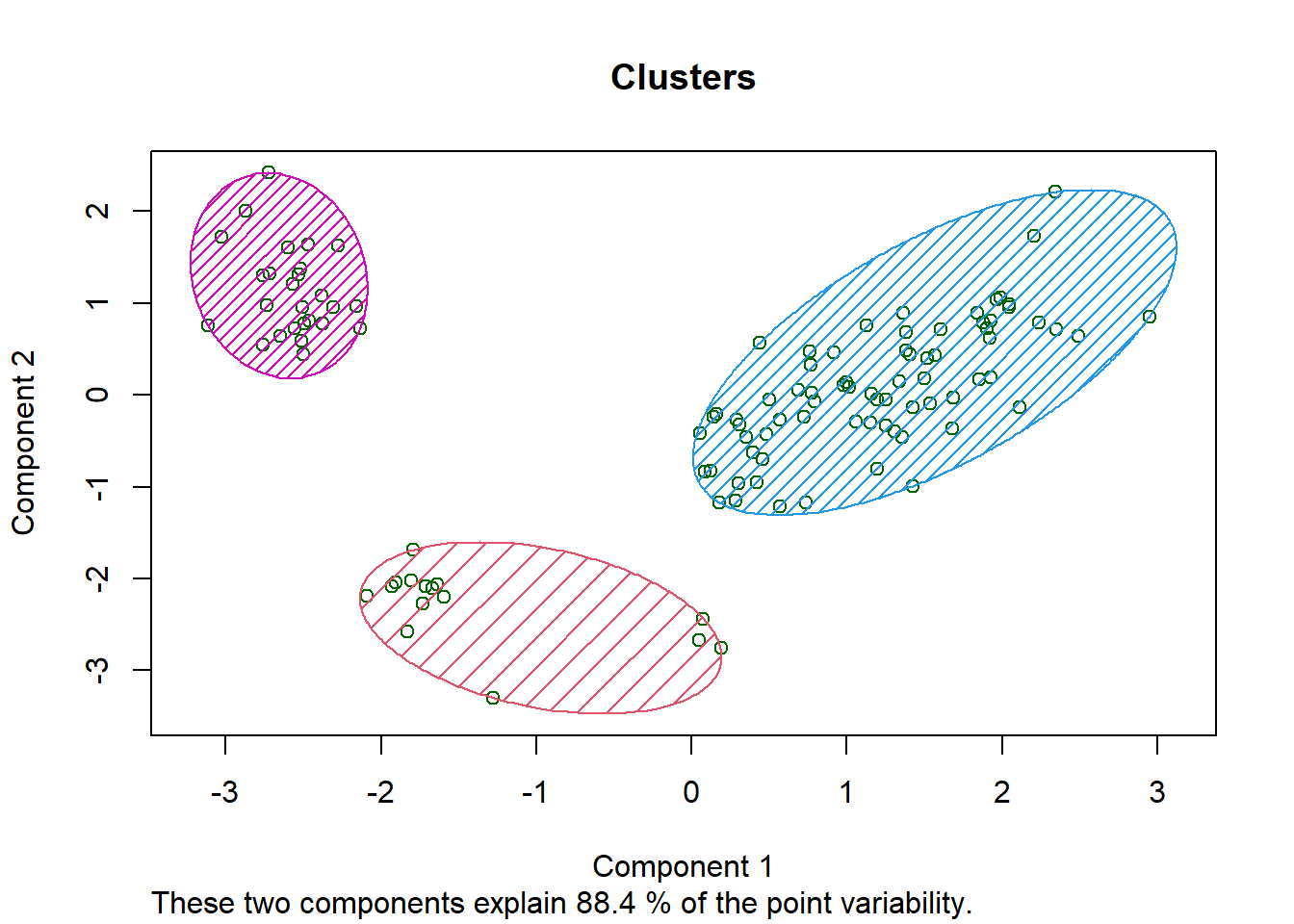

Figure 5.5: 7

Se reentrena el modelo y se hace la predicción

modFit <- train(clusters~.,data=subset(training,select=-c(Species)),method="rpart")
table(predict(modFit,training),training$Species)
#>    
#>     setosa versicolor virginica
#>   1     12          3         0
#>   2      0         35        38
#>   3     26          0         0

testClusterPred <- predict(modFit,testing) 
table(testClusterPred ,testing$Species)
#>                
#> testClusterPred setosa versicolor virginica
#>               1      5          0         0
#>               2      0         12        12
#>               3      7          0         0

7.8.7 Combinación de algoritmos

Una de las grandes ventajas del aprendizaje automático es que se pueden combinar los algoritmos para aumentar la precisión. En el ejemplo utilizaremos un set de datos de mediciones en el fluido cerebroespinal usado para diagnosticar o predecir el Alzheimer

library(caret); library(gbm);library(AppliedPredictiveModeling)
data(AlzheimerDisease)

adData <- data.frame(diagnosis, predictors)
inTrain <- createDataPartition(adData$diagnosis, p=3/4)[[1]]
training <- adData[inTrain, ]
testing <- adData[-inTrain, ]

fitRf <- train(diagnosis ~ ., data=training, method="ranger")
fitGBM <- train(diagnosis ~ ., data=training, method="gbm")
fitLDA <- train(diagnosis ~ ., data=training, method="lda")

predRf <- predict(fitRf, testing)
predGBM <- predict(fitGBM, testing)
predLDA <- predict(fitLDA, testing)
pred <- data.frame(predRf, predGBM, predLDA, diagnosis=testing$diagnosis)


fit <- train(diagnosis ~., data=pred, method="ranger")
predFit <- predict(fit, testing)

c1 <- confusionMatrix(predRf, testing$diagnosis)$overall[1]
c2 <- confusionMatrix(predGBM, testing$diagnosis)$overall[1]
c3 <- confusionMatrix(predLDA, testing$diagnosis)$overall[1]
c4 <- confusionMatrix(predFit, testing$diagnosis)$overall[1]
print(paste(c1, c2, c3, c4))

7.9 Recursos complementarios

6 Análisis de Cluster, Mapas de Calor y Análisis Multivariados

8 Análisis de Series de Tiempo