Chapter 10 Lab 8 - Identifying Near Repeats

Welcome to Lab 8! In this lab we are going to focus on:

Topics Covered
- Identifying Near-Repeat Incidents
- Mapping and Describing Near-Repeats
- Writing up Analysis

10.1 Setting up the Data

Let’s begin by first examining our data. We have two sets of data we’re going to utilize: (1) A list of all motor vehicle thefts and larcenies from motor vehicle and (2) a shapefile of the boroughs in New York City. We’re going to have to eventually isolate just the crimes in a specific borough to help focus our attention.

library(sf)
library(lubridate)
library(tidyverse)

nyc_city <- st_read("C:/Users/gioc4/Desktop/nyc_city.shp")
nyc_mvt <- st_read("C:/Users/gioc4/Desktop/nyc_mvt.shp")

Let’s create a point map to visualize these incidents. Just a quick one to make sure everything looks OK.

# Plot all motor vehicle thefts in NYC
ggplot() +
  geom_sf(data = nyc_city) +
  geom_sf(data = nyc_mvt, color = "darkblue", size = .8) +
  theme_void()

10.1.1 Spatial Clip

Well, that’s quite a lot! Let’s isolate our attention to a single Borough. In this example, we can focus on Staten Island. To do this, we need to create a new shapefile for only Staten Island using filter() and then do a spatial clip using the square brackets []. Remember: A spatial clip isolates just the incidents that are within a given boundary - in this case, the boundaries of a borough.

# Create a shapefile of just Staten Island
nyc_staten <- filter(nyc_city, boro_name == "STATEN ISLAND")

# Spatially clip crimes that are only within Staten Island
mvt_staten <- nyc_mvt[nyc_staten,]

Now let’s plot the crimes in Staten Island and add a descriptive title.

ggplot() +
  geom_sf(data = nyc_staten) +
  geom_sf(data = mvt_staten, color = "darkblue") +
  labs(title = "Larceny from Motor Vehicle, Staten Island NYC") +
  theme_void()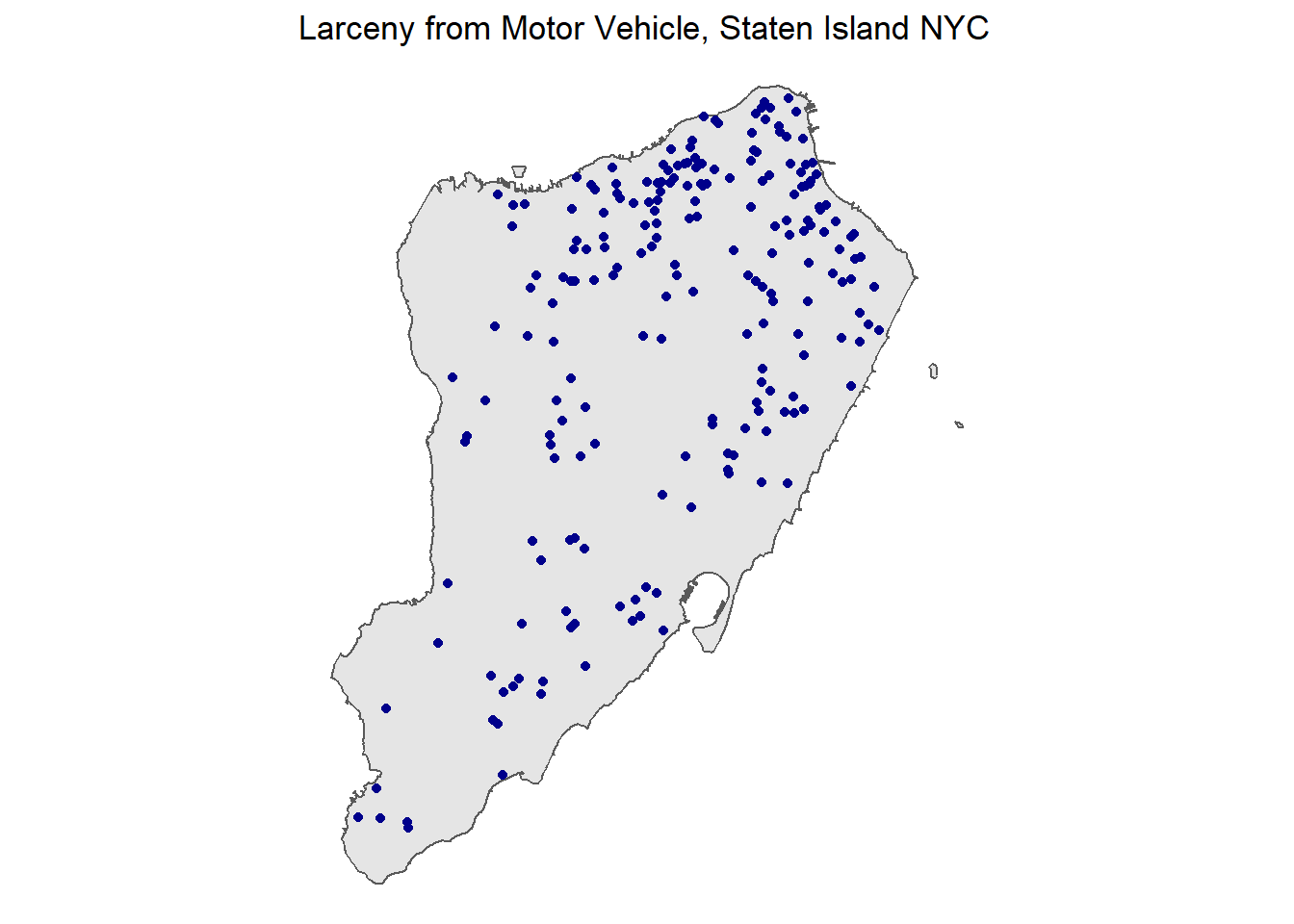

Now we’re ready to start identifying patterns of near-repeat incidents!

10.2 Identifying Near-Repeat Patterns

10.2.1 Setting up the `NearRepeat` package

Ok, now we’re ready to start identifying near-repeats. The first thing we have to do is set up some new software. The program we will be using is the aptly-named NearRepeat package which is written by criminologist Wouter Steenbeek. According to him, the package:

The R package NearRepeat uses the Knox test for space-time clustering to quantify the spatio-temporal association between events. In criminology, this test has been used to identify people and locations that are at disproportionate risk of victimization. Of interest is often not only the ‘same repeat’ victims (people or locations that after a first crime event, are targeted again within a short period thereafter), but also the ‘near repeat’ victims: nearby people or locations that are victimized within a short period after the first crime.

The first thing we need to do is install this new software. Because the NearRepeat tool is still very new, we need to install it directly from the source via Github. Without going too much into detail, we just need to run the code below, which is similar to the install.packages code we’ve used before.

# First-time install for the NearRepeat package
# Remember: Just need to do this one time only!

install.packages("remotes")
remotes::install_github("wsteenbeek/NearRepeat")

After a bit of running we should be good to go! Let’s use library to load it in and get started.

library(NearRepeat)

10.2.2 Running `NearRepeat`

Let’s start by setting up a variable to hold our results. Here I’ll call it nr_results. Next, we need to call the NearRepeat function and fill in a few things:

x = X value variable
y = Y value variable
time = date variable
sds = distance interval
tds = time interval

So, in this case we just need to point the computer to the right variables. Here our x and y values are just called X and Y in the data and the name of the variable holding the date is called DATE. Then we need to specify both the distance and time intervals. These reflect the distances that we want to test for near-repeat incidents (for example: at distances of 0 feet, 100 feet, 200 feet, ect..). Here, we’re going to fill in the X,Y, and time variables with the correct data. For the distance interval tds we’re going to go for 0 to 400 feet, by 100 foot intervals. For our time interval tds we’re going to do 0 to 5 days at 1 day intervals.

Finally, we’re going to put nrep = 99. This makes it run a bit faster by limiting the number of simulations the program does to calculate statistical significance. Depending on the amount of data, this might take a minute or two.

# Run the NearRepeat function
nr_results <- NearRepeat(x = mvt_staten$X,
                         y = mvt_staten$Y,
                         time = mvt_staten$DATE,
                         sds = c(0,100,200,300,400),
                         tds = c(0:5),
                         nrep = 99)

## - [-------------------------------------------------------------------------------------------------------------------] 0%
## \ [>------------------------------------------------------------------------------------------------------------------] 1%
## | [=>-----------------------------------------------------------------------------------------------------------------] 2% /
## [==>----------------------------------------------------------------------------------------------------------------] 3% -
## [====>--------------------------------------------------------------------------------------------------------------] 4% \
## [=====>-------------------------------------------------------------------------------------------------------------] 5% |
## [======>------------------------------------------------------------------------------------------------------------] 6% /
## [=======>-----------------------------------------------------------------------------------------------------------] 7% -
## [========>----------------------------------------------------------------------------------------------------------] 8% \
## [=========>---------------------------------------------------------------------------------------------------------] 9% |
## [===========>-------------------------------------------------------------------------------------------------------] 10% /
## [============>------------------------------------------------------------------------------------------------------] 11% -
## [=============>-----------------------------------------------------------------------------------------------------] 12% \
## [==============>----------------------------------------------------------------------------------------------------] 13% |
## [===============>---------------------------------------------------------------------------------------------------] 14% /
## [================>--------------------------------------------------------------------------------------------------] 15% -
## [==================>------------------------------------------------------------------------------------------------] 16% \
## [===================>-----------------------------------------------------------------------------------------------] 17% |
## [====================>----------------------------------------------------------------------------------------------] 18% /
## [=====================>---------------------------------------------------------------------------------------------] 19% -
## [======================>--------------------------------------------------------------------------------------------] 20% \
## [=======================>-------------------------------------------------------------------------------------------] 21% |
## [=========================>-----------------------------------------------------------------------------------------] 22% /
## [==========================>----------------------------------------------------------------------------------------] 23% -
## [===========================>---------------------------------------------------------------------------------------] 24% \
## [============================>--------------------------------------------------------------------------------------] 25% |
## [=============================>-------------------------------------------------------------------------------------] 26% /
## [==============================>------------------------------------------------------------------------------------] 27% -
## [================================>----------------------------------------------------------------------------------] 28% \
## [=================================>---------------------------------------------------------------------------------] 29% |
## [==================================>--------------------------------------------------------------------------------] 30% /
## [===================================>-------------------------------------------------------------------------------] 31% -
## [====================================>------------------------------------------------------------------------------] 32% \
## [=====================================>-----------------------------------------------------------------------------] 33% |
## [======================================>----------------------------------------------------------------------------] 34% /
## [========================================>--------------------------------------------------------------------------] 35% -
## [=========================================>-------------------------------------------------------------------------] 36% \
## [==========================================>------------------------------------------------------------------------] 37% |
## [===========================================>-----------------------------------------------------------------------] 38% /
## [============================================>----------------------------------------------------------------------] 39% -
## [=============================================>---------------------------------------------------------------------] 40% \
## [===============================================>-------------------------------------------------------------------] 41% |
## [================================================>------------------------------------------------------------------] 42% /
## [=================================================>-----------------------------------------------------------------] 43% -
## [==================================================>----------------------------------------------------------------] 44% \
## [===================================================>---------------------------------------------------------------] 45% |
## [====================================================>--------------------------------------------------------------] 46% /
## [======================================================>------------------------------------------------------------] 47% -
## [=======================================================>-----------------------------------------------------------] 48% \
## [========================================================>----------------------------------------------------------] 49% |
## [=========================================================>---------------------------------------------------------] 51% /
## [==========================================================>--------------------------------------------------------] 52% -
## [===========================================================>-------------------------------------------------------] 53% \
## [=============================================================>-----------------------------------------------------] 54% |
## [==============================================================>----------------------------------------------------] 55% /
## [===============================================================>---------------------------------------------------] 56% -
## [================================================================>--------------------------------------------------] 57% \
## [=================================================================>-------------------------------------------------] 58% |
## [==================================================================>------------------------------------------------] 59% /
## [====================================================================>----------------------------------------------] 60% -
## [=====================================================================>---------------------------------------------] 61% \
## [======================================================================>--------------------------------------------] 62% |
## [=======================================================================>-------------------------------------------] 63% /
## [========================================================================>------------------------------------------] 64% -
## [=========================================================================>-----------------------------------------] 65% \
## [===========================================================================>---------------------------------------] 66% |
## [============================================================================>--------------------------------------] 67% /
## [=============================================================================>-------------------------------------] 68% -
## [==============================================================================>------------------------------------] 69% \
## [===============================================================================>-----------------------------------] 70% |
## [================================================================================>----------------------------------] 71% /
## [=================================================================================>---------------------------------] 72% -
## [===================================================================================>-------------------------------] 73% \
## [====================================================================================>------------------------------] 74% |
## [=====================================================================================>-----------------------------] 75% /
## [======================================================================================>----------------------------] 76% -
## [=======================================================================================>---------------------------] 77% \
## [========================================================================================>--------------------------] 78% |
## [==========================================================================================>------------------------] 79% /
## [===========================================================================================>-----------------------] 80% -
## [============================================================================================>----------------------] 81% \
## [=============================================================================================>---------------------] 82% |
## [==============================================================================================>--------------------] 83% /
## [===============================================================================================>-------------------] 84% -
## [=================================================================================================>-----------------] 85% \
## [==================================================================================================>----------------] 86% |
## [===================================================================================================>---------------] 87% /
## [====================================================================================================>--------------] 88% -
## [=====================================================================================================>-------------] 89% \
## [======================================================================================================>------------] 90% |
## [========================================================================================================>----------] 91% /
## [=========================================================================================================>---------] 92% -
## [==========================================================================================================>--------] 93% \
## [===========================================================================================================>-------] 94% |
## [============================================================================================================>------] 95% /
## [=============================================================================================================>-----] 96% -
## [===============================================================================================================>---] 97% \
## [================================================================================================================>--] 98% |
## [=================================================================================================================>-] 99% /
## [===================================================================================================================] 100%

10.2.3 Analyzing the results

First, let’s get our table. We can just access these results by getting the observed counts from our nr_results variable

# Get the Knox Table
nr_results$observed

##            
##             [0,1) [1,2) [2,3) [3,4) [4,5)
##   [0,100)       2     0     0     1     0
##   [100,200)     3     3     0     0     0
##   [200,300)     0     1     1     0     0
##   [300,400)     0     1     0     0     0

This shows that there were 2 thefts within 0-200 feet and 0-1 days, while there were 3 thefts within 100-200 feet. If we want to find out where these results are likely to be ‘significant’ - that is, distance and time ranges that are different than what we’d expect to see at random - then we can just plot our nr_results function to see. Here, we’re looking for cells in the table that are highlighted in yellow, orange, or red (corresponding to p-values of 0.05 to 0.00).

# Find out which are statistically significant
plot(nr_results)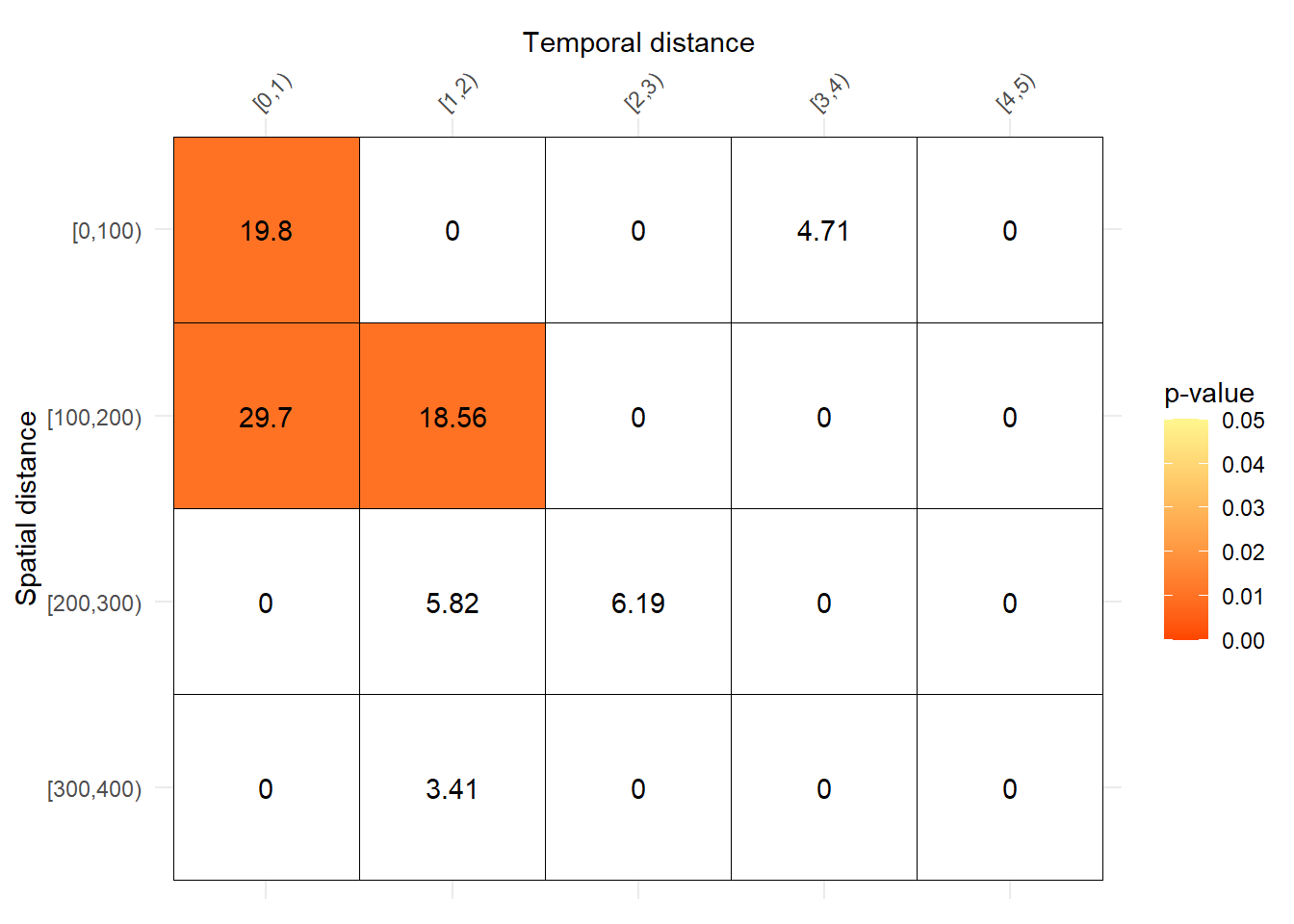

In this example we see that there are some patterns of motor vehicle thefts at ranges of 0-100 and 100-200 feet, between 0-1 days. This also holds for between 1-2 days at 100, 200 feet. What does this mean? In general, this tells us that we might want to concentrate some efforts of repeat incidents of motor vehicle theft within 0-200 feet of previous motor vehicle thefts. From a tactical standpoint, this might reflect deploying officers to areas which have recent had motor vehicle thefts and giving them some proactive activities to implement.

10.3 Lab 8 Assignment

This lab assignment is worth 10 points. Follow the instructions below.

Using the nyc_city.shp and nyc_mvt.shp shapefiles:
- Filter nyc_city by selecting a single borough
- Perform a spatial clip on nyc_mvt to get crimes only in the borough you chose
Create a point map using the two variables you filtered and clipped in step 1
- Change the shape, color, and size of the points
- Add a title and use theme_void to remove the plot background
Use the NearRepeat function to do the following:
- Specify a range of distance intervals
- Specify a range of time intervals
- Print the observed Knox table
- Plot the results with p-values

This lab has specific write-up instructions!

In your write-up, describe why you chose the range of distance and time values. Explain why you think they are relevant to a near-repeat analysis for the crime of motor vehicle theft. Describe how you might address this near-repeat pattern using a tactical approach. Write your response in at least one complete paragraph.