# Example Data
beta_true <- c(-0.5, 2, 1)
N = 100
set.seed(1232)
X <- cbind(1, rnorm(N, 0, 0.1), rnorm(N, 0, 0.1)) # Design matrix (with intercept)
Y <- X %*% beta_true + rnorm(N, 0, sd = 10) # Response vector
# Compute beta-hat
# beta_hat <- =?
# Variance of beta-hat?Module 7: Review
Module 1: Multiple Linear Regression Review
The linear regression model in matrix form is:
\[ \mathbf{Y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\epsilon}, \quad \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \sigma^2 \mathbf{I}) \]
Here:
\(\mathbf{Y}\): \(n \times 1\) vector of responses.
\(\mathbf{X}\): \(n \times p\) design matrix of predictors.
\(\boldsymbol{\beta}\): \(p \times 1\) vector of coefficients.
\(\boldsymbol{\epsilon}\): \(n \times 1\) vector of errors.
The Ordinary Least Squares (OLS) estimate for \(\boldsymbol{\beta}\) is:
\[ \hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{Y} \]
Simulation in R: Below gives the design matrix and response outcome length 3.
- Write code to compute \(\hat{\beta}\).
- What are the properties of the OLS Estimator \(\hat{\beta}\), hint: also review theorems and when is OLS = MLE?
- Interpret the coefficients based on your calculation.
- Inference for Coefficients: Write out the covariance of \(\hat{\beta}\) and add code to calculate the covariance.
- Explain what the diagonal and off-diagonal elements of \(\text{Var}(\hat{\boldsymbol{\beta}})\) represent and how they relate to confidence intervals for the coefficients.
- What is the difference between \(\hat{\sigma}^2\) and \(s^2\)?
Interactions and Effect Modification
Interactions allow the effect of one predictor to depend on the value of another. The model:
\[ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 (X_1 \cdot X_2) + \epsilon \]
Example:
set.seed(123)
# Simulated data
beta <- c(1,2,4,3)
X1 = rnorm(N, 0, 10)
X2 = rnorm(N, 0, 10)
Y = beta[1] + beta[2] * X1 + beta[3] * X2 + beta[4] * X1* X2 + rnorm(N, 0, 1)
# Fit a model with interaction
model <- lm(Y ~ X1 * X2)
summary(model)
Call:
lm(formula = Y ~ X1 * X2)
Residuals:
Min 1Q Median 3Q Max
-1.8719 -0.6777 -0.1086 0.5897 2.3166
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.140983 0.095777 11.91 <2e-16 ***
X1 1.990719 0.010834 183.75 <2e-16 ***
X2 4.003434 0.009881 405.15 <2e-16 ***
X1:X2 3.001591 0.001145 2621.64 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9468 on 96 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 2.406e+06 on 3 and 96 DF, p-value: < 2.2e-16Interpretation: The coefficient for \(X1:X2\) quantifies the interaction effect. If significant, it means the effect of \(X1\) on \(Y\) depends on \(X2\).
- Write the derivation for the prediction interval for a new observation.
- Write the code to calculate the 95% prediction interval using the results above.
Confounding
A variable is a confounder if it influences both the predictor and the outcome, potentially biasing the estimated relationship.
Example:
#Example
data <- data.frame(
smoking = c(0, 1, 0, 1),
age = c(20, 30, 40, 50),
disease = c(0, 1, 1, 1)
)
# Fit a model without adjusting for age
model1 <- glm(disease ~ smoking, family = binomial, data = data)
# Fit a model adjusting for age
model2 <- glm(disease ~ smoking + age, family = binomial, data = data)Warning: glm.fit: fitted probabilities numerically 0 or 1 occurredsummary(model1)
Call:
glm(formula = disease ~ smoking, family = binomial, data = data)
Deviance Residuals:
1 2 3 4
-1.17741 0.00008 1.17741 0.00008
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.238e-16 1.414e+00 0.000 1.000
smoking 1.957e+01 7.604e+03 0.003 0.998
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 4.4987 on 3 degrees of freedom
Residual deviance: 2.7726 on 2 degrees of freedom
AIC: 6.7726
Number of Fisher Scoring iterations: 18summary(model2)
Call:
glm(formula = disease ~ smoking + age, family = binomial, data = data)
Deviance Residuals:
1 2 3 4
-1.197e-05 1.197e-05 1.197e-05 2.110e-08
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -70.078 160246.558 0 1
smoking 23.359 87770.712 0 1
age 2.336 5067.441 0 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 4.4987e+00 on 3 degrees of freedom
Residual deviance: 4.2978e-10 on 1 degrees of freedom
AIC: 6
Number of Fisher Scoring iterations: 23- Compare the coefficient for smoking in both models to see how controlling for age effects the relationship. Interpret the findings for this coefficient in both settings.
- Compare the models to find the optimal model using a F-test statistic.
Module 2 Linear Mixed Models
Linear mixed models (LMMs) are designed to handle correlated data. This arises when: -
Multiple measurements are taken on the same individuals (e.g., repeated measures).
Data are grouped into clusters (e.g., students nested within schools).
The general structure of a mixed model is: \[ Y_{ij} = \beta_0 + \beta_1 X_{ij} + u_j + \epsilon_{ij} \] Where:
\(Y_{ij}\): Response for individual \(i\) in group \(j\).
\(\beta_0 + \beta_1 X_{ij}\): Fixed effects (global trends or population-level effects).
\(u_j\): Random effect for group \(j\), \(u_j \sim \mathcal{N}(0, \tau^2)\).
\(\epsilon_{ij}\): Residual error, \(\epsilon_{ij} \sim \mathcal{N}(0, \sigma^2)\).
Fixed vs. Random Effects
- Fixed Effects:
- Parameters of interest (e.g., \(\beta_0\), \(\beta_1\)).
- Represent the population-level effects.
- Random Effects:
- Account for variability between clusters or groups.
- Allow for partial pooling of information across groups.
Example: In a study of students’ test scores:
Fixed effect: Average effect of study hours on scores.
Random effect: Variation in scores across schools.
Variance Components
Mixed models decompose variability into:
1. Between-cluster variability (\(\tau^2\)): How much clusters differ.
2. Within-cluster variability (\(\sigma^2\)): How much individuals within a cluster differ.
Example Dataset: Sleep study with repeated measures of reaction times for individuals under sleep deprivation. 1. Fit a linear mixed model regressing \(Reaction\) on \(Days\) and a random intercept for \(Subject\)
# Load the lme4 package
library(lme4)Loading required package: Matrix# Example: Sleep study dataset
data("sleepstudy", package = "lme4")
# Fit a mixed-effects model
# Reaction time ~ Days of sleep deprivation + (Random intercept for Subject)
# model <- ?
# summary(model)Write out the interpretation of the fixed effects \(\hat{\beta}\) in this model.
What is the estimates for the between-subject variability and the within-subject variability?
Calculate and interpret the Intraclass Correlation.
Extend this model to include both random intercepts AND slopes. Write out the model, fit the model with the code below, and interpret.
# Random slope and intercept model
# model2 <- ?
# summary(model2)- Is the random intercept or random intercept and slope model preferred? To compare models, we use the \(AIC\). Calculate the AICS and determine which model is better.
Module 3 Generalized Linear Models
- GLMs extend linear regression to handle response variables that are not normally distributed.
- A GLM consists of three components:
- A probability distribution in the Exponential Family (e.g., Binomial, Poisson).
- Systematic Component: A linear model \(\eta = X\beta\), where \(X\) is the design matrix and \(\beta\) are the coefficients.
- Link Function: Transforms the expected value of the response variable to the scale of the linear predictor, \(g(\mu) = \eta\).
The probability distribution must be in the Exponential Family.
- Write out the general form of the Exp Family and show that the Poisson distribution fits this form.
Common GLMs:
- Logistic Regression:
- Used for binary data.
- Link function: \(g(\mu) = \log\left(\frac{\mu}{1 - \mu}\right)\) (logit link).
- Response variable \(y_i \sim \text{Binomial}(n_i, \pi_i)\).
- Probit Regression:
- Also for binary data.
- Link function: \(g(\mu) = \Phi^{-1}(\mu)\), where \(\Phi\) is the standard normal cumulative distribution function.
- Poisson Regression:
- Used for count data.
- Link function: \(g(\mu) = \log(\mu)\).
- Response variable \(y_i \sim \text{Poisson}(\lambda_i)\).
Consider a study on whether students pass an exam (\(y_i = 1\) if pass, \(y_i = 0\) otherwise). The model is:
\[ \text{logit}(\pi_i) = \beta_0 + \beta_1 \text{Hours}_i \]
- Write the logistic regression model where outcomes \(y_i\) regress on the number of hours spent studying \(hours_i\).
- Write out the expectation.
- Interpret the coefficient \(\beta_1\) in the context of the study.
- If \(\beta_1 = 0.5\), compute the odds of passing for a student who studies 4 hours compared to one who studies 2 hours.
- Calculate the 95% CIs for the OR.(Assume \(\text{SE}(\beta_1) = 0.1\))
Load the mtcars dataset in R and fit a logistic regression model to predict whether a car has an automatic transmission (am) using mpg and hp as predictors.
- Write the R code to fit the model using the
glm()function. - Interpret the coefficients of
mpgandhpin the output. - Use the model to predict the probability of an automatic transmission for a car with
mpg = 25andhp = 100.
Poisson Regression with Random Intercept
A hospital administrator is analyzing the number of patients admitted to different wards each day. The number of daily admissions is modeled as a Poisson-distributed outcome. The wards are suspected to have differing baseline admission rates, so a random intercept is included in the model.
The model for daily admissions \(y_{ij}\) in ward \(i\) on day \(j\) is given by:
\[ \begin{align*} y_{ij} & \sim Pois(\mu_{ij})\\ \log(\mu_{ij}) &= \beta_0 + \beta_1 \text{DayType}_{ij} + u_i \end{align*} \]
- \(u_i \sim N(0, \sigma^2_u)\) is the random intercept for ward \(i\).
- \(\text{DayType}_{ij}\) is a binary indicator (0 = weekday, 1 = weekend).
- \(\beta_0\) is the overall fixed intercept.
- \(\beta_1\) is the fixed effect of the day type.
- Identify the fixed and random components of this model.
- Write the expected value of \(y_{ij}\) in terms of \(\mu_{ij}\).
- Interpret the meaning of \(\beta_1\) in this model.
- What does \(\sigma^2_u\) tell you about the variability across wards?
- Write R code to simulate data from this model. Assume the estimated coefficients are \(\beta_0 = 2.5\), \(\beta_1 = -0.3\), and \(\sigma^2_u = 0.2\). Also write code to plot the simulated data.
##Starting you off
set.seed(123)
# Parameters
beta_0 <- 2.5 # Fixed intercept
beta_1 <- -0.3 # Fixed effect of DayType
sigma_u <- sqrt(0.2) # Standard deviation of random intercepts
n_wards <- 15 # Number of wards
n_days <- 30 # Number of days per ward- Predict the expected number of admissions for: - A weekday (\(\text{DayType} = 0\)) in Ward A, where \(u_A = 0.1\).
Module 4: Generalized Estimating Equations (GEEs)
- GEEs are an extension of GLMs used for correlated or clustered data, such as repeated measures.
- Unlike random-effects models, GEEs estimate population-averaged (marginal) effects rather than subject-specific effects.
- Key features include:
- Estimating Equation: An iterative method for parameter estimation.
- Correlation Structures: Specify the within-cluster correlation (e.g., exchangeable, autoregressive, unstructured).
- Robust Standard Errors: Account for misspecification of the correlation structure.
Correlation Structures
- Exchangeable: Equal correlation among all observations within a cluster.
- Autoregressive (AR1): Correlation decreases with increasing time separation.
- Unstructured: No specific structure; each correlation is estimated.
The respiratory dataset includes longitudinal data from a respiratory study. The main variables are: - outcome: Binary outcome indicating the presence or absence of infection. - age: Age of the subject. - visit: Time of the visit. - treatment: Treatment group (placebo or drug).
- Load the dataset and fit a GEE with an exchangeable correlation structure:
library(geepack)
library(gee)
# Load the respiratory dataset
data("respiratory", package = "geepack")
# Fit the GEE
fit_gee <- gee(outcome ~ age + visit + treat, data = respiratory, id = id, corstr = "exchangeable", family = binomial)Beginning Cgee S-function, @(#) geeformula.q 4.13 98/01/27running glm to get initial regression estimate(Intercept) age visit treatP
1.31881870 -0.01217949 -0.06244781 -0.98377461 # Summary of the model
summary(fit_gee)
GEE: GENERALIZED LINEAR MODELS FOR DEPENDENT DATA
gee S-function, version 4.13 modified 98/01/27 (1998)
Model:
Link: Logit
Variance to Mean Relation: Binomial
Correlation Structure: Exchangeable
Call:
gee(formula = outcome ~ age + visit + treat, id = id, data = respiratory,
family = binomial, corstr = "exchangeable")
Summary of Residuals:
Min 1Q Median 3Q Max
-0.7445718 -0.4523645 0.2814629 0.3964276 0.6710428
Coefficients:
Estimate Naive S.E. Naive z Robust S.E. Robust z
(Intercept) 1.31321054 0.47893788 2.7419225 0.47503342 2.7644593
age -0.01205922 0.01143541 -1.0545504 0.01160090 -1.0395071
visit -0.06245418 0.06350982 -0.9833784 0.06561084 -0.9518882
treatP -0.98039084 0.31316711 -3.1305677 0.31275820 -3.1346607
Estimated Scale Parameter: 1.010102
Number of Iterations: 2
Working Correlation
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 1.0000000 0.4890786 0 0 0 0 0 0
[2,] 0.4890786 0.4890786 0 0 0 0 0 0
[3,] 0.4890786 1.0000000 0 0 0 0 0 0
[4,] 0.4890786 0.4890786 0 0 0 0 0 0
[5,] 0.4890786 0.4890786 0 0 0 0 0 0
[6,] 1.0000000 0.4890786 0 0 0 0 0 0
[7,] 0.4890786 0.4890786 0 0 0 0 0 0
[8,] 0.4890786 1.0000000 0 0 0 0 0 0- Interpret the coefficients for age and treat.
- Compare the robust and model-based standard errors in the output. What do they indicate about model assumptions?
- Explain how misspecifying the correlation structure affects the model’s results.
Consider a study on school performance, where test scores are modeled as a function of teacher experience and classroom size, clustered by school.
- Write the general form of a GEE for this scenario, using \(y_{ij}\) for test scores, \(x_1\) for teacher experience, and \(x_2\) for classroom size.
- How does the interpretation of coefficients differ between a GEE and a mixed-effects model?
Simulate data for a Poisson GEE: Run the code below to simulate clustered count data where the response variable represents the number of tasks completed by workers in teams, with predictors for experience (exp) and workload (load).
library(gee)
library(geepack)
# Simulate clustered Poisson data
set.seed(123)
n_teams <- 10
n_workers <- 5
exp <- rnorm(n_teams * n_workers, mean = 5, sd = 2)
load <- rpois(n_teams * n_workers, lambda = 10)
team <- rep(1:n_teams, each = n_workers)
tasks <- rpois(n_teams * n_workers, lambda = exp(0.5 + 0.3 * exp - 0.1 * load))
# Create a data frame
data <- data.frame(team, exp, load, tasks)
# Fit a Poisson GEE
fit_pois_gee <- gee(tasks ~ exp + load, data = data, id = team, corstr = "exchangeable", family = poisson)Beginning Cgee S-function, @(#) geeformula.q 4.13 98/01/27running glm to get initial regression estimate(Intercept) exp load
0.65183432 0.25481011 -0.09221407 # Summary of the model
summary(fit_pois_gee)
GEE: GENERALIZED LINEAR MODELS FOR DEPENDENT DATA
gee S-function, version 4.13 modified 98/01/27 (1998)
Model:
Link: Logarithm
Variance to Mean Relation: Poisson
Correlation Structure: Exchangeable
Call:
gee(formula = tasks ~ exp + load, id = team, data = data, family = poisson,
corstr = "exchangeable")
Summary of Residuals:
Min 1Q Median 3Q Max
-2.5792704 -0.9928465 -0.2308147 0.8542432 3.1320614
Coefficients:
Estimate Naive S.E. Naive z Robust S.E. Robust z
(Intercept) 0.68090576 0.30291226 2.247865 0.33007871 2.062859
exp 0.25262895 0.03879274 6.512274 0.04602186 5.489325
load -0.09397882 0.02651737 -3.544047 0.01494948 -6.286427
Estimated Scale Parameter: 0.6964406
Number of Iterations: 2
Working Correlation
[,1] [,2] [,3] [,4] [,5]
[1,] 1.0000000 0.1138303 0.1138303 0.1138303 0.1138303
[2,] 0.1138303 1.0000000 0.1138303 0.1138303 0.1138303
[3,] 0.1138303 0.1138303 1.0000000 0.1138303 0.1138303
[4,] 0.1138303 0.1138303 0.1138303 1.0000000 0.1138303
[5,] 0.1138303 0.1138303 0.1138303 0.1138303 1.0000000Interpret the coefficients for
expandload.Change the correlation structure to unstructured and compare the results. What differences do you observe?
Robust Standard Errors
- GEEs provide robust standard errors to account for potential misspecification of the working correlation structure.
- These standard errors are derived using a sandwich estimator, ensuring valid inference even if the assumed correlation structure is incorrect.
Formula for Robust Variance-Covariance Matrix: The robust variance-covariance matrix of the estimated coefficients \(\hat{\beta}\) is given by:
\[ \text{Var}(\hat{\beta}) = A^{-1} B A^{-1}, \]
where:
\(A = -\frac{\partial U(\beta)}{\partial \beta}\) is the sensitivity matrix.
\(B = \text{Cov}[U(\beta)]\) is the variability of the score function \(U(\beta)\).
- Compare the implications of using model-based standard errors versus robust standard errors when the working correlation structure is misspecified.
- Based on the \(R\) output above compare and interpret the model-based and Robust SEs for the covariate coefficients. What do differences indicate aboutthe correlation structure?
Variance-Covariance Derivation in GEEs
- GEEs handle within-cluster correlations using a working correlation matrix, denoted by \(R(\alpha)\), where \(\alpha\) is a parameter that specifies the correlation structure (e.g., exchangeable, AR1).
- The total variance-covariance matrix is derived as:
\[ \Sigma_i = \phi V(\mu_i)^{1/2} R(\alpha) V(\mu_i)^{1/2}, \]
where:
\(V(\mu_i)\) is the variance function (e.g., \(\mu_i\) for Poisson, \(\mu_i(1-\mu_i)\) for Binomial).
\(\phi\) is the dispersion parameter.
Module 5: Smoothing Functions
Basis Expansion and Parametric Splines
Consider the regression model below: \[ \begin{align*} y_i &= g(x_i) + \epsilon_i\\ g(x_i)& = \sum_{m=1}^M \beta_m b_m (x_i) \end{align*} \] 1. Write out the model cubic spline
- Using the
splinespackage, fit a piecewise cubic spline model to theGAbirthdataset.
library(splines)
# Load GAbirth dataset
load(paste0(getwd(), "/data/GAbirth.RData"))
GAbirth <- dat
# Fit cubic spline model
fit_spline <- lm(bw ~ ns(age, knots = c(20, 30, 40)), data = GAbirth)
# Summarize results
summary(fit_spline)
Call:
lm(formula = bw ~ ns(age, knots = c(20, 30, 40)), data = GAbirth)
Residuals:
Min 1Q Median 3Q Max
-2555.55 -66.43 68.93 168.19 576.66
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3111.81 25.01 124.401 < 2e-16 ***
ns(age, knots = c(20, 30, 40))1 291.67 26.12 11.168 < 2e-16 ***
ns(age, knots = c(20, 30, 40))2 231.37 38.82 5.961 2.69e-09 ***
ns(age, knots = c(20, 30, 40))3 300.16 66.00 4.548 5.55e-06 ***
ns(age, knots = c(20, 30, 40))4 146.26 61.86 2.364 0.0181 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 309.5 on 4995 degrees of freedom
Multiple R-squared: 0.05464, Adjusted R-squared: 0.05388
F-statistic: 72.18 on 4 and 4995 DF, p-value: < 2.2e-16Interpret the coefficients for age and explain how the knots affect the model fit.
Use the AIC function to compare this model to a simple linear regression of bw ~ age.
We pre-defined the knots in the above code. Now let’s use automatic knot selection with the L2-penalty.
a. Write out the objective function with the penalty constraint.
b. Derive the closed form solution for \(\hat{\beta}\) and describe the impact of the penalty term.
The Generalized Cross-Validation Error (GCV) is defined as
\[ GCV = \frac{1}{n} \frac{\sum_i (y_i - \hat{y})^2}{[1-\frac{1}{n} tr(S)]^2} \]
- Fitting GAM with \(mgcv\): Fit two models where (1) default \(k=10\), and (2) \(k=30\). Compare GCV values and determine the model with best fit.
- Check the diagnostic plots using \(plot()\) for the most optimal model from (6). Interpret the findings from the diagnostic plot.
- Using the optimal model chosen from (6), interpret the parametric coefficients.
Generalized Additive Models for Non-Normal Data.
- Generalized Additive Models (GAMs): Extend GLMs by allowing additive non-linear relationships between predictors and the response.
\[ g(E(y)) - \beta_0 + \sum_{j=1}^p s_j(X_j) \]
- Bivariate Splines: Used for modeling interactions between two continuous variables.
- Interpreting Non-Linear Effects: GAMs provide smooth terms (\(s(x)\)) that capture non-linear patterns in the data.
- Use the
gam()function from themgcvpackage to fit a model predicting binary outcomes (e.g., infection status) from age and time of visit.
library(mgcv)Loading required package: nlme
Attaching package: 'nlme'The following object is masked from 'package:lme4':
lmListThis is mgcv 1.8-42. For overview type 'help("mgcv-package")'.# Simulate binary data
set.seed(123)
age <- runif(100, 20, 60)
time <- runif(100, 0, 10)
outcome <- rbinom(100, 1, plogis(0.5 + 0.03 * age - 0.1 * time))
# Fit GAM
fit_gam <- gam(outcome ~ s(age) + s(time), family = binomial, method = "REML")
# Summarize and plot
summary(fit_gam)
Family: binomial
Link function: logit
Formula:
outcome ~ s(age) + s(time)
Parametric coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.1390 0.2461 4.629 3.68e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(age) 1.895 2.373 4.705 0.146
s(time) 2.107 2.637 2.002 0.416
R-sq.(adj) = 0.053 Deviance explained = 8.7%
-REML = 56.127 Scale est. = 1 n = 100plot(fit_gam, pages = 1)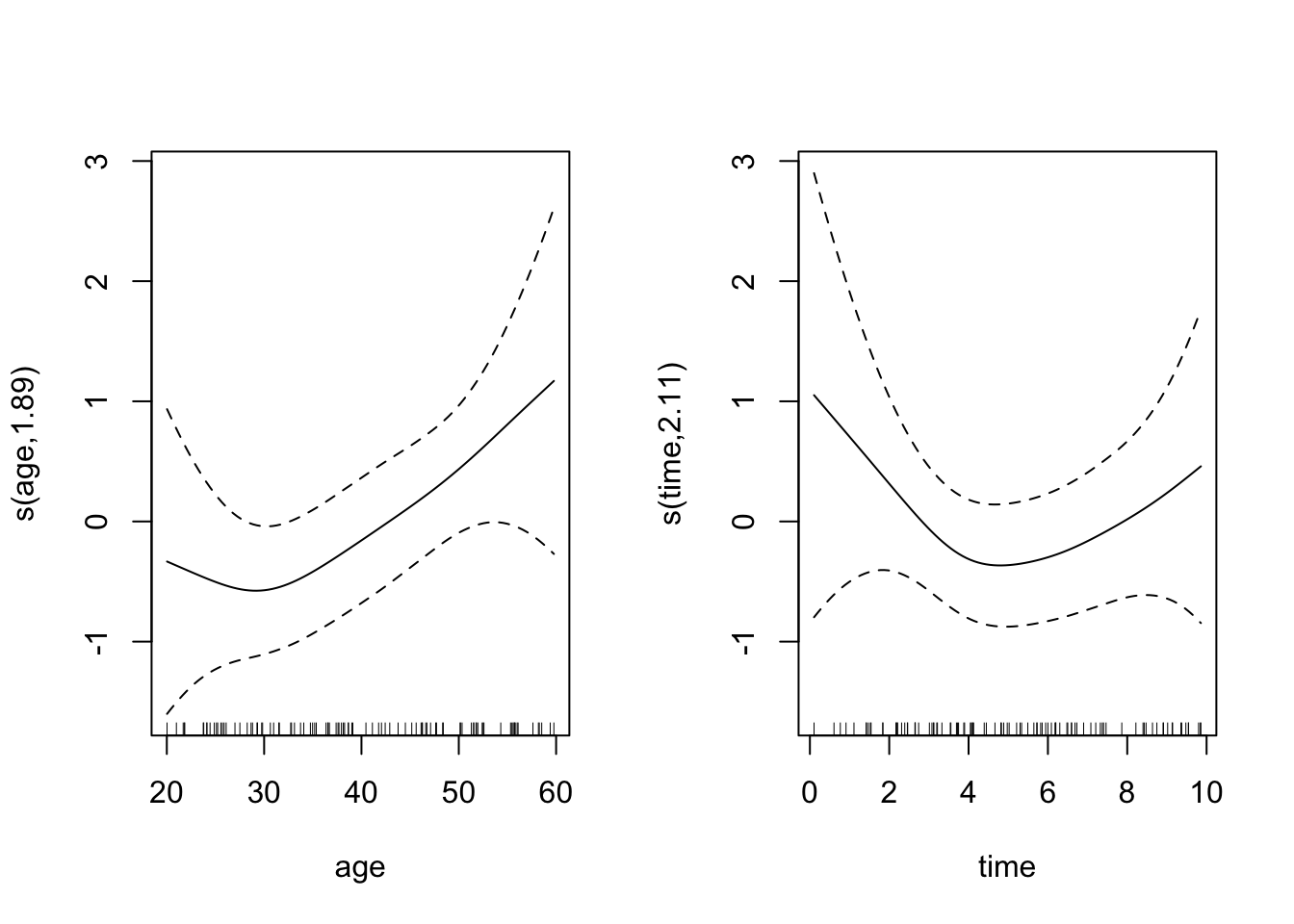
- Extend the GAM model to include a bivariate spline for age and time.
fit_gam_bivariate <- gam(outcome ~ te(age, time), family = binomial, method = "REML")
# Summarize and plot
summary(fit_gam_bivariate)
Family: binomial
Link function: logit
Formula:
outcome ~ te(age, time)
Parametric coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.1874 0.2571 4.618 3.87e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
te(age,time) 6.026 7.806 7.497 0.469
R-sq.(adj) = 0.0472 Deviance explained = 10.8%
-REML = 50.367 Scale est. = 1 n = 100plot(fit_gam_bivariate, scheme = 1)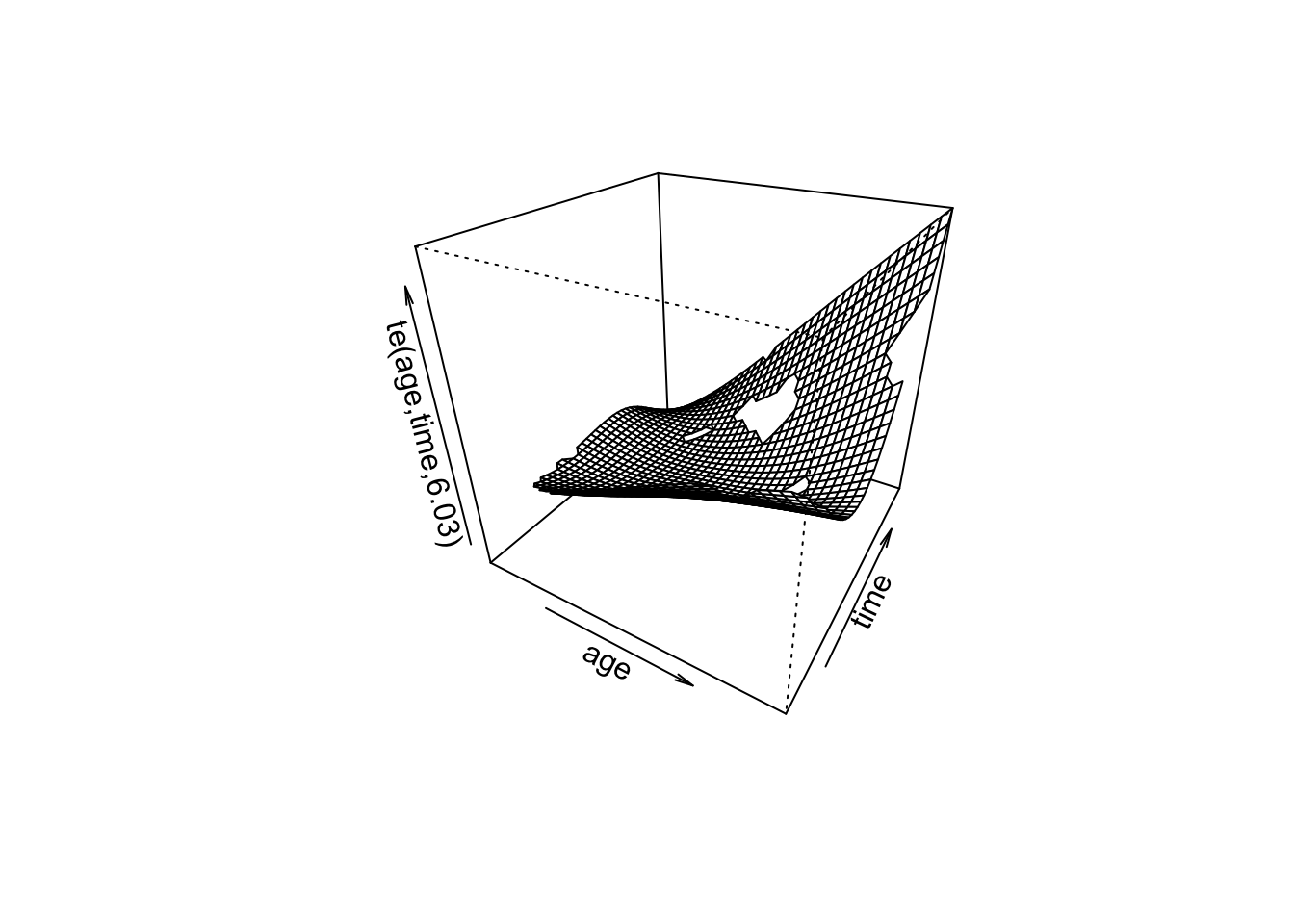
- What does the bivariate spline capture that separate univariate smooths do not?
- Visualize the interaction between age and time using the plot() function.
Module 6: Principal Component Analysis
PCA is a method for dimensionality reduction that identifies principal components (PCs), which are uncorrelated linear combinations of the original variables. These PCs are ordered by the amount of variance they explain in the data.
Steps in PCA
- Standardize the data if variables are measured on different scales.
- Compute the covariance matrix \(\Sigma\) or correlation matrix.
- Perform eigenvalue decomposition (EVD) or singular value decomposition (SVD).
- Eigenvalues (\(\lambda_i\)) represent the variance explained by each PC.
- Eigenvectors (\(v_i\)) define the weights for each variable in the PCs.
- Transform the data into the principal component space.
Variance Explained by PCs
The proportion of variance explained (PVE) by the \(k\)th PC is given by: \[ \text{PVE}_k = \frac{\lambda_k}{\sum_{i=1}^p \lambda_i}, \] where \(\lambda_k\) is the eigenvalue corresponding to the \(k\)th PC.
Principal Component Regression (PCR)
PCR uses PCs as predictors in regression models instead of the original variables. This approach is particularly useful when predictors are highly correlated.
Consider a dataset with three variables \(X_1\), \(X_2\), and \(X_3\). The covariance matrix \(\Sigma\) is: \[ \Sigma = \begin{bmatrix} 2 & 1 & 0.5 \\ 1 & 2 & 0.3 \\ 0.5 & 0.3 & 1 \end{bmatrix}. \]
- Compute the eigenvalues and eigenvectors of \(\Sigma\) (use R if needed).
- Write the first principal component as a linear combination of \(X_1\), \(X_2\), and \(X_3\).
- Perform PCA on the numerical variables in the
mtcarsdataset:
# Load mtcars dataset
data(mtcars)
# Perform PCA
pca_mtcars <- prcomp(mtcars, scale. = TRUE)
# Summary of PCA
summary(pca_mtcars)Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7
Standard deviation 2.5707 1.6280 0.79196 0.51923 0.47271 0.46000 0.3678
Proportion of Variance 0.6008 0.2409 0.05702 0.02451 0.02031 0.01924 0.0123
Cumulative Proportion 0.6008 0.8417 0.89873 0.92324 0.94356 0.96279 0.9751
PC8 PC9 PC10 PC11
Standard deviation 0.35057 0.2776 0.22811 0.1485
Proportion of Variance 0.01117 0.0070 0.00473 0.0020
Cumulative Proportion 0.98626 0.9933 0.99800 1.0000# Plot PCA
biplot(pca_mtcars, scale = 0)
- How many PCs explain at least 90% of the variance?
- Interpret the first two PCs using the loadings \((pca\_mtcars\)rotation)$.
Using the PCA output from the mtcars dataset: 6. Calculate the proportion of variance explained (PVE) for the first three PCs. 7. Create a scree plot to visualize the PVE for all components.
pve <- (pca_mtcars$sdev)^2 / sum((pca_mtcars$sdev)^2)
plot(pve, type = "b", xlab = "Principal Component", ylab = "Proportion of Variance Explained")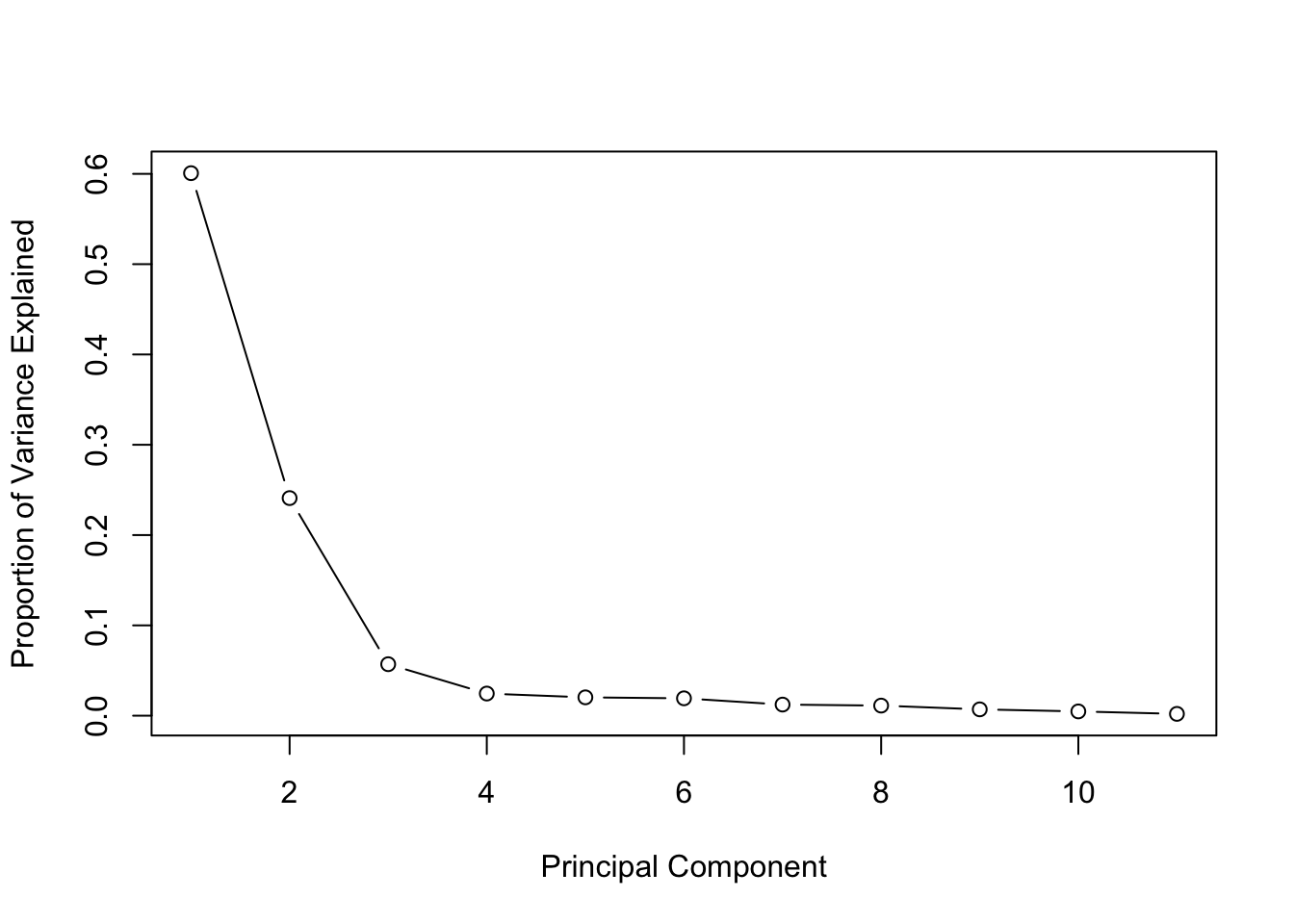
- Write out the model for a PCA regression of mpg (miles per gallon) on the first 3 PCs from the mtcars dataset.
- Perform this regression in R
# PCA for regression
pca_data <- data.frame(pca_mtcars$x[, 1:3], mpg = mtcars$mpg)
# Regression on PCs
fit_pcr <- lm(mpg ~ PC1 + PC2 + PC3, data = pca_data)
summary(fit_pcr)
Call:
lm(formula = mpg ~ PC1 + PC2 + PC3, data = pca_data)
Residuals:
Min 1Q Median 3Q Max
-3.5769 -1.1683 -0.1571 1.0958 4.1058
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 20.09062 0.35240 57.010 < 2e-16 ***
PC1 -2.18495 0.13928 -15.688 2.12e-15 ***
PC2 0.09718 0.21992 0.442 0.66197
PC3 -1.36055 0.45210 -3.009 0.00549 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.993 on 28 degrees of freedom
Multiple R-squared: 0.9012, Adjusted R-squared: 0.8906
F-statistic: 85.12 on 3 and 28 DF, p-value: 3.496e-14- Compare the results to a regression using all original predictors.
- Interpret the coefficients of the PCs and discuss why they differ from coefficients in a regression on the original variables.