Module 2 Linear Mixed Models

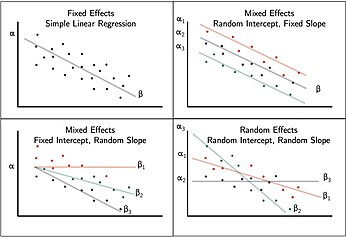
Reading

Basic Concepts

Examples of clustered data
  • Longitudinal data: Repeated measures data on each subject
    • \(y_{it}\) denotes the measure at time \(t\) for individual \(i\).
  • Clustered or multilevel data: Observations within nested group structures.
    • A collection of units from a population of similar units, e.g., \(y_{ij}\) denotes measure from person \(i\) in demographic group \(j\).

Motivating Example

Example of both longitudinal data and grouped/nested data:

The Treatment of Lead-Exposed Children (TLC) was examined using a placebo-controlled randomized study of succimer (a chelating agent) in children with blood lead levels of 20-44 micrograms/dL. These data consist of four repeated measurements of blood lead levels obtained at baseline (or week 0) , week 1, week 4, and week 6 on 100 children who were randomly assigned to chelation treament with succimer or placebo.

Variables:

  • ID: Child ID number

  • Treatment Group: Placebo vs. Succimer

  • Week: week X (x=0, 1, 4, 6)

  • Lead: lead level

tlcdata <- readRDS("data/tlc.RDS")
head(tlcdata)
    id treatment week lead
1    1   placebo    0 30.8
101  1   placebo    1 26.9
201  1   placebo    4 25.8
301  1   placebo    6 23.8
2    2  succimer    0 26.5
102  2  succimer    1 14.8
library(ggplot2)
library(dplyr)
library(gridExtra) 

placebo <- tlcdata %>% 
  filter(treatment == "placebo") %>%
  ggplot() +
  geom_line(aes(x = week, y = lead, col = id)) +
  labs(x = "Week", y="Lead", title = "Placebo") +
  theme(legend.position = "none")

succimer <- tlcdata %>% 
  filter(treatment == "succimer") %>%
  ggplot() +
  geom_line(aes(x = week, y = lead, col = id, linetype = treatment)) +
  labs(x = "Week", y="Lead",title = "Succimer") +
  theme(legend.position = "none")

gridExtra::grid.arrange(placebo, succimer)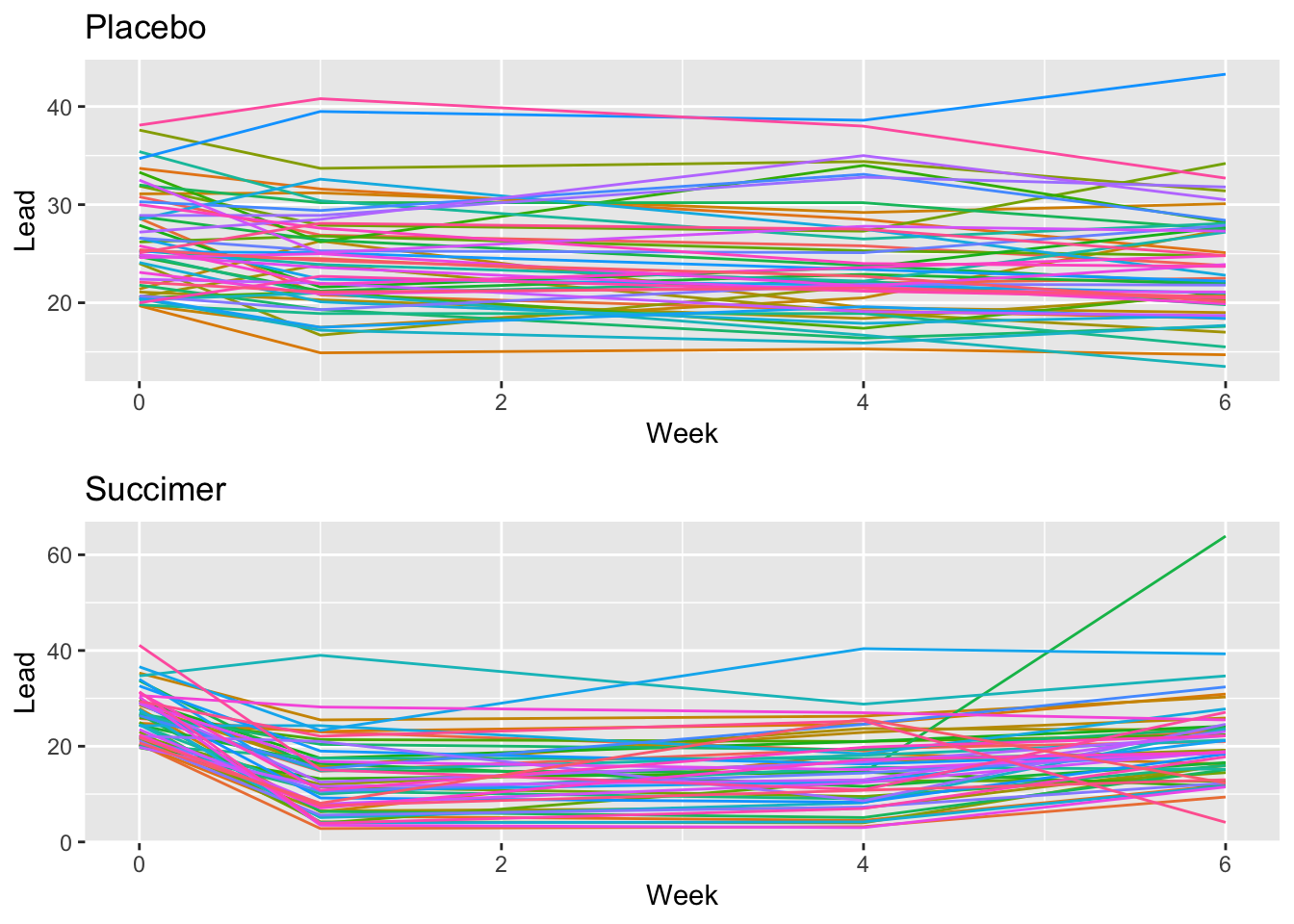

  • What are some scientific questions we may be interested in studying?

The Wrong Approach : Ignoring clustered or longitudinal structure= The wrong way to do it!!!

\[ \begin{align*} y_{ij}& = \beta_0 + \hat{\beta}_1 x_{ij} + \epsilon_{ij}\\ \epsilon_{ij} & \overset{iid}{\sim} N(0, \sigma^2) \end{align*} \]

fit.lm = lm(lead ~ week, data = tlcdata)
summary(fit.lm)

Call:
lm(formula = lead ~ week, data = tlcdata)

Residuals:
    Min      1Q  Median      3Q     Max 
-19.775  -3.749   0.328   4.454  43.330 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  22.9760     0.6079  37.793   <2e-16 ***
week         -0.4010     0.1670  -2.401   0.0168 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 7.966 on 398 degrees of freedom
Multiple R-squared:  0.01428,   Adjusted R-squared:  0.0118 
F-statistic: 5.765 on 1 and 398 DF,  p-value: 0.01681
  • What assumptions of OLS are we violating?

  • If observations were uncorrelated, i.e., if we had measured different subjects at 0, 1, 4, and 6 weeks post-exposure, then we could fit the standard linear model:

    \[ y_{it} = \beta_0 + \beta_1I(t=1) + \beta_2 I(t=4) + \beta_3 I(t=6) + e_{it} \]

    • There is an indicator for each time point, where \(t=0\) is treated as the reference group.

    • BUT the data are correlated. How do we handle this?

    • We extend the linear model to allow correlation (covariance).

    • A Better Approach: Linear Mixed Models

Approach 2: Mixed Models

Linear Mixed Models or LMMs

  • LMMs are extensions of regression in which intercepts and/or slopes are allowed to vary across individuals.

  • Mixed models were developed to deal with correlated data.

  • They allow for the inclusion of both fixed and random effects.

    • Fixed effect: a global or constant parameter that does not vary.

    • Random effect: Parameters that are random variables and are assigned a distributional assumption, e.g., \(\beta \sim N(\mu, \sigma^2)\).

Fixed effects parametrization

  • Taking our motivating example, we can assign a separate intercept for each child:

    \[ \begin{align*} y_{ij} &= \beta_{0i} + \beta_1 x_{ij} + \epsilon_{ij}, \\ \epsilon_{ij} & \overset{iid}{\sim} N(0, \sigma^2) \end{align*} \]

Interpretation:

  • \(\beta_{0i}\) is the child-specific weight at zero and \(\beta_1\) is the constant slope.
  • \(\sigma^2\) captures within child variability.

  • Limitations:

    • Estimating lots of parameters: subject-specific coefficients do not leverage overall population information and have less precision because of smaller sample size.

    • Cannot forecast the grow curve of a new child.

Fitting a fixed effects model in R:

We treat the “group” or “nested” unit as a factor/dummy variable. Therefore, we DO NOT include the intercept (see Module 1). Including the “cluster” as a factor allows for individual intercepts across children. Use the \(factor(id)\) function to create a factor variable for child ID.

fit.strat = lm(lead ~week + factor(id)-1, data =tlcdata) #do not include the intercept!!
summary(fit.strat$coefficients[1])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 -0.401  -0.401  -0.401  -0.401  -0.401  -0.401 
summary(fit.strat$coefficients[2])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  27.93   27.93   27.93   27.93   27.93   27.93

  • Data are balanced (same number of observations for each child).

  • The slope of week is the same in the model with a single intercept and the model with child-specific intercepts.

  • Controlling for group-specific intercepts gives a smaller standard error for the slope of week because week is the same for all children.

  • Note that oftentimes, the standard error will be larger if there is sparse or unbalanced data.

In class exercise

What is the interpretation of \(\hat{\beta_j}\) in this model?

Random Intercept Model

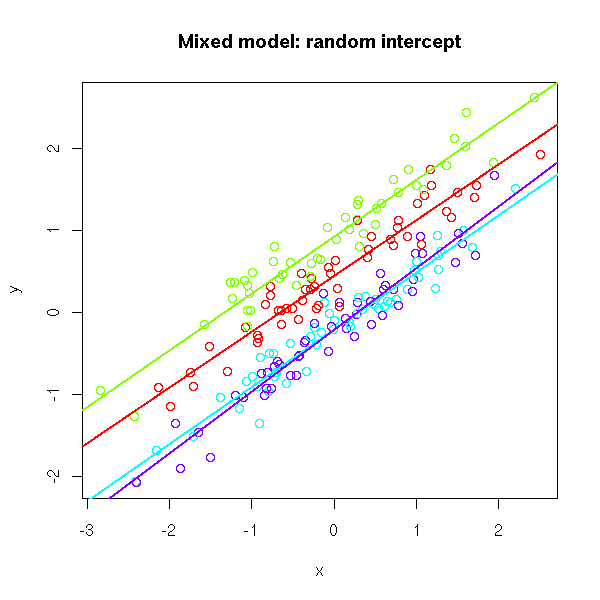
Consider the random intercept model with a vector of predictors \(x_{ij}\):

\[ \begin{align*} y_{ij} &=\mu + \theta_i + x_{ij}^T \beta + \epsilon_{ij}\\ \epsilon_{ij} & \overset{iid}{\sim} N(0, \sigma^2)\\ \theta_i & \overset{iid}{\sim} N(0, \tau^2) \\ \theta_i& \perp \epsilon_{ij} \end{align*} \]

  • \(\mu\) denotes the overall intercept (population mean when \(x_{ij}=0\).

  • \(\theta_i\) denotes the child specific difference from \(\mu\).

  • \(\beta_{0i} = \mu + \theta_i\) participant specific intercept or child specific average.

  • \(\beta\) time coefficient that does not vary across participants.

  • \(\tau^2\) denotes the between participant variability and here is the random effect variance.

  • \(\sigma^2\) denotes residual variance or within group variability “measurement error”.

What makes this a mixed model?

\(\beta_{0i}\) is random vs. \(\beta\) is global or fixed.

The following two models are equivalent:

Model 1: \(y_{ij} = (\mu + \theta_i) + x_{ij}^T\beta + \epsilon_{ij} , \quad \theta_i \sim N(0, \tau^2) \quad and \epsilon_{ij} \sim N(0, \sigma^2)\)

Model 2: The hierarchical model framework

\[ \begin{align*} y_{ij} &= \beta_{0i} + x_{ij}'\beta + \epsilon_{ij}\\ \beta_{0i}& \sim N(\mu, \tau^2)\\ \epsilon_{ij} & \sim N(0, \sigma^2) \end{align*} \]

  • Model 2 is an example of a hierarchical model in which there are hierarchical structures placed on random effects. Here the random coeffcient \(\beta_{0i}\) have a higher level mean \(\mu\).

  • Assumptions:

    • \(\epsilon_{ij} \perp \theta_i\) for all \(i\) and \(j\).

    • \(\theta_i\) are indentical and independent and normal for all \(i\).

    • \(\epsilon_{ij}\) are identical and independent and normal for all \(i\) and \(j\).

Properties of the Random Intercept Model

In-class exercise

  1. What is the overall (average) trend?

  2. What is total variability around the overall trend?

  3. What is the conditional (group-specific) trend?

  4. What is the conditional (within-group) residual variance?

Fitting a mixed effects model with a random intercept in R:

library(lmerTest)
Loading required package: lme4
Loading required package: Matrix

Attaching package: 'lmerTest'
The following object is masked from 'package:lme4':

    lmer
The following object is masked from 'package:stats':

    step
fit.randomeffects = lmer(lead ~ week + (1|id), data = tlcdata)
summary(fit.randomeffects)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: lead ~ week + (1 | id)
   Data: tlcdata

REML criterion at convergence: 2695.1

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-2.6337 -0.3461  0.0601  0.4131  6.1167 

Random effects:
 Groups   Name        Variance Std.Dev.
 id       (Intercept) 29.63    5.444   
 Residual             33.98    5.829   
Number of obs: 400, groups:  id, 100

Fixed effects:
            Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)  22.9760     0.7030 161.6442  32.683  < 2e-16 ***
week         -0.4010     0.1222 299.0000  -3.281  0.00116 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
     (Intr)
week -0.478
  • Compared to a model fitted with group dummy variables, the week slope estimate and SE are identical.

Model Interpretation

Interpretation: The fixed effect captures the global or average change in lead level for every one unit change in time, i.e., from week 1 to week 2 \(\hat{\beta}_1 = -0.410\) meaning that there is an average 0.4 decrease in lead for every unit increase in week which was found to be statistically significant \(p<0.01\).

Now the intercept 22.97 corresponds to the population-average lead at week 0.

The SE of the slope \(se(\hat{\beta_1}) = 0.122\) capturing uncertainty associated with the estimate.

The random effect of child \(\beta_{0i}\) allows for child-specific random intercepts, where the variance of the intercepts is 29.63.

#Extracting the random effects theta_i's
random.eff = ranef(fit.randomeffects)$id
hist(random.eff$`(Intercept)`)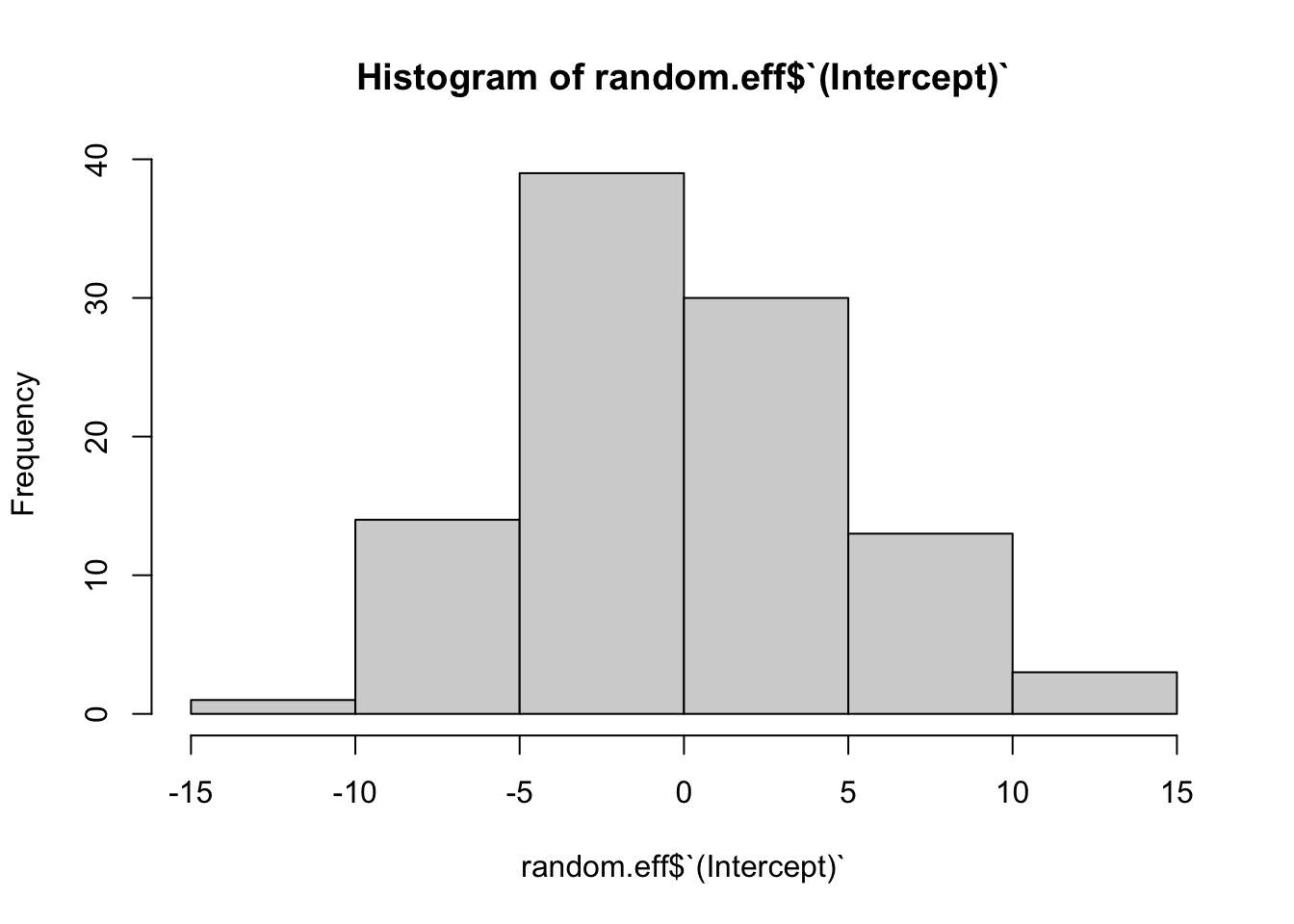

Let’s fit an alternative model to the data including a treatment effect:

library(lmerTest)
fit.randomeffects = lmer(lead ~ week + treatment +  (1|id), data = tlcdata)
summary(fit.randomeffects)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: lead ~ week + treatment + (1 | id)
   Data: tlcdata

REML criterion at convergence: 2670.2

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-2.4885 -0.3686 -0.0176  0.4514  6.3428 

Random effects:
 Groups   Name        Variance Std.Dev.
 id       (Intercept) 22.09    4.700   
 Residual             33.98    5.829   
Number of obs: 400, groups:  id, 100

Fixed effects:
                  Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)        25.7648     0.8512 136.0165  30.269  < 2e-16 ***
week               -0.4010     0.1222 299.0000  -3.281  0.00116 ** 
treatmentsuccimer  -5.5775     1.1060  98.0000  -5.043  2.1e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr) week  
week        -0.395       
trtmntsccmr -0.650  0.000
In class exercise

What are the overall findings from this model? And how does this model differ from the previous model?

Covariance Structure

  • A random intercept model is also known as a two-level variance component model:

\[ \begin{align*} y_{ij} &= \mu + \theta_i + \beta x_{ij} + \epsilon_{ij}\\ \theta_i & \overset{iid}{\sim} N(0, \tau^2)\\ \epsilon_{ij} & \overset{iid}{\sim} N(0, \sigma^2) \end{align*} \]

Random Intercept Model in Matrix Form

Random intercept model

Consider the mixed model with random intercepts for \(n\) groups and define \(N = \sum_{i=1}^n r_i\).

\[ \mathbf{y} = \mathbf{Z} \mathbf{\theta} + \mathbf{X}\mathbf{\beta} + \mathbf{\epsilon} \]

where

  • \(\mathbf{y} = N \times 1\) vector of response

  • \(\mathbf{Z} = N \times n\) design matrix of indicator variables for each group.

  • \(\mathbf{\theta} = n \times 1\) vector of random intercepts.

  • \(\mathbf{X} = N\times p\) design matrix of fixed effects (including overall intercept).

  • \(\mathbf{\beta} = p\times 1\) vector of fixed effects.

  • \(\mathbf{\epsilon} = N \times 1\) vector of residual error.

Assumptions of the above model

  • \(\mathbf{\theta} \sim N(0, \tau^2 I_{n \times n}\).

  • \(\mathbf{\epsilon} \sim N(0, \sigma^2 I_{N \times N}\)).

Summary I

What is the model?
  • In the random intercept model, we regress a vector of outcomes \(y_{ij}\) for individual \(i\) and within measure \(j\) on values on a vector of predictor values \(x_{ij}\) with:
  • \(Y = \mu + \theta_i + x_{ij}'\beta + \epsilon_{ij}\)
  • \(\mu\) is the population mean or overall average across all subjects-times.
Model Assumptions
  • \(\epsilon_{ij} \sim N(0, \sigma^2)\)
  • \(Var(\epsilon) = \sigma^2\) constant within subject variance
  • \(\theta_i \sim N(0, \tau^2)\).
  • \(Var(\theta_i) = \tau^2\) across subject variance.
  • \(\theta_i \perp \epsilon_{ij}\)
Interpretation
  • \(\theta_i\) *individual deviations away from the population mean \(\mu\).
  • \(\beta_1\) the global value of the change of \(Y\) for every one unit change of \(X\).
  • \(\sigma^2 + \tau^2\) is the total variance.

Intraclass Correlation

  • Note that the within-group covariance is: \(Cov(y_{ij}, y_{ij'}) = \tau^2\) .

  • So the correlation between observations within within the same group is

\[ \rho = Corr(y_{ij}, y_{ij'}) = \frac{\tau^2}{\tau^2 + \sigma^2} \text{ for all }j \neq j'. \]

  • The value \(\rho\) is often called the intraclass correlation. It measures the degree of similarity among same-group observations compared to the residual error \(\sigma^2\).
  • Describes how strongly units in the same group resemble eachother.
  • \(\rho \rightarrow 0\) when \(\tau^2 \rightarrow 0\) (i.e. same intercept)
  • \(\rho \rightarrow 0\) when \(\sigma^2 \rightarrow \infty\) (i.e., growing measurement error).
  • \(\rho \rightarrow 1\) when \(\tau^2 \rightarrow \infty\) (i.e., large separation in intercepts).
  • \(\rho \rightarrow 1\) when \(\sigma^2 \rightarrow 0\) (i.e., zero measurement error).
  • The above ICC has an exchangeable structure because the correlation is constant between any pair of within-group observations.

Simulation Varying Between Subject Variability

Simulation Varying Measurement Error

Shrinkage and Random Effects

  • To simplify the derivation first consider a random effects model without fixed effects:

\[ y_{ij} = \theta_i + \epsilon_{ij}, \quad \theta_i \overset{iid}{\sim} N(0, \tau^2), \quad \epsilon_{ij} \overset{iid}{\sim} N(0, \sigma^2) \] - The join density of the data and random effects is given by:

\[ \prod_{i,j} f(y_{ij}, \theta_i) = \prod_{i,j} f(y_{ij}|\theta_i) \cdot \prod_i g(\theta_i) \]

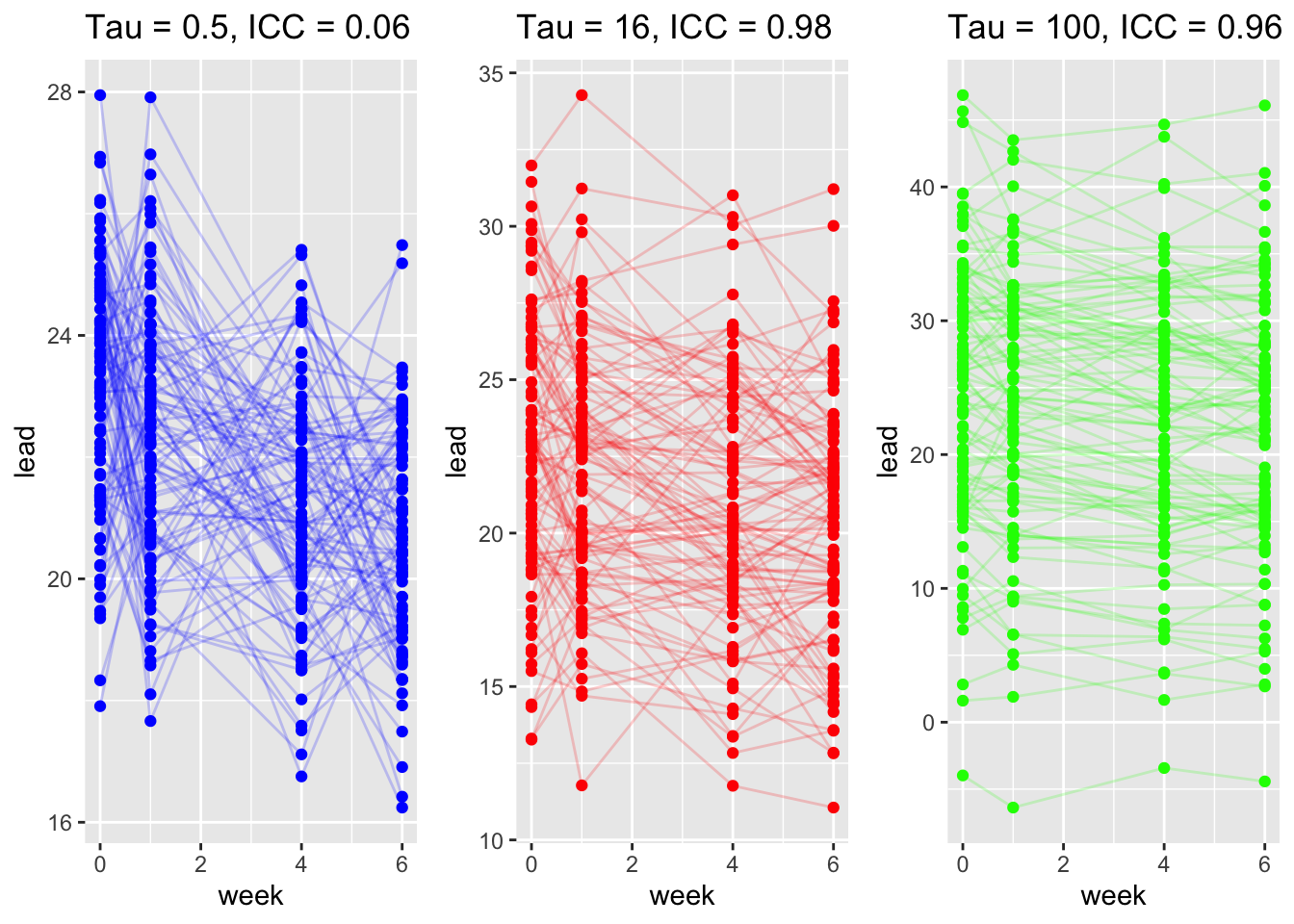
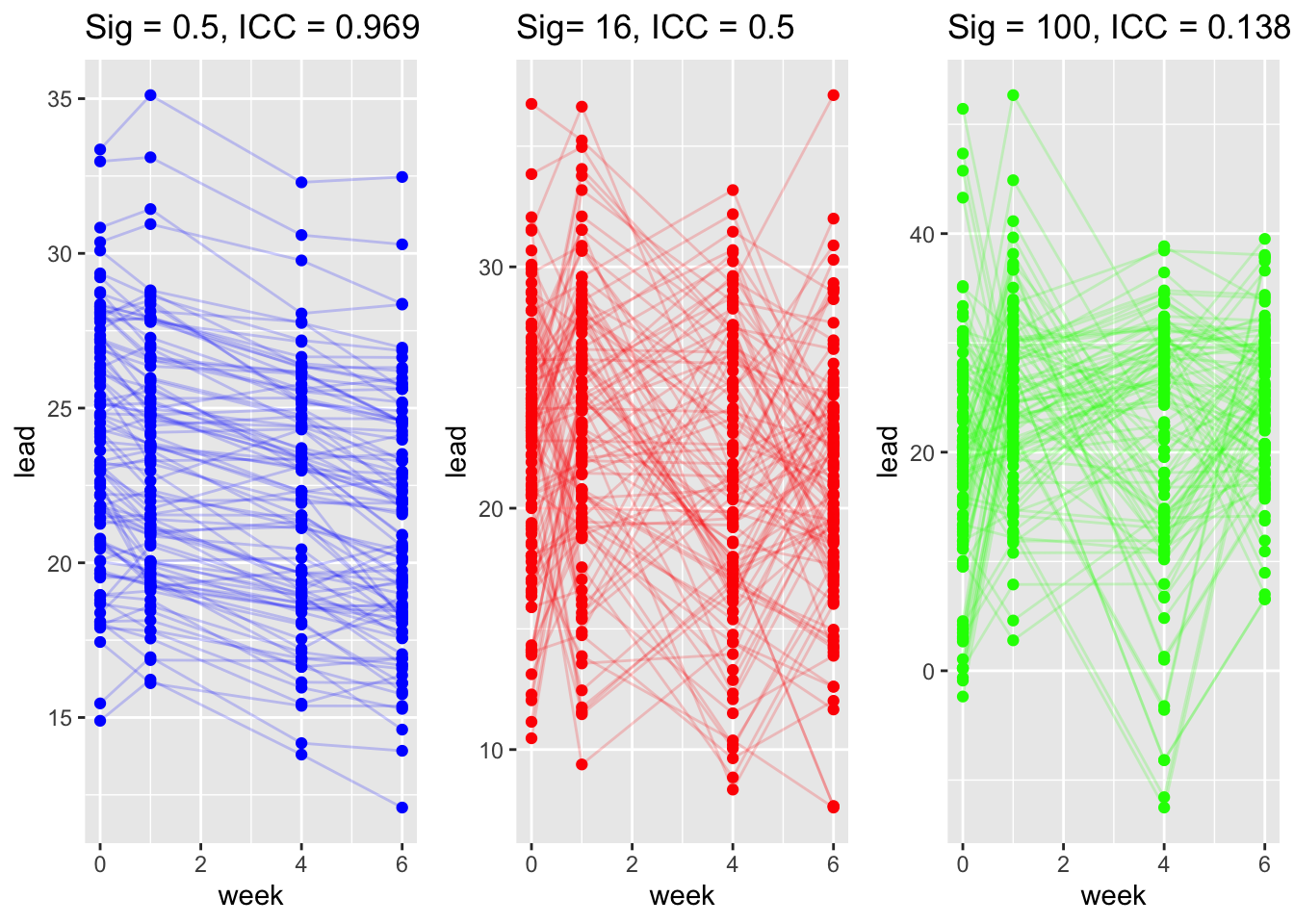
  • Now consider the matrix formulation \(\mathbf{y} = \mathbf{Z} \mathbf{\theta} + \mathbf{\epsilon}\) where \(\mathbf{Z}=\) deisgn matrix of indicator variables denoting the \(ij^{th}\) observation belongs to group \(i\).

  • Given the values of \(\sigma^2\) and \(\tau^2\), it is easy to find the closed form solution to this.

  • Note that:

    • \(\hat{\theta}_i \rightarrow 0\) when \(\tau^2 \rightarrow 0\) (shrinks all random intercepts to zero).
    • \(\hat{\theta}_i \rightarrow \bar{y}_{i.}\) when \(\tau^2 \rightarrow \infty\) (no shrinkage = raw group mean estimates).
    • \(\hat{\theta}_i \rightarrow \bar{y}_{i.}\) when \(\sigma^2 \rightarrow 0\) (no shrinkage = raw group mean estimates).
    • \(\hat{\theta}_i \rightarrow \bar{y}_{i.}\) when \(r \rightarrow \infty\) (no shrinkage = raw group mean estimates).

    \(\tau^2\) controls the amount of shrinkage and how much information to borrow across groups.

Hierarchical Formulation

  • Now we assume the random effects are centered around a common mean. \(\mu\). Let’s take look at the hierarchical formulation.

\[ y_{ij} = \theta_i + \epsilon_{ij}, \quad \theta_i \sim N(\mu, \tau^2), \quad \epsilon_{ij} \sim N(0, \sigma^2) \]

  • The joint density of the data and random effects is a multivariate normal given by:

\[ \begin{align*} \prod_{i,j} f(y_{ij}, \theta_i) & =\prod_{i,j} f(y_{ij}|\theta_i) \cdot \prod_i g(\theta_i)\\ & \propto exp\left(-\frac{1}{2\sigma^2} [( \mathbf{y} - \mathbf{Z}\mathbf{\theta})^T (\mathbf{y} - \mathbf{Z} \mathbf{\theta}) + \frac{\sigma^2}{\tau^2} (\mathbf{\theta} - \mathbf{\mu})^T (\mathbf{\theta}- \mathbf{\mu})]\right) \end{align*} \]

Taking the first derivative, setting to 0, and solve! (On your own time).

Borrowing of Information
  • We can express \(\hat{\theta}_i\) as

\[ \hat{\theta}_i = \frac{(1/\tau^2)\mu + (r_i/\sigma^2) \bar{y}_{i.}}{1/\tau^2 + (r_i /\sigma^2)} \]

  • Since \(\sigma^2/r_i\) is the sample variance of the estimated sample mean \(\bar{y}_{i.}\), the above form shows that random effects can be viewed as weighted average of:

    • subject-specific mean: \(\bar{y}_{i.}\).
    • overall mean \(\mu\)

  • We can also express \(\hat{\theta}_i\) in terms of the intraclass correlation \(\rho = \tau^2/(\tau^2 + \sigma^2)\).

    \[ \hat{\theta}_i = \frac{\rho^{-1} \mu + r_i (1-\rho)^{-1} \bar{y}_{i.}}{\rho^{-1} + r_i (1-\rho)^{-1}} \]

  • Less shrinkage is expected for \(\rho \rightarrow 1\).

  • For unknown variance parameters \(\hat{\theta}_i\) is the BLUP: Best Linear Unbiased Predictor.

    • Unbiased: \(E(\hat{\theta}_i) = \mu\).
    • Best Linear Unbiased Prediction (BLUP) = Best means unbiased and minimum variance: \(E(\hat{\theta}_i - \theta_i)^2\) is minimized.

  • Note that

    • \(\hat{\theta}_i \rightarrow \mu\) when you \(\tau^2 \rightarrow 0\) (shrink ALL random intercepts to a common mean \(\mu\)).
    • \(\hat{\theta}_i \rightarrow \bar{y}_{i.}\) when \(\tau^2 \rightarrow \infty\) (no shrinkage = raw mean estimates).

Parameter Estimation

\[\mathbf{y} = \mathbf{Z\theta} + \mathbf{X \beta} + \mathbf{\epsilon}\] - Since \(\mathbf{\theta}\) and \(\mathbf{\epsilon}\) are random effects, we can rewrite the above as

\[ \begin{align*} \mathbf{y} &= \mathbf{X \beta} + \mathbf{\epsilon^*}\\ \mathbf{\epsilon*}& = \mathbf{Z \theta} + \mathbf{\epsilon} \end{align*} \] - This is equivalent to integrating out the random effects. Then the marginal model is:

\[ \mathbf{y} \sim N(X\beta, \mathbf{V}) \]

  • The MLE approach from simple linear regression does not work because data are now correlated. We extend the simple OLS estimate to include covariance \(V\):
MLE estimation

\[ \mathbf{\hat{\beta}} = (\mathbf{X}^T \mathbf{V}^{-1} \mathbf{X})^{-1} \mathbf{X^T} \mathbf{V}^{-1} \mathbf{y} \]

  • The MLE estimate of the variances is biased! (Similar to the estimate in simple linear regression).

  • An alternative is the restricted maximum likelihood (REML):

\[ \hat{\sigma}^2_{MLE} = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2 \]

vs.

\[ \hat{\sigma}^2_{REML} = \frac{1}{n-1} \sum_{i=1}^n (x_i -\bar{x})^2 \]

Random Intercept and Random Slope Model

  • What are some scientific questions we may be interested in studying?
  • Consider the mixed effects model with a vector of predictors \(x_{ij}\):

\[ y_{ij} = (\beta_0 + \theta_{0i}) + (\beta_1 + \theta_{1i}) x_{ij} + \epsilon_{ij}, \quad \epsilon_{ij} \overset{iid}{\sim} N(0, \sigma^2) \]

  • $_{0i} = _0 + $ participant specific intercept or child specific average.

  • \(\beta_{1i} = \beta_1 + \theta_{1i}\) participant specific rate of change or slope.

  • \(\beta_0, \beta_1\) the intercept and slope that does not vary across participants.

  • \(\sigma^2\) within subject variability ie measurement error.

In class exercise

What do we do for \(\theta_{1i}\)?

Fitting the Random Intercept and Slope model in R

Let’s fit the model using the tlc data:

placebo_data = tlcdata %>% filter(treatment == "placebo")
fit_random <- lmer(lead ~ week + (week|id), data = placebo_data)
summary(fit_random)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: lead ~ week + (week | id)
   Data: placebo_data

REML criterion at convergence: 1053.3

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.20808 -0.49837 -0.02268  0.47100  2.30541 

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 id       (Intercept) 23.3113  4.8282       
          week         0.1581  0.3976   0.02
 Residual              4.5016  2.1217       
Number of obs: 200, groups:  id, 50

Fixed effects:
            Estimate Std. Error       df t value Pr(>|t|)    
(Intercept) 25.68536    0.72018 49.01076  35.665  < 2e-16 ***
week        -0.37213    0.08437 49.00066  -4.411 5.64e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
     (Intr)
week -0.164

Interpretation:

  • Child-specific intercept: \((\beta_0 + \theta_{0i}) \sim N(25.68, 23.31)\).
  • Child-specific slope: \((\beta_1 + \theta_{1i}) \sim N(-0.372, 0.158)\).
  • The correlation \(rho\) between \((\beta_{0i} \beta_{1i}) = 0.02\).
  • The 95% CIs of the subject-specific slopes does not include zero in the distribution. This we reject the null that a child’s lead levels do not increase with time.

Comparing Models

  • Is the random intercept plus slope preferred over random intercept only?
AIC

  • AIC: Akaike’s Information Criterion.

  • AIC is often used in model selection. It is a popular approach to choosing which variables should be in the model. \[ AIC = -2l(\mathbf{\theta}) + 2p \] where \(l(\mathbf{\theta})\) is the log-likelihood for all parameters \(\mathbf{\theta}\) and \(p\) is the number of parameters.

  • The MLE estimate of the variances is biased! (Similar to the estimate in simple linear regression).

  • The general rule of thumb is a differenc of 2+ is substantially better. A lower AIC is better.

  • The AIC uses the maximum likelihood so use \(REML=FALSE\) to set the parameter estimation to MLE.

BREAKOUT SESSION 2
  1. Read in the Nepalese Children data from Canvas.

Motivating Example

Study Design:

  1. Time-varying variables of 200 children collected up to 5 time points about 4 months apart.
  • age (month), indicator for current breastfeeding status, arm circumference (cm), height (cm), weight(kg).
  1. Time invariant baseline information:
  • sex of the child, mother’s age at birth, indicator of mother’s literacy.
load("/Users/emilypeterson/Library/CloudStorage/OneDrive-EmoryUniversity/BIOS 526/BIOS526_Book/data/Nepal200.RData")
  1. Review the data to make sure you understand the variables. \
  2. Fit the random intercept model using the code given above where arm circumference is regressed on age .
  3. Interpret the findings from this model.
  4. Fit the same model, but using MLE instead. Do this by setting \(REML=FALSE\) as a parameter in your code.
  5. Identify the differences in coefficient estimates.
  6. Fit the random intercept and slope model using the code given above where arm circumference is regressed on age.
  7. Interpret the findings of this model.
  8. Compare the random intercept only, and the random intercept plus slope model using AIC metrics. \(REML=FALSE\) must be included in the \(fit <- lmer(y\sim ..., REML=F)\) function call. To get the AIC from a model fit using the function \(AIC(fit)\).
  9. Based on the AIC findings, which model is better?