Module 5 Part 1: Basis Expansion and Parametric Splines
Reading
Chapter 5- Elements of Statistical Learning (Hastie)
Chapter 5- Introduction to Statistical Learning (James et al. )
Basic Concepts
- Basis Functions and knots
- Piecewise Linear Splines
- Piecewise Cubic Splines
- Bias-Variance Tradeoff
- Criteria for model prediction performance (CV, GCV, AIC).
Parametric Splines
Let’s fit a linear regression here
Call:
lm(formula = bw ~ gw, data = dat)
Residuals:
Min 1Q Median 3Q Max
-761.50 -83.01 16.80 100.80 348.80
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2177.513 39.351 -55.34 <2e-16 ***
gw 141.808 1.019 139.10 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 144.2 on 4998 degrees of freedom
Multiple R-squared: 0.7947, Adjusted R-squared: 0.7947
F-statistic: 1.935e+04 on 1 and 4998 DF, p-value: < 2.2e-16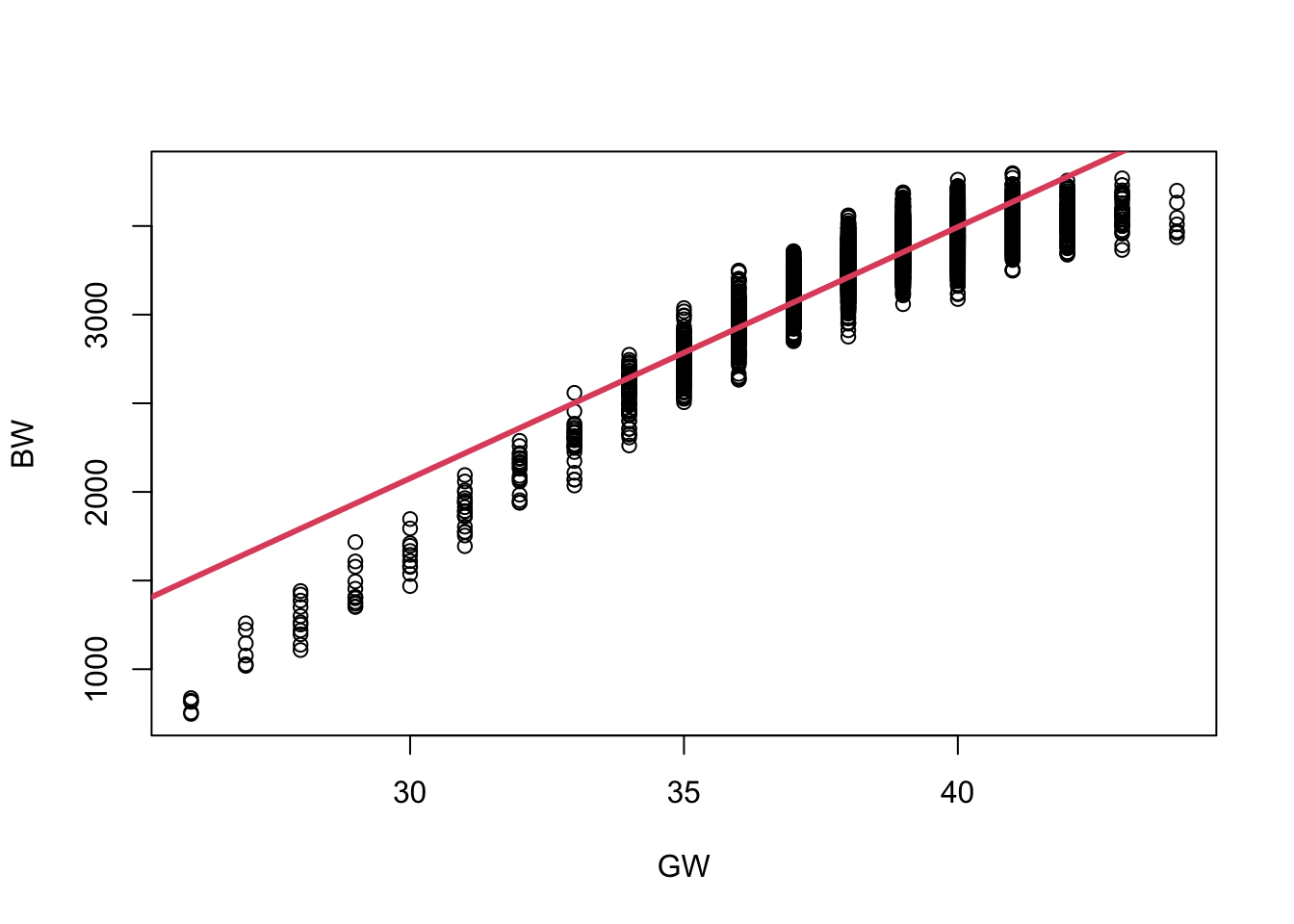
Important
Basis Expansion
- Consider the regression model:
\[ y_i = \textcolor{blue}{g(x_i)} + \epsilon_i \]
- One approach: assume \(g(x_i)\) is a linear combination of \(M\) functions of \(x_i\).
\[ g(x_i) = \sum_{m=1}^M \beta_m b_m(x_i) \]
We choose and fix \(b_m(x_i)\) so it is known!.
We estimate the coefficients/scalars for the transformed \(b_m(x_i)\).
Note! \(b_m()\) is simply a transformation of the original variable \(x_i\).
\(b_m(x_i)\) is called a Basis Function.
Basis functions are a core tool in the field of functional data analysis and optimizations. We model non-linear curves as piecewise functions.
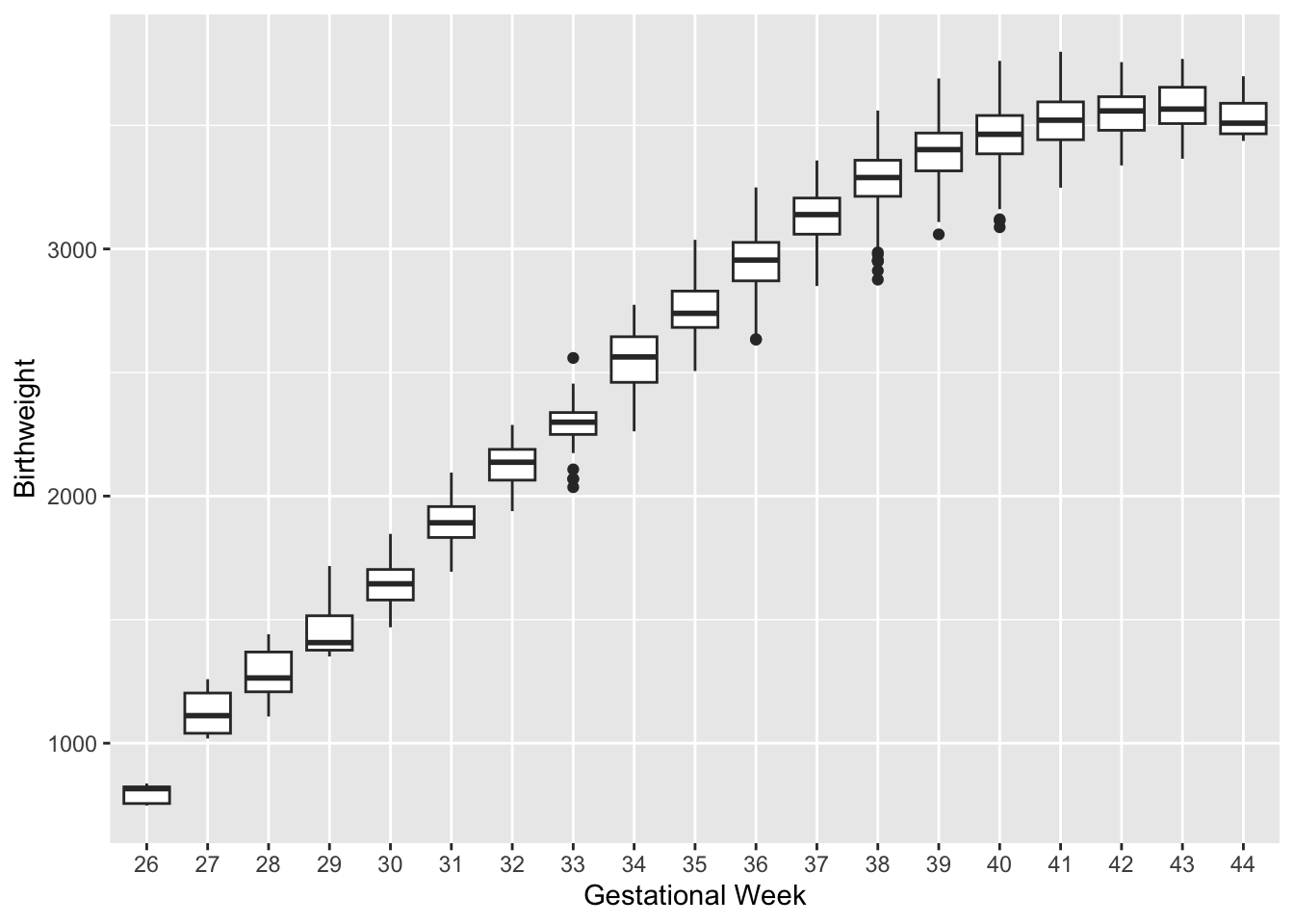
Let’s fit a Polynomial Regression to the birthweight outcomes:
\[ \begin{align*} \text{Quadratic } y_i & = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + e_i\\ \text{Cubic } y_i & = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + + \beta_3 x_i^3 + e_i\\ \end{align*} \]
Note that polynomial functions often cannot model the ends very well.
Piecewise Regression
To model non-linear relationship: divide range of the covariates into some “suitable” regions. E.g. pregnancy length: preterm (<37 weeks), full-term (37-41 weeks), and post-term (>42 weeks).
Model with polynomial functions separately within each region. The interior values that define the regions (cut-points) are called knots.
- Piecewise regression is equivalent to a model where the basis functions of \(x_i\) interact with dummy variables for regions, e.g.,
\[ \begin{align*} y_i & = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \beta_3 D_{1i} \\ & + \beta_4 x_i \times D_{1i} + \beta_5 x_i^2 \times D_{1i}\\ & + \beta_6 D_{2i} + \beta_7 x_i \times D_{2i} + \beta_8 x_i^2 \times D_{2i} \end{align*} \]
where
\[ D_{1i} = \begin{cases} 1 & 37 \leq x_i < 42\\ 0 & OW \end{cases} \]
$$
D_{2i} =
\[\begin{cases} 1 & x_i \geq 42\\ 0 & OW \end{cases}\]$$
We have two cut-points (knots) which yields three regions. We only need two dummy variables for three regions.
The positive association between pregnancy length and birth weight decreases for higher gestational weeks.
Here, linear, quadratic, and cubic result in similar trends in each regions.
Importantly! All three have discontinuities, i.e., they are not continous in the 1st and/or 2nd derivative.
Call:
lm(formula = bw ~ (gw + I(gw^2)) * (Ind1 + Ind2), data = dat)
Residuals:
Min 1Q Median 3Q Max
-403.65 -73.97 5.35 78.00 299.04
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.962e+03 8.043e+02 -6.169 7.42e-10 ***
gw 2.312e+02 5.005e+01 4.619 3.96e-06 ***
I(gw^2) -3.160e-01 7.735e-01 -0.409 0.683
Ind1TRUE -2.142e+04 1.959e+03 -10.937 < 2e-16 ***
Ind2TRUE -4.984e+04 5.279e+04 -0.944 0.345
gw:Ind1TRUE 1.202e+03 1.045e+02 11.494 < 2e-16 ***
gw:Ind2TRUE 2.488e+03 2.470e+03 1.007 0.314
I(gw^2):Ind1TRUE -1.685e+01 1.410e+00 -11.950 < 2e-16 ***
I(gw^2):Ind2TRUE -3.134e+01 2.889e+01 -1.085 0.278
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 109.6 on 4991 degrees of freedom
Multiple R-squared: 0.8816, Adjusted R-squared: 0.8814
F-statistic: 4646 on 8 and 4991 DF, p-value: < 2.2e-16
Call:
lm(formula = bw ~ (gw + (gw^2)) * (Ind1 + Ind2), data = dat)
Residuals:
Min 1Q Median 3Q Max
-396.28 -74.28 4.34 78.34 321.34
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4634.537 74.286 -62.39 <2e-16 ***
gw 210.735 2.158 97.67 <2e-16 ***
Ind1TRUE 4244.229 94.153 45.08 <2e-16 ***
Ind2TRUE 7710.241 711.475 10.84 <2e-16 ***
gw:Ind1TRUE -114.351 2.620 -43.65 <2e-16 ***
gw:Ind2TRUE -199.521 16.853 -11.84 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 111.8 on 4994 degrees of freedom
Multiple R-squared: 0.8766, Adjusted R-squared: 0.8764
F-statistic: 7092 on 5 and 4994 DF, p-value: < 2.2e-16
Piecewise polynomials have limitations:
Positive association between pregnancy length and birthweight decreases for higher gestational weeks.
Linear, quadratic, and cubic result in similar trend in each region.
Limitations
The regression functions do not match at knot locations.
Requires many regression coefficients (degrees of freedom).
Linear Splines
Splines are basis functions for piecewise regressons that are connected at the interior knots.
Splines are continuous, which makes them aesthetically appealing.
A linear piecewise spline at knot locations 36.5 and 41.5 is specified as:
\[ y_i = \beta_0 + \beta_1 x_i + \beta_2 (x_i - 36.5)_{+} + \beta_3 (x_i - 41.5)_{+} + \epsilon_i \]
- For \(x_i<36.5\)
\[ y_i = \beta_0 + \beta_1 x_i \]
- For \(36.5 \geq x_i < 41.5\)
\[ \begin{align*} y_i & = \beta_0 + \beta_1 x_i + \beta_2 (x_i - 36.5) \\ &= (\beta_0 - \beta_2 * 36.5) + (\beta_1 + \beta_2) x_i \end{align*} \]
- For \(41.5 \geq x_i\)
\[ \begin{align*} y_i & = \beta_0 + \beta_1 x_i + \beta_2 (x_i - 36.5) + \beta_3 (x_i - 41.5)\\ & = (\beta_0 - \beta_2 * 36.5 - \beta_3 * 41.5) + (\beta_1 + \beta_2 + \beta_3) x_i \end{align*} \]
- \(\beta_2\) and \(\beta_3\) represent changes in slope compared to the previous region.
Note here we only need 4 regression coefficients compared to 6 in the model that does not force connections at knots.
#Linear Splines
Sp1 = (dat$gw - 36.5) * as.numeric(dat$gw >= 36.5)
Sp2 = (dat$gw - 41.5) * as.numeric(dat$gw >= 41.5)
fit7 <- lm(bw ~ gw + Sp1 + Sp2, data = dat)morepoints = seq(26, 44, .1)
newdata = data.frame(gw=morepoints, Sp1= (morepoints-36.5), Sp2=(morepoints-41.5) )
# non-zero for values greater than 36.5 and greater than 41.5 only:
newdata[ newdata <0] = 0
plot (dat$bw~dat$gw, xlab = "Gestational Week", ylab = "Birth weight")
lines (fit4$fitted[Ind1]~dat$gw[Ind1], col = 2, lwd = 3)
lines (fit4$fitted[Ind2]~dat$gw[Ind2], col = 2, lwd = 3)
lines (fit4$fitted[!Ind1 & !Ind2]~dat$gw[!Ind1 & !Ind2], col = 2, lwd = 3)
lines (predict (fit7, newdata=newdata)~morepoints, col = 4, lwd = 3)
abline (v=c(36.5, 41.5), col = "grey", lwd = 3)
legend ("topleft", legend=c("Piecewise linear", "Linear splines"), col=c(2,4), lwd=3)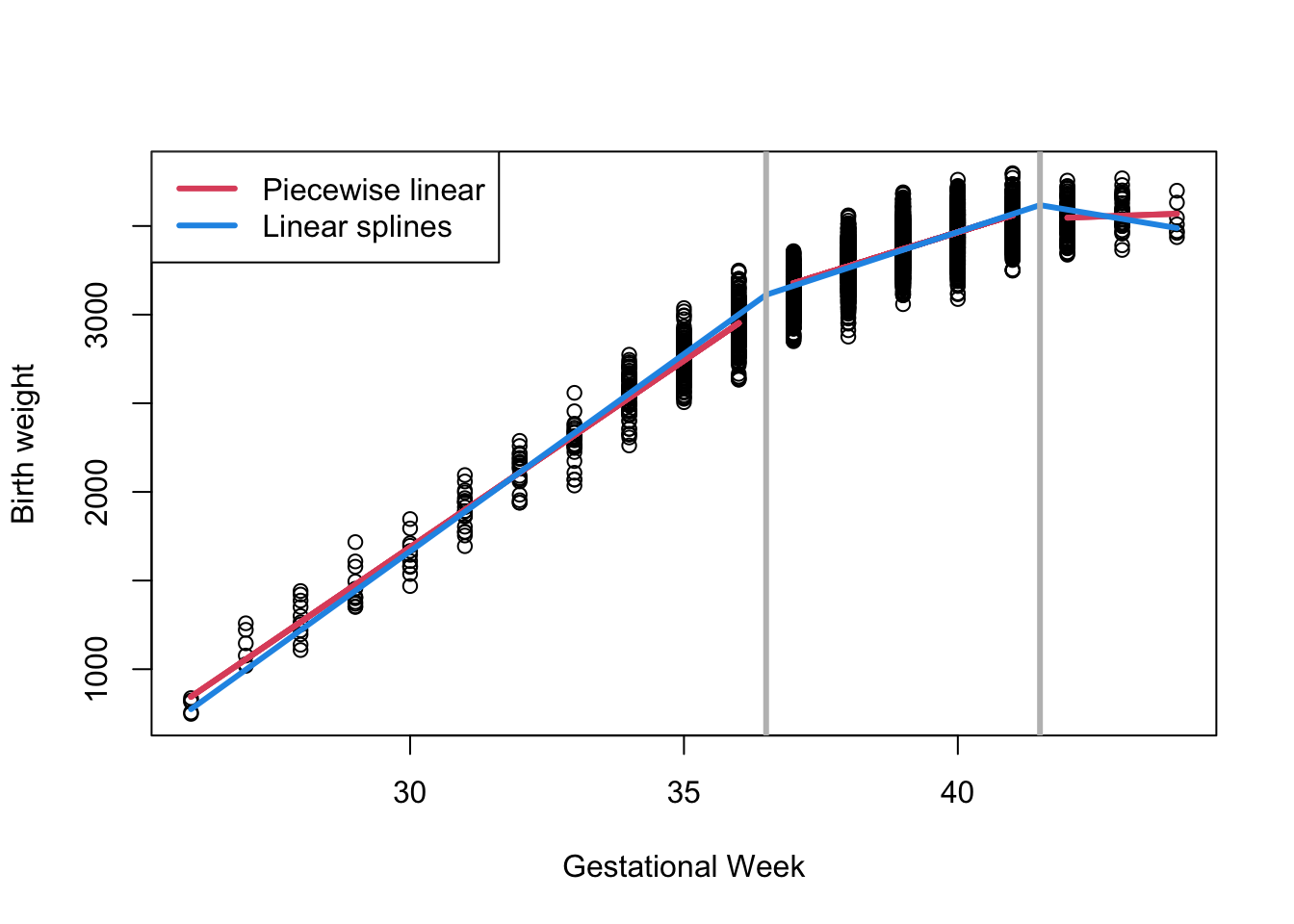
summary(fit7)
Call:
lm(formula = bw ~ gw + Sp1 + Sp2, data = dat)
Residuals:
Min 1Q Median 3Q Max
-387.65 -75.73 5.05 79.96 325.15
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5013.768 62.747 -79.90 <2e-16 ***
gw 222.620 1.757 126.71 <2e-16 ***
Sp1 -121.427 2.549 -47.64 <2e-16 ***
Sp2 -152.948 10.492 -14.58 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 113 on 4996 degrees of freedom
Multiple R-squared: 0.874, Adjusted R-squared: 0.8739
F-statistic: 1.155e+04 on 3 and 4996 DF, p-value: < 2.2e-16Cubic Splines
Linear splines are easily interpretable.
The resulting function \(g(x_i)\) is NOT smooth. The 1st deriv is discontinuous at the knots.
Instead we can work with piecewise cubic functions that are connected at the knots, i.e., 1st and 2nd derivs are continous (ensures continuity and smoothness):
\[ g(x_i) = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \beta_3 x_i^3 + \beta_4 (x_i - 36.5)_{+}^3 + \beta_5 (x_i - 41.5)_{+}^3 \]
- Cubic splines are popular because continuous 2nd derivs, typically view as a smooth function.
#Cubic Splines
Sp1 = (dat$gw - 36.5)^3*as.numeric(dat$gw >= 36.5 )
Sp2 = (dat$gw - 41.5)^3*as.numeric(dat$gw >= 41.5)
fit8 = lm (bw~ gw+I(gw^2) + I(gw^3) + Sp1 + Sp2, data = dat)
plot(dat$gw, dat$bw, col = "black", xlab = "GW", ylab = "BW")
abline(v = 36.5)
abline(v = 41.5)
lines (predict (fit7, newdata=newdata)~morepoints, col = "red", lwd = 3)
lines(sort(dat$gw), sort(fit8$fitted.values), col = "blue", lwd = 2)
legend("topleft", legend = c("Linear splines", "Cubic splines"),
col = c("red", "blue"), lwd = 2)
Important
Polynomial Splines
- The general formulation of a d-degree polynomial spline model with \(M\) knots \(k_1, k_2, k_3, ..., k_M\) is
\[ y_i = \beta_0 + \sum_{j=1}^d \beta_j x_i^{(j)} + \sum_{m=1}^M \beta_{d+m} (x_i - k_m)^d_{+} \]
the above is known as the truncated power formulation.
Linear \(d=1\)
\[ y_i = \beta_0 + \beta_1 x_i+ \sum_{m=1}^M \beta_{1+m} (x_i - k_m)_{+} \] - Quadratic \(d=2\)
\[ y_i = \beta_0 + \beta_1 x_i+ + \beta_2 x_i^2 + \sum_{m=1}^M \beta_{2+m} (x_i - k_m)^2_{+} \]
Linear splines are a good choice for interpretability - the coefficients at the knots represent the change in slope from previous region.
Cubic splines appear smooth, which is often biologically reasonable. Generally, we do not interpret the individual coeffs of the truncated polynomials.
summary(fit8)
Call:
lm(formula = bw ~ gw + I(gw^2) + I(gw^3) + Sp1 + Sp2, data = dat)
Residuals:
Min 1Q Median 3Q Max
-399.13 -74.61 4.47 77.06 301.40
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.890e+04 3.717e+03 7.776 9.02e-15 ***
gw -2.968e+03 3.335e+02 -8.901 < 2e-16 ***
I(gw^2) 9.972e+01 9.900e+00 10.073 < 2e-16 ***
I(gw^3) -1.036e+00 9.734e-02 -10.641 < 2e-16 ***
Sp1 7.732e-01 2.482e-01 3.115 0.00185 **
Sp2 7.455e+00 3.471e+00 2.148 0.03177 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 109.8 on 4994 degrees of freedom
Multiple R-squared: 0.881, Adjusted R-squared: 0.8809
F-statistic: 7397 on 5 and 4994 DF, p-value: < 2.2e-16Basis Splines (B-Splines)
- Goal: Find a flexible function \(\mu(x)\) for the model:
\[ \begin{align*} y &= \mu(x) + \epsilon, \quad \epsilon \sim N(0, \sigma^2)\\ \mu(x)& = \sum_{k=1}^K \beta_k \cdot b_k(x)\\ \mu_i & = \mathbf{B_i} \mathbf{\beta} \end{align*} \]
where \(\mathbf{B}_{i,1:K} = (v1(x_i), b2(x_i), ..., b_k (x_i))\).
We consider B-splines (basis splines) to model \(\mu(x)\). Where \(\mu(x)\) is a linear combination of basis functions. (A broader family of splines)
B-splines have nice properties and are computationally convenient because they are non-zero on a limited range only.
Computationally more accurate- avoid overflow errors.
Provide better numerical stability.
Any spline function of given degree can be expressed as a linear combination of B-splines of that degree.
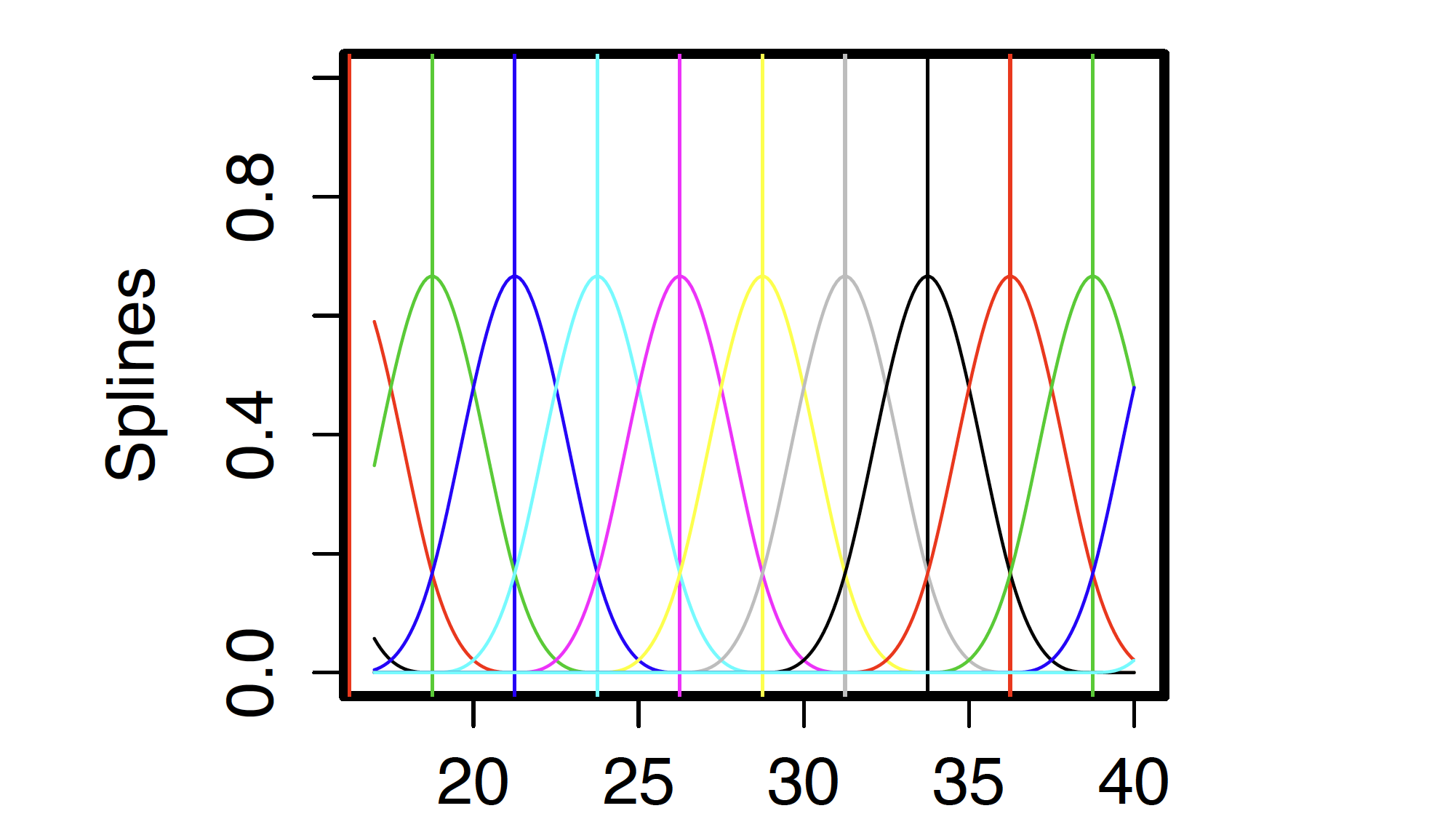
Example of B-Splines
- Define a set of knots or breakpoints (of the x-axis), denoted by:
\[ \tau_1 < \tau_2 < \ldots < \tau_g; \]
Knot placement is determined in advance. Want them close enough together to capture true fluctuations in \(x\). An example above is equally spaced knots.
A cubic B-spline \(b_k(x)\) is:
- a piecewise polynomial function of degree \(d = 3\) in variable \(x\);
- non-zero for a range \(\tau_{k-2} \leq x \leq \tau_{k+2}\);
- at its maximum at knot \(\tau_k\).
For each \(x_i\):
\[
x_i: \sum_{k=1}^K b_k(x_i) = 1
\] 
B-splines and computation
The \(bs()\) function in R will create the design matrix
library(splines) set.seed(123) Blinear = bs(dat$gw, knots = c(36.5, 41.5), degree=1) #basis matrix where each column represents piecewise linear basis functions. #Each row. = obs of GW and each column = one linear BF Bquad = bs(dat$gw, knots = c(36.5, 41.5), degree=2) Bcubic = bs(dat$gw, knots = c(36.5, 41.5), degree=3)
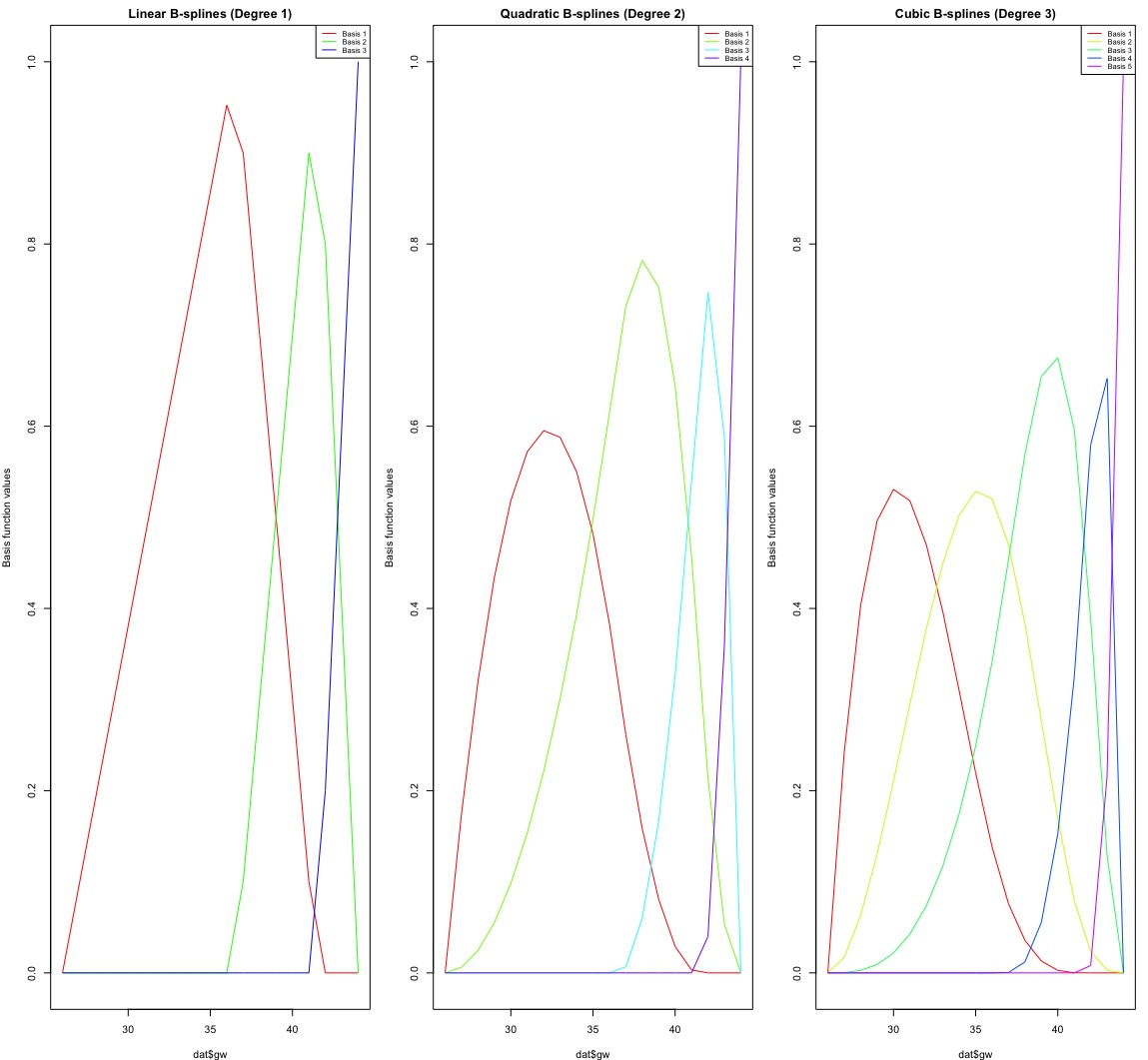
Summary:
Linear B-Splines (Degree 1):
Piecewise straight lines.
3 basis functions (one for each interval between knots).
Less flexibility, only changes slope at the knots.
Quadratic B-Splines (Degree 2):
Piecewise parabolas (curved lines).
4 basis functions.
Smoother than linear, with a continuous slope at the knots.
Cubic B-Splines (Degree 3):
Piecewise cubic curves.
5 basis functions.
Even smoother, with continuous slope and curvature at the knots.
#Linear splines
fit1 <- lm(bw ~ bs(gw, knots = c(36.5, 41.5), degree=1), data = dat)
#Quadratic splines
fit2 <- lm(bw ~ bs(gw, knots = c(36.5, 41.5), degree=2), data = dat)
#Cubic splines
fit3 <- lm(bw ~ bs(gw, knots = c(36.5, 41.5), degree=3), data = dat)
summary(fit3)
Call:
lm(formula = bw ~ bs(gw, knots = c(36.5, 41.5), degree = 3),
data = dat)
Residuals:
Min 1Q Median 3Q Max
-399.13 -74.61 4.47 77.06 301.40
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 937.45 34.65 27.056 < 2e-16
bs(gw, knots = c(36.5, 41.5), degree = 3)1 408.19 57.92 7.048 2.07e-12
bs(gw, knots = c(36.5, 41.5), degree = 3)2 2037.52 32.46 62.779 < 2e-16
bs(gw, knots = c(36.5, 41.5), degree = 3)3 2655.45 38.15 69.608 < 2e-16
bs(gw, knots = c(36.5, 41.5), degree = 3)4 2582.17 35.94 71.851 < 2e-16
bs(gw, knots = c(36.5, 41.5), degree = 3)5 2633.37 52.76 49.912 < 2e-16
(Intercept) ***
bs(gw, knots = c(36.5, 41.5), degree = 3)1 ***
bs(gw, knots = c(36.5, 41.5), degree = 3)2 ***
bs(gw, knots = c(36.5, 41.5), degree = 3)3 ***
bs(gw, knots = c(36.5, 41.5), degree = 3)4 ***
bs(gw, knots = c(36.5, 41.5), degree = 3)5 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 109.8 on 4994 degrees of freedom
Multiple R-squared: 0.881, Adjusted R-squared: 0.8809
F-statistic: 7397 on 5 and 4994 DF, p-value: < 2.2e-16Example: Daily Death Counts in NYC
- Daily non-accidental mortality counts in 5-county NYC 2001-2006
load(paste0(getwd(), "/data/NYC.RData"))
fit1 = lm (alldeaths~bs (date, df = 10, degree = 1), data = health)
fit2 = lm (alldeaths~bs (date, df = 10, degree = 2), data = health)
fit3 = lm (alldeaths~bs (date, df = 10, degree = 3), data = health)
# NOTE: To see where knots are
temp = bs(health$date,df=10,degree=1) # allows 9 knots; bs does not create column of ones...
# bs(health$date,df=10,degree=2) # allows 8 knots
# bs(health$date,df=10,degree=3) # allows 7 knots
plot (health$alldeaths~health$date, col = "grey", xlab = "Date", ylab = "Death", main = "Knots at quantiles, df = 10")
lines (fit1$fitted~health$date, col = 2, lwd = 3)
lines (fit2$fitted~health$date, col = 4, lwd = 3)
lines (fit3$fitted~health$date, col = 5, lwd = 3)
legend ("topleft", legend=c("Linear splines", "Quadratic splines", "Cubic splines"), col=c(2,4, 5), lwd=3, cex = 1.3, bty= "n")
fit1 = lm (alldeaths~bs (date, df = 20, degree = 1), data = health)
fit2 = lm (alldeaths~bs (date, df = 20, degree = 2), data = health)
fit3 = lm (alldeaths~bs (date, df = 20, degree = 3), data = health)
plot (health$alldeaths~health$date, col = "grey", xlab = "Date", ylab = "Death", main = "Knots at quantiles, df = 20")
lines (fit1$fitted~health$date, col = 2, lwd = 3)
lines (fit2$fitted~health$date, col = 4, lwd = 3)
lines (fit3$fitted~health$date, col = 5, lwd = 3)
legend ("topleft", legend=c("Linear splines", "Quadratic splines", "Cubic splines"), col=c(2,4, 5), lwd=3, cex = 1.3, bty= "n")
Model Selection
We need to pick:
Which basis function? Linear versus Cubic
How many knots?
Where to put the knots?
Main Ideas
Choice of basis function usually does not have a large impact on model fit, especially when there are enough knots and \(g(x)\) is smooth.
When there are enough knots, their locations are less important too! By “enough” this means distance between them is small enough to capture fluctuations.
So how many knots? is the question.
Important
Bias- Variance Tradeoff
More knots->
can better capture fine scale trends
Need to estimate more coefficients (risk of overfitting)
Below shows cubic splines with different number of knots.
Assume \(Y\) comes from some true model.
\[ Y = g(X) + \epsilon, \quad \epsilon \sim (0, \sigma^2) \]
where \(g()\) is some unknown function.
For a given \(x_i\), we estimate \(Y\) with \(\hat{g}(x_i)\) where here we assume \(g(x) \perp \epsilon\)
The expected squared difference between \(Y\) and \(\hat{g}(x)\) is the population mean squared error (MSE):
MSE = \[ E[Y-\hat{g}(x)]^2 = \sigma^2 + E[g(x_i) - \hat{g}(x_i)]^2 = \text{Bias}^2 + \text{Variance} \]
We want to minimize the population MSE, but it is made up of 2 components.
Cross-Validation Error
- Let \(\hat{g}^{(-i)}\) be the fitted value of \(y_i\) at \(x_i\) using all the data except \(y_i\). The ordinary leave-one-out cross-validation (LOOCV) is given by
\[ CV = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{g}^{(-i)}(x_i))^2 \]
- Intuitively, \(CV\) estimates the population Mean Squared Error (MSE), \(E[(Y - \hat{g}(X))^2]\), with a sample MSE.
Note here we are averaging across the values of \(x_i\).
- We want to pick a model that minimizes CV!
Caveat from Hastie et al:
“Discussions of error rate estimation can be confusing, because we have to make clear which quantities are fixed and which are random…”
Overfitting
- If you overfit, then you start to fit the noise in the data, i.e., you estimate \(g(x_i) + \epsilon_i\), instead of \(g(x_i)\).
- With overfitting, new data are poorly predicted.
From Bias-Variance perspective:
- In splines, lines that are very wiggly = high variance.
- If you underfit, then you tend to estimate a smoothed version of \(g(x_i)\), and at the extreme, fit a mean such that \(\hat{g}(x_i) = \bar{y}_i\).
From Bias-Variance perspective:
- In splines, lines that vary little = low variance.