7 サブグループ解析

C hapter 5 では、研究間異質性の概念と、それがメタ分析においてなぜ重要であるかについて説明した。また、外れ値分析や影響力分析の一環として、どの研究が観察された異質性に寄与しているかを特定するための手法も学んだ。この分析では、純粋に統計学的な立場からメタ分析にアプローチする。データ中のかなりの異質性を「測定」し、その結果、統計的特性に合わない研究（すなわち、外れ値や影響力のある研究）を除外して、モデルの頑健性を向上させる。

この方法は、post hoc な手続きと見なすことができる。外れ値や影響力の分析は、データを見た後に行われ、多くの場合、見つけた結果のために行われるのである。また、データそのもの以外のものには注意を払わない。影響力分析の方法論は、ある研究がモデルの予測に適切に沿わないことを教えてくれるとしても、それがなぜなのかは教えてくれない。原因は、この研究がわずかに異なる研究手法や治療法を用いているからかもしれない。しかし、このことは研究の影響力だけではわからないのである。

ある治療法の効果を調べるためにメタ分析を行うとする。その結果、全体としてその治療には効果がないことが分かったとする。しかし、大きな治療効果が認められた研究が 3 つあるとしよう。これらの研究を影響力分析で検出することは可能だろうが、なぜその研究が影響力があるのかはわからない。この 3 つの研究では、他のすべての研究で使用された治療法とわずかに異なる治療法が使用され、この小さなディテールが治療効果に大きな影響を与えたということがあり得るのである。これは画期的な発見だろう。しかし、外れ値解析や影響力分析だけではできない発見である。

このことから、データから特定の異質性パターンを見出すためには、別のアプローチが必要であることは明らかである。サブグループ解析は、これを行うための一つの方法であり、モデレータ分析とも呼ばれる。ある種の研究が、なぜ他の研究よりも低い効果や高い効果をもたらすのかを説明し、特定の仮説を検証することが可能である。

Chapter 1.4.2 で学んだように、サブグループ検定は a priori で定義されるべきである。メタ分析を始める前に、観察された効果量に影響を与える可能性のあるさまざまな研究特性を定義し、それに従って各研究をコーディングする必要がある。効果量が異なる理由は無数にあるが、分析の文脈上、重要なものに限定すべきである。

例として、ある種の薬が他の薬より高い効果をもたらすかどうかを調べることができる。あるいは、追跡期間が短い研究と長い研究を比較することもできる。また、研究が実施された文化的地域によって、観察された効果が異なるかどうかを調べることも可能である。メタ分析では、その分野に特化した専門知識があると、その分野の他の科学者や実務者に実際に関連する質問を見つけることができることがある。

サブグループ解析の背景にある考え方は、メタ分析が平均的な効果量を計算するだけでなく、エビデンスのばらつきを調べるツールにもなり得るということである。サブグループ解析では、異質性を単に厄介なものとしてではなく、科学的仮説によって説明できるか否かという興味深い変動としてとらえる。最良の場合、これは私たちを取り巻く世界の理解を深めるものとなる。そうでなくとも、少なくとも将来の意思決定の指針となる実用的な洞察を生み出すものとなる。

この章では、サブグループ解析の背後にある統計モデルと、 R で直接サブグループ解析を行う方法について説明する。

7.1 固定効果（複数）モデル

サブグループ解析では、メタ分析に含まれる研究は、1 つの総体的集団から生じているのではないと仮定する。その代わりに、異なるサブグループに分類され、各サブグループが独自の真の全体効果を持つと仮定する。研究の目的としては、サブグループ間の効果量に差がないという帰無仮説を棄却することになる。

サブグループ解析の計算は、2 つの部分からなる。まず、各サブグループでの効果をプールする。その後、統計的検定を用いて、各サブグループの効果を比較する (Borenstein and Higgins 2013) 。

7.1.1 サブグループにおける効果のプール化

最初の部分は、サブグループなしのメタ分析（Chapter 4.1）と同じ基準が適用されるので、かなり簡単である。もし、サブグループ内のすべての研究が同じ集団から発生し、1つの共有された真の効果を持つと仮定すると、固定効果モデルを使用することが可能である。前に述べたように、研究をより小さなグループに分割しても、実際にはこの仮定が成立しないことがよくある。

したがって、代替案は、ランダム効果モデルを使用することである。これは、サブグループ内の研究は、推定したい平均値を持つ母集団から抽出されると仮定する。通常のメタ分析との違いは、各サブグループごとに別々のランダム効果メタ分析を実施することである。論理的には、この結果、各サブグループ $g$ のプール効果 $\hat\mu_g$ が得られる。

各サブグループはそれぞれ個別のメタ分析を受けるので、$\tau^2$ 異質性の推定値もサブグループごとに異なる。しかし実際には、個々の異質性の値 $\hat\tau^2_g$ は、サブグループ間でプールされた $\tau^2$ に置き換えられることが多いようである。

つまり、すべてのサブグループが研究間の異質性の共通の推定値を共有すると仮定することになる。これは、実用的な理由で行われることがほとんどである。サブグループ内の研究数が少ない場合、例えば $k_g \leq 5$ (Borenstein et al. 2011, chap. 19) の場合、$\tau^2$ の推定値が不正確になる可能性がある。この場合、1 つのサブグループにおける研究間異質性の非常に不正確な推定値に頼るよりも、すべてのサブグループで使用するプールされた $\tau^2$ を計算する方がよいだろう。

7.1.2 サブグループ効果の比較

次のステップでは、$G$ 件のサブグループ間に真の差があるかどうかを評価する。この仮定は、サブグループが異なっていること、つまり、少なくとも 1 つのサブグループが研究の異なる集団の一部であることを意味する。

これをテストするエレガントな方法は、サブグループのプール効果が、実は1つの大規模研究の観察された効果量に過ぎないというふりをすることである (Borenstein et al. 2011、chap. 19 参照)。例えば、$G=3$ のサブグループ解析を行う場合、3 つの大きな研究の観察された効果量（および標準誤差）を計算したふりをするのである。

このようにサブグループを見ると、通常のメタ分析の異質性を評価するときに直面する質問と非常に似ていることがわかる。効果量の差が、サンプルエラーによってのみ存在するのか、それとも効果量の真の差によって存在するのかを知りたいと思っている。

したがって、サブグループの差が、サンプル誤差だけでは説明できないほど大きいかどうかを判断するために、$Q$ の値を使用する。サブグループ効果が観察された効果量であると仮定して、$Q$ の値を計算する。この観察された $Q$ の値は、$\chi^2$ の分布と仮定した場合の期待値と比較され、この場合は自由度 $G-1$ である（Chapter 5.1.1）。

$Q$ の観測値が期待値よりかなり大きい場合、$Q$ 検定の $p$ -値は有意になる。これは、サブグループ間の真の効果量に差があることを示す。この $Q$ 検定は、オムニバス検定である。これは、すべてのサブグループの効果量が等しいという帰無仮説を検定し、少なくとも 2 つのサブグループ、またはそれらの組み合わせが異なる場合に有意であることを示すものである。

通常、サブグループ内の研究はランダム効果モデルに従ってふるまうと仮定するが、プールされたサブグループレベルでは状況は異なるように見える。Borenstein and Higgins (2013) は、多くの分野で、分析するために選択したサブグループは、可能なサブグループの「宇宙」からランダムに抽出したものとは見なせず、調査したい特性の固定レベルを表していると論じている。例として、雇用形態を挙げる。雇用形態には、“employed” と “unemployed” という2つの固定されたサブグループがある。同じことが、例えば、特定の併存疾患を持つ患者と持たない患者における研究にも当てはまる。

Borenstein and Higgins は、サブグループ解析のためのモデルを固定効果（複数）モデル (fixed-effects (plural) model) と呼んでいる。「複数」という言葉がついているのは、標準的な固定効果モデル (fixed-effect model) と区別するためである。固定効果（複数）モデルは、固定効果モデルとランダム効果モデルの両方の特徴を含むハイブリッドな生き物と見ることが可能である。ランダム効果モデルと同様に、データにはサブグループが存在するため、真の効果量は1つではないと仮定する。

ただし、サブグループは、サブグループの全宇宙からのランダムな抽選とは見なさない。サブグループの水準は固定で、網羅的であり、一般化が必要ないことを意味する。これは、私たちがサブグループデータを生成するプロセスを固定効果「複数」モデルと呼ぶ理由を明確にする：なぜなら、複数の真の効果量が存在するが、真の効果量は、固定と仮定されるサブグループレベルを表しているからである。

Borenstein ら (2011, chap. 19) は、「固定」という言葉が統計学では二つの意味を持つため、少し混乱しているように見えるかもしれないと論じている。従来のメタ分析では、「固定効果」という言葉は「共通効果」と同義に使われる。しかし、サブグループ解析の文脈では、「ランダムではない」ことを強調するために「固定効果」という言葉を使う。固定効果は、一般化することを目的とする包括的な分布の単なるランダムな現れではなく、変数が入ることができる現実かつ唯一のカテゴリである。

Figure 7.1 は、サブグループ内の研究がランダム効果モデルに従うと仮定して、固定効果（複数）モデルを可視化する。

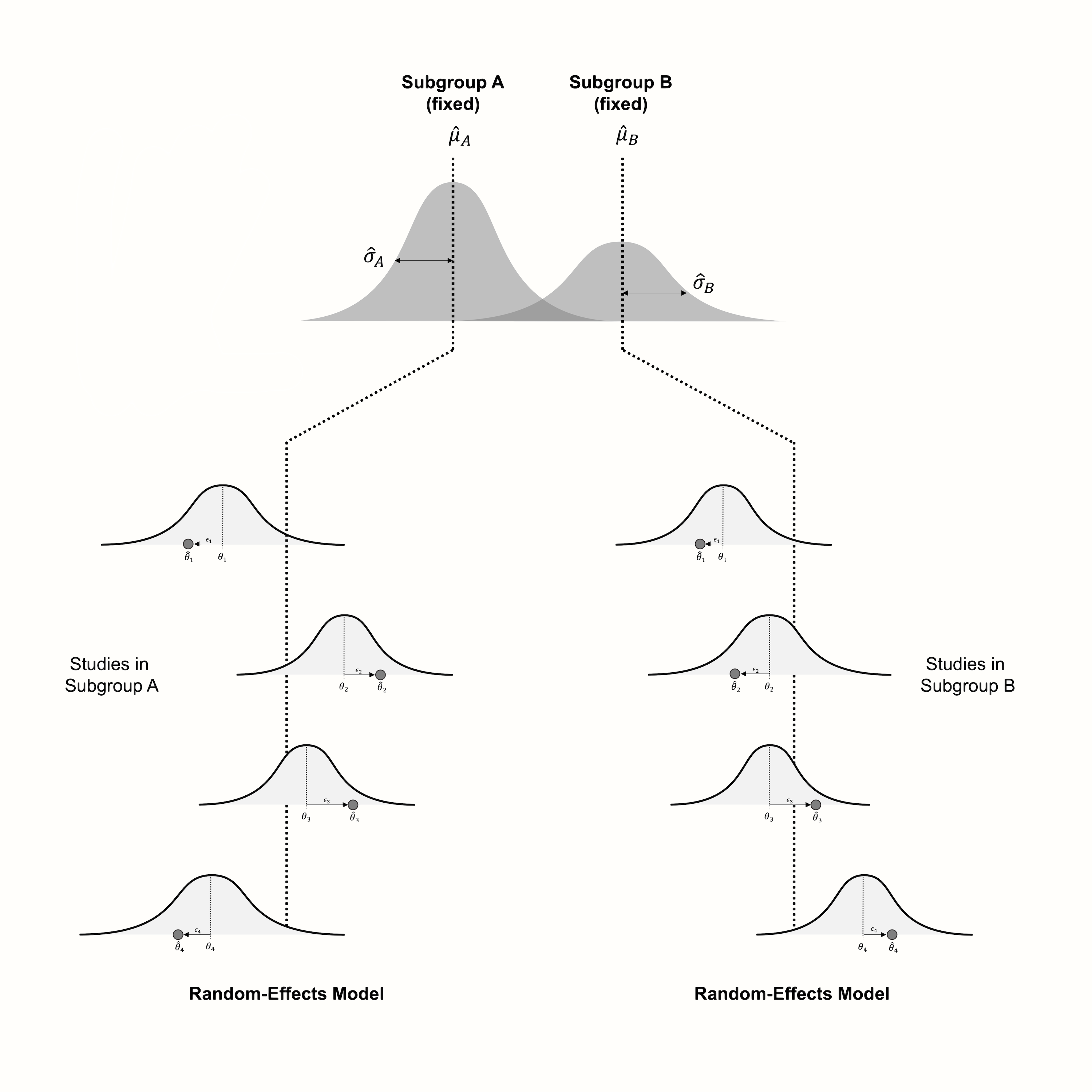
Figure 7.1: サブグループ内でランダム効果モデルを想定した固定効果（複数）モデルの可視化。

水準が固定されたサブグループ変数の例

年齢層: 小児、若年成人 (young adults)、成人、高齢者

文化的背景: 西洋、非西洋

対照群: 代替療法、最小限治療、治療なし

アウトカム測定手法: 自己報告、専門家判断

研究の質: 高、低、不明

種: 植物、動物

セッティング: 学校、病院、家庭

サブグループの具体的な選択と定義は、メタアナリシスの目的と範囲に基づいて適合させることができ、またそうすべきであることに注意。

固定効果（複数）モデルは、ランダム効果（サブグループ内）と固定効果（サブグループは固定されていると仮定されているため）の両方を含むので、文献上では混合効果モデル (mixed-effects model) としても知られている。Chapter 4.2.6 ですでにこの用語に触れている。たとえば、割合をプールするために使用できる異なるタイプの（一般化）混合効果モデルについて議論してきた。

サブグループ解析に使用するモデルは、メタ分析でよく使用される他の手法と大きく関連している。Chapter 8 では、サブグループ解析が単なるメタ分析の特殊なケースであり、そのために混合効果モデルも使用することを示す予定である。

さらに、サブグループの水準が固定であると仮定できない可能性もある。効果が観察された場所によって、効果の大きさが異なるかどうかを評価したいと想像してみよう。ある研究はイスラエルで、ある研究はイタリアで、ある研究はメキシコで、ある研究は中国本土で、効果を評価してきたとする。世界にはたくさんの国があり、国を水準数の固定された因子とはみなすことはできないため、「ランダム」な選択を含んでいることにする。

この場合、サブグループを固定的にモデル化するのではなく、ランダム効果として国ごとのばらつきを推定するようにすることが理にかなっている。これは、Chapter 10 で扱うマルチレベル・モデルにつながる。

7.2 サブグループ解析の限界と落とし穴

直感的には、サブグループ解析は、効果を弱める因子を検出するのに非常に優れたツールであると考えるかもしれない。結局のところ、メタ分析の目的は、利用可能なすべてのエビデンスを調査することである。これは、メタ分析で分析される個体の総数は、通常、一次研究のそれを桁違いに上回ることを意味した。

しかし、残念ながら、この方法では、サブグループの違いを検出するための統計的検出力は必ずしも高くはない。これにはいくつかの理由がある (L. V. Hedges and Pigott 2004)。

まず、サブグループ解析では、サブグループ内の結果は通常ランダム効果モデルを使用してプールされることを覚えておこう。サブグループ内の研究間異質性が大きい場合、プール効果の精度が低下する（すなわち、標準誤差が増加する）ことになる。しかし、サブグループの効果推定値が非常に不正確な場合、これは、それらの信頼区間が大きく重なることを意味する。結果的に、たとえ差が存在するとしても、サブグループ間の有意差を見つけることを難しくする。
同じように、サブグループ解析で検出したい効果は、通常のメタ分析よりもはるかに低いため、統計的検出力も低くなりがちである。例えば、あるアウトカムを自己報告と専門家の評価で評価する研究間で、効果に差があるかどうかを調べるとした。たとえ差があったとしても、それは非常に小さいものだろう。治療群と対照群の間に有意差を見出すことはしばしば可能である。しかし、研究間の効果量の差を検出することは、差が小さいため、通常より多くの統計的検出力が必要とされ、より困難である。
上記の点から、重要な注意事項がある： エビデンスの欠如は、欠如のエビデンスではない。もし、サブグループ間の効果量に差がないとしても、それは自動的にサブグループが同等のアウトカムをもたらすということにはならない。上で述べたように、私たちのサブグループ解析が、効果の真の差を確認するのに必要な統計的検出力を持たないかもしれない様々な理由があるのである。この場合、サブグループが同じ効果を持つと言うのは重大な誤訳である–私たちは、差が存在するかどうか単に知らないのである。このことは、ある治療法が他の治療法よりも優れているかどうかを評価したい場合に、特に問題となる。企業を含む一部の利害関係者は、しばしば治療の同等性を示すことに既得権益を有している。しかし、サブグループ解析は、通常、これを証明する適切な方法ではない。
事前にサブグループ検出力分析を行うことで、サブグループ解析において統計的検出力が問題となるかどうかを確認することが可能である。このような分析では、サブグループ解析で検出できる最小の効果量の差を確認することが可能である。各種ツールの Chapter 14.3 では、 R でどのようにサブグループ検出力分析を行うことができるかを説明している。しかし、検出力分析は、せいぜい有用な診断として見られるだけで、私たちの分析の検出力が十分に高く、サブグループが同等であることを示す証明にはならないことに注意してみよう。Schwarzer ら (Schwarzer, Carpenter, and Rücker 2015, chap. 4.3) は、一般的な経験則として、サブグループ解析は、メタ分析が少なくとも $K=$ 10 件の研究を含むときにのみ意味をなすと言及している。

サブグループ解析のもう一つの重要な限界は、純粋に観察的であることである (Borenstein and Higgins 2013)。メタ分析には、参加者が治療群または対照群のいずれかにランダムに割り付けられたランダム化比較試験（RCT）しか含まれていないことが多い。このような RCT は、適切に実施されれば、研究で観察された群間差を治療が引き起こしたというエビデンスを提供することが可能である。これは、評価されたアウトカムに影響を与える可能性のあるすべての関連変数が 2 つのグループで等しいために言うことができる。唯一の違いは、一方のグループが治療を受け、もう一方のグループが受けなかったということである。

サブグループ解析は、ランダム化された研究のみからなる場合でも、因果関係を示すことができない。サブグループ解析で、ある種の治療が他の治療より効果的であることがわかったとした。この発見が偽りかもしれない理由は無数にある；たとえば、治療 A を調査した研究では、治療 B を調査した研究とは別の対照群を使用していた可能性がある。これは、両方の治療が同じように有効である可能性があり、治療タイプが方法論の因子と交絡 (confound) するので、違いを見ているだけだということである。この例は、サブグループ解析の結果を常に批判的に評価する必要があることを強調するものである。

最後の重要な落とし穴は、サブグループの定義の仕方である。しばしば、集合的な情報に基づいて研究をサブグループに分類したくなることがある。Schwarzer ら (Schwarzer, Carpenter, and Rücker 2015, chap. 4.3) は、よくある例として、研究の平均年齢を挙げている。例えば、高齢者（65歳以上）と一般成人との間で効果が異なるかどうかを評価したいとする。そこで、報告された平均年齢が65歳以上か以下かによって、研究をこの2つのカテゴリに分類する。

もし、平均年齢の高いサブグループで効果が高いことがわかれば、直感的に、高齢者ほど効果が高いことを示していると考えるかもしれない。しかし、この推論には深い欠陥がある。一次研究の平均年齢が 65 歳以上である場合、それよりも若い個人の割合がかなり含まれている可能性がある。その逆もまた然りで、平均年齢が 65 歳より低い場合でも、65 歳より上の人が多く含まれている可能性は十分にあるのである。

つまり、「高齢者」サブグループに見られる高い効果は、実際には 65 歳未満の個人によってのみもたらされる可能性がある。逆に、「若い」サブグループでは、低い効果は 65 歳以上の研究対象者によってもたらされた可能性がある。

このことは、逆説的な状況をもたらす。すなわち、全体レベルでは、平均年齢が高い研究ほど効果が高いことがわかる。しかし、個人レベルではその逆で、年齢が上がるにつれて効果は低くなる。

今述べたシナリオは、いわゆる生態学的バイアス (S. G. Thompson and Higgins 2002; Piantadosi, Byar, and Green 1988) によって引き起こされるものである。このバイアスは、個人（ミクロ）レベルの関連を予測するために、集合体（マクロ）レベルの関係を利用したいときに発生するものである。

生態学的バイアスを回避する最善の方法は、サブグループ解析やメタ回帰において、集計情報を決して使用しないことである。しかし、ある研究のすべての個人が 1 つのカテゴリに分類されるとわかっている場合は、状況が違ってくる。例えば、18 歳未満の青少年のみを対象としたいくつかの研究と、成人（18 歳以上）のみを対象としたいくつかの研究があれば、生態学的バイアスのリスクはほぼ排除される。しかし、効果の違いは、参加者の年齢ではなく、交絡変数によって引き起こされた可能性が残っている。

サブグループ解析: やって良いことと悪いこと

サブグループ解析は統計的検出力に依存するため、研究数が小さい場合は通常実施する意味がない（つまり $K$ < 10）。

サブグループ間の効果量に差がない場合、これは自動的にサブグループが同等な結果をもたらすことを意味するものではない。

サブグループ解析は純粋に観察的なものなので、効果の違いは交絡変数によっても引き起こされる可能性があることを常に念頭に置いておく必要がある。

サブグループ解析において、集合的な研究情報を使用することは、生態学的なバイアスをもたらす可能性があるため、良くない考えである。

7.3 R のサブグループ解析

R で学んだことを実行する時が来た。{meta} パッケージを使ってサブグループ解析を行うのは比較的簡単である。{meta} のすべてのメタ分析関数において、 subgroup 引数を指定することが可能である³⁰。これは、どの効果量がどのサブグループに該当するかを関数に伝え、サブグループ解析を実行する。引数 subgroup には、character、factor、logical、numeric の変数を指定することが可能である。唯一気をつけなければならないのは、同じサブグループに属する研究は絶対に同じラベルを持つということである。

この例では、再び m.gen メタ分析オブジェクトを使用する。メタ分析の計算に使用した ThirdWave データセットには、サブグループ情報を持ついくつかの列が含まれている。ここでは、バイアスのリスクが高い研究と低い研究の間で効果量に差があるかどうかを調べたい。バイアスリスクの情報は、RiskOfBias 列に格納されている。

まず、この列を見てみよう。このコードでは、データセットの最初の数行だけが表示されるように head 関数を使用している。

# 研究名と 'RiskOfBias' 列、最初のデータを表示
head(ThirdWave[,c("Author", "RiskOfBias")])

##            Author RiskOfBias
## 1     Call et al.       high
## 2 Cavanagh et al.        low
## 3   DanitzOrsillo       high
## 4  de Vibe et al.        low
## 5  Frazier et al.        low
## 6  Frogeli et al.        low

データセット内の各研究は、バイアスのリスク評価を指定するラベルを持っていることがわかる。metagen を使用してメタ分析を計算した際、この情報は内部的に m.gen オブジェクトに保存された。サブグループ解析を行うには、update.meta 関数を使用して m.gen オブジェクトを指定し、subgroup 引数を使用してデータセットのどの列にサブグループラベルが含まれるかを指定する。

前に、サブグループ解析は、サブグループ間で共通の推定値（$\tau^2$ ）の有無で実施できることも取り上げた。これは、{meta} で tau.common を TRUE または FALSE に設定することで制御することが可能である。とりあえず、各サブグループでの研究間異質性分散の別々の推定値を使用することにしよう。

この例では、固定効果（複数）モデルを適用し、サブグループ内の研究はランダム効果モデルを使用してプールされると仮定する。m.gen にランダム効果モデルの結果が含まれているので、（comb.fixed を FALSE、comb.random を TRUE に設定したので）何も変更する必要はない。元のメタ分析はランダム効果モデルを用いて行われたため、update.meta は自動的に、サブグループ内の研究もランダム効果モデルを用いてプールすることを想定している。

したがって、出来上がったコードは次のようになる。

update.meta(m.gen, 
            subgroup = RiskOfBias, 
            tau.common = FALSE)

## Review:     Third Wave Psychotherapies
## 
## Number of studies combined: k = 18
## 
##                         SMD           95%-CI    t  p-value
## Random effects model 0.5771 [0.3782; 0.7760] 6.12 < 0.0001
## Prediction interval              [-0.0572; 1.2115]     
## 
## Quantifying heterogeneity:
##  tau^2 = 0.0820 [0.0295; 0.3533]; tau = 0.2863 [0.1717; 0.5944]
##  I^2 = 62.6% [37.9%; 77.5%]; H = 1.64 [1.27; 2.11]
## 
## Test of heterogeneity:
##      Q d.f. p-value
##  45.50   17  0.0002
## 
## Results for subgroups (random effects model (HK)):
##                     k    SMD           95%-CI  tau^2    tau     Q   I^2
## RiskOfBias = high   7 0.8126 [0.2835; 1.3417] 0.2423 0.4922 25.89 76.8%
## RiskOfBias = low   11 0.4300 [0.2770; 0.5830] 0.0099 0.0997 13.42 25.5%
## 
## Test for subgroup differences (random effects model (HK)):
##                     Q d.f. p-value
## Between groups   2.84    1  0.0917
## 
## Details on meta-analytical method:
## - Inverse variance method
## - Restricted maximum-likelihood estimator for tau^2
## - Q-profile method for confidence interval of tau^2 and tau
## - Hartung-Knapp (HK) adjustment for random effects model (df = 17)
## - Prediction interval based on t-distribution (df = 16)

この出力では、Results for subgroups と呼ばれる新しいセクションが表示される。出力のこの部分は、各サブグループで別々にプール効果量を示している。バイアスのリスクが高い研究が $k=$ 7 件、バイアスのリスクが低い研究が 11 件であることがわかる。推定された研究間の異質性はかなり異なっており、バイアスのリスクの高い研究では $I^2=$ 77% であるが、リスクの低い研究では 26% にすぎない。

また、サブグループの効果量も異なっている。$g=$ 0.43 で、バイアスリスクの低い研究の効果推定値は、バイアスリスクの高い研究よりも小さい。バイアスのかかった研究は治療効果を過大評価する可能性が高いので、このことはよく見られる所見である。

しかし、その差は統計的に有意なのだろうか？Test for subgroup differences には、$Q$-検定を示している結果があるので、これで確認することができる。この例では、2つのサブグループがあり、自由度1に基づいている。この検定の $p$-値は 0.09 で、従来の有意水準より大きいが、それでも傾向レベルの差を示している。

また、両方のサブグループで共通の $\tau^2$ 推定値を仮定した場合の結果も確認することができる。tau.common を TRUE に設定するだけである。

update.meta(m.gen, subgroup = RiskOfBias, tau.common = TRUE)

## [...]
##                     k    SMD           95%-CI  tau^2    tau     Q   I^2
## RiskOfBias = high   7 0.7691 [0.2533; 1.2848] 0.0691 0.2630 25.89 76.8%
## RiskOfBias = low   11 0.4698 [0.3015; 0.6382] 0.0691 0.2630 13.42 25.5%
## 
## Test for subgroup differences (random effects model (HK)):
##                    Q d.f. p-value
## Between groups  1.79    1  0.1814
## Within groups  39.31   16  0.0010
## 
## Details on meta-analytical method:
## - Inverse variance method
## - Restricted maximum-likelihood estimator for tau^2 
##   (assuming common tau^2 in subgroups)
## [...]

この出力では、推定された研究間異質性分散が $\tau^2=$ 0.069 で、両方のサブグループで同じであることがわかる。２つの $Q$ -検定が提示される。すなわち、between groups の異質性（実際のサブグループ）と within-subgroup の異質性（サブグループ内の異質性）である。

通常のメタ分析と同様に、後者は単にサブグループに過剰な変動があることを示している ($p=$ 0.001)。サブグループ差の検定でも、バイアスリスクが低い研究と高い研究の間に有意な差がないことが示された ($p=$ 0.181)。

ここで、$\tau^2$ が独立しているか、あるいは共通のであるかを仮定して結果を探った。両サブグループの異質性が等しいと仮定する十分な理由がなく、また、各サブグループに最低 $k=$ 7 件の研究があることから、$\tau^2$ の別々の推定が適切であると考えられる。しかし、少なくともこの例では、どちらのアプローチでも結果の解釈は同じようなものだとわかった。

サブグループ解析の結果を報告

サブグループ解析の結果は、通常、各サブグループにおける推定効果と異質性、およびサブグループの差の検定の $p$ 値を表示した表で報告される。

	$g$	95%CI	$p$	$I^2$	95%CI	$p$_subgroup
Risk of Bias						0.092
High	0.81	0.28-1.34	0.009	0.77	0.51-0.89
Low	0.43	0.28-0.58	$<$ 0.001	0.25	0.00-0.63

上の表で、第３列の $p$ 値はサブグループに特有の効果が有意であることを示している。これは、高バイアスと低バイアスのどちらでも発生する。また、$p_{\textsf{subgroup}}$ より小さい値は高リスクと低リスクの効果の差は有意ではないことを示している。

サブグループに特有の $p$ 値を抽出するには、update.meta の結果をオブジェクトとして保存し、このオブジェクトから pval.random.w 要素を $ 演算子を使って抽出する。

複数のサブグループ解析が行われた場合は、表にさらに行を追加することができる。

\[\tag*{$\blacksquare$}\]

7.4 演習問題

知識を試そう！

影響力分析や外れ値分析ではわからないことのうち、何がサブグループ解析ではわかることがあるか？

サブグループ解析の背景にあるモデルが、なぜ固定効果（複数）モデルと呼ばれるのか。

メタ分析の一環として、ある教育研修プログラムの効果が、実施された学区によって異なるかどうかを調べたいと考えている。この問いに答えるために、固定効果（複数）モデルを用いたサブグループ解析は適切か？

あなたの友人が、合計9つの研究を含むメタ分析を行った。これらの研究のうち5つが1つのサブグループに分類され、4つが他のサブグループに分類されている。彼女は、サブグループ解析を行うことに意味があるかどうかをあなたに尋ねている。あなたならどうするか？

メタ分析で、分析した治療法が男性よりも女性でより効果的であると著者が主張しているものがあった。この知見は、研究対象者に含まれる女性の割合に基づいて研究をサブグループに分けたサブグループ解析に基づいている。この知見は信頼できるか、またその理由は？

問題の解答は、本書の巻末 Appendix A にある。

7.5 要約

メタ分析の不均一性を評価する方法はいろいろあるが、これらのアプローチでは、データに過剰な変動が見られる理由を知ることはできない。サブグループ解析では、ある研究の真の効果量が他の研究よりも高い、または低い理由についての仮説を検証することが可能である。
サブグループ解析では、通常、固定効果（複数）モデルを仮定する。サブグループ内の研究は、ほとんどの場合、ランダム効果モデルを用いてプールされる。その後、全体のサブグループの結果に基づいた $Q$ -検定を使用して、グループが有意に異なるかどうかを判断する。
サブグループ解析モデルは、異なるカテゴリ自体が固定されていると仮定されているため、「固定効果」モデルと呼ばれる。サブグループの水準は、可能なカテゴリの宇宙からのランダムな抽選とは見なされない。それらは、サブグループ変数が取り得る唯一の値を表す。
サブグループ解析を計算する場合、サブグループ内の結果をプールするために、研究間の異質性の推定値を別々にするか、共通にするかを決めなければならない。
サブグループ解析は万能ではない。サブグループの差を検出するのに必要な統計的検出力が不足していることが多い。したがって、サブグループの差について有意でない検定は、自動的にサブグループが同等の結果をもたらすことを意味するものではない。

6 フォレストプロット

8 メタ回帰