11 構造方程式モデリングメタ分析

前 章で、メタ分析モデルにはマルチレベル構造が内在していることを示した。この性質を利用して、例えば、従来のメタ分析を3レベルモデルに拡張することができる。
統計的手法に関しては、よく別々の箱に入れられることがあるが、これは非常におかしなことである。研究や実務では、統計のそれぞれの手法は無関係なものとして扱われることが多いが、実際はそうではない。例えば、分散分析(ANOVA)とカテゴリ予測変数の線形回帰は本質的に同じことを行なっていると教えると、多くの社会科学の学生はたいてい驚く58。2つの方法が異なる文脈で使われ、別個のものとして教えられてきたときに、このようになることがある。
この例と同じように、マルチレベルモデルを構造方程式モデル(Structural Equation Model, SEM)の特殊な形態として捉え始めたのはごく最近のことである (Mehta and Neale 2005; Bauer 2003) 。すでに学んだように、すべてのメタ分析はマルチレベルモデルに基づいている。結果として、プール効果量が潜在(または未観測)変数として扱われる構造方程式モデルとしてメタ分析を扱うことが可能である (Cheung 2015a, chap. 4.6)。要するに、メタ分析はマルチレベルモデルなので、構造方程式モデルとしても表現できるのである。
これは、これまで取り上げられてきた種類のメタ分析を構造方程式モデリングの観点から概念化できることを意味するだけではない。SEM を使って、より複雑なメタ分析モデルを構築することもできるようになるのである。メタ分析的な SEM を用いて、因子分析的なモデルを検証したり、アウトカムを複数含む多変量メタ分析を実行することが可能である(これらは、応用例の一部に過ぎない)。
メタ分析 SEM は、利用可能なすべてのエビデンスを考慮した上で、文献中のあるモデルが実際に成り立っているかどうかを評価したい場合に役立つ。逆に、ある理論がエビデンスに裏付けられていないかどうか、あるいはさらに興味深いことに、その理論がサブグループにしか適用されないかどうかをチェックするためにも使用することが可能である。
メタ分析的な SEM の手法を適用するには、もちろん構造方程式モデリングに基本的に慣れていることが前提になる。そこで次のセクションでは、構造方程式モデリングの背後にある一般的な考え方と、そのメタ分析的な拡張について簡単に説明する。
11.1 メタ分析構造方程式モデリングとは?
構造方程式モデリングは、顕在(観測)変数と潜在変数の関係に関する仮説を検定するために用いられる統計手法である (Kline 2015, chap. 1)。潜在変数は、観測されないか、観測可能のどちらかである。例えば、パーソナリティは、例えば、アンケートの様々な項目を通して間接的にしか測定できない構成要素である。SEM では、顕在変数と潜在変数の間の仮定された関係(「構造」)が、測定された顕在変数を用いて、その測定誤差を考慮しながらモデル化される。
SEM 分析は、「従来の」統計的仮説検定(例えば、\(t\)-検定など)とは多少違う点がある。通常、統計的検定は、\(H_0: \mu_1 = \mu_2\)(ここで、\(\mu_1\) と \(\mu_2\) は2つのグループの平均)のような帰無仮説に対する検定を伴う。このような検定では、研究者は、帰無仮説を棄却することを「目的」とし、これによって、2つのグループが異なると結論づけることができることがある。しかし、SEM では、特定の構造モデルが事前に提案され、適合度が十分であれば、このモデルを受け入れることを「目的」とする (Cheung 2015a, chap. 2.4.6)。
11.1.1 モデル仕様
一般に、SEM は一連の行列によって指定され、数学的に表現される。行列は、 R の data.frame オブジェクトのように、行と列を含む単純な表と考えることができる(実際、ほとんどのデータフレームは、as.matrix 関数を用いて簡単に行列に変換することが可能)。視覚的には、SEM はパス図として表現することができる。このようなパス図は、通常、非常に直感的であり、その解釈も簡単である。したがって、まず最初に SEM を視覚的に示し、その後、行列表記に移行しよう。
11.1.1.1 パス図
パス図は、SEM をグラフィカルに表現したものである。パス図の描き方について完全なコンセンサスは得られていないが、いくつかの規約がある。ここでは、パス図の主な構成要素と、それらが表現するものを紹介した。
| Symbol | Name | Description |
|---|---|---|
| \(\square\) | 長方形 | 観測変数。 |
| \(\circ\) | 円 | 潜在(非観測)変数 |
| \(\triangle\) | 三角形 | 切片 (fixed vector of 1s). |
| \(\rightarrow\) | 矢印 | 予測。矢印の末端の変数が、先端の変数を予測する。Predictor \(\rightarrow\) Target。 |
| \(\leftrightarrow\) | 二重矢印 | (共)変量。双方向の矢印が2つの変数(長方形/円)を結ぶ場合、2つの変数間の共分散・相関を意味する。双方向矢印が1つの変数の上にループを形成している場合、その変数の分散を意味する。 |
例として、単純な線形(「非メタ分析」)回帰モデルのパス図を作成してみよう。このモデルでは、\(y\) を \(x\) で予測したい。モデル式は次のようなものである。
\[\begin{equation} y_i = \beta_0 + \beta_1x_i + e_i \tag{11.1} \end{equation}\]
さて、この数式を「分解」してみよう。このモデルにおいて、\(x_i\) と \(y_i\) は観測された変数である。観測されない(潜在)変数はない。\(y\) の真の母平均は回帰切片 \(\beta_0\) であり、\(\mu_x\) は \(x\) の母平均を示す。観測された予測変数の分散 \(x\) は \(\sigma^2_x\) で示される。 \(x\) が \(y\) の完全な予測因子でない場合、\(y\) に関連する残留誤差分散 \(\sigma^2_{e_y}\) がある程度存在することになる。以下の通り、2つの回帰係数がある。\(\beta_0\) は切片で、\(\beta_1\) は \(x\) の傾きである。
これらの構成要素を用いて、線形回帰モデルのパス図を作成すると、以下のようになる。
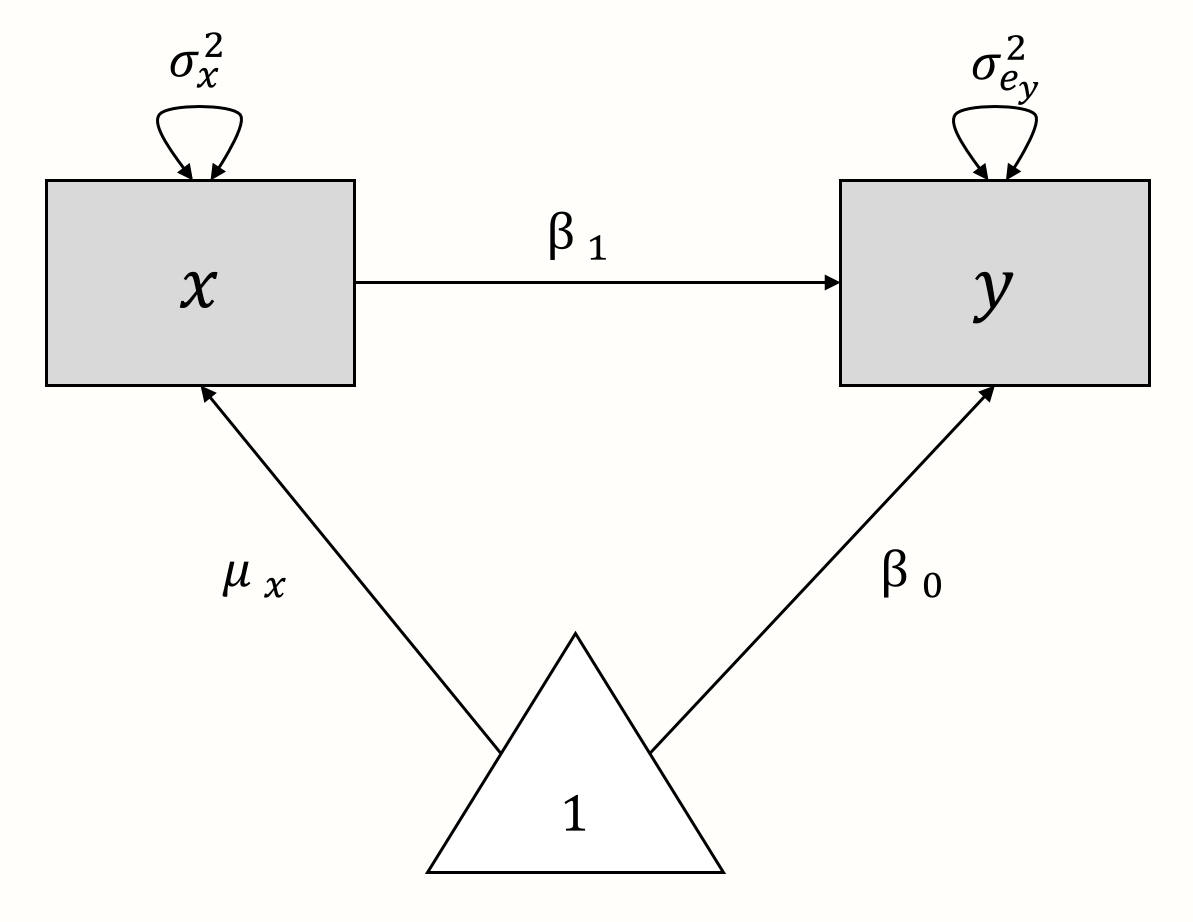
また、このグラフモデルを出発点として、回帰モデルの式を組み立て直すことができる。このモデルから、\(y\) は、\(x \times \beta_1\) と \(1 \times \beta_0\) という二つの要素に影響されていることが推測できる。 この二つの要素を足し合わせると、再び先ほどの \(y\) の式にたどり着く。
11.1.1.2 行列表現
SEM を行列で表現する方法はいくつかある (Jöreskog and Sörbom 2006; Muthén and Muthén 2012; McArdle and McDonald 1984)。ここでは、Reticular Action Model (RAM) の定式化に焦点を当てることにする (McArdle and McDonald 1984)。なぜなら、この後に紹介する {metaSEM} パッケージでは、この式が使用されているからである。RAM は4つ行列を使用する。\(\boldsymbol{F}\)、\(\boldsymbol{A}\)、\(\boldsymbol{S}\)、\(\boldsymbol{M}\) という4つ行列を使用する。 \(\boldsymbol{M}\) 行列は、今回取り上げるメタ分析的SEMに適合させる必要はないので、ここでは省略した(より広範な紹介は Cheung 2015a を参照)。
先ほどの線形回帰モデルに、残りの \(\boldsymbol{A}\) , \(\boldsymbol{F}\) , \(\boldsymbol{S}\) 行列を指定する。この3つ行列は、すべて同じ行と列数で、モデルで持っている変数 \(x\) と \(y\) に対応している。したがって、回帰モデルの一般的な行列構造は、常に次のようになる。
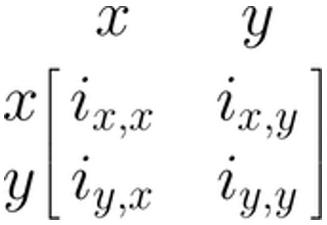
\(\boldsymbol{A}\) 行列: 一方向矢印
\(\boldsymbol{A}\) 行列は、パス・モデル中の非対称(単一方向)矢印を表す。この行列は、矢印が始まる変数の列のエントリを検索し ( \(x\) )、次に矢印が終わる変数行列の行のエントリを検索することによって埋めることが可能である ( \(y\) )。矢印の値 \(\beta_1\) は、選択された列と行が行列の中で交差する場所に置かれる ( \(i_{y,x}\) )。このモデルには、変数間の他のパスがないので、残りのフィールドを0で埋める。したがって、例の \(\boldsymbol{A}\) 行列は次のようになる。
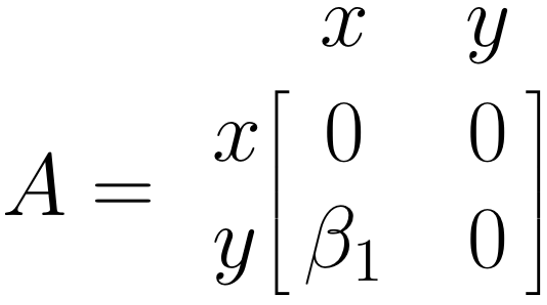
\(\boldsymbol{S}\) 行列: 一方向矢印
\(\boldsymbol{S}\) 行列は、含まれる変数について推定したい(共)分散を表している。予測変数である \(x\) については、分散 \(\sigma^2_x\)(「シグマ x 二乗」と読む)を推定する必要がある。予測変数 \(y\) については、予測誤差の分散 \(\sigma^2_{e_y}\)(「シグマ e y 二乗」と読む) を知りたい。したがって、\(\boldsymbol{S}\) をこのように指定する。
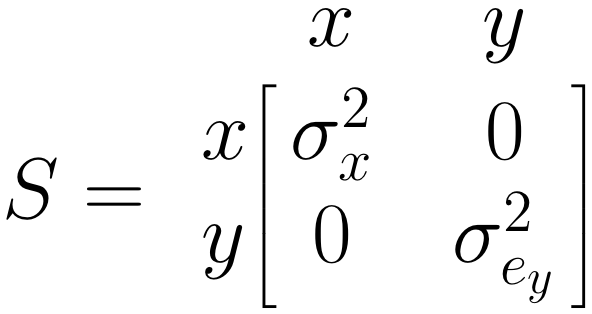
\(\boldsymbol{F}\) 行列: 一方向矢印
\(\boldsymbol{F}\) 行列は、モデルで観測された変数を指定することが可能である。変数が観測されたことを指定するために、単に行列のそれぞれの対角フィールドに1を挿入する。このモデルでは、\(x\) と \(y\) の両方が観測されているので、両方の対角フィールドに 1 を挿入する。
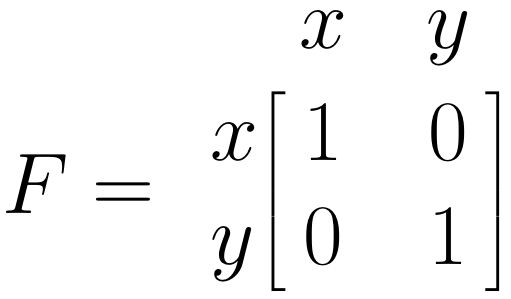
これらの行列が設定されると、SEM のパラメータを推定することができ、指定されたモデルがどれだけデータに適合しているかを評価することができるようになる。これにはいくつか行列代数と最尤推定によるパラメータ推定が含まれるが、数学的な細かい説明はここでは省略する。このステップの背後にある詳細を理解したい場合は、Cheung (2015a) の4.3章を参照。
11.1.2 SEM の観点からのメタ分析
ここで、メタ分析モデルと SEM に関する知識を組み合わせて、メタ分析を構造方程式モデル (Cheung 2008) として定式化しよう。
はじめに、ランダム効果モデルの式に戻りよう。前回、メタ分析モデルがマルチレベル構造に従っていることをすでに説明してきたが(Chapter 10.1)、これは次のようなものである。
レベル 1
\[\begin{equation} \hat\theta_k = \theta_k + \epsilon_k \tag{11.2} \end{equation}\]
レベル 2
\[\begin{equation} \theta_k = \mu + \zeta_k \tag{11.3} \end{equation}\]
最初のレベルでは、研究 \(k\) で報告された効果量 \(\hat\theta_k\) が、真の効果量 \(\theta_k\) の推定値であると仮定する。観測された効果量が真の効果から乖離しているのは、サンプリングエラー \(\epsilon_k\)、分散 \(\widehat{\text{Var}}(\hat\theta_k)=v_k\) で表されるからである。
ランダム効果モデルでは、各研究の真の効果量でさえ、レベル2の真の効果量の母集団からしか抽出されないと仮定する。この真の効果量の母集団の平均 \(\mu\) が推定したいものであり、プール効果量を表す。これを推定するためには、真の効果量の分散 \(\widehat{\text{Var}}(\theta)=\tau^2\) (つまり、研究間異質性)も推定する必要がある。固定効果モデルはランダム効果モデルの特殊なケースで、\(\tau^2\) がゼロであると仮定する。
このモデルを SEM グラフとして表現することは、非常に簡単である。レベル1のパラメータを潜在変数として、観察している効果量がどのように生まれたかを「説明」する (Cheung 2015a, chap. 4.6.2)。
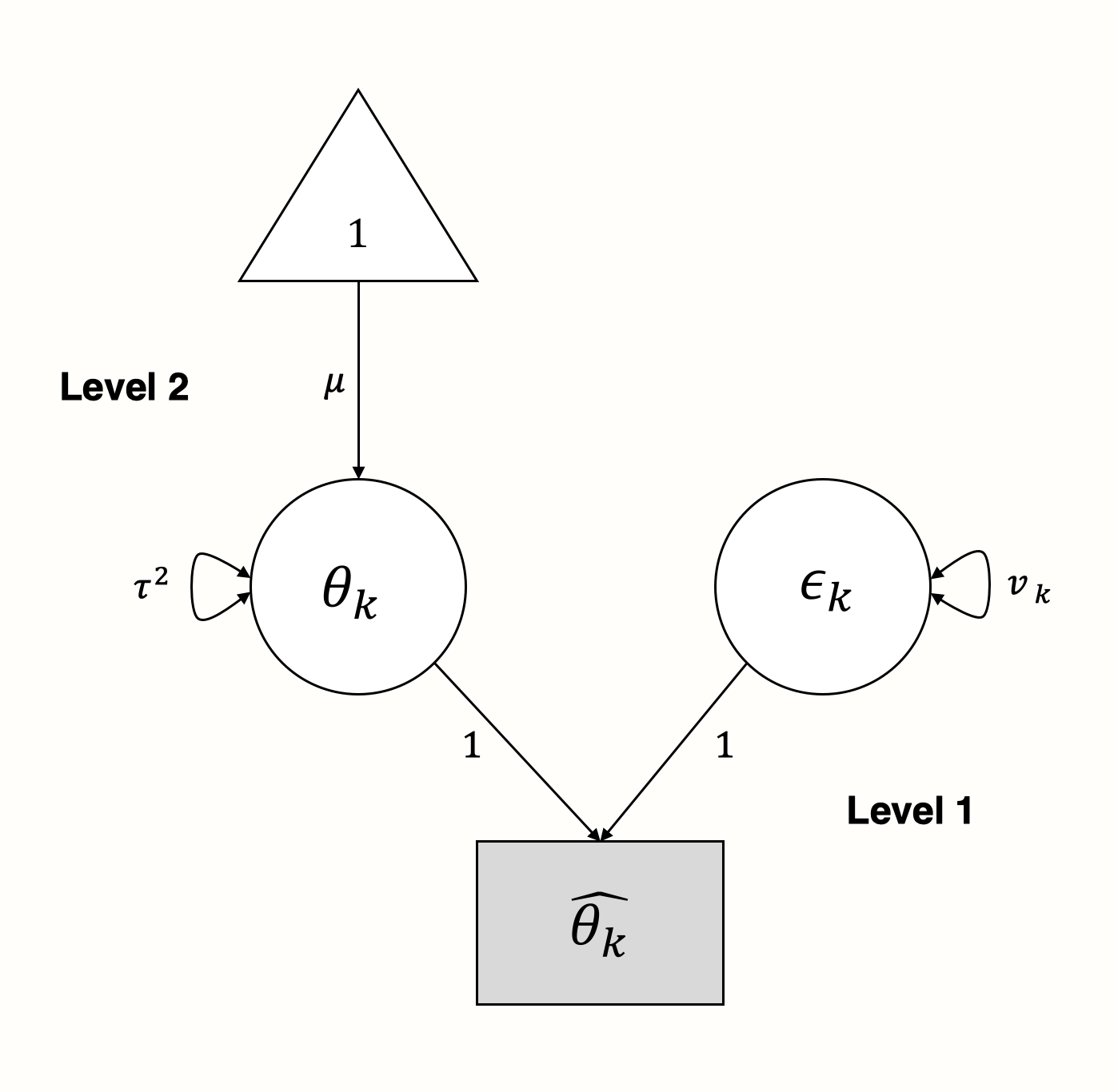
モデルの図では、ある研究 \(k\) の観察された効果量 \(\hat\theta_k\) は、2つのアームによって「影響」されていることがわかる。2つのアームとは、分散 \(v_k\) を持つサンプルエラー \(\epsilon_k\)、および分散 \(\tau^2\) を持つ真の効果量 \(\theta_k\) である。
11.1.3 2段階メタ分析 SEM アプローチ
上記では、SEM の観点から(ランダム効果)メタ分析モデルを定義してみた。これは理論的には面白いが、このモデルは以前取り上げたメタ分析手法と比較して能力が高いわけでも低いわけでもない。単に、ランダム効果モデルを仮定して効果量をプールすることを記述しているだけである。
メタ分析 SEM の汎用性を本当に生かすには、2段階アプローチが必要である (Tang and Cheung 2016; Cheung 2015a, chap. 7)。2段階構造方程式モデリング(Two-Stage Structural Equation Modeling, TSSEM)では、まず、各研究の効果量をプールする。通常、これらの効果量は、モデリングに使用する複数の変数間の相関である。 各研究 \(k\) の相関は、ベクトル \(\boldsymbol{r_k} = (r_1, r_2, \dots, r_p)\) で表される。ここで、 \(p\) は、(ユニークな)相関の総数である。通常のランダム効果モデルと同様に、サンプリングエラー \(\epsilon_k\) と研究間の異質性 \(\zeta_k\)(「ゼータ・k」と読む)により、研究 \(k\) で観測された各相関は真の平均相関 \(\rho\)(「ロー」と読む)から乖離すると仮定する。
\(\boldsymbol{r_k}\) が1つの研究に含まれる複数の相関を表すことを考慮すると、ランダム効果モデルの式は次のようになる。
\[\begin{align} \boldsymbol{r_k} &= \boldsymbol{\rho} + \boldsymbol{\zeta_k} + \boldsymbol{\epsilon_k} \notag \\ \begin{bmatrix} r_1 \\ r_2 \\ \vdots \\ r_p \end{bmatrix} &= \begin{bmatrix} \rho_1 \\ \rho_2 \\ \vdots \\ \rho_p \end{bmatrix} + \begin{bmatrix} \zeta_1 \\ \zeta_2 \\ \vdots \\ \zeta_p \end{bmatrix} + \begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_p \end{bmatrix} \tag{11.4} \end{align}\]
このモデルを用いて、プール相関のベクトル \(\boldsymbol{r}\) を計算することが可能である。この最初のプール化ステップにより、研究間の効果の異質性を評価し、ランダム効果モデルまたはサブグループ分析を使用すべきかどうかを判断することが可能である。{metaSEM} パッケージで使用されている最尤法に基づくアプローチのおかげで、部分的にデータが欠損している研究であっても、このステップに含めることが可能である。
次に、第二段階として、加重最小二乗法( Chapter 8.1.3 参照)を用いて、指定した構造方程式モデルを当てはめる。指定したモデル \(\rho(\hat\theta)\) の関数は、以下の式で表される (Cheung and Chan 2009; Cheung 2015a, chap. 7.4.2)。
\[\begin{equation} F_{\text{WLS}}(\hat\theta) = (\boldsymbol{r} - \rho(\hat\theta))^\top \boldsymbol{V}^{-1} (\boldsymbol{r} - \rho(\hat\theta)) \tag{11.5} \end{equation}\]
ここで、\(\boldsymbol{r}\) はプール相関ベクトルである。この式の重要な部分は、\(\boldsymbol{V}^{-1}\)(「ブイ・インバース」と読む)で、これは \(\boldsymbol{r}\) の共分散を含む逆行列である。この行列は、重み付けに使用される。重要なのは、この第2ステップの式は、ランダム効果モデルでも固定効果モデルでも同じである。なぜなら、研究間の異質性が存在する場合は、第1ステップですでに考慮されているからである。
11.2 多変量メタ分析
メタ分析 SEM の最初の事例を紹介しよう。まずは、SEM 法を使った多変量メタ分析から始めたい。多変量メタ分析では、1つ以上の効果を同時に推定しようとする。このようなメタ分析は、主なアウトカムが1つだけでなく、複数あるような研究テーマを研究している場合に有効である。
ある種の治療の効果を調べることを想像してみよう。この治療法では、ほとんどの専門家が2種類のアウトカムを重要とみなし、したがってほとんどの研究で評価されているとしよう。多変量メタ分析では、1つのモデルで両方のアウトカムに対する効果量を共同で推定することで、この問題に対処することができる。この多変量解析のアプローチでは、2つのアウトカム間の相関を考慮することも可能である。これは、一方のアウトカムで高い効果量を持つ研究が、もう一方のアウトカムでも高い効果量を持つかどうかを判断するために使用することができる。あるいは、2つのアウトカムに負の関係があるか、まったく関係がないかがわかるだろう。
なお、多変量メタ分析は、SEMの枠組み以外でも実行可能となる (Schwarzer, Carpenter, and Rücker 2015, chap. 7; Gasparrini, Armstrong, and Kenward 2012)。しかし、ここでは、SEMの観点からそれらを実行する方法を紹介した。この例と次の例では、Mike Cheung (2015b)によって開発されたメタ分析 SEM のための偉大なパッケージである {metaSEM} を使用することになる。いつものように、まず {metaSEM} パッケージをインストールし、ライブラリからロードする必要がある。
今回の例でも、 {dmetar} の ThirdWave データセットを使用する( Chapter 4.2.1 を参照)。デフォルトでは、このデータセットには、知覚されたストレスに対する効果というアウトカムしか含まれていない。さて、このメタ分析のほとんどの研究が、もう1つの重要なメンタルヘルス関連のアウトカムである不安に対する効果も測定していると想像してみよう。多変量メタ分析を使用して、ストレスと不安に対する効果、および両者がどのように互いに関連しているかを共同で推定したい。
したがって、先に進むために両方のアウトカムのデータが含まれる新しいデータフレームを作成する必要がある。まず、各研究で報告された不安に対する効果(Hedges’ \(g\) と表す)、およびその標準誤差を含むベクトルを定義する。また、各研究で報告されたストレスと不安の間の共分散を含むベクトルも定義する必要がある。1つの研究では、不安のアウトカムを評価していないので、情報がないことを示すために、3つのベクトルで NA を使用する。
# 不安の効果(Hedges g) を定義
Anxiety <- c(0.224,0.389,0.913,0.255,0.615,-0.021,0.201,
0.665,0.373,1.118,0.158,0.252,0.142,NA,
0.410,1.139,-0.002,1.084)
# 不安の効果の標準偏差
Anxiety_SE <- c(0.193,0.194,0.314,0.165,0.270,0.233,0.159,
0.298,0.153,0.388,0.206,0.256,0.256,NA,
0.431,0.242,0.274,0.250)
# ストレスと不安の共変量
Covariance <- c(0.023,0.028,0.065,0.008,0.018,0.032,0.026,
0.046,0.020,0.063,0.017,0.043,0.037,NA,
0.079,0.046,0.040,0.041)そして、このデータを ThirdWave の情報と合わせて、ThirdWaveMV という新しいデータフレームを作成する。このデータセットには、効果量の分散である Stress_var と Anxiety_var を設定する。分散は、標準誤差を二乗することで得られる。
ThirdWaveMV <- data.frame(Author = ThirdWave$Author,
Stress = ThirdWave$TE,
Stress_var = ThirdWave$seTE^2,
Anxiety = Anxiety,
Anxiety_var = Anxiety_SE^2,
Covariance = Covariance)
format(head(ThirdWaveMV), digits = 2)## Author Stress Stress_var Anxiety Anxiety_var Covariance
## 1 Call et al. 0.71 0.068 0.224 0.037 0.023
## 2 Cavanagh et al. 0.35 0.039 0.389 0.038 0.028
## 3 DanitzOrsillo 1.79 0.119 0.913 0.099 0.065
## 4 de Vibe et al. 0.18 0.014 0.255 0.027 0.008
## 5 Frazier et al. 0.42 0.021 0.615 0.073 0.018
## 6 Frogeli et al. 0.63 0.038 -0.021 0.054 0.032
見てわかるように、新しいデータセットには、ストレスと不安の両方の効果量が、それぞれのサンプル分散と一緒に含まれている。Covariance 列は、各研究で測定されたストレスと不安の間の共分散を格納している。
実際の研究でよくある問題は、2つのアウトカム間の共分散(または相関)がオリジナルの研究で報告されていないことである。この場合、アウトカム間の相関に関する合理的な仮定に基づいて、共分散を推定する必要がある。
各研究の共分散がまだわかっていないとしよう。どのように推定できるだろうか?良い方法は、2つのアウトカム間の相関を評価した過去の文献を探すことで、今扱っているのと同じようなコンテキストで探すことができると最適である。例えば、臨床試験の介入後テストにおいて、ストレスと不安は非常に高い相関があり、\(r_{\text{S,A}} \approx\) 0.6であると文献で見つけたとしよう。この想定される相関に基づいて、ある研究 \(k\) の共分散を次の公式を使って近似可能である (Schwarzer, Carpenter, and Rücker 2015, chap. 7)。
\[\begin{equation} \widehat{\text{Cov}}(\theta_{1},\theta_{2}) = SE_{\theta_{1}} \times SE_{\theta_{2}} \times \hat\rho_{1, 2} \tag{11.6} \end{equation}\]
今回のデータを使って、\(r_{\text{S,A}} \approx\) 0.6とすると、この式は R で次のように実装可能である。
# SE = sqrt(var) より、分散の2乗根を使用
cov.est <- with(ThirdWaveMV,
sqrt(Stress_var) * sqrt(Anxiety_var) * 0.6)なお、このように共分散を計算する場合、想定する相関の選択によって結果に大きな影響を与えることがある。したがって、(1)常に想定した相関係数を報告し、(2)感度分析を行い、選んだ相関によって結果がどう変わるかを検証することが強く望まれる。
11.2.1 モデルの指定
多変量メタ分析モデルを指定するために、プログラム的に TSSEM 手順(前章参照)に従う必要はないし、RAM 行列を指定する必要もない。このような比較的単純なモデルであれば、 {metaSEM} の meta 関数を使用すれば、たった1ステップでメタ分析 SEM を適用することが可能である。meta を使用するには、3つの必須引数を指定するだけである。
y. 効果量データを含むデータセットの列である。多変量メタ分析では、cbindを用いて、効果量を含む列を結合する必要がある。v. 効果量の分散を含むデータセットの列。多変量メタ分析では、cbindを用いて、対象とする分散列を結合する必要がある。また、効果量間の共分散を含む列も含める必要がある。引数の構造はcbind(variance_1, covariance, variance_2)である。data. 効果量と分散が格納されたデータセット。
適合したモデルを m.mv という名前で保存する。ひとつ重要な点として、meta を実行する前に、{meta} パッケージがロードされていないことを確認しておこう。{meta} と {metaSEM} の関数は同じ名前を持って流物がいくつかあり、 R でコードを実行するときにエラーにつながる可能性がある。detach 関数を使ってパッケージを “unload” することが可能である。
結果として得られる m.mv オブジェクトは、summary を用いて検証したい。
m.mv <- meta(y = cbind(Stress, Anxiety),
v = cbind(Stress_var, Covariance, Anxiety_var),
data = ThirdWaveMV)
summary(m.mv)## [...]
## Coefficients:
## Estimate Std.Error lbound ubound z value Pr(>|z|)
## Intercept1 0.570 0.087 0.399 0.740 6.5455 5.9e-13 ***
## Intercept2 0.407 0.083 0.244 0.570 4.9006 9.5e-09 ***
## Tau2_1_1 0.073 0.049 -0.023 0.169 1.4861 0.1372
## Tau2_2_1 0.028 0.035 -0.041 0.099 0.8040 0.4214
## Tau2_2_2 0.057 0.042 -0.025 0.140 1.3643 0.1725
## ---
## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## [...]
##
## Heterogeneity indices (based on the estimated Tau2):
## Estimate
## Intercept1: I2 (Q statistic) 0.6203
## Intercept2: I2 (Q statistic) 0.5292
##
## Number of studies (or clusters): 18
## [...]
## OpenMx status1: 0 ("0" or "1": The optimization is considered fine.
## Other values may indicate problems.)11.2.2 結果の評価
SEM モデルが最尤法を使って適合していることを考えると、まず出力の最後にある OpenMx status を最初にチェックする。最尤推定は最適化手順であり、手元のデータに対する最適解が見つかるまで、パラメータが繰り返し変更される。しかし、特に複雑なモデルでは、何度繰り返しても最適解に到達しないことがある。その場合、最尤法は停止して、これまでに近似したパラメータ値を出力した。しかし、このようなモデルの構成要素の値は間違っている可能性が高く、信用するべきではない。
このモデルの OpenMx status は 0 であり、最尤推定がうまくいったことを示している。もし、このステータスが 0 または 1 以外であった場合、このコードを使ってモデルを再実行する必要がある。
rerun(m.mv)この出力では、プールされた2つの効果量が Intercept1 と Intercept2 として表示される。効果量は、meta の呼び出しに挿入した順番に番号が振られている。プールされた効果量は、\(g_{\text{Stress}}\) = 0.57 および \(g_{\text{Anxiety}}\) = 0.41であることがわかる。どちらの効果量も有意である。異質性指標では、\(I^2\) の値も見ることが可能である。 \(I^2_{\text{Stress}}\) = 62% と \(I^2_{\text{Anxiety}}\) = 53%で、両方のアウトカムにかなりの研究間異質性があることがわかる。
また、研究間異質性分散 \(\tau^2\) の直接推定値も示されている。2つの推定値だけでなく、3つの推定値があることがわかる。この意味を理解するために、m.mv オブジェクトから「ランダム」な値を抽出することが可能である。
tau.coefs <- coef(m.mv, select = "random")次に、vec2symMat 関数を使用して、係数行列を作成する。行列の行と列には、変数名である Stress と Anxiety を付ける。
# 行列を作成
tc.mat <- vec2symMat(tau.coefs)
# 列名と行名をつける
dimnames(tc.mat)[[1]] <- dimnames(tc.mat)[[2]] <- c("Stress",
"Anxiety")
tc.mat## Stress Anxiety
## Stress 0.07331199 0.02894342
## Anxiety 0.02894342 0.05753271ここで、\(\tau^2\) の3つの値の意味がよくわかる。これらは、行列の対角線上の研究間分散(異質性)を表している。他の2つのフィールドでは、行列はストレスと不安の間の推定共分散を示している。共分散は相関の未標準化バージョンに過ぎないので、cov2cor 関数を用いて、これらの値を相関に変換することが可能である。
cov2cor(tc.mat)## Stress Anxiety
## Stress 1.0000000 0.4456613
## Anxiety 0.4456613 1.0000000極めて論理的に、行列の対角要素の相関は1であることがわかる。ストレスと不安に対する効果の相関は、\(r_{\text{S,A}}\) = 0.45 である。これは興味深い発見で、治療法の知覚ストレスに対する効果と不安に対する効果との間に正の相関があることを示している。ストレスに対する効果が高い治療法は、不安に対する効果も高いようだと言うことが可能である。
m.mv の要約で示される信頼区間は Wald 型の区間であることに注意しておこう(Chapter 4.1.2.2 を参照)。このような Wald タイプの信頼区間は、特に小さなサンプルでは不正確な場合がある (DiCiccio and Efron 1996)。したがって、尤度に基づく信頼区間を用いて、別の方法で信頼区間を構築することが重要である場合がある。meta 関数を再実行し、さらに intervals.type = "LB" を指定することで、これらの CI を得ることが可能である。
m.mv <- meta(y = cbind(Stress, Anxiety),
v = cbind(Stress_var, Covariance, Anxiety_var),
data = ThirdWaveMV,
intervals.type = "LB")m.mv の出力には、研究間異質性 \(\tau^2\) のゼロでない推定値が含まれていることがすでにわかった。したがって、今適合したモデルは、ランダム効果モデルであると結論づけることが可能である。meta 関数は自動的にランダム効果モデルを使用する。出力された \(I^2\) の値を考慮すると、これは確かに適切であると結論づけることが可能である。しかし、固定効果モデルを適用したい場合は、解析を再実行し、パラメータ RE.constraints = matrix(0, nrow=2, ncol=2) を追加することで、適用することが可能である。これは、\(\tau^2\) の値をすべて0に拘束する零行列を作成する。
m.mv <- meta(y = cbind(Stress, Anxiety),
v = cbind(Stress_var, Covariance, Anxiety_var),
data = ThirdWaveMV,
RE.constraints = matrix(0, nrow=2, ncol=2))11.2.3 結果の可視化
多変量メタ分析モデルをプロットするには、plot 関数を使用する。また、プロットの外観を変更するために、いくつかの追加指定を行う。全てのスタイリングオプションを見たい場合は、コンソールに ?metaSEM::plot.meta を貼り付けて、Enterキーを押してみよう。
plot(m.mv,
axis.labels = c("Perceived Stress", "Anxiety"),
randeff.ellipse.col = "#014d64",
univariate.arrows.col = "gray40",
univariate.arrows.lwd = 9,
univariate.polygon.col = "gray40",
estimate.ellipse.col = "gray40",
estimate.col = "firebrick")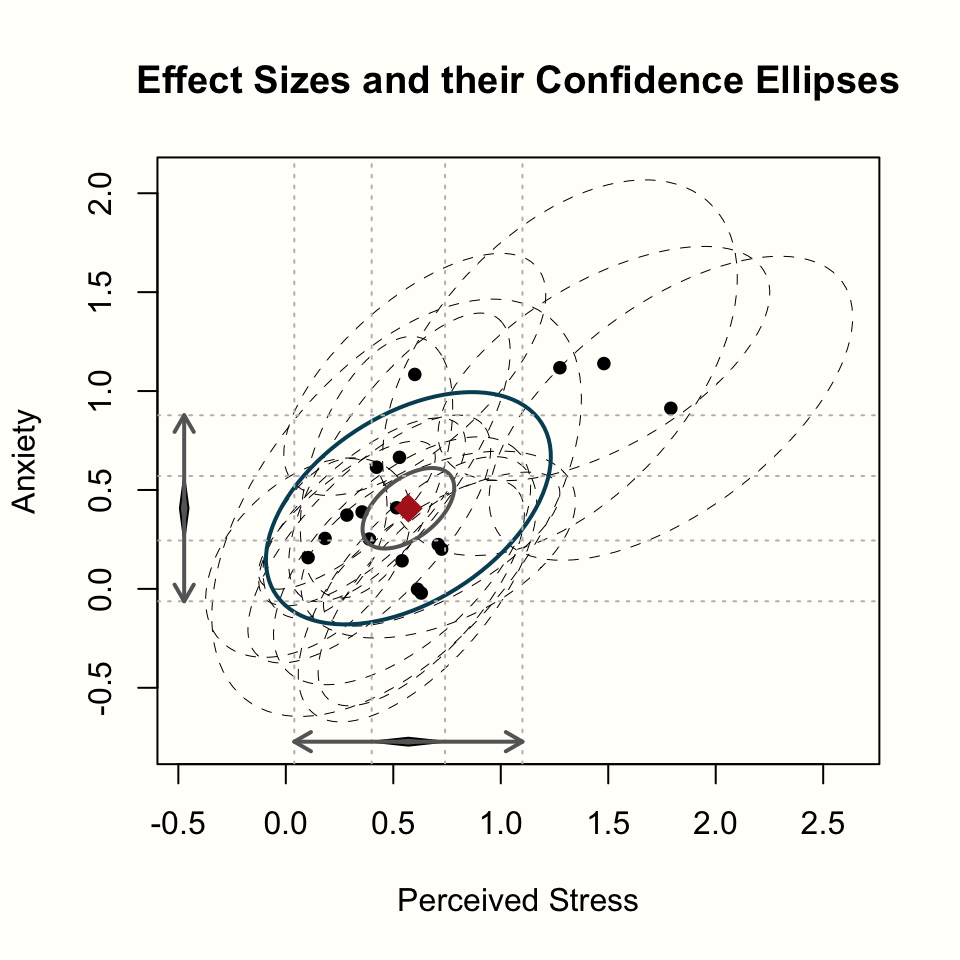
それでは、見ていこう。プロットには2つの軸がある:ストレスへの効果を示す x 軸と、不安への効果を示す y 軸である。また、両方のアウトカムに対するプール効果とその95%信頼区間が表示されている(黒い菱形で表されている)。
プロットの中央には、両変数のプール効果が赤い菱形で示されている。小さい青い楕円は、私たちのプールされた効果の95%信頼区間を表し、大きい黒い楕円は、95%予測区間を表している(Chapter 5.2)59。
最後に、黒丸は個々の研究を示し、破線の楕円は95%信頼区間を表す。
11.3 確証的因子分析
確証的因子分析 (Confirmatory Factor Analysis, CFA) は、観測された変数が仮定された潜在変数にどのように関係するかを特定する一般的な SEM 手法である (B. Thompson 2004, chap. 1.1 and 1.2)。CFA は、アンケートや他のタイプのアセスメントの心理測定特性を評価するためによく使用される。それは、研究者が、評価された変数が、測定しようとする潜在変数を本当に測定しているかどうか、および複数の潜在変数がお互いにどのように関係するかを決定することを可能にする。
頻繁に使用されるアンケートについては、通常、異なるアンケート項目間の相関を報告する多くの実証研究が存在した。このようなデータは、メタ分析的な SEM に使用することが可能である。これにより、すべての利用可能なエビデンスに基づいて、どの潜在因子構造が最も適切であるかを評価することが可能である。
この例では、睡眠の問題についての(架空の)質問票の潜在的な因子構造を確認したい。質問票には、睡眠の問題を特徴づける2つの異なる潜在変数を測定すると仮定する。不眠症(insomnia)と倦怠感(lassitude、一般的に倦怠感は fatigue)である。Koffel and Watson (2009) は、睡眠の訴えは、実際にこれらの2つの潜在因子によって記述され得ると主張した。
メタ分析 CFA を実践するために、私たちが想像した睡眠アンケートを評価した11件の研究結果をシミュレートした。このデータセットを SleepProblems と名付けた。これらの研究のそれぞれには、私たちの質問票によって直接測定された睡眠に関する不満の症状間の相互相関が含まれている。これらの測定指標には、睡眠の質、睡眠潜時、睡眠効率、日中機能不全、hypersomnia(すなわち、寝過ぎ)が含まれる。最初の3つの症状は、いずれも不眠症を潜在変数として測定しているので関連があり、日中機能不全と過眠症は、倦怠感要因の症状なので関連があると推測される。
提案された構造をグラフィカルなモデルとして表現すると、次のようになる60。

11.3.1 データ準備
まず、モデルに使用する SleepProblems データを見てみよう。このデータセットは特殊な構造を持っている。それは list オブジェクトであり、 (1) 行列の list と (2) 数値ベクトルを含んでいる。リストは非常に汎用性の高い R オブジェクトであり、異なる要素を 1 つの大きなオブジェクトに結合することが可能である。リストは $ 演算子を用いて、データフレームのようにアクセスすることができる。names 関数を使用すると、リスト内のオブジェクトの名前を表示すことが可能である。
## [1] "data" "n"このリストには、実際の data と、各研究のサンプルサイズである n の 2 つの要素が含まれていることがわかる。data オブジェクトはそれ自体が list であるため、 names 関数を使用してそのコンテンツの名前を取得することも可能である。
names(SleepProblems$data)## [1] "Coleman et al. (2003)" "Salazar et al. (2008)"
## [3] "Newman et al. (2016)" "Delacruz et al. (2009)"
## [5] "Wyatt et al. (2002)" "Pacheco et al. (2016)"
## [...]また、$ 演算子を使って data に含まれる特定の要素を表示すことも可能である。
SleepProblems$data$`Coleman et al. (2003)`## Quality Latency Efficiency DTDysf HypSomnia
## Quality 1.00 0.39 0.53 -0.30 -0.05
## Latency 0.39 1.00 0.59 0.07 0.44
## Efficiency 0.53 0.59 1.00 0.09 0.22
## DTDysf -0.30 0.07 0.09 1.00 0.45
## HypSomnia -0.05 0.44 0.22 0.45 1.00data リストには11の要素があり、含まれる11の研究ごとに1つずつある。Coleman et al. (2003) の研究を詳しく見ると、データは5つの変数を持つ相関行列として格納されていることがわかる。行列の各行と列は、私たちの質問票で評価された睡眠の不定愁訴の症状の1つに対応した。
Coleman et al. (2003) の研究では、各症状の組み合わせについて相関が報告されている。しかし、いくつかのフィールドで欠損値( NA としてコード化)を持つ研究を使用することも可能である。これは、メタ分析SEMが、少なくともある程度は、欠損データを扱うことができることがある。
先に進む前に、このようなリストを自分で作成する方法を簡単に説明しよう。2つの研究の相関行列を抽出し、それをデータフレームとして R にインポートしたい。データフレームを df1 と df2 と呼ぶとすると、以下の「レシピ」を使用して、さらなる解析に適した list オブジェクトを作成することが可能である。
# データフレームを行列に変換
mat1 <- as.matrix(df1)
mat2 <- as.matrix(df2)
# 行ラベルを定義
dimnames(mat1)[[1]] <- c("Variable 1", "Variable 2", "Variable 3")
dimnames(mat2)[[1]] <- c("Variable 1", "Variable 2", "Variable 3")
# リストに相関係数行列を結合
data <- list(mat1, mat2)
names(data) <- c("Study1", "Study2")
# 二つの研究のサンプルサイズを定義
n <- c(205, # N of study 1
830) # N of study 2
# 行列とサンプルサイズを結合
cfa.data <- list(data, n)11.3.2 モデル仕様
CFA モデルを指定するためには、先に述べた RAM 指定と2段階メタ分析 SEM 手順を使用する必要がある。{metaSEM} パッケージは、2段階のそれぞれについて、tssem1 と tssem2 という別々の関数を含んでいる。最初の関数は、すべての研究の相関行列をプールし、2番目の関数は、提案されたモデルをデータに適合させる。
11.3.2.1 ステージ 1
最初の段階では、tssem1 関数を用いて相関行列をプールする。この関数では、4つの重要な引数を指定する必要がある。
Cov. プールしたい相関行列のlistを指定する。リスト内のすべての相関行列は、同一の構造を持っている必要があることに注意。n. 各研究のサンプルサイズを含む数値ベクトルで、Covに含まれる行列と同じ順序で並べられる。method. 固定効果モデル("FEM")またはランダム効果モデル("REM")を使用するかどうかを指定。RE.type. ランダム効果モデルを利用する場合、ランダム効果の推定方法を指定する。デフォルトは"Symm"で、2つの変数間の共分散を含む、すべての \(\tau^2\) の値を推定する。"Diag"に設定すると、ランダム効果行列の対角要素のみが推定される。これは、ランダム効果が独立であると仮定していることを意味する。"Diag"を設定すると、モデルは非常に単純化されるが、推定しなければならないパラメータが少なくなるため、多くの場合、この方法が望ましい。これは変数の数が多い場合や研究の数が少ない場合に特に意味がある。
この例では、ランダム効果モデルを仮定し、RE.type = "Diag" を使用する。モデルを cfa1 として保存し、出力を取得するために summary 関数を呼び出す。
##
## Call:
## meta(y = ES, v = acovR, RE.constraints = Diag(paste0(RE.startvalues,
## "*Tau2_", 1:no.es, "_", 1:no.es)), RE.lbound = RE.lbound,
## I2 = I2, model.name = model.name, suppressWarnings = TRUE,
## silent = silent, run = run)
##
## 95% confidence intervals: z statistic approximation (robust=FALSE)
## Coefficients:
## Estimate Std.Error lbound ubound z value
## Intercept1 0.444432236 0.057467775 0.331797465 0.557067006 7.7336
## Intercept2 0.478173063 0.042506058 0.394862720 0.561483407 11.2495
## Intercept3 0.032786305 0.071282427 -0.106924685 0.172497295 0.4599
## Intercept4 0.132711876 0.048151188 0.038337281 0.227086471 2.7561
## Intercept5 0.509594150 0.036490787 0.438073522 0.581114778 13.9650
## Intercept6 0.120881305 0.040915599 0.040688204 0.201074406 2.9544
## Intercept7 0.192545120 0.060739565 0.073497760 0.311592481 3.1700
## Intercept8 0.221265205 0.039608121 0.143634715 0.298895695 5.5864
## Intercept9 0.189786602 0.045589099 0.100433611 0.279139594 4.1630
## Intercept10 0.509204468 0.023983697 0.462197284 0.556211651 21.2313
## Tau2_1_1 0.032324879 0.015012416 0.002901083 0.061748674 2.1532
## Tau2_2_2 0.016349084 0.008326703 0.000029047 0.032669121 1.9635
## Tau2_3_3 0.049769970 0.023797989 0.003126768 0.096413171 2.0914
## Tau2_4_4 0.019828043 0.010038215 0.000153503 0.039502583 1.9753
## Tau2_5_5 0.010963532 0.006133040 -0.001057005 0.022984070 1.7876
## Tau2_6_6 0.012511016 0.007794974 -0.002766852 0.027788883 1.6050
## Tau2_7_7 0.034863896 0.016839497 0.001859088 0.067868704 2.0704
## Tau2_8_8 0.012156429 0.006571848 -0.000724157 0.025037015 1.8498
## Tau2_9_9 0.017532003 0.009481599 -0.001051590 0.036115595 1.8491
## Tau2_10_10 0.003543432 0.002549068 -0.001452649 0.008539512 1.3901
## Pr(>|z|)
## Intercept1 0.00000000000001044 ***
## Intercept2 < 0.00000000000000022 ***
## Intercept3 0.645553
## Intercept4 0.005849 **
## Intercept5 < 0.00000000000000022 ***
## Intercept6 0.003133 **
## Intercept7 0.001524 **
## Intercept8 0.00000002318788406 ***
## Intercept9 0.00003141179890975 ***
## Intercept10 < 0.00000000000000022 ***
## Tau2_1_1 0.031302 *
## Tau2_2_2 0.049594 *
## Tau2_3_3 0.036497 *
## Tau2_4_4 0.048239 *
## Tau2_5_5 0.073838 .
## Tau2_6_6 0.108491
## Tau2_7_7 0.038418 *
## Tau2_8_8 0.064346 .
## Tau2_9_9 0.064450 .
## Tau2_10_10 0.164502
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Q statistic on the homogeneity of effect sizes: 908.1438
## Degrees of freedom of the Q statistic: 100
## P value of the Q statistic: 0
##
## Heterogeneity indices (based on the estimated Tau2):
## Estimate
## Intercept1: I2 (Q statistic) 0.9316
## Intercept2: I2 (Q statistic) 0.8837
## Intercept3: I2 (Q statistic) 0.9336
## Intercept4: I2 (Q statistic) 0.8547
## Intercept5: I2 (Q statistic) 0.8315
## Intercept6: I2 (Q statistic) 0.7800
## Intercept7: I2 (Q statistic) 0.9093
## Intercept8: I2 (Q statistic) 0.7958
## Intercept9: I2 (Q statistic) 0.8366
## Intercept10: I2 (Q statistic) 0.6486
##
## Number of studies (or clusters): 11
## Number of observed statistics: 110
## Number of estimated parameters: 20
## Degrees of freedom: 90
## -2 log likelihood: -100.688
## OpenMx status1: 0 ("0" or "1": The optimization is considered fine.
## Other values may indicate problems.)[...]
Coefficients:
Estimate Std.Error lbound ubound z value Pr(>|z|)
Intercept1 0.444 0.057 0.331 0.557 7.733 < 0.001 ***
Intercept2 0.478 0.042 0.394 0.561 11.249 < 0.001 ***
Intercept3 0.032 0.071 -0.106 0.172 0.459 0.645
Intercept4 0.132 0.048 0.038 0.227 2.756 0.005 **
Intercept5 0.509 0.036 0.438 0.581 13.965 < 0.001 ***
Intercept6 0.120 0.040 0.040 0.201 2.954 0.003 **
Intercept7 0.192 0.060 0.073 0.311 3.170 0.001 **
Intercept8 0.221 0.039 0.143 0.298 5.586 < 0.001 ***
Intercept9 0.189 0.045 0.100 0.279 4.163 < 0.001 ***
Intercept10 0.509 0.023 0.462 0.556 21.231 < 0.001 ***
Tau2_1_1 0.032 0.015 0.002 0.061 2.153 0.031 *
Tau2_2_2 0.016 0.008 0.000 0.032 1.963 0.049 *
Tau2_3_3 0.049 0.023 0.003 0.096 2.091 0.036 *
Tau2_4_4 0.019 0.010 0.000 0.039 1.975 0.048 *
Tau2_5_5 0.010 0.006 -0.001 0.022 1.787 0.073 .
Tau2_6_6 0.012 0.007 -0.002 0.027 1.605 0.108
Tau2_7_7 0.034 0.016 0.001 0.067 2.070 0.038 *
Tau2_8_8 0.012 0.006 -0.000 0.025 1.849 0.064 .
Tau2_9_9 0.017 0.009 -0.001 0.036 1.849 0.064 .
Tau2_10_10 0.003 0.002 -0.001 0.008 1.390 0.164
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
[...]
Heterogeneity indices (based on the estimated Tau2):
Estimate
Intercept1: I2 (Q statistic) 0.9316
Intercept2: I2 (Q statistic) 0.8837
Intercept3: I2 (Q statistic) 0.9336
Intercept4: I2 (Q statistic) 0.8547
Intercept5: I2 (Q statistic) 0.8315
Intercept6: I2 (Q statistic) 0.7800
Intercept7: I2 (Q statistic) 0.9093
Intercept8: I2 (Q statistic) 0.7958
Intercept9: I2 (Q statistic) 0.8366
Intercept10: I2 (Q statistic) 0.6486
[...]
OpenMx status1: 0 ("0" or "1": The optimization is considered fine.
Other values may indicate problems.)OpenMx status を見ると、モデルの推定値が信頼できるものであることが確認可能である。結果をより消化しやすくするために、coef 関数を用いて固定効果(私たちの推定したプール相関)を抽出することが可能である。次に、vec2symMat を用いて係数から対称行列を作成し、解釈を容易にするために次元名を追加する。
# 固定係数(相関)を抽出
fixed.coefs <- coef(cfa1, "fixed")
# 対称行列を作成
fc.mat <- vec2symMat(fixed.coefs, diag = FALSE)
# 列名と行名をつける
dimnames(fc.mat)[[1]] <- c("Quality", "Latency",
"Efficiency", "DTDysf", "HypSomnia")
dimnames(fc.mat)[[2]] <- c("Quality", "Latency",
"Efficiency", "DTDysf", "HypSomnia")
# 相関行列を表示(3桁)
round(fc.mat, 3)## Quality Latency Efficiency DTDysf HypSomnia
## Quality 1.000 0.444 0.478 0.033 0.133
## Latency 0.444 1.000 0.510 0.121 0.193
## Efficiency 0.478 0.510 1.000 0.221 0.190
## DTDysf 0.033 0.121 0.221 1.000 0.509
## HypSomnia 0.133 0.193 0.190 0.509 1.000これで、変数のプールされた相関行列を見ることが可能である。モデルの出力を見てみると、すべての相関係数が有意であることがわかる ( \(p<\) 0.05) ただし、1つだけ、睡眠の質と日中機能不全の相関は有意ではなかった。私たちの想定したモデルの観点からは、これらの変数が異なる因子に負荷されると予想されるので、これは理にかなっている。また、異なる推定値の \(I^2\) 値が非常に大きい(65-93%)ことがわかる。
11.3.2.2 ステージ 2
相関行列をプールした後、提案した因子モデルがデータにうまく適合しているかどうかを判断することになる。モデルを指定するために、今回は RAM 式を使用し、\(\boldsymbol{A}\), \(\boldsymbol{S}\), \(\boldsymbol{F}\) という行列を指定する必要がある。これら行列の各フィールドを埋めるために、最初に空行列を構築することが最善であることがよくある。構造的には、私たちが定義したすべて行列は、観測変数だけでなく、仮定した潜在変数である f_Insomnia と f_Lassitude も含んでいる。ここでは、出発点としてゼロ行列を作成する方法を示した。
# 行と列の名称のベクトルを作成
dims <- c("Quality", "Latency", "Efficiency",
"DTDysf", "HypSomnia", "f_Insomnia", "f_Lassitude")
# 7x7 のゼロ行列を作成
mat <- matrix(rep(0, 7*7), nrow = 7, ncol = 7)
# 列名と行名をつける
dimnames(mat)[[1]] <- dimnames(mat)[[2]] <- dims
mat## Qlty Ltncy Effcncy DTDysf HypSmn f_Insmn f_Lsstd
## Quality 0 0 0 0 0 0 0
## Latency 0 0 0 0 0 0 0
## Efficiency 0 0 0 0 0 0 0
## DTDysf 0 0 0 0 0 0 0
## HypSomnia 0 0 0 0 0 0 0
## f_Insomnia 0 0 0 0 0 0 0
## f_Lassitude 0 0 0 0 0 0 0\(\boldsymbol{A}\) 行列
\(\boldsymbol{A}\) 行列では、モデルにおける非対称(つまり単一)矢印を指定する。各単一矢印は列変数から始まり、列が行変数のエントリと交差するところで終わる。矢印を表さない他のフィールドはすべて 0 で埋められる。
\(\boldsymbol{A}\) 行列に文字列を追加することで、矢印を「推定」しなければならないことを指定する。この文字列は、最適化手順の開始値(通常は 0.1 から 0.3 の間のどこか)で始まり、その後に * が続く。記号の後に、その値のラベルを指定する。\(\boldsymbol{A}\) 行列の2つのフィールドが同じラベルを持つ場合、これはそのフィールドが同じ値を持つと仮定することを意味する。
この例では、すべての推定矢印の開始値を 0.3 とし、先に示した経路図に従ってフィールドにラベル付けを行う。
A <- matrix(c(0, 0, 0, 0, 0, "0.3*Ins_Q", 0 ,
0, 0, 0, 0, 0, "0.3*Ins_L", 0 ,
0, 0, 0, 0, 0, "0.3*Ins_E", 0 ,
0, 0, 0, 0, 0, 0 , "0.3*Las_D",
0, 0, 0, 0, 0, 0 , "0.3*Las_H",
0, 0, 0, 0, 0, 0 , 0 ,
0, 0, 0, 0, 0, 0 , 0
), nrow = 7, ncol = 7, byrow=TRUE)
# 列名と行名をつける
dimnames(A)[[1]] <- dimnames(A)[[2]] <- dims最後のステップは、\(\boldsymbol{A}\) 行列を as.mxMatrix 関数に入れて、ステージ2モデルで使用できるようにすることである。
A <- as.mxMatrix(A)\(\boldsymbol{S}\) 行列
\(\boldsymbol{S}\) 行列では、推定したい分散を指定する。この例では、これらはすべての観測変数の分散と、2つの潜在要因の間の相関である。まず、潜在要因の自分自身との相関を1に設定した。さらに、観測された変数の分散は 0.2、相関は 0.3 という開始値を使用する。これらはすべてこのコードで指定することができる。
# 分散を表す対角行列を作る
Vars <- Diag(c("0.2*var_Q", "0.2*var_L",
"0.2*var_E", "0.2*var_D", "0.2*var_H"))
# 潜在変数に対する行列を作成する
Cors <- matrix(c(1, "0.3*cor_InsLas",
"0.3*cor_InsLas", 1),
nrow=2, ncol=2)
# 結合する
S <- bdiagMat(list(Vars, Cors))
# 列名と行名をつける
dimnames(S)[[1]] <- dimnames(S)[[2]] <- dimsそして、再び、as.mxMatrix を用いて行列に変換する。
S <- as.mxMatrix(S)\(\boldsymbol{F}\) 行列
最後に、\(\boldsymbol{F}\) 行列を指定するのは簡単である。観測された変数の対角要素には 1 を記入し、それ以外は 0 を使用する。さらに、行列の少なくとも 1 つの要素が 0 でない行だけを選択する(つまり、最後の 2 行は 0 しか含まれていないので削除する)。
# 対角行列を作成
F1 <- Diag(c(1, 1, 1, 1, 1, 0, 0))
# ヌルでない行だけを選択
F1 <- F1[1:5,]
# 行ラベルと列ラベルの指定
dimnames(F1)[[1]] <- dims[1:5]
dimnames(F1)[[2]] <- dims
F1 <- as.mxMatrix(F1)11.3.3 モデル適合
さて、いよいよ提案したモデルをプールされたデータに適合させる。これを行うには、 tsem2 関数を使用する。ステージ1のモデル cfa1、3つ行列、そして diag.constraints=FALSE を指定するだけである(mediation モデルを適用しているわけではないため)。結果として得られるオブジェクトを cfa2 として保存し、summary を用いてアクセスする。
cfa2 <- tssem2(cfa1,
Amatrix = A,
Smatrix = S,
Fmatrix = F1,
diag.constraints = FALSE)
summary(cfa2)##
## Call:
## wls(Cov = pooledS, aCov = aCov, n = tssem1.obj$total.n, RAM = RAM,
## Amatrix = Amatrix, Smatrix = Smatrix, Fmatrix = Fmatrix,
## diag.constraints = diag.constraints, cor.analysis = cor.analysis,
## intervals.type = intervals.type, mx.algebras = mx.algebras,
## mxModel.Args = mxModel.Args, subset.variables = subset.variables,
## model.name = model.name, suppressWarnings = suppressWarnings,
## silent = silent, run = run)
##
## 95% confidence intervals: z statistic approximation
## Coefficients:
## Estimate Std.Error lbound ubound z value Pr(>|z|)
## Las_D 0.688251 0.081845 0.527838 0.848665 8.4092 < 0.00000000000000022
## Ins_E 0.789438 0.060605 0.670654 0.908221 13.0260 < 0.00000000000000022
## Las_H 0.741372 0.088425 0.568063 0.914681 8.3842 < 0.00000000000000022
## Ins_L 0.658587 0.053650 0.553435 0.763739 12.2756 < 0.00000000000000022
## Ins_Q 0.613591 0.051384 0.512879 0.714303 11.9412 < 0.00000000000000022
## cor_InsLas 0.330274 0.045607 0.240886 0.419662 7.2418 0.0000000000004428
##
## Las_D ***
## Ins_E ***
## Las_H ***
## Ins_L ***
## Ins_Q ***
## cor_InsLas ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Goodness-of-fit indices:
## Value
## Sample size 3272.0000
## Chi-square of target model 5.2640
## DF of target model 4.0000
## p value of target model 0.2613
## Number of constraints imposed on "Smatrix" 0.0000
## DF manually adjusted 0.0000
## Chi-square of independence model 809.5366
## DF of independence model 10.0000
## RMSEA 0.0098
## RMSEA lower 95% CI 0.0000
## RMSEA upper 95% CI 0.0297
## SRMR 0.0413
## TLI 0.9960
## CFI 0.9984
## AIC -2.7360
## BIC -27.1086
## OpenMx status1: 0 ("0" or "1": The optimization is considered fine.
## Other values indicate problems.)## [...]
## Coefficients:
## Estimate Std.Error lbound ubound z value Pr(>|z|)
## Las_D 0.688 0.081 0.527 0.848 8.409 < 0.001 ***
## Ins_E 0.789 0.060 0.670 0.908 13.026 < 0.001 ***
## Las_H 0.741 0.088 0.568 0.914 8.384 < 0.001 ***
## Ins_L 0.658 0.053 0.553 0.763 12.275 < 0.001 ***
## Ins_Q 0.613 0.051 0.512 0.714 11.941 < 0.001 ***
## cor_InsLas 0.330 0.045 0.240 0.419 7.241 < 0.001 ***
## ---
## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
##
## Goodness-of-fit indices:
## Value
## Sample size 3272.0000
## Chi-square of target model 5.2640
## DF of target model 4.0000
## p value of target model 0.2613
## [...]
## RMSEA 0.0098
## RMSEA lower 95% CI 0.0000
## RMSEA upper 95% CI 0.0297
## [...]
## OpenMx status1: 0 ("0" or "1": The optimization is considered fine.
## Other values indicate problems.)OpenMxの状態 が 0 であり、最適化がうまくいったことがわかる。出力では、Lassitude \(\rightarrow\) Daytime Dysfunction(Las_D)の 0.69 のように、2つの潜在因子と観察された症状の間のパスの推定値が提供される。私たちはまた、モデルによると、2つの潜在的な要因の間に有意な相関があることがわかる。\(r_{\text{Ins,Las}}\) = 0.33.
しかし、最も重要なことは、想定したモデルがどの程度データに適合しているかをチェックすることである。これは Goodness-of-fit indices を見ることによって達成可能である。適合度検定は、\(\chi^2_4=\) 5.26、\(p=\) 0.26 で、有意でないことがわかる。他の統計検定とは異なり、このアウトカムは、私たちのモデルがデータによく適合するという帰無仮説を受け入れることを意味するので、望ましい結果である。
さらに、近似値の二乗平均平方根誤差 (Root Mean Square Error of Approximation, RMSEA) の値は 0.0098 であることがわかる。経験則では、RSMEA の値が 0.05 以下であれば、モデルはデータによく適合していると考えることができ、値が小さいほど適合度が高いことを示している (Browne and Cudeck 1993)。したがって、この適合度指数も、モデルが私たちのデータによく適合していることを示している。
代替モデル
SEM 研究によくある問題は、研究者が自分の提唱するモデルにのみ注目し、それがデータにうまく適合するかどうかに注目しがちなことである。もし、想定したモデルがデータに近い適合を示すことがわかれば、多くの研究者は、データが自分の理論を証明したと直接結論づけることが多い。
しかし、同じデータに対して複数のモデルがうまく適合する可能性があるため、これは問題である。したがって、代替モデルの仮説や構造も確認する必要がある。もし、代替モデルもデータにうまくフィットすれば、我々の提案した構造が本当に「正しい」ものなのかどうかがわからなくなる。
11.3.4 パス図
モデルの適合後、{metaSEM} はそれをグラフィカルに可視化することを非常に簡単にしてくれる。パス図を描くためには、まず、{semPlot} パッケージ (Epskamp 2019) をインストールし、ロードする必要がある。
モデルをプロットするために、{semPlot} が使用できる形式に変換する必要があるので、meta2semPlot 関数を使用して行っておこう。
cfa.plot <- meta2semPlot(cfa2)そして、グラフを生成するために、{semPlot} の semPaths 関数を使ってみよう。この関数は多くのパラメータを持っており、コンソールに ?semPaths と入力し、Enter キーを押すことでアクセスすることが可能である。以下がコードと結果のプロットである。
# macOS 用文字化け対策
par(family= "HiraKakuProN-W3")
# プロットラベルを作成(左から右、下から上)
labels <- c("睡眠\nの質",
"睡眠\n潜時",
"睡眠\n効率",
"日中機\n能障害",
"過眠症","不眠",
"倦怠感")
# プロット
semPaths(cfa.plot,
whatLabels = "est",
edge.color = "black",
nodeLabels = labels,
sizeMan = 10,
sizeLat = 10,
edge.label.cex = 1)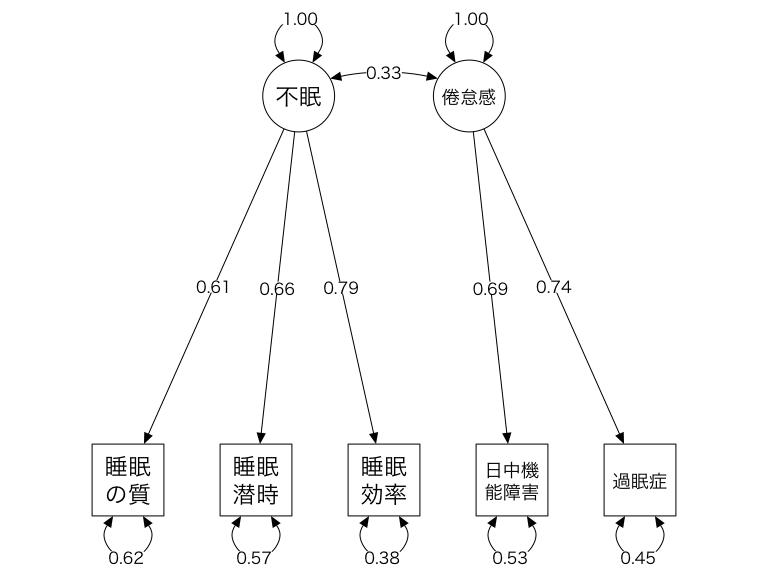
更なる学習
この章で取り上げたことは、メタアナリシス SEM の初歩的な入門として捉えていただきたい。より詳細なメタアナリシス SEM の議論は、Mike Cheung の決定的な本である Meta-Analysis: A Structural Equation Modeling Approach (2015a) に記載されている。この本は、ここでカバーしていない他のさまざまな種類のメタ分析構造方程式モデルについても記述しており、 R を使用してどのように実装できるかを説明されている。
短めの(そして、オープンにアクセスできる)リソースを探すのであれば、{metaSEM}
パッケージの vignette をお読みいただきたい。この vignette
には、メタアナリシスSEMの理論について簡単に説明し、 R
を使ったいくつかの図解を掲載している。{metaSEM}
をロードした後、コンソールで vignette(“metaSEM”)
を実行することにより、インターネットからヴィネットをダウンロードすることができる。
\[\tag*{$\blacksquare$}\]
11.4 演習問題
知識を試そう!
- 構造方程式モデリングとは何か、何のために使うのか。
- SEM の表現方法として、どのようなものがあるか?
- ランダム効果メタ分析を SEM の観点から説明しなさい。
- 多変量メタ分析とは何か、どのような場合に有用か。
- 提案したメタ分析 SEM がデータによく適合することがわかったとき、このモデルが自動的に「正しい」モデルであることを意味するのだろうか。
問題の解答は、本書の巻末 Appendix A にある。
11.5 要約
構造方程式モデリング(SEM)は、観測される(=顕在)変数と観測されない(=潜在)変数の間の複雑な関係を検証するために使用できる統計手法である。
メタ分析はマルチレベルモデルに基づいているため、SEM の観点からも定式化することが可能である。これは、ランダム効果メタ分析を構造方程式モデルとして「複製」するために使用することが可能である。しかし、より重要なことは、観測された効果量間のより複雑な関係をモデル化したメタ分析を行うことができることである。
メタ分析 SEM は、例えば、多変量メタ分析を行うために適用することができる。多変量メタ分析では、2つ以上のアウトカムを、両アウトカム間の相関を考慮しながら、共同で推定する。
メタ分析的 SEM のもう一つの応用は、確証的因子分析である。含まれるすべての研究にわたって提案された因子モデルの適合性をテストするために、2段階の手順を使用しなければならない。第一段階では、個々の研究の相関行列がプールされる。そして、このプールされた相関行列は、想定された SEM を適合させるために使用される。