13 ベイズメタ分析

---

こ れまでの章では、「マルチレベル」モデル（Chapter 10）、メタ分析的構造方程式モデリング（Chapter 11）、ネットワークメタ分析（Chapter 12）など、メタ分析のやや高度な拡張を掘り下げてきた。さて、一歩下がって、もう一度「従来の」メタ分析を見直そう。ただし、今回はこれまでとは異なる角度でベイズメタ分析を扱う。

すでに一つ前のネットワークメタ分析に関する章でベイズモデルを取り上げた。そこでは、ベイズの定理や事前分布の考え方など、ベイズ統計の背後にある主要な考え方について議論してきた（Chapter 12.3.1 参照）。本章では、この知識をもとに、メタ分析を行うための「ベイズ的な方法」をより深く理解したい。例えば、ベイジアンネットワークのメタ分析モデルを設定するとき、{gemtc} パッケージは自動的に優先順位を指定したが、ここでは、これを自分たちで行っていきたい。

背景は少し複雑であるが、ベイズメタ分析も本質的に「従来の」メタ分析と同じことをしていることがわかる。しかし、ベイズモデルを使用することは、頻度論的アプローチと比較して、いくつかの実用的な利点もある。そのため、 R を使用して利点のあるモデルを実装する方法を学ぶことは価値がある。

13.1 ベイズ型階層モデル

---

ベイズメタ分析を行うために、いわゆるベイズ階層モデル (Röver 2017; Julian Higgins, Thompson, and Spiegelhalter 2009) を採用する。このタイプのモデルについては、すでにネットワークメタ分析の章（Chapter 12.3.2）で簡単に取り上げた。

Chapter 10 では、すべてのメタ分析モデルには固有の「マルチレベル」、つまり階層的な構造があることを学んだ。最初のレベルには、個々の参加者がいる。このレベルのデータは、通常、各研究 \(k\) の計算された効果量 \(\hat\theta_k\) という形で届く。参加者が第２レベルにネストされると、それぞれの研究の真の効果量 \(\theta_k\) は、独自の分布に従うと仮定する。この真の効果の分布は、平均 \(\mu\)（推定したい「真の」効果のプール値）と分散 \(\tau^2\) （研究間の異質性を表す）を持っている。

これを定式化してみよう。最初のレベルでは、研究 \(k\) で報告された観察された効果量 \(\hat\theta_k\) が、この研究での「真の」効果 \(\theta_k\) の推定値であると仮定した。観察された効果 \(\hat\theta_k\) は、サンプル誤差 \(\epsilon_k\) のために \(\theta_k\) から乖離している。これは、\(\hat\theta_k\) が \(k\) の基礎となる母集団から抽出（サンプル）されたと仮定している。この母集団は、平均 \(\theta_k\)、研究の「真の」効果、および分散 \(\sigma^2\) を持つ分布と見なすことが可能である。

第2ステップでは、真の効果量 \(\theta_k\) 自身は、真の効果量の包括的な分布のサンプルに過ぎないと仮定する。この分布の平均 \(\mu\) は、推定したい効果量のプール値である。包括的な分布は分散 \(\tau^2\) も持っているので、研究別の真の効果 \(\theta_k\) は、\(\mu\) から乖離している。この分散は、研究間の異質性を表す。まとめると、この2つの方程式が得られる。

\[\begin{align} \hat\theta_k &\sim \mathcal{N}(\theta_k,\sigma_k^2) \notag \\ \theta_k &\sim \mathcal{N}(\mu,\tau^2) \tag{13.1} \end{align}\]

ここでは、\(\mathcal{N}\) を使って、左側のパラメータが正規分布からサンプルされたことを示す。これは2番目の式に対して不必要に厳しい仮定であるという意見もあるが (Julian Higgins, Thompson, and Spiegelhalter 2009)、ここで示したような定式化は、ほとんどの場合に使用されているものである。前にも述べたように、固定効果モデルはこのモデルの特殊なケースで、\(\tau^2 = 0\) 、つまり研究間の異質性がなく、すべての研究が1つの真の効果量を共有していると仮定している（すなわち、すべての研究 \(k\) に対して、\(\theta_k = \mu\)）。

また、この式を簡略化するために、合わせた形式を用いることができる。

\[\begin{equation} \hat\theta_k \sim \mathcal{N}(\mu,\sigma_k^2 + \tau^2) \tag{13.2} \end{equation}\]

これらの公式は、ランダム効果（Chapter 4.1.2）や３レベルメタ分析（Chapter 10.1）モデルを議論したときに定義したものとよく似ていることに、すでに気づいただろう。実際、この定式化には特に「ベイズ的」なものはない。しかし、次の式 (Williams, Rast, and Bürkner 2018) を追加すると、この点は変わる。

\[\begin{align} (\mu, \tau^2) &\sim p(.) \notag \\ \tau^2 &> 0 \tag{13.3} \end{align}\]

最初の行が特に重要で、パラメータ \(\mu\) と \(\tau^2\) の事前分布（prior distributions）を定義している。これにより、真のプール効果量 \(\mu\) と研究間異質性 \(\tau^2\) がどのように見えるか、またそれについてどの程度確信が持てるかを a priori に指定することが可能である。2番目の式は、研究間異質性分散が0より大きくなければならないという制約を加えている。しかし、この式は、\(\mu\) と \(\tau^2\) で使用される事前分布の正確な種類 を指定していない。それは、何らかの事前分布が仮定されていることを教えてくれるだけである。ベイズメタ分析モデルのための合理的で特別な事前分布については、後で詳しく説明する。

ネットワークメタ分析の章では、ベイズアプローチがモデルパラメータを推定する方法について説明した。要約すると、マルコフ連鎖モンテカルロに基づくサンプリング手続き、例えば Gibbs サンプリングを使用することである。本章で使用する {brms} パッケージでは、いわゆる No-U-Turn サンプリング (NUTS, Hoffman and Gelman 2014) を使用する⁶⁷。

これまでの章では、主に {meta} と {metafor} パッケージを使用してきた。この二つのパッケージは、非ベイズ的、つまり頻度論的なフレームワークに基づいてメタ分析を行うことが可能である。したがって、「従来の」アプローチですでにこのような強力なツールに頼ることができるのに、なぜベイズ法を使い始めなければならないのかと疑問に思うだろう。その理由は、以下のようなベイズメタ分析には明確な利点があるからである (Williams, Rast, and Bürkner 2018; McNeish 2016; Chung et al. 2013)。

• ベイズ法は、\(\tau^2\) の推定値における不確実性を直接モデル化することが可能である。また、特に対象研究の数が少ない場合（実際には非常に多い）、効果のプール推定に優れている場合がある。

• ベイズ法は、\(\mu\) と \(\tau^2\) の両方について、完全な事後分布 (posterior distribution) を生成する。これにより、\(\mu\) または \(\tau^2\) がある指定された値より小さいまたは大きい正確な確率を計算することが可能である。これは、信頼区間だけを計算する頻度論的方法とは対照的である。しかし、（95％）信頼区間は、データサンプリングが何度も繰り返された場合、母集団のパラメータ（例えば、\(\mu\) や \(\tau^2\)）の真の値が、サンプルの95％において信頼区間の範囲に収まることを述べているに過ぎないのである。真のパラメータが2つの指定された値の間にある確率は教えてくれない。

• ベイズ法は、メタ分析を計算する際に、事前知識と仮定を統合することができる。

13.2 事前分布の設定

---

これまで、ベイズメタ分析で効果をプールするために使用できる階層モデルを定式化した。しかし、このようなモデルを実行するためには、\(\mu\) と \(\tau^2\) の事前分布を指定しなければならない。特に、研究数が少ない場合、事前分布は結果にかなりの影響を与えるので、賢く選択する必要がある。

一般的に、良いアプローチは、弱情報事前 (weakly informative prior) を使用することである (Williams, Rast, and Bürkner 2018)。弱情報事前分布は、無情報事前 (non-informative priors) 分布と対比することが可能である。無情報的事前分布は、事前分布の最も単純な形式である。これは通常、一様分布に基づいており、すべての値が等しく信頼できることを表現する時に使用される。

一方、弱情報事前分布は、もう少し洗練されたものである。これは、ある値が他の値よりも信頼できるという弱い確信を持っていることを表す分布に依存する。しかし、データから推定されるパラメータの値については、まだ具体的な記述はしていない。

直感的には、これは非常に理にかなっている。たとえば、多くのメタ分析では、真の効果がSMD = -2.0 と 2.0 の間のどこかにあると仮定することは妥当であるが、SMD = 50 になることはまずないだろう。この理論的根拠に基づいて、ここでの \(\mu\) 事前分布は、平均 0、分散 1の正規分布から出発すると良いだろう。これは、真のプールされた効果量 \(\mu\) が -2.0 と 2.0 の間にあることを、約95%の事前確率で認めることを意味する。

\[\begin{equation} \mu \sim \mathcal{N}(0,1) \tag{13.4} \end{equation}\]

次に指定しなければならない事前分布は、\(\tau^2\) の事前分布である。\(\tau^2\) は常に非負であるが、0（またはゼロに近い値）であってもよいことがわかっているので、これは少し難しい。この場合に推奨される分布で、\(\tau^2\) のような分散によく使われるものは、Half-Cauchy 事前分布である。Half-Cauchy 分布は、Cauchy 分布の特殊なケースで、分布の「半分」（もちろん、正の側）に対してのみ定義されている⁶⁸。

Half-Cauchy 分布は2つのパラメータで制御される。最初のものは、分布のピークを指定する位置パラメータ \(x_0\) である。もう1つは、スケーリングパラメータ \(s\) である。これは、分布がどの程度裾が重い (heavy-tailed) か（すなわち、どの程度高い値まで「広がる」か）を制御する。Half-Cauchy 分布は \(\mathcal{HC}(x_0,s)\) と表記される。

以下のグラフは、\(x_0\) の値を 0 に固定し、\(s\) の値を変化させた場合の Half-Cauchy 分布を可視化したものである。

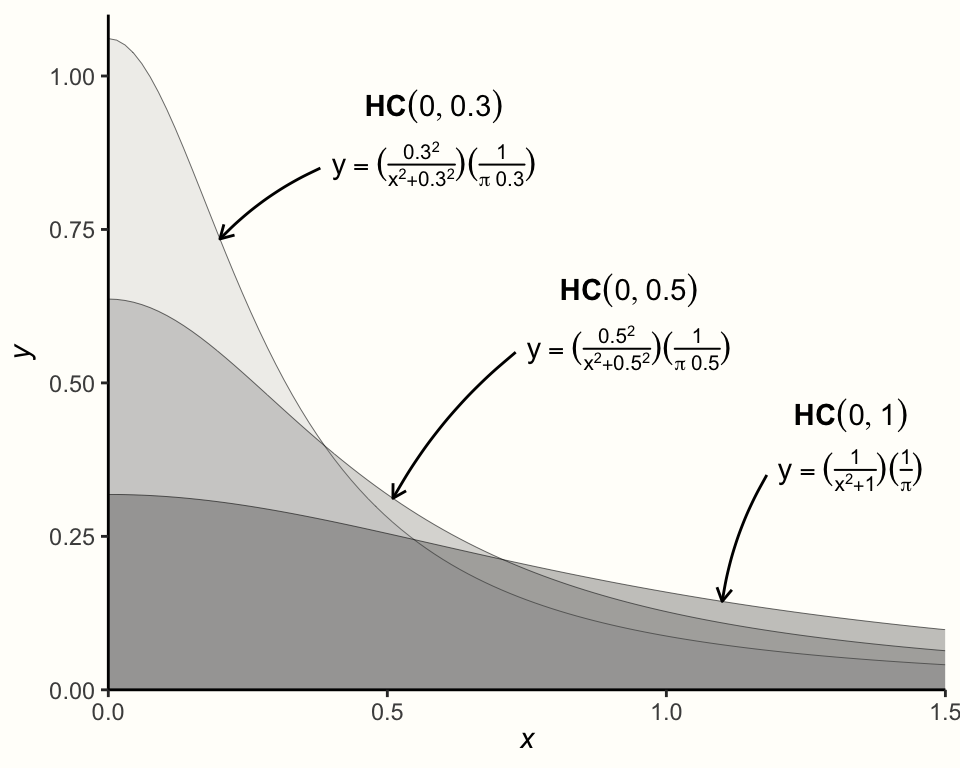
Half-Cauchy 分布は通常、かなり重い裾を持つので、\(\tau\) の事前分布として特に有用である。この重い尾は、\(\tau\) の非常に高い値を何らかの確率で与えることを保証すると同時に、低い値の方がより可能性が高いと想定している。

多くのメタ分析では、\(\tau\)（\(\tau^2\) の平方根）は 0.3 近辺にあるか、少なくとも同じような範囲にある。したがって、Half-Cauchy 事前分布を指定するために、\(s =\) 0.3 を使用することが可能である。これにより、\(\tau =\) 0.3 より小さい値は50%の確率で存在することが保証される (Williams, Rast, and Bürkner 2018)。このことは、{extraDistr} パッケージの phcauchy 関数で実装されている Half-Cauchy 分布関数を用いて確認することが可能である (Wołodźko 2020)。

library(extraDistr)
phcauchy(0.3, sigma = 0.3)

## [1] 0.5

しかし、これはすでに \(\tau\) の真の値に関するかなり具体的な仮定である。より保守的なアプローチとして、この実践例では、\(s\) を0.5に設定する。これは、分布をよりフラットにできる。一般的に、常に異なる事前分布を用いた感度分析を行い、それが結果に大きな影響を与えるかどうかを確認することを勧める。 \(s =\) 0.5 を Half-Cauchy 分布のパラメータとして使用し、\(\tau\) の事前分布を次のように書くことが可能である。

\[\begin{equation} \tau \sim \mathcal{HC}(0,0.5) \tag{13.5} \end{equation}\]

これで、階層モデルの式と事前指定をまとめることが可能である。これは、ベイズ・メタ分析に使用できる完全なモデルにつながる。

\[\begin{align} \hat\theta_k &\sim \mathcal{N}(\theta_k,\sigma_k^2) \notag \\ \theta_k &\sim \mathcal{N}(\mu,\tau^2) \notag \\ \mu &\sim \mathcal{N}(0,1) \notag \\ \tau &\sim \mathcal{HC}(0,0.5) \tag{13.5} \end{align}\]

13.3 R でのベイズメタ分析

---

メタ分析のためのベイズモデルを定義したので、いよいよ R で実装してみよう。ここでは、{brms} パッケージ (Bürkner 2017b, 2017a) を使ってモデルの適合を行う。{brms} パッケージは、ベイズ回帰モデルを適合させるための非常に多機能で強力なツールである。マルチレベル（混合効果）モデル、一般化線形モデル、多変量モデル、一般化加法モデルなど、幅広い用途に使用することが可能である。モデルの多くは人レベルのデータを必要とするが、{brms} は（重み付けされた）研究レベルデータを扱うメタ分析にも使用可能である⁶⁹。

モデルの適合を始める前に、まず {brms} パッケージをインストールし、ロードする必要がある。

library(brms)

13.3.1 モデルの適合

---

このデータセットには、大学生における「第3の波」心理療法の効果を調査したメタ分析からの情報が含まれている（Chapter 4.2.1）。モデルを適合させる前に、まず、全体の効果量 \(\mu\) と研究間の異質性 \(\tau\) の事前分布を指定しよう。前に、\(\mu \sim \mathcal{N}(0,1)\) と \(\tau \sim \mathcal{HC}(0,0.5)\) と定義した。

分布を指定するには、prior 関数を使用する。この関数は2つの引数を取る。最初の引数では、分布パラメータを含む、事前分布として想定される分布を指定する。2番目の引数では、事前分布の class を定義する必要がある。\(\mu\) の場合、母集団レベルの固定効果であるため、適切なクラスは Intercept である。\(\tau\) の場合は、分散（より正確には、標準偏差）なので、クラスは sd である。両方の prior を prior 関数で定義し、それらを連結したものを priors という名前で保存する。

priors <- c(prior(normal(0,1), class = Intercept),
            prior(cauchy(0,0.5), class = sd))

さて、次にモデルの適合を行う。これを行うには、{brms} の brm 関数を使用する。この関数には多くの引数があるが、私たちに関係するのはごく一部である。

引数 formula には、モデルの数式が指定される。{brms} パッケージは回帰式の表記法を用いており、アウトカム（ここでは観測された効果量） y が一つ以上の予測変数 x によって予測されることを表している。チルダ（ ~ ）は、y ~ x という予測関係があることを指定するために使用される。

メタ分析はやや特殊で、効果量を予測する変数を持っていない（メタ回帰を実行する場合を除く）。つまり、切片のみのモデルであることを示すために、x を 1 に置き換える必要がある。さらに、単純に各研究の効果量をそのまま y に使うことはできないので、y|se(se_y) を使う。また、精度の高い研究（すなわち、サンプルサイズ）にはより大きな重みを与える必要がある。ここで、se(se_y) の部分は、データセット中の各効果量 y の標準誤差を表している。

ランダム効果モデルを使用したい場合、最後のステップは、式の右側にランダム効果項 (1|study) を追加することである。これは、y の効果量が研究内で入れ子になっていると仮定し、その真の効果量は、真の効果量の包括的な母集団からランダムに抽出されたものであることを指定するものである。固定効果モデルを使用したい場合は、この項を省略すればよい。したがって、ランダム効果モデルの一般的な完全式は、次のようになる。y|se(se_y) ~ 1 + (1|random)。モデルの計算式の詳細については、コンソールで ?brmsformula と入力すると、ドキュメントが表示される。

他の引数はかなり単純である。prior には、モデルに定義したい prior を指定する。この例では、以前に作成した priors オブジェクトを代入することが可能である。iter 引数は、MCMC アルゴリズムの反復回数を指定する。モデルが複雑であればあるほど、この数値は大きくなるはずである。しかし、反復回数が多ければ多いほど、関数が終了するまでに時間がかかるということでもある。最後に、data を指定する。ここでは、データセットの名前を指定する。

適合したベイズメタ分析モデルを m.brm という名前で保存する。コードは以下のようになる。

m.brm <- brm(TE|se(seTE) ~ 1 + (1|Author),
             data = ThirdWave,
             prior = priors,
             iter = 4000)

ベイズ法は、以前取り上げた標準的なメタ分析手法に比べ、計算量が非常に多いことに注意。そのため、サンプリングが完了するまで数分かかる場合がある。

13.3.2 収束性とモデルの妥当性の評価

---

結果の解析を始める前に、モデルが収束すること（つまり、MCMC アルゴリズムが最適解を見つること）を確認する必要がある。もし収束しなければ、パラメータは信頼できないので、解釈すべきではない。収束しないことはベイズモデルで頻繁に起こり、反復回数（iter）を大きくしモデルを再実行することで解決することが多い。モデルの収束と全体的な妥当性を評価するために、常に2つのことを行うべきである。まず、パラメータ推定値の \(\hat{R}\)（「R ハット」と読む） 値をチェックし、次に、事後予測チェック（posterior predictive checks）を行う。

\(\hat{R}\) の値は、ベイジアンネットワークメタ分析（Chapter 12.3.3.5 ）を議論する際にすでに取り上げた Potential Scale Reduction Factor (PSRF) を表している。推定 \(\hat{R}\) 値は 1.01 より小さいはずである。これを確認するために、m.brm オブジェクトの summary を生成しよう。

summary(m.brm)

## Family: gaussian 
##   Links: mu = identity; sigma = identity 
## Formula: TE | se(seTE) ~ 1 + (1 | Author) 
##    Data: ThirdWave (Number of observations: 18) 
## Samples: 4 chains, each with iter = 4000; warmup = 2000; thin = 1;
##          total post-warmup samples = 8000
## 
## Group-Level Effects: 
## ~Author (Number of levels: 18) 
##               Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS 
## sd(Intercept)     0.29      0.10     0.11     0.51 1.00     2086   
## 
## Population-Level Effects: 
##           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS 
## Intercept     0.57      0.09     0.39     0.76 1.00     3660    
## 
##
## [...]
## 
## Samples were drawn using sampling(NUTS). For each parameter, 
## Bulk_ESS and Tail_ESS are effective sample size measures, 
## and Rhat is the potential scale reduction factor on split 
## chains (at convergence, Rhat = 1).

見ての通り、両パラメータの Rhat 値は 1 であり、収束した。つまり、結果を解釈できることを意味する。

一方、事後予測チェックでは、事後予測分布からランダムに抽出してデータをシミュレートし、観測データと比較する。モデルが収束してデータをよく捉えていれば、再現分布の密度は観測データの密度とほぼ同じになると予想される。これは、関数 pp_check の出力で簡単に確認することが可能である。

pp_check(m.brm)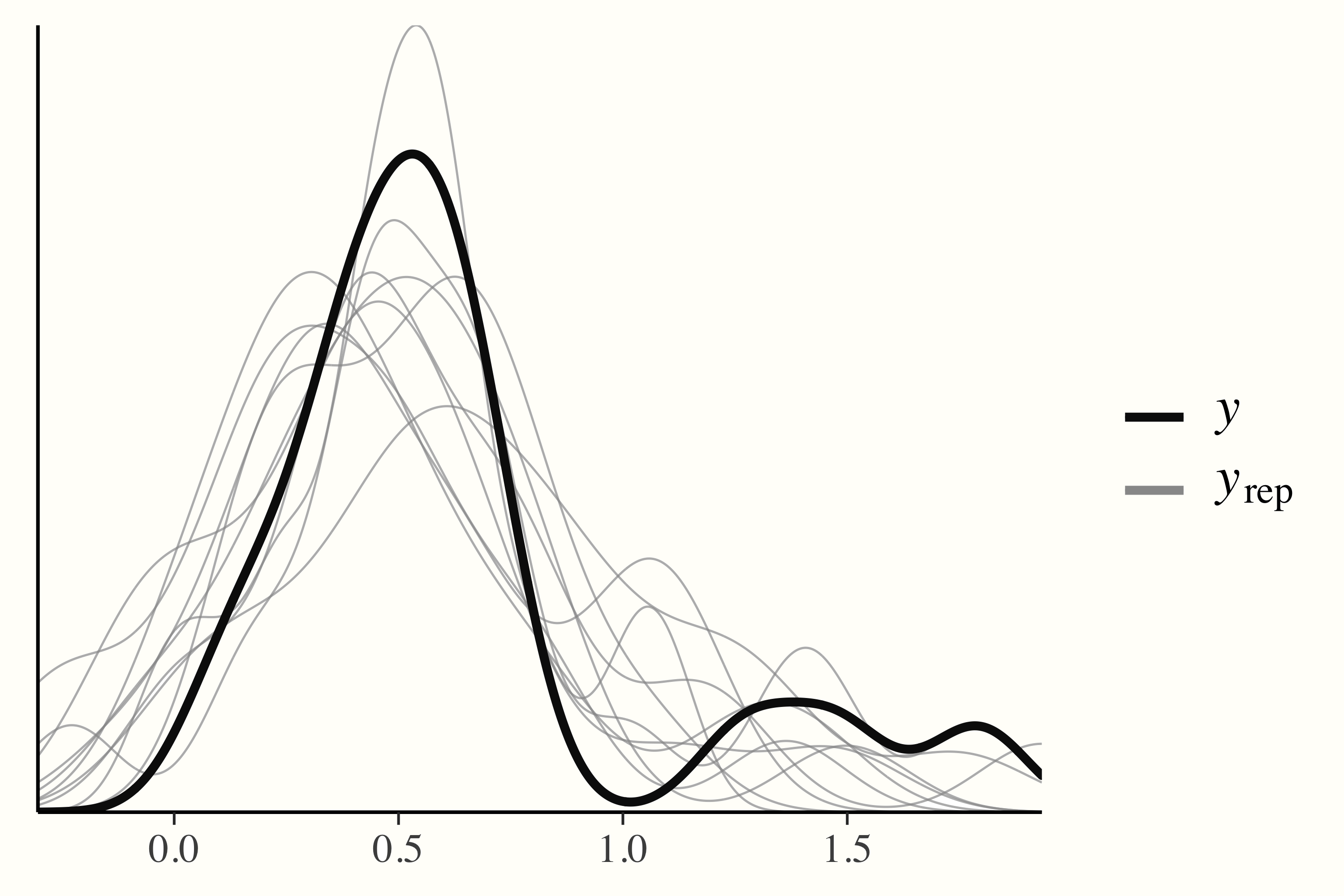

13.3.3 結果の解釈

---

まず、要約出力の Group-Level Effects を見ることによって、結果の解釈を始めていこう。このセクションは、数式で定義したランダム効果のために予約されている。ランダム効果のメタ分析モデルを適用したので、個々の研究を意味する変数 ~Author は、ランダム切片でモデル化された。前に説明したように、これはレベル２において、各研究がそれ自身の「真の」効果量を持ち、それは真の効果量の包括的な分布からサンプルされた、というの仮定を表している。また、グループレベルの効果は 18 あり、これは結果のデータ中の \(K =\) 18 件の研究に対応している。

研究間異質性の推定値 sd(Intercept) である \(\tau =\) 0.29 である、したがって、prior を設定する際の最初の「最良の推測」に近いものである。ranef 関数を使用すると、プール効果から各研究の「真の」効果量の推定偏差を抽出することも可能である。

ranef(m.brm)

## $Author
## , , Intercept
##                           Estimate Est.Error         Q2.5       Q97.5
## Call et al.             0.06836636 0.1991649 -0.327463365  0.47663987
## Cavanagh et al.        -0.14151644 0.1767123 -0.510165576  0.18799272
## DanitzOrsillo           0.48091338 0.2829719 -0.003425284  1.08636421
## de Vibe et al.         -0.31923470 0.1454819 -0.612269461 -0.03795683
## Frazier et al.         -0.11388029 0.1497128 -0.417029387  0.17085917
## [...]

次に解釈できるのは、Population-Level Effects である。このセクションは、モデル化した「固定」母集団パラメータを表す。ここでは \(\mu\) のことで、メタ分析の全体的な効果量である。

出力では、推定値は（バイアス補正された）SMD が 0.57 であり、95％信用（確信）区間は95％CrI：0.39-0.76であることがわかる。これは、このメタ分析で研究された介入は、中程度の大きさの全体的な効果を有することを示している。

これはベイズモデルなので、\(p\) -値は見当たらない。しかし、この例は、古典的な有意性検定に頼ることなく、合理的な推論を行うことができることを強調するものである。頻度論的なメタ分析になりベイズモデルの利点として、推定したいパラメータを確率的にモデル化することができる。ベイズモデルで、興味のあるパラメータを推定するだけでなく、\(\tau^2\) と \(\mu\) の事後分布全体を推定するには、posterior_samples 関数を使用するだけでよい。

post.samples <- posterior_samples(m.brm, c("^b", "^sd"))
names(post.samples)

## [1] "b_Intercept"          "sd_Author__Intercept"

この結果、データフレームには2つの列が含まれる。b_Intercept はプール効果量 \(\tau\) の事後サンプルデータ、sd_Author_Intercept は研究間異質性データである。列の名前をより分かりやすくするために、smd と tau に改名しよう。

names(post.samples) <- c("smd", "tau")

post.samples のデータを用いて、事後分布の密度プロットを作成してみよう。プロットには、{ggplot2} パッケージを使用する。

ggplot(aes(x = smd), data = post.samples) +
  geom_density(fill = "lightblue",                # 色を指定
               color = "lightblue", alpha = 0.7) +  
  geom_point(y = 0,                               # 平均に点を追加
             x = mean(post.samples$smd)) +
  labs(x = expression(italic(SMD)),
       y = element_blank()) +
  theme_minimal()

ggplot(aes(x = tau), data = post.samples) +
  geom_density(fill = "lightgreen",               # 色を指定
               color = "lightgreen", alpha = 0.7) +  
  geom_point(y = 0, 
             x = mean(post.samples$tau)) +        # 平均に点を追加
    labs(x = expression(tau),
       y = element_blank()) +
  theme_minimal()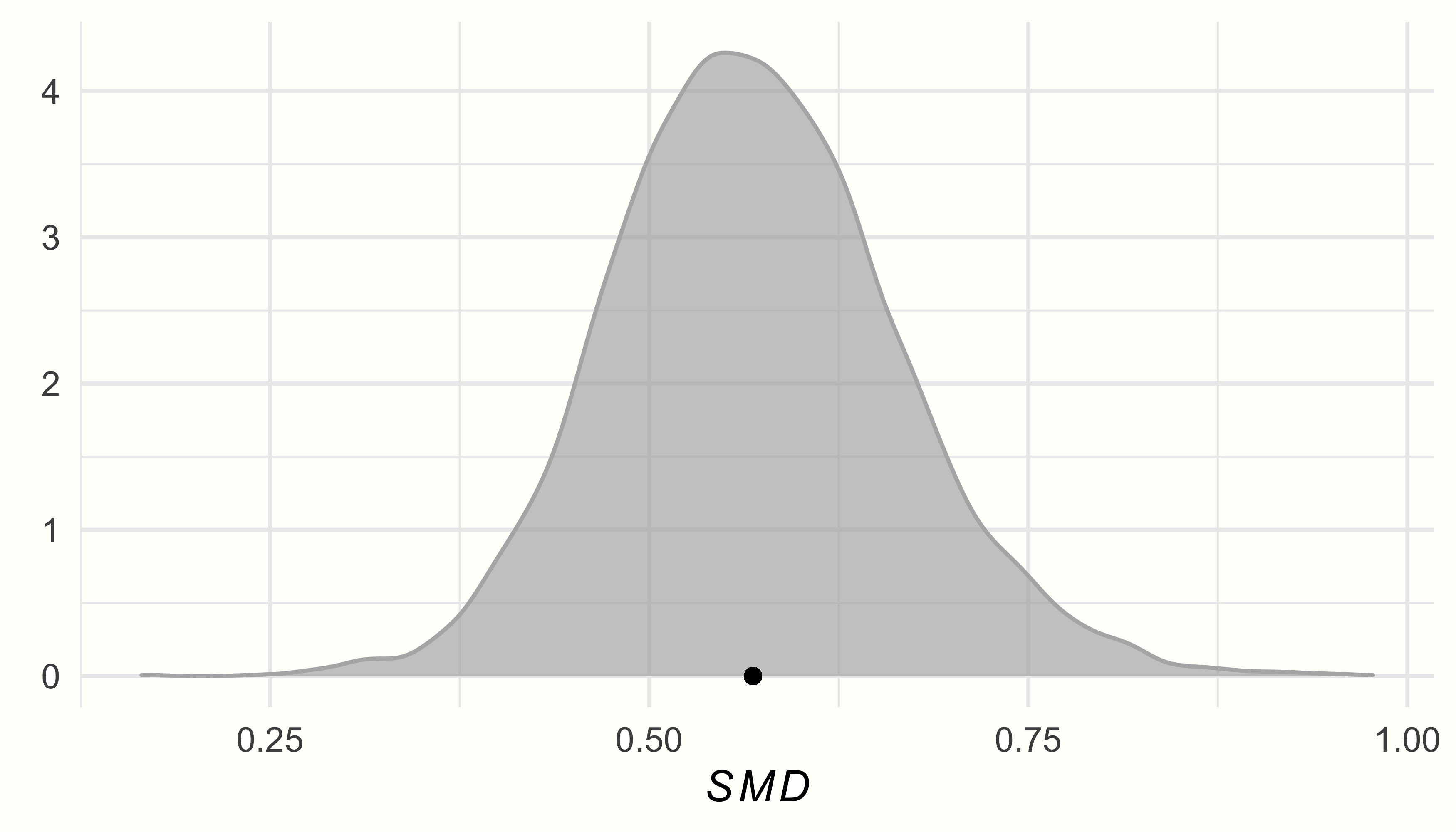

事後分布はほぼ、一峰性の正規分布に従い、\(\mu\) と \(\tau\) の推定値付近でピークを示すことがわかる。

ベイズ法は、関心のあるパラメータの実際のサンプル分布を作成するということは、\(\mu\) または \(\tau\) がある特定の値より大きいか小さいかという正確な確率を計算することができるということである。以前の文献で、介入の効果が SMD = 0.30 以下であれば、もう意味がないことがわかったとする。そこで、このメタ分析における真の全体効果が SMD = 0.30 より小さい確率を、このモデルに基づいて計算してみよう。

これは、経験的累積分布関数 (Empirical Cumulative Distribution Function, ECDF) を見ることによって行うことが可能である。ECDF は、ある特定の値 \(X\) を選択することができ、提供されたデータに基づいて、ある値 \(x\) が \(X\) より小さい確率を返す。この例での \(\mu\) の事後分布の ECDF は、以下のようになる。

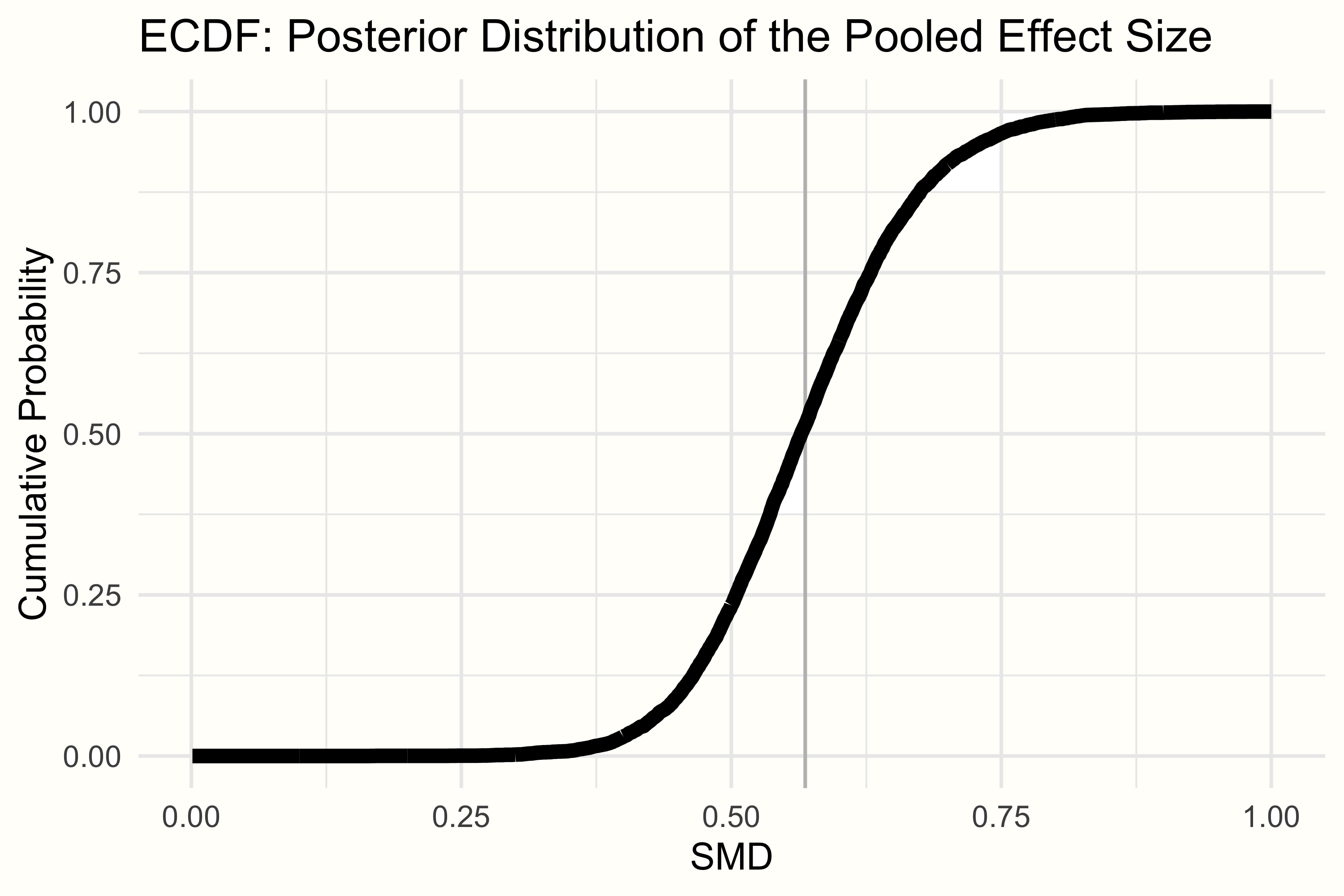
ECDF 関数を使って、 R で ECDF を定義し、プールした効果が 0.30 より小さい確率を調べることができる。コードは以下のようになる。

smd.ecdf <- ecdf(post.samples$smd)
smd.ecdf(0.3)

## [1] 0.002125

0.21% ということは、プール効果が 0.30 より小さい確率は非常に低いことがわかる。このカットオフが有効であると仮定すると、このメタ分析で見出された介入の全体的な効果は、意味のあるものである可能性が非常に高いということになる。

13.3.4 フォレストプロットの生成

---

これまで見てきたように、ベイズモデルによって、そのサンプル事後分布を抽出することが可能である。これは、モデルが与えられたときの特定の値の確率を直接評価するのに非常に役立つ。また、この機能を利用して、非常に有益で見栄えのする拡張フォレストプロット（Chapter 6）を作成することも可能である⁷⁰。

残念ながら、現在のところ、{brms} モデルから直接フォレストプロットを作成するパッケージは整備されていない。しかし、{tidybayes} パッケージ (Kay 2020) の関数を使用することにより、自分で作成することが可能である。そこで、まずパッケージを読み込んでから先に進もう。

library(tidybayes)
library(dplyr)
library(ggplot2)
library(ggridges)
library(glue)
library(stringr)
library(forcats)

プロットを作成する前に、データを準備する必要がある。特に、各研究の事後分布を個別に抽出する必要がある（フォレストプロットは各研究の特定の効果量も描写しているため）。これを実現するために、{tidybayes} パッケージの spread_draws 関数を使用することが可能である。この関数は3つの引数を入力として必要とする。適合 {brms} モデル、結果をインデックス化するランダム効果因子、そして抽出したいパラメータ（ここでは固定項：効果量を抽出したいので b_Intercept）である。

パイプ演算子を使うことで、出力を直接操作することが可能である。{dplyr} の mutate 関数を用いて、各研究の推定偏差にプール効果量 b_Intercept を加算して、各研究の実際の効果量を計算する。その結果を study.draws として保存する。

study.draws <- spread_draws(m.brm, r_Author[Author,], b_Intercept) %>% 
  mutate(b_Intercept = r_Author + b_Intercept)

次に、同様の方法でプール効果の分布を生成したい（フォレストプロットでは、効果の要約は通常最後の行に表示されるため）。そこで、先ほどのコードを少しアレンジして、プール効果だけを得るために第2引数を削除する。mutate の呼び出しは、"Author" という追加の列を追加するだけである。その結果を pooled.effect.draws という名前で保存する。

pooled.effect.draws <- spread_draws(m.brm, b_Intercept) %>% 
  mutate(Author = "Pooled Effect")

次に、study.draws と pooled.effect.draws を一つのデータフレームにバインドしている。そして、パイプを再び立ち上げ、まず ungroup を呼び出し、次に mutate を用いて、(1) 研究ラベルをきれいにし（ドットをスペースに置き換えるなど）、 (2) 研究因子レベルを効果量（高から低）で並べ替える。その結果、プロットに必要なデータができあがり、forest.data として保存する。

forest.data <- bind_rows(study.draws, 
                         pooled.effect.draws) %>% 
   ungroup() %>%
   mutate(Author = str_replace_all(Author, "[.]", " ")) %>% 
   mutate(Author = reorder(Author, b_Intercept))

最後に、フォレストプロットは各研究の効果量（SMD と信用（確信）区間）も表示する必要がある。そのために、新しく作成した forest.data データセットを使用し、Author でグループ化し、mean_qi 関数を使用してこれらの値を計算する。出力は forest.data.summary という名前で保存する。

forest.data.summary <- group_by(forest.data, Author) %>% 
  mean_qi(b_Intercept)

これで、{ggplot2} パッケージでフォレストプロットを生成する準備が整った。プロットを生成するコードは次のようなものである。

ggplot(aes(b_Intercept, 
           relevel(Author, "Pooled Effect", 
                   after = Inf)), 
       data = forest.data) +
  
  # プール効果と信頼区間に縦線を追加
  geom_vline(xintercept = fixef(m.brm)[1, 1], 
             color = "grey", size = 1) +
  geom_vline(xintercept = fixef(m.brm)[1, 3:4], 
             color = "grey", linetype = 2) +
  geom_vline(xintercept = 0, color = "black", 
             size = 1) +
  
  # 密度を追加
  geom_density_ridges(fill = "blue", 
                      rel_min_height = 0.01, 
                      col = NA, scale = 1,
                      alpha = 0.8) +
  geom_pointintervalh(data = forest.data.summary, 
                      size = 1) +
  
  # テキストとラベルを追加
  geom_text(data = mutate_if(forest.data.summary, 
                             is.numeric, round, 2),
    aes(label = glue("{b_Intercept} [{.lower}, {.upper}]"), 
        x = Inf), hjust = "inward") +
  labs(x = "Standardized Mean Difference", # 要約
       y = element_blank()) +
  theme_minimal()

観測に基づく効果量とモデルに基づく効果量

ここで一つ、非常に重要なことを述べておこう。フォレストプロットに表示されている効果量は、元の研究の観測された効果量ではなく、ベイズモデルに基づいた研究の効果量（\(\theta_k\)）の推定値である。フォレストプロットで示された点は、ranef を用いてランダム効果を抽出した際に見た研究ごとの推定値と同等である（ただし、これらの値はプールされた効果を中心にしたもの）。

さらに、効果量が非常に大きい研究（例えば、“DanitzOrsillo” や “Shapiro et al.” などの外れ値）の値を見ると、モデルベースの効果量は、最初の観測値よりも全体効果 \(\hat\mu\) に 近いことがわかる⁷¹。

この平均への縮小は、メタ分析的ランダム効果モデルのような共通の包括的分布を持つ階層的モデルに典型的なものである。推定プロセスにおいて、ベイズモデルは、メタ分析におけるすべての効果量 \(k\) によって共同推定される真の効果量の全体的分布に関する情報で、ある研究 \(k\) の効果に関する情報を「補完」する。

このような「強さの借用」は、極端な効果を持つ研究の値が平均値に向かって引っ張られることを意味する (Lunn et al. 2012, chap. 10.1)。この挙動は、比較的少ない情報を提供する研究（つまり、大きな標準誤差を持つ研究）においてより顕著になる。

\[\tag*{$\blacksquare$}\]

13.4 演習問題

知識を試そう！

1. 「従来の」ランダム効果モデルとベイズ型階層モデルの相違点と類似点は何か？

2. ベイズメタ分析の頻度論的な利点と比較した場合の利点を3つ挙げよ。

3. 弱情報的事前分布と非情報的事前分布の違いを説明しなさい。

4. Half-Cauchy 分布とは何か、なぜベイズメタ分析に有用なのか。

5. ECDF とは何か、ベイズメタ分析にどう使えるか？

問題の解答は、本書の巻末 Appendix A にある。

13.5 要約

• メタ分析は頻度論的な統計で行われることが多いが、ベイズメタ分析も可能である。

• ベイズメタ分析は、ベイズ階層モデルに基づいている。このモデルの核となる考え方は、「従来の」ランダム効果モデルと同じである。ただし、\(\mu\) と \(\tau^2\) 、（情報量が多い、情報量が少ない、または情報量が少ない）事前分布を仮定している点が異なる。

• ベイズメタ分析モデルでは、通常、弱情報事前を仮定するのがよいだろう。弱情報的事前は、ある値が他の値よりも信頼性が高いという弱い信念を表すために使用される。

• 研究間異質性分散 \(\tau^2\) の事前分布を指定するために、Half-Cauchy 分布を使用することができる。Half-Cauchy 分布は、正の値に対してのみ定義され、より重いテールを持つので、このタスクに特に適している。これは、\(\tau^2\) の非常に高い値の可能性は低いけれども、まだ非常に可能性があることを表現するために使うことが可能である。

• ベイズメタ分析モデルを当てはめる際には、（1）モデルが収束するのに十分な反復回数を含んでいるかどうかを常に確認すること（例えば、\(\hat{R}\) の値を確認するなど）、（2）異なる事前仕様を用いた感度分析を行って結果に対する影響を評価することが重要である。