8 メタ回帰

前章では、メタ分析の「ツール」に新しい手法としてサブグループ分析を追加した。前章で学んだのは、サブグループ解析では、1つの全体的な効果を見つけることから解析の焦点をずらすという点である。その代わりとして、データ中の異質性のパターンとその原因を調査することができるのである。

また、サブグループ解析はメタ分析の特殊な形態であることを述べた。「回帰」という言葉を聞いたことがあるかと思われる。回帰分析は、最も一般的な統計手法の1つで、さまざまな分野で使用されている。最も単純な形では、回帰モデルは、ある変数 $x$ の値を使って、別の変数 $y$ の値を予測しようとするものである。通常、回帰モデルは、$x$ と $y$ の両方の値が測定された個人またはサンプルからなるデータに基づいている。

メタ回帰では、このロジックは全ての研究に適用される。変数 $x$ は、研究の特徴、たとえば、実施された年などを表す。この情報に基づいて、メタ回帰モデルは、研究の効果量である $y$ を予測しようとする。しかし、予測される変数として効果量が使用されると、より複雑になる。

Chapter 3.1 ですでに、観察された効果量 $\hat\theta$ は、その標準誤差によって、研究の真の効果のおおよそ正確な推定量になりうることを学んだ。「通常の」メタ分析では、研究に大小の重みを与えることによって、これを考慮に入れている。メタ回帰では、ある研究のサンプル誤差が他より低いとき、その推定値はより「真実」に近いと仮定できるため、モデルはこれらの研究に注意を払う必要がある。

メタ回帰は、混合効果モデルを仮定することによって、これを実現する。このモデルは、観察された研究がサンプルエラーや研究間の異質性によって、真の全体効果から逸脱するという事実を説明する。しかし、より重要なのは、1 つまたは複数の変数 $x$を用いて、真の効果量の差を予測するために使用することである。サブグループ分析も混合効果モデルに基づいていることは、すでに前章で述べたとおりである。この章では、もう少し掘り下げて、なぜサブグループ分析とメタ回帰が本質的に関連しているのかを議論する。

メタ回帰は、それなりの限界はあるものの、メタ分析において非常に強力なツールとなり得る。また、非常に汎用性が高い。たとえば、多重メタ回帰は、1つだけでなく、複数の予測変数とそれらの交互作用 (interaction) を含めることができる。本章の後半では、多重メタ回帰と、 R を用いたメタ回帰の実施方法について説明する。

8.1 メタ回帰モデル

過去に、参加者を分析単位とする一次研究のデータを使って、すでに回帰を行ったことがあるだろう。メタ分析では、通常、各参加者の個別のデータは得られず、集約された結果に頼るしかない。これが、研究レベルの予測因子でメタ回帰を実行しなければならない理由である。

また、一次試験よりもはるかに大きなサンプルで分析を行っても、メタ回帰が有用となるだけのデータポイントが得られない可能性があることを意味する。 Chapter 7.2 で、$K<$ 10 件の時、サブグループ解析が意味をなさないことが多いことを取り上げた。Borenstein ら (2011, chap. 20) は、このガイドラインはメタ回帰モデルにも適用できるかもしれないが、鉄則と見なすべきではないと言及している。

従来の回帰では、人物 $i$ の値 $y_i$ を、予測因子（または共変量） $x_i$ と回帰係数 $\beta$ を使って推定したい。したがって、標準的な回帰式は次のようになる。

\[\begin{equation} \hat{y_i} = \beta_0 + \beta_1x_i \tag{8.1} \end{equation}\]

メタ回帰では、予測したい変数 $y$ は、研究 $k$ の観察された効果量 $\hat\theta_k$（シータハットと読む）である。メタ回帰の式は、正規回帰モデルの式に似ている。

\[\begin{equation} \hat\theta_k = \theta + \beta x_{k} + \epsilon_k+\zeta_k \tag{8.2} \end{equation}\]

この式は、2つの追加項、$\epsilon_k$（イプシロン k と読む）と $\zeta_k$（ゼータ k と読む）を含んでいることに注意されたい。同じ項がランダム効果モデルの式（Chapter 4.1.2 ）にもあり、2 種類の独立した誤差を意味する。1 つ目の $\epsilon_k$ は、研究の効果量が真の効果から逸脱するサンプル誤差である。

2 つ目の誤差、$\zeta_k$ は、研究の真の効果量でさえ、効果量の包括的な分布からサンプルされているに過ぎないことを表している。これは、私たちのデータには研究間の異質性が存在することを意味し、これは異質性分散 $\tau^2$ によって捕捉される。

上記の式は、固定効果（$\beta$ 係数）とランダム効果（$\zeta_k$）を含むので、メタ回帰で使用されるモデルは、混合効果モデルと呼ばれることも多い。概念的には、このモデルは Chapter 7.1.2 で説明した混合効果モデルと同じで、サブグループ解析がどのように機能するかを説明したものである。

8.1.1 カテゴリカル予測変数のメタ回帰

実際、前述のように、サブグループ分析は、カテゴリカル予測変数のメタ回帰にほかならない。そのようなカテゴリカル変数は、たとえば、ダミー・コーディング によって含めることができる。

\[\begin{equation} D_g=\begin{cases} 0: & \text{Subgroup A}\\ 1: & \text{Subgroup B.} \end{cases} \tag{8.3} \end{equation}\]

サブグループ分析をメタ回帰の形で指定するには、共変量 $x_k$ を $D_g$ に置き換えるだけでよい。

\[\begin{equation} \hat\theta_k = \theta + \beta D_g +\epsilon_k+\zeta_k. \tag{8.4} \end{equation}\]

この式を理解するためには、左から右へ読む必要がある。メタ回帰モデルの目的は、他の統計モデルと同様、観測されたデータがどのように生成されたかを説明することである。私たちの場合、これはメタ分析におけるいくつかの研究（$k$）の観察された効果量 $\hat\theta_k$ である。上の式はレシピのように機能し、観察された効果を生み出すためにどの材料が必要かを教えてくれる。

まず、$\theta$ は回帰モデルにおける切片として機能する。$\theta$ の値は、サブグループAの真の全体効果量と同じである。この理由を見るために、次の「成分」である項 $\beta D_g$ を見る必要がある。この項の $\beta$ の値は、サブグループ A とサブグループ B の間の効果量の差 $\theta_{\Delta}$ を表している。$\beta$ の値に、研究がサブグループ A ($D_g = 0$) またはサブグループ B ($D_g = 1$) のどちらに属しているかによって 0 または 1 のどちらかになる $D_g$ を掛けている。

ゼロを掛けるとゼロになるので、サブグループAの研究を扱っているときは、$\beta D_g$ の項は方程式から完全に外れる。一方、$D_g=1$ のとき、1を掛けるので $\beta$ が方程式に残り、$\theta$ に足され、サブグループ B の全体的な効果量が得られる。基本的に、ダミー予測変数は二つの式をひとつに統合する方法である。これは、各サブグループの式を個別に書き出すと、簡単にわかる。

\[\begin{equation} D_g=\begin{cases} 0: & \text{$\hat\theta_k = \theta_A + \epsilon_k+\zeta_k$}\\ 1: & \text{$\hat\theta_k = \theta_A + \theta_{\Delta} +\epsilon_k+\zeta_k$} \end{cases} \tag{8.5} \end{equation}\]

このように書くと、この式は、実際には、サブグループ A とサブグループ B の2つのモデルを含んでいることが明らかになる。モデル間の主な違いは、$\beta$ （上の式では $\theta_{\Delta}$ と表記）の値によって、第2サブグループの効果が上下に「シフト」されることである。

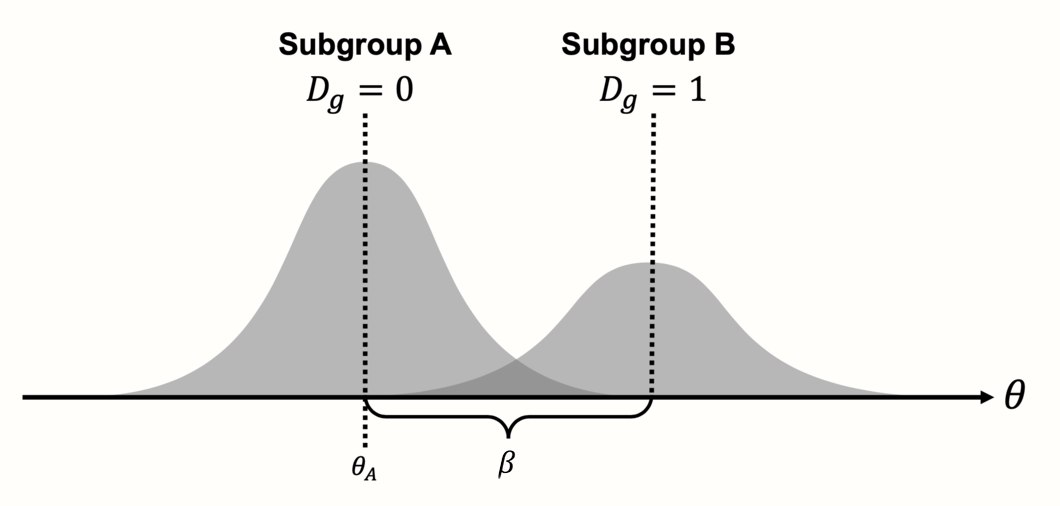
Figure 8.1: カテゴリ予測因子を用いたメタ回帰（サブグループ）。

これは、サブグループ分析が通常の回帰と同じように動作することを明確にするもので、ある変数 $x$ を使って $y$ の値を予測する。特別なのは、$\beta x_k$ が連続的ではなく、ある研究が特定のサブグループに属するかどうかに応じて、予測に追加する固定値であるということである。この固定値 $\beta$ は、2つのサブグループ間の効果量の差の推定値である。

8.1.2 連続予測因子によるメタ回帰

しかし、「メタ回帰」というと、普通は連続変数を予測変数としたモデルを思い浮かべる。そこで、8.2式に示す一般的なメタ回帰の式に戻る。ここでも、前に説明した回帰の用語が使われているが、少し違う目的を持っている。$\theta$ 項は再び切片を表すが、今度は $x = 0$ のときに予測される効果量を表す。

切片に、$\beta x_k$ 項が加えられる。この部分は、回帰傾きを生成する。つまり、連続変数 $x$ と回帰重み $\beta$ が掛け算され、共変量値の予測効果を低くしたり高くしたりする。

メタ回帰モデルの目的は、研究の予測効果量と真の効果量の差を最小化する $\theta$ と $\beta$ の値を見つけることである（ Figure 8.2 を参照）。

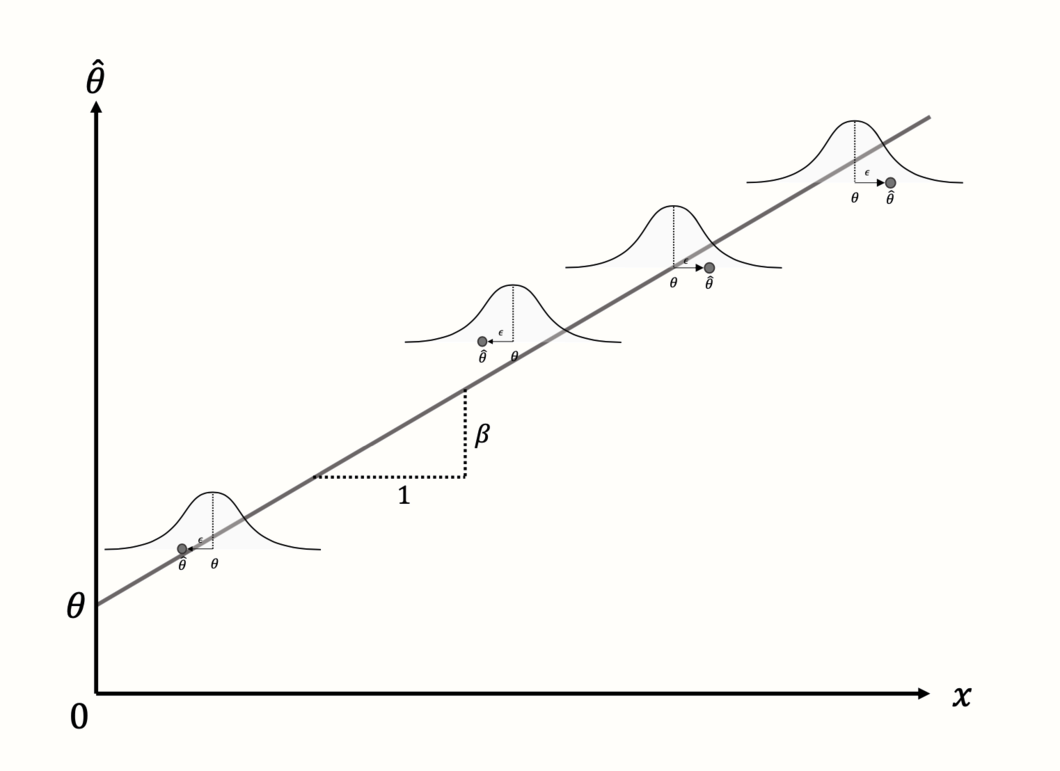
Figure 8.2: 連続変数予測因子と４つの研究のメタ回帰

メタ回帰式をよく見てみると、2種類の項が含まれていることがわかる。いくつかの項には添え字（$k$）があり、他の項には添え字がない。添え字（$k$）は、ある値が研究ごとに異なることを示す。ある項が添え字（$k$）を含んでいない場合、それはすべての研究で同じである。

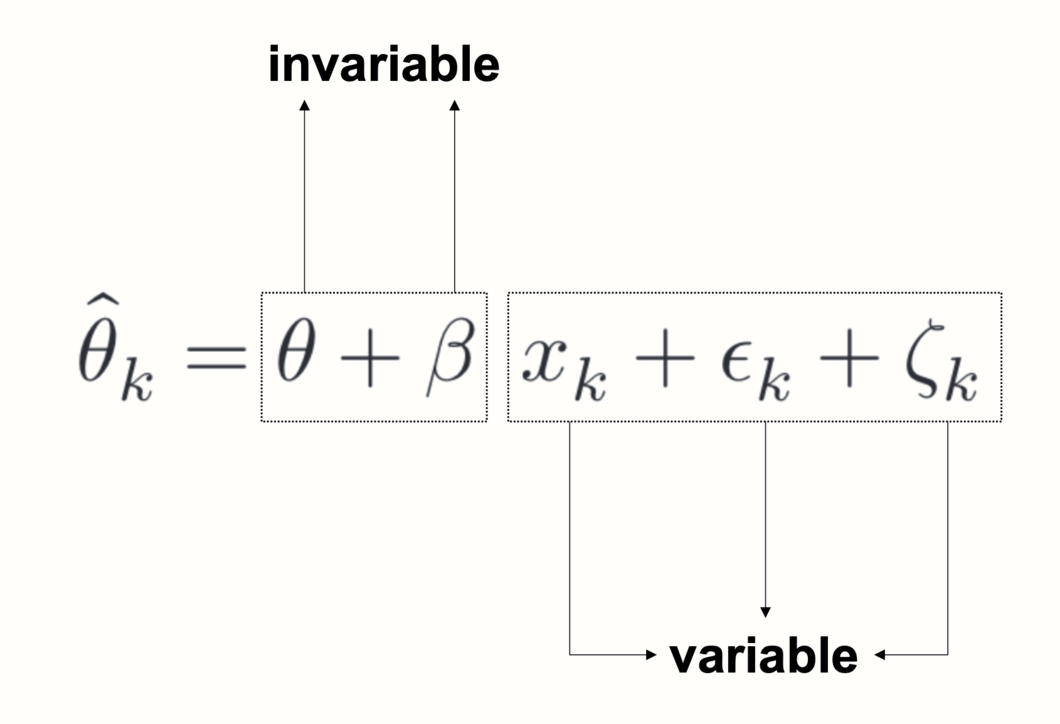
メタ回帰では、$\theta$ と $\beta$ の両方が不変、または固定である。予測変数の変動と観察された効果に基づいて、回帰線の形で、データの根底にある固定パターンを「抽出」しようとするのである。メタ回帰モデルがデータによく当てはまる場合、推定されたパラメータ $\theta$ と $\beta$ は、モデルが今まで見たことのない研究の効果量を予測するのに使うことができる（$x$ がわかっていればの話であるが）。

$\epsilon_k$ と研究間異質性 $\zeta_k$ の両方を考慮すると、メタ回帰は、観察された効果量だけでなく、関心のあるすべての研究の「宇宙」に対して、うまく一般化するモデルを見つけようとするものである。

8.1.3 モデルの適合性を評価

メタ回帰モデルの重要な点は、効果量のプールに使用する「通常の」ランダム効果モデルの拡張とみなすことができる点である。ランダム効果モデルは、傾き項を含まないメタ回帰モデルに過ぎない。傾きがないので、ランダム効果モデルは、各研究について単純に同じ値を予測する。つまり、プールされた効果量の推定値 $\mu$ であり、これは切片と同じである。

最初のステップでは、メタ回帰の計算は、したがってランダム効果メタ分析のものとよく似ており、研究間異質性 $\tau^2$ が Chapter 4.1.2.1 で説明した方法（例えば、DerSimonian-Laird 法または REML 法）のいずれかを使って推定される。次のステップでは、固定重み $\theta$ と $\beta$ が推定される。通常の線形回帰モデルは、通常の最小2乗 (ordinary least squares, OLS) 法を用いて、データに最もよく適合する回帰直線を見つける。メタ回帰では、重み付き最小2乗 (weighted least squares, WLS)と呼ばれる修正された方法が使用され、より小さな標準誤差を持つ研究がより高い重みを与えられるようにする。

最適解が見つかったら、新しく追加された回帰項が効果量の異質性の一部を説明しているかどうかを確認することができる。メタ回帰モデルがデータによく適合している場合、真の効果量は、プール効果量 $\hat\mu$ と比較して回帰直線からの偏差が小さくなる。この場合、予測因子 $x$ は、メタ分析における異質性分散の一部を説明する。

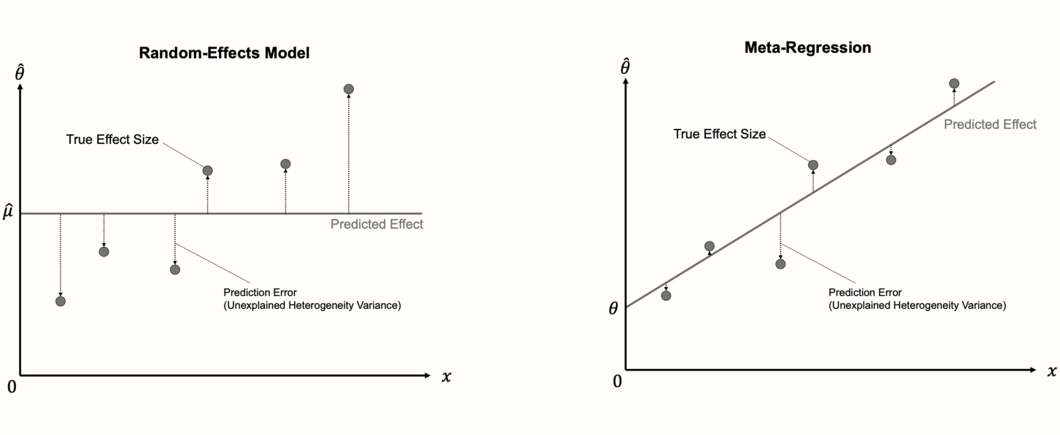
したがって、メタ回帰モデルの適合性は、それが異質性分散のどれだけを説明するかをチェックすることによって評価することができる。混合効果モデルに含まれる予測変数は、残差 (residual)、または説明されない異質性分散の量を最小化する必要があり、これは、$\tau^2_{\text{unexplained}}$ で示される。

回帰分析では、モデルによって説明される変動の割合を定量化するために、$R^2$ 指数が一般的に使用される。類似の指数である $R^2_{*}$ もメタ回帰で計算することができる。ここでは、観測されたデータ点ではなく、真の効果量 を扱うので、メタ回帰の $R^2$ は、従来の回帰で使われるものと若干異なることを示すために、アスタリスク（$*$）を追加している。 $R^2_*$ の式は次のようになる。

\[\begin{equation} R^2_* = 1- \frac{\hat\tau^2_{\text{unexplained}}}{\hat\tau^2_{\text{(total)}}} \tag{8.6} \end{equation}\]

$R^2_*$ は、メタ回帰の傾きでさえ説明できない異質性分散の残差量を使用し、それをメタ分析で最初に発見した異質性の合計で割る。この割合を1から引くと、予測変数によって説明される研究間の異質性のパーセンテージが得られる。

また、$R^2_*$ を定式化する別の方法がある。それは、混合効果モデルが、最初のランダム効果プーリングモデルと比較して、異質性の分散をどれだけ低減させるかをパーセントで表すと言うことができる。この結果、次のような式になる。

\[\begin{equation} R^2_* = \frac{\hat\tau^2_{\text{REM}}-\hat\tau^2_{\text{MEM}}}{\hat\tau^2_{\text{REM}}} \tag{8.7} \end{equation}\]

この式で、$\hat\tau^2_{\text{REM}}$ はランダム効果プーリングモデルで見つかった研究間異質性の量を表し、$\hat\tau^2_{\text{MEM}}$ は混合効果メタ回帰モデルの（残）分散（すなわち、真の効果量に関する「予測誤差」）を表す。

通常、私たちは回帰モデルで説明される異質性の量に興味があるだけでなく、私たちの予測因子 $x$ の回帰重量が有意であるかどうかにも興味がある。もしそうであれば、$x$ が研究の効果量に影響を及ぼしていると確信できる。従来の回帰でもメタ回帰でも、回帰重みの有意性は、一般的に Wald-type 検定で評価される。これは、$\beta$ の推定値をその標準誤差で割ることによって、検定統計量 $z$ を計算することを含む。

\[\begin{equation} z = \frac{\hat\beta}{SE_{\hat\beta}} \tag{8.8} \end{equation}\]

$\beta = 0$ という帰無仮説のもとでは、この $z$ -統計量は、標準正規分布に従う。これは、対応する $p$ -値を計算することができ、予測変数が有意であるかどうかを決定するものである。

しかし、$z$-統計量に基づく検定は、予測変数の有意性を評価する唯一の方法ではない。通常のメタ分析モデルのように、$t$-分布に基づく検定統計量になる Knapp-Hartung 調整も使用できる（ Chapter 4.1.2.2 を参照）。以前学んだように、Knapp-Hartung 法は、偽陽性のリスクを減らすので、使用することが推奨される。

8.2 R のメタ回帰について

{meta} パッケージには、メタ回帰を行うための関数 metareg が含まれている。この metareg 関数は、入力として {meta} メタ分析オブジェクトと共変量名のみを必要とする。

この例では、再び ThirdWave データセット（ Chapter 4.2.1 参照）に基づいた m.gen メタ分析オブジェクトを使用する。メタ回帰を用いて、研究の出版年がその効果量を予測するのに使えるかどうかを調べたいと思われる。デフォルトでは、ThirdWave データセットには出版年を格納する変数がないので、この情報を格納する新しい numeric 変数を作成する必要がある。そのため、この情報を含む新しい numeric 変数を作成する必要がある。ここでは、すべての研究の出版年を ThirdWave データセットに現れるのと同じ順序で単純に連結している。この変数を year³¹ という名前で保存する。

year <- c(2014, 1998, 2010, 1999, 2005, 2014, 
          2019, 2010, 1982, 2020, 1978, 2001,
          2018, 2002, 2009, 2011, 2011, 2013)

これで、メタ回帰を実行するために必要な情報はすべて揃った。metareg 関数では、最初の引数にメタ分析オブジェクトの名前 m.gen を指定し、2番目の引数に予測変数の名前 year を指定する。結果は m.gen.reg という名前になる。

m.gen.reg <- metareg(m.gen, ~year)

では、その結果を見てみよう。

m.gen.reg

## Mixed-Effects Model (k = 18; tau^2 estimator: REML)
## 
## tau^2 (estimated amount of residual heterogeneity):     0.019 (SE = 0.023)
## tau (square root of estimated tau^2 value):             0.1371
## I^2 (residual heterogeneity / unaccounted variability): 29.26%
## H^2 (unaccounted variability / sampling variability):   1.41
## R^2 (amount of heterogeneity accounted for):            77.08%
## 
## Test for Residual Heterogeneity:
## QE(df = 16) = 27.8273, p-val = 0.0332
## 
## Test of Moderators (coefficient 2):
## F(df1 = 1, df2 = 16) = 9.3755, p-val = 0.0075
## 
## Model Results:
## 
##         estimate     se   tval   pval    ci.lb    ci.ub 
## intrcpt   -36.15  11.98  -3.01  0.008  -61.551  -10.758  ** 
## year        0.01   0.00   3.06  0.007    0.005    0.031  ** 
## 
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

ここでわかることを見ていこう。最初の行では、意図したとおりに混合効果モデルがデータに適合されたことが出力されている。次の数行は、モデルによって説明される異質性の量に関する詳細である。残差異質性分散（予測変数によって説明されない分散）の推定値が、$\hat\tau^2_{\text{unexplained}}=$ 0.019である。

出力には、$I^2$ もある。これは、予測変数の包含後、データの変動の29.26%が残りの研究間異質性に帰着することができることを教えてくれる。通常のランダム効果メタ分析モデルでは、$I^2$ 異質性が 63% であることがわかっていた。これは、予測変数が真の効果量における差のかなりの量を「説明する」ことができたということになる。

最後の行では、$R^2_*$ の値が表示され、この例では 77% となっている。これは、真の効果量の差の77%が出版年によって説明できることを意味し、非常に大きな値である。

次のセクションは、Test for Residual Heterogeneity を含み、本質的には、すでに以前知った $Q$-検定である（ Chapter 5.1.1 を参照）。ここでは、予測変数で説明されない異質性が有意であるかどうかを検定する。$p$ = 0.03 であることから有意である。しかし、私たちは $Q$-検定（Chapter 5.1.1）の限界を知っているので、この結果にはあまり依存しない方がよいだろう。

次の部分は、Test of Moderators を示している。この検定も有意であることがわかる ($p$ = 0.0075)。これは、私たちの予測因子である出版年が、実際に研究の効果量に影響を与えることを意味する。

最後のセクションでは、推定された回帰係数の詳細を説明する。最初の行は、切片（intrcpt）の結果を示している。これは、予測因子である出版年がゼロの場合に期待される効果量（私たちの場合：Hedges’ $g$）である。この例では、少し不自然なシナリオを表している。これは、0年に実施された研究の予測効果を示しており、$\hat{g}=$ -36.15となっている。優れた統計モデルは現実を完璧に表現している必要はなく、ただ有用であればよいということを改めて思い起こさせるものとなっている。

私たちが主に注目するのは2行目の係数である。このモデルの year の回帰重みの推定値が0.01であることがわかる。これは、1年増えるごとに、研究の効果量 $g$ が0.01ずつ増加することを意味する。したがって、研究の効果量は時間とともに増加していると言えるだろう。95%信頼区間の範囲は 0.005 から 0.3 であり、効果は有意であることがわかる。

重要なのは、各回帰係数( tval )に対応する $t$-統計量も提示されていることである。これは、信頼区間と $p$ -値を計算するために、Knapp-Hartung 法が使用されたことを示す。最初のメタ分析モデルでもこの調整法を使用したので、 metareg はここでも自動的にこの調整法を使用してきた。そうでなければ、$z$ 値と Wald 型信頼区間が提供されるはずであった。

{meta} パッケージでは、 bubble 関数を用いてメタ回帰を可視化することができる。これは、推定回帰勾配と各研究の効果量を示すバブルプロット (bubble plot) を作成する。研究の重みを示すために、バブルは異なる大きさを持ち、大きければ大きいほど重みがあることを表す。

バブルプロットを作成するためには、メタ回帰オブジェクトを bubble 関数に接続するだけである。研究ラベルも表示させたいので、studlab を TRUE に設定する。

bubble(m.gen.reg, studlab = TRUE)

完全性を期すために、前章のサブグループ分析（Chapter 7.3）を、今度はメタ回帰の枠組みで繰り返してみることもできる。これは、カテゴリ予測因子としてバイアスのリスク・アセスメントを使用することを意味する。変数 RiskOfBias はすでに ThirdWave のデータセットに含まれているので、この情報を追加オブジェクトに保存する必要はない。単純に metareg 関数を再度実行すれば良いのであるが、今回は関数の2番目の引数として RiskOfBias を使用する。

metareg(m.gen, RiskOfBias)

## [...]
## R^2 (amount of heterogeneity accounted for):            15.66%
## 
## Test for Residual Heterogeneity:
## QE(df = 16) = 39.3084, p-val = 0.0010
## 
## Test of Moderators (coefficient 2):
## F(df1 = 1, df2 = 16) = 2.5066, p-val = 0.1329
## 
## Model Results:
## 
##               estimate    se   tval    pval  ci.lb ci.ub 
## intrcpt           0.76  0.15   5.00  0.0001   0.44  1.09  *** 
## RiskOfBiaslow    -0.29  0.18  -1.58  0.1329  -0.69  0.10      
## [...]

出力では、$R^2_*$ の値が15.66%で、year の値よりかなり小さいことがわかる。以前の結果と一致して、バイアス・リスク変数が有意な効果量予測因子でないことがわかる ($p$ = 0.13)。

モデル結果の下で、metareg が自動的に RiskOfBias をダミー変数に変換していることがわかる。サブグループ “high risk” のプール効果を表す切片の推定値は、$g$ = 0.76 である。バイアスのリスクが低い研究を表す回帰係数の推定値は -0.29 である。

このサブグループの効果量を得るには、切片に回帰重みを加える必要があり、その結果、$g=$ 0.76 - 0.29 $\approx$ 0.47 となる。これらの結果は、$\tau^2$ の共通の推定値を仮定したサブグループ分析の結果と同じである。

8.3 多重メタ回帰

前回は、メタ回帰モデルで一つのの予測因子 $\beta x_k$ を使用するシナリオのみを検討してきた。この例では、研究の効果量が出版された年に依存するかどうかを調べる。しかし今度は、報告された効果量が、研究が掲載された科学雑誌の名声にも依存していると仮定しよう。高い評価を得ている雑誌に掲載された研究が、より高い効果を報告している可能性があると考えている。なぜなら、一流の雑誌では、選ばれた研究は「画期的」な発見をしていることがほとんどだからである。

一方、評判の良い雑誌は一般的に質の高い研究を掲載しているというのももっともな話である。もしかしたら、より高い効果量と関連するのは、より良い研究の質だけだろう。そこで、ジャーナルの評判が本当に高い効果と関連しているかどうかを確認するために、この関係が、一流のジャーナルが高品質のエビデンスを出版する可能性が高いという事実によって交絡していないことを確認する必要がある。つまり、ジャーナルの名声と効果量の関係を調査する際には、研究の質をコントロールする必要がある。

これや他の多くの研究課題は、多重メタ回帰を使用して対処することができる。多重メタ回帰では、効果の変動を説明するために、1つだけでなく複数の予測変数を使用する。複数の予測変数を使用できるようにするには、前のメタ回帰式（式8.2参照）を修正して、次のようにする必要がある。

\[\begin{equation} \hat \theta_k = \theta + \beta_1x_{1k} + ... + \beta_nx_{nk} + \epsilon_k + \zeta_k \tag{8.9} \end{equation}\]

この式は、メタ回帰モデルに $n-1$ より多くの予測変数 $x$ を追加して、多重メタ回帰に変えることができることを示す。この式の3つの点は、理論的には、望むだけの予測変数を追加できることを象徴している。しかし、現実にはもっとやっかいなことが多い。以下では、多重メタ回帰のいくつかの重要な落とし穴と、どのようにすれば頑健で信頼できるモデルを構築できるかを説明する。その前に、多重メタ回帰のもう一つの重要な特徴である交互作用 (interaction) について説明する。

8.3.1 交互作用

ここまでは、モデル内に複数の予測変数 $x_1, x_2, \dots x_n$ があり、それらの回帰重み $\beta$ と共に加算される場合のみを考えていた。しかし、多重メタ回帰モデルは、このような加算関係に限定されるわけではない。また、予測変数の交互作用 もモデル化することができる。交互作用とは、ある予測変数（例： $x_1$ ）と推定効果量との間の関係が、別の共変量（例： $x_2$ ）の異なる値で変化することを意味する。

2つの予測因子とそれらが効果量とどのように関連するかをモデル化したいとする：出版年 ($x_1$) と研究の質 ($x_2$) である。研究の質は次のようにコード化される。

\[\begin{equation} x_2=\begin{cases} 0: & \text{low}\\ 1: & \text{moderate}\\ 2: & \text{high} \end{cases} \tag{8.10} \end{equation}\]

出版年と研究の質の間に交互作用がないと仮定した場合、$x_1$ と $x_2$ の両方に回帰の重み $\beta$ を与え、数式でその項を一緒に追加することによって、メタ回帰モデルを構築することができる。

\[\begin{equation} \hat \theta_k = \theta + \beta_1x_{1k} + \beta_2x_{2k} + \epsilon_k + \zeta_k \tag{8.11} \end{equation}\]

しかし、$x_1$ と $x_2$ の関係がもっと複雑だとしたらどうだろうか。先ほどの例のように、より新しい出版年がより高い効果と正に関連している可能性がある。しかし、すべての研究がこのような傾向を示すとは限らない。もしかしたら、質の高い研究で顕著に増加し、質の低い研究の結果は時間の経過とともにほとんど変わらなくなるだろう。効果量 ($\hat\theta_k$)、出版年 ($x_1$)、研究の質 ($x_2$)の間のこの想定された関係は、次のように可視化することができる。

このグラフは、交互作用の典型的な例を示している。回帰の傾きの急さは、別の予測変数の値に依存することがわかる。質の高い研究では、回帰線の傾きが非常に急で、発表年と効果の間に強い関係があることを示しているが、低質な研究では状況が異なる。このサブグループの回帰直線はほとんど水平で、出版年は結果に全く、あるいはわずかにマイナスの影響を与えることを示している。

この例は、交互作用の強みの1つである、予測因子の影響がすべての研究で同じかどうか、あるいは他の特性によって緩和されているかどうかを調べることができることを示している。

メタ回帰で交互作用を評価するためには、モデルに交互作用項 を追加する必要がある。私たちの例では、これは私たちのモデルでテストしたい交互作用 $x_{1k}x_{2k}$ を捕捉する3番目の回帰重み $\beta_3$ を追加することで達成できる。これは、次の数式を与える。

\[\begin{equation} \hat \theta_k = \theta + \beta_1x_{1k} + \beta_2x_{2k} + \beta_3x_{1k}x_{2k}+ \epsilon_k + \zeta_k \tag{8.12} \end{equation}\]

線形多重メタ回帰モデルは、このような単純な構成要素で構成されているだけであるが、様々な用途に使用することができる。しかし、 R を用いた多重メタ回帰のフィッティングを始める前に、まずその限界と落とし穴について考えておく必要がある。

8.3.2 多重メタ回帰にありがちな落とし穴

多重メタ回帰は、適切に適用されれば非常に有用であるが、ある種の注意点がある。実際には（多重）メタ回帰は不適切な使い方や解釈が多く、結果の妥当性が低いという意見もある (JPT Higgins and Thompson 2004)。多重メタ回帰モデルを当てはめる際に注意しなければならない点がいくつかあるので、以下に説明する。

8.3.2.1 過適合: シグナルのないところにシグナルを見いだす

メタ回帰モデル（複数）のリスクをより良く理解するためには、過適合 (overfitting) という概念を理解する必要がある。過適合とは、データにあまりにも近く適合するような統計モデルを構築した場合に起こる。簡単に説明すると、手元のデータはうまく予測できるが、将来のデータはうまく予測できない統計モデルを構築してしまうということである。

これは、モデルが、データの変動が真の「シグナル」に由来すると仮定したときに起こるもので、実際にはランダムなノイズしか捉えていない (Iniesta, Stahl, and McGuffin 2016)。その結果、モデルは偽陽性の結果を生成する。つまり、何もないところに関係性を見出すのである。

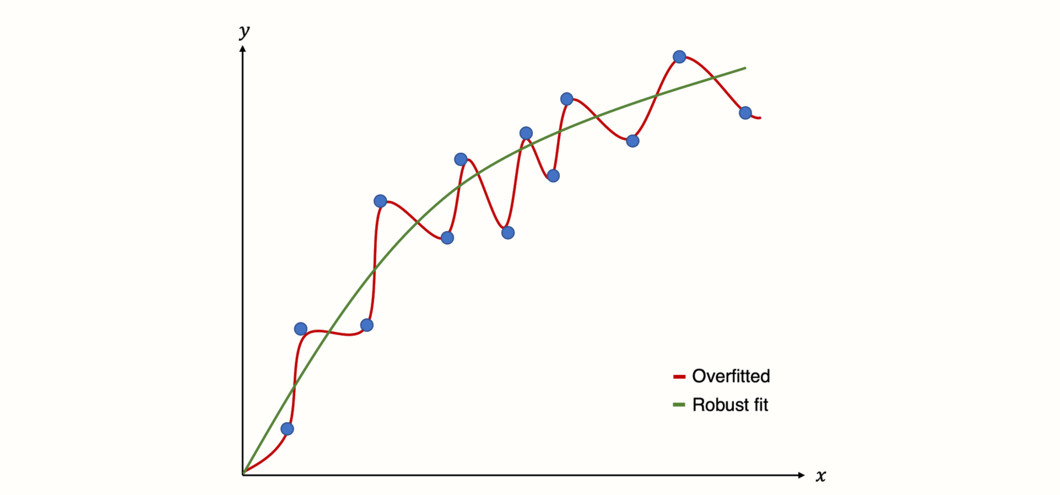
Figure 8.3: 過適合モデルと頑健適合モデルの予測。

モデル適合のために、回帰は通常の最小二乗法や最尤推定などの最適化技術を利用する。すでに学んだように、メタ回帰は普通の最小二乗法の重み付きバージョンを使用するので（Chapter 8.1.3 参照）、これも例外ではない。

「貪欲に」最適化すると、回帰アプローチは過適合に陥りやすい (Gigerenzer 2004)。残念ながら、従来の回帰手法からメタ回帰に移行すると、頑健でないモデルを構築するリスクはさらに高くなる。これにはいくつかの理由がある (JPT Higgins and Thompson 2004)。

メタ回帰では、含まれる研究の集約された情報しか使えないので、通常、データポイントの数は少ない。
メタ分析は、すべての利用可能なエビデンスを包括的に概観することを目的としているので、回帰モデルが未知のデータをどれだけ予測できるかを「テスト」できるような追加データが存在しない。
メタ回帰では、効果量の異質性が存在する可能性に対処しなければならない。２つの研究があり、両者の効果量が異なり、信頼区間が重なっていないケースを想像してみよう。２つの研究で異なる値を持つすべての変数が、効果量の差の説明となり得る。しかし、これらの説明のほとんどが偽の説明であることは明らかだろう。
一般的なメタ回帰、特に多重メタ回帰は、予測変数の「遊び」を非常に簡単にする。データの異質性を説明するために、多数のメタ回帰モデルをテストして、より多くの予測変数を含めたり削除したりすることができる。このアプローチは魅力的で、実際によく見られる。メタ分析では、効果量が異なる理由の説明を見つけたいからである (J. Higgins et al. 2002)。有意なモデルを見つけるまで無限にモデルの一部を変更することができるが、そのモデルは過適合である（つまり、ほとんど統計的ノイズをモデル化している）可能性が非常に高い。

メタ回帰モデルを構築する際に、過度の偽陽性を避けるためのガイドラインがいくつか提案されている。

調査すべき予測変数の数を最小にする。多重メタ回帰では、これは倹約 (parsimony) の概念に変換される。つまり、メタ回帰モデルの適合を評価するとき、少ない予測変数で良い適合を達成するモデルを好む。赤池情報量規準やベイズ情報量規準のような推定量は、この決定を助けることができる。本章の実践例で、これらのメトリックをどのように解釈するかを示す。
予測変数の選択は、あらかじめ定義され、科学的に関連性のある、メタ分析で答えたい質問に基づいて行う必要がある。メタ分析モデルに含まれる予測因子（組み合わせ）を分析レポート（Chapter 1.4.2 ）ですでに定義しておくことが重要である。分析計画に記載されていないメタ分析を実行することになったとしても、それで終わりではない。ただし、この場合は正直に、メタ分析報告書に、データを見た後でモデルの適合を決定したことを記載する必要がある。
研究数が少ない場合（これはよくある）、予測変数の有意性を計算したい場合は、Knapp-Hartung 調整を用いて、より頑健な推定値を得るべきである。

再サンプルされたデータにおけるモデルの頑健性を評価するために、置換を使用することができる。この方法の詳細については後ほど説明する。

8.3.2.2 多重共線性

多重共線性 (multi-collinearity) とは、回帰モデル中の1つ以上の予測変数が、他のモデル予測変数によって高い精度で予測されることである (Mansfield and Helms 1982)。これは通常、モデル中に相関の高い２つ以上の独立変数があることを意味する。

多重共線性の危険性のほとんどは、過適合の問題と関連している。高い共線性は、予測変数の係数推定値 $\hat\beta$ を不安定にさせ、データの小さな変化で大きく変化させることがある。また、モデルによって説明される分散の大きさ（ここでは $R^2_*$）も制限される。

メタ回帰における多重共線性は一般的である (Berlin and Antman 1994)。重回帰は低度の共線性を扱うことができるが、非常に高い相関を持つ予測変数をチェックし、必要ならコントロールする必要がある。多重共線性の有無を判断するための統合されたイエス・ノールールはない。

モデルを適合する前に、非常に高い予測変数の相関（すなわち、$r \geq$ 0.8）をチェックすることは、粗雑ではあるものの効果的な方法である。そして、多重共線性は、(1) 近い冗長な予測変数の１つを除去するか、(2) 予測変数を１つの単一変数に結合しようとするかのいずれかによって削減することができる。

8.3.2.3 過適合のアプローチ

多重メタ回帰モデルを構築するとき、予測変数の選択と包含にさまざまなアプローチがある。ここでは、最も重要なものを、その長所と短所とともに議論する。

強制投入. 強制投入法（または変数指定法）では、すべての関連する予測変数が同時に回帰モデルに強制投入される。 R のほとんどの関数では、これはデフォルトの設定である。これは一般的に推奨される手順であるが、強制投入で使用するすべての予測変数は、やはり事前に定義された、理論に基づいた決定に基づいているべきであることに留意する必要がある。
階層的. 階層的重回帰は、明確に定義された科学的根拠に基づいて、予測変数を段階的に私たちの回帰モデルに含めることを意味する。まず、以前の研究で効果量の差に関係していた予測変数のみが、その重要性の順序で含まれる。このステップの後、既知の予測変数ではまだ捕捉されていない異質性をこれらの変数が説明するかどうかを調べるために、新しい予測変数を追加することができる。

ステップ・ワイズ. ステップ・ワイズ投入法（または逐次選択法）とは、変数/予測変数が次々にモデルに追加されることを意味する。一見すると、これは階層的回帰とよく似ているが、決定的な違いがある：ステップ・ワイズ回帰法は、統計的基準に基づいて予測変数を選択する。変数増加法 (前方選択、フォワード選択、forward selection) と呼ばれる手順では、データ中の最大の変動量を説明する変数が、最初の予測変数として使われる。そして、このプロセスを残りの変数について繰り返し、毎回、データ中の説明できない残留変動のほとんどを説明する変数を選択する。また、変数減少法 (後方選択法、backward selection) と呼ばれる手順もあり、まずすべての変数がモデルの予測変数として使用され、次にあらかじめ定義された統計的基準に基づいて、順次削除される。ステップ・ワイズ法の使用を推奨しない文献が多数ある (Chatfield 1995; Whittingham et al. 2006)。上で示した重回帰モデルの一般的な落とし穴を思い出すと、これらの方法が偽の知見を持つ過剰適合モデルを生成する高いリスクを持つことが明らかになる。とはいえ、ステップワイズ法は今でも実務で頻繁に使われているので、これらの手続きが存在することを知っておくことは重要である。ただし、ステップワイズ法を使う場合は、主に探索的に行い、この手法の限界を念頭に置いておくことを勧める。（訳注：これらのほか、変数増減法、変数減増法がある。）

マルチモデル推論. マルチモデル法（または総当たり法）は、分散の大部分を説明する1つの「最良」モデルを連続的に構築しようとしないので、段階的アプローチとは異なる。その代わりに、この手法では、予測変数のすべての可能な組み合わせがモデル化される。これは、いくつかの異なるメタ回帰が作成され、その後、評価されることを意味する。これは、すべての可能な予測変数の組み合わせと、それらがどのように機能するかを完全に調べることができる。共通の発見は、良いモデル適合をもたらす多くの異なる仕様があることである。そして、予測変数の推定係数は、適合したすべてのモデルにわたってプールされ、特定の変数が全体としてどのくらい重要であるかを推論することができる。

8.3.3 R の多重メタ回帰

すべてのインプットの後、 R を使用して最初の多重メタ回帰の適合を開始する時が来た。以下の例は、{meta} パッケージを使用しない最初の例である。その代わりに {metafor} を見てみよう (Viechtbauer 2010)。このパッケージは、メタ分析のための膨大で高度な機能を、素晴らしいドキュメントとともに提供している³²。そこで、まず、{metafor} がインストールされており、ライブラリからロードされていることを確認する。

library(metafor)

このハンズオンでは、 MVRegressionData データセットを使用する。これは「おもちゃ」のようなデータセットで、説明のためにシミュレートしたものである。

“MVRegressionData” データセット

MVRegressionData のデータセットも {dmetar} パッケージに直接含まれている。{dmetar} をインストールし、ライブラリからロードした後、 data(SuicidePrevention) を実行すると、自動的に R 環境にデータセットが保存される。これでデータセットが利用できる。もし、{dmetar} がインストールされていない場合は、インターネットから .rda ファイルとしてデータセットをダウンロードして作業ディレクトリに保存し、R Studio ウィンドウでクリックするとインポートすることができる。

まず、データフレームの構造を見てみよう。

library(tidyverse)
library(dmetar)
data(MVRegressionData)

glimpse(MVRegressionData)

## Rows: 36
## Columns: 6
## $ yi         <dbl> 0.09437543, 0.09981923, 0.16931607, 0.17511107, 0.27301641,…
## $ sei        <dbl> 0.1959031, 0.1918510, 0.1193179, 0.1161592, 0.1646946, 0.17…
## $ reputation <dbl> -11, 0, -11, 4, -10, -9, -8, -8, -8, 0, -5, -5, -4, -4, -3,…
## $ quality    <dbl> 6, 9, 5, 9, 2, 10, 6, 3, 10, 3, 1, 5, 10, 2, 1, 2, 4, 1, 8,…
## $ pubyear    <dbl> -0.85475360, -0.75277184, -0.66048349, -0.56304843, -0.4308…
## $ continent  <fct> 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1,…

このデータセットには6つの変数があることがわかる。yi 列と sei 列は、特定の研究の効果量と標準誤差を格納する。この列は、前に使った TE 列と seTE 列と対応している。この変数名が、{metafor} が使用している標準的な表記方法である。yi は（メタ）回帰で予測したい観測された効果量 $y_i$ を表し、sei は $SE_i$で、研究 $i$ の標準誤差を表す。

他の4つの変数は、メタ回帰で使用される予測変数である。まず、reputation であるが、これは研究が掲載されたジャーナルの（平均値中心の）インパクト・ファクターである。インパクトファクターは、ジャーナルの論文がどれだけ頻繁に引用されるかを定量化し、ジャーナルの名声の代理として使用する。

その他の変数は、0 から 10 で評価される研究の質である quality、（平均値中心揃えでスケーリングされた）出版年である pubyear、そして研究が行われた大陸である continent である。これらの変数は、continent を除き、すべて連続変数である。continent は、ヨーロッパと北アメリカの2つのレベルを持つカテゴリ変数である。

8.3.3.1 多重共線性の確認

前に述べたように、メタ回帰の係数推定が頑健 (robust) であることを確認するために、予測変数の多重共線性をチェックする必要がある。高い相関をチェックする簡単な方法は、すべての連続変数について相互相関行列を計算することである。これは、cor 関数を用いて行うことができる。

MVRegressionData[,c("reputation", "quality", "pubyear")] %>% cor()

##            reputation    quality    pubyear
## reputation  1.0000000  0.3015694  0.3346594
## quality     0.3015694  1.0000000 -0.1551123
## pubyear     0.3346594 -0.1551123  1.0000000

{PerformanceAnalytics} パッケージ (Peterson and Carl 2020) には chart.Correlation という関数があり、これを使うと相関行列を可視化することができる。まず、PerformanceAnalytics パッケージをインストールしてから、このコードを使用する必要がある。

library(PerformanceAnalytics)

MVRegressionData[,c("reputation", "quality", "pubyear")] %>% 
  chart.Correlation()

変数は確かに相関しているが、おそらくそのうちの 1 つを除外するほどではないだろうということがわかる。

8.3.3.2 多重メタ回帰モデルの適合

さて、最初のメタ回帰モデルは、 {metafor} を使用して適合させることができる。以前は、高いジャーナルの評判がより高い効果量を予測するかどうか、またはこれが単に一流ジャーナルの研究がより高い品質を持つという事実によって引き起こされる思い込みであるかどうかを調べたいと思った。

例えば、先行研究から研究の質が効果量を予測することがよく分かっていると仮定しよう。この場合、階層的回帰を実行することは理にかなっている。まず、既知の予測因子である「品質」を含め、次に「評判」がそれ以上の異質性を説明するかどうかをチェックする。これが正しい場合、一流雑誌の研究がより高い品質を持つ傾向があるという事実を制御しても、雑誌の評判は実際に高い効果と関連していると言うことができる。

そのために、 {metafor} の rma 関数を使用する。この関数はランダム効果メタ分析を実行し、モデレータが追加されると混合効果メタ回帰モデルへと拡張される。rma 関数は無数の引数を取ることができ、 R コンソールで ?rma を実行すると、その引数を調べることができる。しかし、通常はそのうちのいくつかを指定するだけでよい。

yi. 各研究の効果量が格納されているデータフレームの列。
sei. 各研究の効果量の標準誤差が格納されているデータフレームの列。
data. メタ分析データを格納したデータフレーム名。
method. 使用したい $\tau^2$ 推定量。この引数に使用できるコードは、 {meta} のものと同じである（例: "REML" restricted maximum likelihood の略）。"ML"を使用することが推奨される。これは、後で異なるメタ回帰モデルを比較することができるからである。
mods. このパラメータは、メタ回帰モデルを定義する。まず、モデルを ~ (チルダ) で指定する。次に、含める予測変数を + で区切って追加する（例： variable1 + variable2 ）。2 つの変数の間の交互作用は、アスタリスクで表す（例： variable1 * variable2 ）。
test. 回帰係数に適用したい検定である。デフォルトの "z" または "knha" (Knapp-Hartung method) から選択できる。

まず、予測因子として quality だけを用いてメタ回帰を実行してみよう。その結果を m.qual というオブジェクトに保存して、出力を調べてみる。

m.qual <- rma(yi = yi,
              sei = sei,
              data = MVRegressionData,
              method = "ML",
              mods = ~ quality,
              test = "knha")

m.qual

## Mixed-Effects Model (k = 36; tau^2 estimator: ML)
## 
## tau^2 (estimated amount of residual heterogeneity):     0.066 (SE = 0.023)
## tau (square root of estimated tau^2 value):             0.2583
## I^2 (residual heterogeneity / unaccounted variability): 60.04%
## H^2 (unaccounted variability / sampling variability):   2.50
## R^2 (amount of heterogeneity accounted for):            7.37%
## 
## Test for Residual Heterogeneity:
## QE(df = 34) = 88.6130, p-val < .0001
## 
## Test of Moderators (coefficient 2):
## F(df1 = 1, df2 = 34) = 3.5330, p-val = 0.0688
## 
## Model Results:
## 
##          estimate      se    tval    pval    ci.lb   ci.ub 
## intrcpt    0.3429  0.1354  2.5318  0.0161   0.0677  0.6181  * 
## quality    0.0356  0.0189  1.8796  0.0688  -0.0029  0.0740  . 
## 
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

この出力では、予測変数 quality の結果を Model Results の下で確認できる。トレンド・レベルでは有意であるが ($p<$ 0.1)、回帰の重みは有意ではない ($p=$ 0.069)。合計で、このモデルは異質性の $R^2_*=$ 7.37% を説明する。

では、reputation を予測変数に含めるとどうなるか見てみよう。mods の入力に + reputation を追加し、今回は出力を m.qual.rep として保存する。

m.qual.rep <- rma(yi = yi, 
                  sei = sei, 
                  data = MVRegressionData, 
                  method = "ML", 
                  mods = ~ quality + reputation, 
                  test = "knha")

m.qual.rep

## Mixed-Effects Model (k = 36; tau^2 estimator: ML)
## 
## tau^2 (estimated amount of residual heterogeneity):     0.0238 (SE = 0.01)
## tau (square root of estimated tau^2 value):             0.1543
## I^2 (residual heterogeneity / unaccounted variability): 34.62%
## H^2 (unaccounted variability / sampling variability):   1.53
## R^2 (amount of heterogeneity accounted for):            66.95%
## 
## Test for Residual Heterogeneity:
## QE(df = 33) = 58.3042, p-val = 0.0042
## 
## Test of Moderators (coefficients 2:3):
## F(df1 = 2, df2 = 33) = 12.2476, p-val = 0.0001
## 
## Model Results:
## 
##             estimate      se    tval    pval    ci.lb   ci.ub 
## intrcpt       0.5005  0.1090  4.5927  <.0001   0.2788  0.7222  *** 
## quality       0.0110  0.0151  0.7312  0.4698  -0.0197  0.0417      
## reputation    0.0343  0.0075  4.5435  <.0001   0.0189  0.0496  *** 
## 
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

モデル結果のセクションに新しい行が表示され、予測変数 reputation の結果が表示されていることがわかる。モデルは、回帰の重みを 0.034 と推定し、これは非常に有意である ($p$ < 0.001)。

また、メタ回帰モデルは、全体としてかなりの量の異質性を説明していることがわかる。正確には、$R^2_*$ = 66.95% である。これは、研究の質でコントロールした場合でも、ジャーナルの評判がより高い効果量と関連していることを意味する。

しかし、2番目のモデルは本当に最初のモデルよりも適合度が高いのだろうか？これを評価するために、 anova 関数を使用し、比較したい2つのモデルを指定することができる。これは、制限付き最尤法（"REML"）の代わりに最尤法（"ML"）を用いて両方の混合効果モデルを適合させたからこそ可能なことであることに注意しておこう。

anova(m.qual, m.qual.rep)

##         df   AIC   BIC  AICc logLik   LRT   pval    QE tau^2    R^2 
## Full     4 19.86 26.19 21.15  -5.93              58.30  0.03          
## Reduced  3 36.98 41.73 37.73 -15.49 19.11 <.0001 88.61  0.06 48.32%

この関数はモデルのテストを行い、m.qual.rep が m.qual よりも適合度が高いかどうかを評価するためのいくつかの統計情報を提供する。ここでは、quality と reputation の両方を含むフルモデルである m.qual.rep と、quality のみを含む縮小モデルとを比較する。

anova 関数は 尤度比検定を実行し、その結果は LRT 列で見ることができる。この検定は非常に有意であり ($\chi^2_1=$ 19.11, $p<$ 0.001) 、フルモデルが本当に良い適合を提供することを意味する。

もう1つの重要な統計量は AICc 列で報告されていて、小さなサンプルで補正された赤池情報量規準（AIC）を提供する。前に述べたように、AICc は、過適合を避けるために、より多くの予測変数がある複雑なモデルにペナルティを課す。

AIC の値が低いと、モデルの性能が良いということに注意を払うことが重要である。この出力では、より多くのパラメータがあるにもかかわらず、フルモデル (AICc = 21.15) が削減モデル (AICc = 37.73) よりも良いAIC値を持っていることがわかる。これらのことは、重回帰モデルが実際に私たちのデータに対して良い適合を提供することを示唆している。

8.3.3.3 モデリング交互作用

追加予測変数 pubyear (出版年) と continent との交互作用をモデル化したいとする。出版年と効果量の関係がヨーロッパと北米の研究で異なると仮定する。この仮定を rma 関数でモデル化するために、mods パラメータで予測変数を * と接続する必要がある。anova 関数を用いて直接モデルを比較したくないので、今回は "REML" (restricted maximum likelihood) $\tau^2$ 予測因子を使用する。

解釈を容易にするために、モデルを実行する前に MVRegressionData で continent 変数に因子ラベルを追加する。

# 因子ラベルを 'continent' に追加
# 0 = Europe
# 1 = North America
levels(MVRegressionData$continent) = c("Europe", "North America")

# メタ回帰モデルを適合
m.qual.rep.int <- rma(yi = yi, 
                      sei = sei, 
                      data = MVRegressionData, 
                      method = "REML", 
                      mods = ~ pubyear * continent, 
                      test = "knha")

m.qual.rep.int

## Mixed-Effects Model (k = 36; tau^2 estimator: REML)
## 
## tau^2 (estimated amount of residual heterogeneity):     0 (SE = 0.01)
## tau (square root of estimated tau^2 value):             0
## I^2 (residual heterogeneity / unaccounted variability): 0.00%
## H^2 (unaccounted variability / sampling variability):   1.00
## R^2 (amount of heterogeneity accounted for):            100.00%
## 
## Test for Residual Heterogeneity:
## QE(df = 32) = 24.8408, p-val = 0.8124
## 
## Test of Moderators (coefficients 2:4):
## F(df1 = 3, df2 = 32) = 28.7778, p-val < .0001
## 
## Model Results:
## 
##                       estimate    se  tval    pval  ci.lb ci.ub 
## intrcpt                    0.38  0.04  9.24  <.0001   0.30  0.47  *** 
## pubyear                    0.16  0.08  2.01  0.0520  -0.00  0.33    . 
## continentNorth America     0.39  0.06  6.05  <.0001   0.26  0.53  *** 
## pubyear:continent          0.63  0.12  4.97  <.0001   0.37  0.89  *** 
##    North America
## [...]

最後の行の pubyear:continentNorth America には、交互作用項の係数が格納されている。 {metafor} は、自動的に交互作用項だけでなく、「通常の」低次予測変数として pubyear と continent の両方を含むことに注意しておこう（むしろ、注意すべき）。

また、continent は因子であるため、rma はこれがダミーコード化された予測因子であることを検出し、北米のカテゴリーと比較するために、カテゴリー「ヨーロッパ」を $D_g$ = 0 の基準として使用したことに留意してみよう。この交互作用項は正の係数 (0.63) を持ち、非常に有意であることがわかる ($p<$ 0.001)。

これは、近年、効果量が増加していること、また、北米で行われた研究でより強くなっていることを示している。また、私たちがあてはめたモデルは、$R^2_*$ =100% の異質性を説明していることがわかる。

なぜこうなったかというと、このデータが説明のためにシミュレーションされたためである。実際には、データの異質性をすべて説明することはほとんどない。むしろ、現実のデータでこのような結果を見つけたら、モデルを過剰に適合させたことになるかもしれないので、心配する必要がある。

8.3.3.4 並び替え検定

並び替え (permutation) とは、数値や物体を含む集合を取り出し、その集合から繰り返し要素を取り出して順番に並べる数学的な操作である。すでに順序のある数値の集合がある場合、これはデータの順序を並べ替える、つまりシャッフルする処理と同じである。

例として、3つの数を含む集合 $S=\{1,2,3 \}$ があるとする。この集合の可能な並べ換えの1つは $(2,1,3)$ 、別の並べ替えでは $(3,2,1)$ となる。並べ替えの結果は、両方とも前の3つの数字を含んでいるが、順番が違うことがわかる。

並び替えは並び替え検定にも使われるが、リサンプリング法の特別な種類である。大まかに言うと、リサンプリング法は、同じソースまたは生成プロセスからサンプルされた（少し）異なるデータを与えることによって、統計モデルの頑健性を検証するために使用される (Good 2013, chap. 3.1)。これは、モデルの係数が本当にデータの根底にある真のパターンを捉えているかどうか、あるいは、モデルを過適合させ、それによって、実際には統計的ノイズであるのに、データのパターンを誤って仮定していないかどうかをより良く評価する方法である。

並び替え検定は、メタ回帰が未知の効果量を予測する際にどのように実行されるかを評価できる予備の「テスト」データセットを持っている必要はない。このため、特に、並べ替え検定は、メタ回帰モデルの頑健性を評価するために推奨されている (JPT Higgins and Thompson 2004)。

メタ回帰モデルで並べ替え検定をどのように実行するかの詳細については、ここではあまり触れない。最も重要な部分は、元のデータ集合のすべての可能な並べ替え、またはランダムに選ばれた多くの並べ替えで得られた検定統計量に基づいて、私たちのモデルの $p$-値を再計算することである。

ここで重要な指標は、並べ替えデータから得られる検定統計量が、元の検定統計量と等しいか大きいか、またその頻度である。例えば、並べ替えデータ 1000 個のうち 50 個で、検定統計量が元の検定統計量より大きいか等しいとすると、$p$ = 0.05となる。

メタ回帰モデルに対して並べ替え検定を行うには、{metafor} に内蔵されている permutest という関数を使用する。例として、以前適合した m.qual.rep モデルの結果を再計算してみよう。permutest 関数は rma オブジェクトと一緒に提供するだけである。並べ替え検定は、特に大きなデータセットの場合、計算量が多く実行に時間がかかる。

permutest(m.qual.rep)

## Test of Moderators (coefficients 2:3):
## F(df1 = 2, df2 = 33) = 12.7844, p-val* = 0.0010
## 
## Model Results:
## 
##             estimate      se    tval   pval*    ci.lb   ci.ub 
## intrcpt       0.4964  0.1096  4.5316  0.2240   0.2736  0.7193      
## quality       0.0130  0.0152  0.8531  0.3640  -0.0179  0.0438      
## reputation    0.0350  0.0076  4.5964  0.0010   0.0195  0.0505  *** 
## 
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

すべての予測変数の結果を含むおなじみの出力が再び表示される。pval* 列を見ると、評判予測変数の $p$-値が $p$ < 0.001 から $p_*$ = 0.001 に減少していることがわかる。しかし、これはまだ非常に有意であり、予測変数の効果が頑健であることを示している。

メタ回帰モデルの結果を報告する前に、必ずこの並べ換え検定を用いることが推奨されている (JPT Higgins and Thompson 2004)。

データが小さい場合の Permutation 検定

モデルに含まれる研究数 $K$ が少ない場合、従来から使われている統計的有意性の閾値（つまり$p$ < 0.05）に到達できないことに注意。

メタ回帰モデルの場合、permutest を用いた並べ替え検定は、$K$ > 4 の場合のみ統計的有意に達することができる (Viechtbauer et al. 2015) 。

8.3.3.5 マルチモデル推論

私たちはすでに、マルチ・モデル推論と呼ばれる方法で、予測変数の全ての可能な組み合わせをモデル化することができることを述べた。これは、どの予測変数の組み合わせが最良の適合を提供するか、そして、どの予測変数が全体として最も重要であるかを調査することができる。マルチモデル推論を行うには、 multimodel.inference 関数を使用する³³。

“multimodel.inference” 関数

multimodel.inference 関数は、{dmetar} パッケージに含まれている。{dmetar} がインストールされ、コンピュータに読み込まれると、この関数を使用できるようになる。もし、{dmetar} をインストールしていない場合は、以下の手順でインストールできる。

関数のソースコードにアクセスするオンライン.
ソースコード全体をコンソール（R Studio の左下ペイン）にコピー＆ペーストし、Enterキーを押して、 R に関数を「学習」させる。
{metafor}, {ggplot2}, {MuMIn} パッケージがインストールされ、ロードされていることを確認する。

この関数では、以下のパラメータを指定する必要がある。

TE. 各研究の効果量。データセットの効果量列の名前を引用符で囲んで指定する必要がある（例： TE = "effectize"）。
seTE. 効果量の標準誤差。データセットの標準誤差列の名前を指定する必要があい（引用符で囲んで、例えば seTE = "se"）。
data. 効果量、標準誤差、メタ回帰予測変数が含まれるデータフレーム。
predictors. マルチモデル推論に使用する予測因子を指定する文字の連結配列。予測因子の名前は、data に与えられたデータフレームの列名と同じでなければならない。
method. 効果量のプーリングに使用するメタ分析モデル。固定効果モデルには "FE" が用いられる。"DL", "SJ", "ML", "REML" など、複数のランダム効果モデルが利用可能である。"FE" を使用する場合、Knapp-Hartung 法は固定効果モデルで使用することを意図していないため、test 引数は自動的に "z" に設定される。デフォルトは "REML" である。
test. 検定統計量と信頼区間を計算する際に利用する手法。デフォルトは "knha" で、Knapp-Hartung 調整を利用する。コンベンショナルな Wald タイプの検定は、この引数を "z" に設定することで計算される。
eval.criterion. 適合したモデルに適用する評価基準。"AICc" (デフォルト、スモールサンプル補正した赤池情報量規準)、 "AIC" (赤池情報量規準)、または "BIC" (ベイズ情報量規準) のいずれかを指定することが可能である。
interaction. FALSE （デフォルト）に設定すると、予測変数間の交互作用は考慮されていない。このパラメータを TRUE に設定すると、すべての交互作用がモデル化される。

では、データセット MVRegressionData のすべての予測変数を使って、交互作用なしで マルチモデル推論を実行してみよう。multimodel.inference 関数を実行すると、特に予測変数の数が多い場合、時間がかかることに注意しておこう。

multimodel.inference(TE = "yi", 
                     seTE = "sei",
                     data = MVRegressionData,
                     predictors = c("pubyear", "quality", 
                                    "reputation", "continent"),
                     interaction = FALSE)

## Multimodel Inference: Final Results
## --------------------------
##  - Number of fitted models: 16
##  - Full formula: ~ pubyear + quality + reputation + continent
##  - Coefficient significance test: knha
##  - Interactions modeled: no
##  - Evaluation criterion: AICc 
## 
## 
## Best 5 Models
## --------------------------
## [...]
##    (Intrc) cntnn  pubyr   qulty   rpttn df logLik AICc delta weight
## 12       +     + 0.3533         0.02160  5  2.981  6.0  0.00  0.536
## 16       +     + 0.4028 0.02210 0.01754  6  4.071  6.8  0.72  0.375
## 8        +     + 0.4948 0.03574          5  0.646 10.7  4.67  0.052
## 11       +       0.2957         0.02725  4 -1.750 12.8  6.75  0.018
## 15       +       0.3547 0.02666 0.02296  5 -0.395 12.8  6.75  0.018
## Models ranked by AICc(x) 
## 
## 
## Multimodel Inference Coefficients
## --------------------------
##                          Estimate  Std. Error   z value  Pr(>|z|)
## intrcpt                0.38614661 0.106983583 3.6094006 0.0003069
## continentNorth America 0.24743836 0.083113174 2.9771256 0.0029096
## pubyear                0.37816796 0.083045572 4.5537402 0.0000053
## reputation             0.01899347 0.007420427 2.5596198 0.0104787
## quality                0.01060060 0.014321158 0.7402055 0.4591753
## 
## 
## Predictor Importance
## --------------------------
##        model importance
## 1    pubyear  0.9988339
## 2  continent  0.9621839
## 3 reputation  0.9428750
## 4    quality  0.4432826

\[~\]

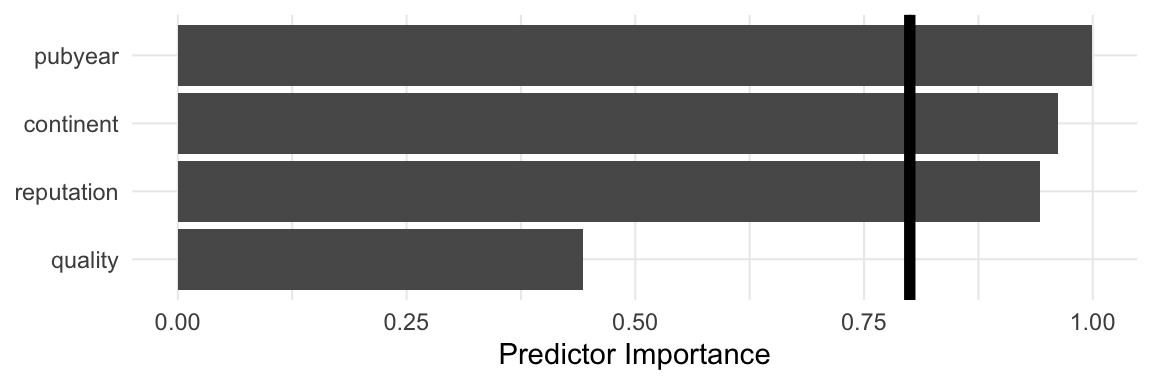
見どころ満載なので、順を追って出力を見ていこう。

Multimodel Inference: Final Results. この部分は、適合したモデルについての詳細な情報を提供する。 $2^4 = 16$ 可能なモデルの総数が適合したことがわかる。また、この関数はモデルの比較に補正済みAIC (aicc) を使用していることがわかる。
Best 5 Models . ここに表示されているのは、AICc が最も低い5つのモデルで、低いものから高いものへとソートされている。予測変数は表の列に、モデルは行に表示される。数字（重み）または + 記号（カテゴリ予測変数の場合）は、予測変数/交互作用項がモデルで用いられたことを示し、空のセルは、予測変数が省略されたことを示す。私たちは、 TE ~ 1 + continent + pubyear + reputation が最良の適合を示すことがわかる（AICc = 6.0）。しかし、他の予測変数の組み合わせは、この値に非常に近い。したがって、どのモデルが本当に「ベスト」モデルであるかを言うのは難しい。しかし、上位5つのモデルはすべて予測変数 pubyear を含んでおり、この変数が特に重要である可能性を示唆している。
Multimodel Inference Coefficients. ここでは、すべての予測変数の係数を、それらが出現するすべてのモデルにわたって集約して見ることができる。係数推定値は、 pubyear ( $\hat\beta$ = 0.378)で最も大きく、これは以前の発見を裏付ける。近似信頼区間は、Std.Error に格納された値に 1.96 を掛けたものを、Estimate と引き算したり足したりすることで得ることができる。
モデル平均予測変数の重要度プロット. このプロットでは、すべてのモデルで各予測変数の平均された重要度が表示される。再び、pubyear が最も重要な予測変数であることがわかる。次に、reputation、continent、quality が続く。

マルチモデル推論の限界

この例から、マルチモデル推論が、効果量の違いを予測するためにどの予測変数が重要であるかを包括的に把握するのに有効な方法であることが明らかになるはずである。

ステップ・ワイズ回帰法の問題のいくつかを回避しているとはいえ、この方法はまだ探索的と見なされるべきで、予測変数が分析する研究分野の効果量とどのように関連しているかについて予備知識がない場合に使用することができることに注意。

マルチモデル推論の結果に基づいてメタ回帰モデルを構築することにした場合、これを報告することが極めて重要である。なぜなら、そのようなモデルは a priori な仮説に基づくものではなく、このサンプルにおける統計的特性に基づいて構築されたためである。

\[\tag*{$\blacksquare$}\]

8.4 演習問題

知識を試そう！

一次研究で用いられる従来の回帰分析と、メタ回帰の違いは何か？

サブグループ解析とメタ回帰は密接な関係がある。メタ回帰の公式をどのようにサブグループデータに適応させることができるか？

メタ回帰において、個々の研究に異なる重みを与えるためにどのような方法が用いられるか？

データによく適合するメタ回帰モデルにはどのような特徴があるか？これを調べるには、どのような指標を用いればよいか？

メタ分析の手法でサブグループ分析を計算する場合、$\tau^2$ の値をサブグループで別々にするか、共通にするか？

（多重）メタ回帰の限界と落とし穴は何か？

（複数の）メタ回帰モデルの頑健性を向上させるために利用できる方法を2つ挙げ、それが有用である理由を述べよ。

問題の解答は、本書の巻末 Appendix A にある。

8.5 要約

メタ回帰では、従来の回帰手法を研究レベルのデータに適応させる。サブグループ分析は、カテゴリカル予測因子と共通の推定値 $\tau^2$ を持つメタ回帰の特別なケースと見なすことができる。
メタ回帰モデルの目的は、データにおける真の効果量の違い（すなわち、研究間異質性分散 $\tau^2$ ）を説明することである。モデルがデータによく合っている場合、回帰直線からの真の効果の偏差は、プール効果からの最初の偏差よりも小さくなるはずである。この場合、説明できない異質性、つまり残差は小さくなる。これは、$R^2_*$ 指数によって捕捉され、モデルによって説明される異質性の変動のパーセンテージを知らせる。
多重メタ回帰では、2つ以上の予測変数が同じメタ回帰モデルで使用される。また、交互作用項を導入することで、ある変数の予測値が他の変数の異なる値に対して変化するかどうかを検定することも可能である。
多重メタ回帰は非常に汎用性の高い手法であるが、限界がある。多重メタ回帰は、真の関係ではなくランダムなノイズがモデル化されることを意味する、オーバーフィットモデルを非常に容易にする。予測変数の多重共線性は、私たちのモデルの妥当性に脅威を与えるだろう。
メタ回帰モデルが頑健であることを保証するために、いくつかのアプローチがある。例えば、定義された理論的根拠に基づいてのみモデルを適合させたり、並べ替え検定を使用したりすることができる。マルチモデル推論は、探索的アプローチとして使用することができる。この方法は、潜在的に重要な予測因子を指摘することができ、将来の研究で検証すべき仮説を導き出すために使用することができる。

7 サブグループ解析

9 出版バイアス