4 効果量のプール

険 しい道はもう過ぎ去った。幸いなことに、私たちは今、すべてのメタ分析の核となる部分、すなわち効果量のプールに到達している。この章から直接始めるという誘惑には勝つことができたと思われる。本書では、研究課題の定義、研究データの検索・選択・抽出のガイドライン、効果量の作成方法など、様々なトピックを既に取り上げている。

徹底的な準備は優れたメタ分析の重要な要素であり、これから続くステップで大いに役立つことだろう。これまでの章に費やした時間は、十分に投資されたと断言できる。

R で効果量をプールすることができるパッケージは数多く存在する。ここでは、Chapter 2.2 で既にインストールした {meta} パッケージの機能を中心に説明する。このパッケージは非常に使い勝手が良く、数行のコードでほぼ全ての重要なメタ分析結果を得ることが可能である。前章では、効果の大きさはアウトカムによって異なる「フレーバー」があることを取り上げた。 {meta} パッケージには、これらの効果量のそれぞれのメトリクス（訳注：標準化平均差やオッズ比など）について特化したメタ分析関数が含まれている。また、全ての関数はほぼ同じ構造をしている。

このように、 {meta} の動作の基本を理解すれば、どの効果量に注目しても、メタ分析のコーディングは簡単にできるようになる。この章では、 {meta} パッケージの一般的な構造について説明する。もちろん、パッケージのメタ分析機能についても、実例を用いてより詳しく解説する。

{meta} パッケージでは、効果量がプールされる方法について、多くの詳細を微調整することが可能である。以前述べたように、メタ分析には多くの 「研究者の自由度」が伴う。適用できる統計手法やアプローチに関する選択肢は無数にあり、ある手法が他の手法より優れているかどうかは、しばしば文脈に依存する。

したがって、 R で分析を始める前に、メタ分析の統計的な前提条件と、その背後にある数学について基本的な理解を深める必要があるのである。メタ分析の背後にある「考え方」についても触れておくことも重要である。統計学では、この「考え方」はモデルと訳されるが、メタ分析のモデルがどのようなものかを見ていきる。

これから見ていくように、メタ分析の性質上、すぐに基本的な判断をしなければならない。固定効果モデルかランダム効果モデルのどちらかを仮定しなければならないのである。他の分析仕様と合わせて、この2つのモデルのうちどの文脈でどちらがより適切なのか、情報に基づいて決定を下すためには、メタ分析プールの背後にある概念についての知識が必要である。

4.1 固定効果モデルとランダム効果モデルの比較

メタ分析モデルを規定する前に、まず統計モデルとは実際にどのようなものかを明らかにする必要がある。統計学には「モデル」がたくさんあり、「モデル」と言う言葉は聞いたことがあるだろう。「線形モデル」「一般化線形モデル」「混合モデル」「ガウス加法モデル」「構造方程式モデル」などがある。

統計学においてモデルが遍在していることは、この概念がいかに重要であるかを示している。統計ツールボックスはすべて、何らかの形でモデルが基礎となっている。\(t\) 検定、ANOVA、回帰の背後にはモデルがある。すべての仮説検定には、それに対応する統計モデルがある。

統計モデルを定義するとき、すでに与えられている情報から始める。これは文字通り、データ¹⁷ である。メタ分析では、データは、含まれる研究で観察された効果量である。私たちのモデルは、これらの観察されたデータが生成されたプロセスを記述するために使用される。

データはブラックボックスの産物であり、私たちのモデルはそのブラックボックスの中で何が起こっているかを明らかにすることを目的としている。

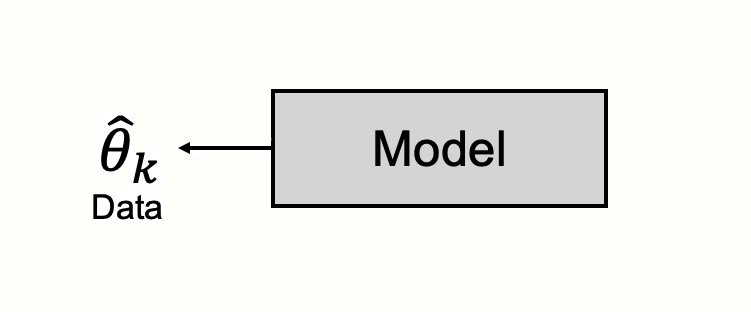
一般に、統計モデルとは特殊な「理論」のようなものである。モデルは、観測されたデータを生成したメカニズムを説明しようとするもので、特にそのメカニズム自体が直接観測できない場合に有効である。特に、そのメカニズム自体が直接観測できない場合、そのメカニズムを説明しようとするものである。

モデルが説明的であるという性格は、現代の統計学に深く根付いており、メタ分析も例外ではない。説明のための手段としてのモデルの概念化は、統計「文化」の特徴である。Breiman (2001) の有名に推定によると、全統計学者の98％が信奉しているようである。

統計モデルを指定することで、データの背後にある「現実」の近似的な表現を見つけようとしている。観測された結果に基づいて、すべての研究の根底にある真の効果量を見つける方法を説明する数式が欲しいのである。Chapter 1.1 で学んだ通り、メタ分析の最終的な目的は、効果量が研究ごとに異なる場合でも、研究全体を特徴づける1つの数値を見つけることである。したがって、メタ分析モデルは、全体的な効果は1つであるにもかかわらず、観察された研究結果がなぜ、どの程度異なるのかを説明する必要がある。

まさにこの問いに答えようとするモデルとして、固定効果モデルとランダム効果モデルの2つがある。両者は異なる仮定に基づいているが、すぐにわかるように、両者の間には強い結びつきがある。

4.1.1 固定効果モデルの場合

固定効果モデルは、すべての効果量が単一の均質な集団に由来すると仮定している。これは、すべての研究が、同じ真の効果量を共有していることを述べている。この真の効果は、メタ分析で計算したい全体的な効果量で、\(\theta\) と表記される。

固定効果モデルによると、ある研究 \(k\) の観測された効果量 \(\hat\theta_k\) （「シータ・ハットk」と読む）が \(\theta\) から逸脱する唯一の理由は、そのサンプル誤差 \(\epsilon_k\) （「イプシロン・k」と読む）のためである。固定効果モデルは、ブラックボックスの中身である研究の効果量の違いを生み出す過程が単純で、すべての研究が同じ真の効果量の推定者であることを教えてくれる。しかし、すべての研究は、無限に大きな研究集団から多少なりとも大きなサンプルを抽出することしかできないため、結果はサンプリングエラーに悩まされることになる。このサンプル誤差は、観察された効果が全体的な真の効果から乖離する原因となる。

このような関係を表現することが可能である (Borenstein et al. 2011, chap. 11)。

\[\begin{equation} \hat\theta_k = \theta + \epsilon_k \tag{4.1} \end{equation}\]

注意深く見ると、この数式が不思議なことに Chapter 3.1 の数式と似ていると思われるだろう。それは間違いではない。先ほどの式では、ある研究 \(k\) の観測された効果量 \(\hat\theta_k\) は、その研究の真の効果量 \(\theta_k\) の推定値であり、研究のサンプル誤差 \(\epsilon_k\) が負担している、と定義する。

先ほどの式と固定効果モデルの式では、ほんのわずかだが重要な違いがある。固定効果モデルの式では、真の効果量を \(\theta_k\) ではなく、\(\theta\) で表し、添え字 \(k\) を削除している。

これまでは、個々の研究 \(k\) の真の効果量についてのみ記述してきた。固定効果モデルでは、さらに一歩踏み込む。研究 \(k\) の真の効果量を見つけると、この効果量は \(k\) だけでなく、メタ分析におけるすべての研究についても真であることを教えてくれる。ある研究の真の効果量 \(\theta_k\) と、全体のプール効果量 \(\theta\) は、同一である。

固定効果モデルの背景にある考え方は、観察された効果量は研究ごとに異なるかもしれないが、それはサンプリング誤差のためだけである、というものである。実際には、真の効果量はすべて同じであり、固定されている。この理由により、固定効果モデルは等効果（“equal effects”）や共通効果（“common effect”）モデルと言われることもある。¹⁸

固定効果モデルの式から、観測された効果量 \(\theta_k\) が真の全体効果から乖離する理由はただ一つ、サンプル誤差 \(\epsilon_k\) によることがわかる。サンプルエラーとサンプルサイズには関連性があることは、Chapter 3.1 で既に述べた。すべての条件が同じであれば、サンプルサイズが大きくなれば、サンプリングエラーは小さくなる。また、サンプリングエラーは標準誤差で数値で表すことができ、これもサンプルサイズが大きくなると小さくなることを学ぶ。

研究の真の全体効果量は不明であるが、この関係を利用して真の全体効果 \(\hat\theta\) の最良の推定値に到達することが可能である。したがって、標準誤差が小さい研究は、標準誤差が大きい研究よりも、真の全体効果のより良い推定値になるはずである。

これをシミュレーションで説明することが可能である。前に使った rnorm 関数を用いて、真の全体効果が \(\theta = 0\) である研究の選択をシミュレートしよう。複数のサンプルを取るが、サンプルサイズを変えて、標準誤差が「観察された」効果間で異なるようにする。シミュレーションの結果は、Figure 4.1 で見ることが可能である。

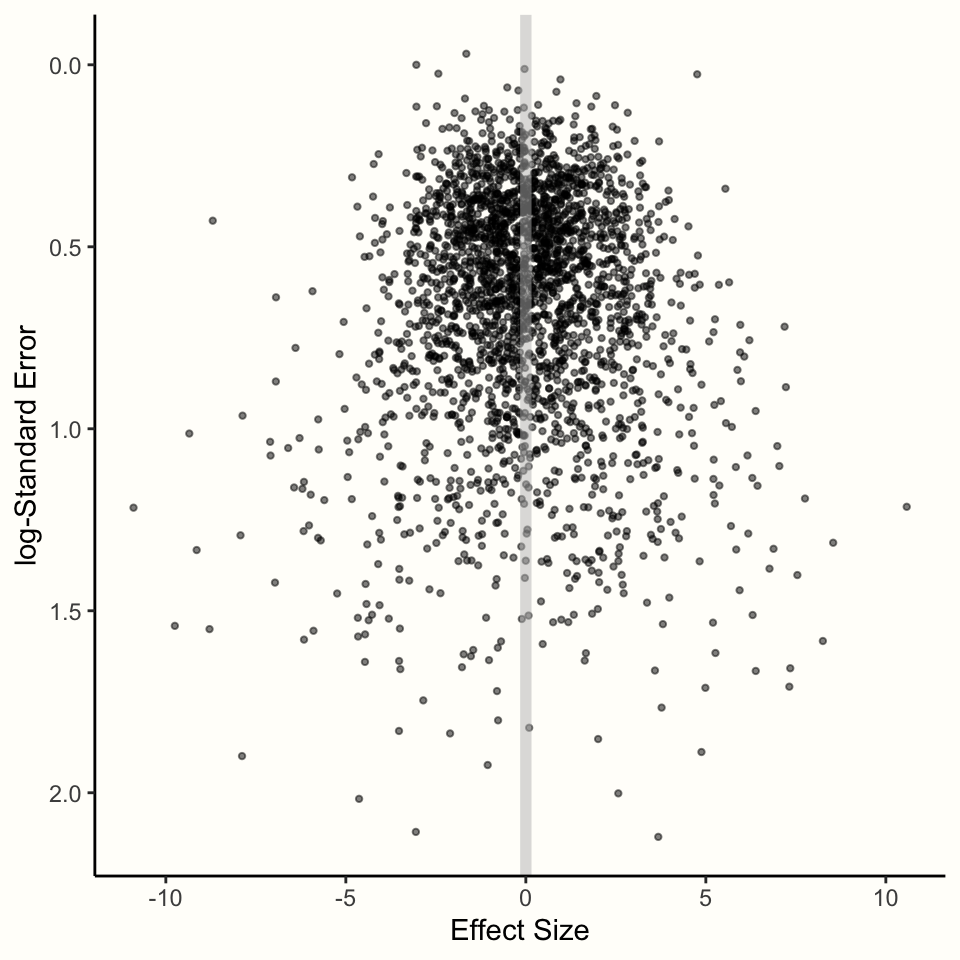
Figure 4.1: 効果量と標準誤差の関係

シミュレーションの結果、興味深いパターンが示された。サンプリング誤差が小さい効果量は、真の効果量 \(\theta = 0\) の周りに凝集していることがわかる。y軸の標準誤差¹⁹が大きくなると、効果量の分散が大きくなり、観測された効果が真の効果からどんどんずれていくことがわかる。

この挙動は、固定効果モデルの式で予測することが可能である。標準誤差が小さい研究は、サンプル誤差が小さく、全体的な効果量の推定値が真実に近い可能性が高いことが分かっている。

観測された効果量はすべて真の効果の推定量であるが、あるものは他のものよりも優れていることを見てきた。したがって、メタ分析で効果をプールする場合、より高い精度（すなわち、より小さい標準誤差）を持つ効果量に、より大きな重みを与える必要がある。固定効果モデルでプール効果量を計算する場合は、全研究の加重平均を使用する。

各研究 \(k\) の重み \(w_k\) を計算するには、標準誤差を用い、それを二乗して各効果量の分散 \(s^2_k\) を求めることができる。分散が小さいほど精度が高いことを示すので、分散の逆数を用いて各研究の重みを決定する。

\[\begin{equation} w_k = \frac{1}{s^2_k} \tag{4.2} \end{equation}\]

重みがわかれば、加重平均を計算し、真のプール効果 \(\hat\theta\) を推定することが可能である。各研究の効果量 \(\hat\theta_k\) に対応する重み \(w_k\) を掛け、メタ分析の全研究 \(K\) で結果を合計し、すべての個々の重みの合計で割ればよい。

\[\begin{equation} \hat\theta = \frac{\sum^{K}_{k=1} \hat\theta_kw_k}{\sum^{K}_{k=1} w_k} \tag{4.3} \end{equation}\]

この方法は、メタ分析で平均効果を計算する最も一般的な方法である。分散の逆数を使用するので、しばしば 逆分散重み付け (Inverse-Variance Weighting) または単に逆分散メタ分析と呼ばれる。

二値効果量データの場合、加重平均を計算する方法として、Mantel-Haenszel 法、Peto 法、あるいは Bakbergenuly によるサンプルサイズ加重法 (2020) などがある。これらの方法については、Chapter 4.2.3.1 で説明する。

{meta} パッケージを使うと、固定効果メタ分析がとても簡単に可能である。しかし、その前に R で 「手動で」逆分散プーリングを試してみよう。この例では、Chapter 2.4 でインポートした SuicidePrevention データセットを使用する。

“SuicidePrevention” データセット

SuicidePrevention のデータセットも {dmetar} パッケージに直接含まれている。{dmetar} をインストールし、ライブラリからロードした後、 data(SuicidePrevention) を実行すると、自動的に R 環境にデータセットが保存される。これでデータセットが利用できる。もし、{dmetar} がインストールされていない場合は、インターネットから .rda ファイルとしてデータセットをダウンロードして作業ディレクトリに保存し、R Studio ウィンドウでクリックするとインポートすることができる。

SuicidePrevention のデータセットには、生の効果量が含まれているので、まず効果量を計算する必要がある。この例では、小サンプル調整済み標準化平均差（Hedges’ \(g\)）を計算する。これを行うには、 {esc} パッケージの esc_mean_sd 関数を使用する（Chapter 3.3.1.2）。

この関数には es.type という追加の引数があり、これを用いてスモールサンプル補正を行うかどうかを指定することが可能である（es.type = "g" と指定; Chapter 3.4.1）。

# dmetar, esc and tidyverse をロード
library(dmetar)
library(esc)
library(tidyverse)

# dmetar からデータセットをロード
data(SuicidePrevention)

# Hedges' g と標準誤差を計算
# - 研究名を "study" に保存
# - その後、パイプを使って
#   結果をデータフレームに変換
SP_calc <- esc_mean_sd(grp1m = SuicidePrevention$mean.e,
                       grp1sd = SuicidePrevention$sd.e,
                       grp1n = SuicidePrevention$n.e,
                       grp2m = SuicidePrevention$mean.c,
                       grp2sd = SuicidePrevention$sd.c,
                       grp2n = SuicidePrevention$n.c,
                       study = SuicidePrevention$author,
                       es.type = "g") %>% 
                     as.data.frame()

# データの glimpse を見よう
# データは Hedges' g ("es") と標準誤差 ("se") を含む
glimpse(SP_calc)

## Rows: 9
## Columns: 9
## $ study       <chr> "Berry et al.", "DeVries et al.", "Fleming et al." …
## $ es          <dbl> -0.14279447, -0.60770928, -0.11117965, -0.12698011 …
## $ weight      <dbl> 46.09784, 34.77314, 14.97625, 32.18243, 24.52054 …
## $ sample.size <dbl> 185, 146, 60, 129, 100, 220, 120, 80, 107data
## $ se          <dbl> 0.1472854, 0.1695813, 0.2584036, 0.1762749 …
## $ var         <dbl> 0.02169299, 0.02875783, 0.06677240, 0.03107286 …
## $ ci.lo       <dbl> -0.4314686, -0.9400826, -0.6176413, -0.4724727 …
## $ ci.hi       <dbl> 0.145879624, -0.275335960, 0.395282029 …
## $ measure     <chr> "g", "g", "g", "g", "g", "g", "g", "g", "g"

# 各研究の 逆分散重みを計算
SP_calc$w <- 1/SP_calc$se^2

# 重みを使って効果量をプール
pooled_effect <- sum(SP_calc$w*SP_calc$es)/sum(SP_calc$w)
pooled_effect

## [1] -0.2311121

計算の結果、固定効果モデルを仮定したプール効果量は \(g \approx\) -0.23 であった。

4.1.2 ランダム効果モデル

これまで見てきたように、固定効果モデルは、メタ分析データの成り立ちや、効果をプールする方法を概念化する一つの方法である。しかし、重要なのは、この方法が現実を適切に反映しているかということである。

固定効果モデルは、すべての研究が均質な母集団の一部であり、観察された効果の差の唯一の原因は研究のサンプリング・エラーであると仮定している。もし、サンプリング・エラーなしに各研究の効果量を計算するとしたら、すべての真の効果量は完全に同じになる。

この考え方を現実的に確認すると、固定効果モデルの仮定は、多くの実世界のアプリケーションにおいて単純すぎる可能性があることがわかる。メタ分析における研究が常に完全に均質であることは、単純に非現実的である。たとえ微妙な違いであっても、研究内容が異なることはよくある。興味のあるアウトカムは、異なる方法で測定されただろう。治療の種類や強さ、長さが全く同じでないこともある。研究の対象者が全く同じでなかっただろうし、使用した対照群に違いがあっただろう。

メタ分析に含まれる研究は、これらの側面のうちの1つだけでなく、同時に複数の側面で異なる可能性がある。もしそうであれば、真の効果におけるかなりの研究間の異質性が予想される。

これらのことは、固定効果モデルの有効性を疑わせるものである。例えば、ある研究が異なるタイプの治療法を用いていた場合、一方の治療法が他方の治療法よりも効果的であることは、ごく普通のことと思われる。このような違いが、研究のサンプル誤差によるノイズに過ぎないと考えるのは、あまりに不自然なことだろう。

その逆で、研究の効果量に本当の差がある理由は無数にあるのである。ランダム効果モデルは、このような懸念に対応するものである。このモデルは、私たちのデータの背後にある現実をよりよく反映するモデルを提供してくれる。

ランダム効果モデルでは、効果量が単一の均質な母集団から抽出された場合よりも分散を示すという事実を考慮したいと思われる (L. V. Hedges and Vevea 1998)。したがって、個々の研究の効果は、サンプル誤差だけによる偏差ではなく、別の分散の原因があると仮定する。

この追加的な分散成分は、研究が1つの集団から生じているわけではないという事実によってもたらされる。その代わり、各研究は、母集団の「宇宙」から独立に抽出されたものとみなされる。

ランダム効果モデルは、真の効果量が1つだけでなく、真の効果量の分布があることを仮定している。したがって、ランダム効果モデルの目的は、すべての研究の1つの真の効果量を推定することではなく、真の効果量の分布の平均値を推定することである。

ランダム効果モデルがどのように数式で表現されるかを見てみよう。ランダム効果モデルは、固定効果モデルと同様に、観測された効果量 \(\hat\theta_k\) が、サンプリングエラー \(\epsilon_k\) を含む研究の真の効果量 \(\theta_k\) の推定値であると仮定することから始まる。

\[\begin{equation} \hat\theta_k = \theta_k + \epsilon_k \tag{4.4} \end{equation}\]

このように、\(\theta\) の代わりに \(\theta_k\) を使っていることが、すでに重要な違いを示している。ランダム効果モデルは、\(\theta_k\) が1個の単一研究 \(k\) の真の効果量であると仮定しているだけである。このモデルでは、\(\theta_k\) の他に、\(\zeta_k\) （訳注: \(\zeta\) は「ゼータ」と読む）で示される第二の誤差要因が存在することを仮定している。この第二の誤差の原因は、研究 \(k\) の真の効果量 \(\theta_k\) でさえ、平均 \(\mu\) を持つ真の効果量の包括的な分布の一部に過ぎないという事実によってもたらされる。

\[\begin{equation} \theta_k = \mu + \zeta_k \tag{4.5} \end{equation}\]

ランダム効果モデルは、ブラックボックス (S. G. Thompson, Turner, and Warn 2001) の内部で、2つのプロセスの階層が起こっていることを教えてくれる：研究の観察された効果量は、サンプル誤差のためにその真の値から逸脱している。しかし、真の効果量でさえも、真の効果の宇宙からの引き出しに過ぎず、その平均 \(\mu\) を、メタ分析のプール効果として推定したい。

2番目の式を1番目の式にあてじはめる（つまり、\(\theta_k\) を2番目の式の定義に置き換える）ことで、ランダム効果モデルを1行で表現可能である (Borenstein et al. 2011, chap. 12)。

\[\begin{equation} \hat\theta_k = \mu + \zeta_k + \epsilon_k \tag{4.6} \end{equation}\]

この式から、観測された効果量がプール効果 \(\mu\) から乖離するのは、\(\zeta_k\) と \(\epsilon_k\) の二つの誤差項のためであることが明らかになった。この関係を可視化したものが Figure 4.2 である。

ランダム効果モデルの重要な前提は、\(\zeta_k\) の大きさは、\(k\) から独立していることことである。つまり、ある研究の \(\zeta_k\) が他の研究の \(\zeta_k\) よりも高いことを事前に示すものは何もないと仮定する。また、\(\zeta_k\) のサイズは偶然の産物だけであると仮定する。

これはランダム効果モデルの交換可能性の仮定として知られている (Julian Higgins, Thompson, and Spiegelhalter 2009; Lunn et al. 2012, chap. 10.1)。データを見る前に、ある研究 \(k\) で \(\zeta_k\) がどの程度大きいかを知ることができるものがない限り、すべての真の効果量は交換可能であると仮定される。

どちらのモデルを使うべきか？

実際には、完全に均質な研究のセレクションを見つけることは非常に稀である。これは、ベストプラクティスに従って、PICO (Chapter 1.4.1) で分析範囲をできるだけ正確にしようと思っても同じである。

医学や社会科学など多くの分野では、ある程度の研究間異質性が予測されるため、常にランダム効果モデルを用いるのが通例である。固定効果モデルは、研究間異質性を検出できなかった場合（異質性の検出方法については、Chapter 5 で説明する）、および真の効果が固定であると仮定する十分な理由がある場合にのみ使用することができる。これは、例えば、ある研究の正確な複製だけを検討する場合や、1つの大きな研究の部分集合をメタ分析する場合などである。言うまでもなく、このようなことはめったにないため、固定効果モデルを「実際に」適用することはむしろ稀である。

a priori にランダム効果モデルを用いるのが通例であるとしても、このアプローチに議論されないわけでもない。ランダム効果モデルは、メタ分析の全体効果を計算する際に、小規模な研究にたいしてより注意を払う (Schwarzer, Carpenter, and Rücker 2015, chap. 2.3)。しかし、特に小規模研究はバイアスがかかっていることが多い（Chapter 9.2.1 参照）。そのため、固定効果モデルが望ましいとする意見もある（場合もある）(Poole and Greenland 1999; Furukawa, McGuire, and Barbui 2003)。Stanley, Doucouliagos, and Ioannidis (2022) は同様の指摘をし、いくつかの分野においてはランダム効果モデルよりも、いわゆる “unrestricted weighted least squares” (UWLS) モデルを使うべきだと議論している。

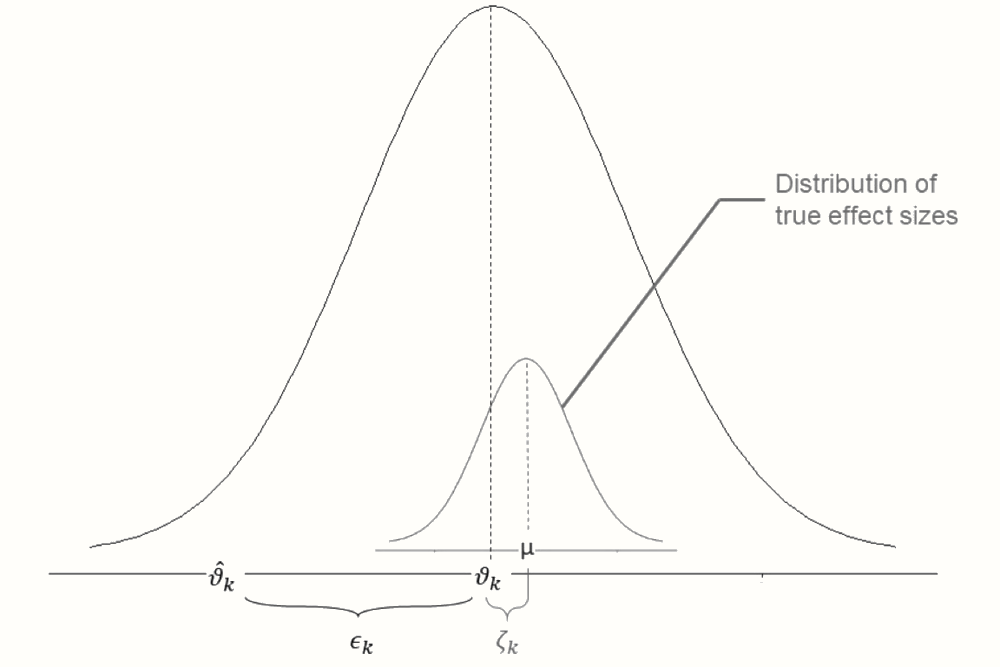
Figure 4.2: ランダム効果モデルのパラメータを示す図。

4.1.2.1 研究間異質性の推定値

ランダム効果モデルに関連する課題は、誤差 \(\zeta_k\) を考慮に入れなければならないことである。これを行うには、真の効果量の分布の分散 を推定する必要がある。この分散は、\(\tau^2\)（タウ２乗）として知られている。いったん \(\tau^2\) の値がわかれば、各効果量の逆分散の重みを決定するときに、研究間の異質性を含めることが可能になる。

したがって、ランダム効果モデルでは、各観測の調整済みランダム効果重み \(w^*_k\) を計算する。その式は次のようになる。

\[\begin{equation} w^*_k = \frac{1}{s^2_k+\tau^2} \tag{4.7} \end{equation}\]

調整済みランダム効果重みを用いて、固定効果モデルを用いた場合と同様に、逆分散法を用いてプール効果量を算出する。

\[\begin{equation} \hat\theta = \frac{\sum^{K}_{k=1} \hat\theta_kw^*_k}{\sum^{K}_{k=1} w^*_k} \tag{4.8} \end{equation}\]

この \(\tau^2\) を推定する方法はいくつかあるが、そのほとんどは手作業で行うには複雑すぎる。しかし、幸運なことに、これらの推定量は {meta} パッケージの関数に実装されており、私たちのために自動的に計算をしてくれるのである。以下は、最も一般的な推定量と、それらが {meta} で参照されるコードのリストである。

• DerSimonian-Laird ("DL") 推定法 (DerSimonian and Laird 1986)。
• 制限付き最尤推定 (Restricted Maximum Likelihood, "REML") または最尤推定 (Maximum Likelihood, "ML") 法 (Viechtbauer 2005)。
• Paule-Mandel ("PM") 法 (Paule and Mandel 1982)。
• Paule-Mandel 法と実質的に同じである Empirical Bayes ("EB") 法 (Sidik and Jonkman 2019)。
• Sidik-Jonkman ("SJ") 推定量 (Sidik and Jonkman 2005)。

これらの推定量のうち、どの推定量が異なる種類のデータに対して最も有効であるかは、現在進行中の研究課題である。研究数 \(k\)、各研究の参加者数 \(n\)、研究ごとに \(n\) がどの程度異なるか、\(\tau^2\) がどの程度大きいかなどのパラメータに依存することが多い。このような様々なシナリオの下での \(\tau^2\) 推定量のバイアスを分析した研究がいくつかある (Veroniki et al. 2016; Viechtbauer 2005; Sidik and Jonkman 2007; Langan et al. 2019)。

おそらく、最もよく使われている推定量は、DerSimonian and Laird によるものであろう。この推定量は、RevMan（Cochraneが開発したプログラム）や Comprehensive Meta-Analysis など、過去にメタ分析者がよく使用したソフトウェアに実装されている。また、{meta} でもデフォルトの推定量として使用されている。この歴史的な遺産により、「ランダム効果モデルの使用」が DerSimonian-Laird 推定量の使用と同義で使用されている研究論文をよく見かける。

しかし、特に研究数が少なく異質性が高い場合、この推定量に偏りが生じることが分かっている (Hartung 1999; Hartung and Knapp 2001a, 2001b; Follmann and Proschan 1999; Makambi 2004)。研究数が少なく異質性の高いメタ分析はよくあることなので、これはかなり問題である。

Veroniki ら (2016) は、概要論文において、様々な\(\tau^2\)推定量の頑健性に関するエビデンスをレビューしている。彼らは、二値・連続効果量のデータには Paule-Mandel 法を、連続アウトカムには制限付き最尤推定量を推奨している。制限付き最尤推定量は、 {metafor} パッケージで使用されるデフォルトの方法でもある。

Langan ら (2019) による最近のシミュレーション研究でも同様の結果が得られているが、研究のサンプルサイズが大きく異なる場合、Paule-Mandel 推定量は最適でない可能性があることが分かっている。また、Bakbergenuly ら (2020) の研究では、特に研究数が少ない場合には Paule-Mandel 推定量がよく適していることが分かっている。Sidik-Jonkman 推定量は、モデル誤差分散法としても知られているが、\(\tau^2\)が非常に大きい場合のみ適している (Sidik and Jonkman 2007)。

どの推定法を使うべきか？

どの推定法を使うべきかという鉄則はない。多くの場合，様々な推定量によって得られる結果にはわずかな違いしかないので，この問題はあまり気にする必要はないだろう．

疑いがあれば、いつでも異なる \(\tau^2\) 推定量を使って分析を再実行し、結果の解釈が変わるかどうかを確認することができる。以下は、メタ分析における暫定的なガイドライン。

1. 連続的なアウトカムデータに基づく効果量については、まず制限付き最尤推定量を使用することができる。

2. バイナリ効果量のデータでは、サンプルサイズに極端なばらつきがなければ、最初に Paule-Mandel 推定量を選択すると良い。

3. サンプル内の効果の不均一性が非常に大きいと信じる十分な理由があり、偽陽性を避けることが非常に高い優先度を持つ場合、Sidik-Jonkman推定量を使用することができる。

4. 他の人があなたの結果を R 外でできるだけ正確に再現できるようにしたい場合は、DerSimonian-Laird 推定量が選択される方法である。

全体として、\(\tau^2\) の推定量は2つのカテゴリに分類される。DerSimonian-Laird や Sidik-Jonkman の推定量のように、閉形式に基づくものもある。つまり、数式を使って直接計算することが可能である。

（制限付き）最尤推定量、Paule-Mandel推定量、経験的ベイズ推定量は、繰り返しアルゴリズムによって \(\tau^2\) の最適値を見つける。そのため、後者の推定量では、計算結果が少し長くなることがある。しかし、ほとんどの場合、このような時間の差はせいぜいわずかなものである。

4.1.2.2 Knapp-Hartung 調整法

また、\(\tau^2\) 推定量の選択に加えて、いわゆる Knapp-Hartung 調整法²⁰を適用するかどうかを決定しなければならない (Knapp and Hartung 2003; Sidik and Jonkman 2002)。この調整は、プール効果量 \(\hat\theta\) の標準誤差（したがって信頼区間）の計算方法に影響する。

Knapp-Hartung 調整法は、研究間異質性の推定値の不確実性を対照しようとするものである。プール効果の有意性検定が通常、正規分布を仮定するのに対して（いわゆる Wald 型 検定）、Knapp-Hartung 法は \(t\) 分布に基づいている。Knapp-Hartung の調整はランダム効果モデルでのみ使用でき、通常、プール効果の信頼区間がわずかに大きくなる。

メタ分析においてモデルの種類を報告

メタ分析を報告する場合、Methods セクションに、使用したモデルの種類を明記することを強く勧める。以下はその例である。（訳注：英文論文を書くことを想定しているため、以下は訳さずそのままとしている。）

“As we anticipated considerable between-study heterogeneity, a random-effects model was used to pool effect sizes. The restricted maximum likelihood estimator (Viechtbauer, 2005) was used to calculate the heterogeneity variance \(\tau^2\). We used Knapp-Hartung adjustments (Knapp & Hartung, 2003) to calculate the confidence interval around the pooled effect.”

Knapp-Hartung調整を適用することは通常賢明である。いくつかの研究 (IntHout, Ioannidis, and Borm 2014; Langan et al. 2019) は、特に研究数が少ない場合に、これらの調整によって偽陽性の可能性を減らすことができることを示す。

しかし、Knapp-Hartung調整の使用は議論の余地がないわけではない。例えば、Wiksten ら (2016) は、効果が非常に均質な場合、この方法は（滅多にない）反保守的な結果を引き起こすことがあると論じている。

4.2 R で効果量をプール

学んだことを実践する時が来た。この章の残りの部分では、 R で直接、異なる効果量のメタ分析を実行する方法を探る。このために使用する {meta} パッケージは特別な構造を持っている。メタ分析関数がいくつか含まれており、それぞれが効果量のデータの1つのタイプに焦点を当てている。例えば、固定効果モデルかランダム効果モデルか、どの \(\tau^2\) 推定量を使うか、などである。それとは別に、特定の種類のデータにのみ関連するメタ分析の詳細を調整することができる関数固有の引数がある。

Figure 4.3 は、 {meta} の構造を概観したものである。どの関数を使うかを決めるには、まず、どのような効果量データを合成したいのかを明確にする必要がある。最も基本的な区別は、生 (raw) と 事前計算済み (pre-calculated) 効果量データの間のものである。「生」のデータとは、目的の効果量を計算するために必要なすべての情報がデータフレームに格納されているが、実際の効果量はまだ計算されていない場合を指す。先ほど使用した SuicidePrevention データセットには、標準化平均差を計算するために必要な2つのグループの平均、標準偏差、サンプルサイズという生データが含まれている。

一方、効果量データには、各研究の最終的な効果量と標準誤差がすでに含まれており、これを「事前計算済み」と呼んでいる。効果指標の補正版（例えば、Hedges’ \(g\)、Chapter 3.4.1）を使用したい場合、プールを始める前に、既に計算済みの効果量データにこの補正が適用されていることが必要である。

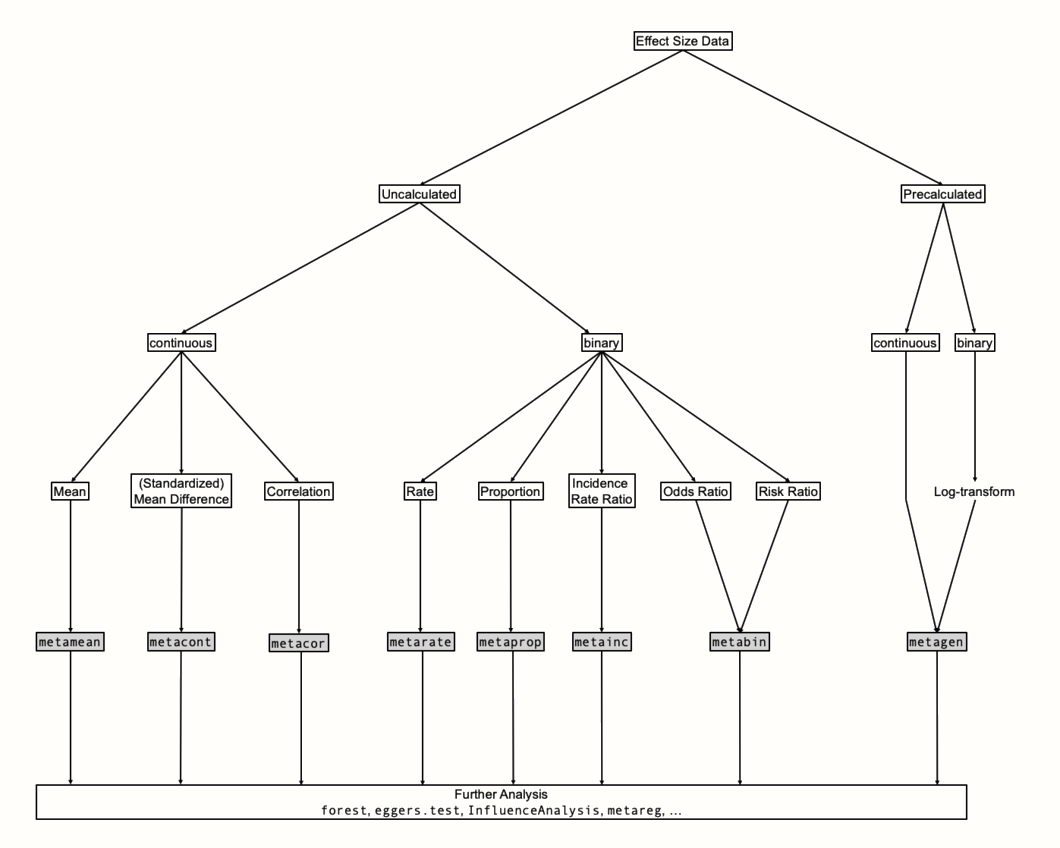
Figure 4.3: メタ分析に関する関数の概略図

可能であれば、メタ分析には生データを使用することが望ましい。そうすれば、他の人が効果量の計算方法を理解し、結果を再現することが容易になる。しかし、研究結果は異なる方法で報告されることが多いため、実際には生データを使用できないことが多い（Chapter 3.5.1）。

このため、各研究の望ましい効果量をすぐに事前計算して、すべての形式が同じになるようにする以外に方法がない。本書の「各種ツール」の Chapter 17 では、報告された効果量を目的のメトリックに変換するのに役立つ公式を紹介している。

あらかじめ計算された効果量に対応する関数として、 metagen がある。この名前は、 generic inverse variance meta-analysis の略である。もし、二値データ（割合、リスク比、オッズ比など）で metagen を使用する場合は、 Chapter 3.3.2 で説明したように、この関数を使用する前に効果量を対数変換しておくことが重要である。

生の効果量データに頼ることができる場合、 {meta} はそれぞれの効果量タイプに特化した関数を提供する。平均、（標準化）平均差、相関には、それぞれ metamean , metacont , metacor 関数を使用可能である。 metarate , metaprop , metainc 関数を用いて、（発生）率、割合、発生率比をプールすることが可能である。 metabin 関数は、リスク比やオッズ比を扱うときに使用する。

{meta} のメタ分析関数はすべて同じ構造を持っている。効果量のデータ（生データまたは計算済みデータ）と、解析の詳細を制御するための引数を関数に与えなければならない。各関数で指定可能なコア引数は6つである。

• studlab. この引数は、各効果量に 研究ラベル を関連付ける。もし、データセットに研究名や著者が保存されている場合は、それぞれの列の名前を指定するだけである（例： studlab = author）。
• sm. この引数は、メタ分析で使用する効果量の指標である要約手法を制御する。このオプションは、生の効果量データを使用する関数で特に重要である。 {meta} パッケージは、例えば "SMD" や "OR" など、異なる効果量のフォーマットに対するコードを使用する。利用できる要約尺度は各関数で同じではないので、以下のセクションでそれぞれのケースで最も一般的な選択肢を説明する。
• fixed. この引数に論理値（TRUE または FALSE）を与える必要があり、固定効果モデルのメタ分析を計算するかどうかを示す²¹。
• random. 同様の方法で、この引数はランダム効果モデルを使用するかどうかを制御する。もし comb.fixed とcomb. random の両方が TRUE に設定されていると、両方のモデルが計算されて表示される²²。
• method.tau. この引数は \(\tau^2\) 推定量を定義する。全ての関数は、前の章で既に紹介した異なる推定量のコードを使用する（例えば、DerSimonian-Laird 法の場合: method.tau = "DL"）。
• hakn. これはまた別の論理的な引数で、ランダム効果モデルを使用する際に、Knapp-Hartung 調整を適用するかどうかを制御する。
• data. この引数では、メタ分析データセットの名前を {meta} で指定する。
• title (必須ではない). この引数には、解析の名前を文字列で指定する。この引数への入力は必須ではないが、後で分析結果を特定するのに役立つ。

また、いくつかの追加の引数もあるが、それは後の章で知ることになる。このガイドでは、 {meta} 関数の引数は100以上あるので、すべての引数を説明することはできない。

ありがたいことに、これらの引数のほとんどはほとんど必要なく、また賢明なデフォルト値が設定されている。疑問がある場合は、 R コンソールで関数名の前にクエスチョンマーク（例： ?metagen）を付けて実行すると、関数のドキュメントを開くことが可能である。

デフォルトの引数とポジションマッチング

R の初心者にとって、関数におけるデフォルト引数と位置ベースのマッチングについて学んでおくと良い。

デフォルトの引数は、関数を書いた人が指定したものである。関数では引数をあらかじめ定義された値に設定し、別の値を明示的に指定しない限り自動的に使用される。{meta} では、すべての引数ではないが、多くの引数がデフォルト値を持っている。

デフォルト値は、関数ドキュメントの「使用法」のセクションに表示される。関数が引数のデフォルト値を定義している場合、デフォルトの動作に満足できない場合を除き、関数呼び出しに含める必要はない。

デフォルト値がない引数は、常に関数呼び出しの中で指定する必要がある。{meta} パッケージには gs という便利な関数があり、これを使うことで特定の引数に使われるデフォルト値を確認することができる。例えば、 gs(“method.tau”) を実行してみよう。もし、デフォルト値がなければ、 gs は NULL を返す。

R 関数のもう一つの興味深い点は、ポジション・マッチングである。通常、関数を呼び出す際には、引数の名前とその値を書かなければならない。しかし、ポジション・マッチングを使えば、引数の名前を書かずに、引数の値だけを入力すればよい。これは、引数をドキュメントに登場するのと同じ 位置 で指定すれば可能である。

例えば、sqrt 関数を考えてみよう。この関数を書き出すと、sqrt(x = 4) となる。しかし、数値である x が最初の引数であることが分かっているので、単に sqrt(4) とタイプしても同じ結果になる。

4.2.1 事前算出された効果量のデータ

それでは、メタ分析関数のツアーを metagen から始めよう。これまで学んだように、この関数は事前に計算された効果量のデータに使用することが可能である。最初の例では、この関数を使用して ThirdWave データセットのメタ分析を実行する。

このデータセットには、いわゆる “Third Wave” の心理療法が大学生の知覚ストレスに及ぼす影響を調べた研究が含まれている。各研究について、試験後における治療群と対照群の標準化平均差を計算し、小サンプル補正を適用する。したがって、このメタ分析で使用される効果量の指標は、Hedges’ \(g\)である。それでは、データを見てみよう。

“ThirdWave” データセット

ThirdWave のデータセットも {dmetar} パッケージに直接含まれている。{dmetar} をインストールし、ライブラリからロードした後、 data(SuicidePrevention) を実行すると、自動的に R 環境にデータセットが保存される。これでデータセットが利用できる。もし、{dmetar} がインストールされていない場合は、インターネットから .rda ファイルとしてデータセットをダウンロードして作業ディレクトリに保存し、R Studio ウィンドウでクリックするとインポートすることができる。

library(tidyverse) # 'glimpse' に必要
library(dmetar)
library(meta)

data(ThirdWave)
glimpse(ThirdWave)

## Rows: 18
## Columns: 8
## $ Author               <chr> "Call et al.", "Cavanagh et al.", "DanitzOrsillo"…
## $ TE                   <dbl> 0.7091362, 0.3548641, 1.7911700, 0.1824552, 0.421…
## $ seTE                 <dbl> 0.2608202, 0.1963624, 0.3455692, 0.1177874, 0.144…
## $ RiskOfBias           <chr> "high", "low", "high", "low", "low", "low", "high…
## $ TypeControlGroup     <chr> "WLC", "WLC", "WLC", "no intervention", "informat…
## $ InterventionDuration <chr> "short", "short", "short", "short", "short", "sho…
## $ InterventionType     <chr> "mindfulness", "mindfulness", "ACT", "mindfulness…
## $ ModeOfDelivery       <chr> "group", "online", "group", "group", "online", "g…

このデータセットには8つの列があり、そのうち最も重要なのは Author、TE 、seTE であることがわかる。TE 列は各研究の \(g\) 値、 seTE は \(g\) の標準誤差を表している。その他の列は、各研究が該当するサブグループカテゴリを記述する変数を表す。これらの変数は今のところ関係ない。

これで、どのようなメタ分析を行いたいかを考え始めることが可能である。サブグループの列を見ると、少なくともバイアスリスク、対照群、介入期間、介入タイプ、実施形態に関して研究が異なっていることがわかる。

このことから、研究間の異質性が予想され、すべての研究の真の効果が一定であると仮定することは意味がないことがよくわかる。したがって、私たちはプールのためにランダム効果モデルを使用することができる。連続アウトカムデータでのロバストなパフォーマンスから、この例では制限付き最尤推定量("REML") を選択する。また、偽陽性結果のリスクを減らすために Knapp-Hartung 調整を使用する。

基本的な疑問が解決されたので、metagen の呼び出し方法もかなり簡単になる。この関数を使用する際には、必ず指定しなければならない関数固有の引数が2つある。

• TE. 計算された効果量が含まれるデータセットの列の名前である。

• seTE. 効果量の標準誤差が格納される列の名前。

残りは、前章ですでに取り上げた一般的な {meta} 引数である。この解析では標準化平均差を扱うので、sm = "SMD" も指定している。しかし、この例では、効果量がすでに各研究で計算されているので、これは結果に対して実際の効果はない。出力で効果量を SMD としてラベル付けするように関数に指示すだけである。

これで metagen の最初の呼び出しを設定するのに必要なすべての情報が得られた。この関数の結果を m.gen というオブジェクトに格納する。

m.gen <- metagen(TE = TE,
                 seTE = seTE,
                 studlab = Author,
                 data = ThirdWave,
                 sm = "SMD",
                 fixed = FALSE,
                 random = TRUE,
                 method.tau = "REML",
                 hakn = TRUE,
                 title = "Third Wave Psychotherapies")

これで m.gen オブジェクトにすべてのメタ分析結果が格納された。概要を知る簡単な方法は summary 関数を使うことである²³。

summary(m.gen)

## Review:     Third Wave Psychotherapies
##                       SMD            95%-CI %W(random)
## Call et al.        0.7091 [ 0.1979; 1.2203]        5.0
## Cavanagh et al.    0.3549 [-0.0300; 0.7397]        6.3
## DanitzOrsillo      1.7912 [ 1.1139; 2.4685]        3.8
## de Vibe et al.     0.1825 [-0.0484; 0.4133]        7.9
## Frazier et al.     0.4219 [ 0.1380; 0.7057]        7.3
## Frogeli et al.     0.6300 [ 0.2458; 1.0142]        6.3
## Gallego et al.     0.7249 [ 0.2846; 1.1652]        5.7
## Hazlett-Steve…     0.5287 [ 0.1162; 0.9412]        6.0
## Hintz et al.       0.2840 [-0.0453; 0.6133]        6.9
## Kang et al.        1.2751 [ 0.6142; 1.9360]        3.9
## Kuhlmann et al.    0.1036 [-0.2781; 0.4853]        6.3
## Lever Taylor…      0.3884 [-0.0639; 0.8407]        5.6
## Phang et al.       0.5407 [ 0.0619; 1.0196]        5.3
## Rasanen et al.     0.4262 [-0.0794; 0.9317]        5.1
## Ratanasiripong     0.5154 [-0.1731; 1.2039]        3.7
## Shapiro et al.     1.4797 [ 0.8618; 2.0977]        4.2
## Song & Lindquist   0.6126 [ 0.1683; 1.0569]        5.7
## Warnecke et al.    0.6000 [ 0.1120; 1.0880]        5.2
## 
## Number of studies combined: k = 18
## 
##                         SMD           95%-CI    t  p-value
## Random effects model 0.5771 [0.3782; 0.7760] 6.12 < 0.0001
## 
## Quantifying heterogeneity:
##  tau^2 = 0.0820 [0.0295; 0.3533]; tau = 0.2863 [0.1717; 0.5944];
##  I^2 = 62.6% [37.9%; 77.5%]; H = 1.64 [1.27; 2.11]
## 
## Test of heterogeneity:
##      Q d.f. p-value
##  45.50   17  0.0002
## 
## Details on meta-analytical method:
## - Inverse variance method
## - Restricted maximum-likelihood estimator for tau^2
## - Q-profile method for confidence interval of tau^2 and tau
## - Hartung-Knapp adjustment for random effects model

さあ、R を使った最初のメタ分析の結果である。解き明かすことがたくさんあるので、順を追って出力を見ていきよう。

• 出力の最初の部分には、個々の研究、その効果量と信頼区間が含まれている。効果は事前に計算されているので、ここで見るべき新しいものはあまりない。%W(random) 列は、ランダム効果モデルが各研究に帰着させた重み（パーセント）を示している。メタ分析では、de Vibe の研究が 7.9% と最も大きな重みを占めていることがわかる。最小の重みは Ratanasiripong による研究に与えられている。この研究の信頼区間を見ると、なぜこのような結果になったのかがわかる。プールされた効果の信頼区間は非常に広く、標準誤差が非常に大きく、したがってこの研究の効果量の推定はあまり正確ではないことを意味している。

• さらに、メタ分析に含まれる研究の総数も出力される。\(K=\) 18件の研究が組み合わされたことがわかる。

• 次節では、その中核となるプール効果量を示す。推定値は約 0.58 であり、95%信頼区間は約 0.38～0.78 であることがわかる。また、効果量が有意であるかどうかの検定結果も示されている。その結果、\(p<\) 0.001 となった。重要なのは、関連する検定統計量も表示されることで、これは t で表示される。これは、\(t\) 分布に基づく Knapp-Hartung 調整を適用する。

• その下に、研究間異質性に関する結果が表示されている。ここで表示される結果のいくつかについては、後の章で詳しく説明するので、ここでは \(\tau^2\) にのみ注目しよう。\(\tau^2\) の横には、真の効果の分散の推定値 \(\tau^2\) = 0.08 が表示されている。\(\tau^2\) の信頼区間は0を含まないので (0.03–0.35) 、\(\tau^2\) は0より有意に大きいことがわかる。これらのことから、私たちのデータには研究間の異質性が存在し、ランダム効果モデルが良い選択であったことがわかる。

• 最後のセクションは、メタ分析についての詳細である。逆分散法を用いて効果をプールしたこと、制限付き最尤推定量を用いたこと、Knapp-Hartung 調整を適用したことなどがわかる。

また、 m.gen に格納されている情報にも直接アクセス可能である。メタ分析の結果である {meta} には、たくさんのオブジェクトがデフォルトで格納されており、ドキュメントの “value” セクションを見れば、これが何を意味しているかが分かる。また、 $ 演算子を使って、特定の分析結果を表示すことが可能である。例えば、プール効果は TE.random として格納される。

m.gen$TE.random

## [1] 0.5771158

fixed = FALSE を指定した場合でも、 {meta} の関数は常に内部で固定効果モデルの結果も計算している。そのため、固定効果モデルを仮定したプール効果にもアクセスすることが可能である。

m.gen$TE.fixed

## [1] 0.4805045

この推定値はランダム効果モデルの結果とはかなり乖離していることがわかる。

分析の詳細を変更したい場合、 update.meta 関数が役に立つ。この関数は、入力として {meta} オブジェクトと、変更したい引数を必要とする。例えば、制限付き最尤推定量の代わりに Paule-Mandel を使用した場合に結果が大きく異なるかどうかをチェックしたいとする。このコードを使ってそれを行うことが可能である。

m.gen_update <- update.meta(m.gen, 
                            method.tau = "PM")

# Get pooled effect
m.gen_update$TE.random

## [1] 0.5873544

# Get tau^2 estimate
m.gen_update$tau2

## [1] 0.1104957

プール効果はあまり変わらないが、Paule-Mandel 推定量では、\(\tau^2\)の近似値がやや大きくなることがわかる。

最後に、結果を保存しておくと後々便利である。 {meta} で生成されたオブジェクトは、save 関数を使って簡単に .rda ( R data) ファイルとして保存することが可能である。

save(m.gen, file = "path/to/my/meta-analysis.rda") # example path

4.2.2 （標準化）平均差

2つの群の平均と標準偏差の形式で表される生の効果量データは、 metacont を使ってプールすることが可能である。この関数は、標準化された群間平均差と標準化されていない群間平均差の両方に使用することが可能である。これらは sm = "SMD" または sm = "MD" を指定することで得ることが可能である。それ以外では、7つの関数固有の引数を指定する必要がある。

• n.e. 治療・実験群の観測数。

• mean.e. 治療・実験群における平均値。

• sd.e. 治療・実験群における標準偏差。

• n.c. 対照群の観測数。

• mean.c. 対照群の平均値。

• sd.c. 対照群の標準偏差。

• method.smd. これは sm = "SMD" のときのみ関係する。 metacont 関数では、3種類の標準化平均差を計算することが可能である。 metacont 関数では、3種類の標準化平均差を計算することが可能である。 method.smd = "Cohen" と設定すると、補正されていない標準化平均差（Cohen’s \(d\)）が効果量指標として使用される。他の2つのオプションは、Hedges’ \(g\) を計算する "Hedges" （デフォルトと推奨）と、Glass’ \(\Delta\)（「デルタ」と読む）を計算する "Glass" である。Glass’ \(\Delta\)は、平均差を標準化するために、プールされた標準偏差の代わりに対照群の標準偏差を使用する。この効果量は、一次研究で複数の治療群がある場合に使われることがあるが、通常、メタ分析では好まれない指標である。

今回の分析例では、Chapter 2.4 と Chapter 4.1.1 で扱った “SuicidePrevention” データセットを再利用している。サンプルに含まれるすべての研究が完全に同一ではないので、ランダム効果モデルを使用することが保証される。また、Knapp-Hartung 調整と\(\tau^2\)の制限付き最尤推定量も再び使用する予定である。 metacont にスモールサンプルバイアスを補正するように指示し、効果量のメトリックとしてHedges’ \(g\) を生成する。結果はオブジェクトに保存され、 m.cont と名付ける。

全体としては、このようなコードになる。

# meta と dmetar がロードされていることを確認
library(meta)
library(dmetar)
library(meta)

# dmetar からデータセットをロード (またはネットからダウンロードし自分で開く)
data(SuicidePrevention)

# metcont を使って結果をプール。
m.cont <- metacont(n.e = n.e,
                   mean.e = mean.e,
                   sd.e = sd.e,
                   n.c = n.c,
                   mean.c = mean.c,
                   sd.c = sd.c,
                   studlab = author,
                   data = SuicidePrevention,
                   sm = "SMD",
                   method.smd = "Hedges",
                   fixed = FALSE,
                   random = TRUE,
                   method.tau = "REML",
                   hakn = TRUE,
                   title = "Suicide Prevention")

その結果を見てみよう。

summary(m.cont)

## Review:     Suicide Prevention
## 
##                     SMD             95%-CI %W(random)
## Berry et al.    -0.1428 [-0.4315;  0.1459]       15.6
## DeVries et al.  -0.6077 [-0.9402; -0.2752]       12.3
## Fleming et al.  -0.1112 [-0.6177;  0.3953]        5.7
## Hunt & Burke    -0.1270 [-0.4725;  0.2185]       11.5
## McCarthy et al. -0.3925 [-0.7884;  0.0034]        9.0
## Meijer et al.   -0.2676 [-0.5331; -0.0021]       17.9
## Rivera et al.    0.0124 [-0.3454;  0.3703]       10.8
## Watkins et al.  -0.2448 [-0.6848;  0.1952]        7.4
## Zaytsev et al.  -0.1265 [-0.5062;  0.2533]        9.7
## 
## Number of studies: k = 9
## Number of observations: o = 1147
## 
##                          SMD             95%-CI     t p-value
## Random effects model -0.2304 [-0.3734; -0.0874] -3.71  0.0059
## 
## Quantifying heterogeneity:
##  tau^2 = 0.0044 [0.0000; 0.0924]; tau = 0.0661 [0.0000; 0.3040]
##  I^2 = 7.4% [0.0%; 67.4%]; H = 1.04 [1.00; 1.75]
## 
## Test of heterogeneity:
##     Q d.f. p-value
##  8.64    8  0.3738
## 
## Details on meta-analytical method:
## - Inverse variance method
## - Restricted maximum-likelihood estimator for tau^2
## - Q-Profile method for confidence interval of tau^2 and tau
## - Hartung-Knapp adjustment for random effects model (df = 8)
## - Hedges' g (bias corrected standardised mean difference; using exact formulae)

この出力を見て、Chapter 4.2.1 で受け取った出力と比較すると、すでに {meta} の最大の資産の1つが見えている。すなわち、metagen や metacont とは異なるデータ型を必要とする異なる関数であるが、出力の構造はほぼ同じように読むことができる。このため、結果の解釈は非常に容易である。ランダム効果モデルによるプール効果は \(g=\) -0.23 であり、95%信頼区間は -0.09 から -0.37 の範囲であることがわかる。この効果は有意である (\(p=\) 0.006)。

効果量が負の符号を持つことがわかる。このメタ分析の文脈では、好ましいアウトカムであることを表し、対照群と比較して治療群で自殺念慮がより低かったことを意味する。これを他の人にわかりやすくするために、効果量の符号を一貫して逆にし（たとえば、代わりに \(g=\) 0.23 と書く）、正の効果量が常に「正の」結果を表すようにしてもよいだろう。

制限付き最尤法では、研究間の異質性分散は \(\tau^2\) = 0.004と推定される。\(\tau^2\) 値を見ると、信頼区間は0を含んでおり、真の効果量の分散は0より有意に大きくないことがわかる。

詳細では、効果量の指標としてHedges’ \(g\) が使われたことが示されている。

4.2.3 二値アウトカム

4.2.3.1 リスク比とオッズ比

metabin 関数は、二値データ、特にリスク比 (Risk Ratio, RR) とオッズ比 (Odds Ratio, OR) に基づく効果量をプールするために使用することが可能である。この関数を使い始める前に、まず、これらの効果量に基づくメタ分析について、いくつかの特殊性を議論する必要がある。

Chapter 4.1.1 と Chapter 4.1.2.1 で取り上げた一般的な逆分散 (generic inverse variance) 法を用いて、二値の効果量をプールすることが可能である。各効果の対数オッズ比または対数リスク比、および標準誤差を計算する必要があり、その後、効果量の分散の逆数を使用してプーリング重みを決定することが可能である。

しかし、この方法は二値アウトカムのデータには最適ではない (Julian Higgins et al. 2019, chap. 10.4.1)。薄いデータを扱っているとき、すなわちイベント数または総サンプルサイズが小さいとき、標準誤差は二値効果量の推定値としては精度が高くない可能性がある。

4.2.3.1.1 Mantel-Haenszel法

このため、Mantel-Haenszel 法 (Mantel and Haenszel 1959; Robins, Greenland, and Breslow 1986) は、二値アウトカム・データを持つ研究の重みを計算する代替手段としてよく使用されている。また、metabin で使用されるデフォルトのアプローチでもある。この方法は、研究の重みを決定するために、治療と対照群におけるイベントと非イベントの数を使用する。リスク比とオッズ比の計算は、それぞれ以下の式で求められる。

リスク比:

\[\begin{equation} w_k = \frac{(a_k+b_k) c_k}{n_k} \tag{4.9} \end{equation}\]

オッズ比:

\[\begin{equation} w_k = \frac{b_kc_k}{n_k} \tag{4.10} \end{equation}\]

式中、Chapter 3.3.2.1 と同じく、\(a_k\) は治療群のイベント数、\(c_k\) は対照群のイベント数、\(b_k\) は治療群の非イベント数、\(d_k\) は対照群の非イベント数、\(n_k\) は全体のサンプルサイズとしている。

4.2.3.1.2 Peto 法

第二のアプローチは、Peto 法 (Yusuf et al. 1985)である。このアプローチの本質は、私たちがすでに知っている逆分散の原則に基づくものである。ただし、特殊な効果量であるPeto オッズ比を使用し、ここでは \(\hat\psi_k\) （訳注: \(\psi\) は「プサイ」と読む）と表記する。

この \(\hat\psi_k\) を計算するためには、治療群で観測された事象である \(O_k\) を知り、治療群の予想例数である \(E_k\) を計算する必要がある。\(O_k-E_k\)の差を \(O_k\) と \(E_k\) の差の分散 \(V_k\) で割ると、対数変換された \(\hat\psi_k\) になる。先ほどと同じセル表記で、\(E_k\)、\(O_k\)、\(V_k\)を計算する式は以下の通りである。

\[\begin{equation} O_k = a_k \tag{4.11} \end{equation}\] \[\begin{equation} E_k = \frac{(a_k+b_k)(a_k+c_k)}{a_k+b_k+c_k+d_k} \tag{4.12} \end{equation}\]

\[\begin{equation} V_k = \frac{(a_k+b_k)(c_k+d_k)(a_k+c_k)(b_k+d_k)}{{(a_k+b_k+c_k+d_k)}^2(a_k+b_k+c_k+d_k-1)} \tag{4.13} \end{equation}\]

\[\begin{equation} \log\hat\psi_k = \frac{O_k-E_k}{V_k} \tag{4.14} \end{equation}\]

そして、効果量のプール時には、\(\log\hat\psi_k\)の分散の逆数を重みとして用いる²⁴。

4.2.3.1.3 Bakbergenuly-サンプルサイズ法

最近、Bakbergenuly ら (2020) は、効果の重みが研究のサンプルサイズだけで決まる別の方法を提案し、この方法が Mantel and Haenszel による方法より望ましい可能性があることを示している。これをサンプルサイズ法と呼ぶことにする。この方法の計算式はとても簡単である。治療群と対照群のサンプルサイズ \(n_{\text{treat}_k}\) と \(n_{\text{control}_k}\) だけ分かれば良い。

\[\begin{equation} w_k = \frac{n_{\text{treat}_k}n_{\text{control}_k}}{n_{\text{treat}_k} + n_{\text{control}_k} } \tag{4.15} \end{equation}\]

このプール法を metabin に実装すると、固定効果モデルとランダム効果モデルによる重みと全体効果は同じになる。プールされた効果の \(p\) 値と信頼区間だけが異なる。

プール方法はどれを使うべきか？

Chapter 3.3.2.1 では、ゼロセルと連続性補正の問題について、すでに詳しく述べた。ゼロセルがある場合、Peto法、サンプルサイズ法ともにそのまま使用できるが、Mantel-Haenszel 法を使用する場合はゼロセルに0.5を加算するのが一般的である。これは metabin のデフォルトの動作でもある。

しかし、連続性補正の使用は、バイアスのある結果につながる可能性があるため、推奨されていない (Efthimiou 2018)。Mantel-Haenszel 法は、ある特定のセルが含まれる研究ですべてゼロである場合にのみ本当に連続性補正を必要とするが、そのようなケースはほとんどない。そのため、通常は metabin で MH.exact = TRUE と設定し、連続性補正を行わない exact Mantel-Haenszel 法を使用することが推奨される。

Peto 法にも限界がある。まず、オッズ比にしか使用できない。また、シミュレーション研究では、(1) 治療群と対照群の観察数が同程度のとき、(2) 観察された事象が稀なとき（<1%）、 (3) 治療効果が過度に大きくないときにのみ, この方法がうまく機能することが示された (Bradburn et al. 2007; Sweeting, Sutton, and Lambert 2004)。

最後に、Bakbergenuly-サンプルサイズ法は、かなり新しい手法であり、他の2つの手法に比べて研究が進んでいない。

全体として，ほとんどの場合，コクランの一般的な評価 (Julian Higgins et al. 2019, chap. 10.4) に従い、Mantel-Haenszel 法（連続性補正なし）を使用することが望ましいと思われる。オッズ比が望ましい効果量の指標であり、関心のある事象が稀であると予想される場合は、Peto 法を用いることができる。

4.2.3.1.4 R における二値効果量のプール

metabin には、8つの重要な関数固有の引数がある。

• event.e. 治療・実験群におけるイベント数。

• n.e. 治療/実験群の観測数。

• event.c. 対照群におけるイベント数。

• n.c. 対照群の観測数。

• method. 使用するプール法。これは、 "Inverse" (一般的な逆分散プール)、 "MH" (Mantel-Haenszel; デフォルトおよび推奨)、 "Peto" (Peto method)、または "SSW" （Bakbergenuly-サンプルサイズ法; sm = "OR" 時のみ）のいずれかになる。

• sm. 計算する要約指標（＝効果量の指標）。リスク比には "RR" を、オッズ比には "OR" を使用することができる。

• incr. ゼロセルの連続性補正のために追加する増分を指定する。incr = 0.5 とすれば、0.5 の増分値が加算される。incr = "TACC" とすると、治療群連続性補正法が用いられる（Chapter 3.3.2.1参照）。前述したように、通常はこの引数を省略し、連続性補正を適用しないことが推奨される。

• MH.exact. もし method = "MH" ならば、この引数を TRUE に設定し、 Mantel-Haenszel 法の連続性補正を使用しないようにすることが可能である。

この実践的な例では、 DepressionMortality データセットを使用する。このデータセットは、Cuijpers and Smit (2002) によるメタ分析に基づいており、全死因死亡率に対するうつ病の影響を調査している。このデータセットには、うつ病のある人とない人の数、そして両群の何人が数年後に死亡したかが含まれている。

“DepressionMortality” データセット

DepressionMortality のデータセットも {dmetar} パッケージに直接含まれている。{dmetar} をインストールし、ライブラリからロードした後、 data(SuicidePrevention) を実行すると、自動的に R 環境にデータセットが保存される。これでデータセットが利用できる。もし、{dmetar} がインストールされていない場合は、インターネットから .rda ファイルとしてデータセットをダウンロードして作業ディレクトリに保存し、R Studio ウィンドウでクリックするとインポートすることができる。

まず、データセットを見てみよう。

library(dmetar)
library(tidyverse)
library(meta)

data(DepressionMortality)
glimpse(DepressionMortality)

## Rows: 18
## Columns: 6
## $ author  <chr> "Aaroma et al., 1994", "Black et al., 1998", "Bruce et al., 19…
## $ event.e <dbl> 25, 65, 5, 26, 32, 1, 24, 15, 15, 173, 37, 41, 29, 61, 15, 21,…
## $ n.e     <dbl> 215, 588, 46, 67, 407, 44, 60, 61, 29, 1015, 105, 120, 258, 38…
## $ event.c <dbl> 171, 120, 107, 1168, 269, 87, 200, 437, 227, 250, 66, 9, 24, 3…
## $ n.c     <dbl> 3088, 1901, 2479, 3493, 6256, 1520, 882, 2603, 853, 3375, 409,…
## $ country <chr> "Finland", "USA", "USA", "USA", "Sweden", "USA", "Canada", "Ne…

この例では、Cuijpers and Smit が行ったように、効果量の指標としてリスク比を計算する。ランダム効果プールモデルを使用し、二値アウトカムデータを扱うので、\(\tau^2\)の Paule-Mandel 推定量を使用する。

データを見ると、サンプルサイズが研究によってかなり異なっており、Paule-Mandel 法がややバイアスされる可能性がある（Chapter 4.1.2.1 参照）。これを踏まえて、感度分析として他の \(\tau^2\) 推定量も試してみて、結果が大きく異なるかどうかを確認することも可能である。

このデータセットにはゼロセルが含まれていないので、連続性補正の心配はなく、すぐに正確な Mantel-Haenszel 法を使うことができる。メタ分析の結果は m.bin というオブジェクトに保存する。

m.bin <- metabin(event.e = event.e, 
                 n.e = n.e,
                 event.c = event.c,
                 n.c = n.c,
                 studlab = author,
                 data = DepressionMortality,
                 sm = "RR",
                 method = "MH",
                 MH.exact = TRUE,
                 fixed = FALSE,
                 random = TRUE,
                 method.tau = "PM",
                 hakn = TRUE,
                 title = "Depression and Mortality")
summary(m.bin)

## Review:     Depression and Mortality
##                           RR        95%-CI %W(random)
## Aaroma et al., 1994     2.09 [1.41;  3.12]        6.0
## Black et al., 1998      1.75 [1.31;  2.33]        6.6
## Bruce et al., 1989      2.51 [1.07;  5.88]        3.7
## Bruce et al., 1994      1.16 [0.85;  1.57]        6.5
## Enzell et al., 1984     1.82 [1.28;  2.60]        6.3
## Fredman et al., 1989    0.39 [0.05;  2.78]        1.2
## Murphy et al., 1987     1.76 [1.26;  2.46]        6.4
## Penninx et al., 1999    1.46 [0.93;  2.29]        5.8
## Pulska et al., 1998     1.94 [1.34;  2.81]        6.2
## Roberts et al., 1990    2.30 [1.92;  2.75]        7.0
## Saz et al., 1999        2.18 [1.55;  3.07]        6.3
## Sharma et al., 1998     2.05 [1.07;  3.91]        4.7
## Takeida et al., 1997    6.97 [4.13; 11.79]        5.3
## Takeida et al., 1999    5.81 [3.88;  8.70]        6.0
## Thomas et al., 1992     1.33 [0.77;  2.27]        5.3
## Thomas et al., 1992     1.77 [1.10;  2.83]        5.6
## Weissman et al., 1986   1.25 [0.66;  2.33]        4.8
## Zheng et al., 1997      1.98 [1.40;  2.80]        6.3
## 
## Number of studies combined: k = 18
## 
##                          RR           95%-CI    t  p-value
## Random effects model 2.0217 [1.5786; 2.5892] 6.00 < 0.0001
## 
## Quantifying heterogeneity:
##  tau^2 = 0.1865 [0.0739; 0.5568]; tau = 0.4319 [0.2718; 0.7462];
##  I^2 = 77.2% [64.3%; 85.4%]; H = 2.09 [1.67; 2.62]
## 
## Test of heterogeneity:
##      Q d.f.  p-value
##  74.49   17 < 0.0001
## 
## Details on meta-analytical method:
## - Mantel-Haenszel method
## - Paule-Mandel estimator for tau^2
## - Q-profile method for confidence interval of tau^2 and tau
## - Hartung-Knapp adjustment for random effects model

プール効果量はRR \(=\) 2.02であることがわかる。このプール効果は有意であり（\(p<\) 0.001）、うつ病にかかると死亡リスクが2倍になることを示している。研究間の異質性分散の推定値は、\(\tau^2 \approx\) 0.19である。

また、\(\tau^2\) の信頼区間はゼロを含まず、研究間の実質的な異質性を示している。最後に、出力の詳細セクションを見ると、 metabin 関数は、意図したようにプールに Mantel-Haenszel 法を使用したことがわかる。

上記で発表したように、\(\tau^2\) の推定方法が結果に影響を与えるかどうか見てみよう。update.meta 関数を使って、分析を再実行するが、今回は制限付き最尤推定量を使用する。

m.bin_update <- update.meta(m.bin, 
                            method.tau = "REML")

ここで、TE.random を調べて、プールされた効果をもう一度見てみよう。ここで忘れてはならないのは、二値アウトカムのメタ分析は、実際には効果量を対数変換したものを使用して行われるということである。結果を表示す際に、metabin は便宜上、効果量のメトリクスを元の形式に再変換しているだけである。このステップは、メタ分析オブジェクトの要素を検査する場合には実行されていない。

対数変換された効果量を再変換するには、その値を指数化する必要がある。指数化は対数変換の「逆関数」であり、 R で exp 関数を使って実行可能である²⁵。これを実際に使ってみよう。

exp(m.bin_update$TE.random)

## [1] 2.02365

制限付き最尤推定量によるプール効果もほぼ同じであることがわかる。次に、\(\tau^2\) の推定値を見てみよう。

m.bin_update$tau2

## [1] 0.1647315

この値は多少乖離しているが、最初の結果の妥当性を心配するほどではない。

metabin の呼び出しは、オッズ比をプールすることにしても、全く同じになる。変更する必要があるのは sm 引数だけで、これは "OR" に設定する必要がある。もう一度関数呼び出し全体を書き出す代わりに、update.meta 関数を再度使用して、プールされた OR を計算することが可能である。

m.bin_or <- update.meta(m.bin, sm = "OR")
m.bin_or

## Review:     Depression and Mortality
##
## [...]
## 
## Number of studies combined: k = 18
## 
##                          OR           95%-CI    t  p-value
## Random effects model 2.2901 [1.7512; 2.9949] 6.52 < 0.0001
## 
## Quantifying heterogeneity:
##  tau^2 = 0.2032 [0.0744; 0.6314]; tau = 0.4508 [0.2728; 0.7946];
##  I^2 = 72.9% [56.7%; 83.0%]; H = 1.92 [1.52; 2.43]
## 
## Test of heterogeneity:
##      Q d.f.  p-value
##  62.73   17 < 0.0001
## 
## Details on meta-analytical method:
## - Mantel-Haenszel method
## - Paule-Mandel estimator for tau^2
## - Q-profile method for confidence interval of tau^2 and tau
## - Hartung-Knapp adjustment for random effects model

出力では、オッズ比を用いたプール効果はOR = 2.29であることがわかる。

4.2.3.1.5 事前に計算された二値効果量のプール

各研究のリスク比やオッズ比を計算するために必要な生の効果量のデータを抽出できないことがある。例えば、主要な研究でオッズ比が報告されていても、この効果量の根拠となるデータがない場合がある。著者が元のデータを提供してくれない場合、事前に計算された効果量のデータに基づいてメタ分析を行う必要が出てくるだろう。学習したように、これを行うために使用できる関数は metagen である。

二値アウトカムデータを扱うとき、事前に計算された効果量データを使う以外に選択肢がない場合は、本当に注意しなければならない。 metagen 関数は逆分散法を用いて効果量をプールし、Mantel-Haenszel 法のようなより良いオプションは使用できない。しかし、他のすべてがうまくいかない場合には、まだ有効な選択肢である。

DepressionMortality のデータセットを使って、事前に計算された効果量のメタ分析を行うシミュレーションをしてみよう。m.bin の TE と seTE オブジェクトを抽出し、各研究の効果量と標準誤差を取得することが可能である。この情報を DepressionMortality データセットに保存する。

DepressionMortality$TE <- m.bin$TE
DepressionMortality$seTE <- m.bin$seTE

ここで、信頼区間の下限と上限はわかっているが、標準誤差がわからない効果が1つあると想像してみよう。このようなシナリオをシミュレートするために、 (1) 研究7 (Murphy et al., 1987) の標準誤差を欠損と定義し（つまり、その値を NA に設定）、 (2) データセットに新しい空の2列、 lower と upper を定義し、 (3) lower と upper に研究7で対数変換した「報告」信頼区間を記入することにする。

# 研究 7 の seTE を NA に設定
DepressionMortality$seTE[7] <- NA

# 空の列 'lower' と 'upper' を作成
DepressionMortality[,"lower"] <- NA
DepressionMortality[,"upper"] <- NA

# 研究 7 の 'lower' と 'upper' に値を入れる
# いつものごとく、二値効果量は対数変換が必要
DepressionMortality$lower[7] <- log(1.26)
DepressionMortality$upper[7] <- log(2.46)

では、先ほど作成したデータを見てみよう。

DepressionMortality[,c("author", "TE", "seTE", "lower", "upper")]

##                   author      TE    seTE  lower  upper
## 1    Aaroma et al., 1994  0.7418 0.20217     NA     NA
## 2     Black et al., 1998  0.5603 0.14659     NA     NA
## 3     Bruce et al., 1989  0.9235 0.43266     NA     NA
## 4     Bruce et al., 1994  0.1488 0.15526     NA     NA
## 5    Enzell et al., 1984  0.6035 0.17986     NA     NA
## 6   Fredman et al., 1989 -0.9236 0.99403     NA     NA
## 7    Murphy et al., 1987  0.5675      NA 0.2311 0.9001
## 8   Penninx et al., 1999  0.3816 0.22842     NA     NA
## [...]

このようなデータセットを見つけることは、実際には珍しいことではない。ほとんどの研究では対数リスク比を計算することができるだろうが、その他のいくつかの研究では、（対数変換した）リスク比とその信頼区間しか情報がないことが多いのである。

幸いなことに、 metagen を使用すると、そのようなデータであってもプールすることが可能である。引数 lower と upper には、信頼区間の下限と上限を含む列の名前を指定するだけでよいのである。標準誤差が利用できない場合、 metagen 関数はこの情報を使って効果に重み付けをする。関数の呼び出しは次のようになる。

m.gen_bin <- metagen(TE = TE,
                     seTE = seTE,
                     lower = lower,
                     upper = upper,
                     studlab = author,
                     data = DepressionMortality,
                     sm = "RR",
                     method.tau = "PM",
                     fixed = FALSE,
                     random = TRUE,
                     title = "Depression Mortality (Pre-calculated)")

summary(m.gen_bin)

## Review:     Depression Mortality (Pre-calculated)
##
## [...]
## 
## Number of studies combined: k = 18
## 
##                          RR           95%-CI    z  p-value
## Random effects model 2.0218 [1.6066; 2.5442] 6.00 < 0.0001
## 
## Quantifying heterogeneity:
##  tau^2 = 0.1865 [0.0739; 0.5568]; tau = 0.4319 [0.2718; 0.7462];
##  I^2 = 77.2% [64.3%; 85.4%]; H = 2.09 [1.67; 2.62]
## 
## [...]

出力では、\(K=\) 18 すべての研究がメタ分析で結合できたことがわかる。これは、 metagen が研究7について提供された lower と upper の情報を使用したことを意味する。また、逆分散法を用いた結果は、先ほどの Mantel-Haenszel 法の結果とほぼ同じであることが出力されている。

4.2.3.2 発生率比

発生率 (incidence rate) に基づく効果量（すなわち、発生率比、Chapter 3.3.3）は、 metainc 関数を使用してプールすることが可能である。この関数の引数は metabin と非常によく似ている。

• event.e: 治療・実験群におけるイベント数。

• time.e: 治療・実験群におけるリスクパーソン時間。

• event.c: 対照群におけるイベント数。

• time.c: 対照群におけるリスクパーソン時間。

• method: metabin と同様に、デフォルトのプール法は Mantel and Haenszel によるもの ("MH") である。また、一般的な逆分散プーリング ("Inverse") を利用することも可能である。

• sm: 要約尺度を指定する。発生率比 ("IRR") と発生率差 ("IRD") のどちらかを選ぶことができる。

• incr: ゼロセルの連続性補正のために追加したいインクリメント。

metabin とは対照的に、 metainc はデフォルトでは連続性補正を使用しない。そのため、 MH.exact を TRUE として指定する必要はない。連続性補正は、一般的な逆分散プール法 (method = "Inverse") を選択したときのみ行われる。

今回の実践例では、 EatingDisorderPrevention データセットを使用する。このデータは、摂食障害の発生率に対する大学ベースの予防的介入の効果を検討したメタ分析に基づいている (Harrer et al. 2020)。このデータセットでは、リスクのある人の時間は人-年として表現されている。

“EatingDisorderPrevention” データセット

EatingDisorderPrevention のデータセットも {dmetar} パッケージに直接含まれている。{dmetar} をインストールし、ライブラリからロードした後、 data(SuicidePrevention) を実行すると、自動的に R 環境にデータセットが保存される。これでデータセットが利用できる。もし、{dmetar} がインストールされていない場合は、インターネットから .rda ファイルとしてデータセットをダウンロードして作業ディレクトリに保存し、R Studio ウィンドウでクリックするとインポートすることができる。

いつものように、まずはデータを見てみよう。

library(dmetar)
library(tidyverse)
library(meta)

data(EatingDisorderPrevention)

glimpse(EatingDisorderPrevention)

## Rows: 5
## Columns: 5
## $ Author  <chr> "Stice et al., 2013", "Stice et al., 2017a", "Stice et al., 20…
## $ event.e <dbl> 6, 22, 6, 8, 22
## $ time.e  <dbl> 362, 235, 394, 224, 160
## $ event.c <dbl> 16, 8, 9, 13, 29
## $ time.c  <dbl> 356, 74, 215, 221, 159

効果量のデータのプールには metainc を用い、効果量の指標は発生率比とする。プールには Mantel-Haenszel 法を用い、研究間異質性分散の計算には Paule-Mandel 推定量を用いている。

m.inc <- metainc(event.e = event.e, 
                 time.e = time.e,
                 event.c = event.c,
                 time.c = time.c,
                 studlab = Author,
                 data = EatingDisorderPrevention,
                 sm = "IRR",
                 method = "MH",
                 fixed = FALSE,
                 random = TRUE,
                 method.tau = "PM",
                 hakn = TRUE,
                 title = "Eating Disorder Prevention")

summary(m.inc)

## Review:     Eating Disorder Prevention
## 
##                        IRR           95%-CI %W(random)
## Stice et al., 2013  0.3688 [0.1443; 0.9424]       13.9
## Stice et al., 2017a 0.8660 [0.3855; 1.9450]       18.7
## Stice et al., 2017b 0.3638 [0.1295; 1.0221]       11.5
## Taylor et al., 2006 0.6071 [0.2516; 1.4648]       15.8
## Taylor et al., 2016 0.7539 [0.4332; 1.3121]       40.0
## 
## Number of studies: k = 5
## Number of events: e = 139
## 
##                         IRR           95%-CI     t p-value
## Random effects model 0.6223 [0.3955; 0.9791] -2.91  0.0439
## 
## Quantifying heterogeneity:
##  tau^2 = 0 [0.0000; 1.1300]; tau = 0 [0.0000; 1.0630]
##  I^2 = 0.0% [0.0%; 79.2%]; H = 1.00 [1.00; 2.19]
## 
## Test of heterogeneity:
##     Q d.f. p-value
##  3.34    4  0.5033
## 
## Details on meta-analytical method:
## - Inverse variance method
## - Paule-Mandel estimator for tau^2
## - Q-Profile method for confidence interval of tau^2 and tau
## - Hartung-Knapp adjustment for random effects model (df = 4)

プールされた効果は IRR = 0.62 であることがわかる。この効果は、前の例よりも従来の有意水準にやや近いとはいえ、有意である (\(p=\) 0.04）。プール効果に基づき、予防的介入は1年以内の摂食障害の発生を38%減少させたと言うことが可能である。最後に、異質性分散 \(\tau^2\) の推定値が0であることがわかる。

4.2.4 相関関係

相関は metacor 関数を用いてプールすることができ、これは一般的な逆分散プーリング法を用いる。Chapter 3.2.3.1 では、相関をプールする前に Fisher’s \(z\) 変形が必要であることを説明した。デフォルトでは、 metacor がこの変換を自動的に行ってくれる。したがって、この関数には、研究で報告されたオリジナルの未変換の相関を与えれば十分である。 metacor 関数には、関数固有の引数が2つだけある。

• cor. （変換前の）相関係数。
• n. 調査における観測数。

metacor の機能を説明するために、 HealthWellbeing のデータセットを使用する。このデータセットは、健康と幸福の関連性を調べた大規模なメタ分析に基づいている (Ngamaba, Panagioti, and Armitage 2017)。

“HealthWellbeing” データセット

HealthWellbeing のデータセットも {dmetar} パッケージに直接含まれている。{dmetar} をインストールし、ライブラリからロードした後、 data(SuicidePrevention) を実行すると、自動的に R 環境にデータセットが保存される。これでデータセットが利用できる。

もし、{dmetar} がインストールされていない場合は、インターネットから .rda ファイルとしてデータセットをダウンロードして作業ディレクトリに保存し、R Studio ウィンドウでクリックするとインポートすることができる。

それでは、データを見てみよう。

library(dmetar)
library(tidyverse)
library(meta)

data(HealthWellbeing)
glimpse(HealthWellbeing)

## Rows: 29
## Columns: 5
## $ author     <chr> "An, 2008", "Angner, 2013", "Barger, 2009", "Doherty, 2013"…
## $ cor        <dbl> 0.620, 0.372, 0.290, 0.333, 0.730, 0.405, 0.292, 0.388, 0.3…
## $ n          <dbl> 121, 383, 350000, 1764, 42331, 112, 899, 870, 70, 67, 246, …
## $ population <chr> "general population", "chronic condition", "general populat…
## $ country    <chr> "South Korea", "USA", "USA", "Ireland", "Poland", "Australi…

このメタ分析では、研究間の異質性がかなり高いと予想されるため、ランダム効果モデルを採用する。また、\(\tau^2\)は制限付き最尤推定量を用いている。

m.cor <- metacor(cor = cor, 
                 n = n,
                 studlab = author,
                 data = HealthWellbeing,
                 fixed = FALSE,
                 random = TRUE,
                 method.tau = "REML",
                 hakn = TRUE,
                 title = "Health and Wellbeing")
summary(m.cor)

## Review:     Health and Wellbeing
##                        COR           95%-CI %W(random)
## An, 2008            0.6200 [0.4964; 0.7189]        2.8
## Angner, 2013        0.3720 [0.2823; 0.4552]        3.4
## Barger, 2009        0.2900 [0.2870; 0.2930]        3.8
## Doherty, 2013       0.3330 [0.2908; 0.3739]        3.7
## Dubrovina, 2012     0.7300 [0.7255; 0.7344]        3.8
## Fisher, 2010        0.4050 [0.2373; 0.5493]        2.8
## [...]
## 
## Number of studies combined: k = 29
## Number of observations: o = 853794
## 
##                         COR           95%-CI     t  p-value
## Random effects model 0.3632 [0.3092; 0.4148] 12.81 < 0.0001
## 
## Quantifying heterogeneity:
##  tau^2 = 0.0241 [0.0141; 0.0436]; tau = 0.1554 [0.1186; 0.2088];
##  I^2 = 99.8% [99.8%; 99.8%]; H = 24.14 [23.29; 25.03]
## 
## Test of heterogeneity:
##         Q d.f. p-value
##  16320.87   28       0
## 
## Details on meta-analytical method:
## - Inverse variance method
## - Restricted maximum-likelihood estimator for tau^2
## - Q-profile method for confidence interval of tau^2 and tau
## - Hartung-Knapp adjustment for random effects model
## - Fisher's z transformation of correlations

プールされた健康と幸福の関連は \(r=\) 0.36 であり、この効果は有意であることがわかる（\(p<\) 0.001）。Cohen の法則に従えば、これは中程度のサイズの相関とみなすことができる。

出力では、 metacor がすでに Fisher’s \(z\) 変換された相関を元の形式に再変換している。しかし、詳細セクションの最後の行を見ると、確かに \(z\) 値が効果をプールするために使用されていることがわかる。最後に、このメタ分析で推定された異質性分散は、0より有意に大きいことがわかる。

4.2.5 プール平均

平均のメタ分析は、 metamean 関数を用いて行うことが可能である。この関数は、データをプールするために一般的な逆分散法を使用する。 metamean を使用する場合、まず、生の平均値と対数変換された平均値のどちらでメタ分析を行うかを決定する必要がある。

オッズ比やリスク比とは対照的に、平均の対数変換は通常必要ない。しかし、非負の量（例えば、身長）の平均を扱うときや、いくつかの平均がゼロに近いときには、変換を使用することが推奨される。これは sm 引数で制御される。sm = "MRAW" と設定すると、生の平均がプールされる。sm = "MLN" とすると、対数変換が行われる。関数固有の引数は以下の通りである。

• n: 観測数。
• mean: 平均値。
• sd: 平均の標準偏差。
• sm: プーリングに使用する要約尺度の種類（上記参照）。

今回の実践例では、 BdiScores データセットを使用する。このデータセットには、心理療法や抗うつ剤の治験に参加しているうつ病患者のサンプルで測定された Beck Depression Inventory II (Beck, Steer, and Brown 1996) の平均スコアが含まれている (Furukawa et al. 2020)。

“BdiScores” データセット

BdiScores のデータセットも {dmetar} パッケージに直接含まれている。{dmetar} をインストールし、ライブラリからロードした後、 data(SuicidePrevention) を実行すると、自動的に R 環境にデータセットが保存される。これでデータセットが利用できる。もし、{dmetar} がインストールされていない場合は、インターネットから .rda ファイルとしてデータセットをダウンロードして作業ディレクトリに保存し、R Studio ウィンドウでクリックするとインポートすることができる。

library(dmetar)
library(tidyverse)
library(meta)
data(BdiScores)

# 最初の４列だけ必要
glimpse(BdiScores[,1:4])

## Rows: 6
## Columns: 4
## $ author <chr> "DeRubeis, 2005", "Dimidjian, 2006", "Dozois, 2009", "Lesperanc…
## $ n      <dbl> 180, 145, 48, 142, 301, 104
## $ mean   <dbl> 32.6, 31.9, 28.6, 30.3, 31.9, 29.8
## $ sd     <dbl> 9.4, 7.4, 9.9, 9.1, 9.2, 8.6

ここでの目標は、この研究のコレクションに基づいて、全体の平均的なうつ病スコアを計算することである。ランダム効果モデルと制限付き最尤推定量を使って、データセット内の生の平均をプールする。その結果を m.mean というオブジェクトに保存する。

m.mean <- metamean(n = n,
                   mean = mean,
                   sd = sd,
                   studlab = author,
                   data = BdiScores,
                   sm = "MRAW",
                   fixed = FALSE,
                   random = TRUE,
                   method.tau = "REML",
                   hakn = TRUE,
                   title = "BDI-II Scores")
summary(m.mean)

## Review:     BDI-II Scores
## 
##                     mean             95%-CI %W(random)
## DeRubeis, 2005   32.6000 [31.2268; 33.9732]       18.0
## Dimidjian, 2006  31.9000 [30.6955; 33.1045]       19.4
## Dozois, 2009     28.6000 [25.7993; 31.4007]        9.1
## Lesperance, 2007 30.3000 [28.8033; 31.7967]       17.0
## McBride, 2007    31.9000 [30.8607; 32.9393]       20.7
## Quilty, 2014     29.8000 [28.1472; 31.4528]       15.8
## 
## Number of studies: k = 6
## Number of observations: o = 920
## 
##                         mean             95%-CI
## Random effects model 31.1221 [29.6656; 32.5786]
## 
## Quantifying heterogeneity:
##  tau^2 = 1.0937 [0.0603; 12.9913]; tau = 1.0458 [0.2456; 3.6043]
##  I^2 = 64.3% [13.8%; 85.2%]; H = 1.67 [1.08; 2.60]
## 
## Test of heterogeneity:
##      Q d.f. p-value
##  14.00    5  0.0156
## 
## Details on meta-analytical method:
## - Inverse variance method
## - Restricted maximum-likelihood estimator for tau^2
## - Q-Profile method for confidence interval of tau^2 and tau
## - Hartung-Knapp adjustment for random effects model (df = 5)
## - Untransformed (raw) means

ランダム効果モデルを仮定したプール平均は \(m\) = 31.12である。また、このメタ分析における研究間異質性分散 \(\tau^2\) は、0より有意に大きいことがわかる。

4.2.6 割合

metaprop 関数は、割合のプールに使用することが可能である。Chapter 3.2.2で、メタ分析を行う前に割合を logit 変換しておくとよいことを既に説明した。sm = "PLOGIT" を指定すると、 metaprop 関数が自動的にこれを行う。もし、生の比率をプールしたい場合は、 sm = "PRAW" を使用することができるが、これは推奨されていないことを覚えていただきたい。

metaprop が割合のプールを行うデフォルトの方法は、少々特殊である。logit 変換された値を使用する場合、この関数はプールのために逆分散法を使用せず、一般化線形混合効果モデル (generalized linear mixed-effects model, GLMM) を構築する。基本的には、この関数はロジスティック回帰モデルをデータに当てはめ、真の効果量が研究間で異なるという事実を説明するために、ランダム効果を含んでいる。

「混合効果モデル」という言葉を聞いたことがあるだろう。このようなモデルは、多くの研究分野の一次研究でよく使用されている。この章では、混合効果モデルの特殊な応用例であるサブグループ解析やメタ回帰について説明し、このテーマをもう少し深く掘り下げていきる。しかし、今のところ、混合効果モデルとは何かという一般的な考え方を理解しておけば十分である。

混合効果モデルは、「固定」成分と「ランダム」成分の両方を含む回帰モデルである。固定要素は、\(\beta\) 重みである。非常に単純な回帰モデルでは、切片 \({\beta_0}\) と回帰項 \({\beta_1}x\) の2つの \(\beta\) 項が含まれる。これらを組み合わせて、他の量 \(x\) を通じて観測データ \(y\) を予測する。この予測は完全とは言い難く、ランダムな誤差 \(\epsilon_i\) が残る。これを合わせると、次のような式になる。

\[\begin{equation} {y}_i = {\beta_0} + {\beta_1}x_i + \epsilon_i \tag{4.16} \end{equation}\]

重要なのは、この式の\(\beta\) 重みの値は各観測 \(i\) で同じままであることである。\(x\) の値は観測ごとに変わるだろうが、\(\beta_0\) と \(\beta_1\) は固定なので変わることはない。

この回帰式は、ランダム効果を加えると混合効果モデルになる。このランダム効果項を \(u_i\) と表記する。添え字 \(i\) で示すように、ランダム効果項は各オブザベーションで異なる値を持つことができる。\(u_i\) 項は0を中心とし、固定効果による推定値を増加させたり、減少させたりすることができる。

\[\begin{equation} {y}_i = {\beta_0} + {\beta_1}x_i + u_i + \epsilon_i \tag{4.17} \end{equation}\]

メタ分析は、このモデルの特殊なタイプで、\(\beta_1x_i\) 項が存在しないものと見なすことができる。このモデルは切片 \(\beta_0\) のみを含み、これはランダム効果モデルにおける全体の効果量 \(\mu\) に相当する。\(u_i\) と \(\epsilon_i\) の部分は、メタ分析における \(\zeta_k\) と \(\epsilon_k\) の誤差項に相当する。このことから、メタ分析は混合効果回帰モデルと等価であることがわかる。しかし、この混合効果モデルには切片とそれに連なるランダム効果しか含まれていない。二項ロジットリンクを用いると²⁶、したがって、（一般化）ロジスティック混合効果モデルを適用してプール効果を推定することが可能である。

GLMM は割合だけでなく、オッズ比や発生率比のような二値やカウントデータに基づく他のアウトカム指標にも適用できる (Stijnen, Hamza, and Özdemir 2010) 。GLMMは二値アウトカムデータのメタ分析に普遍的に推奨されているわけではないが (Bakbergenuly and Kulinskaya 2018) 、割合についてはその使用が提唱されている (Schwarzer et al. 2019)。

GLMM を metaprop の一部として使用すると、次の3つの意味がある：(1) 出力は、各効果のメタ分析重みを表示しない、 (2) \(\tau^2\)推定量は "ML" にしか設定できない（最尤法を使用してGLMMを推定するので）、 (3) \(\tau^2\) の推定量の信頼区間が存在しなくなる。この情報が必要な場合は、逆分散メタ分析の実行に切り替えることが可能である。 metaprop には、5つの関数固有の引数がある。

• event. イベント数。

• n. 観測数。

• method. プーリング手法。GLMM (method = "GLMM") あるいは逆 (Inverse) 分散プーリング (method = "Inverse") のいずれかを指定することができる。

• incr. ゼロセルでの連続性補正のために追加される増分。これは、逆分散プーリングが使用される場合にのみ関係する。

• sm. 使用する要約尺度を指定する。sm = "PLOGIT" (デフォルト)とすることで、logit 変換された比率を使用することが推奨される。

metaprop 関数の説明のために、 OpioidMisuse データセットを使用することにする。このデータは、米国の青年・若年成人における処方オピオイドの誤用12ヶ月有病率を調査したメタ分析から得られたものである (Jordan et al. 2017)。

“OpioidMisuse” データセット

OpioidMisuse のデータセットも {dmetar} パッケージに直接含まれている。{dmetar} をインストールし、ライブラリからロードした後、 data(SuicidePrevention) を実行すると、自動的に R 環境にデータセットが保存される。これでデータセットが利用できる。もし、{dmetar} がインストールされていない場合は、インターネットから .rda ファイルとしてデータセットをダウンロードして作業ディレクトリに保存し、R Studio ウィンドウでクリックするとインポートすることができる。

データセットをロードして見てみよう。

library(dmetar)
library(meta)
library(tidyverse)

data(OpioidMisuse)
glimpse(OpioidMisuse)

## Rows: 15
## Columns: 3
## $ author <chr> "Becker, 2008", "Boyd, 2009", "Boyd, 2007", "Cerda, 2014", "Fie…
## $ event  <dbl> 2186, 91, 126, 543, 6496, 10850, 86, 668, 843, 647, 11521, 1111…
## $ n      <dbl> 21826, 912, 1084, 7646, 55215, 114783, 527, 9403, 11274, 8888, …

GLMM と logit 変換された割合を用いて有病率データをプールする。

m.prop <- metaprop(event = event,
                   n = n,
                   studlab = author,
                   data = OpioidMisuse,
                   method = "GLMM",
                   sm = "PLOGIT",
                   fixed = FALSE,
                   random = TRUE,
                   hakn = TRUE,
                   title = "Opioid Misuse")
summary(m.prop)

## Review:     Opioid Misuse
##                proportion           95%-CI
## Becker, 2008       0.1002 [0.0962; 0.1042]
## Boyd, 2009         0.0998 [0.0811; 0.1211]
## Boyd, 2007         0.1162 [0.0978; 0.1368]
## Cerda, 2014        0.0710 [0.0654; 0.0770]
## Fiellin, 2013      0.1176 [0.1150; 0.1204]
## [...]
## 
## 
## Number of studies combined: k = 15
## Number of observations: o = 434385
## Number of events: e = 41364
## 
##                      proportion           95%-CI
## Random effects model     0.0944 [0.0836; 0.1066]
## 
## Quantifying heterogeneity:
##  tau^2 = 0.0558; tau = 0.2362; I^2 = 98.3% [97.9%; 98.7%]; H = 7.74 [6.92; 8.66]
## 
## Test of heterogeneity:
##       Q d.f.  p-value             Test
##  838.21   14 < 0.0001        Wald-type
##  826.87   14 < 0.0001 Likelihood-Ratio
## 
## Details on meta-analytical method:
## - Random intercept logistic regression model
## - Maximum-likelihood estimator for tau^2
## - Hartung-Knapp adjustment for random effects model
## - Logit transformation
## - Clopper-Pearson confidence interval for individual studies

出力では、選択された研究における処方オピオイドの誤用のプールされた12ヶ月の有病率は9.4％であり、信頼区間の範囲は8.36から10.66％であることがわかる。

前述したように、この出力には各効果の個別の重みが表示されていない。同じように、研究間の異質性の推定値（\(\tau^2 =\) 0.056）が得られるが、その周りの信頼区間はない。

\[\tag*{$\blacksquare$}\]

4.3 演習問題

知識を試そう！

1. 固定効果モデルとランダム効果モデルの違いは何か？

2. 固定効果モデルとランダム効果モデルの結果が同じになるケースは考えられるか。

3. \(\tau^2\) とは何か？どのように推定するのか？

4. Knapp-Hartung の調整はどの分布に基づいているか？どのような効果があるか？

5. 「逆分散」 (inverse-variance) プーリングとはどういう意味か？この方法が最適解でないのはどのような場合か？

6. 二値アウトカムデータをメタ分析したい。試験群の観察数はほぼ同じで、観察された事象は非常にまれで、治療効果が大きくなることは期待できない。どのようなプール方法を使用するか？

7. GLMM はどのようなアウトカム指標に使用できるのか。

問題の解答は、本書の巻末 Appendix A にある。

4.4 要約

• 統計学において、モデルは、観測されたデータが生成された過程を記述する、簡略化された「理論」と見なすことができる。メタ分析には、固定効果モデルとランダム効果モデルの2つのモデルがある。

• 固定効果モデルが真の効果量が1つであることを仮定しているのに対し、ランダム効果モデルは真の効果量がメタ分析内でも変化することを述べている。したがって、ランダム効果モデルの目的は、データの根底にある真の効果量の分布の平均を見つけることである。

• ランダム効果メタ分析では、真の効果量の分散 \(\tau^2\) （研究間異質性分散とも呼ばれる）を推定する必要がある。これにはいくつかの方法があり、どれが一番効果的かは文脈によって異なる。

• プール効果量を計算する最も一般的な方法は、逆分散法である。しかし、二値アウトカム・データでは、Mantel-Haenszel 法のような他のアプローチが望ましい場合がある。

• {meta} パッケージには、事前に計算された効果量データのメタ分析を行う関数と、さまざまな種類の「生の」アウトカムデータに対して使用できる関数群がある。