10 「マルチレベル」メタ分析

高度な分析へようこそ。このガイドの前のパートでは、ほとんどすべてのメタ分析に非常に関連すると思われるトピックに深く潜ってみよう。この背景を踏まえて、より高度なテクニックに進む。

以下の方法は、基礎となる数学あるいは R での実装がより複雑であるため、「高度」であるとみなした。しかし、このガイドの前の章を読んでいれば、この後に続く内容を理解し、実装するのに十分な能力を備えているはずである。以下のトピックの多くは、それ自身の本に値するものであり、ここで取り上げるものは、簡単な紹介としてのみ考慮されるべきである。ここで取り上げた内容は、あくまでも簡単な紹介と考えていただきたい。

最初の章では、「マルチレベル」メタ分析というトピックを扱う。なぜ「マルチレベル」という言葉をカギカッコで囲むのか、不思議に思われるだろう。ある研究を「マルチレベル」メタ分析と表現することは、暗に「標準的な」メタ分析に比べて特別なものであることを示している。

しかし、これは正しくはない。あらゆるメタ分析モデルは、結果をプールするために、データのマルチレベル構造を前提にしている (Pastor and Lazowski 2018)。前の章で、私たちはすでに何度かマルチレベル (メタ分析) モデルを、知らないうちに使っている。

マルチレベルメタ分析というと、すぐに思いつくのは 3 レベルメタ分析モデルではないだろうか。このモデルは、確かに私たちが既に知っている固定効果モデルやランダム効果モデルとは多少異なる。そこで、この章では、まず、なぜメタ分析が自然にデータのマルチレベル構造意味をするのか、そして、従来のメタ分析をどのようにして 3 レベルモデルに拡張できるのかを説明する。また、いつものように、このようなモデルを R でどのように適合させることができるかを、実際の例を使って見ていこう。

10.1 メタ分析のマルチレベル性

メタ分析がなぜデフォルトでマルチレベルになるのかを知るために、Chapter 4.1.2 で説明したランダム効果モデルの式に戻ってみよう。

\[\begin{equation} \hat\theta_k = \mu + \epsilon_k + \zeta_k \tag{10.1} \end{equation}\]

ランダム効果モデルで $\epsilon_k$ (「イプシロン・k」と読む) と $\zeta_k$ (「ゼータ・k」と読む) という項が導入されているのは、2 つの変動源があると仮定しているからだと説明してきた。1つ目は、個々の研究のサンプルエラー( $\epsilon_k$ )によるもので、これにより効果量推定値が真の効果量 $\theta_k$ から差が出ることになる。

2 つ目の $\zeta_k$ は、研究間の異質性を表している。この異質性は、ある研究 $k$ の真の効果量が、やはり真の効果量の包括的な分布の一部に過ぎないという事実によって引き起こされる。この分布は、個々の真の効果量 $\theta_k$ が引き出されたところから導かれる。したがって、ランダム効果モデルにおける私たちの目的は、$\mu$ (「ミュー」と読む) で示される真の効果量の分布の平均を推定することである。

$\epsilon_k$ と $\zeta_k$ の 2 つの誤差項は、メタ分析データにおける「参加者」レベル (レベル 1) と「研究」レベル (レベル2) の 2 つのレベルに対応している。以下の Figure 10.1 は、この構造を象徴している。

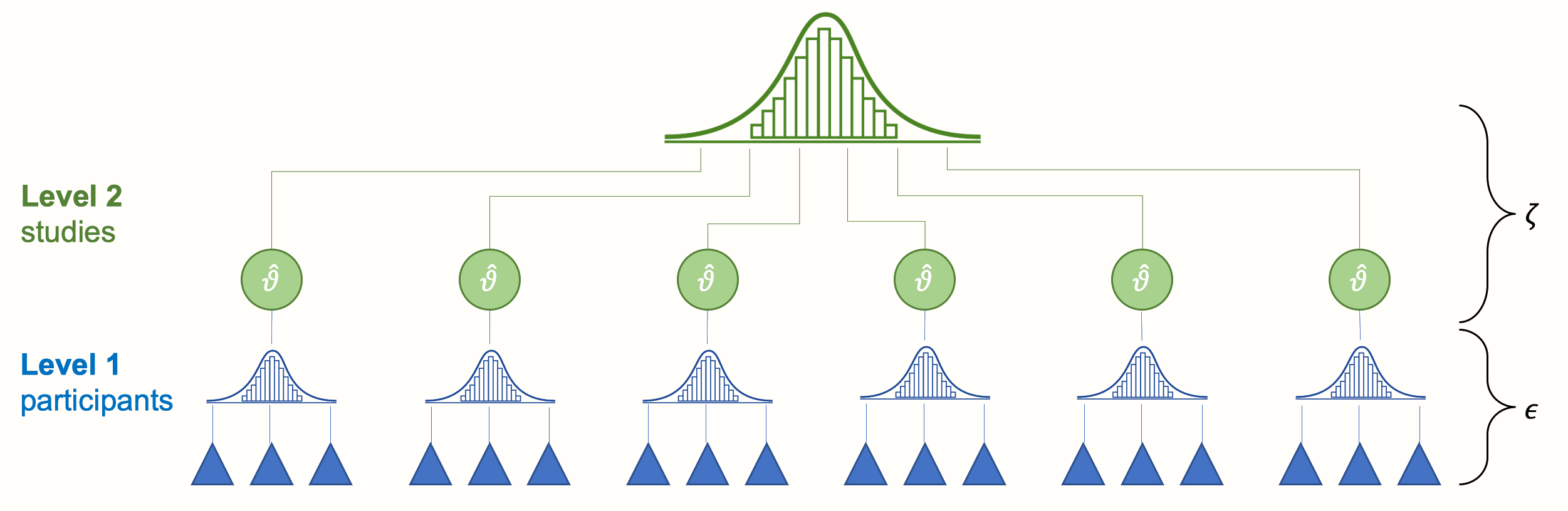
Figure 10.1: 従来のランダム効果モデルのマルチレベル構造

最下層 (レベル 1) には、参加者 (研究分野によっては、患者、検体など) がいる。これらの参加者は、より大きな単位であるメタ分析に含まれる研究の一部である。この上にある研究の層は、私たちの第２レベルを構成している。

メタ分析を行う場合、レベル1のデータは通常すでに「プール」された形で届く (例えば、論文の著者は生データの代わりに研究サンプルの平均と標準偏差を提供してくれる)。しかし、レベル 2 (研究レベル) のプールは、メタ分析の一部として実行されなければならない。伝統的に、このようなタイプのデータはネストと呼ばれ、参加者が研究内に「ネスト」されていると言うことが可能である。

ここで、ランダム効果モデルの式 (10.1) に戻ってみよう。この式は暗黙のうちにメタ分析データのマルチレベル構造を記述している。これをより明確にするために、式を 2 つに分割し、それぞれが 2 つのレベルのうちの 1 つに対応するようにする必要がある。そうすると、次のような結果が得られる。

レベル1 (参加者) モデル：

\[\begin{equation} \hat\theta_k = \theta_k + \epsilon_k \tag{10.2} \end{equation}\]

レベル2 (研究) モデル：

\[\begin{equation} \theta_k = \mu + \zeta_k \tag{10.3} \end{equation}\]

すでにお気づきかもしれないが、最初の式の $\theta_k$ を 2 番目の式の定義に置き換えればよい。そうすると、先ほどのランダム効果モデルの式とまったく同じ式が得られる。固定効果モデルもこのように書くことが可能である。$\zeta_k$ をゼロに設定するだけである。明らかに、私たちのメタ分析モデルは、すでにマルチレベルの特性を「内蔵」している。これは、私たちのデータでは、参加者が研究内でネストされていると仮定しているので、この特性を示している。

このように、メタ分析には多階層構造が備わっていることがわかる。データを生成した特定のメカニズムをよりよく捉えるために、この構造をさらに拡張することが可能である。そこで、3 レベルモデル (Cheung 2014; Assink, Wibbelink, et al. 2016) の出番となる。

統計的独立性は、メタ分析で効果量をプールするときの中心的な前提条件の一つである。効果量の間に依存関係がある (効果量に相関がある) 場合、異質性を人為的に減少させ、その結果、偽陽性の結果につながる可能性がある。この問題は分析単位エラーとして知られており、以前すでに取り上げた (Chapter 3.5.2 参照)。効果量の依存性は、様々な原因から生じる可能性がある (Cheung 2014)。

個々の研究の著者によって導入された依存性: 例えば、研究を実施する科学者が複数のサイトからデータを収集したり、複数の介入を一つの対照群と比較したり、同じアウトカムを測定するために異なる質問票を使用したりすることがある。これらのシナリオのすべてにおいて、報告されたデータには何らかの依存性があると考えることが可能である。
メタ分析者自身によって導入される依存性: 例として、ある心理メカニズムに注目したメタ分析を考えてみよう。このメタ分析には、世界の異なる文化圏 (例えば、東アジアと西欧社会) で行われた研究が含まれている。心理メカニズムの種類によっては、同じ文化圏で行われた研究の方が、異なる文化圏で行われた研究よりも結果が似ていることもあり得る。

メタ分析モデルの構造に第 3 の層を組み込むことで、このような依存性を考慮することができる。例えば、異なる質問票に基づく効果量が研究内でネストされているモデルが考えられる。あるいは、研究が文化圏にネストされているモデルを作成することもできる。これにより、次の図に示すような 3 階層のメタ分析モデルが構築される。

3 レベルのモデルには 3 つのプール段階があることがわかる。まず、研究者自身が、一次研究の個々の参加者の結果を「プール」し、集約した効果量を報告する。次に、レベル 2 において、これらの効果量は、$\kappa$ (「カッパ」と読む) で示されるいくつかのクラスタ内にネストされている。これらのクラスタは、個々の研究 (すなわち、多くの効果量が1つの研究にネストされている)、または研究のサブグループ (すなわち、多くの研究が1つのサブグループにネストされており、各研究は 1 つの効果量にのみ寄与する) のいずれかである可能性がある。

最後に、集計されたクラスタ効果をプールすると、全体の真の効果量 $\mu$ になる。概念的には、この平均効果は、固定効果モデルまたはランダム効果モデルでプールされた真の効果 $\mu$ (「ミュー」と読む) に非常に近いものである。しかし、その違いは、私たちのデータにおける依存効果量を明示的に考慮したモデルに基づいている点にある。

3 レベルモデルの式は、これまでと同じレベル表記で書き表すことができる。最大の違いは、2 つの数式ではなく、3 つの数式を定義する必要があることだ。

レベル1モデル：

\[\begin{equation} \hat\theta_{ij} = \theta_{ij} + \epsilon_{ij} \tag{10.4} \end{equation}\]

レベル2モデル：

\[\begin{equation} \theta_{ij} = \kappa_{j} + \zeta_{(2)ij} \tag{10.5} \end{equation}\]

レベル3モデル：

\[\begin{equation} \kappa_{j} = \mu + \zeta_{(3)j} \tag{10.6} \end{equation}\]

ここで、$\hat\theta_{ij}$ は、真の効果量 $\theta_{ij}$ の推定値である。 $ij$ という用語は、「クラスタ $j$ にネストされているある効果量 $i$ 」と読み替えることができる。パラメータ $\kappa_{j}$ はクラスタ $j$ の平均効果量であり、$\mu$ は全体的な平均母集団効果である。前と同じように、これらの数式をつなぎ合わせて、数式を 1 行に減らすことができる。

\[\begin{equation} \hat\theta_{ij} = \mu + \zeta_{(2)ij} + \zeta_{(3)j} + \epsilon_{ij} \tag{10.7} \end{equation}\]

ランダム効果モデルとは異なり、この式には2つの不均質性項が含まれていることがわかる。一つは $\zeta_{(2)ij}$で、これはレベル２のクラスタ内 (within-cluster) 異質性である (つまり、クラスタ $j$ 内の真の効果量は、平均 $\kappa_j$ の分布に従う)。もう一つは $\zeta_{(3)j}$ で、これはレベル 3 のクラスタ間 (between-cluster) 異質性である。結果、3 レベルメタ分析適合モデルでは、異質性分散 $\tau^2$ は一つではなく、レベル 2 用とレベル 3 用の 2 つ推計しなければならない。

{metafor} パッケージは、特にメタ分析的な 3 レベルモデルの適合に適している。これは、 (制限付き) 最尤法を用いて行う。以前は、メタ分析の実行に主に {meta} パッケージの関数を使用していた。なぜなら {meta} の方が若干専門的でなく、初心者に適しているためである。しかし、Chapter 8.3.3 で見たように、 {metafor} パッケージも、データを正しく準備すればかなり使いやすくなっている。具体的にどのように {metafor} を使って R の 3 レベルモデルに適合させるかは、次のセクションのトピックになる⁴⁶。

10.2 R で３レベルのメタ分析モデルを適合

前述したように、３レベルのメタ分析モデルを適合させるためには、 {metafor} パッケージが必要である。そのため、まずライブラリからロードする必要がある。

library(metafor)

この例では、Chernobyl データセットを使用する。このデータセットは、1986年のチェルノブイリ原発事故 (Møller and Mousseau 2015) によって引き起こされた電離放射線 (「核汚染」) とヒトの突然変異率の相関を調べた実際のメタ分析に緩く基づいている。

“Chernobyl” データセット

Chernobyl データセットは {dmetar} パッケージに含まれている。{dmetar} をインストールし、ライブラリからロードした後、 data(TherapyFormats) を実行すると、自動的に R 環境にデータセットが保存される。これでデータセットが使用できるようになる。

{dmetar} がインストールされていない場合は、Internet から .rda ファイルとしてデータセットをダウンロードし、作業ディレクトリに保存してから、R Studio ウィンドウでクリックしてインポートすることが可能である。

# Load data set from 'dmetar'
library(dmetar)
data("Chernobyl")

データの一般的な構造を見るために、head 関数を使用しよう。これは、先ほどグローバル環境にロードしたデータフレームの最初の 6 行を表示する。

head(Chernobyl)

##                       author  cor   n    z se.z var.z radiation es.id
## 1 Aghajanyan & Suskov (2009) 0.20  91 0.20 0.10  0.01       low  id_1
## 2 Aghajanyan & Suskov (2009) 0.26  91 0.27 0.10  0.01       low  id_2
## 3 Aghajanyan & Suskov (2009) 0.20  92 0.20 0.10  0.01       low  id_3
## 4 Aghajanyan & Suskov (2009) 0.26  92 0.27 0.10  0.01       low  id_4
## 5     Alexanin et al. (2010) 0.93 559 1.67 0.04  0.00       low  id_5
## 6     Alexanin et al. (2010) 0.44 559 0.47 0.04  0.00       low  id_6

このデータセットには 8 つの列がある。最初の列は author で、研究の名前が表示されている。cor 列は放射線被曝と突然変異率の (未変換の) 相関を示し、n はサンプルサイズを示す。z、se.z、var.z 列は Fisher- $z$ で変換した相関 (Chapter 3.2.3.1) とその標準誤差および分散である。radiation 列はモデレーターとして機能し、効果量を全体的に放射線被曝量の低い (low) サブグループと高いサブグループに分割する。es.id 列には、各効果量 (すなわち、データフレームの各行) の識別用 ID を格納している。

このデータセットで特徴的なことは、 author に繰り返し入力されていることである。これは、このメタ分析におけるほとんどの研究が、1つ以上の観察された効果量に貢献しているからである。いくつかの研究では、突然変異を測定するためにいくつかの方法を用いたり、複数のタイプの指標となる人物 (例えば、被曝した両親とその子孫) を用いたりしており、これらすべてが研究ごとに複数の効果をもたらす。

この構造を見ると、このデータセットの効果量が独立していないことは明らかである。これらはネスト構造になっており、様々な効果量が 1 つの研究にネストされている。したがって、私たちのデータにおけるこれらの依存性を適切にモデル化するために、3 レベルのメタ分析に適合させることは良いアイデアだろう。

10.2.1 モデルの適合

3 レベルのメタ分析モデルは、{metafor} の rma.mv 関数を使用して適合させることが可能である。以下は、この関数の最も重要な引数のリストと、それらの引数の指定方法である。

yi. 計算された効果量を含むデータセットの列の名前。この例では、これは z である。Fisher- $z$ で変換された相関は、“未変換”の相関よりも数学的特性が優れていることがある。
V. 計算された効果量の分散を含む、データセットの列の名前。この場合、var.z となる。また、$SE_k^2 = v_k$ であるから、効果量の 2 乗標準誤差を使用することも可能である。
slab. {meta} の studlab と同様に、研究ラベルを含むデータセットの列の名前。
data. データセットの名前。
test. 回帰係数に適用する検定。"z" (デフォルト) と "t" (推奨; Knapp-Hartung 法に類似した検定を使用) から選択することが可能である。
method. モデルのパラメータを推定するために用いる手法。REML (推奨; 制限付き最尤法) と ML (最尤法) の両方が利用可能。他のタイプの研究間不均一性推定量 (例えば Paule-Mandel) はここでは適用できないことに注意しておこう。

しかし、最も重要な議論は、randomである。間違いなく、最も厄介なものでもある。この引数では、(ネストされた) ランダム効果を定義する数式を指定する。3 レベルモデルの場合、式は常に ~ 1 で始まり、縦棒 | が続く。縦棒の後ろでは、グループ化変数 (研究、測定、地域など) にランダム効果を割り当てる。このグルーピング変数は、各グループに異なる効果 (すなわち切片) を仮定するようにモデルに指示すので、しばしば ランダム化切片 と呼ばれる。

3 レベルモデルでは、2 つのグループ化変数がある。1 つはレベル 2 で、もう 1 つはレベル 3 である。私たちは、これらのグルーピング変数がネストになっていると仮定する。すなわち、レベル 2 でのいくつかの効果が一緒になって、レベル 3 でのより大きなクラスタを構成している。

このようなネストしたランダム効果を仮定するために、rma.mv に特別な方法を指示すことが可能である。これは、スラッシュ (/) を使用して、上位と下位のグループ化変数を分離するものである。/ の左側には、レベル 3 (クラスタ) 変数を入れる。右側には、大きなクラスタにネストされた低次の変数を入れる。したがって、式の一般的な構造は ~ 1 | cluster/effects_within_cluster のようになる。

この例では、個々の効果量 (レベル2； es.id で定義) は、研究 (レベル 3; author で定義) 内にネストされていると仮定している。この結果、以下の式が得られる: ~ 1 | author/es.id。完全な rma.mv 関数呼び出しは次のようになる。

full.model <- rma.mv(yi = z, 
                     V = var.z, 
                     slab = author,
                     data = Chernobyl,
                     random = ~ 1 | author/es.id, 
                     test = "t", 
                     method = "REML")

出力には full.model という名前を付けることとした。結果の概要を表示すには、summary 関数を使用する。

summary(full.model)

## Multivariate Meta-Analysis Model (k = 33; method: REML)
## [...]   
## Variance Components:
## 
##             estim    sqrt  nlvls  fixed        factor 
## sigma^2.1  0.1788  0.4229     14     no        author 
## sigma^2.2  0.1194  0.3455     33     no  author/es.id 
## 
## Test for Heterogeneity:
## Q(df = 32) = 4195.8268, p-val < .0001
## 
## Model Results:
## 
## estimate      se    tval    pval   ci.lb   ci.ub 
##   0.5231  0.1341  3.9008  0.0005  0.2500  0.7963  *** 
## [...]

まず、「分散成分」 (Variance Components) を見てみよう。ここでは、モデルの各レベルについて計算されたランダム効果分散を見ることが可能である。最初の sigma^2.1 は、レベル 3 のクラスタ間分散 (between cluster variance) を示している。この例では、 (クラスタがこのモデルにおける研究を表しているため) これは従来のメタ分析における研究間異質性分散 $\tau^2$ に相当する。

2 番目の分散成分 sigma^2.2 は、クラスタ内の分散 (within cluster variance) (レベル 2) を示している。nlvls の列では、各レベルのグループの数を示している。レベル 3 は 14 グループあり、$K=$ 14 件の研究に相当する。2 行目に示すように、これらの 14 の研究は、33 の効果量を含む。

Model Results の下に、プール効果の推定値がある。$z=$ 0.52 (95%CI: 0.25–0.80) である。解釈を容易にするために、効果を正規の相関に変換することが推奨される。これは、 {esc} パッケージの convert_z2r 関数を使用して行うことが可能である。

library(esc)
convert_z2r(0.52)

## [1] 0.4777

この結果、約 $r \approx$ 0.48 の相関が得られることがわかる。これは大きいといえるだろう。チェルノブイリの放射線被曝と突然変異率の間には、かなりの相関があるようだ。

出力された「異質性の検定」は、私たちのデータにおける真の効果量の差を指摘している ($p<$ 0.001)。しかし、この結果は、あまり有益ではない。私たちは、私たちのモデルの各レベルによって捕捉された異質性の分散の正確な量に、より興味がある。異質性のどれだけが研究内の差 (レベル 2) に起因し、どれだけが研究間の差 (レベル 3) に起因しているかを知ることは良いことだろう。

10.2.2 レベル間の分散分布

$I^2$ のマルチレベル版を計算することでこの疑問に答えることができる (Cheung 2014)。従来のメタ分析では、$I^2$ はサンプリングエラーに起因しない変動量を表した (Chapter 5.1.2 ;すなわち、研究間異質性)。3 レベルモデルでは、この異質性の分散は 2 つの部分に分けられる。1 つはクラスタ内の真の効果量の差に起因し、もう 1 つはクラスタ間の変量に起因するものである。したがって、レベル 2 またはレベル 3 のいずれかに関連する全変動のパーセンテージを定量化する 3 つの値 ($I^2$) が存在する。

“var.comp” 関数

var.comp 関数は、{dmetar} パッケージに含まれている。{dmetar} がインストールされ、コンピュータに読み込まれると、この関数を使用できるようになる。もし、{dmetar} をインストールしていない場合は、以下の手順でインストールできる。

関数のソースコードにアクセスするオンライン.
ソースコード全体をコンソール (R Studio の左下ペイン) にコピー＆ペーストし、Enterキーを押して、 R に関数を「学習」させる。
{ggplot2} パッケージがインストールされ、ロードされていることを確認する。

var.comp 関数は、適合した rma.mv モデルのみを入力として必要とする。出力を i2 に保存し、summary 関数で結果を表示する。

i2 <- var.comp(full.model)
summary(i2)

##         % of total variance    I2
## Level 1            1.254966   ---
## Level 2           39.525499 39.53
## Level 3           59.219534 59.22
## Total I2: 98.75%

出力では、3 つのレベルのそれぞれに起因する全分散のパーセンテージが表示される。レベル 1 のサンプル誤差の分散は非常に小さく、およそ 1% を占めるだけである。クラスタ内の異質性の分散である $I^2_{\text{Level 2}}$ の値ははるかに高く、合計で約 40% になる。しかし、最も大きな割合を占めるのはレベル 3 である。クラスタ間 (ここでは研究間) の異質性は、私たちのデータにおける全変動のうち、$I^2_{\text{Level 3}}=$ 59% を占めている。

全体として、3 番目のレベルではかなりの研究間異質性があることを示している。しかし、全体の分散の 3 分の 1 以上という大きな割合が、研究内の差 (differences within studies) によって説明できることもわかる。

また、var.comp の出力を plot 関数に代入すると、この全分散の分布を視覚化することができる。

plot(i2)

10.2.3 モデルの比較

3 レベルモデルの適合は、2 レベルモデルよりもデータの変動をよりよく表す場合にのみ意味がある。2 レベルモデルが 3 レベルモデルに匹敵する適合度を示すことがわかったら、オッカムのカミソリを適用すべきである。というのも、3 レベルモデルより 2 レベルモデルの方が複雑でなく、かつデータをうまく説明できることがある。

幸運なことに、{metafor} パッケージは、3 レベルモデルとレベルを一つ取り除いたモデルを比較することが可能である。これを行うには、再び rma.mv 関数を使用した。しかし、今回は、1 つのレベルの分散成分をゼロに設定した。これは、 sigma2 パラメータを指定することにより可能である。c(level 3, level 2)という一般的な形式のベクトルを用意する必要がある。このベクトルには、分散成分をゼロにする場合は 0 を記入し、データからパラメータを推定する場合は NA を使用する。

この例では、個々の効果量を研究に入れ込むことでモデルが改善されたかどうかを確認することは理にかなっている。したがって、私たちは、研究間の異質性を表すレベル3分散がゼロに設定されたモデルを適合させる。これは、すべての効果量が独立であると仮定する (独立でないことは分かっている) 単純なランダム効果モデルの適合と同じである。レベル 3 はゼロで一定なので、sigma2 の入力は c(0, NA) となる。この結果、以下のように rma.mv が呼び出され、その出力が l3.removed という名前で保存される。

l3.removed <- rma.mv(yi = z, 
                     V = var.z, 
                     slab = author,
                     data = Chernobyl,
                     random = ~ 1 | author/es.id, 
                     test = "t", 
                     method = "REML",
                     sigma2 =  c(0, NA))

summary(l3.removed)

## [...]
## Variance Components:
## 
##             estim    sqrt  nlvls  fixed        factor 
## sigma^2.1  0.0000  0.0000     14    yes        author 
## sigma^2.2  0.3550  0.5959     33     no  author/es.id 
## 
## Test for Heterogeneity:
## Q(df = 32) = 4195.8268, p-val < .0001
## 
## Model Results:
## 
## estimate      se    tval    pval   ci.lb   ci.ub 
##   0.5985  0.1051  5.6938  <.0001  0.3844  0.8126  *** 
## [...]

出力では、 sigma^2.1 がゼロに設定されていることがわかる。全体の効果も変化している。しかし、この結果は 3 レベルモデルのものよりも良いのだろうか？これを評価するために、anova 関数を使って両モデルを比較することが可能である。

anova(full.model, l3.removed)

##         df   AIC   BIC  AICc logLik   LRT   pval      QE 
## Full     3 48.24 52.64 49.10 -21.12              4195.82 
## Reduced  2 62.34 65.27 62.76 -29.17 16.10 <.0001 4195.82

2 レベルの「縮小」モデルに比べ、「完全」 (3 レベル) モデルはより適合度が高いことがわかる。赤池情報量規準 (Akaike Information Criterion, AIC) とベイズ情報量規準 (Bayesian Information Criterion, BIC) は、このモデルの方が低く、良好な性能を示している。両モデルを比較した尤度比検定 (Likelihood Ratio Test, LRT) は有意であり ( $\chi^2_1=$ 16.1, $p<$ 0.001)、同じ方向を向いている。

3 レベルモデルは、1 つの追加パラメータを導入したが (すなわち、自由度が 2 ではなく 3)、この追加された複雑さは正当化されるようだと言える。ネストのデータ構造のモデリングは、おそらく良いアイデアで、プール効果の推定値を改善してきた。

しかし、3 レベル構造を維持することには、たとえそれが有意に優れた適合性を提供しない場合であっても、しばしば正当な理由があることに留意してみよう。特に、3 レベルモデルが確かな理論的根拠に基づいていると考えられる場合には、3 レベルモデルを維持することは理にかなっている。

例えば、複数の効果量を持つ研究がデータに含まれている場合、これらの効果が独立していることはありえないということがわかる。したがって、ネストされたモデルを維持することは、データがどのように「生成」されたかをより適切に表現しているため、理にかなっている。もし、この例の anova の結果が 2 レベル解を支持していたなら、私たちは研究内の効果は大きく均質であると結論付けたことだろう。しかし、いずれにせよ、3 レベルモデルの結果を報告しただろう。これは、3 レベルモデルがデータ生成過程をよりよく表現していることを知っていることがある。

クラスタ変数の重要性が不明確な場合、状況は多少異なる。たとえば、３レベル・モデルにおいて、レベル 3 のクラスタが異なる文化圏を表すとした。研究対象の現象が文化間の変化を示さないことがわかったら、3 番目のレベルを削除して、代わりに 2 レベル・モデルを使用してもまったく問題ない。

10.3 ３レベルモデルにおけるサブグループ解析

３レベルモデルが設定されると、全体効果の推定モデレータを評価することも可能になる。このガイドの前では、サブグループ解析が、ダミー・コード化された予測変数 ( Chapter 8.1 ) のメタ回帰モデルとして表現できることを発見してきた。同様にして、私たちは「マルチレベル」モデルに回帰項を追加することができ、これは ３レベル混合効果モデル につながる。

\[\begin{equation} \hat\theta_{ij} = \theta + \beta x_i + \zeta_{(2)ij} + \zeta_{(3)j} + \epsilon_{ij} \tag{10.8} \end{equation}\]

ここで、$\theta$ は切片、$\beta$ は予測変数 $x$ の回帰重みである。$x_i$ をダミー (Chapter 8.1) に置き換えると、サブグループ解析に使用できるモデルが得られる。$x$ が連続的であるとき、上記の式は 3 レベルのメタ回帰モデルを表す。

カテゴリまたは連続の予測変数は、rma.mv で mods 引数を用いて指定することが可能である。この引数には、チルダ (~) で始まる数式と、その後に予測変数の名前を指定する。複数の予測変数 (例： ~ var1 + var2) を指定することで、多重メタ回帰を行うことも可能である。

チェルノブイリの例では、サンプルに含まれる放射線の量 (低、中、高) によって相関が異なるかどうかを確認したい。この情報は、データセットの radiation 列で提供されている。このコードを使って３レベルモデレータモデルを適合させることができる。

mod.model <- rma.mv(yi = z, V = var.z, 
                    slab = author, data = Chernobyl,
                    random = ~ 1 | author/es.id, 
                    test = "t", method = "REML",
                    mods = ~ radiation)

summary(mod.model)

## [...]
## Test of Moderators (coefficients 2:3):
## F(df1 = 2, df2 = 28) = 0.4512, p-val = 0.6414
## 
## Model Results:
##                 estimate    se   tval  pval  ci.lb ci.ub 
## intrcpt             0.58  0.36   1.63  0.11  -0.14  1.32    
## radiationlow       -0.19  0.40  -0.48  0.63  -1.03  0.63    
## radiationmedium     0.20  0.54   0.37  0.70  -0.90  1.31    
## [...]

最初の重要な出力は Test of Moderators である。$F_{2,28}=$ 0.45、$p=$ 0.64 であることがわかる。これは、サブグループ間に有意な差がないことを意味する。

Model Results はメタ回帰の枠組みで表示される。これは、サブグループ内のプール効果量を得るために、推定値を直接抽出することができないことを意味する。

$z$ 最初の値である切片 (intrcpt) は、全体の放射線被曝量が高い場合 ($z=$ 0.58) の値を示している。低線量群および中線量群における効果は、切片の値にそれらの推定値を加えることによって求めることができる。したがって、低線量被曝群における効果は $z$ = 0.58 - 0.19 = 0.39 であり、中線量被曝群における効果は $z$ = 0.58 + 0.20 = 0.78 である。

3 レベル (調整効果) モデルの結果を報告

3 レベルモデルの結果の報告に際しては、プール効果だけでなく推定分散についても言及するべきである。関数 rma.mv は、レベル 3 とレベル 2 のランダム効果分散を、それぞれ $\sigma^2_1$ と $\sigma^2_2$ で示す。

しかしながら、この推定分散は、$\tau^2_{\text{Level 3}}$ と $\tau^2_{\text{Level 2}}$ を使うことが望ましい。この方が、真の (研究) 効果 (つまり異質性の分散) の分散を扱っていることが明確になる。マルチレベルの $I^2$ 値も、解釈しやすいという点では適しているが、最初に何を表しているかを説明するという条件が必要である。

を使ってモデルを比較する場合、少なくとも尤度比検定を報告するべききである。調整効果 (moderator) 分析の結果は、Chapter 7.3 で示したような表で報告することができる。以下に、anova の結果の報告例を示す。

“The pooled correlation based on the three-level meta-analytic model was $r=$ 0.48 (95%CI: 0.25-0.66; $p$ < 0.001). The estimated variance components were $\tau^2_{\text{Level 3}}=$ 0.179 and $\tau^2_{\text{Level 2}}=$ 0.119. This means that $I^2_{\text{Level 3}}=$ 58.22% of the total variation can be attributed to between-cluster, and $I^2_{\text{Level 2}}=$ 31.86% to within-cluster heterogeneity. We found that the three-level model provided a significantly better fit compared to a two-level model with level 3 heterogeneity constrained to zero ($\chi^2_1=$ 16.10; $p$< 0.001).”

10.4 ロバスト分散推定

前章では、3 レベルメタ分析モデルを紹介し、データにおける効果量間の依存性をモデル化するために、どのように使用できるかを説明してきた。前章で取り入れた階層型モデルは、効果量が完全に独立しているとする「従来の」メタ分析よりも、明らかに私たちのデータセットをより良く表現している。しかし、これはまだ現実の単純化である。実際には、効果量間の依存関係は、現在のネストモデルで捉えられるものよりも複雑であることが多いのである。

チェルノブイリのデータセットに戻ると、すでにこのことがわかる。このデータでは、ほとんどの研究が複数の効果量を提供しているが、その理由は研究によって異なっている。いくつかの研究では、異なる対象集団における放射線の影響を比較しており、そのため複数の効果量を報告している。また、同じサンプルに対して異なる方法を用いた研究もあり、これも複数の効果量が報告されていることを意味する。

一つの研究の複数の効果量が同じサンプルに基づいている場合、それらのサンプリングエラー (Chapter 10.1 と Chapter 10.3 の式 10.7 and 10.8 における $\epsilon_ {ij}$) には相関があると期待される。しかし、このことは、今回の３レベルモデルではまだ捉えられていない。上記のモデルは、クラスタ/研究内では、サンプル誤差の相関 (つまり共分散) がゼロであることを仮定している。つまり、1 つのクラスタまたは研究内では、効果量の推定値は独立であると仮定している。

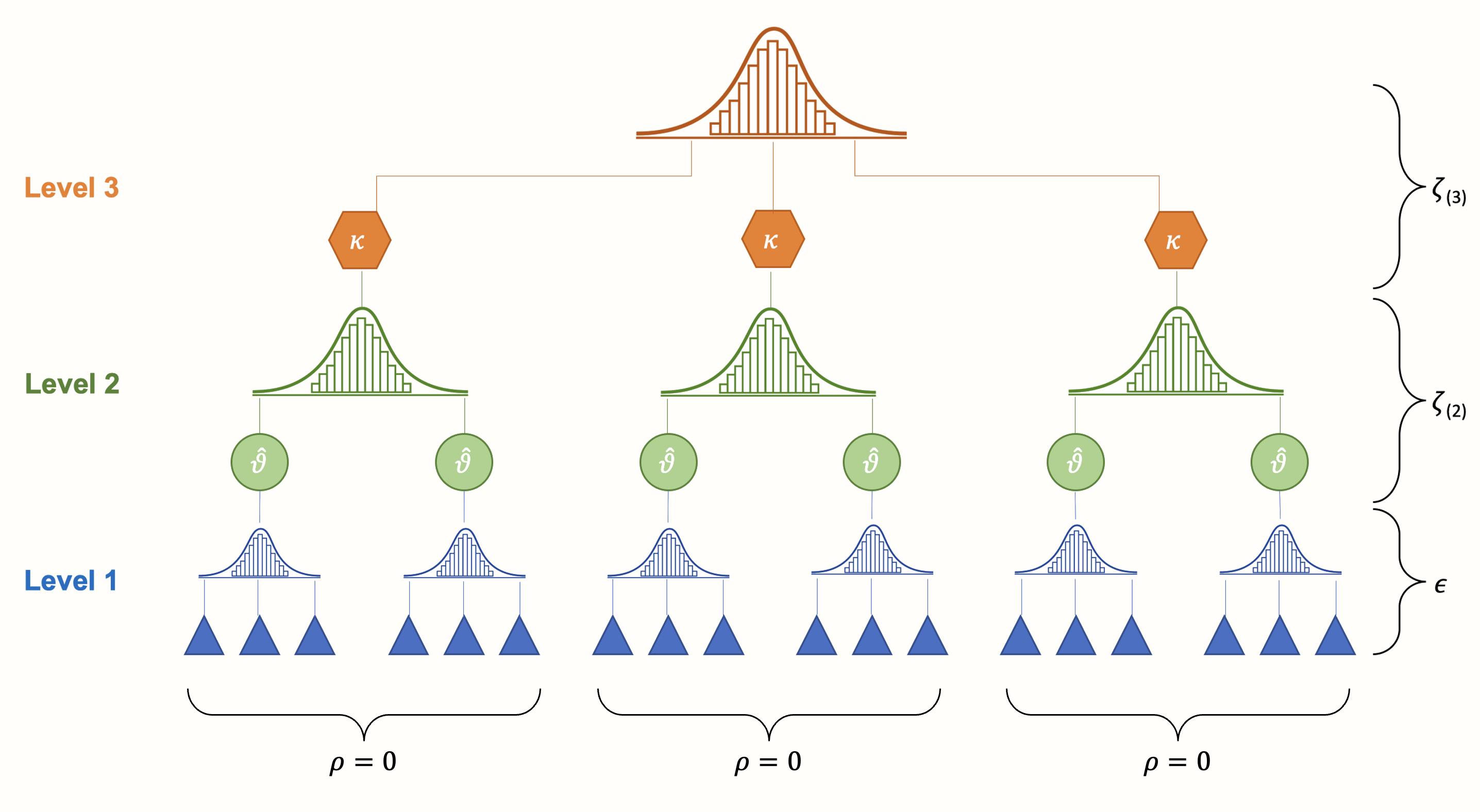
Figure 10.2: もともと、３レベル (階層) モデルは研究官あるいはクラスタ間の効果量は独立であると仮定している。

このセクションでは、拡張された 3 レベル構造、いわゆる相関・階層効果 (Correlated and Hierarchical Effects, CHE) モデル (J. E. Pustejovsky and Tipton 2021)に時間を割こう。以前の (階層的) 3 レベルモデルと同様に、CHE モデルは、ある共通点 (例えば、同じ研究、作業グループ、文化的地域などに由来する) に基づいて、いくつかの効果量を大きなクラスタに結合することが可能である。

このことに加えて、このモデルでは、クラスタ内のいくつかの効果量が同じサンプルに基づいており (例えば、複数の測定が行われたため)、したがってそれらのサンプル誤差は相関していることを明示的に考慮している。現実には、特に、データの依存性構造が複雑であったり、部分的にしか知られていない場合、CHE モデルから始めるとよい (J. E. Pustejovsky and Tipton 2021)⁴⁷。

CHE モデルとともに、メタ分析の文脈におけるロバスト分散推定 (Robust Variance Estimation, RVE) についても説明する (L. Hedges, Tipton, and Johnson 2010; Tipton and Pustejovsky 2015; Tipton 2015)。これは、過去にメタ分析で従属効果量を扱うために頻繁に使用されてきた一連の方法である。RVE の中核は、いわゆるサンドイッチ推定量を中心に展開されている。この推定量は、CHEモデル (および他のメタ分析モデル) と組み合わせて、ロバストな信頼区間と $p$-値を得るために使用することができる。選択したモデルが、データの複雑な依存構造を完全にうまく捉えていない場合も可能である。

そこで、最初の CHE モデルの適合の前に、メタ分析 RVE の概要と サンドイッチ推定量 について、後者がなぜそのような魅力的な名前を持っているのかを探ってみよう。

10.4.1 サンドイッチ型分散推定量

発表されたメタ分析では、「ロバスト分散推定」という言葉が特殊な使われ方をしていることがあり、これが依存効果量を持つメタ分析データにのみ適用できる特殊な方法であると思われることがある。その逆である。ロバスト分散推定量は、もともと従来の回帰モデルのための手法として開発されたもので、回帰重みの分散 $\hat\beta$ を計算するために使われる (Aronow and Miller 2019, chap. 4.2.2 など参照)。

この推定量は、線形モデルの通常の仮定が満たされない場合でも、漸近的な標準誤差の一貫性のある推定値が得られるため、「ロバスト」推定量と呼ばれる ⁴⁸ 。回帰モデルにおける係数分散のロバスト推定は非常に重要である。分散推定値 ⁴⁹ は、$p$-値と同様に、推定回帰重量の周りの信頼区間を計算するために使われ、したがってモデルから引き出す推測に直接影響を持つ。

ここで取り上げるロバスト分散推定量は、「通常の」回帰モデルで使用されるオリジナルの手法の特別バージョン に過ぎないのである。Hedges, Tipton and Jackson (2010) は、依存効果量のあるメタ回帰モデルに使用できる適応型の RVE を発表し、このアプローチはここ数年で拡張されている。

これを理解するためには、まずメタ回帰の式をもう一度見てみる必要がある。概念的には、この式は Chapter 8.1 で紹介した式 8.2 と非常によく似ている。それを単に行列表記で表示すだけですある⁵⁰。

\[\begin{equation} \boldsymbol{T}_{j}=\boldsymbol{X}_{j}\boldsymbol{\beta} + \boldsymbol{u}_j +\boldsymbol{e}_j \tag{10.9} \end{equation}\]

この式は、単純に、$\boldsymbol{T}$ のある効果量が、$\boldsymbol{X}$ のある共変量と関連した回帰の重み $\beta$ によって予測されることを教えてくれる。また、サンプル誤差 ($\boldsymbol{e}_j$ で記号化) 以外に、各研究のランダム効果 ($\boldsymbol{u}_j$ で表記) があり、それによって (混合効果) メタ回帰モデルを生成していることも教えてくれる。

特別なのは、この式の添え字 $j$ である。これは、式中の文字が太字であることとともに、データセット中の各研究またはクラスタ $j$ が複数の効果量を提供する、または提供できることを示している。$n_j$ は、ある研究 $j$ における効果量の数であるとする。そして、$j$ の効果量は、式 $\boldsymbol{T}_j = (T_{j,1}, \dots, T_{j,{n_j}})^\top$ で見る列ベクトルとして書き下すことが可能である。同様に、$\boldsymbol{X}_j$ は、ある研究 $j$ の共変量を含むデザイン行列であり、次のように書くことができる。

\[\begin{equation} \boldsymbol{X}_j = \begin{bmatrix} x_{1,1} & \cdots & x_{1,p} \\ \vdots & \ddots & \vdots \\ x_{n_j,1} & \cdots & x_{n_j,p} \end{bmatrix} \tag{10.10} \end{equation}\]

ここで $p-1$ は共変量の総数である⁵¹。推定したい回帰係数のベクトル $\boldsymbol{\beta} = (\beta_1, \dots, \beta_{p})^\top$ には、添字 $j$ は含まれていない。なぜなら、回帰係数は全ての研究で同じと仮定されているからである。

全体として、この表記は、研究が複数の効果量に貢献できる場合、私たちのデータは、いくつかの小さなデータセットを積み重ねたように見えることを強調している。$J$ は、このデータにおける研究またはクラスタの合計数である。

\[\begin{equation} \begin{bmatrix} \boldsymbol{T}_1 \\ \boldsymbol{T}_2 \\ \vdots \\ \boldsymbol{T}_J \end{bmatrix} = \begin{bmatrix} \boldsymbol{X}_1 \\ \boldsymbol{X}_2 \\ \vdots \\ \boldsymbol{X}_J \end{bmatrix} \boldsymbol{\beta} + \begin{bmatrix} \boldsymbol{u}_1 \\ \boldsymbol{u}_2 \\ \vdots \\ \boldsymbol{u}_J \end{bmatrix} + \begin{bmatrix} \boldsymbol{e}_1 \\ \boldsymbol{e}_2 \\ \vdots \\ \boldsymbol{e}_J \end{bmatrix}. \tag{10.11} \end{equation}\]

この式に基づいて、メタ回帰の係数 $\boldsymbol{\hat\beta}$ を推定することができる。信頼区間を計算し、係数の有意性検定を行うには、その分散の推定が必要である。これはロバストサンプリング分散推定量 $\boldsymbol{V_{\hat\beta}}$ を使って実現可能である。その式は次のようになる (L. Hedges, Tipton, and Johnson 2010; J. E. Pustejovsky and Tipton 2021, suppl. S1)。

\[\begin{equation} \scriptsize\boldsymbol{V}^{\text{R}}_{\boldsymbol{\hat\beta}} = \left(\sum^J_{j=1}\boldsymbol{X}_j^\top\boldsymbol{W}_j\boldsymbol{X}_j \right)^{-1} \left(\sum^J_{j=1}\boldsymbol{X}_j^\top\boldsymbol{W}_j \boldsymbol{A}_j\Phi_j \boldsymbol{A}_j \boldsymbol{W}_j \boldsymbol{X}_j \right) \left(\sum^J_{j=1}\boldsymbol{X}_j^\top\boldsymbol{W}_j\boldsymbol{X}_j \right)^{-1} \tag{10.12} \end{equation}\]

この式はかなり複雑に見えるので、細部まで理解する必要はないだろう。今重要なのは、形式と、その「成分」の一部である。

まず、この式が三分木構造であることがわかる。左右の括弧で囲まれた部品は、真ん中の部品を取り囲むように同じものが並んでいる。これは、外側の部分が「パン」で内側の部分が「肉」であるサンドイッチのように見え、「サンドイッチ推定量」と名付けられた所以である。この式の重要な「材料」は、$\boldsymbol{\Phi}_j$, $\boldsymbol{W}_j$ and $\boldsymbol{A}_j$ の行列である。

まず1つ目。$\boldsymbol{\Phi}_j=\text{Var}(\boldsymbol{u}_j +\boldsymbol{e}_j)$, は、$n_j$ 行と $n_j$ 列の分散共分散行列 (variance-covariance matrix) である。これは、研究 $j$ の真の依存構造を表している (J. E. Pustejovsky and Tipton 2021, Suppl. S1)。残念ながら、効果量が研究内でどのように、どの程度相関しているかはほとんど知られておらず、私たちのメタ分析ですべての研究に関してこれを知ることはさらに困難である。したがって、このモデルでは、いくつかの単純化した仮定を置く必要がある⁵²。CHE モデルは、例えば、効果量間の既知の相関 (known correlation) $\rho$ があり、 $\rho$ は全ての研究で同じ値という仮定がある (「一定標本相関 (constant sampling correlation)」の仮定、 J. E. Pustejovsky and Tipton 2021)。
$\boldsymbol{W}_j$ 行列には、各効果量の重みが含まれている。前の章 ( 4.1.1 and 8.1.3 参照) で、効果量推定値の精度を考慮に入れてからプールする必要があることを既に学びんだ。これを行う最適な方法は、分散の逆数を取ることであり、これは、$\boldsymbol{W}_j = \boldsymbol{\Phi}^{-1}_j$ を意味する。先ほど述べたように、$\boldsymbol{\Phi}_j$ の真の値はほとんど知られていないので、私たちのモデルに基づく推定値、$(\boldsymbol{\hat\Phi}_j)^{-1}$ が使われる⁵³.
最後の $\boldsymbol{A}_j$ は調整行列で、メタ分析の研究数が少ない (例えば 40 以下、 L. Hedges, Tipton, and Johnson 2010; Tipton and Pustejovsky 2015) でも推定量が有効な結果を提供できるようにするものである。推奨されるアプローチは、バイアス低減線形化 (bias-reduced linearization)、つまり“CR2” 法に基づく行列を使うことである(Tipton and Pustejovsky 2015)⁵⁴。

10.4.2 ロバスト分散推定を用いた CHE モデルの適合

それでは、最初の相関・階層効果モデルを R で適合させ、同時にロバスト分散推定を採用し、モデルの誤指定を防ぐ。これまで同様に、{metafor} の rma.mv 関数を使用してモデルを実行できる。今回は、{clubSandwich} パッケージ (J. Pustejovsky 2022)が提供するいくつかの追加関数も必要である。そのため、必ずパッケージをインストールし、ライブラリからロードしておこう。

library(clubSandwich)

上記のように、CHE モデルは、研究またはクラスタ内の効果量が相関しており、この相関は研究内および研究間で同一であると仮定している。

したがって、モデル内で使用する相関係数を定義する必要がある。今回のチェルノブイリのデータでは、相関が大きいと仮定して、$\rho$ =0.6としよう。これは推測に過ぎず、$\rho$ の値を変えながら複数の感度分析を行うことを強く勧める。

# 想定される定数相関係数
rho <- 0.6

さて、この相関を利用して、各研究の仮定された分散共分散行列を計算することが可能である。これは、{clubSandwich} の impute_covariance_matrix 関数を使用して行う。

vi の引数には、各効果量の分散 (すなわち、標準誤差の二乗) を含むデータセットの変数名を指定した。
cluster 引数は、各効果量を study または cluster に関連付ける変数を定義する。Chernobyl データセットでは、これは author である。
引数 r は、効果量間の定数相関係数を想定している。

# サンプル定数相関係数の実行モデル
V <- with(Chernobyl, 
          impute_covariance_matrix(vi = var.z,
                                   cluster = author,
                                   r = rho))

V で準備した分散共分散行列を用いて、rma.mv モデルの適合を行うことができるようになる。 Chapter 10.3 と同じメタ回帰モデルで、共変量として radiation を用いて解析するとする。

最初の引数は formula オブジェクトで、効果量 z が切片 (1) と共変量 radiation によって予測されることを関数に渡した。V 引数には、先ほど作成した分散共分散行列のリストを渡す。また、sparse 引数を TRUE に設定することで、計算を高速化することが可能である。

引数 random と data だけが同じである。結果は che.model という名前で保存される。

che.model <- rma.mv(z ~ 1 + radiation,
                    V = V,
                    random = ~ 1 | author/es.id,
                    data = Chernobyl,
                    sparse = TRUE)

{clubSandwich} の conf_int 関数を使用することで、メタ回帰係数の信頼区間を計算することができる。計算は、適合したモデルと vcov で使用する小サンプル調整 を指定するだけである。推奨通り、"CR2" 調整を使用する (Chapter 10.4.1 参照)。

conf_int(che.model, 
         vcov = "CR2")

##            Coef. Estimate    SE d.f. Lower 95% CI Upper 95% CI
##          intrcpt    0.584 0.578 1.00        -6.76         7.93
##     radiationlow   -0.190 0.605 1.60        -3.52         3.14
##  radiationmedium    0.207 0.603 1.98        -2.41         2.83

Estimate の点推定値は、Chapter 10.3 で得たものと同様であることがわかる。しかし、推定された標準誤差と信頼区間は、はるかに大きくなっている。また、coef_test関数を用いて、回帰重みの $p$ 値を計算することが可能である。

coef_test(che.model, 
          vcov = "CR2")

##            Coef. Estimate    SE t-stat d.f. (Satt) p-val (Satt) Sig.
##          intrcpt    0.584 0.578  1.010        1.00        0.497     
##     radiationlow   -0.190 0.605 -0.315        1.60        0.789     
##  radiationmedium    0.207 0.603  0.344        1.98        0.764

ロバスト分散推定を用いた場合、どの係数も有意ではないことがわかる⁵⁵。

ロバスト分散推定とモデルの誤同定

読者の中には、なぜ私たちがロバスト分散推定を使ったモデルに大騒ぎするのか不思議に思われるかもしれない。その主な理由は、多変量・マルチレベルのモデルは、簡単に誤った仕様になりうるからである。CHE モデルでさえ、相関が研究内と研究間で同一であると仮定することで、やや粗雑なモデルであることをすでに学んだ。モデルがデータ中の複雑な依存関係を適切に近似しているかどうかが不明確なことがよくある。

この点、ロバスト分散推定は、モデルの潜在的な誤記定に対して、私たちの推論 (すなわち、我々が計算する信頼区間と$p$値) を保護することができるため、有用である。

{robumeta} パッケージ

このセクションでは、相関・階層効果モデルと組み合わせたロバスト分散推定を取り上げた。このモデルは、他のいくつかの革新的な技術とともに、Pustejosky and Tiptonによって提案されている (2021)。

Hedges, Tipton and Jackson (2010) による “original” RVE approach と、いくつかの小サンプルの拡張は、 {robumeta} パッケージを使って適用することができる (Z. Fisher, Tipton, and Zhipeng 2017)。このパッケージは、Hedges, Tipton and Jackson が最初に提案した2種類のモデル、階層的モデルと相関効果モデル (ただし両方を組み合わせたモデルは不可) を使ってメタ回帰を適合させることができる。

10.5 クラスタワイルドブートストラップ

前章では、相関効果モデルと階層効果モデルの適合方法、ロバスト分散推定を用いた信頼区間と係数検定の計算方法について学んだ。

もう一つの、そして時には私たちのモデルの係数を検定するのに有利な方法は、ブートストラップ法で、その特別な変種がいわゆるクラスタワイルドブートストラップ (Joshi, Pustejovsky, and Beretvas 2021) である。この方法は、メタ分析における研究の総数 $J$ が小さい場合に適している。特に、 (私たち自身の チェルノブイリ の例で見たように) 小さなサンプルで過度に保守的な結果につながる可能性がある RVE と比較して、この方法は適している。

この方法は、いわゆる多重対比仮説 (multiple-contrast hypothesis) を検定したいときにも有効である。多重対比仮説は、たとえば、ダミー・コード化されたカテゴリ共変量の全体効果を検定したい場合に必要である。

クラスタワイルドブートストラップのアルゴリズム

ワイルドブートストラップは、Null モデル (共変量を追加せずに適合させたモデル) の残差に基づく方法である。クラスタワイルドブートストラップでは、依存効果量を扱うために、例えば CR2 法に基づく調整行列 $\boldsymbol{A}_j$ を用いて残差を変換する (Chapter 10.4.1 参照)。ワイルドブートストラップの一般的なアルゴリズムは以下のようなものである (Joshi, Pustejovsky, and Beretvas 2021)。

元のデータからフルモデルを計算し、目的の検定統計量 ($t$ 値または $F$ 値) を導出する。
元のデータに基づいてヌルモデルを適合し、その残差 $\boldsymbol{e}$ を抽出する。
各研究またはクラスタ $j$ について、分布⁵⁶からランダムな値を引き、$j$ の残差にこのランダムな値をかける。
元のデータに基づく Null モデルの予測値に変換された残差を加えることで、新しいブートストラップされた効果量を生成する。
ブートストラップされた効果量値を用いて，再度フルモデルを適合させ，再度検定統計量を計算する。

そして、ステップ 3 から 5 を $R$ 回繰り返す。Boostrap $p$ 値は、boostrap 検定統計量が元データに基づくものより極端であった回数の割合として導出される。

ブートストラップを用いて多重対比仮説を検定するには、{wildmeta} パッケージを使用することができる (Joshi and Pustejovsky 2022)。次の例のためにこのパッケージをインストールし、ライブラリからロードしておく必要がある。さらに、{tidyverse} の関数を用いて、Chernobyl データセットに新しい変数を生成し、そこに各研究の年号を保存する。

# {wildmeta} と {tidyverse} をロードする
library(wildmeta)
library(tidyverse)

# year という変数を追加
Chernobyl$year <- str_extract(Chernobyl$author, 
                              "[0-9]{4}") %>% as.numeric()

次に、この変数をメタ回帰モデル rma.mv の 新しい予測変数 として使用した。これは、単に最初の引数で year を数式に追加し、共変数をセンタリング、スケールするために scale 関数を適用した。また、この式ではもう一つ、切片の 1 を 0 に変更している。これは切片がないことを意味し、「年」の予測値は放射線のレベルごとに層別される⁵⁷。この結果を che.model.bs として保存する。

che.model.bs <- rma.mv(z ~ 0 + radiation + scale(year),
                       V = V,
                       random = ~ 1 | author/es.id,
                       data = Chernobyl,
                       sparse = TRUE)

ブートストラップを始める前に、実施したい検定について線形対比を定義する必要がある。例えば、変数 radiation の全体的な調整効果を検定したいとする。これを行うには、 {clubSandwich} の constrain_equal 関数を使用して、検定のための制約行列を作成する必要がある。帰無仮説は、変数 radiation の3つのレベルの間で効果が等しいというもので、constraints 引数を 1:3 にセットする。さらに、coefs 引数には先ほどフィットしたモデルの係数を指定した。結果は rad.constraints という名前で保存される。

rad.constraints <- constrain_equal(constraints = 1:3,
                                   coefs = coef(che.model.bs))
rad.constraints

##      [,1] [,2] [,3] [,4]
## [1,]   -1    1    0    0
## [2,]   -1    0    1    0

{wildmeta} の Wald_test_cwb 関数を用いて、多重対比仮説のブートストラップ $p$ -値を計算することができる。適合したフルモデル、制約行列、使用したいスモールサンプル調整の種類、そしてブートストラップ複製の数である R を指定する必要がある。検出力が向上するため、高い複製数 (例：1000以上) を使用することを勧める。この例では、2000 回を使用し、結果を cw.boot として保存する。繰り返しの回数にもよるが、この処理は終了までに数分かかることがある。

cw.boot <- Wald_test_cwb(full_model = che.model.bs,
                         constraints = rad.constraints,
                         adjust = "CR2",
                         R = 2000)
cw.boot

##           Test Adjustment CR_type Statistic    R  p_val
## 1 CWB Adjusted        CR2     CR0   Naive-F 2000 0.3595

調整効果の検定の結果、$p$ -値は 0.36 で、有意ではないことがわかる。私たちは以前、Chapter 10.3 の放射強度の調整効果分析でも同様の所見を得た。

plot 関数を使用すると、すべてのブートストラップ複製における検定統計量の密度を可視化することも可能である。

plot(cw.boot, 
     fill = "lightblue", 
     alpha = 0.5)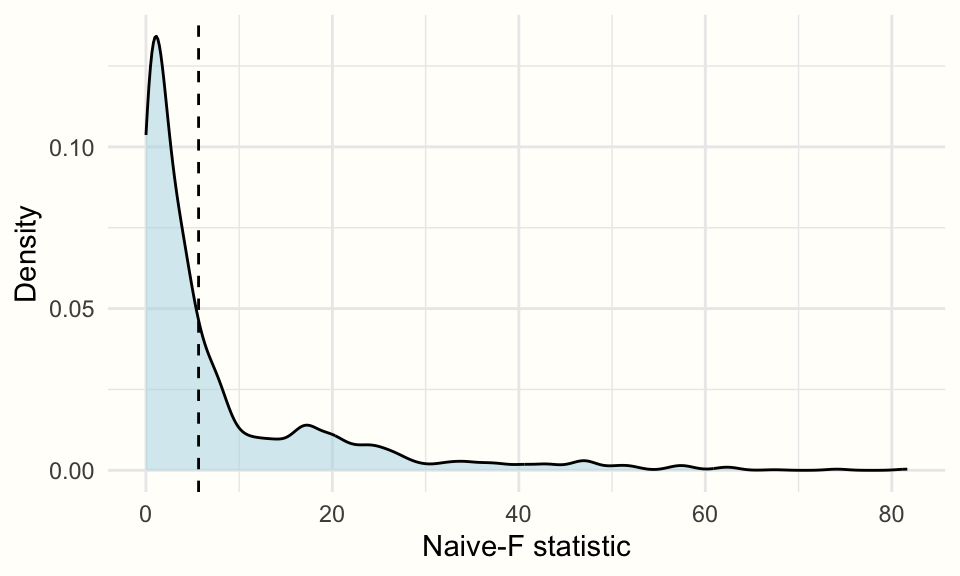

10.6 演習問題

知識を試そう！

なぜ「マルチレベル」モデルではなく「３レベル」モデルと言う方が正確なのか？

３レベルメタ分析モデルはいつ有用か？

効果量依存性の一般的な原因を2つ挙げなさい。

マルチレベル $I^2$ の統計量はどのように解釈すればよいか。

調整効果 (moderator) 変数の効果を取り入れるために、どのように３レベルモデルを拡張することができるのか？

問題の解答は、本書の巻末 Appendix A にある。

\[\tag*{$\blacksquare$}\]

10.7 要約

すべてのランダム効果メタ分析は、マルチレベルモデルに基づいている。3 レベル目が追加された場合、3 レベルメタ分析モデルと呼ばれる。このようなモデルは、クラスタ化した効果量データの取り扱いに適している。
3 レベルモデルは、従属効果量に使用することができる。例えば、1 つの研究が複数の効果量に寄与している場合、これらの結果が独立しているとは通常仮定できない。3 レベルモデルは、効果量がより大きなクラスタ (研究など) に ネストされていると仮定することで、この問題を制御する。
従来のメタ分析とは異なり、3 レベルモデルでは、クラスタ内のランダム効果分散と、クラスタ間の 2 つの異質性分散を推定することが可能である。
3 レベルモデルを用いて、カテゴリまたは連続予測変数を検定することも可能である。これは、3 レベル混合効果モデルをもたらす。

9 出版バイアス

11 構造方程式モデリングメタ分析