Rozdział 8 Rozkłady prawdopodobieństwa
8.1 Rozkłady jednowymiarowe
8.1.2 Uogólniony rozkład t Studenta
\[ f(x \mid \mu, \sigma, \nu) = \frac{1}{\sigma} \sqrt{\frac{\nu}{\nu-2}} \cdot t_\nu\!\left( \frac{x - \mu}{\sigma} \cdot \sqrt{\frac{\nu}{\nu-2}} \right) \]
gdzie \(t_\nu(\cdot)\) to funkcja gęstości zwykłego rozkładu t Studenta:
\[ t_\nu(y) = \frac{\Gamma\!\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi} \; \Gamma\!\left(\frac{\nu}{2}\right)} \left(1 + \frac{y^2}{\nu}\right)^{-\frac{\nu+1}{2}} \]
Wzór ten można zapisać w następujący sposób:
\[ f(x \mid \mu, \sigma, \nu) = \frac{\Gamma\!\left(\frac{\nu+1}{2}\right)}{\sigma\sqrt{(\nu-2)\pi} \; \Gamma\!\left(\frac{\nu}{2}\right)} \left(1 + \frac{1}{\nu-2}\left(\frac{x-\mu}{\sigma}\right)^{2}\right)^{-\frac{\nu+1}{2}} \]
Własności:
Średnia: \(\mathbb{E}[X] = \mu\) (dla \(\nu > 1\))
Wariancja: \(\text{Var}(X) = \sigma^2\) (dla \(\nu > 2\))
Kurtoza nadwyżkowa: \(3\frac{6}{\nu - 4}\) (dla \(\nu > 4\))
Uwaga: Taka parametryzacja gwarantuje, że parametr \(\sigma\) to wprost odchylenie standardowe. Dla \(\nu \to \infty\) rozkład zbiega do rozkładu normalnego \(\mathcal{N}(\mu, \sigma^2)\).
8.1.3 Uogólniony skośny rozkład t Studenta
Gęstość uogólnionego skośnego rozkładu t-Studenta z parametrem położenia \(\mu\), parametrem skali \(\sigma > 0\), parametrem skośności \(\xi > 0\) oraz liczbą stopni swobody \(\nu > 2\) wynosi:
\[ f(x \mid \mu, \sigma, \xi, \nu) = \frac{1}{\sigma} \cdot f_{\text{SSTD}}\!\left( \frac{x - \mu}{\sigma} \;\Big|\; \xi, \nu \right) \]
gdzie \(f_{\text{SSTD}}\) jest gęstością standaryzowanego skośnego rozkładu t-Studenta:
\[ f_{\text{SSTD}}(y \mid \xi, \nu) = \frac{2}{\xi + \xi^{-1}} \cdot \sqrt{\frac{\nu}{\nu-2}} \cdot t_\nu\!\left( \frac{w}{\xi^{\text{sign}(w)}} \cdot \sqrt{\frac{\nu}{\nu-2}} \right) \cdot s \]
z transformacją:
\[ w = y \cdot s + m \]
oraz \(t_\nu(\cdot)\) jest gęstością standardowego rozkładu t-Studenta:
\[ t_\nu(y) = \frac{\Gamma\!\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi} \; \Gamma\!\left(\frac{\nu}{2}\right)} \left(1 + \frac{y^2}{\nu}\right)^{-\frac{\nu+1}{2}} \]
Stałe standaryzujące:
\[ m_1 = \frac{2\sqrt{\nu-2}}{(\nu-1) \cdot B\!\left(\frac{1}{2}, \frac{\nu}{2}\right)} \]
\[ m = m_1 \left( \xi - \xi^{-1} \right) \]
\[ s = \sqrt{(1 - m_1^2)(\xi^2 + \xi^{-2}) + 2m_1^2 - 1} \]
gdzie \(B(a,b)\) oznacza funkcję beta.
Własności:
Wartość oczekiwana: \(\mathbb{E}[X] = \mu\)
Wariancja: \(\text{Var}(X) = \sigma^2\)
Skośność: Kontrolowana przez \(\xi\) (prawostronna skośność gdy \(\xi > 1\), lewostronna gdy \(\xi < 1\), symetryczny gdy \(\xi = 1\))
Przypadki szczególne:
| Warunek | Rozkład |
|---|---|
| \(\xi = 1\) | Uogólniony rozkład t-Studenta |
| \(\xi = 1, \; \nu \to \infty\) | Rozkład normalny \(\mathcal{N}(\mu, \sigma^2)\) |
| \(\mu = 0, \; \sigma = 1\) | Standaryzowany skośny rozkład t-Studenta |
Uwaga: Ta parametryzacja zapewnia, że \(\mu\) i \(\sigma\) są rzeczywistą wartością oczekiwaną i odchyleniem standardowym rozkładu, niezależnie od parametrów skośności i grubości ogonów. Stałe \(m\) i \(s\) wewnętrznie korygują skośny rozkład t Fernándeza-Steela, aby osiągnąć tę standaryzację.
8.2 Wartość zagrożona (VaR)
Wartość zagrożona (Value at risk, VaR4) to ilościowy miernik ryzyka inwestycji. Informuje, jaka jest maksymalna potencjalna strata, której nie przekroczy się z ustalonym prawdopodobieństwem \(\alpha\) (np. 5%, 0,1%…) w określonym okresie (np. jeden dzień), przy normalnych warunkach rynkowych. Jest to (lub kiedyś było) popularne narzędzie pomiaru ryzyka stosowane przez instytucje finansowe.
Innymi słowy:
przyjmujemy poziom, np. \(\alpha= 0{,}01\) lub \(\alpha = 0{,}001\),
zakładamy określony rozkład prawdopobieństwa,
zadajemy pytanie: jaka jest wartość, która „odcina” \(\alpha \cdot 100\%\) najmniejszych wartości (największych strat).
Value at Risk możemy wyznaczyć, używając funkcji odwrotnej do dystrybuanty, funkcji kwantylowej.
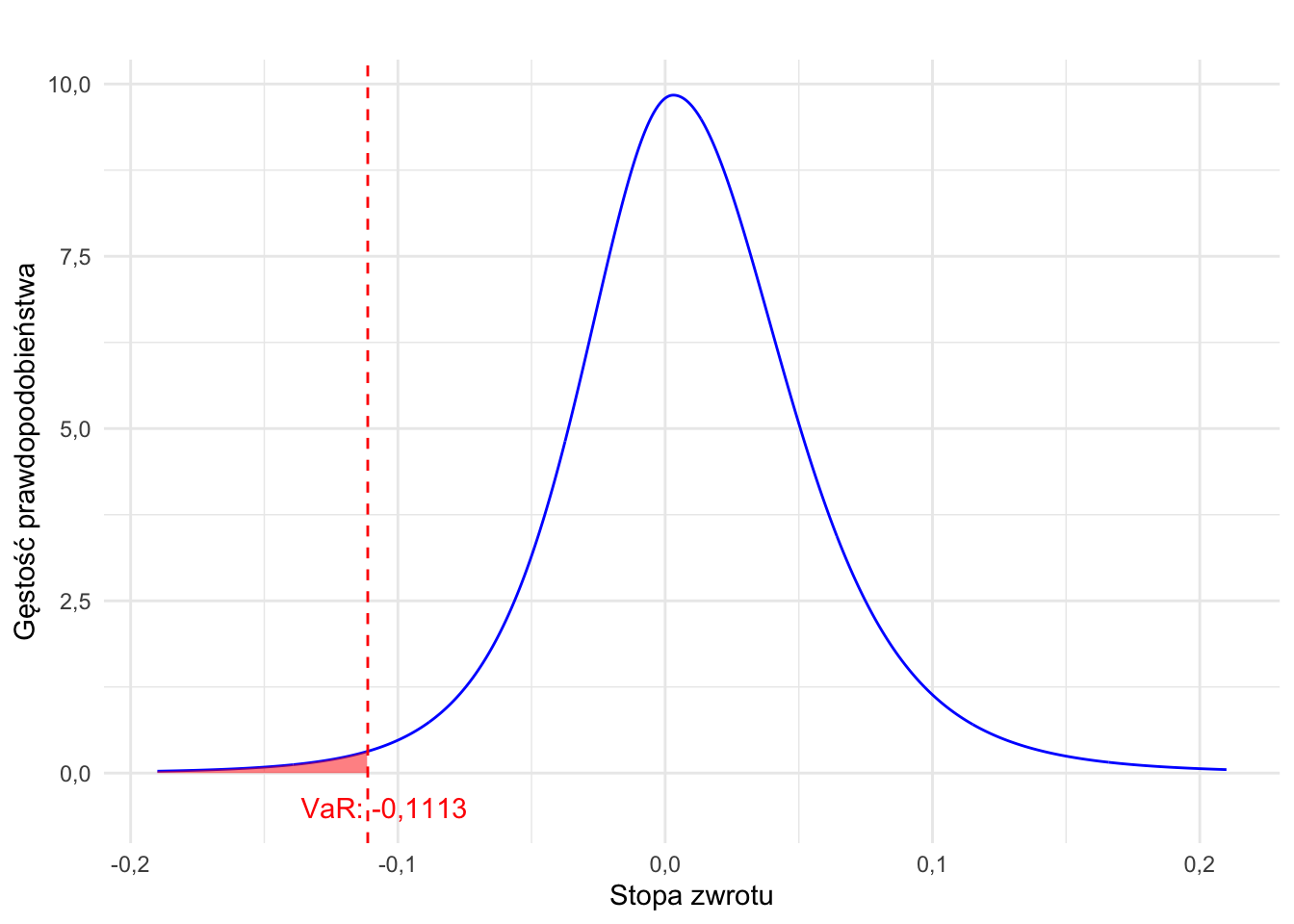
Rysunek 8.1: Value at Risk (VaR) – ilustracja
Matematycznie zapisując powyższe, otrzymamy:
\[\text{VaR}_\alpha = x_\alpha \quad \text{takie, że} \quad \int_{-\infty}^{x_\alpha} f_X(x) dx = \alpha\]
\(\text{VaR}_\alpha\) – wartość zagrożona, czyli strata nieprzekraczana z prawdopodobieństwem (\(\alpha\)),
\(f_X(t)\) – gęstość rozkładu zwrotów (X).
Miernikiem opartym na VaR jest Expected shortfall (oczekiwany niedobór). Jest to przeciętna (mówiąc językiem matematycznym: oczekiwana) wartość straty poniżej VaR:
\[\text{ES}_\alpha = \int_{-\infty}^{VaR_\alpha}xf_X(x)dx\]
Chcąc podać wartość zagrożoną oraz oczekiwany niedobór, należy ustalić konwencję raportowania. W praktyce, w przedsiębiorstwach finansowych podaje się wartość kwotową – nie procentową – straty, pomija się również znak minus.
Wielke/małe litery mają znaczenie! W ekonometrii finansowej „var” lub „Var” często oznacza wariancję, „VaR” wartość zagrożoną, zaś „VAR” to Vector Autoregression, model autoregresji wektorowej.↩︎