Rozdział 9 Model GARCH

Typowe modele procesów stochastycznych (ARMA/ARIMA) zawierają założenie homoskedastyczności, czyli stałości wariancji warunkowej. Dla finansowych szeregów czasowych jest to założenie nierealistyczne, w szeregach występują zgrupowania zmienności: można oczekiwać, że zwiększona zmienność zaobserwowana w niedawnej przeszłości może wskazywać na zwiększoną zmienność warunkową w najbliższym czasie.

Model GARCH umożliwia modelowanie zgrupowań zmienności. Skrótowiec ARCH oznacza autoregresyjny model warunkowej heteroskedastyczności (ang. Auto-Regressive Conditional Heteroskedasticity), GARCH to z kolei uogólnienie tego modelu (ang. Generalized ARCH).

9.1 Stała i zmienna wariancja

Załóżmy, że mamy model ze stałą wariancją warunkową $\mathbb{V}(Y_t|X_{1,t}, ..., X_{p,t}) = \sigma^2$. Wtedy ogólny model regresji ze zmienną objaśnianą $Y_t$ i zmiennymi objaśniającymi $X_{1,t}, ..., X_{p,t}$ przyjmie następującą postać:

$$Y_t = f(X_{1,t}, ..., X_{p,t}) + \varepsilon_t, \tag{9.1}$$ gdzie $\varepsilon_t$ to niezależne od $X_{1,t}, ..., X_{p,t}$ zakłócenie o średniej równej $0$ i wariancji równej $\sigma^2_\varepsilon$. Funkcja $f(\cdot)$ opisuje warunkową wartość oczekiwaną $\mathbb{E}(Y_t|X_{1,t}, ..., X_{p,t})$. Warunkowa wariancja $Y_t$ to $\sigma^2_\varepsilon$.

Równanie (9.1) można rozszerzyć, dopuszczając zmienność wariancji w następujący sposób:

$$Y_t = f(X_{1,t}, ..., X_{p,t}) + \varepsilon_t\sigma(X_{1,t}, ..., X_{p,t}), \tag{9.2}$$ gdzie zakłócenie standaryzowane $\varepsilon_t$ ma (warunkowy) rozkład normalny ze średnią $0$ i odchyleniem standardowym równym $1$, natomiast funkcja $\sigma(X_{1,t}, ..., X_{p,t})$ umożliwia modelowanie warunkowej zmienności. Funkcja $\sigma(\cdot)$ powinna zwracać wartości dodatnie, ponieważ ma to być warunkowe odchylenie standardowe. Wartość $\sigma^2(X_{1,t}, ..., X_{p,t})$ to warunkowa wariancja.

Modele umożliwiające modelowanie warunkowej wariancji to modele funkcji wariancji. Do takich modeli należą modele z rodziny GARCH.

9.2 Model ARCH(1)

Załóżmy, że $\varepsilon_t$ to ścisły (Gaussowski) biały szum z jednostkową wariancją.

Wartość oczekiwana w takiej sytuacji to:

$$\mathbb{E}(\varepsilon_t|\varepsilon_{t-1}, ...) = 0, \tag{9.3}$$

a warunkowa wariancja to:

$$\mathbb{V}(\varepsilon_t|\varepsilon_{t-1}, ...) = 1 \tag{9.4}$$

Model ARCH(1) można sformułować przy użyciu takiego wzoru:

$$a_t = \varepsilon_t\sqrt{\omega + \alpha a^2_{t-1}}, \tag{9.5}$$ gdzie $\omega > 0$ i $0 \leqslant \alpha < 1$.

Równanie (9.5) można uznać za przypadek specjalny modelu (9.2) z $f(\cdot) = 0$ i $\sigma(\cdot) = \sqrt{\omega + \alpha a^2_{t-1}}$. Można je zapisać również w następujący sposób:

$$a_t^2 = \varepsilon_t^2\left(\omega + \alpha a^2_{t-1}\right), \tag{9.6}$$

Niech $\sigma^2_t$ będzie wariancją warunkową procesu opisywanego przez $a_t$:

$$\sigma_t^2 = \mathbb{V}(a_t|a_{t-1}, ...)$$

Wtedy:

$$\sigma_t^2 = \omega + \alpha a^2_{t-1} \tag{9.7}$$

Równanie (9.7) pozwala na zrozumienie, jak działają modele GARCH. Gdy $a_{t-1}$ jest co do wartości bezwzględnej duże, to odchylenie $\sigma_t$ również będzie większe niż zwykle, a tym samym zwiększone jest prawdopodobieństwo otrzymania dużego $a_t$. I odwrotnie.

Wariancja brzegowa (bezwarunkowa) w procesie ARCH(1) równa się:

$$\gamma_a(0) = \frac{\omega}{1-\alpha}$$

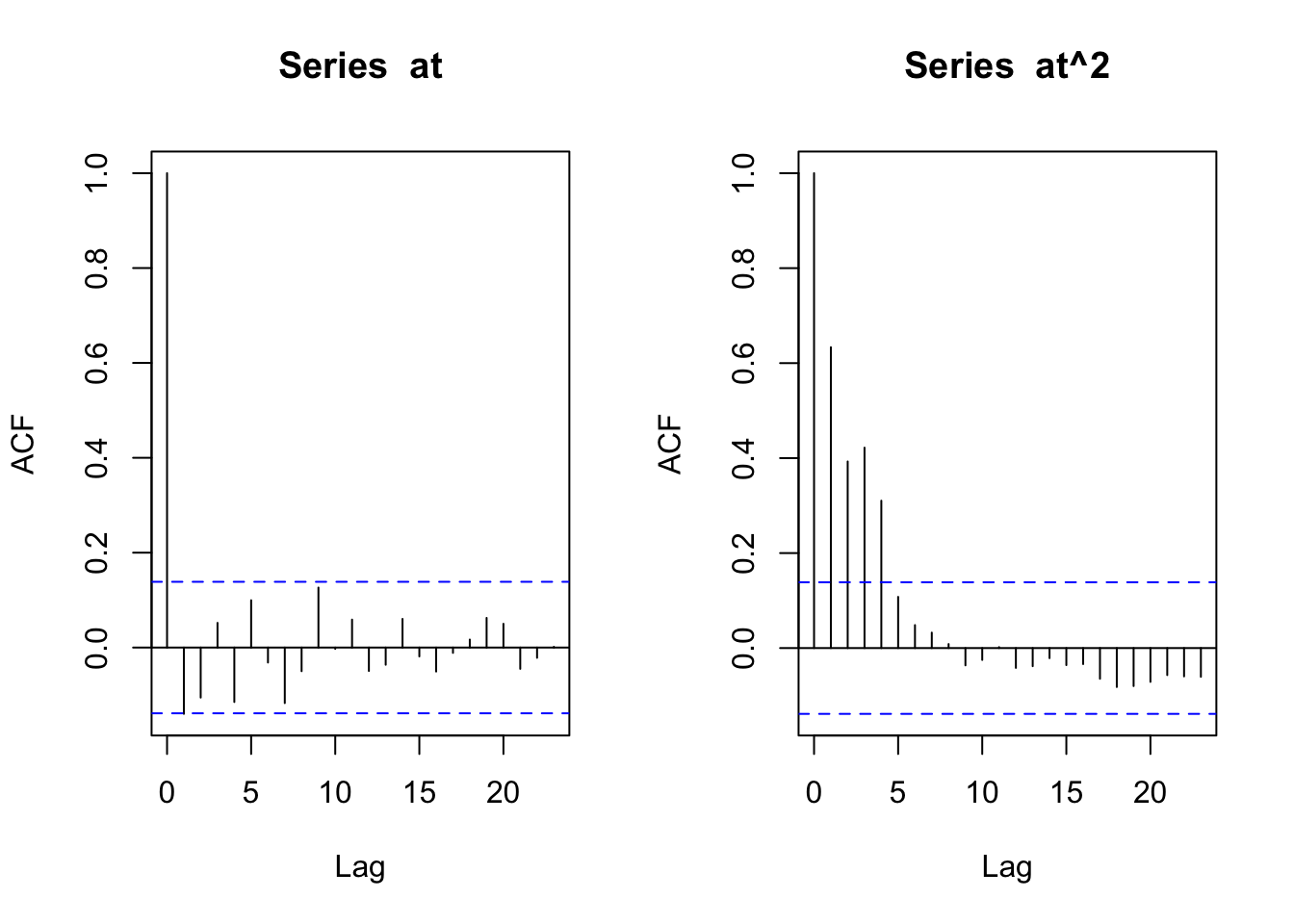
Autokorelacje w procesie ARCH(1) wynoszą zero.

Symulacja:

# pojedynczy szereg
set.seed(124)
T  <- 200
alpha <- .8
omega <- .4
at <- numeric(T)
at[1] <- omega/(1-alpha)
for (t in 2:T) {
  at[t] <- sqrt(omega + alpha*(at[t-1])^2) * rnorm(1, 0, 1) 
}
plot(at, type="l")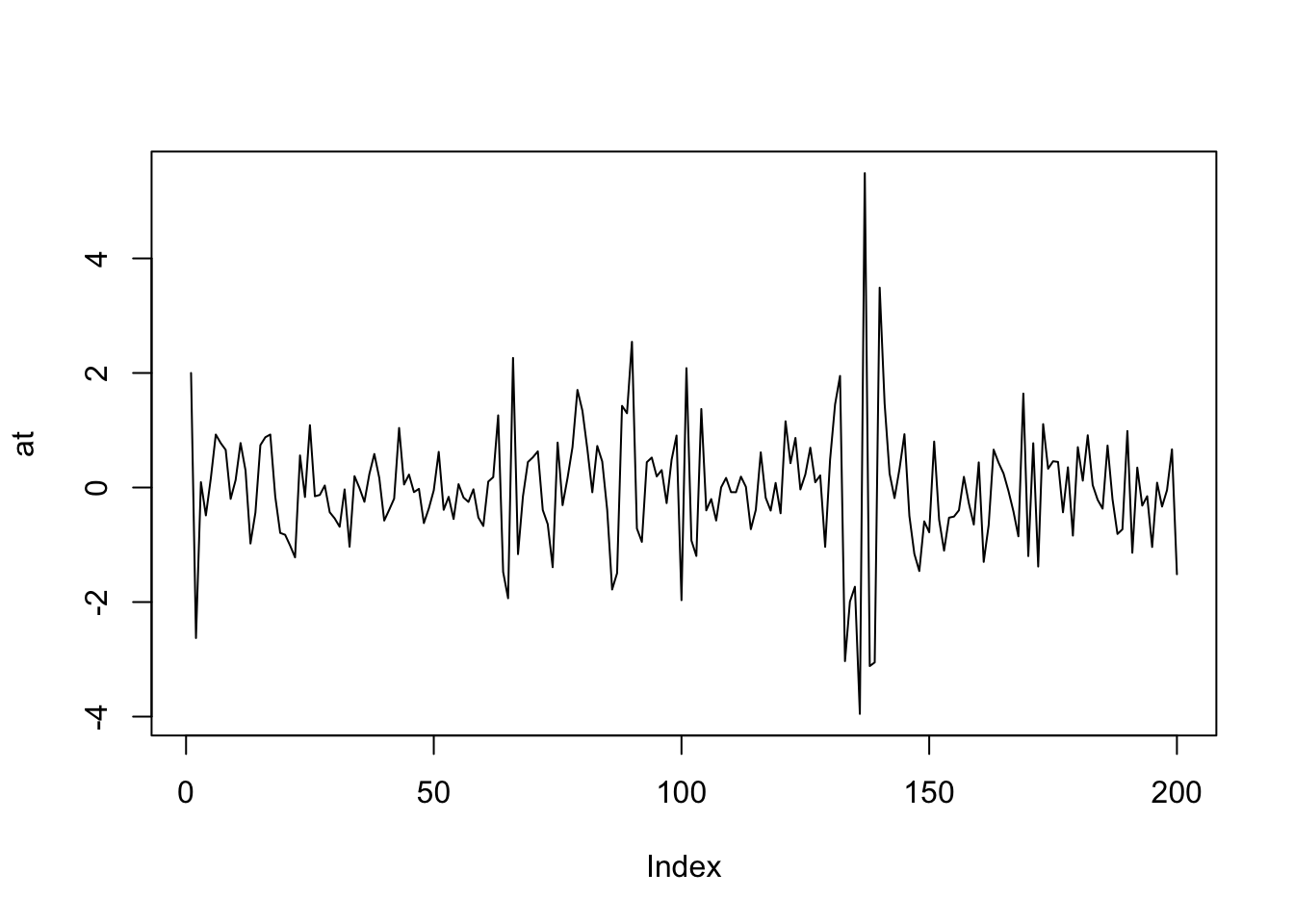

# autokorelacje w próbce
op<-par(mfrow=c(1,2))
acf(at)
acf(at^2)

par(op)


# wiele szeregów plus wykresy pudełkowe
nsim <- 1e3
w <- replicate(nsim,{ 
  at <- numeric(T)
  at[1] <- sqrt(omega/(1-alpha))
  for (t in 2:T) {
    at[t] <- sqrt(omega + alpha*(at[t-1])^2) * rnorm(1, 0, 1) 
  }
  at}
)
boxplot(t(w), pch='.', ylim=c(-5,5))

9.3 Model AR(1) + ARCH(1)

Model AR(1) ma stałą wariancję warunkową, ale zmienną średnią warunkową. Proces ARCH(1) wręcz przeciwnie. Można połączyć oba modele:

$$y_t - \mu = \phi(y_{t-1}-\mu) + a_t\\ a_t = \varepsilon_t\sigma_t \\ \sigma_t = \sqrt{\omega + \alpha a^2_{t-1}}\\ \varepsilon_t \sim \text{i.i.d.}\:\mathcal{N}(0,1) \tag{9.8}$$

Należy założyć następujące ograniczenia: $|\phi|<1$, $\omega > 0$, $0 \leqslant \alpha < 1$.

Symulacja:

# pojedynczy szereg
# set.seed(124)
T  <- 200
alpha <- 0.55
omega <- 1
mu = 0.1
phi = 0.8

at <- numeric(T)
at[1] <- omega/(1-alpha)
for (t in 2:T) {
  at[t] <- sqrt(omega + alpha*(at[t-1])^2) * rnorm(1, 0, 1) 
}
yt <- numeric(T)
yt[1] <- mu/(1-phi)
for (t in 2:T) {
  yt[t] <- mu + phi*(yt[t-1]-mu) + at[t]
}

plot(yt, type="l")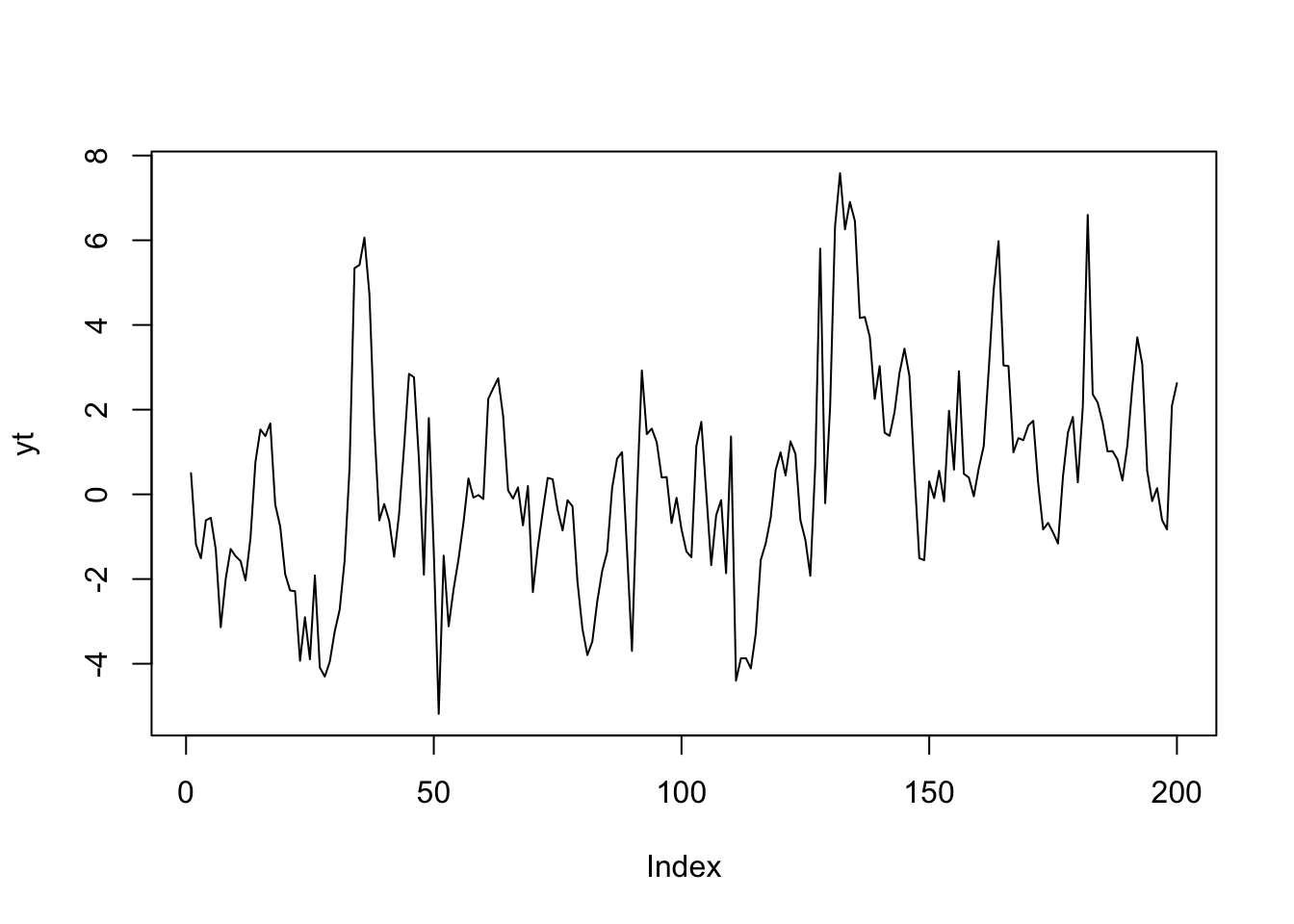

# wiele szeregów plus wykresy pudełkowe
nsim <- 1e3
w <- replicate(nsim,{ 
  at <- numeric(T)
  at[1] <- omega/(1-alpha)
  for (t in 2:T) {
    at[t] <- sqrt(omega + alpha*(at[t-1])^2) * rnorm(1, 0, 1) 
  }
  yt <- numeric(T)
  yt[1] <- mu/(1-phi)
  for (t in 2:T) {
    yt[t] <- mu + phi*(yt[t-1]-mu) + at[t]
  }
  yt}
)
boxplot(t(w), pch='.', ylim=c(-7,7))

9.4 Modele ARMA + GARCH

Powyżej opisane modele można dalej rozbudowywać. Można na przykład wprowadzić modele ARCH z większą liczbą opóźnień (oznaczane „ARCH(p)”, gdzie p to liczba opóźnień):

$$a_t = \varepsilon_t\sigma_t \\ \sigma_t = \sqrt{\omega + \sum_{i=1}^p\alpha_i a^2_{t-i}}\\ \varepsilon_t \sim \text{i.i.d.}\:\mathcal{N}(0,1) \tag{9.9}$$

Jednak wadą modeli ARCH jest to, że zwiększone oscylacje występują w krótkich okresach. Dlatego wprowadza się modele GARCH umożliwiające modelowanie bardziej trwałej zmienności.

Model GARCH(p, q) definiuje się następująco:

$$a_t = \varepsilon_t\sigma_t \\ \sigma_t = \sqrt{\omega + \sum_{i=1}^p\alpha_i a^2_{t-i}+\sum_{j=1}^q\beta_j \sigma^2_{t-j}}\\ \varepsilon_t \sim \text{i.i.d.}\:\mathcal{N}(0,1) \tag{9.9}$$

Model GARCH można połączyć z modelem ARMA. Na przykład model AR(1)+GARCH(1,1) wygląda tak:

$$y_t - \mu = \phi(y_{t-1}-\mu) + a_t\\ a_t = \varepsilon_t\sigma_t \\ \sigma_t = \sqrt{\omega + \alpha a^2_{t-1}+\beta \sigma^2_{t-1}}\\\ \varepsilon_t \sim \text{i.i.d.}\:\mathcal{N}(0,1) \tag{9.8}$$

Symulacja:

# pojedynczy szereg
set.seed(111)
T  <- 200
alpha <- 0.08
beta <- 0.7
omega <- 1
mu = 0.1
phi = 0.8

at <- numeric(T)
at[1] <- omega/(1-alpha)
sigma2t <- numeric(T)
sigma2t[1] <- omega
for (t in 2:T) {
  sigma2t[t] <- omega + alpha*(at[t-1])^2 + beta*sigma2t[t-1]
  at[t] <- sqrt(sigma2t[t]) * rnorm(1, 0, 1) 
}
yt <- numeric(T)
yt[1] <- mu/(1-phi)
for (t in 2:T) {
  yt[t] <- mu + phi*(yt[t-1]-mu) + at[t]
}

plot(yt, type="l")

# wiele szeregów plus wykresy pudełkowe
nsim <- 1e3
w <- replicate(nsim,{ 
  at <- numeric(T)
  at[1] <- omega/(1-alpha)
  sigma2t <- numeric(T)
  sigma2t[1] <- omega
  for (t in 2:T) {
    sigma2t[t] <- omega + alpha*(at[t-1])^2 + beta*sigma2t[t-1]
    at[t] <- sqrt(sigma2t[t]) * rnorm(1, 0, 1) 
  }
  yt <- numeric(T)
  yt[1] <- mu/(1-phi)
  for (t in 2:T) {
    yt[t] <- mu + phi*(yt[t-1]-mu) + at[t]
  }
  yt}
)

boxplot(t(w), pch='.', ylim=c(-12,12))

W praktyce najczęściej stosuje się model GARCH(1,1). Model charakteryzuje się empiryczną trafnością i jest wystarczająco elastyczny.

Parametr $\alpha$ ($\alpha_1$) umożliwia modelowanie efektu szoku. Parametr $\beta$ ($\beta_1$) umożliwia modelowanie autoregresji zmienności. Parametr $\omega$ umożliwia modelowanie długookresowej zmienności.

Jeżeli $\alpha_1 + \beta_1<1$ model GARCH(1,1) jest stacjonarny.

Najlepiej proces GARCH(1,1) interpretować od strony autokorelacji $a^2_t$. Można wykazać, że autokorelacja rzędu 1 to:

$$\rho_{a^2}(1) = \frac{\alpha\left(1-\alpha\beta-\beta^2\right)}{1-2\alpha\beta-\beta^2} \tag{9.10}$$

zaś korelacje dalszych rzędów to:

$$\rho_{a^2}(h) = \left(\alpha+\beta\right)^{h-1}\rho_{a^2}(1) \text{ dla } h \geqslant 2 \tag{9.11}$$

Jak wynika ze wzoru (9.10), tę samą autokorelację rzędu 1 można uzyskać dla różnych zestawów $\alpha$ i $\beta$, wzór (9.11) powoduje w uproszczeniu, że dla większych wartości $\beta$ autokorelacja zanika wolniej. Umożliwia to elastyczne modelowanie zgrupowań zmienności.

9.5 Modele GARCH – reszty i grube ogony rozkładów

9.5.1 Dwa typy reszt w modelach GARCH

Gdy dopasowuje się model ARIMA($p_M, d, q_M$)+GARCH($p_V, q_V$) do szeregu czasowego $y_t$, istnieją dwa typy reszt. Zwykła reszta, oznaczana tutaj $\widehat{a}_t$, jest różnicą między wartością rzeczywistą $y_t$ i warunkową wartością oczekiwaną i stanowi oszacowanie $a_t$. Aby otrzymać oszacowanie ${\varepsilon}_t$ należy podzielić $\widehat{a}_t$ przez oszacowane warunkowe odchylenie standardowe $\widehat{\sigma}_t$. Standaryzowane reszty $\widehat{\varepsilon_t}$ powinny być używane do sprawdzania modelu: jeśli model dobrze pasuje do danych, to ani $\widehat{\varepsilon_t}$, ani $\widehat{\varepsilon_t}^2$ nie powinny wykazywać autokorelacji. Ponadto, jeśli założono, że $\varepsilon_t$ ma rozkład normalny, to założenie to można sprawdzić za pomocą normalnego wykresu standaryzowanych reszt $\widehat{\varepsilon_t}$.

9.5.2 Modele GARCH a „ciężkie ogony”

Zwroty akcji mają rozkłady mające „ciężkie ogony”, co oznacza, że wartości odstające są bardziej intensywne niż rozkładzie normalnym. Jednym z powodów wzmożonego występowania wartości odstających może być to, że wariancja warunkowa nie jest stała. Zmienną wariancję można modelować za pomocą procesów GARCH. I rzeczywiście, szeregi generowane przez procesy GARCH mają grube ogony, nawet gdy $\varepsilon_t$ ma rozkład normalny. Niemniej jednak wiele szeregów czasowych finansowych ma ogony, które są cięższe niż wynikałoby to z procesu GARCH, gdzie $\varepsilon_t$ ma rozkład Gaussa. Dlatego zamiast założenia:

$$\varepsilon_t \sim \text{i.i.d.}\:\mathcal{N}(0,1)$$

stosuje się biały szum o rozkładzie innym niż rozkład Gaussa. Na przykład:

$$\varepsilon_t \sim \text{i.i.d.}\:\mathcal{STD}(0,1, \nu)$$

gdzie $\mathcal{STD}$ to uogólniony standaryzowany rozkład t Studenta z parametrem $\nu$ sterującym grubością ogonów rozkładu.

9.6 Dopasowywanie modelu GARCH – przykład

9.7 Prognozowanie z wykorzystaniem modelu GARCH

9.8 Uogólnienie modelu GARCH: model APARCH

APARCH to skrót o asymmetric power GARCH. Model wprowadza asymetrię w reakcji na ujemne i dodatnie szoki (stąd asymmetric) oraz pozwala modelować $\sigma_t$ za pomocą innej potegi niż dwa ($\sigma^2$). Jest to możliwe dzięki wprowadzonym do modelu nowym parametrom: $\gamma_i$ i $\delta$.

Model APARCH można opisać w następujący sposób:

$$a_t = \varepsilon_t\sigma_t \\ \sigma_t = \left({\omega + \sum_{i=1}^p\alpha_i \left(|a_{t-i}|-\gamma_i a_{t-i}\right)^\delta+\sum_{j=1}^q\beta_j \sigma^\delta_{t-j}}\right)^{1/\delta}\\ \varepsilon_t \sim \text{i.i.d.}\:\mathcal{D}(0,1), \quad \mathcal{D} \in \{\mathcal{N}, \mathcal{STD}_{\nu}, \dots \} \tag{9.12}$$

Można zauważyć, że gdy $\delta = 2$ i $\forall_i(\gamma_i=0)$, model APARCH staje się modelem GARCH.

Inne szczególne przypadki modelu APARCH również mają swoje nazwy:

• TS-GARCH: $\delta = 1$ i $\forall_i(\gamma_i=0)$

• GJR-GARCH: $\delta = 2$

• TARCH: $\delta = 1$

• NARCH: $\forall_i(\gamma_i=0)$ i $\forall_j(\beta_j=0)$

Model APARCH(1, 1) wyglądałby w następujący sposób:

$$a_t = \varepsilon_t\sigma_t \\ \sigma_t = \left({\omega + \alpha \left(|a_{t-i}|-\gamma a_{t-1}\right)^\delta+\beta \sigma^\delta_{t-1}}\right)^{1/\delta}\\ \varepsilon_t \sim \text{i.i.d.}\:\mathcal{D}(0,1), \quad \mathcal{D} \in \{\mathcal{N}, \mathcal{STD}_{\nu}, \dots \} \tag{9.13}$$