Chapter 7 Statistics

In earlier chapters, we learned some techniques for using Excel to clean data and to construct common statistics and charts. We also learned the basics of probability theory, simple random variables, and more complex random variables.

Our next step is to bring these two sets of concepts together. In this chapter, we will develop a framework for talking about data and the statistics calculated from that data as a random process that can be described using the theory of probability and random variables. We will also explore one of the most important uses of statistics: to estimate or guess at the value at, some unknown parameter of the DGP.

Chapter goals

In this chapter we will:

Model the random process generating a data set.
Apply and interpret the assumption of simple random sampling, and compare it to other sampling schemes.
Use the theory of probability and random variables to model the statistics we have calculated from a data set.
Calculate and interpret the mean and variance of a statistic from its sampling distribution.
Calculate and interpret bias and mean squared error.
Explain the law of large numbers, Slutsky’s theorem, and the idea of a consistent estimator.

7.1 Data and the data generating process

Having invested in all of the probabilistic preliminaries, we can finally talk about data. Suppose for the rest of this chapter that we have a data set called \(D_n\).

In this chapter, we will assume that \(D_n = (x_1,x_2,\ldots,x_n)\) is a data set with one variable and \(n\) observations. We use \(x_i\) to refer to the value of our variable for an arbitrary observation \(i\).

In real-world analysis, data tends to be more complex:

In most applications, it will be a simple table of numbers with \(n\) observations (rows) and \(K\) variables (columns).
However, it is occasionally something more abstract. For example, the data set at https://www.kaggle.com/c/dogs-vs-cats is a big folder full of dog and cat photos.
- A great deal of research in the statistical field of machine learning has been focused on developing methods for determining if a particular photo in this data set shows a dog or a cat.

Although our examples will all be based on simple data sets, many of our concepts and results can be applied to more complex data.

Example 7.1 Data from 3 roulette games

Suppose we have a data set \(D_3\) providing the result of \(n=3\) independent games of roulette. Let \(b_i\) be the outcome in game \(i\), and let \(x_i\) be the result of a bet on red: \[x_i = I(b_i \in RED) = \begin{cases} 1 & b_i \in RED \\ 0 & b_i \notin RED \\ \end{cases}\] Then \(D_n = (x_1,x_2,x_3)\). For example, if red loses the first two games and wins the third game we have \(D_n = (0,0,1)\).

Our data set \(D_n\) is a set of \(n\) numbers, but we can also think of it as a set of \(n\) random variables with unknown joint distribution \(P_D\). The distinction here is a hard one for students to make, so give it some thought before proceeding.

The joint distribution of \(D_n\) is called its data generating process or DGP. The exact DGP is assumed to be unknown, but we usually have at least some information about it.

Example 7.2 The DGP for the roulette data

The joint distribution of \(D_n\) can be derived. Let \[p = \Pr(b \in Red)\] We showed in a previous chapter that \(p \approx 0.486\) if the roulette wheel is fair. But rather than assuming it is fair, let’s treat \(p\) as an unknown parameter.

The PDF of \(x_i\) is \[f_x(a) = \begin{cases}(1-p) & a = 0 \\ p & a = 1 \\ 0 & \textrm{otherwise} \\ \end{cases} \] Since the random variables in \(D_n\) are independent, their joint PDF is: \[\Pr(D_n) = f_x(x_1)f_x(x_2)f_x(x_3) = p^{x_1+x_2+x_3}(1-p)^{3-x_1-x_2-x_3}\] Note that even with a small data set of a simple random variable, the joint PDF is not easy to calculate. Once we get into larger data sets and more complex random variables, it can get very difficult. That’s OK, we don’t usually need to calculate it - we just need to know that it could be calculated.

7.1.1 Simple random sampling

In order to model the data generating process, we need to model the entire joint distribution of \(D_n\). As mentioned earlier, this means we must model both:

The marginal probability distribution of each \(x_i\)
The relationship between the \(x_i\)’s

Fortunately, we often can simplify this joint distribution quite a bit by assuming that \(D_n\) is independent and identically distributed (IID) or a simple random sample from a large population.

A simple random sample has two features:

Independent: Each \(x_i\) is independent of the others.
Identically distributed: Each \(x_i\) has the same (unknown) marginal distribution.

This implies that its joint PDF can be written: \[\Pr(D_n = (a_1,a_2,\ldots,a_n)) = f_x(a_1)f_x(a_2)\ldots f_x(a_n)\] where \(f_x(a) = \Pr(x_i = a)\) is just the marginal PDF of a single observation. Independence allows us to write the joint PDF as the product of the marginal PDFs for each observation, and identical distribution allows us to use the same marginal PDF for each observation.

The reason we call this “independent and identically distributed” is hopefully obvious, but what does it mean to say we have a “random sample” from a “population?” Well, one simple way of generating an IID sample is to:

Define the population of interest, for example all Canadian residents.
Use some purely random mechanism⁶ to choose a small subset of cases from this population.
- The subset is called our sample
- “Purely random” here means some mechanism like a computer’s random number generator, which can then be used to dial random telephone numbers or select cases from a list.
Collect data from every case in our sample, usually by contacting them and asking them questions (survey).

It will turn out that a moderately-sized random sample provides surprisingly accurate information on the underlying population.

Example 7.3 Our roulette data is a random sample

Each observation \(x_i\) in our roulette data is an independent random draw from the \(Bernouilli(p)\) distribution where \(p = \Pr(b \in Red)\).

Therefore, this data set satisfies the criteria for a simple random sample.

7.1.2 Time series data

Our employment data set is an example of time series data; it is made of observations of each variable at regularly-spaced points in time. Most macroeconomic data - GDP, population, inflation, interest rates - are time series.

Time series have several features that are inconsistent with the random sampling assumption:

They usually have clear time trends.
- For example, Canada’s real GDP has been steadily growing for as long as we have data.
- This violates “identically distributed” since 2010 GDP is drawn from a distribution with a higher expected value than the distribution for 1910 GDP.
They usually have clear recurring cyclical patterns or seasonality.
- For example, unemployment in Canada is usually lower from September through December.
- This also violates “identically distributed” since February unemployment has a higher expected value than November unemployment.
They usually exhibit what is called autocorrelation.
- For example, shocks to the economy that affect GDP in one month or quarter (think of COVID or a financial crisis) are likely to have a similar (if smaller) effect on GDP in the next month or quarter.
- This violates “independence” since nearby time periods are positively correlated.

We can calculate statistics for time series, and we already did in Chapter 6. However, time series data often requires more advanced techniques than we will learn in this class. ECON 433 addresses time series data.

7.1.3 Other sampling models

Not all useful data sets come from a simple random sample or a time series. For example:

A stratified sample is collected by dividing the population into strata (subgroups) based on some observable characteristics, and then randomly sampling a predetermined number of cases within each strata.
- Most professional surveys are constructed from stratified samples rather than random samples.
- Stratified sampling is often combined with oversampling of some smaller strata that are of particular interest.
  - The LFS oversamples residents of Prince Edward Island (PEI) because a national random sample would not catch enough PEI residents to accurately measure PEI’s unemployment rate.
  - Government surveys typically oversample disadvantaged groups.
- Stratified samples can usually be handled as if they were from a random sample, with some adjustments.
A cluster sample is gathered by dividing the population into clusters, randomly selecting some of these clusters, and sampling cases within the cluster.
- Educational data sets are often gathered this way: we pick a random sample of schools, and then collect data from each student within those schools.
- Cluster samples can usually be handled as if they were from a random sample, with some adjustments.
A census gathers data on every case in the population.
- For example, we might have data on all 50 US states, or all 10 Canadian provinces, or all of the countries of the world.
- Data from administrative sources such as tax records or school records often cover the entire population of interest as well.
- Censuses are often treated as random samples from some hypothetical population of “possible” cases.
A convenience sample is gathered by whatever method is convenient.
- For example, we might gather a survey from people who walk by, or we might recruit our friends to participate in the survey.
- Convenience samples are the worst-case scenario; in many cases they simply aren’t usable for accurate statistical analysis.

Many data sets combine several of these elements. For example, Canada’s unemployment rate is calculated using data from the Labour Force Survey (LFS). The LFS is built from a stratified sample of the civilian non-institutionalized working-age population of Canada. There is also some clustering: the LFS will typically interview whole households, and will do some geographic clustering to save on travel costs. The LFS is gathered monthly, and the resulting unemployment rate is a time series.

7.1.4 Sample selection and representativeness

Random samples and their close relatives have the feature that they are representative of the population from which they are drawn. In a sense that will be made more clear over the next few chapters, any sufficiently large random sample “looks just like” the population.

Unfortunately, a simple random is quite difficult to collect from humans. Even if we are able to randomly select cases, we often run into the following problems:

Nonresponse occurs when a sampled individual does not provide the information requested by the survey
- Survey-level nonresponse occurs when the sampled individual does not answer any questions.
  - This can occur if the sampled individual cannot be found, refuses to answer, or cannot answer (for example, is incapacitated due to illness or disability).
  - Recent response rates to telephone surveys have been around 9%, implying over 90% of those contacted do not respond.
- Item-level nonresponse occurs when the sampled individual does not answer a particular question.
  - This can occur if the respondent refuses to answer, or the question is not applicable or has no valid answer.
  - Item-level nonresponse is particularly common on sensitive questions including income.
Censoring occurs when a particular quantity of interest cannot be observed for a particular case. Censored outcomes are extremely common in economics, for example:
- In labour market analysis, we cannot observe the market wage for individuals who are not currently employed.
- In supply/demand analysis, we only observe quantity supplied and quantity demanded at the current market price.

When observations are subject to nonresponse or censoring, we must interpret the data carefully.

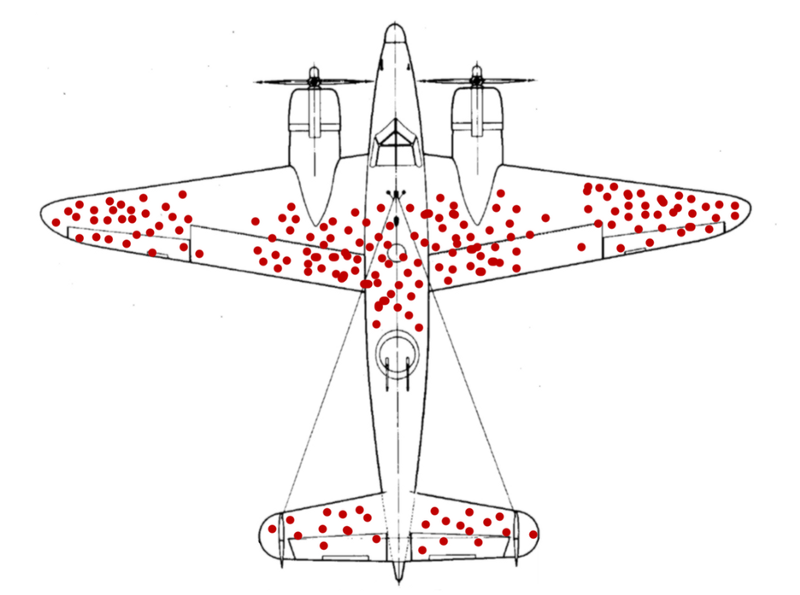
Example 7.4 Wald’s airplanes

Abraham Wald was a Hungarian/American statistician and econometrician who made important contributions to both the theory of statistical inference and the development of economic index numbers such as the Consumer Price Index.

Like many scientists of his time, he advised the US government during World War II. As part of his work, he was provided with data on combat damage received by airplanes, with the hopes that the data could be used to help make the planes more robust to damage. The data looked something like this (this isn’t the real data, just a visualization constructed for the example):

Seeing this data, some military analysts concluded that planes were mostly being shot in the wings and in the middle of the fuselage (body), and that they should be reinforced with additional steel in these locations.

Wald quickly realized that this was wrong: the data were taken from planes that returned, which is not a random sample of planes that went out. Planes were probably shot in the nose, the engines, and the back of the fuselage just as often as anywhere else, but they did not appear often in the data because they crashed. Wald’s insight led to a counter-intuitive policy recommendation: reinforce the parts of the plane that rarely show damage.

There are two basic solutions to nonresponse and censoring:

Imputation: we assume or impute values for all missing quantities. For example, we might assume that the wage of each non-employed worker is equal to the average wage among employed workers with similar characteristics.
Redefinition: we redefine the population so that our data can be correctly interpreted as a random sample from that population. For example, instead of having a random sample of Canadians, we can interpret our data as a random sample of Canadians who would answer these questions if asked.

This is not an issue that has a purely technical solution, but requires careful thought instead. If we are imputing values, do we believe that our imputation method is reasonable? If we are redefining the population, is the redefined population one we are interested in? There is no right or wrong answers to these questions, and sometimes our data are simply not good enough to answer our questions.

Nonresponse bias in recent US elections

Going into both the 2016 and 2020 US presidential elections, polls indicated that the Democratic candidate had a substantial lead over the Republican candidate:

Hillary Clinton led Donald Trump by 4-6% nationally in 2016
Joe Biden led Trump by 8% nationally in 2020.

The actual vote was much closer:

Clinton won the popular vote (but lost the election) by 2%
Biden won the popular vote (and won the election) by about 4.5%.

The generally accepted explanation among pollsters for the clear disparity between polls and voting is systematic nonresponse: for some reason, Trump voters are less likely to respond to polls. Since most people do not respond to standard telephone polls any more (response rates are typically around 9%), it does not take much difference in response rates to produce a large difference in responses. For example, suppose that:

We call 1,000 voters
These voters are equally split, with 500 supporting Biden and 500 supporting trump.
10% of Biden voters respond (50 voters)
8% of Trump voters respond (40 voters)

The overall response rate is 9% (similar to what we usually see in surveys), Biden has the support of \(50/90 = 56\%\) of the respondents while Trump has the support of \(40/90 = 44\%\). Actual support is even, but the polls show a 12 percentage point gap in support, entirely because of the small difference in response rates.

Polling organizations employ statisticians who are well aware of this problem, and they made various adjustments after 2016 to address it. For example, most now weight their analysis by education, since more educated people tend to have a higher response rate. Unfortunately, the 2020 results indicate that this adjustment was not enough. Some pollsters have argued that it makes more sense to just assume the nonresponse bias is 2-3% and adjust the numbers by that amount directly.

7.2 Statistics and their properties

Suppose we have some statistic \(s_n =s(D_n)\), i.e., a number that is calculated from the data.

Since the data is observed/known, the value of the statistic is observed/known.
Since the elements of \(D_n\) are random variables, \(s_n\) is also a random variable with a well-defined (but unknown) probability distribution that depends on the unknown DGP.

Example 7.5 Roulette wins

In our roulette example, the total number of wins is: \[R = x_1 + x_2 + x_3\] Since this is a number calculated from our data, it is a statistic.

Since \(x_i \sim Bernoulli(p)\), we can show that \(R \sim Binomial(3,p)\).

7.2.1 Some important statistics

I will use \(s_n\) to represent an abstract statistic, but we will often use other notation to talk about specific statistics.

The most important statistic is the sample average which is defined as: \[\bar{x}_n = \frac{1}{n} \sum_{i=1}^n x_i\] We will also consider several other commonly-used univariate statistics:

The sample variance of \(x_i\) is defined as: \[s_x^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2\] A closely-related statistic is the sample standard deviation \(s_x = \sqrt{s_x^2}\) which is the square root of the sample variance.
The sample frequency or relative sample frequency of the event \(x_i \in A\) is defined as the proportion of cases in which the event occurs: \[\hat{f}_A = \frac{1}{n} \sum_{i=1}^n I(x_i \in A)\] A closely-related statistic is the absolute sample frequency \(n\hat{f}_A\) which is the number of cases in which the event occurs.
The sample median of \(x_i\) is defined as: \[\hat{m}_x = m: \begin{cases} \hat{f}_{x < m} \leq 0.5 \\ \hat{f}_{x > m} \leq 0.5 \\ \end{cases}\]

7.2.2 The sampling distribution

Since the data itself is a collection of random variables, any statistic calculated from that data is also a random variable, with a probability distribution that can be derived from the DGP.

Example 7.6 The sampling distribution of the sample frequency

Calculating the exact probability distribution of most statistics is quite difficult, but it is easy to do for the sample frequency. Let \(p =\Pr(x_i \in A)\). Then: \[n\hat{f}_A \sim Binomial(n,p)\] In other words, we can calculate the exact probability distribution of the sample frequency using the formula for the binomial distribution.

Unfortunately, most statistics typically have sampling distributions that are quite difficult to calculate.

To see why the sampling distribution of a statistic is so difficult to calculate, suppose we have a discrete random variable \(x_i\) whose support \(S_x\) has five elements. Then we need to calculate the sampling distribution of our statistic by adding its probability up across the support of \(D_n\). The support has \(5^n\) elements, a number that can quickly get very large.

For example, a typical data set in microeconomics has at least a few hundred or a few thousand observations. With 100 observations, \(D_n\) can take on \(5^{100} \approx 7.9 \times 10^{69}\) (that’s 79 followed by 68 zeros!) distinct values. With 1,000 observations , \(D_n\) can take on \(5^{1000}\) distinct values, a number too big for Excel to even calculate.

7.2.3 The mean and variance

If our statistic has a probability distribution, it (usually) has a mean and variance as well. Under some circumstances, we can calculate them.

Example 7.7 The mean of the sample average

Let \(\mu_x = E(x_i)\) be the mean of \(x_i\) Then the mean of \(\bar{x}\) is: \[E(\bar{x}_n) = E\left( \frac{1}{n} \sum_{i=1}^n x_i\right) = \frac{1}{n} \sum_{i=1}^n E\left( x_i\right) = \frac{1}{n} \sum_{i=1}^n \mu_x = \mu_x\]

This is an important and general result in statistics. The mean of the sample average in a random sample is identical to the mean of the random variable being averaged. \[E(\bar{x}_n) = E(x_i)\] We have shown this property specifically for a random sample, but it holds under many other sampling processes.

The variance of the sample average is not equal to the variance of the random variable being averaged, but they are closely related.

Example 7.8 The variance of the sample average

To keep the math simple, suppose we only have \(n = 2\) observations. Then the sample average is: \[\bar{x} = \frac{1}{2}(x_1 + x_2)\] By our earlier formula for the variance: \[\begin{align} var(\bar{x}) &= var\left(\frac{1}{2}(x_1 + x_2)\right) \\ &= \left(\frac{1}{2}\right)^2 var(x_1 + x_2) \\ &= \frac{1}{4} \left( \underbrace{var(x_1)}_{\sigma_x^2} + 2 \underbrace{cov(x_1,x_2)}_{0 \textrm{(independence)}} + \underbrace{var(x_2)}_{\sigma_x^2} \right) \\ &= \frac{1}{4} \left( 2 \sigma_x^2 \right) \\ &= \frac{\sigma_x^2}{2} \\ \end{align}\]

More generally, the variance of the sample average in a random sample of size \(n\) is: \[var(\bar{x}_n) = \frac{\sigma_x^2}{n}\] where \(\sigma_x^2 = var(x_i)\).

Other commonly-used statistics also have a mean and variance.

Example 7.9 The mean and variance of the sample frequency

Since the absolute sample frequency has the binomial distribution, we have already seen its mean and variance. Let \(p = \Pr(x_i \in A)\). Then \(n\hat{f}_A \sim Binomial(n,p)\) and: \[E(n\hat{f}_A) = np\] \[var(n\hat{f}_A) = np(1-p)\]

Applying the usual rules for expected values, the mean and variance of the relative sample frequency is: \[E(\hat{f}_A) = \frac{E(n\hat{f}_A)}{n} = \frac{np}{n} = p\] \[var(\hat{f}_A) = \frac{var(n\hat{f}_A)}{n^2} = \frac{np(1-p)}{n^2} = \frac{p(1-p)}{n} \]

7.3 Estimation

Statistics are often used to estimate, or guess the value of, some unknown feature of the population or DGP.

7.3.1 Parameters and estimators

A parameter is an unknown number characterizing a DGP.

Example 7.10 Examples of parameters

Sometimes a single parameter completely describes the DGP:

In our roulette data set, the joint distribution of the data depends only on the single parameter \(p = \Pr(b \in Red)\).

Sometimes a group of parameters completely describe the DGP:

If \(x_i\) is a random sample from the \(U(L,H)\) distribution, then \(L\) and \(H\) are both parameters.

And sometimes a parameter only partially describes the DGP

If \(x_i\) is a random sample from some unknown distribution with unknown mean \(\mu_x = E(x_i)\), then \(\mu_x\) is a parameter.
If \(x_i\) is a random sample from some unknown distribution with unknown median \(m_x = q_{0.5}(x_i)\), then \(m_x\) is a parameter.

Typically there will be particular parameters whose value we wish to know. Such a parameter is called a parameter of interest. Our model may include other parameters, which are typically called auxiliary parameters or nuisance parameters.

An estimator is a statistic that is being used to estimate (guess at the value of) an unknown parameter of interest. The distinction between estimator and estimate is a subtle one: we use “estimate” when talking about our statistic as a number calculated for a specific data set and “estimator” when talking about it as a random variable.

Example 7.11 Commonly used estimators

Our four example statistics are commonly used as estimators:

The relative sample frequency \(\hat{f}_A\) is typically used as an estimator of the probability \(p_A = \Pr(x_i \in A)\)
The sample average \(\bar{x}\) is typically used as an estimator of the population mean \(\mu_x = E(x_i)\).
The sample variance \(s_x^2\) is typically used as an estimator of the population variance \(\sigma_x^2 = var(x_i)\).
The sample median \(\hat{m}_x\) is typically used as an estimator of the population median \(m_x = q_{0.5}(x_i)\).

Estimators are statistics, so they have all the usual characteristics of a statistic, including a sampling distribution, a mean, a variance, etc.

In addition estimators have properties specific to their purpose as a statistic that is supposed to take on a value close to the unknown parameter of interest.

7.3.2 Sampling error

Let \(s_n\) be a statistic we are using as an estimator of some parameter of interest \(\theta\). We can define its sampling error as: \[err(s_n) = s_n - \theta\] In principle, we want \(s_n\) to be a good estimator of \(\theta\), i.e., we want the sampling error to be as close to zero as possible.

There are several major complications to keep in mind:

Since \(s_n\) is a random variable with a probability distribution, \(err(s_n)\) is also a random variable with a probability distribution.
Since the value of \(\theta\) is unknown, the value of \(err(s_n)\) is also unknown.

Always remember that \(err(s_n)\) is not an inherent property of the statistic - it depends on the relationship between the statistic and the parameter of interest. A given statistic may be a good estimator of one parameter, and a bad estimator of another parameter.

7.3.3 Bias

In choosing an estimator, we can consider several criteria.

The first is the bias of the estimator, which is defined as its expected sampling error: \[\begin{align} bias(s_n) &= E(err(s_n)) \\ &= E(s_n - \theta) \\ &= E(s_n) - \theta \end{align}\] Note that bias is always defined relative to the parameter we wish to estimate, and is not an inherent property of the statistic.

Ideally we would want \(bias(s_n)\) to be zero, in which case we would say that \(s_n\) is an unbiased estimator of \(\theta\).

Example 7.12 Two unbiased estimators of the mean

Consider the sample average \(\bar{x}_n\) in a random sample as an estimator of the parameter \(\mu_x = E(x_i)\). The bias is: \[bias(\bar{x}_n) = E(\bar{x}_n) - \mu_x = \mu_x - \mu_x = 0\] That is, the sample average is an unbiased estimator of the population mean.

However, it is not the only unbiased estimator. For example, suppose we simply take the value of \(x_i\) in the first observation and throw away the rest of the data. This “first observation estimator” is easier to calculate than the sample average, and is also an unbiased estimator of \(\mu_x\): \[bias(x_1) = E(x_1) - \mu_x = \mu_x - \mu_x = 0\] This example illustrates a general principle: there is rarely exactly one unbiased estimator. There are either none, or many.

Example 7.13 An unbiased estimator of the variance

The sample variance is an unbiased estimator of the population variance: \[E(s_x^2) = \sigma_x^2 = var(x_i)\] This is not hard to prove, but I will skip it for now.

If there are multiple unbiased estimators available for a given parameter, we need to apply a second criterion to choose one. A natural second criterion is the variance of the estimator: \[var(s_n) = E[(s_n-(E(s_n))^2]\] If \(s_n\) is unbiased, then a low variance means it is usually close to \(\theta\), while a high variance means that it is often either much larger or much smaller than \(\theta\). Clearly, low variance is better than high variance.

The minimum variance unbiased estimator (MVUE) of a parameter is the unbiased estimator with the lowest variance.

Example 7.14 The variance of the sample average and and first observation estimators

In our previous example, we found two unbiased estimators for the mean, the sample average \(\bar{x}_n\) and the first observation \(x_1\).

The variance of the sample average is: \[var(\bar{x}_n) = \sigma^2/n\] and the variance of the first observation estimator is: \[var(x_1) = \sigma^2\] For any \(n > 1\), the sample average \(\bar{x}_n\) has lower variance than the first observation estimator \(x_1\). Since they are both unbiased, it is the preferred estimator of the two.

In fact, we can prove that \(\bar{x}_n\) is the minimum variance unbiased estimator of \(\mu_x\).

7.3.4 Mean squared error

Unfortunately, once we move beyond the simple case of estimating the population mean, we run into several complications:

The first complication is that an unbiased estimator may not exist for a particular parameter of interest. If there is no unbiased estimator, there is no minimum variance unbiased estimator. So we need some other way of choosing an estimator.

Example 7.15 The sample median

There is no unbiased estimator of the median of a random variable with unknown distribution. To see why, consider the simplest possible data set: a random sample of size \(n=1\) on the random variable \(x_i \sim Bernoulli(p)\), where \(0 < p < 1\). The median of \(x_i\) in this case is: \[m_x = I(p > 0.5)\]

First we show that the sample median is a biased estimator of \(m_x\). The sample median is: \[\hat{m}_x = x_1\] and its expected value is: \[E(\hat{m}_x) = E(x_1) = p \neq I(p > 0.5)\] So the sample median \(\hat{m}_x\) is a biased estimator for the population median \(m_x\).

More generally, any statistic calculated from this data set must take the form \(s = a_0 + a_1x_1\), where \(s = a_0\) when \(x_1 = 0\) and \(s = a_0+a_1\) is its value when \(x_1 = 1\). This statistic has expected value \(E(a_0 + a_1x_1) = a_0 + a_1p\), so any unbiased estimator would need to solve the equation: \[a_0 + a_1 p = I(p > 0.5)\] and there is no such solution.

The second complication is that we often have access to an unbiased estimator and a biased estimator with lower variance.

Example 7.16 The relationship between age and earnings

One common question in labour economics is how earnings vary by various characteristics such as age.

Suppose we have a random sample of 800 Canadians, and we want to estimate the earnings of the average 35-year old Canadian. Assuming for simplicity that ages are equally-spaced between 0 and 80, our data set will have only 10 Canadians at each age. So we have several options:

Average earnings of the 10 35-year-olds in our data.

This estimator will be unbiased, but 10 observations isn’t very much and so its variance will be high. We can reduce the variance by adding more observations from people who are almost 35 years old:

Average earnings of the 30 34-36 year olds in our data.
Average earnings of the 100 30-39 year olds in our data.
Average earnings of the 800 0-80 year olds in our data.

By including more data, these estimators will have lower variance but will introduce bias. My guess is introducing 34 and 36 year olds is a good idea since they probably have similar earnings to 35 year olds, but including children and the elderly is not such a good idea.

This suggests that we need a criterion that

Can be used to choose between biased estimators
Can choose slightly biased estimators with low variance over unbiased estimators with high variance.

The mean squared error of an estimator is defined as the expected value of the squared sampling error: \[\begin{align} MSE(s_n) &= E[err(s_n)^2] \\ &= E[(s_n-\theta)^2] \\ &= var(s_n) + [bias(s_n)]^2 \end{align}\] The MSE criterion allows us to choose a biased estimator with low variance over an unbiased estimator with high variance, and also allows us to choose between biased estimators when no unbiased estimator exists.

Example 7.17 The MSE of the sample mean and first observation estimators

The mean squared error of the sample average is: \[MSE(\bar{x}_n) = var(\bar{x}_n) + [bias(\bar{x}_n)]^2 = \frac{\sigma_x^2}{n} + 0^2 = \frac{\sigma_x^2}{n}\] and the mean squared error of the first observation estimator is: \[MSE(x_1) = \sigma_x^2\] The sample average is the preferred estimator by the MSE criterion, so in this case we get the same result as applying the MVUE criterion.

7.3.5 Standard error

Parameter estimates are typically reported along with their standard errors. The standard error of a statistic is an estimate of its standard deviation.

Example 7.18 The standard error of the average

We have shown that the sample average provides a good estimate of the population mean, and that its variance is: \[var(\bar{x}_n) = \frac{\sigma_x^2}{n} = \frac{var(x_i)}{n}\] Since \(s_x^2\) is an unbiased estimator of \(var(x_i)\) we can use it to construct an unbiased estimator of \(var(\bar{x})\): \[E\left(\frac{s_x^2}{n}\right) = \frac{E(s_x^2)}{n} = \frac{var(x_i)}{n} = var(\bar{x}_n)\]

We might also want to estimate the standard deviation of \(\bar{x}\). A natural approach would be to take the square root of the estimator above, yielding: \[se(\bar{x}_n) = \frac{s_x}{\sqrt{n}}\] This is the conventional formula for the standard error of the sample average, and is typically reported next to the sample average.

Standard errors are usually biased estimators of the statistic’s true standard deviation, but the bias is typically small.

7.4 The law of large numbers

So far, we have described statistics and estimators in terms of their probability distribution and the mean, variance and mean squared error associated with that probability distribution.

We are able to do this fairly easy with both sample averages and sample frequencies (which are also sample averages) because they are sums. Unfortunately, this is not so easy with other statistics (e.g. standard errors, medians, percentiles, etc.) that are nonlinear functions of the data.

In order to deal with those statistics, we need to construct approximations based on the asymptotic properties of the statistics. Asymptotic properties are properties that hold approximately, with the approximation getting closer and closer to the truth as the sample size gets larger.

Properties that hold exactly for any sample size are sometimes called exact or finite sample properties. All of the results we have discussed so far are finite sample results.

We will state two main asymptotic results in this chapter: the law of large numbers and Slutsky’s theorem. A third asymptotic result called the central limit theorem will be stated in the next chapter.

All three results rely on the concept of a limit, which you would have learned in your calculus course. If you need to review that concept, please see the section on limits in the math appendix. However, I will not expect you to do any significant amount of math with these results. Please focus on the intuition and interpretation and don’t worry too much about the math.

7.4.1 Defining the LLN

The law of large numbers (LLN) says that for a large enough random sample, the sample average is almost identical to the corresponding population mean.

In order to state the LLN, we need to introduce some concepts. Consider a data set \(D_n\) of size \(n\), and let \(s_n\) be some statistic calculated from \(D_n\). We say that \(s_n\) converges in probability to some constant \(c\) if: \[\lim_{n \rightarrow \infty} \Pr( |s_n - c| < \epsilon) = 1\] for any positive number \(\epsilon > 0\).

Intuitively, what this means is that for a sufficiently large \(n\) (the \(\lim_{n \rightarrow \infty}\) part), \(s_n\) is almost certainly (the \(\Pr(\cdot) = 1\) part) very close to \(c\) (the \(|s_n-c| < \epsilon\) part).

We have a compact way of writing convergence in probability: \[w_n \rightarrow^p c\] means that \(w_n\) converges in probability to \(c\).

Having defined our terms we can now state the law of large numbers.

LAW OF LARGE NUMBERS: Let \(\bar{x}_n\) be the sample average from a random sample of size \(n\) on the random variable \(x_i\) with mean \(E(x_i) = \mu_x\). Then \[\bar{x}_n \rightarrow^p \mu_x\]

Example 7.19 The LLN in the economy

The law of large numbers is extremely powerful and important, as it is the basis for the gambling industry, the insurance industry, and much of the banking industry.

A casino works by taking in a large number of independent small bets. As we have seen for the case of roulette, these bets have a small house advantage, so their average benefit to the casino is positive. The casino can lose any bet, but the LLN virtually guarantees that the gains will outweigh the losses as long as the casino takes in a large enough number of independent bets.

An insurance company works almost the same as a casino. Each of us faces a small risk of a catastrophic cost: a house that burns down, a car accident leading to serious injury, etc. Insurance companies collect a little bit of money from each of us, and pay out a lot of money to the small number of people who have claims. Although the context is quite different, the underlying economics are identical to those of a casino: the insurance company prices its products so that its revenues exceed its expected payout, and takes on a large number of independent risks.

Sometimes insurance companies do lose money, and even go bankrupt. The usual cause of this is a big systemic event like a natural disaster, pandemic or financial crisis that affects everyone. Here the independence needed for the LLN does not apply.

7.4.2 Consistent estimation

The law of large numbers applies to the sample mean, but we are interested in other estimators as well.

In general, we say that the statistic \(s_n\) is a consistent estimator of a parameter \(\theta\) if: \[s_n \rightarrow^P \theta\] It will turn out that most of the statistics we use are consistent estimators of the thing we typically use them to estimate.

The key to this property is a result called Slutsky’s theorem. Slutsky’s theorem roughly says that if the law of large numbers applies to a statistic \(s_n\), it also applies to \(g(s_n)\) for any continuous function \(g(\cdot)\).

SLUTSKY THEOREM: Let \(g(\cdot)\) be a continuous function. Then: \[s_n \rightarrow^p c \implies g(s_n) \rightarrow^p g(c)\]

What is the importance of Slutsky’s theorem? Most commonly used statistics can be written as continuous functions of a sample average (or several sample averages). Slutsky’s theorem extends the LLN to these statistics, and ensures that these commonly used statistics are consistent estimators of the corresponding population parameter. For example:

The sample variance is a consistent estimator of the population variance: \[s_x^2 \rightarrow^p var(x)\]
The sample standard deviation is a consistent estimator of the population standard deviation: \[s_x \rightarrow^p sd(x)\]
The relative sample frequency is a consistent estimator of the population probability: \[\hat{f}_A \rightarrow^p \Pr(A)\]
The sample median is a consistent estimator of the population median, and all other sample quantiles are consistent estimators of the corresponding population quantile.

The math needed to make full use of Slutsky’s theorem and prove these results is beyond the scope of this course, so all I am asking here is for you to know that it can be used for this purpose.

Chapter review

In this chapter we have learned to model a data generating process, describe the probability distribution of a statistic, interpret a statistic as an estimator of some unknown parameter of the underlying data generating process.

Almost by definition, estimators are rarely identical to the parameter of interest, so any conclusions based on estimators have a degree of uncertainty. To describe this uncertainty in a rigorous and quantitative manner, we will next learn some principles of statistical inference.

Practice problems

Answers can be found in the appendix.

SKILL #1: Identify whether a data set is a random sample

Suppose we have a data set \(D_n = (x_1,x_2)\) of size \(n = 2\). For each of the following conditions, identify whether it implies that \(D_n\) is (i) definitely a random sample; (ii) definitely not a random sample; or (iii) possibly a random sample.
1. The two observations are independent and have the same mean \(E(x_1) = E(x_2) = \mu_x\).
2. The two observations are independent and have the same mean \(E(x_1) = E(x_2) = \mu_x\) and variance \(var(x_1)=var(x_2)=\sigma_x^2\).
3. The two observations are independent and have different means \(E(x_1) \neq E(x_2)\).
4. The two observations have the same PDFs, and are independent.
5. The two observations have the same PDFs, and have \(corr(x_1,x_2) = 0\)
6. The two observations have the same PDFs, and have \(cov(x_1,x_2) > 0\)

SKILL #2: Classify data sets by sampling types

Identify the sampling type (random sample, time series, stratified sample, cluster sample, census, convenience sample) for each of the following data sets.
1. A data set from a survey of 100 SFU students who I found waiting in line at Tim Horton’s.
2. A data set from a survey of 1,000 randomly selected SFU students.
3. A data set from a survey of 100 randomly selected SFU students from each faculty.
4. A data set that reports total SFU enrollment for each year from 2005-2020.
5. A data set from administrative sources that describes demographic information and postal code of residence for all SFU students in 2020.

SKILL #3: Describe the probability distribution of a very simple data set

Suppose we have a data set \(D_n = (x_1,x_2)\) that is a random sample of size \(n = 2\) on the random variable \(x_i\) which has discrete PDF: \[\begin{align} f_x(a) &= \begin{cases} 0.4 & a = 1 \\ 0.6 & a = 2 \\ \end{cases} \end{align}\] Let \(f_{D_n}(a,b) = \Pr(x_1=a \cap x_2 = b)\) be the joint PDF of the data set
1. Find the support \(S_{D_n}\)
2. Find \(f_{D_n}(1,1)\)
3. Find \(f_{D_n}(2,1)\)
4. Find \(f_{D_n}(1,2)\)
5. Find \(f_{D_n}(2,2)\)

SKILL #4: Find the sampling distribution of a very simple statistic

Suppose we have the data set described in question 3 above. Find the support \(S\) and sampling distribution \(f(\cdot)\) for each of the following statistics:
1. The sample frequency \(\hat{f}_1 = \frac{I(x_1=1) + I(x_2=1)}{2}\).
2. The sample average \(\bar{x} = (x_1 + x_2)/2\).
3. The sample variance \(\hat{\sigma}_x^2 = (x_1-\bar{x})^2 + (x_2-\bar{x})^2\).
4. The sample standard deviation \(\hat{\sigma}_x = \sqrt{\hat{\sigma}_x^2}\).
5. The sample minimum \(xmin = \min(x_1, x_2)\).
6. The sample maximum \(xmax = \max(x_1, x_2)\).

SKILL #5: Find the mean and variance of a statistic from its sampling distribution

Suppose we have the data set described in question 3 above. Find the mean of each of the following statistics:
1. The sample frequency \(\hat{f}_1 = \frac{I(x_1=1) + I(x_2=1)}{2}\).
2. The sample average \(\bar{x} = (x_1 + x_2)/2\).
3. The sample variance \(\hat{\sigma}_x^2 = (x_1-\bar{x})^2 + (x_2-\bar{x})^2\).
4. The sample standard deviation \(\hat{\sigma}_x = \sqrt{\hat{\sigma}_x^2}\).
5. The sample minimum \(xmin = \min(x_1, x_2)\).
6. The sample maximum \(xmax = \max(x_1, x_2)\).
Suppose we have the data set described in question 3 above. Find the variance of the following statistics:
1. The sample frequency \(\hat{f}_1 = \frac{I(x_1=1) + I(x_2=1)}{2}\).
2. The sample average \(\bar{x} = (x_1 + x_2)/2\).
3. The sample minimum \(xmin = \min(x_1, x_2)\).
4. The sample maximum \(xmax = \max(x_1, x_2)\).

SKILL #6: Find the mean and variance of a linear statistic

Suppose we have a data set \(D_n = (x_1,x_2)\) that is a random sample of size \(n = 2\) on the random variable \(x_i\) which has mean \(E(x_i) = 1.6\) and variance \(var(x_i) = 0.24\). Find the mean and variance of the following statistics:
1. The first observation \(x_1\).
2. The sample average \(\bar{x} = (x_1 + x_2)/2\).
3. The weighted average \(w = 0.2*x_1 + 0.8*x_2\).

SKILL #7: Distinguish between parameters and statistics

Suppose \(D_n\) is a random sample of size \(n=100\) on a random variable \(x_i\) which has the \(N(\mu,\sigma^2)\) distribution. Which of the following are unknown parameters of the DGP? Which are statistics calculated from the data?
1. \(D_n\)
2. \(n\)
3. \(x_i\)
4. \(i\)
5. \(N\)
6. \(\mu\)
7. \(\sigma^2\)
8. \(E(x_i)\)
9. \(E(x_i^3)\)
10. \(var(x_i)\)
11. \(sd(x_i)/\sqrt{n}\)
12. \(\bar{x}\)
Suppose we have the data set described in question 3 above. Find the true value of each of the following parameters:
1. The probability \(\Pr(x_i=1)\).
2. The population mean \(E(x_i)\)
3. The population variance \(var(x_i)\)
4. The population standard deviation \(sd(x_i)\)
5. The population minimum \(\min(S_x)\).
6. The population maximum \(\max(S_x)\).

SKILL #8: Calculate sampling error

Suppose we have the data set described in question 3 above. Suppose we use the sample maximum \(xmax = \max(x_1,x_2)\) population maximum \(\max(S_x)\).
1. Find the support \(S_{err}\) of the sampling error \(err = \max(x_1,x_2) - max(S_x)\).
2. Find the PDF \(f_{err}(\cdot)\) for the sampling distribution of the sampling error \(err\).

SKILL #9: Calculate bias and classify estimators as biased or unbiased

Suppose we have the data set described in question 3 above. Classify each of the following estimators as biased or unbiased, and calculate the bias.
1. The sample frequency \(\hat{f}_1\) as an estimator of the probability \(\Pr(x_i=1)\).
2. The sample average \(\bar{x}\) as an estimator of the population mean \(E(x_i)\)
3. The sample variance \(\hat{\sigma}_x^2\) as an estimator of the population variance \(var(x_i)\)
4. The sample standard deviation \(\hat{\sigma}_x\) as an estimator of the population standard deviation \(sd(x_i)\)
5. The sample minimum \(xmin\) as an estimator of the population minimum \(\min(S_x)\).
6. The sample maximum \(xmax\) as an estimator of the population maximum \(\max(S_x)\).
Suppose we are interested in the following parameters:
- The average earnings of Canadian men: \(\mu_M\).
- The average earnings of Canadian women: \(\mu_W\).
- The male-female earnings gap in Canada: \(\mu_M - \mu_W\).
- The male-female earnings ratio in Canada: \(\mu_M/\mu_W\).
and we have calculated the following statistics from a random sample of Canadians:
- The average earnings of men in our sample \(\bar{y}_{M}\)
- The average earnings of women in our sample \(\bar{y}_{W}\)
- The male-female earnings gap in our sample \(\bar{y}_{M} - \bar{y}_{W}\).
- The male-female earnings ratio in our sample \(\bar{y}_{M}/\bar{y}_{W}\).
We already know that \(\bar{y}_{M}\) is an unbiased estimator of \(\mu_M\) and \(\bar{y}_{W}\) is an unbiased estimator of \(\mu_W\).
1. Is the sample earnings gap \(\bar{y}_M - \bar{y}_W\) a biased or unbiased estimator of the population gap \(\mu_M - \mu_W\)? Explain.
2. Is the sample earnings ratio \(\bar{y}_M/\bar{y}_W\) a biased or unbiased estimator of the population earnings ratio \(\mu_M/\mu_W\)? Explain.

SKILL #10: Calculate mean squared error

Suppose we have the data set described in question 3 above. Calculate the mean squared error for each of the following estimators.
1. The sample frequency \(\hat{f}_1\) as an estimator of the probability \(\Pr(x_i=1)\).
2. The sample average \(\bar{x}\) as an estimator of the population mean \(E(x_i)\)
3. The sample minimum \(xmin\) as an estimator of the population minimum \(\min(S_x)\).
4. The sample maximum \(xmax\) as an estimator of the population maximum \(\max(S_x)\).

SKILL #11: Apply MVUE and MSE criteria to select an estimator

Suppose you have a random sample of size \(n=2\) on the random variable \(x\) with mean \(E\left(x\right)=\mu\) and variance \(var(x_i)=\sigma^2\). Two potential estimators of \(\mu\) are the sample average \[\bar{x} = \frac{x_1 + x_2}{2}\] and the last observation \[x_2\]
1. Are these estimators biased or unbiased?
2. Find \(var(\bar{x})\)
3. Find \(var(x_2)\)
4. Find \(MSE(\bar{x})\)
5. Find \(MSE(x_2)\)
6. Which estimator is preferred under the MVUE criterion?
7. Which estimator is preferred under the MSE criterion?

SKILL #12: Calculate the standard error for a sample average

Suppose that we have a random sample \(D_n\) of size \(n=100\) on the random variable \(x_i\) with unknown mean \(\mu\) and unknown variance \(\sigma^2\). Suppose that the sample average is \(\bar{x} = 12\) and the sample variance is \(\hat{\sigma}^2 = 4\). Find the standard error of \(\bar{x}\).

SKILL #13: Explain and interpret the law of large numbers

Suppose we have a random sample of size \(n\) on the random variable \(x_i\) with mean \(E(x_i) = \mu\). Which of the following statistics are consistent estimators of \(\mu\)?
1. The sample average \(\bar{x}\)
2. The sample median.
3. The first observation \(x_1\).
4. The average of all even-numbered observations.
5. The average of the first 100 observations.

As a technical matter, the assumption of independence requires that we sample with replacement. This means we allow for the possibility that we sample the same case more than once. In practice this doesn’t matter as long as the sample is small relative to the population.↩︎