15 Pearl and Mackenzie (2018)

摘要自 Pearl and Mackenzie (2018) 之中文版《因果革命：人工智慧的大未來》。

前言

因果推論（causal inference）這門新科學以簡單的數學語言，來表達我們已知和想知道的因果關係。近三十年，因果模型已經造成了因果革命（causal revolution）。因果革命所蘊含的數學可說是因果的微積分，其包含兩種語言。一是因果圖（causal diagram），用以描述已知事物，為「知識語言」，由點線構成；一是類似代數的符號語言，用以描述我們想知道的事物，為「查詢語言」，例如我們若想知道藥物 $D$ 對壽命 $L$ 的影響，可以寫成 $P(L|do(D))$。

請注意，觀察到服用藥物 $D$ 而壽命是 $L$ 的機率不同於 $P(L|do(D))$，是 $P(L|D)$。「觀察到某個現象」與「刻意造成某個現象」有相當大的區別。因果革命的成就包含說明如何不需實際介入就能預測介入效果。不過在此之前，我們就須定義 $do\mbox{-}$ 這個運算子，並找出方法以非侵入性的方式模擬介入。而科學推理涉及回顧過去時，我們需要反事實（counterfactual）的思考，即「如果⋯⋯會怎樣？」

圖 15.1 的因果推論發動機（causal inference engine）可以協助人工智慧處理因果推論工作。

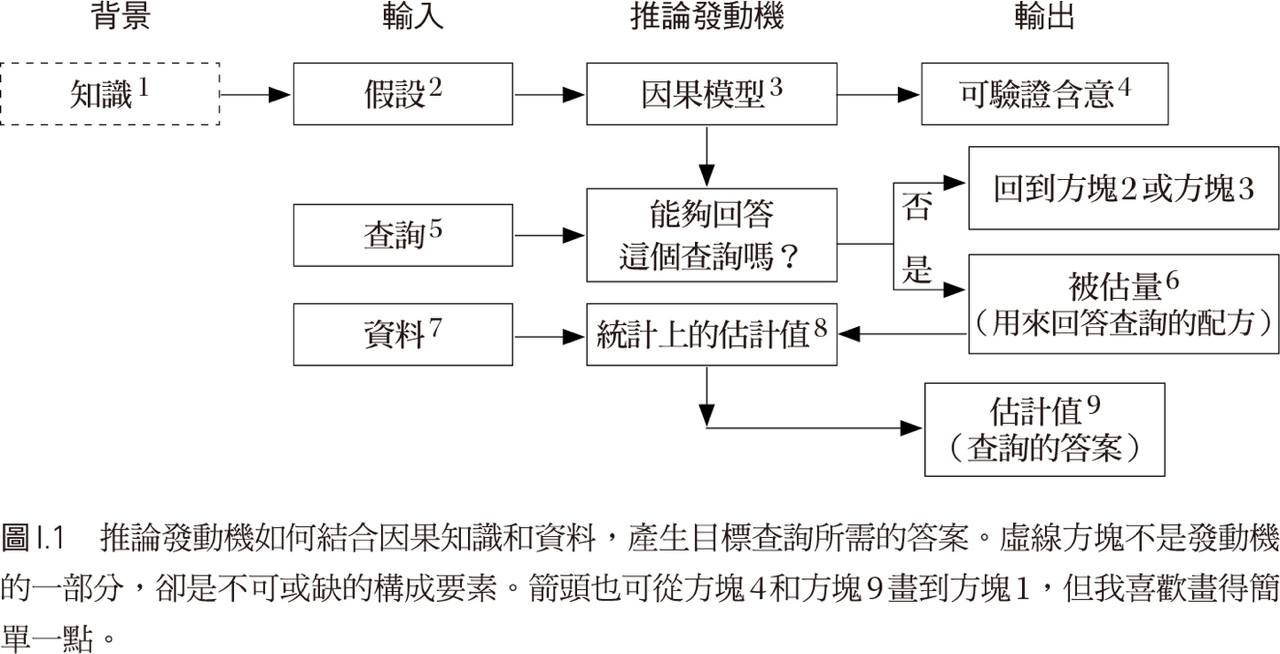
Figure 15.1: 推論發動機。

15.1 因果階梯

Lucky is he who has been able to understand the causes of things.

— Virgil (29 BC)

I would rather discover one true cause than gain the kingdom of Persia.

— Democritus

15.1.1 因果的三個層級

因果學習者至少必須掌握三個不同層級的認知能力，如圖 15.2：

1. 觀看：透過關聯學習（learning from association）探知環境規律。多數動物和深度學習都還停留於此。

2. 實行：預測可以改變環境的效果並從中獲得想要的結果。少數動物才能辦到。

3. 想像：想像不存在的世界，推知眼前現象的原因。唯有人類具備如此能力。

Figure 15.2: 因果階梯（the ladder of causation）。

15.1.2 迷你圖靈測驗與因果圖範例

Figure 15.3: 行刑隊因果圖範例。

假設有囚犯將被槍決。圖 15.3 表示，槍決完成先要法院要下令執行，行刑隊隊長再命令士兵 $A$ 與 $B$ 開槍（其中一人有開槍，囚犯就會死亡）。而每個未知數（$CO$、$C$、$A$、$B$、$D$）都是真假變數。例如 $D$ 為假則囚犯存活，$CO$ 為真代表法院確有下達命令。我們可以利用因果圖回答因果階梯上每層的因果問題：

1. 關聯：如果囚犯死亡，是否表示法院已下達命令？如圖 15.3，只要不斷回溯，就知道法院已下達命令。

2. 介入：如果士兵 $A$ 未獲命令而自作主張開槍，那囚犯會存活或死亡？乍看之下矛盾的問題，如圖 15.4，造成事件時，去除所有指向事件的箭頭，擦去所有指向 $A$ 的箭頭，那電腦可知如果 $A$ 為真（開槍）則 $D$ 為真（囚犯死亡）。注意看見與實行的區別。

Figure 15.4: 介入的因果推理。

3. 反事實：假設囚犯已死，我們利用「關聯」可知 $A$ 已開槍、$B$ 已開槍、隊長已下命令、法院也發出命令；而如果當時 $A$ 決定不開槍會如何？如圖 15.5，顯然囚犯仍會死亡。

Figure 15.5: 反事實推理內容。

能通過迷你圖靈測驗，即能回答因果問題，電腦才能算是了解因果關係。

15.1.3 機率與因果

條件機率無法說明因果關係。「$X$ 使 $Y$ 的機率提高」表為 $P(Y|X) > P(Y)$ 其實是不正確的。$P(Y|X) > P(Y)$ 只提到觀察，事實上是意味著「如果我們看見 $X$，則 $Y$ 的機率提高」，但 $Y$ 的機率提高的理由或有許多原因。所以說，條件機率還停留在因果階梯的第一層，無法回答第二層或第三層問題。或有以背景因素（background factors）或干擾因子（confounders）來描述，即 $P(Y|X, K=k) > P(Y|k=k)$，其中 $K$ 為背景因素，例如給定氣溫 32 度之下，冰淇淋的銷售量 $Y$ 會因為 $X$ 而提高。但哪些變數必須納入為背景因素 $K$？

使用 $do\mbox{-}$ 運算子可以表達「機率提高」的概念，我們可以說如果 $P(Y|do(X)) > P(Y)$ 則 $X$ 是 $Y$ 的原因。

15.2 從海盜到天竺鼠

E pur si muove.

— Galilei

高爾頓想研究人類智慧的遺傳，而從身高開始研究起。他發現，親代與子代之間，身高有迴歸均值（regression toward mediocrity, regression to the mean）的現象。他也提出了相關（correlated）的概念，其學生皮爾森（Karl Pearson）後來提出迴歸線斜率的公式，稱為相關係數（correlation coefficient）。本來高爾頓是要追尋因果，最後卻發現了相關。遺傳的因果模型由 Hardy 與 Weinberg 提出，採用孟德爾遺傳理論。

皮爾森把因果掃出統計學。他指出：

That a certain sequence has occurred and reoccurred in the past is a matter of experience to which we give expression in the concept causation…. Science in no case can demonstrate any inherent necessity in a sequence, nor prove with absolute certainty that it must be repeated.

— The Grammar of Science (Pearson, 1892)

皮爾森後來創立期刊 Biometrica，皮爾森生物統計實驗室成為全世界的統計學中心，他並把意見相左者逐出生物統計學界。皮爾森本人還指出假相關（spurious correlation），例如人均巧克力食用越多的國家，諾貝爾獎得主越多。這要用因果性解釋，但他在解釋某些相關有意義，某些卻沒有時，卻說「真相關是指出變項間的『有機關係』，假相關則否」。但「有機關係」是什麼？就是因果關係嗎？

萊特（Sewall Wright）研究遺傳學與天竺鼠的過程中，提出了路徑圖。²他的路徑圖是史上首次發表的因果圖。後來，他又發表 Wright (1921)，說明如何將路徑分析運用到天竺鼠以外的領域，但卻遭皮爾森的學生 Henry Niles 大力反駁，且再來幾十年內也未獲重視。不提出因果假說，就不可能得出因果結論，並非「一切都在資料中」。

會受到這麼嚴重的忽視，有論者認為，是因為萊特的路徑分析需要人主觀地繪製因果圖，這背離了傳統的統計學。貝氏統計學雖然也有主觀的成分，但與傳統的統計學相仿，也使用機率的語言，因此後來與古典統計學和解了，因果圖卻沒有。

15.3 從證據到原因

因果圖就是貝氏網路，圖中的忝頭代表直接或可能存在的因果關係，以箭頭方向為準。貝氏網路不見得有因果性，但如果我們想要詢問因果階梯上第二層或第三層的問題，我們就需要注意因果性並繪製因果圖。

15.3.1 貝氏法則

貝氏機率由 Thomos Bates 提出，貝氏網路也是由此命名。Bayes 想要解決逆機率（inverse probability）的問題，所以提出了貝氏法則。例如 $P(T)$ 為顧客點茶的機率，$P(S)$ 代表點司康的機率，而 $P(S|T)$ 是已知某位顧客點了茶，他點司康的機率。我們可知， $$\begin{aligned} P(S \mbox{ and } T) &= P(S|T)\times P(T),\\ P(S \mbox{ and } T) &= P(T|S)\times P(S). \end{aligned}$$ 因此可得 $$P(S|T)\times P(T) = P(T|S)\times P(S).$$

以四十歲女性接受乳房造影為例，假設檢測如癌結果為陽性。如果 $D$ 為罹患癌症，而檢測 $T$ 為造影結果，這個人該多相信這個假設？應該動手術嗎？改寫貝氏法則後可得 $$(D \mbox{ 的修正後機率}) = P(D|T) = (\mbox{概似比}) \times (D \mbox{ 的事前機率}).$$ 而概似比（likelihood ratio）為 $P(T|D)/P(T)$，用以計算疾病患者檢測結果為陽性的可能性比一般人高出多少。

15.3.2 貝氏網路

作者從認知科學的文獻獲得啟發，提出了貝氏網路。貝氏網路成為機器學習的實用選擇。但貝氏網路與因果圖不同，不假設箭頭具有因果意義；箭頭只代表我們知道正向機率 $P(S|T)$，貝氏法則告訴我們如何把事前機率乘以概似比，反轉這個程序。

不過，貝氏網路與因果網路仍有相同之處，都由 junctions 所建構。Junctions 分為三種基本的類型，如下。

Chain or mediation: $A\rightarrow B\rightarrow C$.

$B$ 是把 $A$ 的效果傳送給 $C$ 的中介變數（mediator）；例如「起火 $\rightarrow$ 冒煙 $\rightarrow$ 警報」。如果我們切斷這個 chain 中的這個 junction，例如以通風管吸去所有煙，那就不會有警報。Chain 的關鍵在於，中介變數 $B$ 把關於 $A$ 的資訊與 $C$ 隔離開來。在條件化（conditioning）——即給定中介變數 $B$ 的值時，$A$ 與 $C$ 為條件獨立；已知「冒煙」值時，「起火」和「警報」為條件獨立，如「冒煙」值等於 1，則無論有無起火，肯定有警報。

Fork: $A \leftarrow B \rightarrow C$.

$B$ 是 $A$ 與 $C$ 的共同原因（common cause）或干擾因子（confounder）。干擾因子可以在沒有直接因果連結的 $A$ 和 $C$ 之間產生統計相關，例如「鞋子尺寸 $\leftarrow$ 兒童年齡 $\rightarrow$ 閱讀能力」。這兩者不是因果關係，所以給小孩穿大鞋，不會讓他的閱讀能力變好。條件化鞋子尺寸以後我們就會發現鞋子尺寸與閱讀能力的相關就消失了；即條件化 $B$ 將使得 $A$ 與 $C$ 條件獨立。

Collider: $A\rightarrow B \leftarrow C$.

例如「才華 $\rightarrow$ 成名 $\leftarrow$ 外貌」。我們會認為才華和外貌都能讓演員成功，但才華和外貌無關。將 $B$ 條件化，$A$ 與 $C$ 將會變成相依。例如只觀察著名演員（「成名」$=1$），會發現才貌為負相關，某名人外貌平庸，肯定是相當有才華。這類的負相關有時候稱為衝突偏誤（collider bias）或自圓其說效應（explain-away effect）。

15.4 干擾與去干擾

控制實驗（controlled experiment）的原理即找兩組相似的人，一組接受處置，一組則否，比較兩者的結果。並且，前瞻性（prospective）相當重要，即要事先選擇各組的成員，不能像是減肥廣告一樣只是找了成效很好的使用者來背書。另外，也要注意干擾偏差（confounding bias）

Figure 15.6: $Z$ 是 $X$ 與 $Y$ 之間因果關係的干擾因子。

15.5 煙霧瀰漫的爭議

15.6 破解悖論

15.7 超越調整

15.8 反事實

15.9 中介

15.10 大數據、人工智慧與大問題

參考文獻

Pearl, Judea, and Dana Mackenzie. 2018. The Book of Why: The New Science of Cause and Effect. Basic books.

Wright, Sewall. 1921. “Correlation and Causation.”

---

2. 其父 Philip Wright 為一經濟學家，是最早提出工具變數的人。↩︎