Les 1 Wat is data?

Neem de voorbereiding (paragraaf 1.2) door voor de les begint.

1.1 Lesinhoud en leerdoelen

In deze les maken we een begin met Excel, en we bespreken de basis van dataverwerking.

Theorie:

  • wat is data
  • onderzoeksvragen
  • steekproeven
  • variabelen
  • experimental design
  • welke grafiek past bij welk soort experiment

Vaardigheden:

  • Datafiles openen in Excel
  • Data kopieren en verplaatsen in Excel
  • Data organiseren in Excel: transpose
  • Grafieken maken

1.2 Voorbereiding

1.2.1 Wat is data?

Wat is eigenlijk data, en waarom maken we daar zo’n punt van? Data zijn “units of information”, vaak getallen maar dat hoeft niet, die verzameld zijn en opgeslagen. Dat kan van alles zijn: de staartlengtes van alle katten in Utrecht, welk cijfer (op een schaal van 1-10) alle studenten in je klas de les geven, de gemeten extincties in de laatste vaardighedenles met de spectrofotometer, hoeveel studenten we per leergroep hebben met blond haar, een lijst van alle oscar-nominaties van de afgelopen 5 jaar…

Uit data kun je informatie halen. Vaak wordt dit gezien als het bekijken van patronen in data, of het plaatsen van data in context. Als docent zijn we bijvoorbeeld geinteresseerd in de beoordeling van een les, want uit die data kunnen we informatie halen: vinden studenten de les over het algemeen prettig of niet?

In de loop van je studie ga je een heleboel data verzamelen en bekijken. Maar met data die je niet netjes opslaat of analyseert, kun je later niets mee. De informatie die je er uit had kunnen halen is dan verloren. In deze cursus leer je daarom meer over data en hoe je die kunt bewaren en verwerken met Excel. Ook leer je om die data te visualiseren (bijv. grafiekjes maken), en informatie eruit te halen (statistiek).

1.2.2 Soorten data

Data kun je grofweg verdelen in 2 soorten:

  • kwantitatief: nummers, kan je meten, heeft een eenheid (bijv cm, ml etc)
    • voorbeeld: haarlengte in centimeter
  • kwalitatief: woorden, plaatjes, symbolen etc, kan je niet meten, heeft geen eenheid
    • voorbeeld: haarkleur van de studenten in VL1224

Kwantitatieve data

Bij kwantitatieve schalen maken we onderscheid tussen de datatypes interval en ratio.

Bij ratio data is de verhouding tussen twee uitkomsten een zinvolle grootheid: zo is bv. de lengte van een stuk hout van 2 meter ook 2 keer zo lang als van een stuk hout van 1 meter. 0 meter betekent ook echt nul: niks. Nul gram weegt niets.

Bij interval data geldt dat niet: een gebouw uit het jaar 2000 is niet 2x zo oud als een gebouw uit het jaar 1000 (de jaartelling is immers een relatieve maat); de hoeveelheid warmte-energie in een voorwerp van 20 graden Celcius is niet twee keer zoveel als in een voorwerp van 10 graden Celcius. Dat komt omdat het nulpunt bij dit soort data niet echt “niks” betekent. Nul uur op de klok is niet “geen tijd”. En in het jaar 0 gebeurde er van alles, er was niet “geen jaar”. De intervallen zijn wel steeds gelijk. Van 15:00h tot 16:00h duurt precies even lang als van 16:00h tot 17:00h.

Kwalitatieve data

Kwalitatieve data kun je opdelen in nominale en ordinale data.

Bij nominale data heb je categorieen, maar de ene categorie is niet hoger of lager dan de andere categorie. Als je bijvoorbeeld vraagt of docenten met de fiets, auto of trein naar de HU komen, dan is hun antwoord (“fiets”, “auto”, “trein”) nominaal.

Bij ordinale data is er wel een rangorde te maken (de ene waarde is groter dan de andere), maar niet uit te drukken in een nummertje dat iets betekent (dan zou het kwantitatieve data zijn). Bijvoorbeeld als je docenten vraagt of ze er erg lang, lang of kort over doen om op de HU te komen. Lang is meer dan kort, maar hoeveel meer? Geen idee. De intervallen zijn dus niet steeds gelijk.

Table 1.1: Data Types
type kenmerk voorbeelden
kwantitatief (scale in het Engels)
ratio meetbaar, absoluut nulpunt leeftijd, gewicht, eiwitconcentratie, hemoglobineconcentratie
interval meetbaar, geen absoluut nulpunt, gelijke intervallen tijd (nulpunt is een keuze), temperatuur in graden Celsius
kwalitatief
nominaal niet rangschikbaar bloedgroep, geslacht, godsdienst, ras
ordinaal rangschikbaar mate van activiteit, kwaliteitsoordeel, aantal sterren van een restaurant
Opdracht 1

Welk type data is:

  • pH
  • goud, zilver en bronzen medailes op de olympische spelen
  • bloedgroepen van je leerteam
  • aantal van deze vragen dat je fout beantwoordt
  • beoordeling van je stoel op een schaal van 1 tot 5 (1 = zit slecht, 5 = zit fantastisch)
Klik hier voor het antwoord


  • pH: interval (pH 0 is niet “geen zuurtegraad”, pH 7 is niet 2x zoveel als pH 3.5)
  • medailes: ordinaal
  • bloedgroepen: nominaal
  • aantal vragen fout: ratio (nul fout = niks fout, 4 fout is twee keer zoveel fout als 2 fout.)
  • stoelbeoordeling: ordinaal. het zijn wel nummertjes, maar die staan eigenlijk voor kwalitatieve beoordelingen. Ze zijn niet meetbaar. Het interval tussen die nummertjes is niet gelijk: het precieze verschil tussen een score van 2 en een score van 3 is onbekend. 3 is beter dan 2, maar meer kan je niet zeggen. En een stoel met een score van 2 zit niet twee keer zo lekker als een stoel met een score van 1.

1.2.3 Data rapporteren

Data is een kostbaar goedje in onderzoeksland. Het is dus belangrijk om je data goed op te slaan, en netjes over te dragen als je over data communiceert!

Een aantal regels voor het delen van excelsheets en andere bestanden met data:

  • Als je een verslag inlevert, lever dan ook een excelbestand met de ruwe data in, en een ander excelbestand met je berekeningen / bewerkingen van die data en grafiekjes.
  • Zorg dat je data kopieert en niet overtypt waar ook maar enigszins mogelijk. Overtypen zorgt voor fouten.
  • Pas nooit je ruwe data aan. Bewaar die in een aparte excelfile, zodat je altijd terug kunt vinden wat je precies op het lab opgeschreven hebt.
  • Zorg dat elke kolom in excel waar gegevens in staat, voorzien is van een kolomheader die aangeeft wat er in die kolom staat.
  • Herhaal kolomheaders niet. Twee kolommen mogen niet dezelfde header hebben.

Dus bijvoorbeeld, niet goed is:

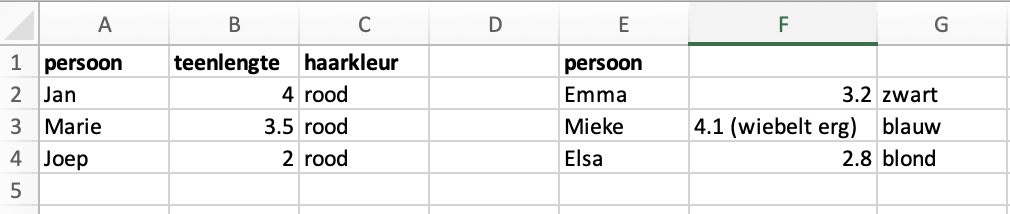
Opdracht 1

Waarom is dit geen nette excelsheet?

Klik hier voor het antwoord


  • twee kolommen hebben geen kolomheader. Is dat ook teenlengte? of misschien wat anders? Joost mag het weten.
  • kolomheaders worden herhaald (persoon)
  • het is onduidelijk wat de eenheid is
  • er staat een notitie in dezelfde cel als een datapunt. Dat zorgt ervoor dat je niet meer automatisch met dat datapunt kunt rekenen.

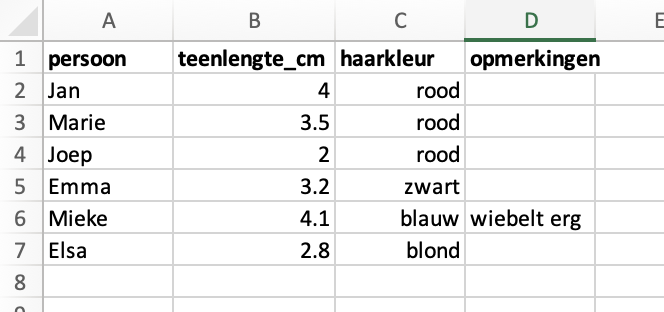
Dit zou beter zijn:

Dit is in ieder geval duidelijk. Je kan niet per ongeluk denken dat er wat anders in de kolommen staat.

Het worden wel een beetje lange kolomnamen, maar dat is beter dan onduidelijkheid.

Een nettere oplossing ( voor nu nog niet verplicht, maar wel sterk aangeraden) is om je data “tidy” op te slaan: 1 variabele per kolom, 1 observatie per rij, 1 waarde per cel:

1.2.4 Onderzoeksvraag

Data verzamel je over het algemeen om een antwoord te geven op een vraag: een onderzoeksvraag. Die zijn vrij specifiek. “Hoe zit het eigenlijk met konijnenoren?” is een vraag, maar “Zijn konijnenoren op de Uithof langer dan die van het gemiddelde konijn?” is een onderzoeksvraag: je kan een onderzoek doen om een antwoord te vinden op je vraag.

De onderzoeksvraag bepaalt dus ook voor een deel wat voor onderzoek of experiment je zou kunnen doen! Vergelijk bijvoorbeeld (en er zijn veel meer voorbeelden denkbaar):

1.2.5 Steekproef

Heel soms kun je de hele populatie meten, bijvoorbeeld als alle studenten in VL1205 en VL1206 wel bereid zijn om sinaasappels te tellen en je had de eerste van bovenstaande onderzoeksvragen.

Bij de andere voorbeelden is het echter al snel duidelijk dat het niet haalbaar gaat zijn om de hele populatie inwoners van Utrecht op te roepen voor een bloedonderzoekje. Dat gaat ’m niet worden. Toch gaat je onderzoeksvraag over alle Utrechters: over de populatie. Maar hoe komen we dan achter de ijzerconcentratie van Utrechters?

Oplossing: we doen een steekproef. Bij een steekproef meet je niet de hele populatie, maar een deel ervan. Een steekproef moet representatief zijn voor de populatie en wordt gebruikt om voorspellingen te doen over de gehele populatie. Het aantal objecten (elementen) in een steekproef wordt weergegeven met n. Dus meet je 50 Utrechters, dan zeg je: n = 50.

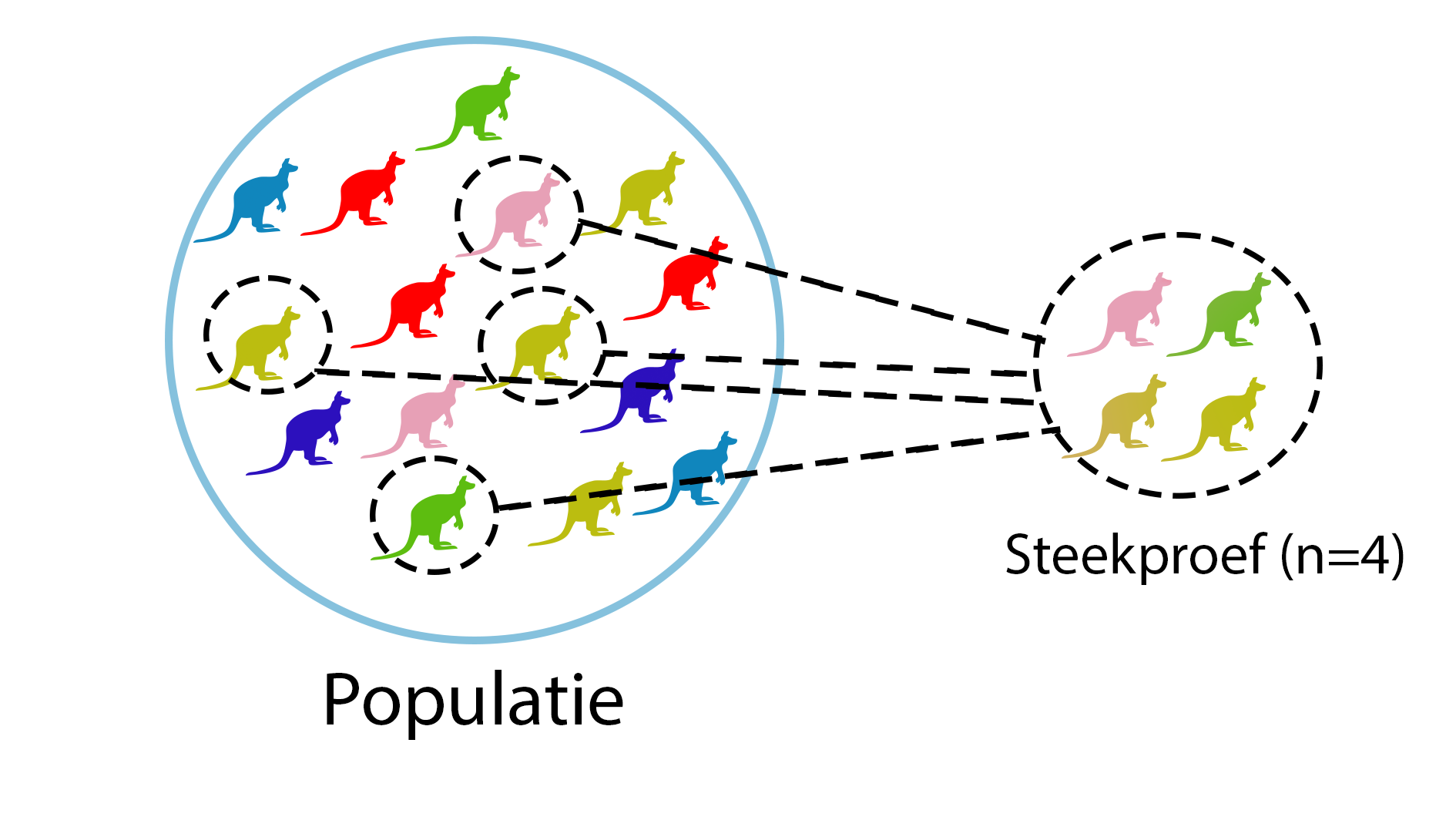
Een steekproef van 4 kangaroes uit een totale populatie van 15

Figure 1.1: Een steekproef van 4 kangaroes uit een totale populatie van 15

Representatief betekent dat de steekproef ongeveer dezelfde samenstelling heeft als de hele populatie, maar dan in het klein. Dus als je bloed-ijzergehalte in Utrecht onderzoekt, moet je random (=willekeurige) mensen in Utrecht gaan vragen of je hun bloedijzergehalte mag meten, en niet alleen studenten op de Uithof. En ook niet alleen de mensen die sowieso naar de dokter gingen om ijzer te laten testen, want die zitten wellicht wat lager dan de meeste Utrechters…

Maar… Al die Utrechters hebben andere bloed-ijzerwaarden. Dus als je een steekproef doet van 100 random mensen, krijg je andere bloedijzerwaarden dan als je nog een keer een steekproef doet van 100 random mensen. Of in het plaatje hierboven (figuur 1.1): Nu zijn de 4 kangaroes in de steekproef roze, geel, geel en groen. Maar als je nog een keer 4 random kangaroes uit de populatie kiest zijn ze waarschijnlijk andere kleuren. Het is dus bijna zeker zo dat als je verschillende steekproeven uit 1 populatie neemt, de data wel wat verschillend is.

1.2.6 inductieve en beschrijvende statistiek

Als je een steekproef doet, heb je niet de hele populatie gemeten. En elke steekproef gaat dus andere data opleveren. Maar je vraag ging over de populatie! Hoe kun je dan toch iets zeggen over die populatie? Dus in het plaatje hierboven: kun je op basis van die 4 kangaroes iets zeggen over de kleuren in de hele populatie? En hoe betrouwbaar is die inschatting? Hiervoor gebruik je inductieve statistiek: de bewerking van data uit een steekproef om een uitspraak te doen over een eigenschap van een populatie. Dit is waar mensen aan denken bij het woord “statistiek”. We gaan het hier in de komende lessen veel vaker over hebben, en je zult termen tegenkomen als “significant”, “hypothese” en “betrouwbaarheidsinterval”.

Een andere tak van statistiek is beschrijvende statistiek: Beschrijvende statistiek is de term die wordt gegeven aan de analyse van gegevens waarmee gegevens op een zinvolle manier kunnen worden beschreven, weergegeven of samengevat. Denk bijvoorbeeld aan het beschrijven van de staartlengte van 20 Utrechtse katten met een gemiddelde. Het CBS is bekend om de grote hoeveelheid beschrijvende statistiek.

Beschrijvende statistiek heeft altijd betrekking op de werkelijk gemeten waardes en kan niet gebruikt worden om hypotheses te testen of om een uitspraak te doen over de populatie aan de hand van een steekproef. Beschrijvende statistiek laat het niet toe om conclusies te trekken die verder gaan dan de gegevens die we hebben geanalyseerd. Dan zou je namelijk inductieve statistiek aan het doen zijn. Ze zijn gewoon een manier om gegevens te beschrijven over de populatie (alleen als je de hele populatie gemeten hebt) of de steekproef.

1.2.7 Variabelen

In je steekproef zit welke objecten in je populatie je gaat meten (wen je al aan de terminologie?). Maar wat ga je dan meten? Kijk, nu komen we bij de data.

Een variabele is “iets dat kan varieren”, oftewel, het is niet altijd hetzelfde. Als bloedijzerconcentratie altijd bij iedereen exact hetzelfde is, maakt niet uit wat je eet, hoe oud je bent, waar je woont…. dan hoeven we ook geen onderzoek te doen. Welke groepen we ook gaan vergelijken, ze zullen toch niet verschillend zijn.

Voorbeelden van variabelen zijn: lengte, bloeddruk, bloedgroep van proefpersonen, gewicht, IQ, politieke voorkeur, aantal HIV deeltjes in de tijd, uitbraak van influenza virus per regio, grootte van een tumor, hartslag in watervlooien, ijzergehalte in het bloed. Anything!

Variabelen heb je in onderzoek in twee smaken:

De onafhankelijk variabele is wat je weet De onafhankelijk variabele is iets wat je zelf definieert. Een onafhankelijke variabele is bijvoorbeeld de groepsindeling van een experiment (controle vs behandelde groep, man vs vrouw of een tijdsreeks).

De afhankelijke variabele is wat je meet De afhankelijke variabele of “dependent variable” hangt dus af van de onafhankelijke variabele

  • populatie: alle objecten (personen, dieren, planten, voorwerpen, cellen, eiwitten enz) waar je vraag over gaat.
  • steekproef: (als het goed is random) selectie van n objecten uit een populatie.
  • onafhankelijke variabele: wat je weet, iets wat de onderzoeker zelf bepaalt of controleert in het experiment
  • afhankelijke variabele: wat je meet, Een meetbaar kenmerk van zo’n object
Opdracht 1

Wat is bij deze onderzoeksvragen de populatie, onafhankelijke en afhankelijke variabele? Wat zou een mogelijke steekproef zijn?

  1. onderzoeksvraag: Wat is het effect van verschillende hoeveelheden kunstmest op het bladoppervlak van brandnetels?
Klik voor het antwoord
  • populatie: alle brandnetels ter wereld
  • onafhankelijke variabele: hoeveelheid kunstmest
  • afhankelijke variabele: bladoppervlak
  • mogelijke steekproef: stuk of 100 brandnetels (bijvoorbeeld)
  1. Onderzoeksvraag: Wat is de gemiddelde staartlengte van de honden in mijn straat?
Klik voor het antwoord
  • populatie: alle hondenstaarten in de straat
  • onafhankelijke variabele: geen
  • afhankelijke variabele: staartlengte
  • mogelijke steekproef: misschien is hier een steekproef niet nodig, het lijkt haalbaar om alle hondenstaarten in de straat te meten.
  1. Onderzoeksvraag: Zijn mensen in Amersfoort langer dan mensen in Utrecht?
Klik voor het antwoord
  • populatie: alle inwoners van Amersfoort en alle inwoners van Utrecht
  • onafhankelijke variabele: woonplaats
  • afhankelijke variabele: lichaamslengte
  • mogelijke steekproef: bijvoorbeeld in beide steden 200 mensen

1.2.8 Onderzoeksvragen aanpakken

Experimenten doe je niet zomaar uit de losse pols, maar met een gestructureerde planning. Deze structuur: welke variabelen gaan we meten of manipuleren en hoe gaan we die metingen met elkaar vergelijken, vormt de proefopzet. Belangrijk is hierbij dat je met die opzet objectief en zo precies mogelijk een antwoord kunt gaan geven op je onderzoeksvraag.

De proefopzet hangt af van het type onderzoeksvraag. Als je een onderzoek doet, is het belangrijk dat de volgende dingen met elkaar kloppen: je onderzoeksvraag, de variabelen die je meet of manipuleert, en de dingen die je vervolgens met elkaar gaat vergelijken.

Soorten kwantitatieve onderzoeksvragen

Kwantitatieve onderzoeksvragen (vragen die gaan over iets dat je kunt meten, zie hier) kun je grofweg onderverdelen in drie groepen:

  • verschilvragen (bijv: Zijn mannen langer dan vrouwen?)
  • verbandvragen (bijv: Wat is het verband tussen hoeveel water per dag gedronken wordt en lichaamslengte bij mannen?)
  • beschrijvende vragen (bijv: hoe lang is de gemiddelde Nederlandse man eigenlijk?)

Let op: beschrijvende statistiek over je steekproef doe je daarnaast eigenlijk altijd als je met data werkt. Ook als je een verschilvraag of een verbandvraag hebt. Stel, je vraagt je af of (onderzoeksvraag:) medicijn X het herstel bij griep versnelt ten opzichte van geen medicijnen gebruiken. Dan is het antwoord op je onderzoeksvraag “ja” of “nee”… Maar iedereen wil natuurlijk ook weten hoeveel sneller! Dus vermeld je dan even de gemiddelde ziekteduur in jouw onderzoek met en zonder medicijn X.

  • Verschilvragen:
    • is A meer/minder/anders dan B?
    • is A meer/minder/anders dan een verwachte waarde?
    • is A meer/minder/anders dan nul? (is ook een verwachte waarde eigenlijk)
    • etc
  • Verbandvragen:
    • als A meer/minder wordt, wordt B dan meer/minder?
    • is er een verband tussen A en B?
    • wat is het effect van A op B?
    • etc
  • Beschrijvende vragen:
    • hoeveel is A?
    • hoe zijn A en B verdeeld?
    • etc

Een veelgemaakte fout (op het tentamen en daarbuiten) is een dataset die over een verbandvraag gaat, analyseren alsof het een verschilvraag is (of andersom). Als we ons afvragen wat het verband is tussen waterintake en lichaamslengte bij mannen, willen we geen analyse die gaat kijken of waterintake en lichaamslengte verschillend zijn! Een andere veelgemaakte fout is dan ook: niet heel precies zijn in hoe je zinnen zoals onderzoeksvragen opschrijft. Zoals je ziet maakt het nogal uit. “Wat is het verschil tussen een dood vogeltje?” werkt niet als vraag.

Voorbeeld van een dood vogeltje. Rijksmuseum, CC0, via Wikimedia Commons

Figure 1.2: Voorbeeld van een dood vogeltje. Rijksmuseum, CC0, via Wikimedia Commons

Opdracht 1

Wat voor soort vraag is dit? Verschil, verband of beschrijvend?

  1. Wat is het effect van verschillende hoeveelheden kunstmest op de lengte van brandnetels?
Klik voor het antwoord

verband

  1. Zijn brandnetels grotere planten dan dovenetels?
Klik voor het antwoord verschil
  1. Hoeveel groeit mijn muis per dag?
Klik voor het antwoord beschrijvend
  1. Zijn Amsterdammers even zwaar als Utrechters?
Klik voor het antwoord verschil (“is er geen verschil in gewicht tussen Amsterdammers en Utrechters?”)
  1. Zijn mensen in Zwolle gemiddeld 1,75 meter lang?
Klik voor het antwoord

verschil

(“Is er een verschil tussen de lengte van mensen in Zwolle en 1,75?” Oftewel: je hebt een verwachte waarde, en je vraagt je af of de populatie anders is (verschilt) dan die verwachte waarde of niet.)

  1. Hoe lang zijn mensen in Amersfoort?
Klik voor het antwoord

beschrijvend

(Hier verwacht je verder niets, geen specifieke verschil- of verband-vraag, je wilt alleen beschrijven)

Voorbeeld: De onderzoeksvraag gaat over een verband

Bijvoorbeeld: Is er een verband tussen staartlengte en hoeveelheid blikvoer per dag in Siamezen (katten)?

variabelen

Heb je een verbandsvraag, dan zijn er dus sowieso 2 variabelen. Die variabelen zijn vaak continue: een continue variabele kan (binnen bepaalde grenzen) iedere waarde aannemen. Lichaamslengte is een voorbeeld van een continue variabele: lichaamslengtes zijn niet beperkt tot hele decimeters (150, 160, 170, 180 cm etc.), je kan 170,2 cm zijn, maar ook 169,89 cm.

Minstens 1 van de twee variabelen meet je. De andere variabele kan je meten of in een experimenteel onderzoek manipuleren. Bij dit katten-voorbeeld kun je kiezen: Je kan van je hele steekproef aan Siamezen achterhalen hoeveel blikvoer ze eten, of je kunt een experiment doen en je steekproef aan Siamezen op een dieet zetten van verschillende hoeveelheden blikvoer.

grafiek

Data van een verbandsvraag zet je meestal in een scatterplot. We gaan verderop in de les kijken hoe je die maakt in Excel. Heb je een van beide variabelen gemanipuleerd in een experiment in plaats van gemeten, dan staat die variabele altijd op de X-as.

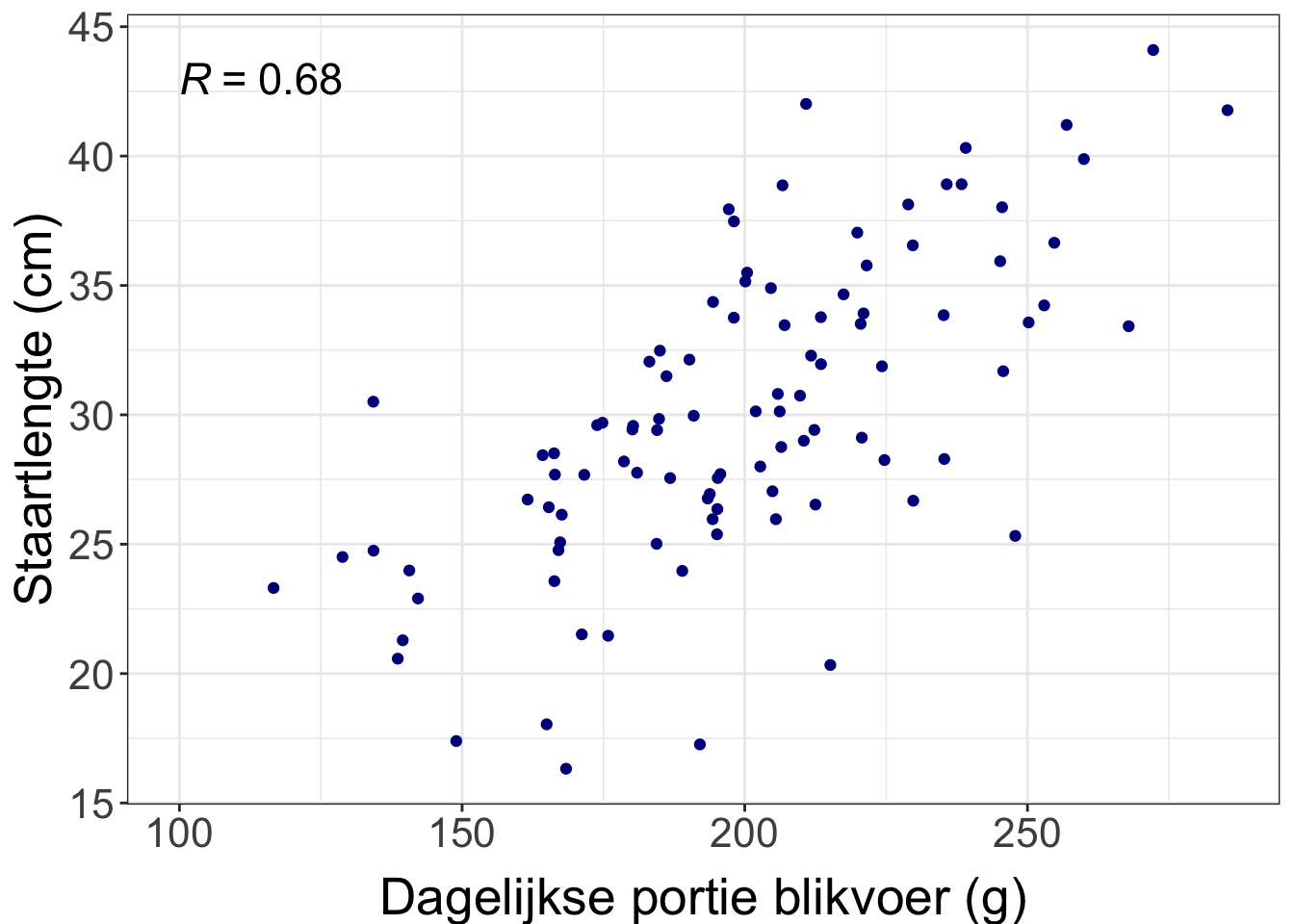
Dagelijkste portie blikvoer en staartlengte van 100 Siamezen. Elk stipje is een Siamees. Te zien is dat Siamezen die meer blikvoer eten, langere staarten lijken te hebben. Die R links in beeld zegt iets over de sterkte van die verband, dit behandelen we in een volgende les. (Dit is verzonnen voor het voorbeeld, ik verwacht niet een dergelijk sterk verband tussen hoeveelheid blikvoer en staartlengte in real live.)

Figure 1.3: Dagelijkste portie blikvoer en staartlengte van 100 Siamezen. Elk stipje is een Siamees. Te zien is dat Siamezen die meer blikvoer eten, langere staarten lijken te hebben. Die R links in beeld zegt iets over de sterkte van die verband, dit behandelen we in een volgende les. (Dit is verzonnen voor het voorbeeld, ik verwacht niet een dergelijk sterk verband tussen hoeveelheid blikvoer en staartlengte in real live.)

Voorbeeld: De onderzoeksvraag is beschrijvend

Bijvoorbeeld: Hoe lang is de staart van een Siamees?

variabelen

Je doet 1 steekproef met als afhankelijke variabele “staartlengte”.

grafiek

Hier kun je alle kanten op, afhankelijk van wat je zou willen laten zien over die staartlengtes. Een mogelijke grafiek voor de beschrijving van kwantitatieve data is een histogram. In een histogram laat je zien hoe vaak bepaalde staartlengtes voorkomen. Op de X-as zie je de staartlengtes, opgedeeld in ranges (15-18 cm, 18-20 cm, 20-22 cm enzovoorts). Op de Y-as zie je hoeveel Siamezen een staartlengte in die range hadden. In totaal zijn 1000 staarten van 1000 Siamezen opgemeten.

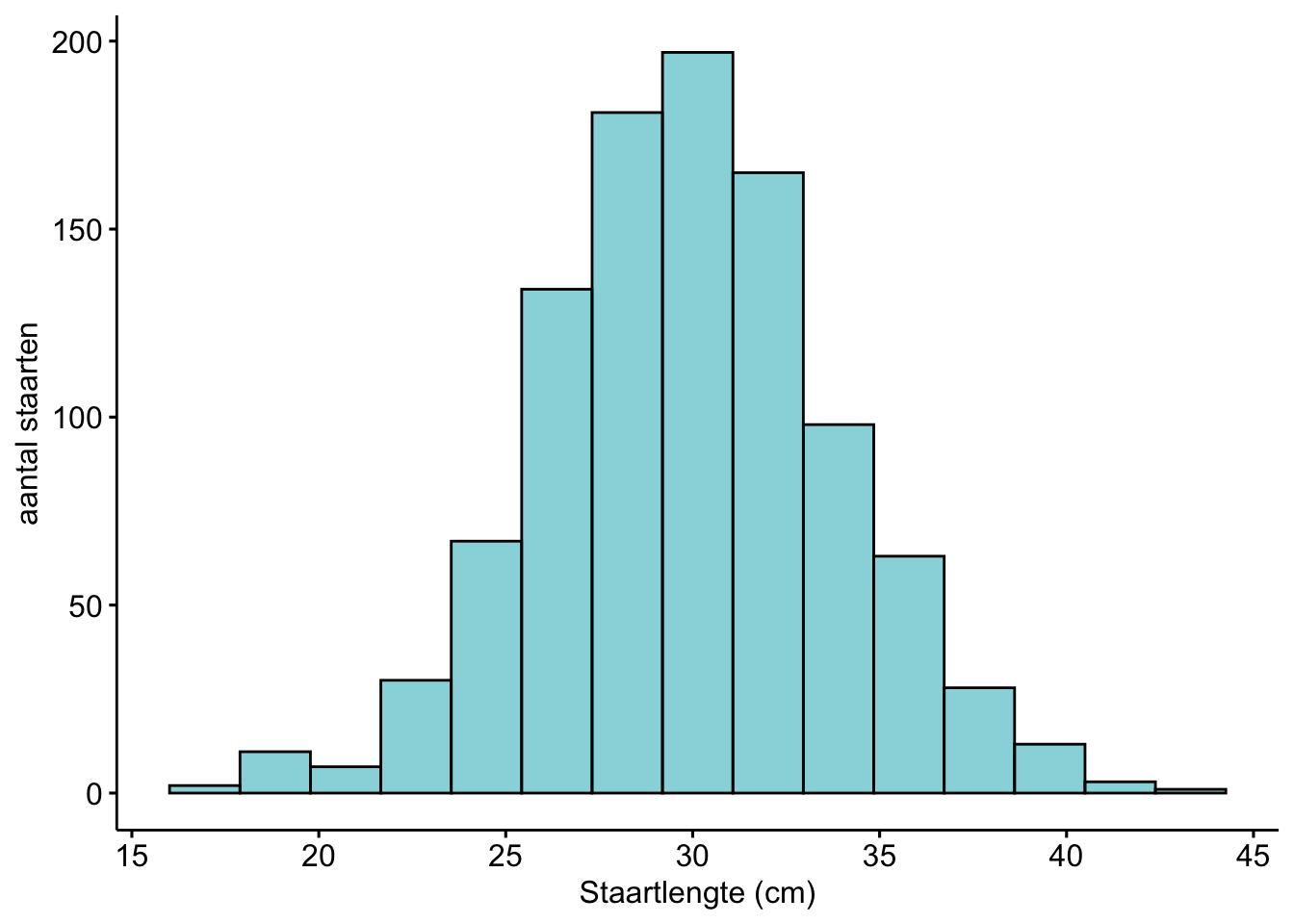
Histogram van 1000 staartlengtes van Siamezen. Te zien is dat de gemiddelde siamezenstaart ongeveer 30 cm is.

Figure 1.4: Histogram van 1000 staartlengtes van Siamezen. Te zien is dat de gemiddelde siamezenstaart ongeveer 30 cm is.

Zorg dat je het histogram hierboven begrijpt. We gaan nog veel histogrammen tegenkomen in deze cursus.

Voorbeeld: De onderzoeksvraag gaat over een verschil

Bijvoorbeeld: Hebben Siamezen langere staarten dan Abessijnen (ook katten)?

variabelen

In het voorbeeld zou je twee steekproeven moeten doen: je moet de staarten van een aantal Siamezen opmeten, en de staarten van een aantal Abessijnen.

Je meet dus 1 afhankelijke variabele: staartlengte. De onanfhankelijke variabele hier is kattenras: Siamees of Abessijn.

(Een verschilvraag kan ook over 1 steekproef gaan. Dan vergelijk je bijvoorbeeld niet Siamezen met Abessijnen, maar Siamezen met de jou bekende gemiddelde staartlengte van Nederlandse katten. Dus in plaats van 2 steekproeven, doe je dan je dan 1 steekproef.)

grafiek

Je zou best 2 van die histogrammen in hetzelfde grafiekje kunnen maken: 1 histogram voor de siamezen en 1 histogram voor de abessijnen.

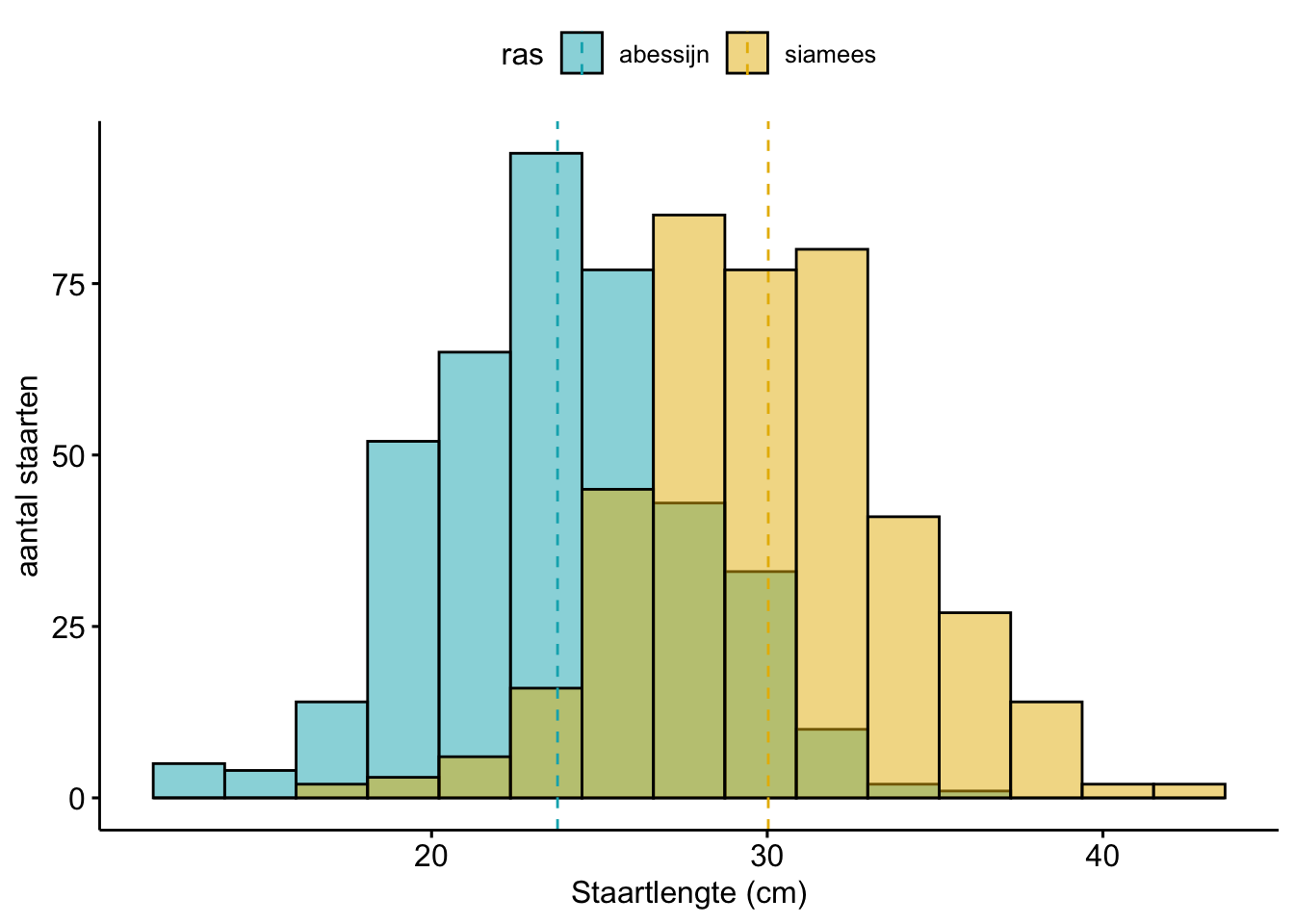
Histogram van de staartlengtes van Siamezen. Te zien is dat de gemiddelde siamezenstaart ongeveer 30 cm is.

Figure 0.1: Histogram van de staartlengtes van Siamezen. Te zien is dat de gemiddelde siamezenstaart ongeveer 30 cm is.

Maar gebruikelijker is om een staafdiagram te maken. In een staafdiagram geef je dan het gemiddelde staartlengte per ras weer (de gestippelde lijn in het histogram hierboven, in het staafdiagram hieronder is dat de hoogte van de staaf) en een indicatie van hoe breed die histogrammen dan zijn (dat streepje met twee dwarsbalkjes bovenop de staaf). Dat zegt dus iets over hoe verschillend de staartlengtes bij dat ras zijn: de spreiding. We gaan in volgende lessen bespreken op welke manier je spreiding kunt uitdrukken en hoe je dat in een grafiekje zet.

Bij een staafgrafiek: op de X-as zet je de onafhankelijke variabele (ras). Op de Y-as zet je de afhankelijke variabele (staartlengte in cm).

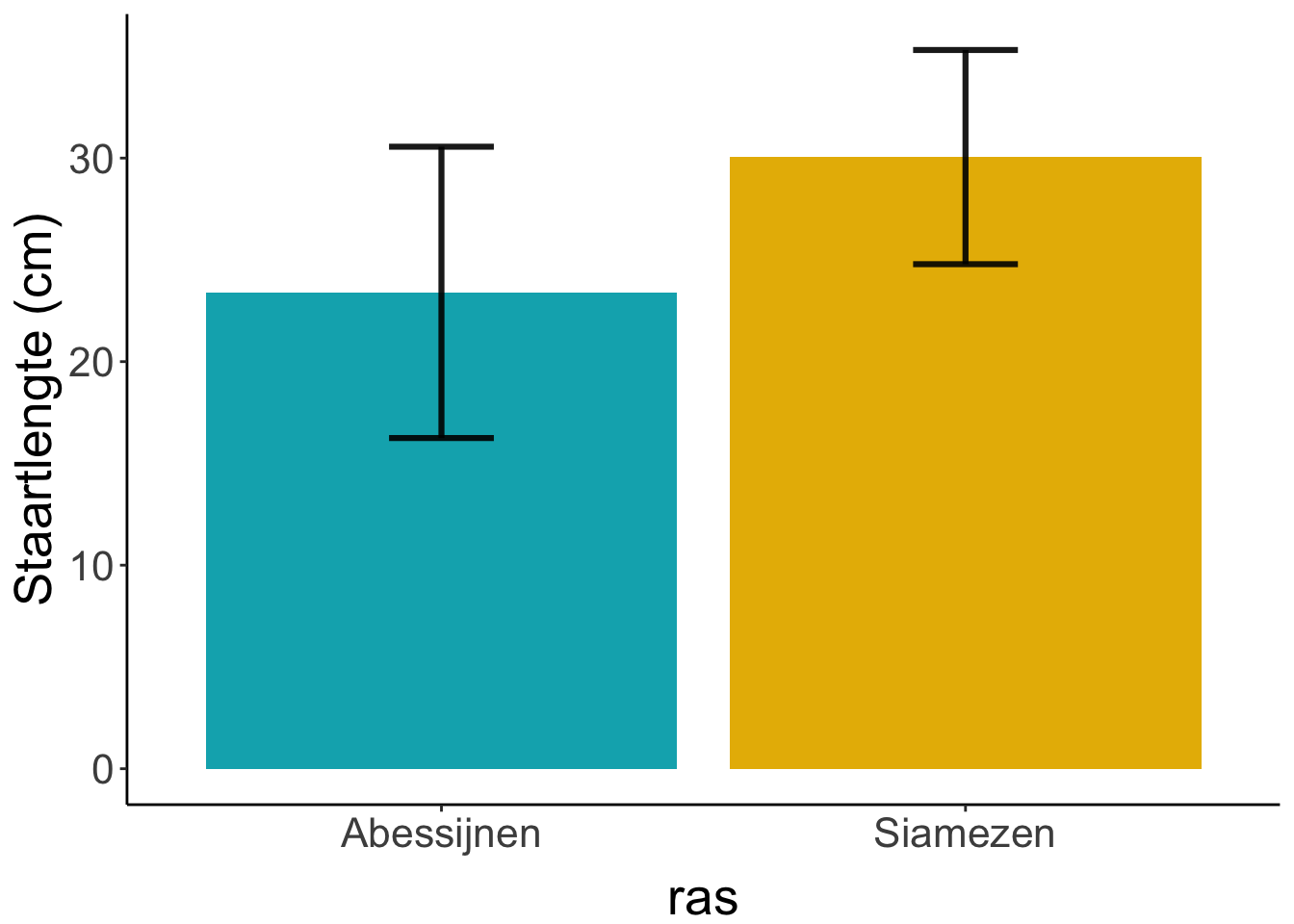
Gemiddelde staartlengte van Abesijnen en Siamezen. In de foutenbalken staat de standaarddeviatie (komt terug in een latere les)

Figure 1.5: Gemiddelde staartlengte van Abesijnen en Siamezen. In de foutenbalken staat de standaarddeviatie (komt terug in een latere les)

1.2.9 Introductie Excel

Sommige mensen hebben op de middelbare school al met Excel gewerkt. In dat geval kun je van deze blauwe paragraaf alleen even de bovenste opdracht maken om te checken of je decimal separator goed staat en ben je klaar met de voorbereiding. Klik hier voor het werkcollege. Deze paragraaf is voor mensen voor wie Excel echt helemaal nieuw is.

Heb je op canvas de datasets voor dit vak nog niet gedownload doe dat dan nu!: klik voor de voltijd of klik voor de deeltijd.

In deze les maken we een start met dataverwerking en met het gebruik van Excel. Excel is een programma dat gebruikt maakt van spreadsheets (zie figuur 1.6). Zo’n spreadsheet is een digitaal rekenblad, dat bestaat uit 1 of meerdere tabellen. In die tabellen kunnen getallen staan, maar ook berekeningen om op die getallen los te laten.

Excel is een van de meest gebruikte programma’s voor het invoeren en verwerken van data. En Excel kan ook wat statistiek, en grafieken maken.

Een spreadsheet in Excel ziet er zo uit:

Excel spreadsheet met bovenin de menubalk. De standaard instelling is de Home tab. Andere veelgebruikte tabbladen van de menubalk zijn File, Insert, Formulas en Data.

Figure 1.6: Excel spreadsheet met bovenin de menubalk. De standaard instelling is de Home tab. Andere veelgebruikte tabbladen van de menubalk zijn File, Insert, Formulas en Data.

Een spreadsheet in Excel heet een “werkblad” of “sheet”, en bestaat uit “cellen”: allemaal (nu nog lege) hokjes. Die cellen staan in kolommen (vertikaal) en rijen (horizontaal), en elke cel heeft een coördinaat. Een cel in de eerste rij, kolom B, heeft coördinaat B1. In iedere cel kan iets ingevuld worden.

Je kan ook een aantal cellen tegelijk beschrijven. De range D11:D15 omvat alle cellen D11, D12, D13, D14, en D15.

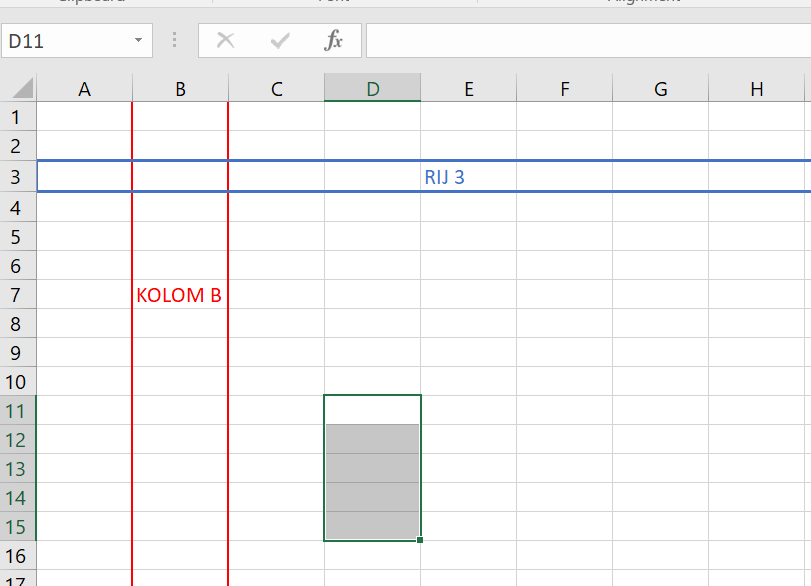
Rijen en Kolommen. Cellen D11 t/m D15 zijn geselecteerd.

Figure 1.7: Rijen en Kolommen. Cellen D11 t/m D15 zijn geselecteerd.

Binnen een bestand is het mogelijk om meerdere werkbladen te hebben.

Bekijk de instructievideo: “werkbladen in Excel” als je Excel niet eerder gebruikt hebt:

Opdracht 1
  1. Open Excel en maak een leeg werkblad aan met de naam “les1”.
  2. Type een getal in cel D5
  3. Type 5.2 in cel D10
  4. Type =D10*2 in cel D11. Krijg je een foutmelding? klik hieronder
Klik hier als stap 4 een foutmelding gaf


  • Controleer eerst of je echt =D10*2 hebt ingetypt.
  • Klopt dat, kijk dan naar cel D10. Heb je 5-komma-2 getypt en niet 5-punt-2? Dit is een dingetje in Excel. Excel gaat uit van een bepaalde “decimal separator”, in ons geval als je Excel goed ingesteld hebt: een komma. Ziet Excel dan ergens een punt, dan gaat het er vanuit dat die gegevens tekst zijn (en aligned de tekst aan de linker kant van de cel)..
  • Heb je 5-komma-2 getypt en doet hij het alsnog niet? Dan staat Excel misschien niet goed ingesteld. Ga terug naar de startpagina van deze cursus (klik op het logo helemaal links bovenin) en volg de instructies. Werkt dat niet, waarschuw dan je docent.


In de bovenste balk staan de verschillende tabbladen van Excel. Ieder tabblad bevat weer andere opties om de data in Excel te bewerken. Bekijk de instructievideo “navigeren in Excel” voor verdere uitleg als je Excel nog niet eerder gebruikt hebt:

Net als in de andere Microsoft Office programma’s werken shortcut keys. Dit zijn veelgebruikte:

Table 1.2: Shortkeys in Excel.
functie toetscombinatie
nieuw werkblad ctrl+n
alles selecteren ctrl+a
kopieren van data ctrl+c
knippen van data ctrl+x
plakken van data ctrl+v
laatste actie ongedaan maken ctrl+z
opslaan ctrl+s

Type iedere 5 minuten ctrl + s zodat je werk opgeslagen wordt !!

Een werkblad Kopiëren

Opdracht 1

Doe mee met de volgende stappen tenzij je al een doorgewinterd werkblad-kopieerder bent.

  • Ga onderin beeld met de cursor op de naam van het werkblad staan (die je wilt kopiëren)

  • klik op de rechtermuisknop

  • Select “Move or Copy”

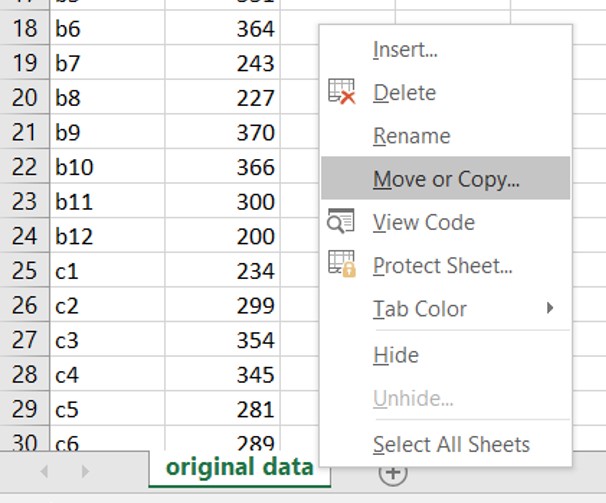
    Een werkblad kopiëren binnen een Excelbestand

    Figure 1.8: Een werkblad kopiëren binnen een Excelbestand

  • Vink onderaan het venster de optie “Create a copy” aan

  • Selecteer bij “To book:” het bestand waarin je werkt (of een ander bestand als je je werkblad naar een andere Excelfile wilt kopiëren.)

  • Selecteer waar het werkblad geplaatst moet worden in je bestand, bijvoorbeeld “move to end” (zie figuur 5). Klik op “OK”

  • Er verschijnt nu een extra werkblad met de naam van het originele werkblad met (2) erachter

1.3 Werkcollege

Heb je op canvas de datasets voor dit vak nog niet gedownload doe dat dan nu!: klik voor de voltijd of klik voor de deeltijd.

Van de voorbereiding verwachten we dat je die voor de les even doorneemt. Met de opdrachten hieronder mag je natuurlijk voor de les al beginnen, maar dat is niet verplicht.

1.3.1 Deel 1 - Data in Excel krijgen

De eerste stap in data analyse is het invoeren van je data. Je kunt dit op verschillende manieren doen:

  • data intypen (als het niet zoveel is, of tijdens het labwerk)
  • data kopieren en plakken
  • data importeren

Intypen en kopieren/plakken

Als je een kleine dataset hebt die je wilt analyseren kan je de getallen handmatig invullen. Vaak is het ook mogelijk om de data van een bestand te kopiëren en direct te plakken in Excel.

Stel, je leerteam verzamelt de volgende data (waarschijnlijk voor een beschrijvende onderzoeksvraag. welke onderzoeksvraag denk je?):

Table 1.3: Bepaling van het alcohol % van een fles rode wijn door 5 studenten
Student perc_alcohol
Boris 11.2
Evelien 13.9
Iris 12.5
John 12.3
Marcel 11.9
Opdracht 1

Data intypen

  • Open een nieuw werkblad.

  • Plaats de cursor in “cell” A1 en type Student.

    Selectie van de cell met de cursor. Vul de cel met tekst of getallen

    Figure 1.9: Selectie van de cell met de cursor. Vul de cel met tekst of getallen

  • Met de pijlen op je toetsenbord of met de muis selecteer je cell B1 en type perc_alcohol

  • Selecteer de cellen A1:B1 (klik op A1, hou de muis ingedrukt, sleep naar B1, laat de muis los) en maak de tekst dikgedrukt (bovenin beeld of ctrl+b)

  • vul nu de tabel aan met de data uit tabel 1.3 hierboven.

    Handmatig invullen van de gegevens van Tabel I

    Figure 1.10: Handmatig invullen van de gegevens van Tabel I

Opdracht 1

Data kopieren

  • Selecteer alle data in de tabel in Excel (klik A1, hou de muis ingedrukt, sleep naar B6, laat los). kopieer deze data (ctrl+c) en plak hem op cel D1 (ctrl+v). Als het goed is vult Excel nu automatisch cel D1:E6

  • Maak nu een nieuw werkblad aan. Selecteer weer alle data en kopieer en plak de data in het nieuwe werkblad.

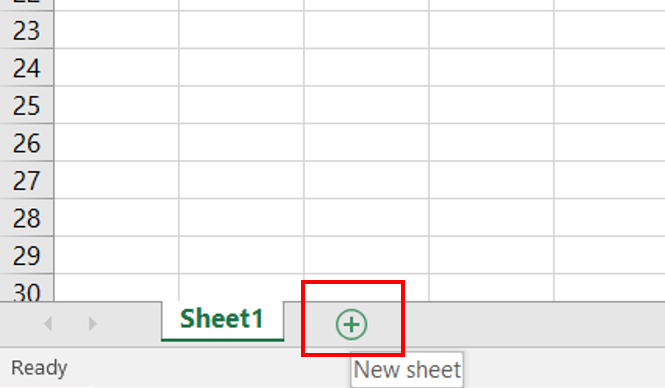
    Een nieuw werkblad maken binnen een Excelbestand

    Figure 1.11: Een nieuw werkblad maken binnen een Excelbestand

  • Selecteer weer alle data en kopieer (ctrl+c). Klik wat rond in een leeg werkblad, type op een random plaats je naam en probeer dan de data te plakken (ctrl+v). Je zult merken dat dit niet werkt. Excel onthoudt niet wat je gekopieerd hebt als je tussendoor andere dingen gaat doen.

  • Probeer nu de informatie uit de tabel hier op de website te kopieren en plakken naar cel G1. Lukt dat? Soms lukt het wel, soms lukt het niet. Opletten dus als je dit doet! Check altijd of Excel de cijfers herkent als cijfers en niet denkt dat het tekst is (aligned rechts in de cel = cijfer).

Opdracht 1

Data verplaatsen

Selecteer weer je cellen met data en probeer ze naar een andere plek in het werkblad te verplaatsen:

  • selecteer de data
  • ga met de cursor op de rand staan van de geselecteerde data totdat de cursor verandert van een wit kruis naar een zwart kruis in de vorm van pijlen.
  • Als de cursor de vorm heeft van een kruis met pijlen, Hou je de linkermuisknop continue ingedrukt en sleep met de muis of touchpad de data naar de gewenste “cell” in het werkblad.

Data wordt niet altijd op een overzichtelijke manier aangeleverd. Een veelvoorkomende handeling is het wisselen van de kolommen en de rijen (transpose). Een goede organisatie van de data betekent dat iedere observatie (hier een meting van een student ) in rijen staat en de meetwaarde in kolommen. In figuur 1.12 staat het juist andersom en dat maakt verdere bewerking van de data lastiger (maar niet onmogelijk).

Voorbeeld van data die je zou willen transponeren (transpose). De meetwaarden staat in een rij en de observaties in een kolom weergegeven.

Figure 1.12: Voorbeeld van data die je zou willen transponeren (transpose). De meetwaarden staat in een rij en de observaties in een kolom weergegeven.

Opdracht 1

Transpose

  • open excelbestand verkeerdom.xlsx

  • Selecteer en kopieer de data (A1:F2)

  • klik op cel A4

  • klik op het pijltje v onder Paste linksboven in beeld

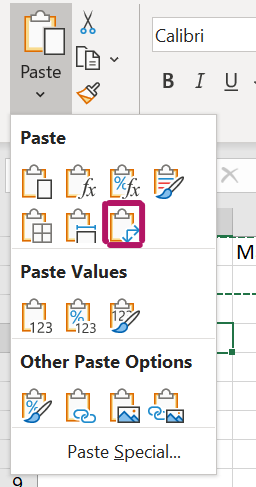
    Verschillende Paste Options. Met rood gemarkeerde icoontje is Transpose

    Figure 1.13: Verschillende Paste Options. Met rood gemarkeerde icoontje is Transpose

  • De data is nu gekopieerd waarbij de kolommen en rijen zijn verwisseld

    Resultaat van de Transpose optie: kolommen en rijen zijn verwisseld.

    Figure 1.14: Resultaat van de Transpose optie: kolommen en rijen zijn verwisseld.

Kopieren-plakken naar excel is een snelle manier om data in te voeren, maar het gaat ook makkelijk mis! Controleer dus altijd of het goed gegaan is als je dit doet.

Openen en importeren

Data handmatig invoeren is foutgevoelig: je maakt makkelijk een typefoutje. Je kan data ook laten importeren door Excel, als je die al in een ander bestand hebt. Oefen hier goed mee!

Excel kan verschillende type bestanden openen. De meest voorkomende data formats zijn

  • .xlsx / .xls bestanden: Excel bestanden (ook van eerdere versies)
  • .txt bestanden: De kolommen zijn meestal gescheiden door een Tab
  • .csv bestanden (Comma Separated Values - De kolommen zijn gescheiden door een comma (,) of een punt-comma (;)
Als je een Excel bestand wilt openen:

  • Klik op de File tab (links bovenin)

  • klik op open en dan op browse

    Klik op Browse om Excel bestanden te zoeken en te openen

    Figure 1.15: Klik op Browse om Excel bestanden te zoeken en te openen

  • Navigeer door je folders en selecteer je Excel bestand. Klik op “Open”

Als je een .txt bestand wilt openen:

Bij tekstbestanden is het even goed opletten: welk tekentje wordt gebruikt als decimal separator? En met welk teken zijn de kolommen gescheiden? De volgende kolommen zijn bijvoorbeeld gescheiden met een #

persoon1#5

persoon2#7

persoon3#8.5

Gebruikelijker zijn een Tab, een comma (,) of een punt-comma (;) maar open dus altijd eerst je tekstbestand in bijvoorbeeld Notepad (programma op de PC) of TextEdit (Mac) om het te bekijken.

Opdracht 1

Zoek in de gedownloade datamap het textbestand /les1/alcoholpercentages.txt en doe mee met de volgende stappen:

Stappen om een textbestand te openen:

  • Open het textbestand in Notepad (Windows) of TextEdit (Mac) en kijk welk teken er tussen de kolommen staat en wat de decimal separator is.

  • In Excel: klik File tab –> open –> browse

  • Selecteer “Text Files” in het drop down menu rechtsonder

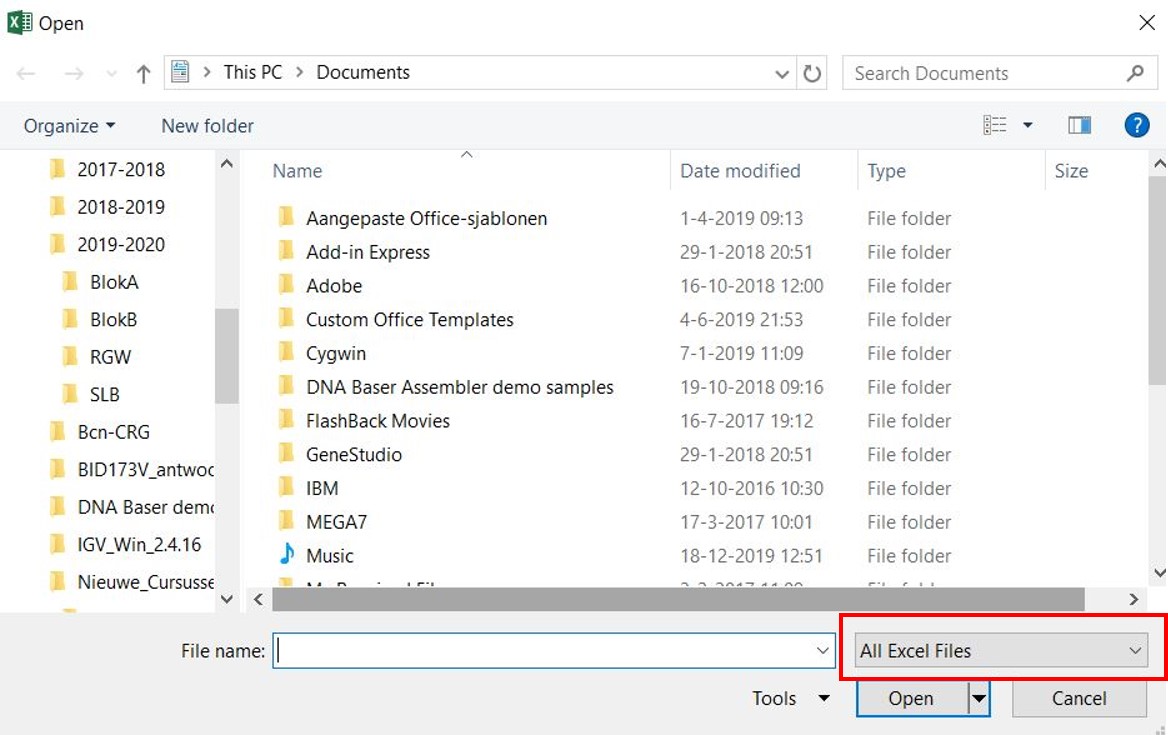
    Standaard zoekt Excel alleen naar Excel-bestanden

    Figure 1.16: Standaard zoekt Excel alleen naar Excel-bestanden

  • Zoek en selecteer het txt bestand dat je wilt openen, klik op open.

  • Na het openen van het tekstbestand verschijnt de “Text Import Wizard”. Kies in het eerste scherm of de kolommen in je textbestand een delimiter gebruiken of altijd even breed zijn (meestal dat eerste) en of er “headers” (kolomnamen in de eerst rij) in staan. Kies en klik op next.

    De Text Import Wizard

    Figure 1.17: De Text Import Wizard

  • kies voor de juiste “delimiter” (wat staat er tussen de kolommen). klik next (nog niet finish).

    Kies de juiste delimiter, in dit geval een ;

    Figure 1.18: Kies de juiste delimiter, in dit geval een ;

  • Nu staan de “decimal separators” nog verkeerd (er staat 11,2 en niet 11.2). Klik op Advanced:

    Text import Wizard scherm 3/3. We zijn er bijna.

    Figure 1.19: Text import Wizard scherm 3/3. We zijn er bijna.

  • kies bij decimal separator het teken dat je textdocument gebruikt. Excel zet die dan om in het teken dat Excel gebruikt.

    Kies de juiste decimal separator, in dit geval een komma

    Figure 1.20: Kies de juiste decimal separator, in dit geval een komma

  • Als het goed is heb je nu een werkblad dat er precies zo uit ziet als het werkblad waarin je de data handmatig getypt had (minus de dikgedrukte letters in rij 1).

  • Heb je de verkeerde delimiter gekozen, dan is alles in 1 kolom gepropt:

    Verkeerd geimporteerde data

    Figure 1.21: Verkeerd geimporteerde data

decimaal symbool en het duizend scheidingsteken

In Nederland gebruiken standaard de komma als decimaal symbool en de punt als duizend scheidingsteken. (Dus wij zouden typen: 10.000,5 voor tienduizend-en-een-half) In andere landen waaronder de Verenigde Staten is dit precies andersom: de punt als decimaal symbool en de komma als duizend scheidingsteken (10,000.5). Op sommige computers staat de Amerikaanse versie ingesteld. Dit geeft problemen als we data met decimalen willen invoeren (Excel denkt namelijk dat het duizendtallen zijn).

Controleer dus bij het invoegen van data goed of je getallen niet opeens 1000x zo groot zijn geworden! Is dat gebeurt, gebruik dan de optie om de thousands separator in te vullen (te zien in figuur 1.20)

1.3.2 Deel 2: Excel als rekenmachine

Nu we data in excel kunnen krijgen, kunnen we eens wat beschrijvende statistiek gaan doen! Dan moeten we wat gaan rekenen.

Met Excel kun je eenvoudig berekeningen uitvoeren. Hieronder leggen we stap voor stap uit hoe je dat doet.

  • Typ het = teken in een cel.
  • Typ de berekening.
  • Druk op Enter

De uitkomst van de berekening verschijnt in de cel A1. De onderliggende berekening wordt weergeven in de formule balk (zie rode vierkant in het figuur hieronder).

Als alternatief kan je de cijfers eerst in Excel typen en de berekening in een aparte cel doen. Dit is overzichtelijker omdat je direct ziet welke getallen er gebruikt zijn voor de berekening. In kolom A en B staan de data. In kolom C is de berekening ingevoerd zoals rechtsboven in de formule balk is weergegeven.

Je kan altijd dubbel klikken op een cel om te zien wat er daadwerkelijk in een cel zit: data of een formule. Dubbel klikken op C1 laat in dit geval de formule zien en geeft met welke data er gerekend wordt (cel A1 en B1).

We kunnen ook de getallen van elkaar aftrekken, zoals gebeurt in C2:

In C3 worden de getallen in A3 en B3 met elkaar vermenigvuldigd:

In C4 worden de getallen door elkaar gedeeld:

Ten slotte wordt in C5 gedemonstreerd hoe je een machtsverheffing kunt uitvoeren in Excel:

Worteltrekken kan op twee manieren worden uitgevoerd. Ten eerste kan je worteltrekken door middel van machtsverheffen. Als je een grondgetal heft tot de macht 0,5 is dat hetzelfde als worteltrekken van het grondgetal:

Als alternatief kan je ook de Excel formule gebruiken voor het uitrekenen van een wortel, sqrt():

Met de uitkomsten van een berekening kunnen nieuwe berekeningen worden uitgevoerd:

Door dubbel te klikken op een cel kun je de inhoud zien (data of een formule):

Als we de andere getallen in kolom C ook willen vermenigvuldigen met 10 dan kunnen we de formule in cel D1 kopiëren:

Vervolgens selecteer je de cellen waar je de formule naar toe wilt kopiëren:

En plak je de formule:

1.3.2.1 Volgorde van berekeningen in Excel

Excel volgt BEDMAS om de volgorde van de berekeningen te bepalen:

  • Brackets (= haakjes)
  • Exponents (= machten)
  • Division (= delen)
  • Multiplication (= vermenigvuldigen)
  • Addition (= optellen)
  • Subtraction (= aftrekken)

Bij twijfel is het dus belangrijk om haakjes te gebruiken!

Voorbeeld 1

  • 3^2 *2 / 6 -2 + 9 =
  • 9 * 2 / 6 -2 +9 =
  • 18 / 6 -2 + 9 =
  • 3 - 2 + 9 =
  • 1 + 9 = 10

Voorbeeld 2

  • 3^(2*2) / 6 -2 + 9 =
  • 3^4 / 6 -2 +9 =
  • 81 / 6 -2 + 9 =
  • 13,5 - 2 + 9 =
  • 11,5 + 9 = 20,5

Voorbeeld 3

  • 3^ 2 *2 / (6 -2) + 9 =
  • 3 ^ 2 * 2 / 4 +9 =
  • 9 * 2 / 4 + 9 =
  • 18 / 4 + 9 =
  • 4,5 + 9 = 13,5

Opdracht 1

Type

= 3^ 2 *2 / (6 -2) + 9

in Excel en kijk of het antwoord klopt met de berekening hierboven.

1.3.2.2 Formules in Excel

Excel heeft honderden verschillende formules die op zowel numerieke als tekst data toegepast kunnen worden. Voor gedetailleerde informatie / instructies over het gebruik van formules in Excel, raadpleeg je deze website.

De formules kan je vinden in de menu balk onder Formulas. Onder iedere categorie staan een lijst met formules. Bij de optie More Functions staat nog een lijst met categorieën waaronder Statistical. Hieronder staan veelgebruikte formules zoals het gemiddelde (average).

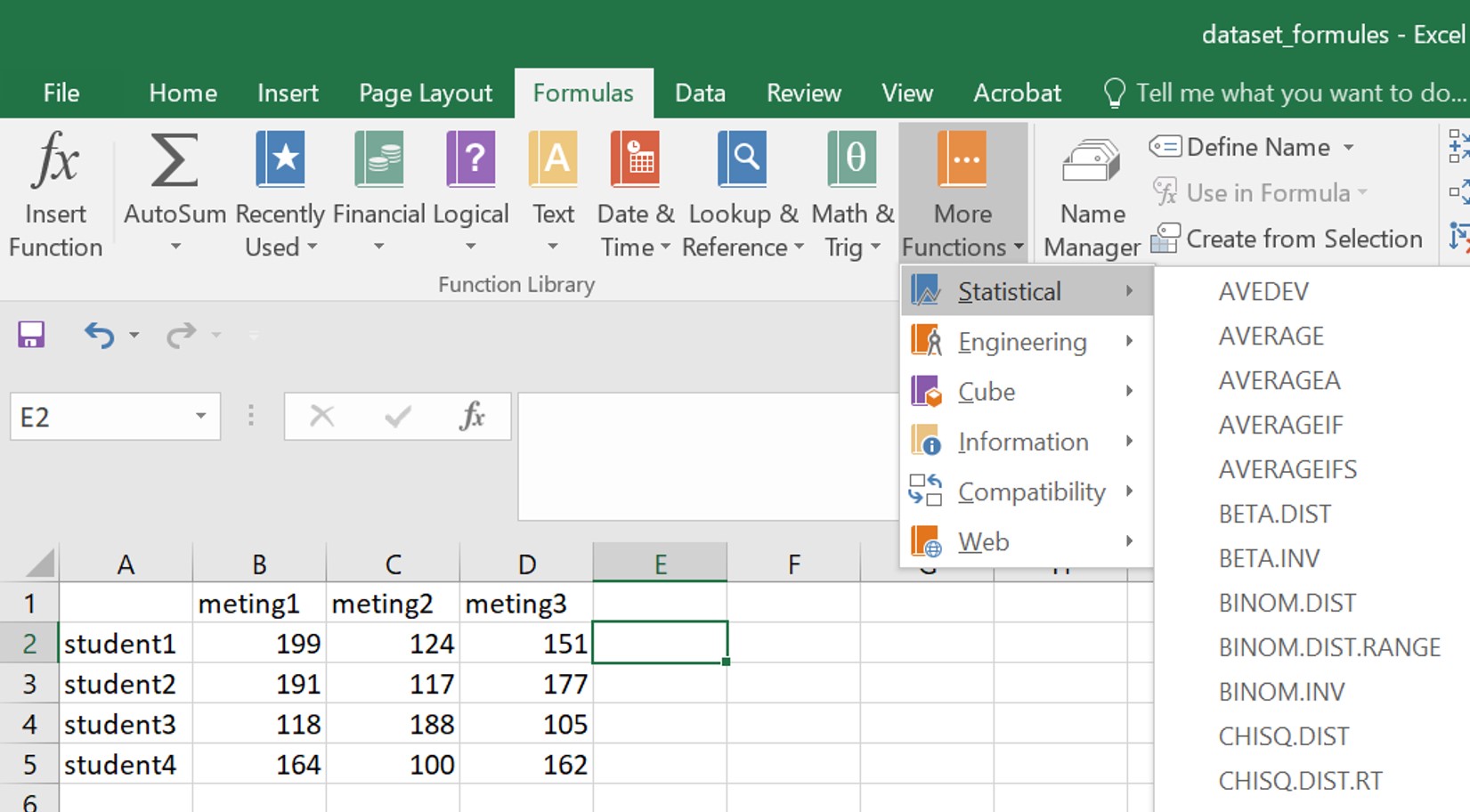
In de les maken we vaak gebruik van de Engelse namen van de formules. Als je de Nederlandse naam van de formule wilt weten, kun je deze website raadplegen of kijken op het formuleblad.

Er zijn twee manieren om een functie te gebruiken in Excel. In beide gevallen is de eerste stap het selecteren van een lege cel in je Excel werkblad.

Manier 1

Als je de naam van een functie weet, kan je de formule direct invullen in de cel. Type in de cel het = teken gevolgd door de naam van de formule. Na de naam van een formule volgt een linker haakje, selectie van de data en als laatste haakje sluiten.

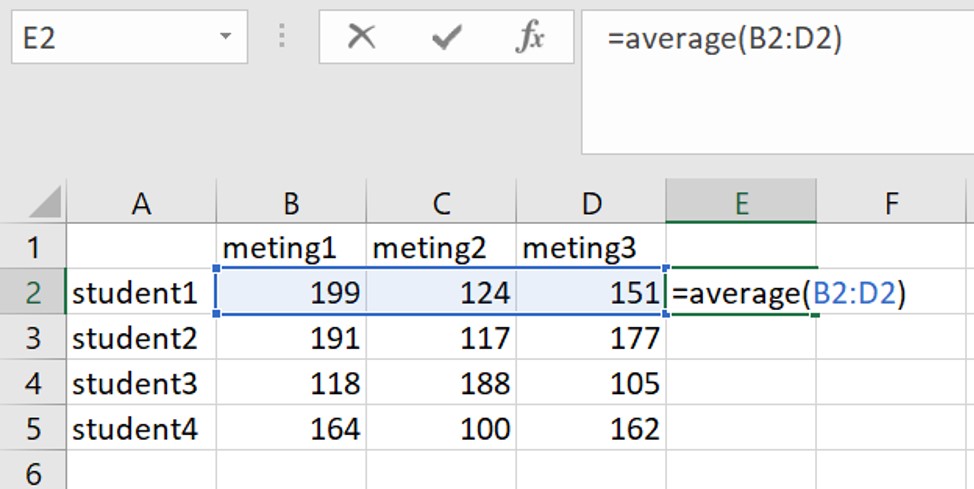
Manier 2

Je kunt ook de Insert Function van de Formulas balk gebruiken.

  • Selecteer een lege cel in Excel.
  • Klik op de Insert Function van de Formulas balk.

  • Selecteer een functie uit het keuze menu (bijvoorbeeld AVERAGE).

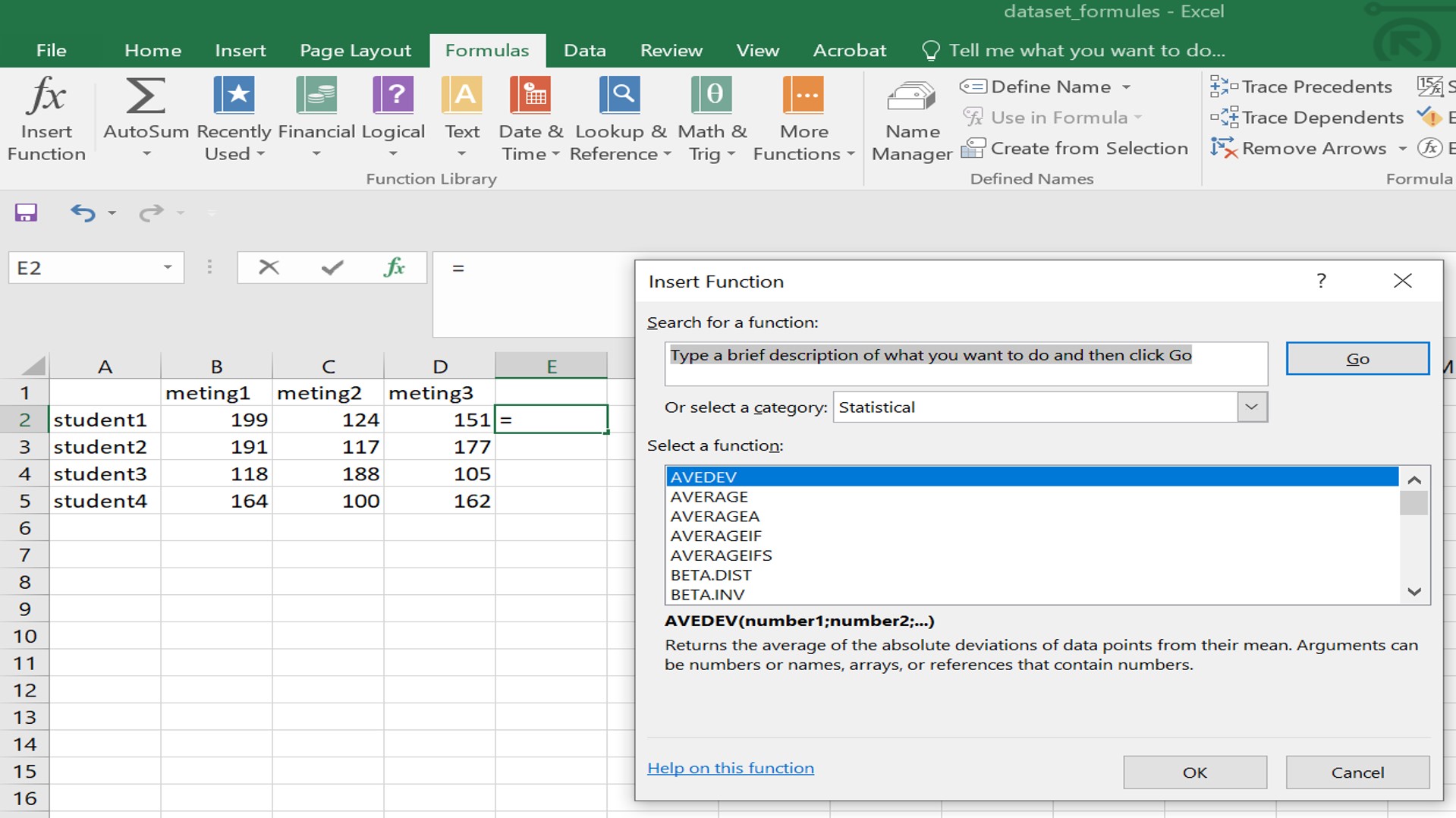
Er verschijnt een venster voor de Function Arguments (zie figuur 1e). Function Arguments zijn alle gegevens die een functie nodig heeft om de functie uit te voeren. Voor de functie AVERAGE zijn dat de meetwaarden waarvan het gemiddelde uitgerekend moet worden.

  • Selecteer met de cursor de cellen waarvan het gemiddelde moet worden uitgerekend.

In plaats van een formule te zoeken met de Insert Function van de Formulas balk, kun je de functie die je wilt gebruiken ook direct aanklikken in de Formulas balk.

1.3.2.3 Het gemiddelde berekenen

Hierboven hebben we laten zien hoe je een formule invoert in Excel met als voorbeeld de functie van het gemiddelde AVERAGE(). Tussen de haakjes worden de cellen genoteerd waarvan het gemiddelde uitgerekend moet worden. De functie AVERAGE() negeert lege cellen en tekst maar niet het nummer 0. Indien aanwezig wordt de 0 waarde ook gebruikt voor het uit uitrekenen van het gemiddelde.

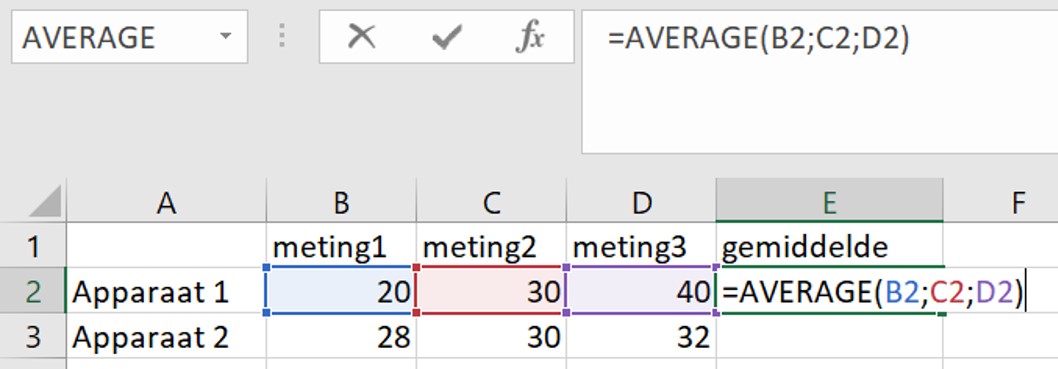
Je kunt het gemiddelde van een aantal cellen als volgt berekenen:

  • Selecteer de cel waarin het gemiddelde moet komen te staan.
  • Typ in deze cel =AVERAGE(
  • Selecteer met de cursor de cellen met data waarvan je het gemiddelde wilt berekenen.
  • Sluit af met een ) en druk op Enter.

Als alternatief kan je de invoer cellen ook individueel selecteren:

  • Selecteer de cel waarin het gemiddelde moet komen te staan.
  • Typ in deze cel =AVERAGE(
  • Selecteer met de cursor de eerste cel.
  • Typ ;
  • Herhaal de vorige twee stappen totdat je alle data hebt geselecteerd.
  • Sluit af met een ) en druk op Enter.

Opdracht 1

Importeer de data uit staartlengtes.txt in Excel en bereken de gemiddelde staartlengte van de katten in deze steekproef met een formule.

Klik hier voor het antwoord

31.36 cm (correct afgerond: 31 cm. merk op dat Excel niet automatisch voor je afrondt)

Krijg je 30.5? dan heb je waarschijnlijk vergeten om de decimal separator aan te geven bij het importeren. Importeer de data uit de .txt file nog een keer. Check hier bij figuur 1.19 hoe je de decimal separator ook al weer instelt bij het importeren.

1.3.3 Grafieken

Het is altijd belangrijk om je data in een grafiek weer te geven. Maar Excel kan een heleboel verschillende grafieken maken. Welke moeten we kiezen? Dat hangt er weer vanaf wat je vraag is.

1.3.3.1 Scatterplot

Een scatterplot maak je vaak bij een verbandvraag. Bijvoorbeeld: “Is er een verband tussen staartlengte en oorlengte bij de katten in mijn straat?”

Opdracht 1

Open het Excelbestand oorlengtes.xlsx.

en doe mee met de volgende stappen:

  • selecteer de kolommen staartlengte en oorlengte.
  • kies bovenin de menubalk-tabjes Insert –> charts-blokje –> Selecteer in het submenu Insert - XY scatter een scatter grafiek.
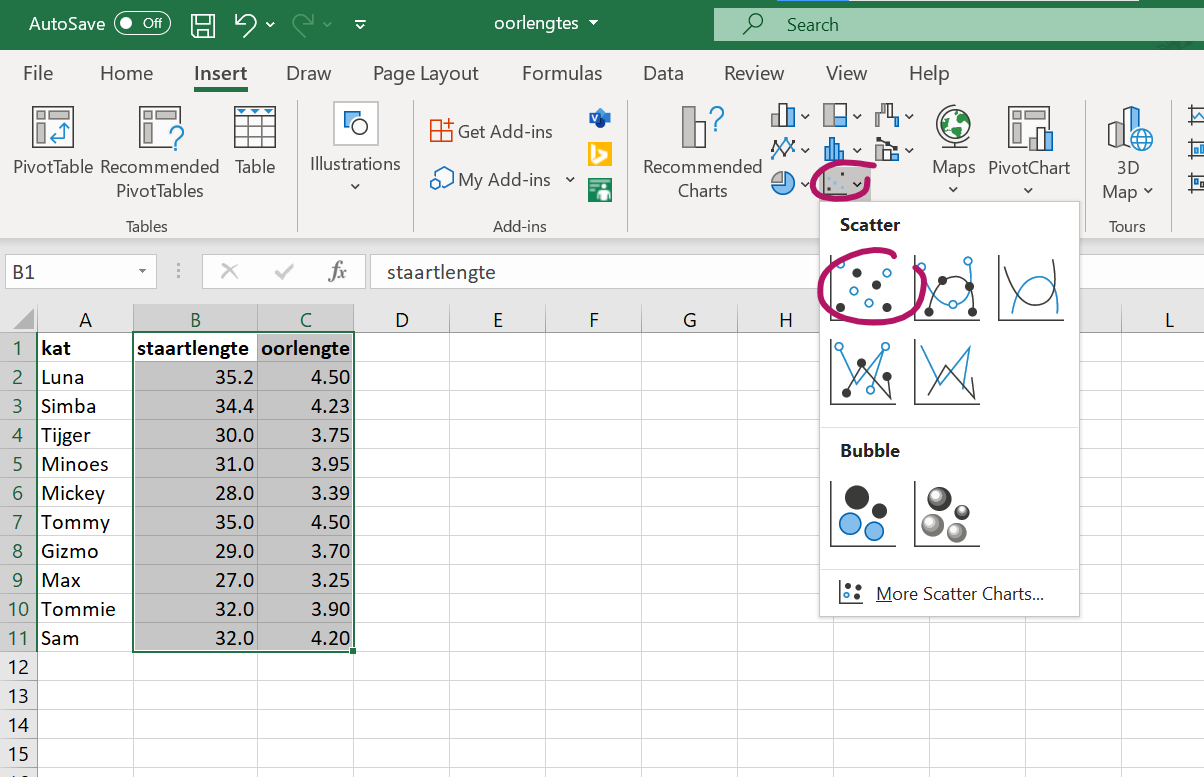
Kies hier echt de met rood aangegeven scatterplots.

Figure 1.22: Kies hier echt de met rood aangegeven scatterplots.

  • dubbelklik op de grafiektitel en type een betere titel
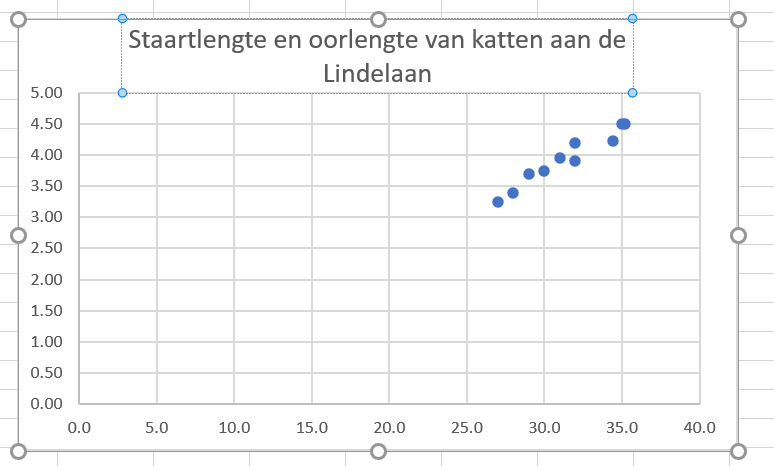
Grafiektitels moeten goed passen bij wat er in de grafiek staat

Figure 1.23: Grafiektitels moeten goed passen bij wat er in de grafiek staat

  • klik nu ergens naast de grafiek in een lege cel, en klik dan in het witte deel van het grafiekje naast de grafiektitel om de hele grafiek te selecteren. Klik daarna links bovenin beeld op Add chart element en voeg asbijschriften toe.
Voeg altijd asbijschriften toe!

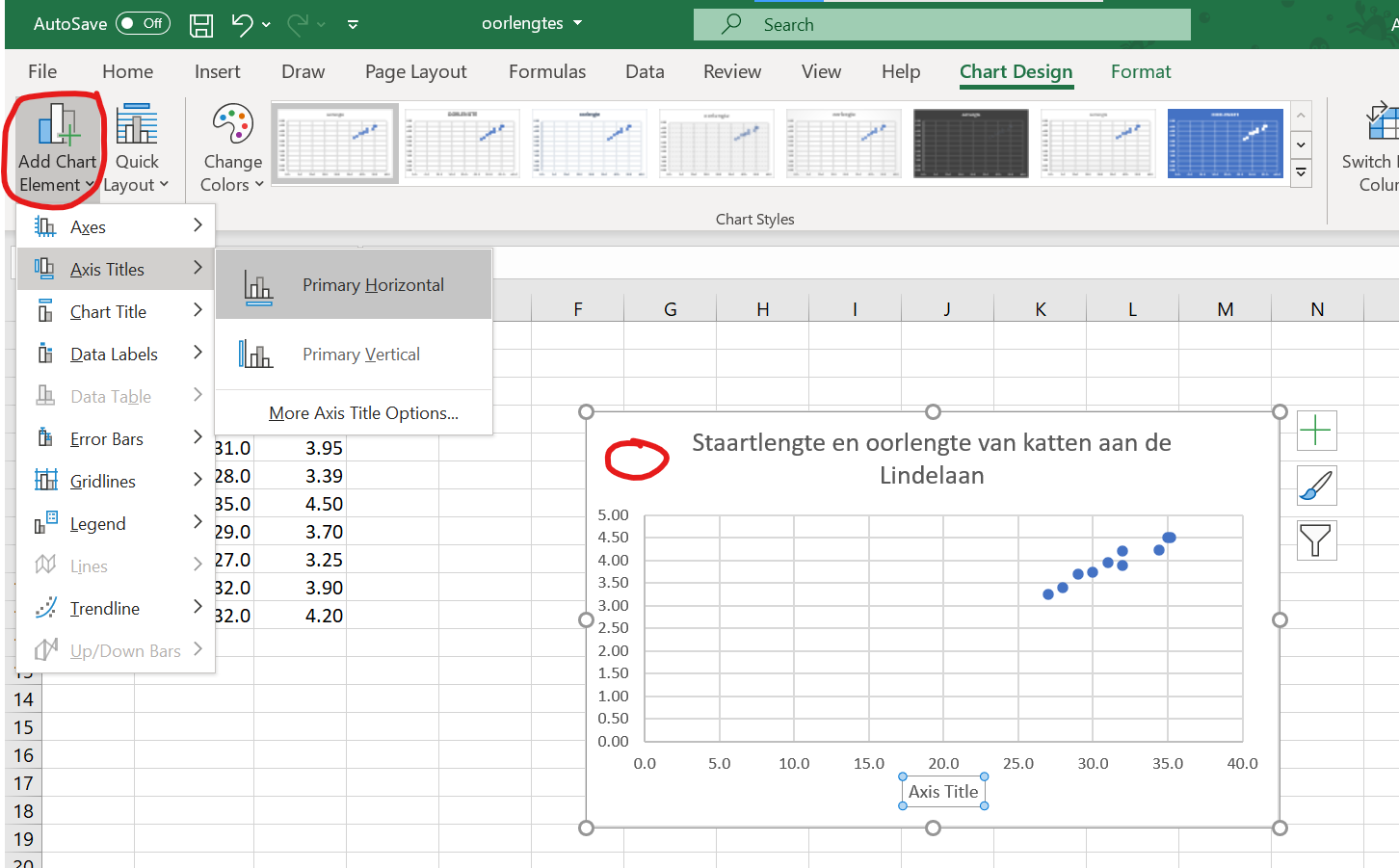
Figure 1.24: Voeg altijd asbijschriften toe!

  • Op de x-as staat staartlengte in centimeters, op de y-as staat oorlengte in centimeters. Grafieken zonder asbijschriften kun je niet aflezen en zullen dus tijdens je hele studie foutgerekend worden!
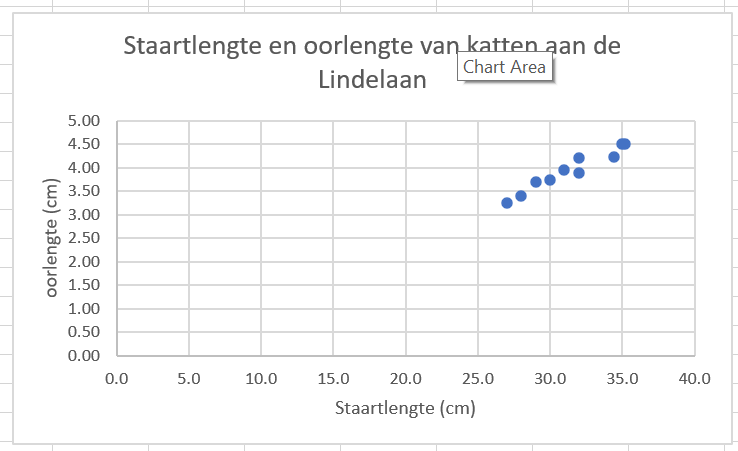
Zo ziet je grafiek er uiteindelijk uit

Figure 1.25: Zo ziet je grafiek er uiteindelijk uit

1.3.3.2 Ijklijnen

Een veel voorkomend voorbeeld van een verbandvraag is wat je doet als je een ijklijn maakt bij fotospectrometrie:

Voor het bepalen van de hoeveelheid glucose in een bloedmonster maak je gebruik van een chemische reactie waarbij het reactiemengsel een rode kleur krijgt in aanwezigheid van glucose. De hoeveelheid rode kleur die ontstaat kun je meten met een spectrofotometer. Om aan de hand de absorptie vervolgens de concentratie glucose te kunnen bepalen, zul je eerst aan de hand van oplossingen met bekende glucose concentraties moeten vaststellen wat het verband is tussen de concentratie glucose en de extinctie. Met andere woorden, je zult een ijklijn moeten opstellen. De ijklijn wordt in een volgende les uitgebreid behandeld, maar omdat jullie hem al snel in het lab gaan tegenkomen maken we er nu alvast een.

De data

In het kort, van een bekende concentratie glucose worden verdunningen gemaakt en van deze verdunningen worden na een chemische reactie de extincties gemeten m.b.v een spectrofotometer. De gemeten extincties worden uitgezet tegen de bekende concentraties glucose in de verdunde oplossingen (Rode stippen). Vervolgens laat je het bloedmonster met de onbekende concentratie glucose dezelfde reactie ondergaan en je meet de extinctie (Paarse stip).

Zo ziet je grafiek er uiteindelijk uit

Figure 1.26: Zo ziet je grafiek er uiteindelijk uit

Opdracht 1

In deze eerste opdracht ga je zelf een ijklijn opstellen en de concentratie van glucose in een onbekende oplossing bepalen.

We beginnen met de ijklijn. Hiervoor werd van vier bekende concentraties glucose de extinctie drie keer gemeten (in triplo dus).

Open het bestand eerste_ijklijn.xlsx

Bereken de gemiddelde extincties per concentratie in kolom F (oranje vakjes)

Tip: je kunt de formule typen in de bovenste oranje cel (F3) en dan kopieren naar de cellen er onder door op de rechtsonderhoek op het zwarte blokje te klikken (je muiswijzer wordt een zwart kruisje) en naar beneden te slepen.

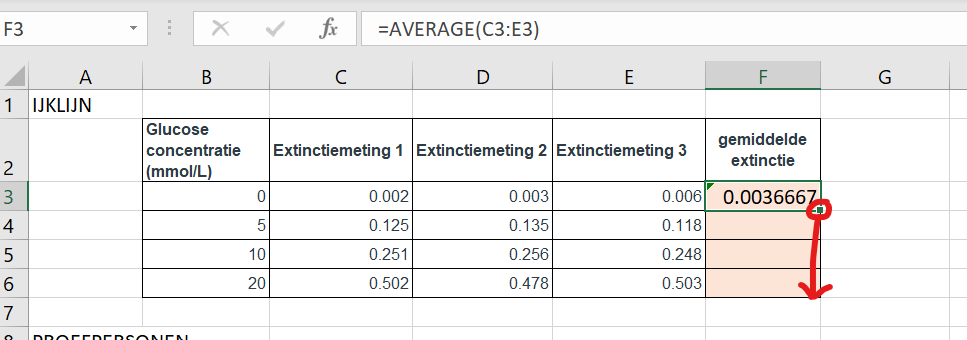
klik hier en sleep om een formule te kopieren naar de cellen er onder. Je kunt ook dubbelklikken op het zwarte blokje, dan vult Excel de tabel vanzelf aan.

Figure 1.27: klik hier en sleep om een formule te kopieren naar de cellen er onder. Je kunt ook dubbelklikken op het zwarte blokje, dan vult Excel de tabel vanzelf aan.

Maak nu een scatterplot met concentratie op de x-as en gemiddelde extinctie op de y-as. Vergeet de titel en asbijschriften niet. Een geschikte titel is hier bijvoorbeeld “Ijklijn glucose”.

Je kunt twee kolommen data selecteren door CTRL te gebruiken:

  • selecteer cel B3 tot en met B6
  • druk CTRL en houd ingedrukt
  • selecteer F3 tot en met F6
  • kies insert en voeg een scatterplot toe

Nu hebben we een scatterplot, maar we kunnen de blauwe vakjes nog niet invullen! Daarvoor moeten we kunnen omrekenen van extinctie naar concentratie glucose. Oftewel, we hebben een formule nodig. Excel kan voor je berekenen wat de meest waarschijnlijke formule is. We gaan in een van de komende lessen zien hoe Excel dat aanpakt.

Opdracht 1
  • Windows: klik op je grafiek om hem te selecteren en klik dan op het kruisje rechtsbovenin. Kies trendline en klik op het pijltje naar rechts en dan op “more options”
  • Mac: (niet op plaatje) klik op een van de punten in je grafiek. ctrl-click (rechter muisklik) en kies add trendline.
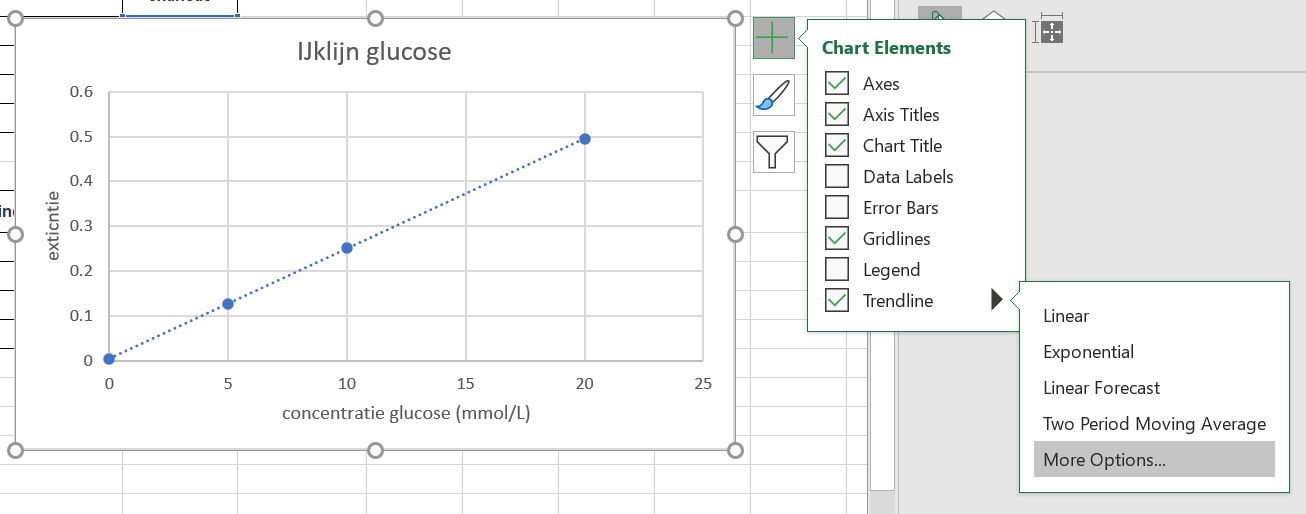
klik hier om de ijklijn toe te voegen

Figure 1.28: klik hier om de ijklijn toe te voegen

  • Windows: klik dan op trendline options, scroll omlaag en vink Display equation on chart en Display R-squared value on chart. Dat eerste is de formule, dat tweede is een maat voor hoe goed je ijklijn is. 1 is uitstekend.

  • Mac: Vink in het menu rechts aan: Display equation on chart en Display R-squared value on chart. Dat eerste is de formule, dat tweede is een maat voor hoe goed je ijklijn is. 1 is uitstekend.

Als het goed is, dan heb je de volgende relatie tussen de concentratie en extinctie gevonden:

y=0.0246x + 0,0041.

Y is de extinctie (die staat op de y-as in je grafiek) en x is de concentratie (die staat op de x-as in de grafiek).

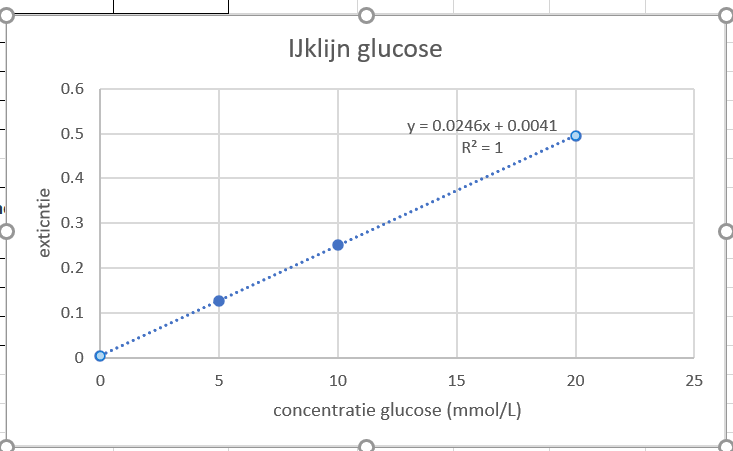
Als het goed is ziet je grafiek er nu zo uit

Figure 1.29: Als het goed is ziet je grafiek er nu zo uit

Van de monsters van de proefpersonen is y (extincties) bekend. Met de gevonden formule kun je de x, de concentraties, berekenen. We moeten hem alleen even omdraaien.

Opdracht 1

Hoe kun je de formule van de ijklijn y=0.0246x + 0.0041 omschrijven zodat je de concentratie x kunt uitrekenen wanneer y bekend is?

\[0.0246x = y+0.0041\]

of

\[ x = \frac{y}{0.0246} - 0.0041 \]

of

\[ x = \frac{y - 0.0041}{0.0246} \]

Klik voor het antwoord \[ x = \frac{y - 0.0041}{0.0246} \]
Opdracht 1

Bereken de gemiddelde extincties van de proefpersonen (groene cellen).

Gebruik de formule uit de vorige vraag om die gemiddelde extincties om te rekenen naar concentraties (blauwe cellen). Rond de waardes af op net zoveel significante cijfers als de extinctiemetingen.

Als je ze in Excel met het goede aantal significante cijfers weergegeven wilt hebben (Excel onthoudt stiekem gewoon alle cijfers), gebruik dan deze knoppen:

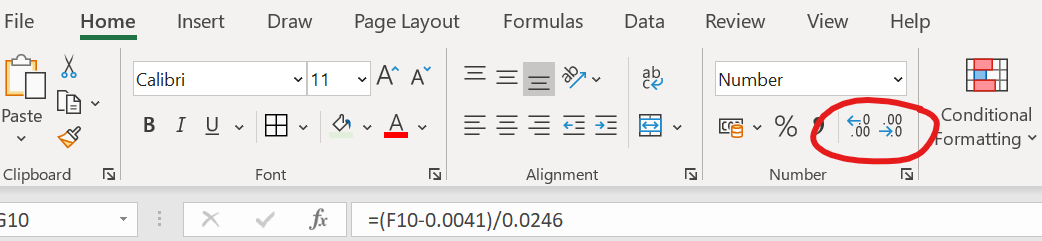
Knoppen om meer of minder decimalen TE LATEN ZIEN in Excel

Figure 1.30: Knoppen om meer of minder decimalen TE LATEN ZIEN in Excel

Klik voor het antwoord

De formule was \[ x = \frac{y - 0.0041}{0.0246} \]

  • Selecteer de cel rechts van de gemiddelde extinctie van proefpersoon Jeroen. In ons voorbeeld is dit cel G10.
  • Voer het volgende in: =(F10-0.0041)/0.0246
  • Selecteer opnieuw cel G13 en beweeg met je muis naar de rechteronderhoek van de cel totdat een zwart kruisje verschijnt. Druk op de linker muisknop en sleep de muis naar beneden zodat de glucose concentratie ook voor de andere proefpersonen berekend wordt.

De concentraties zijn 14.9 , 4.71, 32.4 en 2.11 mmol/L (vergeet de eenheid niet).

Opdracht 1

EXTRA oefenopdracht

In een experiment wordt de hoeveelheid cholesterol in triplo gemeten in patiëntenmonsters. De gemeten extincties zijn als volgt:

Patient Extinctie 1 Extinctie 2 Extinctie 3
Ronald 0.338 0.315 0.271
Ivo 0.103 0.092 0.125
Erica 0.210 0.198 0.242
Ans 0.268 0.285 0.258

Om de cholesterol concentraties te kunnen berekenen, dien je eerst een ijklijn op te stellen.

Stel de ijklijn op aan de hand van de volgende meetwaarden en vergeet niet om de ijklijn formule weer te geven in je grafiek

Concentratie cholesterol (mmol/L) Extinctie 1 Extinctie 2 Extinctie 3
0 0.002 0.003 0.006
2.5 0.135 0.145 0.138
5 0.278 0.286 0.281
10 0.521 0.578 0.533

Bereken de concentraties cholesterol in de verschillende patientenmonsters en rond deze af op 3 decimalen

Klik voor het antwoord
Patient concentratie
Ronald 5.591 mmol/L
Ivo 1.870 mmol/L
Erica 3.903 mmol/L
Ans 4.895 mmol/L

1.3.3.3 Staafgrafiek

We hebben gezien dat bij een verschilvraag een staafdiagram vaak handig is. Hoe maak je die?

Opdracht 1

Open staartvergelijking.xlsx voor het bestand met kattenstaartlengtes in cm van katten in de Lindelaan en aan de Hoofdweg. Doe de volgende stappen mee:

  • Selecteer beide kolommen, klik insert en kies een staafdiagram (zie figuur).
Voorbeeld van hoe een staafdiagram er NIET uit moet zien

Figure 1.31: Voorbeeld van hoe een staafdiagram er NIET uit moet zien

Oei. Dat was niet de bedoeling. Elke kat heeft opeens een staaf gekregen. Daar kunnen we niet zoveel mee. We willen graag de gemiddelden kunnen vergelijken.

  • Gooi dit grafiekje weer weg!
  • De gemiddelde staartlengte voor de katten in de Lindelaan en die voor de Hoofdweg is berekend in cellen A13 en B13. Check met welke formule dit gedaan is.
  • Selecteer de twee gemiddelde kattenstaartlengtes en insert een staafdiagram.
  • Geef de grafiek astitels en een grafiektitel. Hij ziet er nu zo uit:
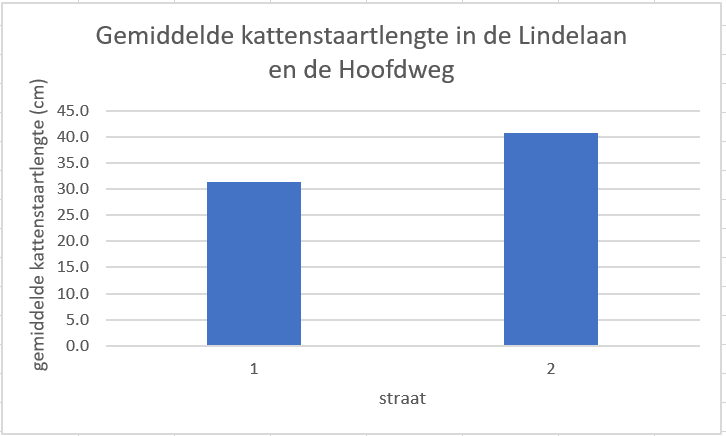
Staafgrafek met oninformatieve groepslabels

Figure 1.32: Staafgrafek met oninformatieve groepslabels

  • Dat ziet er al heel aardig uit, nu moeten die 1 en 2 nog vervangen door de straatnamen. Als je de data waar de grafiek op gebaseerd is wilt aanpassen (in dit geval: labels toevoegen), klik je op chart filters en dan op `select data”
Staafgrafek met oninformatieve groepslabels

Figure 1.33: Staafgrafek met oninformatieve groepslabels

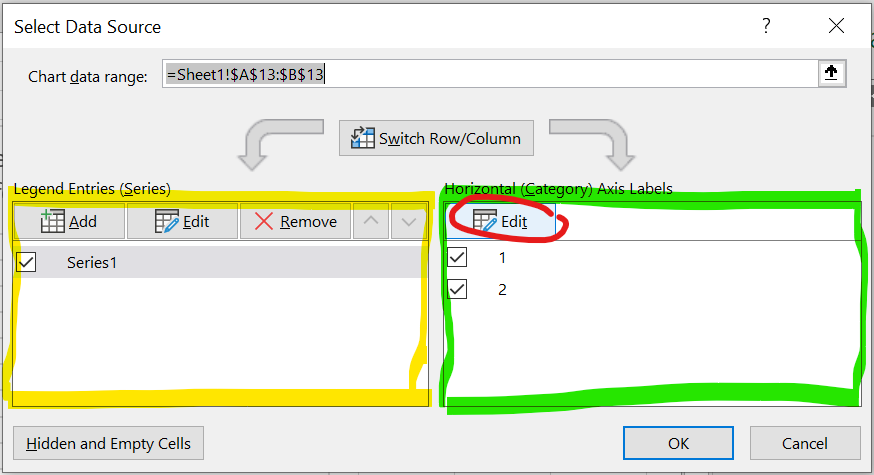
Het Select data source menu.

Figure 1.34: Het Select data source menu.

  • in het linker vak zou je de data aan kunnen passen (geel)

  • In het rechter vak (groen) kun je de labels aanpassen: klik op edit en selecteer de cellen (beide tegelijk) met de juiste labels, of type : “Lindelaan,Hoofdweg” (als dat niet werkt: “Lindelaan;Hoofdweg”, sommige versies van Excel willen een ; )

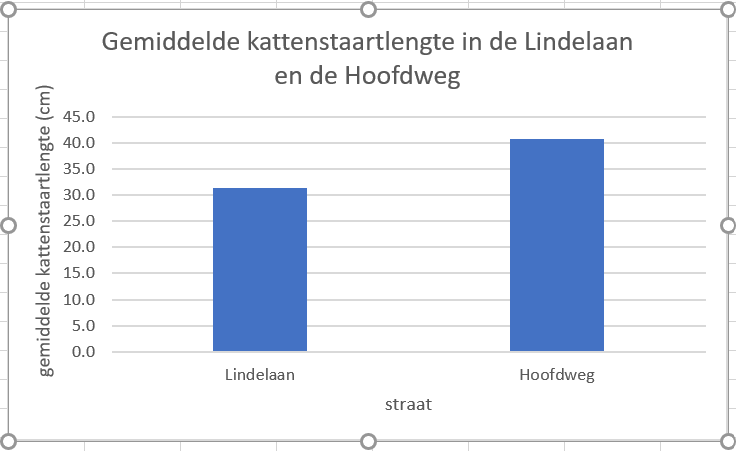
Het staafdiagram aan het eind van deze opdracht.

Figure 1.35: Het staafdiagram aan het eind van deze opdracht.

Hoera, een staafgrafiek!

Sla je Excel-bestand op, we hebben hem komende les nog nodig!

Opdracht 1

Welke katten lijken langere staarten te hebben? Welke informatie kun je in de grafiek niet zien, die je wel nodig hebt om daar echt een inschatting van te kunnen maken?

Klik hier voor het antwoord

Katten aan de Hoofdweg lijken langere staarten te hebben. Maar in de grafiek is niet te zien hoe verschillend kattenstaarten in deze steekproef zijn. Stel je voor dat kattenstaarten kunnen varieren tussen de 10 en 70 cm. De hoeveelheid metingen in deze steekproeven was niet enorm groot. Zou je op basis van 2 maal 10 katten dan al durven inschatten dat katten aan de Hoofdweg langere staarten zouden hebben? Misschien is het verschilletje dat je nu in de grafiek ziet dan wel toeval.. We weten immers al dat als je twee keer een steekproef uit dezelfde populatie zou nemen, je ook niet precies hetzelfde steekproef-gemiddelde zou vinden…

Tja, moeilijk.

In de komende lessen gaan we veel verder uitwerken hoe je dit soort vragen kunt beantwoorden.

1.3.4 Extra oefenopgaven

Opdracht 1

EXTRA Oefenopgaven typen data

Geef aan voor elk van de volgende waarden of de data kwalitatief of kwantitatief zijn. Als het gaat om kwalitatieve data, geef aan of het ordinaal of nominaal is. Als het gaat om kwantitatieve data, geef aan of het ratio of interval is.

Concentratie antilichamen in het bloed tegen de SARS-CoV-2 virus

Klik voor het antwoord kwantitatief, ratio

Code rood afgegeven door het KNMI bij een zuidwester storm

Klik voor het antwoord kwalitatief, ordinaal

Aantal kilometer file in Frankrijk op zwarte zaterdag

Klik voor het antwoord kwantitatief, ratio

Bloedgroep van patienten die op de IC zijn opgenomen met covid-19

Klik voor het antwoord kwalitatief, nominaal

Windkracht boven de Noordzee volgens het schaal van Beaufort

Klik voor het antwoord kwalitatief, ordinaal

Gemiddelde snelheid van de winnaar van de Tour de France

Klik voor het antwoord kwantitatief, ratio

Immuun tegen covid-19 na een eerdere besmetting (ja/nee)

Klik voor het antwoord kwalitatief, nominaal

Drie sterren voor een camping volgens de reviews op een online vergelijkingsite

Klik voor het antwoord kwalitatief, ordinaal

Gewichtsverlies van herstelde patienten na 19 dagen IC opname

Klik voor het antwoord kwantitatief, ratio

De datum van vandaag

Klik voor het antwoord kwantitatief, interval