Les 2 Meten en Onnauwkeurigheid

2.1 Lesinhoud en leerdoelen

Tijdens deze les maak je kennis met enkele basisbegrippen en concepten in de statistiek. In een biomedisch laboratorium zal je regelmatig (kwantitatieve en kwalitatieve) metingen verrichten. Het is belangrijk om je daarbij bewust te zijn van mogelijke meetfouten en de effecten van deze meetfouten op je conclusies. Je leert in deze les de nauwkeurigheid van gemeten kwantitatieve waarden op een juiste manier te noteren.

Aan het einde van deze les kun je:

uitleggen welke verschillende soorten fouten en foutoorzaken er bij het meten bestaan;
aangeven wat het effect van toevallige variatie is op een meting;
uitleggen wat de normaalverdeling is;
en het gemiddelde en de standaarddeviatie berekenen in Excel.

Theorie:

meetfouten
biologische variatie
de normaalverdeling
spreiding: de standaarddeviatie

Vaardigheden:

meetwaarden met meetfouten afronden
kopieren van formules in Excel
error bars toevoegen aan grafieken in Excel
beschrijvende statistiek: gemiddelde en standaarddeviatie
een lijngrafiek maken

2.2 Voorbereiding

Statistiek is net zo’n dingetje dat veel mensen **bijna* door hebben. Statistiek is dus een onderwerp dat heel (!) vaak op internet verkeerd uitgelegd wordt. Echt heel vaak. Pas daar dus mee op. Wikipedia heeft het heel regelmatig niet correct. Maar ook allerlei statistics-websites, zeker van commerciele partijen als adviesbureaus, huiswerkbegeleiders en aanbieders van software, en ook absoluut sites als studeersnel en stuvia zitten er heel regelmatig naast. Dit kan erg verwarrend worden als je probeert om je informatie op internet bij elkaar te googlen.

Wil je graag verder lezen of kijken, dan kun je bijvoorbeeld Crash course wel vertrouwen, of Kahn academy.

2.2.1 Meetfouten

De perfecte meting bestaat niet. Wanneer we de temperatuur van een vloeistof meten, zal de gemeten waarde altijd (een klein beetje) afwijken van de werkelijke temperatuur. Met andere woorden, we kunnen de werkelijke temperatuur alleen maar benaderen door te meten. Deze onnauwkeurigheid komt voort uit zogenaamde meetfouten. We onderscheiden drie type meetfouten: toevallige fouten, systematische fouten en vermijdbare fouten.

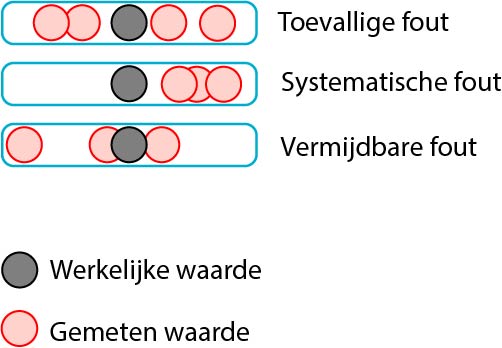
2.2.1.1 Toevallige fouten

Toevallige fouten zijn altijd aanwezig; ze zijn niet te vermijden. (Ze zijn in die zin dus ook niet “fout”, zo heten ze alleen. Statistici houden er van om dingen namen te geven die niet zo handig zijn in een andere context!) Toevallige fouten zijn het gevolg van twee dingen die te maken hebben met je meting:

Fouten bij het aflezen van de apparatuur. Wanneer je een analoge thermometer afleest zal je moeilijk onderscheid kunnen maken tussen 37,2 en 37,3 graden.
Beperkte gevoeligheid van de meetapparatuur. Een goedkope thermometer kan onderscheid maken tussen 37 en 38 graden, maar niet tussen 37 en 37,2 graden.

En tot slot een ding dat te maken heeft met je populatie: - Biologische variatie. Wanneer je bij verschillende mensen de temperatuur exact zou kunnen bepalen, zal je bij de ene persoon 36,5 graden meten en bij de andere 37,5 graden. Oftewel, we zeggen wel dat mensen een lichaamstemperatuur hebben van 37 graden, maar in werkelijkheid is die lichaamstemperatuur gemiddeld 37 graden, maar varieren mensen pak ’m beet tussen de 36.5 en 37.5 graden.

Het gevolg van toevallige meetfouten is dat de gemeten waarde soms hoger en soms lager is dan de werkelijke waarde (zie ook bovenstaande figuur). Je kunt daarom de toevallige meetfout eenvoudig verkleinen door vaker te meten en over de gemeten waarden het gemiddelde te berekenen.

Gevoeligheid van meetapparatuur en significante cijfers

Bij chemisch rekenen (en ook vaak op de HAVO) leren jullie over significante cijfers. Hoe weten we nou op hoeveel significante cijfers je een meetwaarde op zou moeten schrijven? Dat hangt dus af van je meetapparatuur.

Een weegschaal. Ter illustratie. M.Minderhoud, [CC BY-SA 3.0](http://creativecommons.org/licenses/by-sa/3.0/), via Wikimedia Commons

Figure 2.1: Een weegschaal. Ter illustratie. M.Minderhoud, CC BY-SA 3.0, via Wikimedia Commons

Stel je wilt muizen wegen, en je hebt een weegschaal met streepjes om de 10 gram. Je zet een muis op de weegschaal, en je leest af: het wijzertje op de weegschaal zit ergens tussen de 10 en de 20 gram, beetje dichter bij de 20. Dan kun je dus niet 18.54 gram opschrijven met 4 significante cijfers, want zo precies weet je het gewoon niet.

2.2.1.2 Systematische fouten

Systematische fouten geven een consequente overschatting of een onderschatting van de werkelijke waarden. Er zijn verschillende oorzaken van systematische fouten:

Wanneer je de lengte van proefpersonen meet terwijl ze nog schoenen dragen, zal je consequent de lengte van deze proefpersonen overschatten.
Het gevolg zijn van verkeerde kalibratie van je apparatuur, verouderde materialen en oplossingen.

Systematische fouten zijn erg moeilijk om te herkennen en op te sporen. Maar wanneer de oorzaak en de afwijking bekend is kunnen we er wel gemakkelijk voor corrigeren of de fouten geheel elimineren.

2.2.1.3 Vermijdbare fouten

Vermijdbare fouten zijn echte fouten of blunders. Een thermometer geeft bijvoorbeeld aan dat de lichaamstemperatuur 37,5 graad is, maar we noteren 36,5 graad. Ook kan het gebeuren dat een thermometer de temperatuur kan meten in graden Celsius én in Fahrenheit, en we per abuis de temperatuur aflezen in graden Fahrenheit terwijl we denken te meten in graden Celsius. Ook het gebruiken van een verkeerd reagens of het gebruiken van een verkeerde voorschrift zijn voorbeelden van vermijdbare fouten. Vermijdbare fouten leiden tot uitschieters. Gelukkig zie je meestal aan de uitkomst al dat er iets fout is gegaan en is dit soort fouten snel op te sporen.

Exercise 2

Jeroen maakt een bufferoplossing op het lab. In plaats van pH=7,4 schrijft hij pH=7,04 op de fles. Wat voor een fout is dit?

Klik hier voor het antwoord

Een vermijdbare fout.

Exercise 2

De balans van het laboratorium is al twee jaar niet gekalibreerd. Hier door geeft de balans een 5% hogere waarde. Wat voor fout is dit?

Klik hier voor het antwoord

Een systematische fout.

Exercise 2

Het bepalen amylase activiteit in speeksel wordt uitgevoerd bij kamertemperatuur. Op woensdag vindt Chris een significant hogere waarde dan op maandag bij het meten van het zelfde monster. Later blijkt dat de airco op het lab kapot was. Wat voor soort fout is hier sprake van?

Klik hier voor het antwoord

Een systematische fout (altijd dezelfde kant op)

Exercise 2

Om de antistof concentratie in een patiëntenmonster te bepalen heeft Daniël een aantal standaardoplossingen gemaakt voor de ijklijn. Achteraf is gebleken dat bij het verdunnen van de monsteroplossing een P200 volumepipet is gebruikt is in plaats van een P20 pipet. Van welk soort fout is hier sprake?

Klik hier voor het antwoord

Een vermijdbare fout.

Exercise 2

Leonie wil de concentratie van glucose bepalen met een spectrofotometer en heeft daarvoor volgens een bestaand protocol de oplossingen gemaakt. Tijdens de meting van 5 gelijke monsteroplossingen ziet zij echter verschillende absorptie-waarden, die liggen tussen 0,356 en 0,365. Van welk soort fout is hier sprake?

Klik hier voor het antwoord

Een toevallige fout.

2.2.2 Biologische variatie

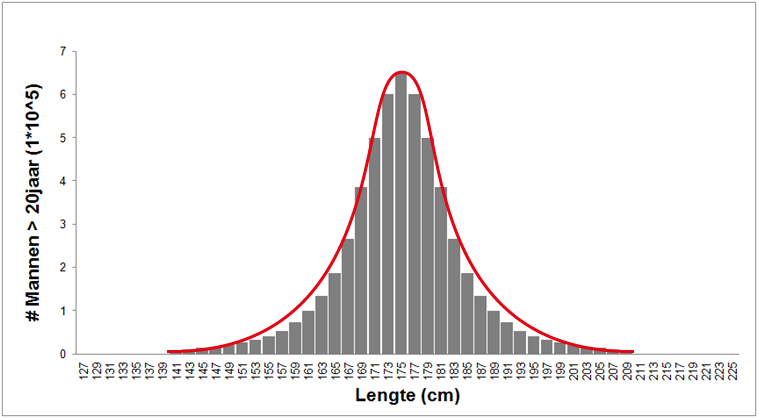
Als gevolg van biologische variatie is niemand even lang. Stel dat je wilt weten wat de gemiddelde lengte van de hedendaagse Nederlandse man is, en hoe groot de kans is dat een willekeurig individu veel groter of veel kleiner is dan dit gemiddelde, hoe pak je dat aan? De doelgroep waarover je iets wilt weten, alle Nederlandse mannen, wordt in de statistiek de populatie genoemd.

Wanneer de lengte van alle Nederlandse mannen bekend is, dan tel je het aantal individuen met een lengte in een bepaald bereik. Het aantal individuen per interval zetten we vervolgens uit in een histogram (zie grijze staven in de onderstaande grafiek). In de onderstaande grafiek is dat bereik verdeeld in intervallen van 2cm. Uit dit histogram blijkt dat relatief veel Nederlandse mannen een lengte hebben van rond de 1,75 meter, en dat er, naarmate de lengte naar boven of naar beneden meer afwijkt van dit gemiddelde, steeds minder mannen zijn met die lengte. Er zijn dus meer Nederlandse mannen met een lengte van 1,75 meter dan mannen met een lengte van 1,45 meter en 2,09 meter.

In dit voorbeeld gaan we er even vanuit dat A) we alle Nederlandse mannen opgementen hebben (niet zo realistisch) en B) dat je mensen uberhaupt zo makkelijk kan indelen in “wel man / niet man” (ook niet zo realistisch). Maar voor het voorbeeld wel even duidelijk.

2.2.3 Normaalverdeling

Een karakteristieke eigenschap van biologische variatie is dat de verdeling van waarden om het gemiddelde symmetrisch is. Er zijn dus ongeveer evenveel mannen 10 cm groter dan het gemiddelde als mannen 10 cm kleiner dan het gemiddelde. Deze verdeling van waarden om het gemiddelde heet een normaalverdeling. Als je data in een histogram zet en het lijkt op deze normaalverdeling, dan noemen we dat normaal verdeelde data.

Wanneer we dan alle waarden verbinden door een continue lijn, ontstaat de normaalcurve (zie de rode lijn in het bovenstaande figuur) die wiskundig kan worden omschreven met de volgende functie (die je niet uit je hoofd hoeft te leren):

$f(x)=\frac{1}{σ\sqrt{2π}}e^{-\frac{1}{2}}(\frac{x-\mu}{\sigma})^2$

Bovenstaande formule is bedacht door Carl Friedrich Gauss (1777-1855) met als doel de normale verdeling zoals die in de natuur voorkomt wiskundig te beschrijven. Er wordt daarom ook wel gesproken over een Gauss-curve. De formule lijkt ingewikkeld, maar omdat π en e beide natuurlijke constanten zijn, wordt de vorm van de curve alleen bepaald door (wel belangrijk om te onthouden):

2.2.4 Populatie

$\boldsymbol{\mu}$ en $\boldsymbol{\sigma}$

Veel biologische variabelen zijn dus “normaal verdeeld”, en dat betekent dat we ze kunnen beschrijven met de twee parameters uit de formule hierboven:

(Let op, we hebben het hier dus niet over een steekproef, maar over de hele populatie. Om dat extra duidelijk te maken, kleuren we de hele achtergrond even roze. )

Het populatiegemiddelde ($\mu$), de gemiddelde waarde van de populatie. Deze is gelijk aan de x-waarde, de lengte in dit geval, op het hoogste punt van de grafiek (zie onderstaande figuur). Dit betekent dat als je de lengte van willekeurig persoon meet de kans het grootst is dat die lengte rond de 1,75 meter zal uitvallen.
De populatiestandaarddeviatie ($\sigma$), de variatie / spreiding van de populatie (zie onderstaande figuur). Deze waarde bepaalt de breedte van de curve. Als de normaalverdeling heel smal is, is $\sigma$ heel klein en is in het voorbeeld iedereen ongeveer even lang. Als de normaalverdeling heel breed is, is $\sigma$ heel groot en is er heel veel verschil in lengte.

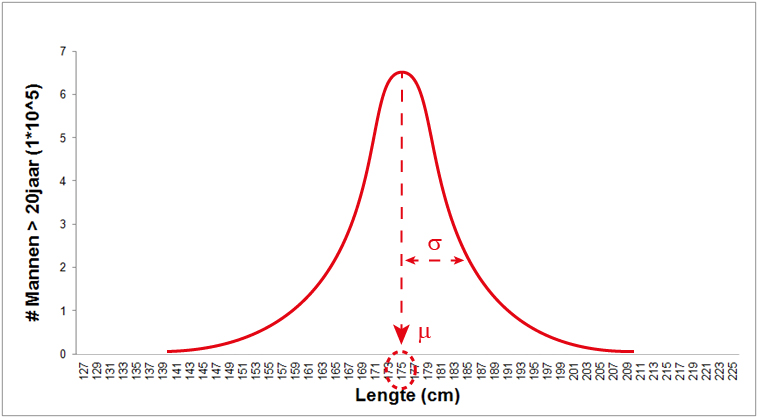
normaalverdeling

Een normaalverdeling is symmetrisch (de linker kant van het midden is het spiegelbeeld van de rechterkant van het midden)
het populatiegemiddelde geeft aan waar het midden ligt (Excel: =AVERAGE() - dan moet je dus wel de complete populatie gemeten hebben)
de populatiestandaarddeviatie geeft aan hoe breed de normaalverdeling is: een maat voor de spreiding. (Excel: =STDEV.P() - dan moet je dus wel de complete populatie gemeten hebben)

2.2.5 Steekproef

$\boldsymbol{\overline{x}}$ en $\boldsymbol{s}$

Het populatiegemiddelde $\mu$ gaf aan waar het midden van de normaalverdeling lag. Meestal is dit populatiegemiddelde iets wat we niet weten, maar wel graag willen schatten. Daarom doen we dan een steekproef.

(We kleuren de hele achtergrond even blauw. )

De data van je steekproef kan ook normaal verdeeld zijn. Sterker nog, als we een steekproef nemen uit een normaal verdeelde populatie, dan wil je graag dat die data ook normaal verdeeld is. Anders heb je namelijk bijkbaar geen random steekproef. Dit soort maten kun je dus ook gebruiken om een steekproef te beschrijven.

Het steekproefgemiddelde ($\overline{x}$), de gemiddelde waarde van de meetpunten.(Excel: =AVERAGE())
De steekproefstandaarddeviatie ($s$), de variatie / spreiding van de meetpunten in je steekproef (Excel: =STDEV.S())

De steekproefstandaarddevaitie bereken je zo (of nou ja, meestal gebruik je Excel, maar dit is de formule):

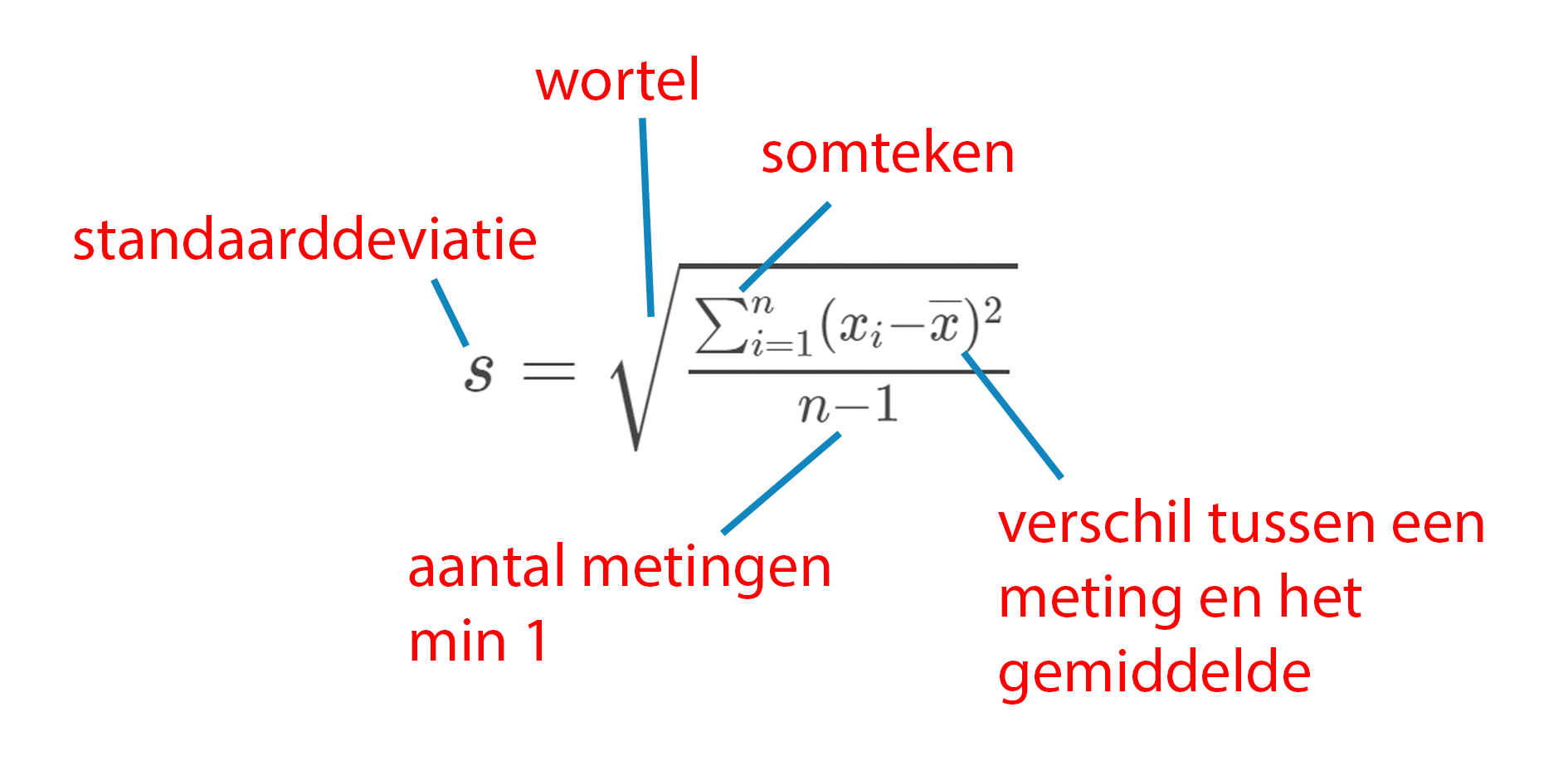
$s$ = steekproefstandaarddeviatie $n$ = aantal metingen $x_i$ = bepaalde meting $\overline{x}$ = steekproefgemiddelde

Oftewel:

Bereken het gemiddelde.
Neem van elk getal de afstand (d) tot het gemiddelde
Neem het kwadraat van die afstanden.
Tel al die kwadraten bij elkaar op.
Deel dat getal door (het aantal metingen - 1)
Neem de wortel van de uitkomst

Kijk, voor dat soort dingen hebben we nou Excel. Excel heeft een functie die de standaard deviatie uit rekent. STDEV.S() voor het uitrekenen van de standaard deviatie van een steekproef (sample) en STDEV.P() voor het uitrekenen van de standaard deviatie van een populatie (population). Kies STDEV.S(), tenzij je echt de hele populatie (!) gemeten hebt. Meestal doe je een steekproef, dus gebruik je STDEV.S().

Typ =STDEV.S( in een cel
Selecteer met de cursor de cellen waarvan de standaard deviatie moet worden uitgerekend.
Sluit af met een haakje en klik op enter

Stel je bijvoorbeeld voor dat we hetzelfde bakje poeder in triplo op 2 weegschalen gemeten hebben:

Het gemiddelde bij beide weegschalen is 30 gram. Maar de spreiding van de metingen is niet gelijk! Kijk maar:

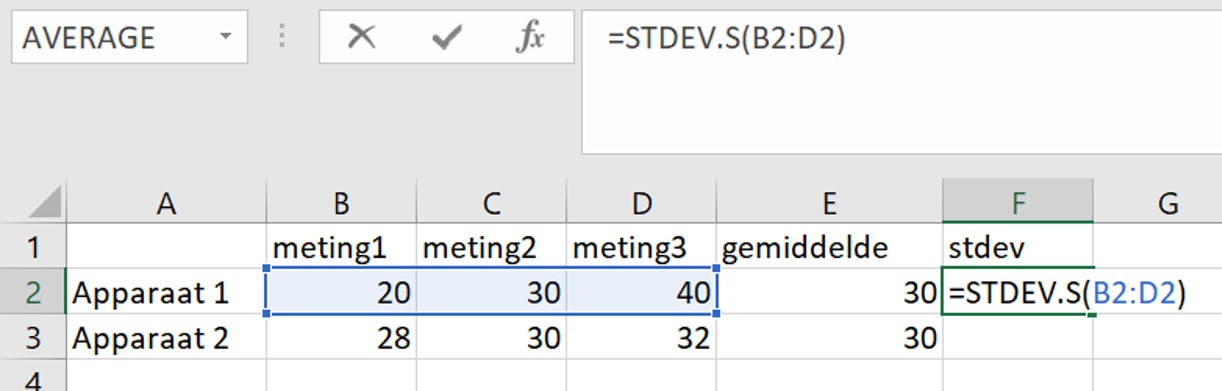
De standaard deviatie is een maat voor de variatie (betrouwbaarheid) van je meetresultaten: Hoe groter de standaard deviatie hoe groter de variatie tussen de metingen (en dus onbetrouwbaarder). Apparaat 1 geeft een grotere variatie van de meetpunten en dus een hogere standaard deviatie in vergelijking met apparaat 2.

2.2.6 Meetwaarden met meetfouten afronden

Bij chemisch rekenen leren jullie over het correct afronden van meetwaarden en rekenregels. Maar als van een meetwaarde een maat van spreiding (meetfout) bekend is, zoals een standaarddeviatie, werkt het net iets anders. Dan bepaalt namelijk de meetfout de precisie waarmee je de meetwaarde op mag schrijven.

Een meetwaarde met meetfout noteer je als meetwaarde ± meetfout.

Dus een steekproefgemiddelde van 5.2 cm met een standaarddeviatie van 0.1 noteer je als: 5.2 ± 0.1 cm.

Voor het afronden van meetwaarden met een meetfout, geldt het volgende:

De meetwaarde en fout schrijven we als dezelfde macht van 10 (of orde van grootte): dus 300 ± 12, of misschien (0,300 ± 0,012) ∙ 10³, maar niet 0,3 ∙ 10³ ± 12 (zie ook het filmpje hierboven over significantie en wetenschappelijke notatie)
We beginnen met het afronden van de meetfout. op 1 significant cijfer
Kijk naar het aantal decimalen die de meetfout nu heeft. Rond je meetwaarde af op hetzelfde aantal decimalen (cijfers na de komma).

Dus 0,16635566 ± 0,02333 wordt 0,17 ± 0,02 of (1,7 ± 0,2)∙ 10^-1 (beide zijn goed)

3556 ± 156,3 wordt (3,6 ± 0,2) ∙ 10³.

2.2.7 Wanneer wetenschappelijke notatie?

Bij Chemie&rekenen leren jullie ook over de wetenschappelijke notatie. Maar in het geval van meetfouten en meetwaarden, wanneer moet je hem dan gebruiken?

mag: Als het lastig wordt om te lezen (bijv. 0.000057 ± 0.000002 cm mag je opschrijven als (5.7 ± 0.2)*10^-5. Maar: 0.000057 ± 0.000002 cm is niet fout, wel slecht leesbaar. Beide antwoorden zijn dus goed.)
moet: als je anders meer dan 1 significant cijfer in de meetfout op zou moeten schrijven. (bijvoorbeeld: 381 ± 128 cm afronden –> 128 afronden op 1 significant cijfer is 1 * 10² en niet 100. Want 100 heeft 3 significante cijfers. –> correcte afgeronde antwoord: (4 ± 1) * 10² cm. In dit geval is 400±100 cm of 381 ± 100 cm wel fout!)

2.2.8 Kopiëren van formules in Excel

Voor we met het werkcollege beginnen eerst nog even dit: kopieren van cellen in Excel met formules er in is even opletten. Kijk mee met het volgende voorbeeld:

Het volgende experiment laat een tijdreeks zien. De onderzoeker wil weten wat de mate van inductie ten opzichte van het nulpunt. Daarvoor worden alle gemiddelde waardes gedeeld door de gemiddelde waarde van tijdspunt 0.

In cel I3 schrijft de onderzoeker een formule waarbij de waarde van cel E3 (blauw gemarkeerd) gedeeld wordt door de waarde in cel E2 (rood gemarkeerd).

De onderzoeker kopieert en plakt de formule van cel I3 voor de andere tijdpunten in cel I4:I7.

De onderzoeker wil nu controleren of het kopiëren van de formule goed is gegaan. Hij klikt daarom op cel I7.

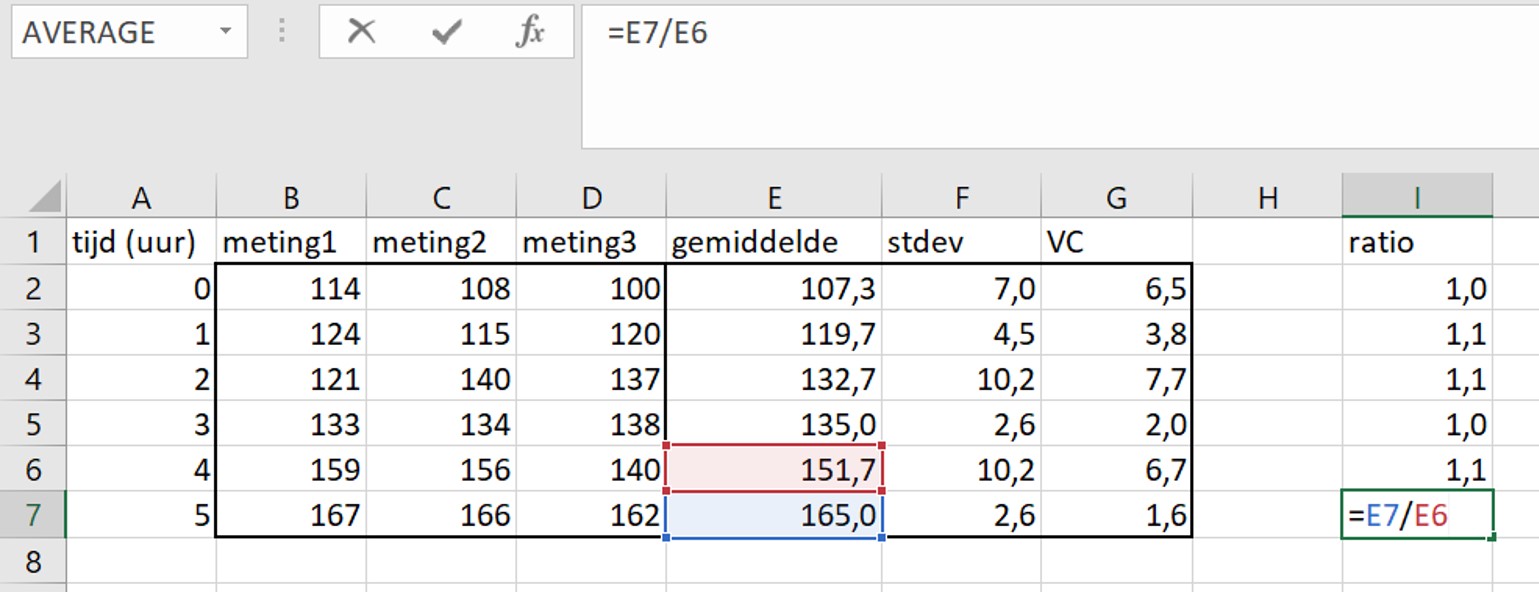
Maar dit klopt niet! De onderzoeker wil dat de waarde van cel E7 (blauw gemarkeerd) wordt gedeeld door de waarde van cel E2 en niet door E6 (rood gemarkeerd). Dit laat een belangrijk principe zien van formules in Excel:

Als je een formule van boven naar beneden kopieert dan verschuiven de cellen waarmee de berekening is uitgevoerd ook mee van boven naar beneden. Dit geldt ook als je kopieert van links naar rechts: de cellen waarmee de berekening is uitgevoerd verschuiven dan mee van links naar rechts.

Om te voorkomen dat cellen van boven naar onder of van links naar rechts verschuiven tijdens het kopiëren van een formule gebruiken we het $ teken om een cel vast te leggen in een formule:

Als je een rij wilt vastleggen plaats je het dollar teken voor het cijfer van de cel (kopiëren van boven naar beneden binnen één kolom). Bijvoorbeeld: E$7 (de rij, 7, staat nu vast).
Als je een kolom wilt vastleggen plaats je het dollar teken voor de letter van de cel (kopiëren van links naar rechts binnen één rij). Bijvoorbeeld: $E7 (de kolom, E, staat nu vast).
Als je beide wilt vast leggen plaats je het dollar teken voor zowel de letter als het cijfer (kopiëren van formules in meerdere rijen en kolommen). Bijvoorbeeld: $E$7 (zowel de rij als de kolom staan nu vast).

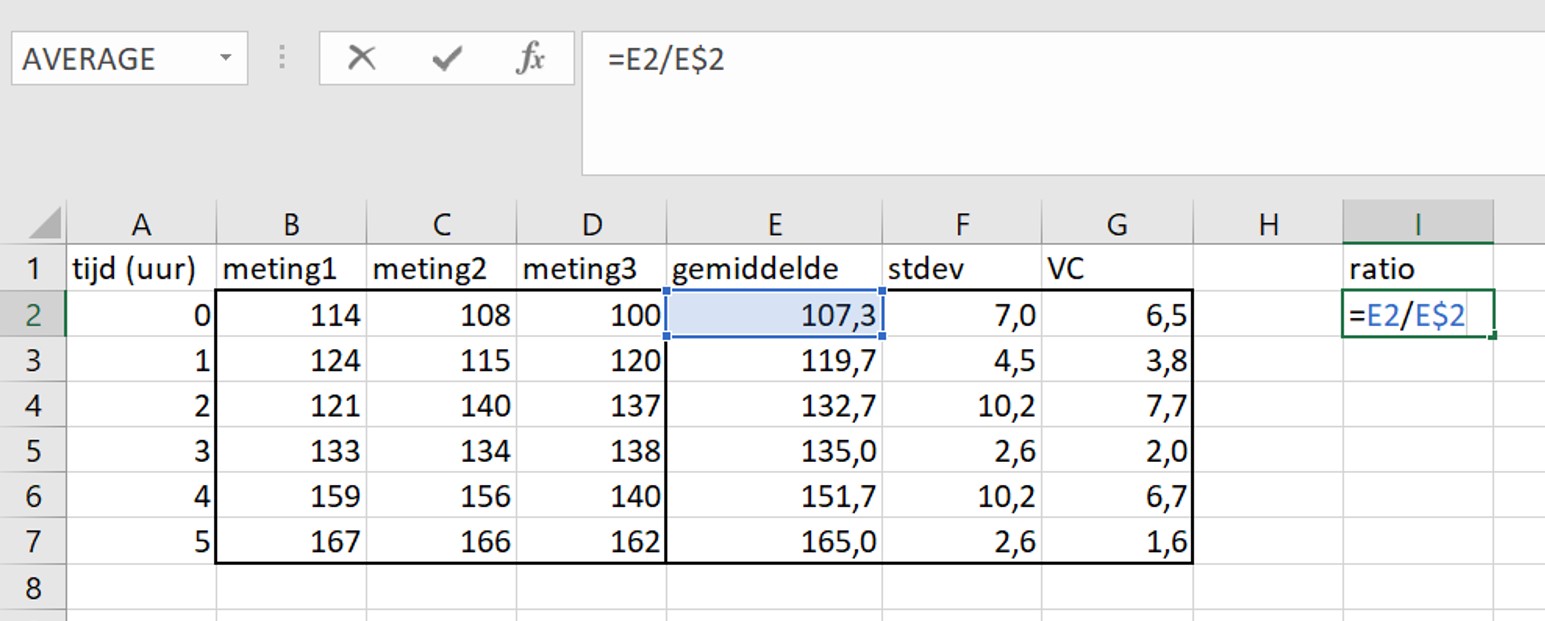
In dit voorbeeld wil de onderzoeker cel E2 vastleggen in de formule zodat deze cel niet verschuift tijdens het kopiëren. In dit voorbeeld wordt de formule van boven naar beneden gekopieerd binnen één kolom. De kolom blijft dus hetzelfde en alleen de rijen (cijfers) verschuiven.

Om het probleem op te lossen noteert de onderzoeker in cel I2 de formule =E2/E$2 waarbij het dollar teken dus voor de twee is geplaatst.

Als de onderzoeker de formule nu kopieert, krijgt hij andere getallen. Voor de zekerheid controleert hij cel I7.

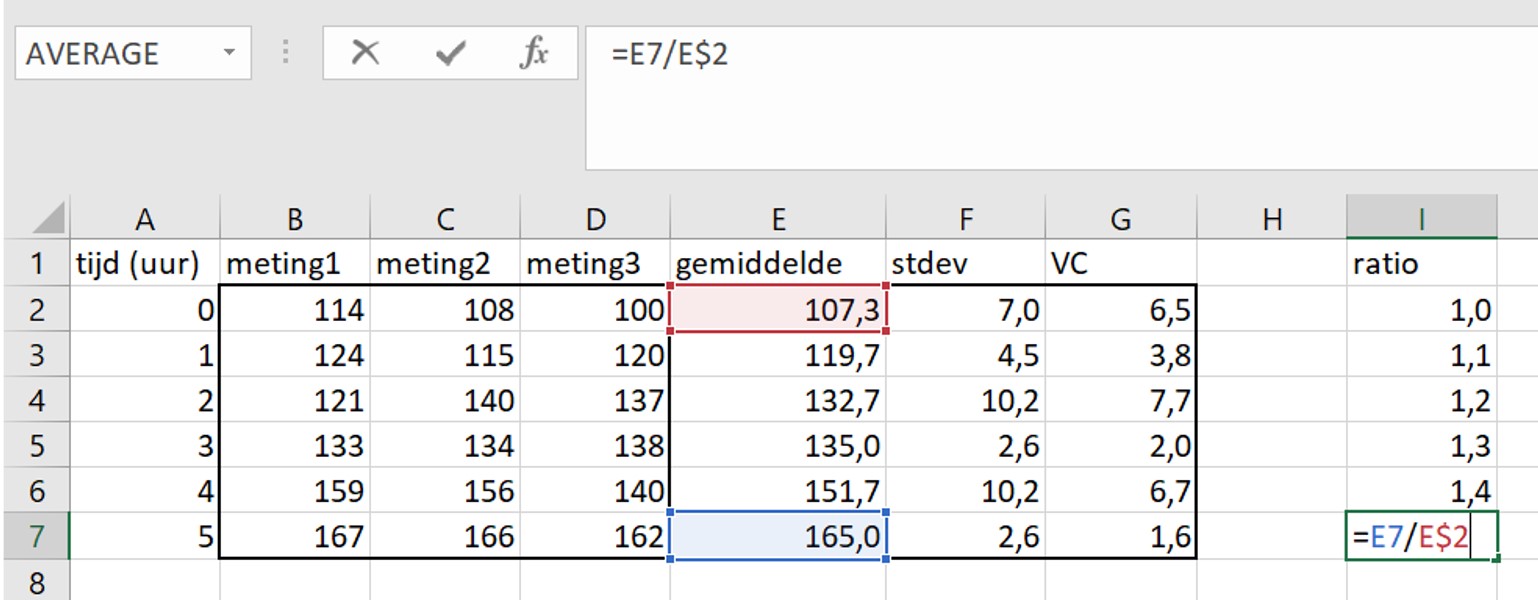
Inderdaad, de juiste cellen zijn nu gebruikt voor de berekening.

2.3 Werkcollege

2.3.1 Deel 1 - afronden

Tijdens het instructiecollege heb je geleerd hoe je meetwaardes en hun fout moet afronden.

Begin met afronden van de meetfout op 1 significant cijfer
Rond vervolgens de meetwaarde af op hetzelfde aantal decimalen als waarop de meetfout is afgerond.
zet in wetenschappelijke notatie als het lastig leesbaar is (kan ook als stap 1, dat maakt niet uit)

Opdracht 2

Rond de volgende meetwaarden met meetfout af volgens de regels:

8,675 ± 1,456
776578 ± 1875
77,87767 ± 0,0356
3445 ± 15
0,0000022333 ± 0,02
0,0023454 ± 0,000244
0,0023454 ± 0,000164
165,45639 ± 0,011467
165,4563946 ± 0,00011467
165,4563946 ± 0,00011567
165,45639 ± 0,11467
165,45639 ± 0,21467
165,45439 ± 0,025
165,45639 ± 0,0250001
165,45669 ± 0,0035
23,5 ± 1
32,5 ± 12
666 ± 19
666 ± 129
5,3 ± 1,65

Klik hier voor de antwoorden

jaar	gemiddelde
8,675 ± 1,456	9 ± 1
776578 ± 1875	(777 ± 2) *10³
77,87767 ± 0,0356	77,88 ± 0,04
3445 ± 15	(345 ± 2) *10¹
0,0000022333 ± 0,02	0,00 ± 0,02
0,0023454 ± 0,000244	(2,3 ± 0,2) * 10^-3
0,0023454 ± 0,000164	(2,3 ± 0,2) * 10^-3
165,45639 ± 0,011467	165,46 ± 0,01
165,4563946 ± 0,00011467	165,4564 ± 0,0001
165,4563946 ± 0,00011567	165,4564 ± 0,0001
165,45639 ± 0,11467	165,5 ± 0,1
165,45639 ± 0,21467	165,5 ± 0,2
165,45439 ± 0,025	165,45 ± 0,03
165,45639 ± 0,0250001	165,46 ± 0,03
165,45669 ± 0,0035	165,457 ± 0,004
23,5 ± 1	24 ± 1
32,5 ± 12	( 3 ± 1) *10¹
666 ± 19	( 67 ± 2) *10¹
666 ± 129	( 7 ± 1) *10²
5,3 ± 1,65	5 ± 2

2.3.2 Deel 2 - De Normaalverdeling

Voor dit deel van het werkcollege heb je het bestand Normaalverdeling.xlsx nodig.

Open dit bestand en klik met de rechtermuisknop op de naam van de worksheet “normaal_verdeling” links onder op de pagina.
In het venster dat opent, klik op Move or Copy.
Selecteer move to end en vink aan Create a copy. Klik OK.

De kopie staat nu als extra werkblad naast het originele werkblad.

Het creëren van een kopie dient als back-up. Bewaar altijd je ruwe data in een apart werkblad (of een apart bestand), maak een kopie en ga de kopie bewerken in Excel.

In het tabblad “normaal_verdeling” is de standaard normaalcurve weergeven volgens de formule van gauss:

$f(x)=\frac{1}{σ\sqrt{2π}}e^{-\frac{1}{2}}(\frac{x-\mu}{\sigma})^2$

De standaard functie heeft een $μ$ van 0 (gele vak B1) en een $σ$ van 1 (groene vak B2).

Stel $μ = 0$ en vul vervolgens voor $σ$ de waardes 1, 2, 3, 4 en 5 in. Voor iedere $σ$, kopieer B5:B65 met paste special > paste values naar respectievelijk:
```
 `M5:M65`     σ=1
 `N5:N65`     σ=2
 `O5:O65`     σ=3
 `P5:P65`     σ=4
 `Q5:Q65`     σ=5
```
Maak een grafiek type scatter plot with smooth lines voor de verschillende normaalcurves.

Exercise 2

Wat gebeurt er met de grafiek als de spreiding ($σ$) toeneemt?

Klik hier voor het antwoord

De grafiek wordt breder en lager (minder hoog).

2.3.3 Deel 3: Beschrijvende statistiek

steekproefgemiddelde en steekproefstandaarddeviatie.

Opdracht 2

Open weer staartvergelijking.xlsx van vorige les voor het bestand met kattenstaartlengtes in cm van katten in de Lindelaan en aan de Hoofdweg. In beide straten deden we een steekproef.

Bereken voor de katten aan de Lindelaan en voor die aan de Hoofdweg de standaarddeviatie van staartlengte.

Klik hier voor het antwoord

2.90 cm voor de Lindelaan en 4.63 cm voor de Hoofdweg.

Die standaarddeviaties zouden best informatief zijn in ons staafgrafiekje. Laten we hem toevoegen.

Klik op je grafiekje van vorige week, en voeg als volgt foutenbalken toe (let op, klik NIET op standard deviation!! Oh Excel…)

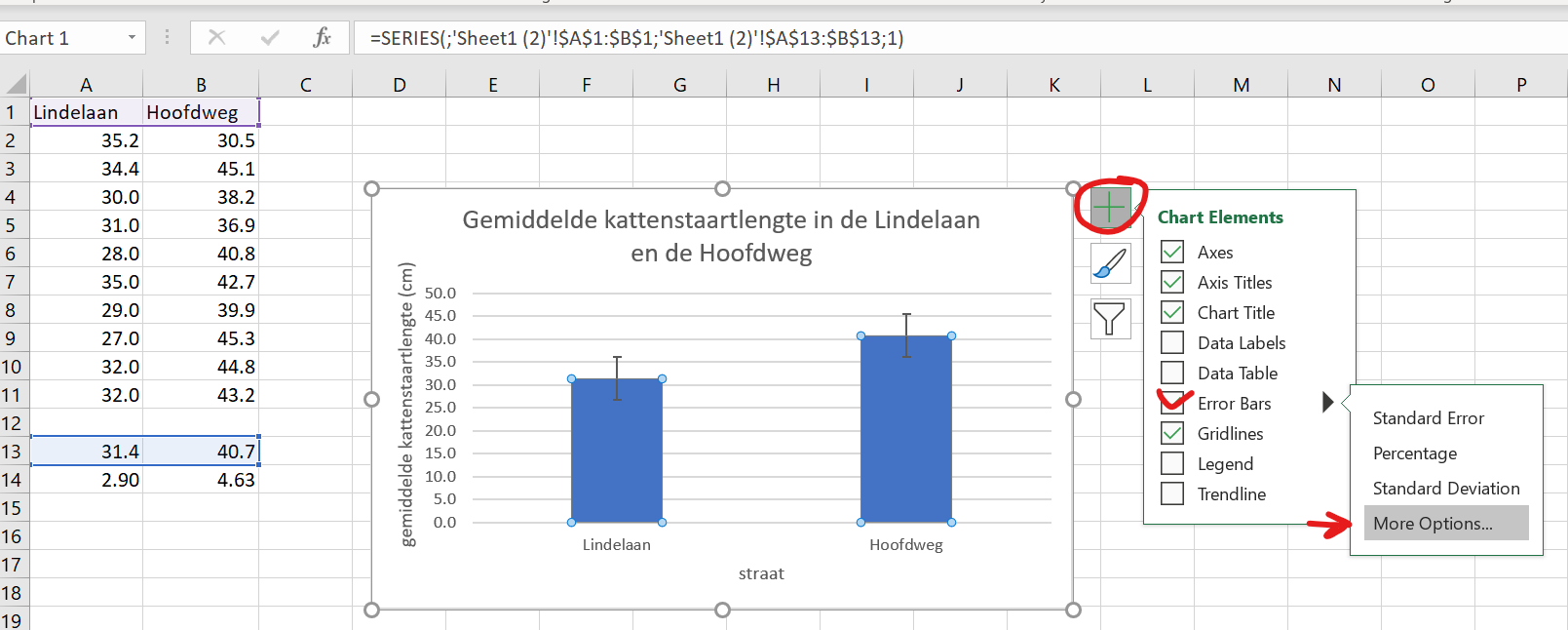
Selecteer voor de errorbars beide standaarddeviaties. Voor zowel de Positive Error Value als de Negative Error Value.

En voila, je hebt spreiding aangegeven in je staafdiagram!

aantal metingen en de som

Opdracht 2

Het Excel-bestand leeftijd_geslacht.xlsx bij deze opdracht bevat informatie over de leeftijd en geslacht van eerstejaars studenten van het Instituut Life Science en Chemistry.

Bereken de gemiddelde leeftijd van de eerstejaars studenten van de opleidingen Life Science en Chemie/Chemische Technologie.
Heeft het zin om het gemiddelde geslacht van de eerstejaars studenten te berekenen? Denk hierbij aan de type data.

Klik hier voor het antwoord

beiden 18 jaar
je kan geen gemiddelde berekenen van nominale data

Voor het bepalen van het aantal waannemingen gebruik je de volgende functies in Excel:

= count(range) : telt het aantal cellen met een cijfer. Negeert lege cellen
= counta(range) : telt het aantal cellen met data (zowel tekst als cijfers). Negeert lege cellen
= countif(range;voorwaarde) : telt het aantal cellen dat voldoet aan een bepaalde voorwaarde

Opdracht 2

Hoeveel eerstejaars studenten van de opleidingen Life Science en Chemie/Chemische Technologie bij elkaar zijn ouder dan 18?

tip: gebruik de volgende formule: =COUNTIF(C2:C297;“>18”)

Klik hier voor het antwoord

Opdracht 2

Welke percentage van de eerstejaars studenten van de opleidingen Life Science en Chemie/Chemische Technologie bij elkaar zijn ouder dan 18?

Klik hier voor het antwoord

0,125 dus 12,5 %

Opdracht 2

Welke percentage van de eerstejaars studenten Life Science is vrouw?

tip: De sum() functie telt de waarde van geselecteerde cellen bij elkaar op. Het negeert tekst en lege cellen. Je kunt sum() hier gebruiken om het aantal vrouwen te tellen.

Klik hier voor het antwoord

60 %

Opdracht 2

Welke percentage van de eerstejaars studenten Chemie/Chemische Technologie is man?

Klik hier voor het antwoord

69%

2.3.4 Deel 4: Lijngrafiek

In de vorige les hadden we het nog niet over lijngrafieken gehad.

Lijngrafieken zijn vooral handig als we veranderingen over veel waarden op de x-as willen laten zien. Dus bijvoorbeeld onze vriend Bas, die kattenstaarten op het Kerkplein al 8 jaar trouw bijhoudt, en elk jaar de gemiddelde kattenstaartlengte berekent:

jaar	gemiddelde staartlengte
2012	25
2013	25.2
2014	26
2015	26.8
2016	32.6
2017	29.5
2018	30.3
2019	31.7
2020	30.9

Een lijngrafiek van deze data doe je door ze naar Excel te kopieren, de kolommen te selecteren, en deze grafiek te kiezen:

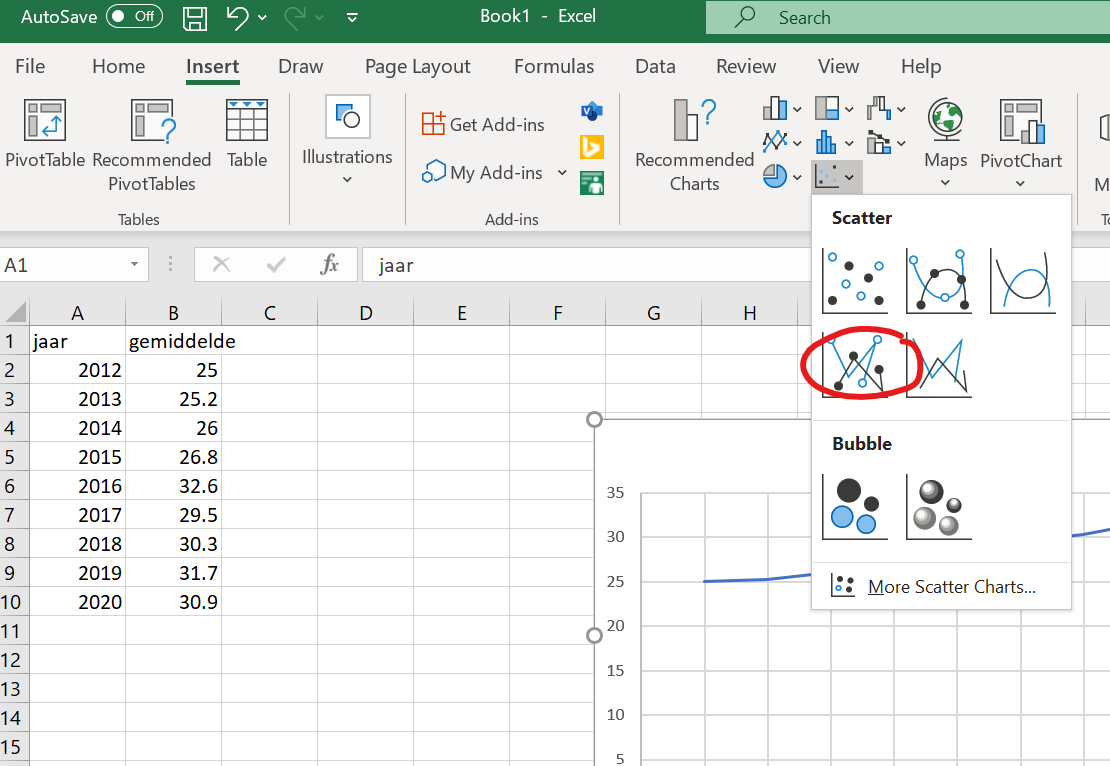
Figure 1.4: Klik hier voor een lijngrafiek

2.3.4.1 Het hele volgende stuk is een opdracht. Doe dus mee!

In dit experiment wordt de hoeveelheid antioxidant gemeten in een aantal verschillende samples. Van deze data gaan we ook een lijngrafiek maken.

Sample	Wat?
A	Vitamine C tablet (Vitamine C is een bekende antioxidant)
B	Sinaasappelsap uit pak merk 1
C	Sinaasappelsap uit pak merk 2
D	Verse jus 1
E	Verse jus 2

10 μl van de onverdunde samples wordt onder elkaar in een plaat gepipetteerd (rij A-E, kolom 1) en vervolgens 7 keer doorverdund in water (kolom 2-8) met telkens een factor 3. De samples in kolom 8 zijn dus 37 = 2187 keer doorverdund. Alleen in welletje A10 wordt water gepipetteerd zonder verdere toevoegingen. Dit is de blanco meting. Hieronder staat aangegeven per welletje hoeveel elk sample is verdund:

Rij/Kolom	1	2	3	4	5	6	7	8	10
A Vitamine C	1	3	9	27	81	243	729	2187	Blanco
B Pak Merk 1	1	3	9	27	81	243	729	2187
C Pak merk 2	1	3	9	27	81	243	729	2187
D Verse jus 1	1	3	9	27	81	243	729	2187
E Verse jus 2	1	3	9	27	81	243	729	2187

In de gevulde welletje van de 96 wells plaat wordt 100 µl DPPH (2,2-Diphenyl-1-picrylhydrazyl) toegevoegd. DPPH is een stof met een vrije radicaal en is met deze vrije radicaal paars van kleur. Het kleurt geel wanneer het geneutraliseerd wordt door anti-oxidanten. Met behulp van een spectrofotometer wordt de kleurintensiteit bij een golflengte van 517 nm (paars) gemeten. Dus: Hoe meer antioxidanten in het welletje, hoe minder paars de kleuring en hoe lager de gemeten extinctie.

2.3.4.2 Importeren van de data

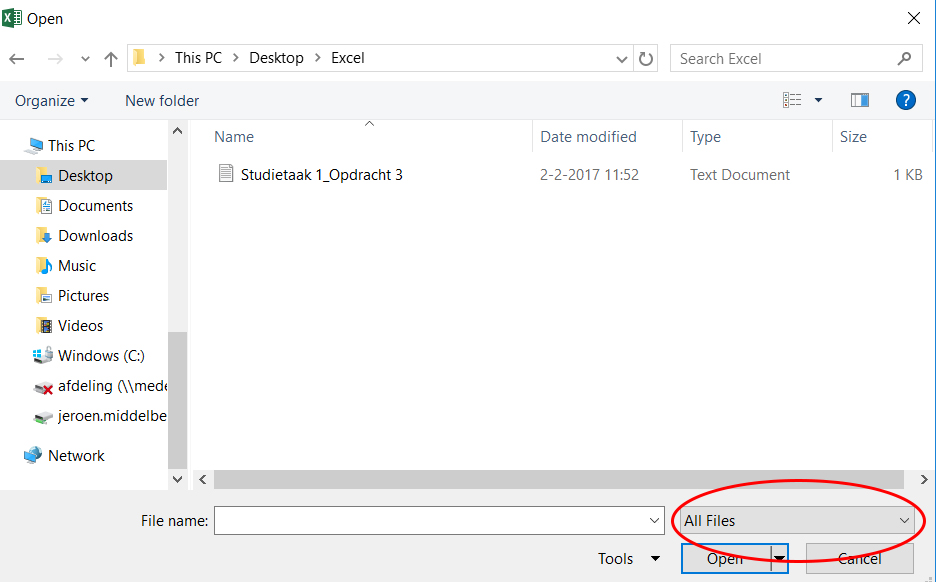
Voor dit deel van het werkcollege heb je het bestand DataImporteren.txt nodig.

Open dit bestand in Excel door via File > Open en Browse het bestand op te zoeken.

Omdat het bestand met meetwaardes geen Excel bestand is, is het niet meteen zichtbaar (alleen Excel bestanden worden weergegeven).

Verander All Excel Files naar All Files
Selecteer het bestand en druk op Open

Het bestand wordt herkent als text bestand. Met behulp van de Text Import Wizard kan deze text eenvoudig worden omgezet naar het Excel format. In een text file worden kolommen gescheiden door een ‘delimiter’. Alle leestekens, spaties en tabs kunnen dienen als delimiter:

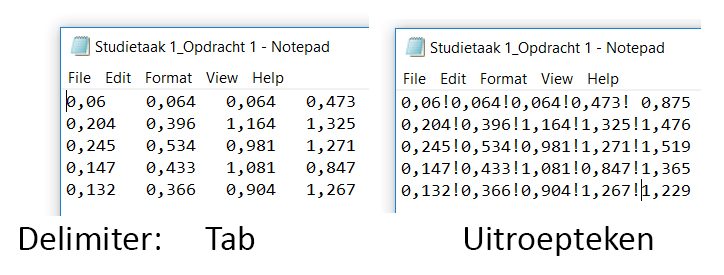
Klik in de Text Import Wizard op Next wanneer de optie Delimited is geselecteerd.

De data in dit bestand zijn gescheiden door een tab. Vink Tab aan en klik op Next.

Klik in het volgende scherm op Finish. De data verschijnt nu in je Excel spreadsheet.

Sla je spreadsheet op als Excel file. Dit doe je door in het menu File te kiezen voor Save As, het bestand een naam te geven en bij File Type te kiezen voor Excel Workbook. De bestandsnaam krijgt nu een ‘.xlsx’ extentie.

2.3.4.3 Organiseren van de data

Je gaat nu aangeven wat de verschillende rijen en kolommen zijn. Om ruimte te maken voor de labels, kun je eerst de data als volgt verplaatsen:

Selecteer de data met je muis van A1:J5. Er zijn verschillende manieren om data te verplaatsen:
- Ga met de muis naar de groene rand. Er verschijnt een zwart kruisje met pijltjes. Sleep de data zodat de inhoud van A1 terecht komt in B3.
- OF: Na selectie klik op de rechtermuisknop en selecteer Cut of gebruik de toetsencombinatie ctrl + x. Selecteer nu cel B3 en plak de data door op de rechtermuisknop de drukken en vervolgens Paste te selecteren óf gebruik de toetsencombinatie ctrl + v.

Data zonder labels zijn zinloos. Label daarom altijd je data in Excel!

Voeg in kolom A labels toe zoals aangegeven in het pipeteerschema zodat je weet welke extincties horen bij welke monsters.
Typ in B2 de verdunningsfactor voor het onverdunde samples (1 staat voor onverdund).

De monsters in kolom C zijn drie keer verdund ten opzichte van de monsters in kolom B. In kolom D zijn de monsters 3 verdund ten opzichte van de monsters in kolom C etc.

Vul in cel C2 de formule =B2*3.
Kopieer cel C2 en plak de formule in de cellen D2:I2. In Excel kopieer je altijd de formule (als er een formule in een cel staat) en niet de uitkomst van de formule.
Label ook de blanco in K3.

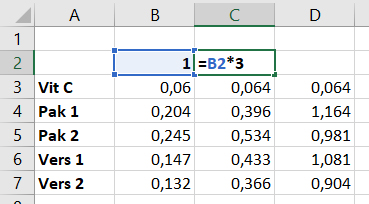
De laatste stap in het organiseren van de data is om de data te transponeren. Dit betekent het omdraaien van de rijen en kolommen.

Selecteer de data zoals aangegeven in de figuur en kopieer de data (ctrl + c).

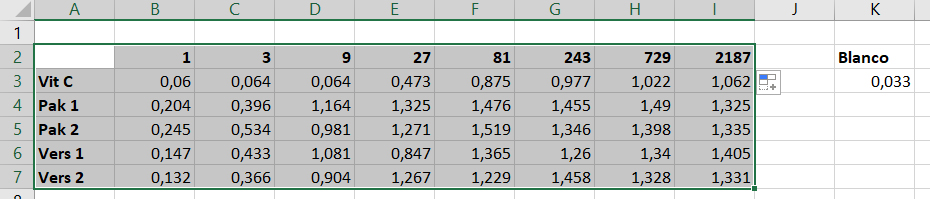
Selecteer met de cursor cel A10.
Druk op de rechter muisknop.
Ga met de muis naar Paste Special (zwarte cirkel)
Je kunt op twee verschillende manier de data getransponeerd plakken: * Transponeer de data door op transpose symbool te klikken (rode cirkel). * OF: Klik weer op Paste Special (oranje cirkel). Nu verschijnt het Paste Special venster. Selecteer Values, None and Transpose zoals hieronder aangegeven en klik op OK.

2.3.4.4 Bewerken van de data

Voordat je begint met de analyse, voeg je nog extra labels toe:

Schrijf in A9 ‘Verduningsfactor’.
Kopieer kolom A9:A18 naar J9:J18. Voeg in kolom K, L en M de labels toe zoals aangegeven in onderstaand figuur.

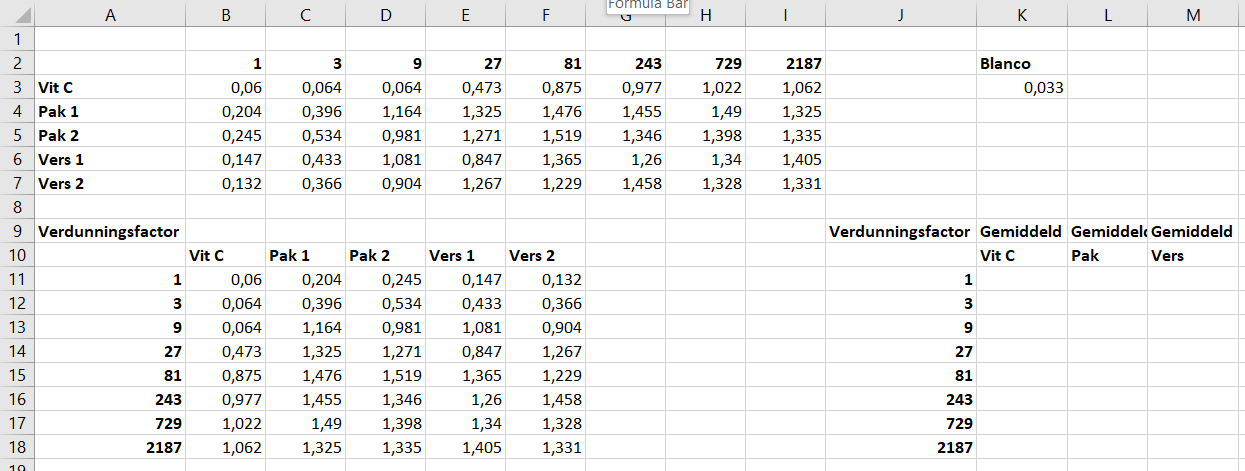
Nu ga je de gemiddelde extinctie per monster uitrekenen in kolom K11:K18, L11:L18 en M11:M18. De extincties van verdunde Vitamine C monsters zijn maar 1 keer gemeten, dus deze waardes kun je direct overnemen uit kolom B.

Typ in cel K11 =B11 en kopieer K11 naar K12:K18.

De extincties van verdunde sinaasappelsap uit pak en verse jus zijn wel in duplo gemeten.

Typ in cel L11 =average(C11:D11) en druk op toets Enter. Kopieer cel L11 naar L12:L18.
Typ in cel M11 =average(E11:F11) en druk op toets Enter. Kopieer cel M11 naar M12:M18.

Vervolgens corrigeer je de gemiddelde meetwaardes voor de blanco meetwaarde. Een blanco meetwaarde is een meetwaarde waarin de reactie NIET heeft plaatsgevonden of waarin de reagentia NIET aanwezig zijn. Dit geeft een achtergrond- of een “baseline” waarde.

Label cellen O9:R18 zoals aangegeven in het onderstaande figuur.
Typ in cel P11 =K11-K3 en druk op de toets Enter.

Kopieer cel P11 naar P12:P18 en naar Q11:R11.
Kijk nu goed naar de waardes waar de blanco van is afgetrokken. Bijvoorbeeld vergelijk K12 met P12. Is de blanco waarde eraf? We zien ook ‘#VALUES’ in cel P17 en P18. Het lijkt alsof alleen P11 gecorrigeerd is voor de blanco. Iets klopt er niet!

We gaan uitzoeken wat er niet goed is gegaan.

Ga naar cel P12 en dubbel klik.

Nu zie je de formule en welke cellen gebruikt zijn voor de formule. De formule is ook zichtbaar in het formulevenster (rode cirkel). Wat valt op? In plaats van =K12-K3 staat er nu =K12-K4. De verwijzing naar de blanco waarde is verschoven van K3 naar K4!

Ga naar cel Q11. Wat valt nu op?

LET OP Als we een formule kopiëren naar beneden/boven, of naar links/rechts dan verschuiven alle cellen waarnaar wordt verwezen ook mee.

De foute formules kun je verbeteren door de verwijzing naar de blanco-waarde in de formules vast te zetten. Dit doe je met een $ teken. De verwijzing naar de blanco-waarde in K3 zet je als volgt vast:

Verwijder alle verkeerde formules.
Ga naar cel P11 en dubbel klik. Je kan ook direct naar het formulevenster gaan en daar je cursor plaatsen.
Plaats een $ teken voor de K om de verwijzing naar kolom K vast te zetten, en plaats het $ teken voor de 3 en druk op de toets Enter.
Kopieer de nieuwe formule in alle cellen van Vit C (P12:P18), Pak (Q11:Q18) en Vers (R11:R18).
Dubbel klik een willekeurige cel in het bereik van P11:R18 en controleer of de formule nu wel goed is.

LET OP Het kan ook voorkomen dat je alleen de verwijzing naar de kolom (in dit voorbeeld $K3) of alleen de rij (K$3) wilt fixeren.

2.3.4.5 Data uitzetten in een grafiek

Je gaat nu de dataset uitzetten in een grafiek.

Voeg een scatter plot in zoals je dat hebt geleerd in de vorige les. Kies nu voor grafiektype Scatter with straight lines and markers.

Voeg de waardes voor Vit C, Pak en Vers in als afzonderlijke series.
Selecteer voor iedere serie de verdunningsfactor als x-waardes en de bijbehorende gecorrigeerde gemiddelde extincties als y-waardes.

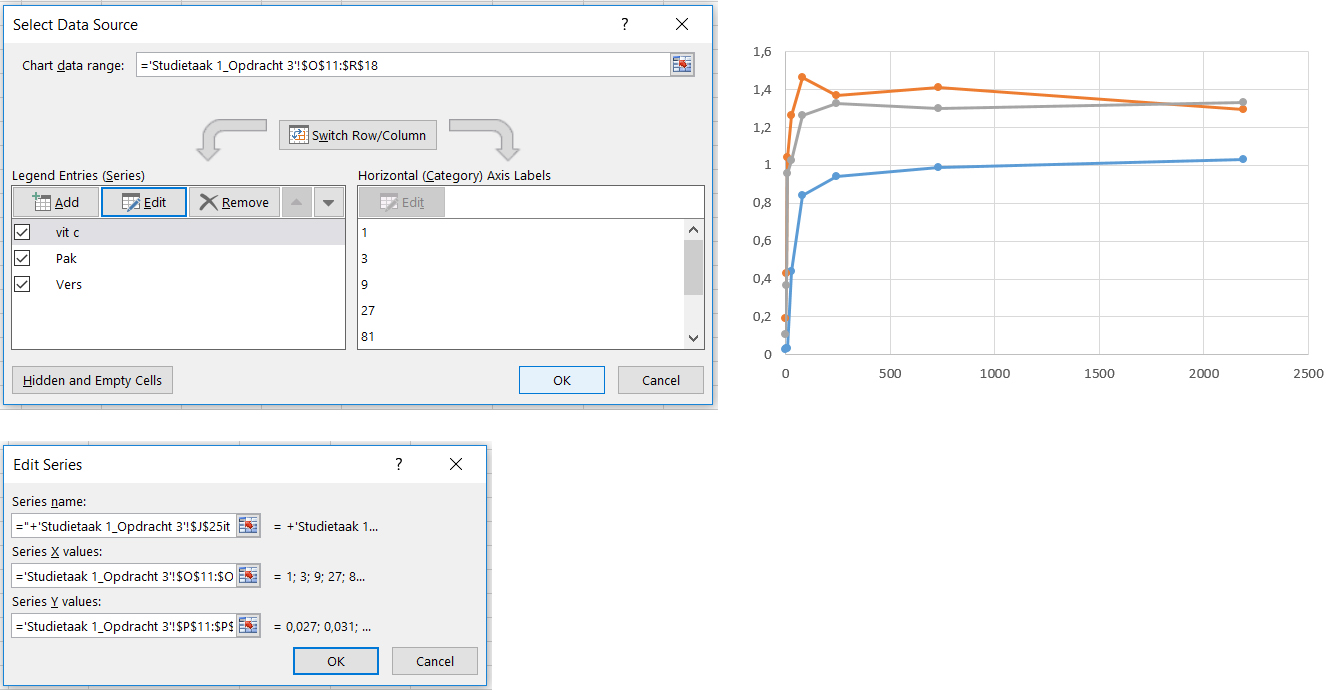
In deze grafiek zijn de meeste datapunten verzameld tussen x-waarden 0 en 100. Waarom zijn de datapunten zo scheef verdeeld? Hoe kunnen we dit corrigeren?

De monsters zijn serieel verdund: In elk van de 7 opeenvolgende verdunningsstappen werd het monster 3 keer verdund. Elke stap op de x-as vertegenwoordigd dus een 3-voudige verdunning t.o.v de vorige stap. De verdeling van de meetpunten op de x-as is niet lineair terwijl de indeling van de x-as dat wel is! Door een logaritmische schaal verdeling te gebruiken op de x-as verdeel je de meetpunten wel gelijk over de x-as.

Dubbel klik op de op de x-as (of een waarde van de x-as). Rechts in je werkblad verschijnt een nieuw panel Format Axis.
Vink de Logaritmic scale optie aan.

De grafiek is nog niet af. Je mist nog duidelijke labels bij de x-as en y-as labels, én een grafiektitel.

Klik op de grafiek en klik op de het groene + teken aan de rechterzijde van de grafiek. Een lijst met Chart Elements verschijnt.
Vink de Axis Titles optie aan. Een x-as en y-as titelvierkant verschijnt. Voeg hier tekst toe.
Vink de Chart Title optie aan. Voeg de grafiektitel toe.
Klik op Legend en rechts op het kleine grijze pijltje. Selecteer de optie Right om de legenda aan de rechterkant te laten verschijnen.

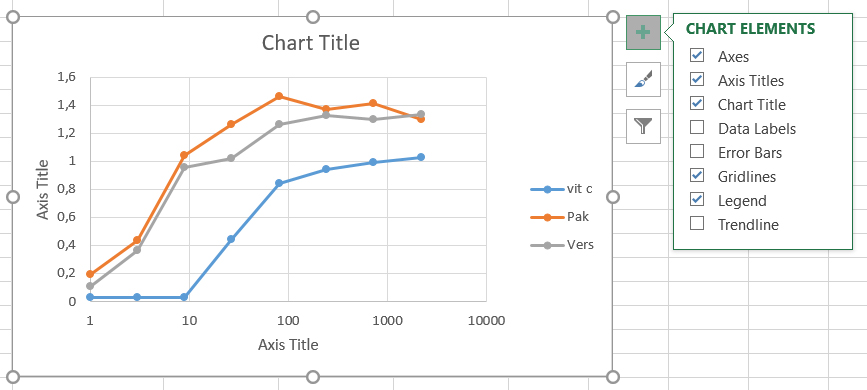
Het is erg belangrijk om een complete grafiek te maken met duidelijke labels. De lezer moet een grafiek kunnen begrijpen zonder extra uitleg of tekst.

In het algemeen, als je een element van een grafiek wilt veranderen, dubbelklik op het element en aan de rechter zijde verschijnt een nieuw venster met allerlei opties. Een alternatieve manier is om het element aan te klikken en vervolgens klik je op de rechtermuisknop. Selecteer een format optie in het popdown menu en rechts verschijnt weer een nieuw venster met allerlei opties.

Exercise 2

Leidt een lage concentratie anti-oxidant tot een hoog of een laag aantal vrije radicalen in de stof DPHH?

Klik hier voor het antwoord

Tot een hoog aantal vrije radicalen.

Exercise 2

Leidt een hoge concentratie anti-oxidant tot een hoog of een laag aantal vrije radicalen in de stof DPHH?

Klik hier voor het antwoord

Tot een laag aantal vrije radicalen.

Exercise 2

Welk monster heeft de hoogste anti-oxidant activiteit?

Klik hier voor het antwoord

Verse sinaasappelsap.

Exercise 2

Waarom zijn de extincties van Vitamine C het laagst?

Klik hier voor het antwoord

Vitamine C is de positieve controle voor de omzetting van DPHH. De hoeveelheid anti-oxidant in de positieve controle is dus hoger.

Exercise 2

Bij welke verdunning van Vitamine C raakt de omzetting van DPHH verzadigd?

Klik hier voor het antwoord

Bij de 10x verdunning.