Les 3 Regressie en correlatie
3.1 Lesinhoud en leerdoelen
Deze les gaat over het beantwoorden van verbandvragen.
In deze les leer je over correlaties en het verschil tussen een causaal en een statistisch verband. Ook leer je wat regressie is. Hierbij maak je kennis met een voorbeeld van regressie, namelijk de ijklijn.
Aan het einde van deze les kan je:
- aangeven wat een correlatiecoëfficiënt is, wat de belangrijkste kenmerken zijn en deze in Excel berekenen;
- het verschil tussen causaal en statistisch verband uitleggen.
- aangeven wat lineaire regressie is en daarmee rekenen;
- het werkingsprincipe van de kleinste kwadraten methode uitleggen en hiermee in Excel rekenen;
- in Excel een regressielijn toevoegen aan een grafiek en deze interpreteren;
- in Excel niet lineaire verbanden lineariseren m.b.v. logaritmische assen;
- aangeven wat de beperkingen en aandachtspunten zijn bij regressie;
3.2 Voorbereiding
In deze les behandelen we twee soorten analyses voor als je een verbandvraag hebt: correlatie-analyse en regressie-analyse. Deze analyses kun je alleen doen met kwantitatieve data.
Correlatie
Als je wilt weten of een variabele samenhangt met een andere variabele, doe je een correlatie-analyse. Bijvoorbeeld als je je afvraagt of er een verband is tussen de hoeveelheid inwoners van een land, en de hoeveelheid medailes die het land haalt op de olympische spelen. Bij een correlatie ga je er niet vanuit dat de ene variabele de andere veroorzaakt. Uit de correlatie-analyse blijkt hoe sterk het verband is tussen de variabelen. Uit een correlatie-analyse blijkt nooit of de ene variabele de andere variabele veroorzaakt. Dus ook al is er een verband, dat betekent niet dat meer inwoners hebben als land, leidt tot meer medailes op de olympische spelen.
Regressie
Als je de uitkomst van een variabele wilt voorspellen op basis van de andere variabele, doe je een regressie-analyse. Je gaat er bij een regressie-analyse dus in beginsel al vanuit dat de ene variabele de andere zou kunnen veroorzaken. Daar is de regressie-analyse op gebouwd. Bijvoorbeeld als je je afvraagt of hamsters die meer eten ook relatief zwaarder worden. Om dat te doen maak je een vergelijking die het beste past op je data. Oftewel: je zet al die hamsters in een grafiek met voedselinname op de x-as en gewicht op de y-as en zoekt de best passende lijn door je datapunten. Met de formule van die lijn kun je vervolgens het gewicht van een willekeurige hamster -ongeveer- voorspellen op basis van zijn/haar voedselinname.
Een voorbeeld van een regressie-analyse is het maken van een ijklijn. De ijklijn zijn we in les 1 al tegengekomen omdat jullie die veel op het lab gebruiken.
3.2.1 Correlatie: Is er een verband tussen X en Y?
(co-relatie: samen-relatie)
Je vraagt je af of er een verband is tussen uren slaap en hoeveelheid gedronken koffie (ml) van docenten. Drinken ze nou sowieso zoveel koffie, of heeft het iets te maken met hoeveel ze slapen?
Je hebt 25 docenten bereid gevonden om een dag bij te houden hoeveel ze geslapen hebben en hoeveel koffie ze dronken in totaal. De data ziet er zo uit:
| Docent | Uren slaap | Koffie_intake (ml) |
|---|---|---|
| docent 1 | 5.8 | 497 |
| docent 2 | 7 | 397 |
| docent 3 | 7.6 | 456 |
| etc … | … | … |
De data kunnen we uitzetten in een grafiek. We kunnen kiezen wat we op de x- en y-as zetten, want bij een correlatie-analyse zijn de twee variabelen allebei afhankelijk. Maar laten we uren slaap op de x-as zetten en koffie op de y-as:
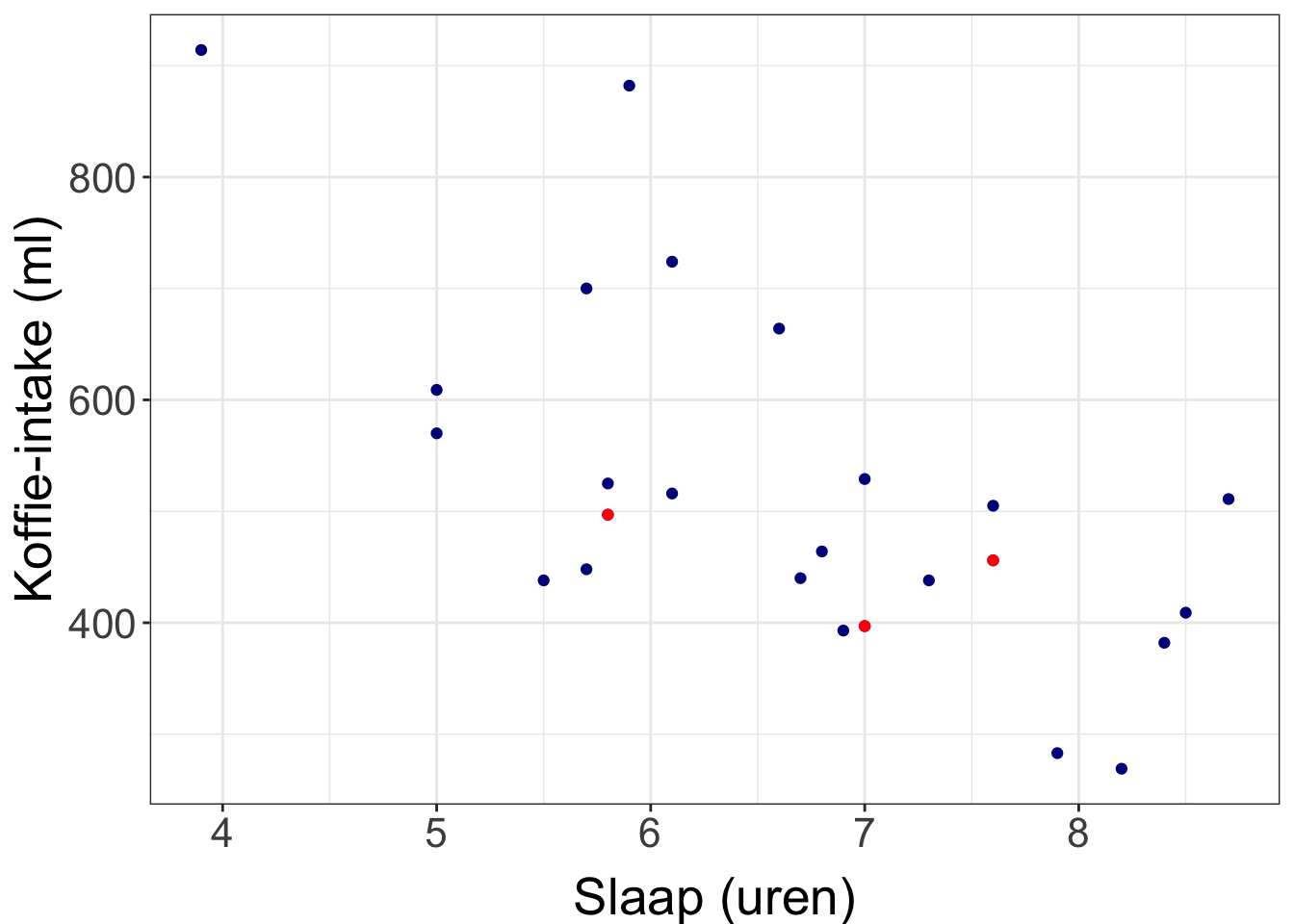
Figure 2.1: Het verband tussen koffie-intake en uren slaap bij docenten. In rood aangegeven zijn de drie docenten die hierboven ook in de tabel te zien zijn. Controleer of je begrijpt waarom die punten op die plek in de grafiek staan.
Elke docent wordt in de grafiek weergegeven als een punt. Als je naar de punten kijkt dan lijkt er inderdaad sprake van een verband tussen de dagelijkse koffieinname en de hoeveelheid slaap.
Dit soort onderzoek naar een verband tussen twee afhankelijke variabelen (in dit geval koffie en slaap) wordt een correlatie-analyse genoemd.
De correlatiecoëfficiënt
We kunnen in de grafiek zien dat docenten die meer slapen vaak minder koffie drinken. Maar hoe sterk is dat verband?
Hoe sterk het verband tussen de variabelen is kunnen we uitdrukken in een getal, de correlatiecoëfficiënt (\(r\)). De formule voor de correlatiecoëfficiënt hoef je niet te kennen, maar is als volgt:
\(r = \frac{\sum_{i=1}^{i=n}{(x_i-\bar{x})(y_i-\bar{y})}}{\sqrt{\sum_{i=1}^{i=n}{(x_i-\bar{x})^2}\sum_{i=1}^{i=n}{(y_i-\bar{y})^2}}}\)
Een correlatiecoëfficiënt heeft een waarde tussen de -1 en de 1 (zie figuur hieronder). Een correlatiecoëfficiënt met een waarde van 0 betekent dat er helemaal geen sprake is van een verband tussen de twee variabelen. Een waarde van 1 of -1 betekent een perfect verband. De correlatiecoëfficiënt van een meting waarbij alle punten exact op een rechte lijn liggen is dus 1 of -1. Dat zou in het voorbeeld betekenen dat alle verschillen tussen docenten in koffie-intake te verklaren zijn door het verschil in slaap. Er zou dan niets anders zijn dat invloed zou hebben op koffie-intake. (Zoals je ziet is dat niet het geval.)
Een correlatie-coefficient vertelt je ook welke richting het verband heeft: Een positieve waarde betekent dat y toeneemt bij een toename van x; een negatieve waarde geeft aan dat y afneemt als x toeneemt.

De correlatie-coefficient geeft je dus twee dingen: hoe sterk is de correlatie en welke richting heeft de correlatie.
Let op: een correlatie-coefficient vertelt je dus niets over hoeveel invloed de hoeveelheid slaap op de hoeveelheid koffie heeft, want hij zegt iets over hoe goed de punten op een lijn liggen, en niet over hoe stijl die lijn is. Een sterke correlatie tussen slaap en koffie, betekent dus niet automatisch dat als de hoeveelheid slaap met tien minuten toeneemt de hoeveelheid koffie veel toeneemt. Alleen dat die met een weinig variabele hoeveelheid toeneemt.
Exercise 3
Kijk naar de grafiek met de data over koffie-intake en slaap bij docenten. Denk je dat dit verband een positieve of negatieve correlatie-coefficient heeft?
Klik hier voor het antwoord
Negatief. Als de hoeveelheid slaap hoger is, is de hoeveelheid koffie lager.Exercise 3
Kijk naar de voorbeeldgrafiekjes hier vlak boven. Hoe groot verwacht je dat de correlatie-coefficient ongeveer is?
Klik hier voor het antwoord
Hij lijkt nog wat minder op een rechte lijn dan het voorbeeld rond de -0.9. Dus een goede schatting zit ergens tussen de -0.5 en -0.75Excel kan dit getal voor je uitrekenen met de CORREL() functie:
Figure 0.1: Correlatie-coefficient berekenen in Excel
Voor het verband tussen koffieinname en hoeveelheid slaap bij docenten vinden we een correlatiecoëfficiënt \(r\) van -0.66. Er is dus sprake van een negatief verband.
Is dat nou veel,-0.66? De interpretatie van de correlatiecoëfficiënt is afhankelijk van het type experiment. Fysische en scheikundige experimenten (zoals de elektrische weerstand in een draad als functie van de lengte van de draad) zijn over het algemeen goed reproduceerbaar en de correlatiecoëfficiënt komt al snel dicht in de buurt van de 1. In een biomedische omgeving heb je te maken met biologische diversiteit en dus spreiding. Om die reden zal een correlatiecoëfficiënt r van 0.91 in een fysisch experiment worden opgevat als ‘onverwacht zwakke correlatie’ , terwijl een \(r\) van 0.91 in een biomedisch experiment vaak erg sterk genoemd wordt.
Exercise 3
Leg uit of je -0.66 een sterk verband vindt gezien het type experiment.
Klik hier voor het antwoord
Tegen de 0.7 is een redelijk sterk verband voor zo’n soort experiment. Er zijn veel andere factoren die invloed hebben op zowel koffie-intake als hoeveelheid slaap. Mensen verschillen sowieso in hoeveel ze slapen en hoeveel koffie ze drinken (biologische variatie).Correlatie versus causaliteit
Wanneer wordt gesproken over een correlatie tussen twee variabelen, zoals tussen de dagelijkse voedselinname en het gewicht, dan wordt bedoeld dat de samenhang tussen de waarden van deze variabelen niet door het toeval verklaard kan worden. Met andere woorden, er is een statistisch verband tussen de variabelen.
Een statistisch verband betekent lang niet altijd dat er ook sprake is van een causaal verband. Een bekend voorbeeld hiervan is dat wanneer er meer ijsjes worden verkocht, het aantal verdrinkingen toeneemt. Er is dus een zeer sterk statistisch verband tussen het aantal verkochte ijsjes en het aantal verdrinkingen. Maar betekent dit dat je door het eten van ijsjes meer kans loopt op verdrinking? Het is veel waarschijnlijker dat het eten van ijsjes en het aantal verdrinkingen beiden het gevolg zijn van hoge buitentemperaturen en er helemaal geen causaal verband bestaat tussen het eten van ijsjes en de kans op verdrinking. Wees bij het beoordelen van data en zeker nieuwsartikelen daarom altijd kritisch over de conclusies die worden getrokken!
3.2.2 Regressie: Hoeveel verandert Y als X verandert?
Nu een ander soort vraag:
Stel je voor dat je gevraagd zou worden om te onderzoeken wat het effect is van verschillen in de dagelijkse voedselinname op het gewicht van hamsters. Wat zou je hypothese zijn? Waarschijnlijk verwacht je dat er inderdaad een verband is tussen de dagelijkse voedselinname en het gewicht van hamsters: hoe meer een hamster eet, hoe zwaarder de hamster zal zijn.
Om het verband te onderzoeken ga je gegevens verzamelen van 36 hamsters gedurende een maand. Elke hamster krijgt een verschillende hoeveelheid eten per dag (elke hamster krijgt een verschillende hoeveelheid, van 1.5 tot 5 gram met verschillen van 0.1 gram per hamster), en aan het eind van het experiment weeg je de hamsters. Je zou dan van tevoren een tabel krijgen die er als volgt uit ziet:
| Hamster | Dagelijkse voedselinname (g) | Gewicht (g) |
|---|---|---|
| hamster 1 | 1.5 | ? |
| hamster 2 | 1.6 | ? |
| hamster 3 | 1.7 | ? |
| … | … | … |
| hamster 35 | 4.9 | ? |
| hamster 36 | 5 | ? |
En na het onderzoek kun je je data invullen:
| Hamster | Dagelijkse voedselinname (g) | Gewicht (g) |
|---|---|---|
| hamster 1 | 1.5 | 20 |
| hamster 2 | 1.6 | 23 |
| hamster 3 | 1.7 | 25 |
| … | … | … |
| hamster 35 | 4.9 | 42 |
| hamster 36 | 5 | 38 |
De data kunnen we uitzetten in een grafiek. In deze grafiek komt de dagelijkse voedselinname op de x-as en het gewicht op de y-as:
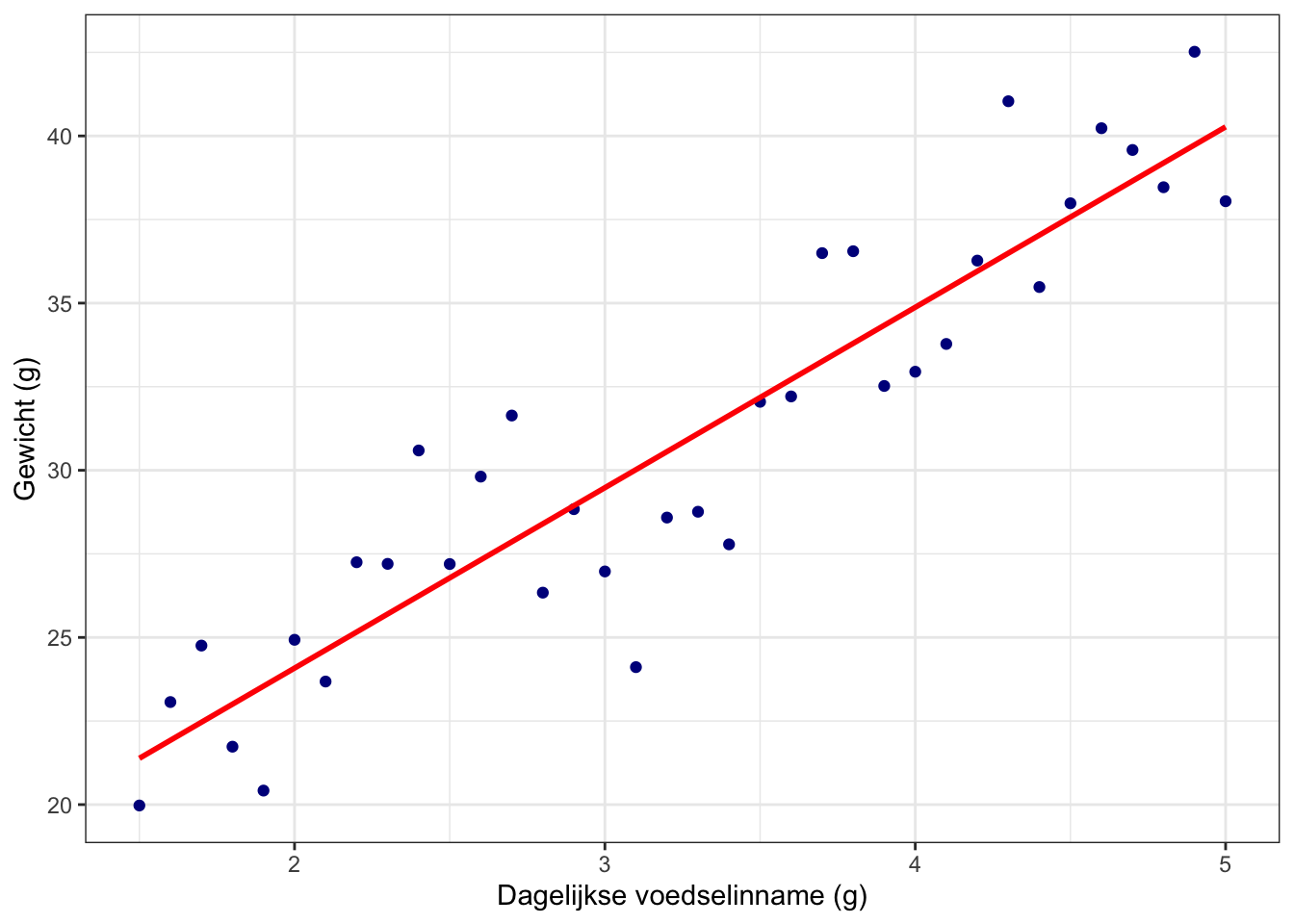
Elke hamster wordt in de grafiek weergegeven als een donkerblauwe punt. Als je naar de punten kijkt dan lijkt er inderdaad sprake van een verband tussen de dagelijkse voedselinname en het gewicht. We kunnen in de grafiek zien dat hamsters die dagelijks meer eten vaak ook zwaarder zijn.
Let op het verschil met de correlatie: de spreiding op de x-as staat nu vast. Die hebben we namelijk zelf zo ingesteld: 1.5 tot 5, met stapjes van 0.1. De spreiding op de y-as lag niet vast, die variabele hebben we gemeten.
Nu gaan we wat anders doen dan bij de correlatie-analyse. We gaan kijken of we een formule aan dit verband kunnen hangen. Met die formule zou je van een willekeurige nieuwe hamster kunnen voorspellen hoe zwaar hij/zij gaat zijn als je weet hoeveel voer hij/zij krijgt.
Het verband kunnen we weergeven door een lijn te trekken door de punten (zie de rode lijn in de grafiek). Zo’n lijn noemen we een regressielijn.
Dit soort onderzoek naar een verband tussen een afhankelijke variabele (in dit geval gewicht) en een of meer onafhankelijke variabalen (in dit geval dagelijkse voedselinname) wordt ook wel regressie analyse genoemd.
De regressielijn
Een regressielijn in een simpele lineaire regressie geldt is een rechte lijn. De vergelijking voor een rechte lijn (lineair verband) is als volgt:
\(y = ax+b\)
In deze formule is \(a\) de richtingscoëfficiënt van de grafiek en \(b\) het snijpunt met de y-as. \(y\) is je afhankelijke variabele (wat je meet: gewicht) en \(x\) is je onafhankelijke variabele (wat je al weet: voedselinname). Voor de regressielijn in het voorbeeld hierboven geldt de volgende formule:
\(y =\) 5.396 \(x +\) 13.29
Hier is \(a\) gelijk aan 5.396. De richtingscoëfficiënt van de regressielijn is dus 5.396. Dat betekent dat als de dagelijkse voedselinname van een hamster met 1 g toeneemt, het gewicht van de hamster 5.396 g toeneemt. Verder zien we dat \(b\) in deze formule gelijk is aan 13.29. Omdat dit het snijpunt met de y-as is, geeft dit getal aan wat het gewicht (= y) zou zijn van een hamster met een dagelijkse voedselinname (= x) van 0 g. Natuurlijk waren er geen hamsters met een dagelijkse voedselinname van 0 g, dus in dit geval heeft \(b\) geen praktische betekenis.
Kleinste kwadratenmethode
Hoe kom je aan die lijn? We hebben een rode lijn in de grafiek hierboven getekend, maar er kunnen meerdere lijnen door deze punten gaan en het is niet meteen duidelijk welke lijn dan de beste is. Om het verband tussen de dagelijkse voedselinname en het gewicht te bepalen, kun je op het oog zo goed mogelijk een rechte lijn door de punten trekken, maar dit is niet erg nauwkeurig. Wanneer je ‘op het oog’ een lijn gaat trekken, proberen we een lijn te trekken waar alle punten zo dicht mogelijk bij liggen; sommige erboven, andere punten eronder. Met behulp van een beetje wiskunde kun je dit veel nauwkeuriger doen.
Het wiskundige equivalent van een rechte lijn trekken waar alle punten zo dicht mogelijk bij liggen wordt lineaire regressie genoemd. De rekenmethode die daarvoor wordt gebruikt heet de kleinste kwadratenmethode. Die methode komt hierop neer: voor een gegeven lijn bereken je de afstanden van alle meetpunten tot de lijn. Je kwadrateert alle afstanden en telt ze op. De beste lijn is de lijn waarbij deze som het kleinst is (zie figuur hieronder voor een grafische weergave van de kleinste kwadratenmethode). Gelukkig kan met behulp van Excel de best passende ijklijn eenvoudig worden vastgesteld (zie ook de Excel opdrachten die bij deze les horen).

Determinatiecoëfficiënt
Hoe goed onze voorspelling voor het gewicht van een nieuwe ongewogen hamster gaat zijn, hangt af van hoe goed die lijn op onze punten past (de x- en y-waarden). Dit wordt uitgedrukt in de determinatiecoëfficiënt (\(R^2\)). En we hebben geluk: in het geval van een lineair verband tussen twee variabelen (dus een rechte lijn), is dat gewoon het kwadraat van de correlatiecoëfficiënt (dus hier geldt: \(R^2 = r^2\)).
\(R^2\) geeft aan welk gedeelte van de variatie in de ene variabele door de andere wordt ‘verklaard’, de “verklaarde variantie”. Dit heeft een waarde tussen 0 en 1, waarbij 0 betekent dat de lijn totaal niet op de meetgegevens past (als we weten hoeveel X is, weten we nog steeds helemaal niets over Y), en 1 betekent dat de lijn de meetgegevens heel erg goed omschrijft (als we weten wat X is, weten we ook precies wat Y is). Dat laatste wil je graag zien bij een regressie analyse. Je kunt aan een determinatiecoëfficiënt alleen niet zien welke richting het verband tussen x en y heeft (zoals je wel kon zien aan de correlatiecoëfficiënt).
Excel rekent de determinatiecoëfficiënt voor je uit als je om een regressielijn vraagt, en je krijgt van Excel dan ook de formule van die lijn (in de vorm \(y = ax + b\)). We gaan dit in het werkcollege doen.
Voor het verband tussen de dagelijkse voedselinname en het gewicht geldt een \(R^2\) van 0.85. De determinatiecoëfficiënt voor dit verband is dus niet erg hoog. De verschillen in voedselinname verklaren dus niet een heel groot deel van de verschillen in gewicht.
3.2.3 Afronden van correlatie- en determinatiecoëfficiënten
Voor het afronden van een correlatiecoëfficiënt of determinatiecoëfficiënt gelden aparte regels. Omdat correlatiecoëfficiënten dichtbij de 1, zoals 0,992332545, met de gebruikelijke afrondregels meestal een waarde van 1 zouden opleveren zou je de (onterechte) conclusie trekken dat je data perfect gecorreleerd zijn. Om te voorkomen dat je informatie kwijtraakt, worden correlatiecoëfficiënten anders dan gebruikelijk afgerond:
Trek de absolute waarde van \(r\) af van 1:
\(r = -0,992332545\)
\(1 - |r| = 1 - |-0,992332545| = 1 - 0,992332545 = 0,007667455\)Rond de verkregen waarde af volgens de gebruikelijke regels (dus op 1 significant cijfer):
\(0,007667455 \approx 0,008\)
Bepaal de afgeronde waarde van \(r\) door de afgeronde waarde van 1 af te trekken (en maak de uitkomst zo nodig weer negatief):
\(-(1 - 0,008)=-0,992\)
Het afronden van de determinatiecoëfficiënt gaat precies hetzelfde.
3.2.4 Lineariseren van niet-lineaire verbanden
In het voorgaande deel is lineaire regressie besproken. Maar wat moet je nu doen als die lijn niet recht is? Vaak kun je met behulp van een wiskundige truc de data zodanig bewerken dat er weer een rechtlijnig verband ontstaat. Dit wordt lineariseren genoemd. Wanneer die aanpak ook niet werkt, maar je weet wel wat het onderliggende verband is tussen de ingestelde en gemeten variabele (de x en y), dan kun je je toevlucht nemen tot Excel dat de beste passende lijn en de bijbehorende formule door de gegeven punten bepaalt. In de natuur en techniek hebben we regelmatig te maken met een verband dat niet lineair is. We onderscheiden verschillende niet-lineaire verbanden:
- Exponentiële functies: voor een exponentiële functie geldt de formule \(y = a\cdot10^{bx}\). Een voorbeeld van een exponentieel verband is de groei van bacteriën en cellen. Bacteriën en cellen groeien exponentieel, ofwel, hun aantal neemt exponentieel toe in de tijd.
- Machtsfuncties: voor machtsfuncties geldt de formule \(y = a\cdot x^b\). Voor de afstand die een vallend voorwerp vanuit stilstand en zonder wrijving aflegt verloopt volgens een machtsfunctie, namelijk \(y(t) = a\cdot t^2\).
- Logaritmische functie: voor een logaritmische functie geldt de formule \(y = a\cdot log(bx)\). Een voorbeeld van een logaritmisch verband is het verband tussen de concentratie van een oplossing en de intensiteit van het doorgelaten licht. De samenstelling van een vloeistof wordt vaak met licht gemeten, denk aan het bepalen van de concentratie glucose. Bepaalde kleuren licht worden dan geabsorbeerd. Door de intensiteit van het doorgelaten licht te meten is het mogelijk iets te zeggen over de soort en de concentratie van de stoffen in de vloeistof. De logaritme van deze intensiteit blijkt evenredig te zijn aan de concentratie.
Kijk hier een kennisclip over het lineariseren van verbanden:
De verschillende niet-lineaire verbanden kun je als volgt lineariseren:
- Exponentiële functies zijn te lineariseren door x tegen y uit te zetten op een enkel-logaritmische schaal met logaritmische y-as:
- Machtsfunties zijn te lineariseren door x tegen y uit te zetten op een dubbel-logaritmische schaal:
- Logaritmische functies zijn te lineariseren door x tegen y uit te zetten op een enkel-logaritmische schaal met logaritmische x-as:
Als dat allemaal niet werkt, zou de computer natuurlijk ook de best passende kromme lijn in plaats van een rechte lijn kunnen gaan zoeken. Dat behandelen we niet in deze cursus, maar heet -zoals je zou verwachten- een nonlineaire regressie.
3.2.5 Beperkingen van regressie
De computer is erg goed in lijnen berekenen (recht of krom) maar kan niet voor jou nadenken. Je moet je daarom altijd afvragen wat het antwoord is op de volgende vragen:
- Is de juiste formule gekozen, d.w.z. is het onderliggende verband ook echt een rechte lijn/ logaritme/wortelfunctie/etc.?
- Geldt die formule voor alle \(x\) waarden?
- Is de gekozen \(x\) ook de enige onafhankelijke variabele?
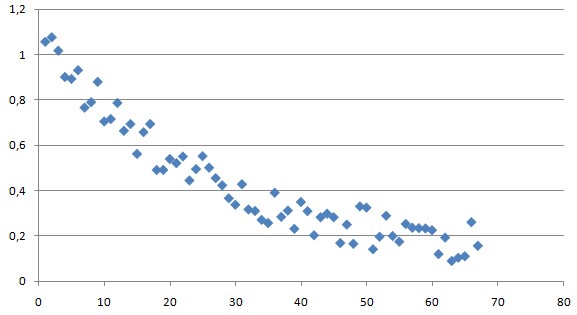
De beste manier om bovenstaande vragen te beantwoorden is door goed naar de data te kijken: in een plaatje zie je vaak al in één oogopslag wat er aan de hand is. Zo kun je in onderstaand plaatje al herkennen dat het verband krom loopt; een rechte lijn is hier waarschijnlijk niet de beste keuze.
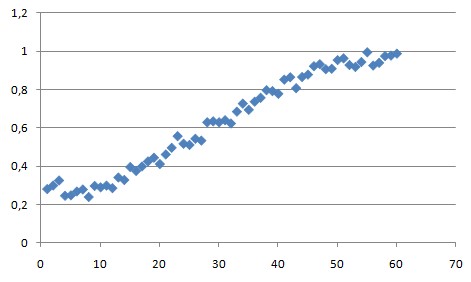
De tweede vraag is lastiger. Geldt het verband ook bij álle gemeten waarden? In onderstaande figuur lijkt een rechte lijn de beste oplossing. Maar als je goed kijkt, dan zie je dat de lijn eigenlijk een flauwe S-vorm heeft; voor \(x < 10\) en \(x > 50\) lijkt het verband ‘platter’. In dat geval is het wellicht beter om metingen behorend bij \(x < 10\) en \(x > 50\) weg te laten. Dat mag uiteraard alleen maar als je daar een goede reden voor hebt en die ook vermeldt in je verslag. Als het onderstaand plaatje een gemeten extinctie zou zijn, dan vertonen de meetwaarden van zeer lage en zeer hoge concentraties afwijkingen ten opzichte van het ideaal voorspelde (lineaire) gedrag vanwege beperkingen van de meetmethoden. Er is namelijk vaak sprak van een ondergrens voor detectie (door beperkte gevoeligheid van de meetapparatuur) en een bovengrens voor detectie (door verzadiging).
Ook de derde vraag kan lastig te beantwoorden zijn. Het kan zijn dat er een andere, verborgen variabele, ook een rol speelt. Dergelijke verborgen variabelen kunnen regressie misleidend maken. Zie de onderstaande figuur waarbij er twee groepen blijken te zijn die je niet op één hoop kunt gooien.
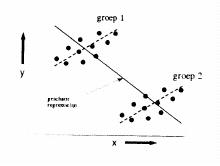
Zie ook de video met uitleg hier:
3.2.6 Een voorbeeld van de regressielijn: de ijklijn
In veel vaardighedenlessen en projecten op school, én in je latere werk op het laboratorium zal je te maken krijgen met het maken en interpreteren van ijklijnen. Ijklijnen zijn regressielijnen (elke ijklijn is een regressielijn, maar niet elke regressielijn is een ijklijn). We kunnen de bovenstaande theorie voor regressielijnen dus toepassen op ijklijnen.
Bekijk hier de uitleg over ijklijnen:
Maar er zijn beperkingen! Een ijklijn is gewoon een voorbeeld van een regressie-analyse, en zoals we hierboven al zagen moet je dus opletten dat je bij het vinden van een goed passende rechte lijn, het lineaire stuk van je data gebruikt. Bekijk hier nog wat extra uitleg:
Laten we eens kijken naar een voorbeeld. Tijdens vaardighedenles 4 in deze periode krijg je de opdracht om de concentratie glucose in verschillende monsters te bepalen. Met behulp van de “Glucose GOD-PAP” methode kleurt de aanwezige glucose rood. De intensiteit van de rode kleuring meet je vervolgens met behulp van een spectrofotometer. Echter, aan de hand van de gemeten extinctie kan je niet zomaar de glucose concentratie bepalen. Om de onbekende glucose concentratie in een oplossing (bijv. bloed) te berekenen aan de hand van de gemeten extinctie, zal je eerst het verband tussen de hoeveelheid glucose en de extinctie moeten vaststellen. Dit kun je doen door van bekende concentraties glucose de extinctie te meten en dit uit te zetten in een grafiek. De regressielijn die door deze punten wordt getrokken noemen we de ijklijn. In een ijklijn worden de gemeten waarden, in dit geval extincties, altijd uitgezet op de y-as, en de bekende concentraties, in dit geval glucose, op de x-as (zie het onderstaande figuur).
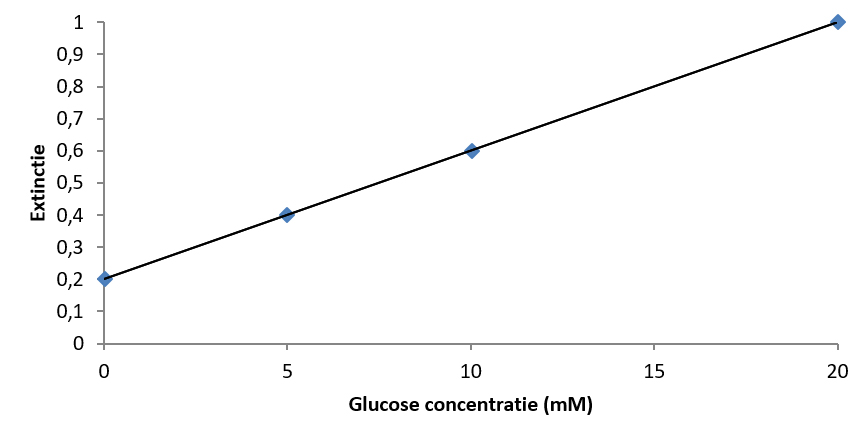
In Excel kun je eenvoudig de vergelijking van de ijklijn bepalen. In dit geval is de vergelijking van de ijklijn:
\(y=0,042x+0,21\)
Met deze vergelijking kun je de concentratie van een onbekend monster bepalen. In dat geval meet je \(y\) en wil je \(x\) met de vergelijking bepalen. We moeten daarvoor de vergelijking omschrijven:
\(x = \frac{y - 0,21}{0,042}\)
Wanneer je bijvoorbeeld voor een onbekende oplossing een extinctie meet van \(0,63\) dan bereken je de bijbehorende glucose concentratie als volgt:
\(x = \frac{0,63 - 0,21}{0,042} = 9,523 mM \approx 9,6 mM\)
Bij het maken van een ijklijn streef je naar een zo betrouwbaar mogelijke manier om met de formule van de ijklijn \(x\) te berekenen als je \(y\) hebt gemeten of andersom. Een ijklijn wordt als voldoende betrouwbaar beschouwd als de determinatiecoëfficiënt \(R^2 > 0,99\). Deze regel geldt alleen voor ijklijnen! Niet voor alle regressie-analyses.
ijklijn
- Een ijklijn is een voorbeeld van een lineaire regressie-analyse, en heeft een formule in de vorm \(y=ax+b\)
- A geeft de richtingscoefficient aan van de lijn
- B geeft de asafsnede aan van de lijn (de waarde van \(y\) op het punt \(x=0\))
- Je middelt eerst je herhaalde metingen (bijv. als je elke concentratie in triplo hebt gemeten), en vraagt dan aan excel om een ijklijn te berekenen.1
- Een ijklijn trek je door het lineaire gebied van de meetpunten. Dus als er bij hoge concentraties verzadiging optreedt en je ziet dat een denkbeeldige lijn door alle punten af zo gaan buigen, dan laat je die hoogste meetwaarde(n) weg.
- Errorbars hoeven niet, mogen wel. Als je metingen te beroerd zijn om een ijklijn van te bouwen dan zie je dat ook aan je \(R^2\).
- Pas op: je mag niet zomaar meetpunten weggooien omdat de \(R^2\) niet hoog genoeg is. Dat mag alleen als die meetpunten niet in het lineare gebied vallen.
- Je kunt de ijklijn alleen gebruiken om y-waarden om te rekenen naar x-waarden als die y-waarden binnen de ijklijn vallen. Dus als bijvoorbeeld de extinctie van een meting hoger is dan de hoogste extinctie die je mee hebt genomen bij het berekenen van de ijklijn, dan kun je daar geen concentratie voor berekenen.
3.3 Werkcollege
3.3.1 Deel 1 - Toepassen van de kleinste kwadratenmethode
Macrofagen zijn witte bloedcellen die bacteriën fagocyteren. Na aanraking met een bacterie wordt een macrofaag geactiveerd; er worden allerlei eiwitten tot expressie gebracht die ervoor zorgen dat de bacterie onschadelijk gemaakt wordt. Activatie van macrofagen gebeurt door componenten in de bacteriewand die binden aan bepaalde receptoren op het membraan van de macrofaag. Een van die componenten is LPS. In de onderstaande grafiek is het verband aangegeven tussen de LPS concentratie in het groeimedium van een macrofaag cellijn en de expressie van een eiwit (NOS2). De LPS concentratie hebben we zelf bepaald. Dit is dus een voorbeeld van een regressie-analyse.
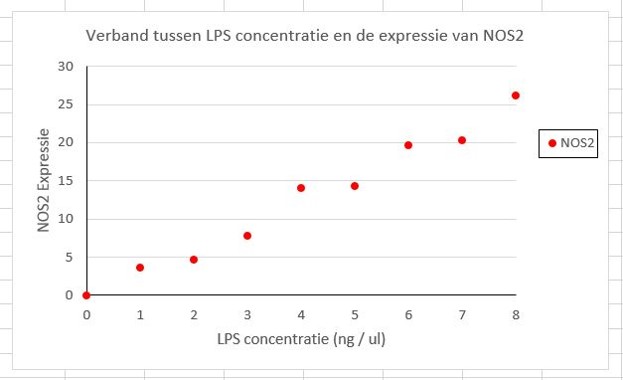
We willen weten of er een lineair verband is tussen de LPS concentratie en expressie van NOS2 d.m.v. een regressielijn. Door deze datapunten kunnen we in theorie oneindig veel regressielijnen trekken. Maar welke is nu de beste? In de onderstaande figuur zijn twee willekeurige regressielijnen getrokken. Met behulp van de kleinste kwadratenmethode gaan we in Excel uitrekenen welke van deze twee lijnen het beste “past” binnen de meetwaardes.

Voor deel 1 van dit werkcollege dien je het bestand KleinsteKwadratenMethode.xlsx te openen. Het bestand ziet er als volgt uit:
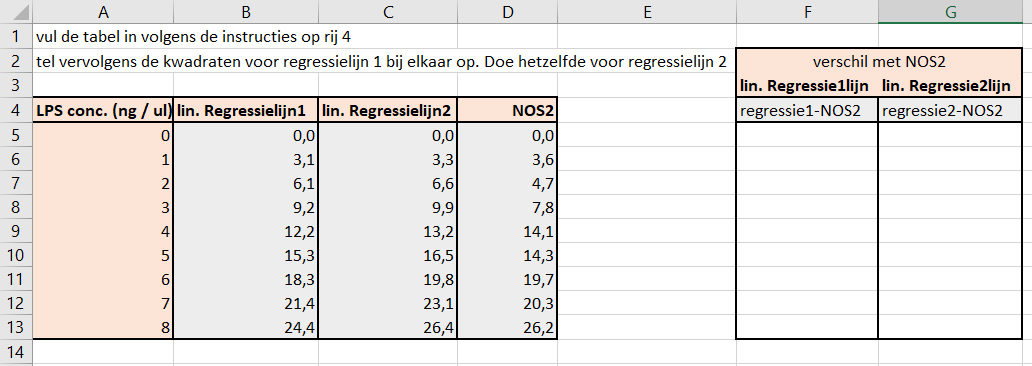
Bereken in Excel de kleinste kwadraat van regressielijn 1 & 2. Beantwoord daarna de volgende vragen.
Exercise 3
Wat is de som van de kwadraten van de verschillen tussen regressielijn 1 en de NOS2 meetwaarden?
Klik hier voor het antwoord
\(14,90\)Exercise 3
Wat is de som van de kwadraten van de verschillen tussen regressielijn 2 en de NOS2 meetwaarden?
Klik hier voor het antwoord
\(21,65\)Exercise 3
Wat is de beste regressielijn gebaseerd op deze methode?
Klik hier voor het antwoord
Regressielijn 1, want de som is voor deze lijn het kleinste.3.3.2 Deel 2 - Ijklijn voor Lowry methode
Doe mee met alle stappen!
We willen de hoeveelheid eiwit meten in spiercellen m.b.v. van de Lowry methode.
We maken eerst een ijklijn m.b.v. de extincties van een bekende eiwitconcentraties (BSA) in μg/μl. Het monster met alleen maar de reagens is de blanco. Dit monster geeft ook een meetwaarde in de spectrofotometer (zie figuur hieronder). De ijklijn moet gecorrigeerd worden voor deze achtergrondwaarde, door van alle meetwaardes de gemiddelde waarde van de blanco’s af te trekken. De extinctie van het monster van de spiercellen wordt gemeten en m.b.v. de ijklijn kunnen we terugrekenen hoeveel eiwit er in het monster aanwezig is.
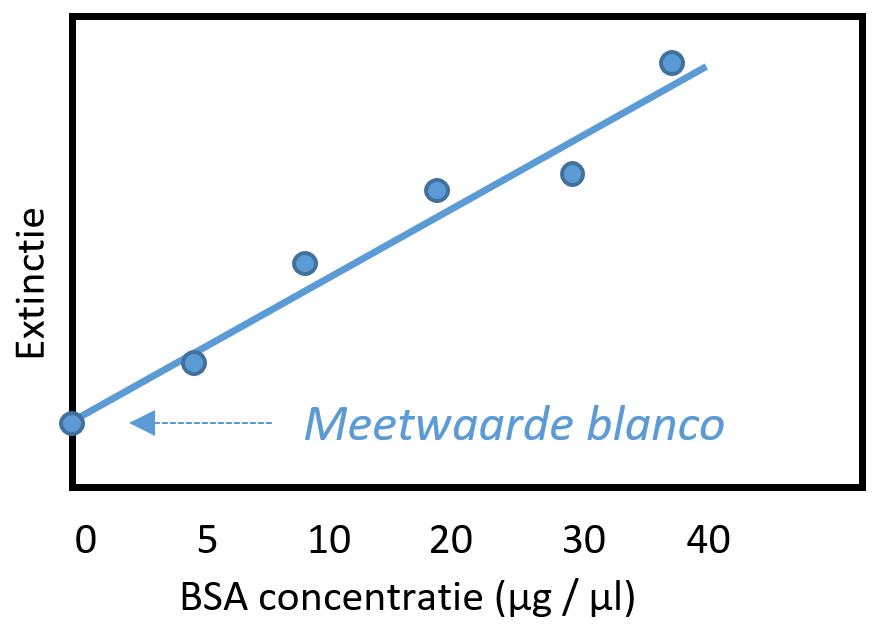
Voor dit deel van het werkcollege heb je de file IjklijnLowry.txt nodig. Deze zat niet in de zip die je gedownload hebt, hier is hij voor de
voltijd en
deeltijd.
- importeer de data in Excel
- Voeg de headers toe zoals aangegeven in de figuur hieronder:
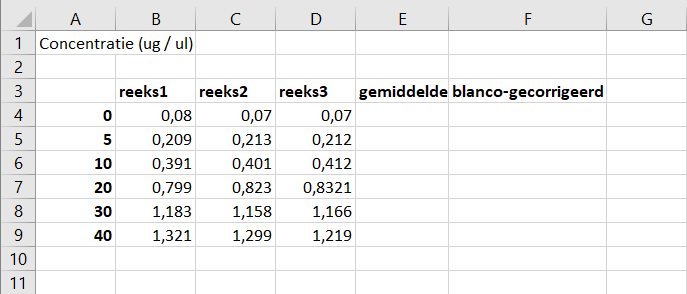
- welke header mist? Voeg die ook toe.
Klik hier voor het antwoord
concentratie BSA in μg/μl- Bereken het gemiddelde van iedere concentratie.
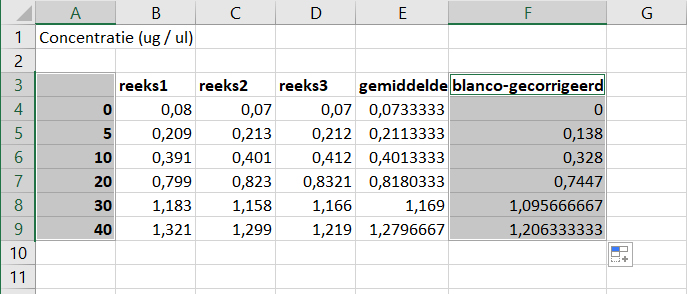
- Corrigeer de meetwaardes door de blanco meetwaarde er af te halen.

We gaan de gecorrigeerde extincties nu uitzetten tegen de concentraties BSA.
- Selecteer
A3:A9enF3:F9. (Selecteer eerstA3:A9, daarna houd je de “ctrl” toets ingedrukt terwijl jeF3:F9selecteert).
- Klik op de
INSERTtab en selecteer deScatter plotonder deChartsoptie. Kies deScatter with smooth lines. (note: dat is eigenlijk de verkeerde grafiek. Maar je kan zo goed het antwoord op de volgende vraag zien.)

Klik op het plus-teken naast de grafiek en maak een complete grafiek met 1) X en Y-as labels, 2) een geschikte titel en 3) een legenda:

Exercise 3
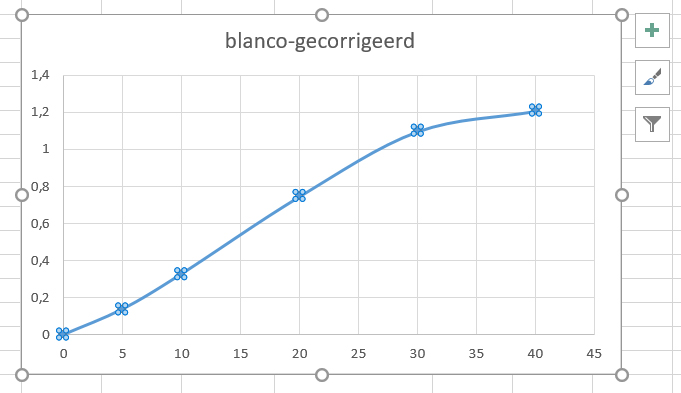
Wat valt je op als je naar het verloop van de grafiek ten opzichte van de datapunten kijkt?
Klik hier voor het antwoord
De extinctie bij 40 ug/ul BSA ligt buiten het lineaire deel van de ijklijn.We gaan de ‘smooth line’ veranderen in een ‘scatter plot’. Dat is de goede grafiek voor een ijklijn, en nu leer je meteen om het grafiektype te veranderen.
- Selecteer de grafiek en klik op de lijn van de grafiek.
- Klik op de rechtermuis knop en klik op
Change Chart Type....
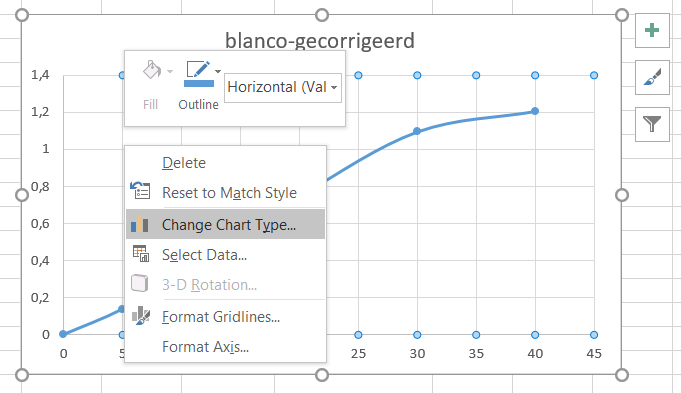
- Klik op de
X Y (Scatter)optie enOK.
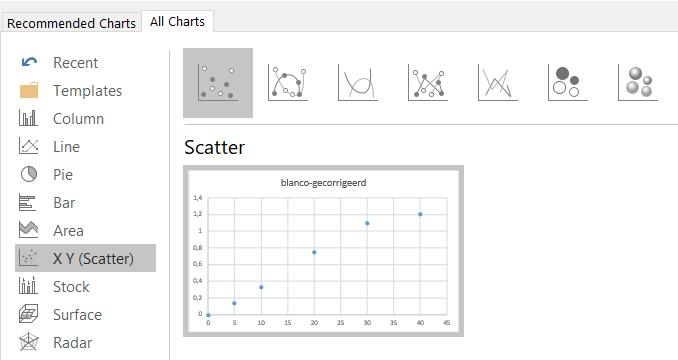
Let op: die smooth line kan dus handig zijn om te zien of je data wel lineair is, maar haal hem altijd weer weg. Hij hoort niet thuis in je uiteindelijke ijklijn-grafiekje.
We gaan nu een (lineaire) regressielijn toevoegen aan de grafiek. Excel trekt oneindig veel regressielijnen door de datapunten en berekent de kleinste kwadraat. De regressielijn met het kleinste kwadraat wordt de regressielijn.
- Laat dat datapunt bij de hoogste concentratie nog gewoon even staan.
- Klik op het plusje naast de grafiek.
- Voeg een regressielijn (
Trendlinein Excel) toe en ga naarMore Options....
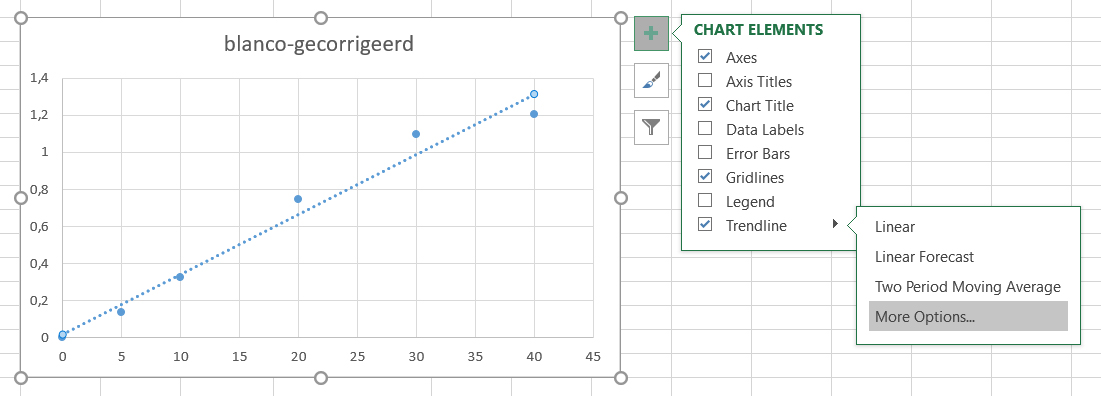
- Selecteer de opties zoals aangegeven in de figuur hieronder:

Exercise 3
Wat is de vergelijking van de regressielijn?
Klik hier voor het antwoord
\(y = 0,0324x + 0,0179\)Exercise 3
Wat is de waarde van de determinatiecoëfficiënt (\(R^2\)) zoals deze door Excel wordt gegeven?
Klik hier voor het antwoord
\(R^2 = 0,9756\)Hierboven hebben we gezien dat de ijklijn verzadigt: de hoge meetwaardes vallen niet meer in het lineaire deel van de grafiek.
- Verwijder nu de hoogste meetwaarde (extinctie bij 40 μg/μl BSA), waarvan we al gezien hadden dat hij buiten het lineaire gebied valt.
- Maak een nieuwe grafiek en voeg een regressielijn toe.
Exercise 3
Wat is de vergelijking van de regressielijn?
Klik hier voor het antwoord
\(y = 0,0375x - 0,0263\)Exercise 3
Wat is de waarde voor determinatiecoëfficiënt (\(R^2\)) zoals deze door Excel gegeven wordt?
Klik hier voor het antwoord
\(R^2 = 0,9974\)Exercise 3
Ben je als onderzoeker tevreden over de waarde van \(R^2\) voor deze ijklijn?
Klik hier voor het antwoord
Ja, want \(R^2 > 0,99\).Een goede \(R^2\) waarde voor een ijklijn is 0,99 of hoger. (Dat geldt niet voor alle regressie-analyses, wel voor ijklijnen)
Exercise 3
Monster 1 heeft een extinctie van 0,64. Bereken de eiwitconcentratie in monster 1 met behulp van de vergelijking van de regressielijn. Wat is de eiwitconcentratie in monster 1?
Klik hier voor het antwoord
18 μg/μl
y=ax+b
a = 0,0375
b = -0,0263 (let op de min)
y = 0,64
x = (y-b)/a = (0,64 - - 0,0263) / 0,0375 = 18 μg/μl
Exercise 3
Monster 2 heeft een extinctie van 1,25. Wat is de eiwitconcentratie in monster 2?
Klik hier voor het antwoord
Dat is niet te bepalen, omdat dit punt buiten het lineaire bereik van de ijklijn ligt.3.3.3 Deel 3 - Ijklijn voor zetmeelmeting
Om in een aantal monsters de zetmeelconcentratie te kunnen bepalen, zijn van bekende concentraties zetmeel de extincties gemeten. Met behulp van de gevonden waarden kan een ijklijn worden opgesteld.
Voor dit deel van het werkcollege dien je het bestand IjklijnZetmeel.xlsx te openen. Dit bestand bevat de metingen voor de ijklijn.
- Maak een scatterplot en voeg een regressielijn toe. Denk hierbij aan de voorwaarden voor een goede ijklijn die je geleerd hebt bij deel 2 van het werkcollege.
- Maak de grafiek netjes af met titel, astitels en eventueel legenda.
Exercise 3
Wat is de vergelijking van de regressielijn?
Klik hier voor het antwoord
\(y = 0,0064x + 0,0394\)
Let op! In dit geval moet je de hoogste 3 meetwaardes weglaten, omdat deze buiten het lineaire gebied van de ijklijn vallen. Laat de regressielijn nooit kunstmatig door (0,0) lopen, want dat maakt de ijklijn minder betrouwbaar (dat is een knopje in Excel. niet aanklikken dus). Het datapunt (0,0) neem je wel gewoon mee (de blanko-gecorrigeerde blankometing is natuurlijk sowieso nul), gooi die niet weg.Exercise 3
Wat is de zetmeelconcentratie van een monster met extinctie 0,6?
Klik hier voor het antwoord
88 mg/LExercise 3
Wat is de zetmeelconcentratie van een monster met extinctie 1,8?
Klik hier voor het antwoord
Dat is niet te bepalen, omdat dit punt buiten het lineaire bereik van de ijklijn ligt.3.3.4 Deel 4 - afronden
Exercise 3
Stel, je maakt een ijklijn en vindt een \(R^2 = 0,99754\)
Noteer deze \(R^2\) correct afgerond.
Klik hier voor het antwoord
\(R^2 = 0,998\)3.3.5 Deel 5 - Lineariseren van verbanden (1)
Vaak is een verband tussen twee variabelen niet lineair. Een voorbeeld is de groei van bacteriën. Tijdens het vermenigvuldigen van Escherichia coli bacteriën in kweekmedium volgt het aantal bacteriën de volgende formule met \(t\) de tijd in uren:
\(N(t) = 300 \cdot e^{2,08t}\)
Exercise 3
Wat voor functie is dit?
Klik hier voor het antwoord
Een exponentiële functie.We gaan nu in Excel een grafiek maken die de groei van het aantal bacteriën weergeeft in de tijd van 0 tot 4 uur (met stapjes van 0,5 uur) volgens onderstaande stappen:
- Open een (nieuwe) Excel werkblad en schrijf “tijd” in
A1en voeg 0 toe in celA3en 0,5 inA4. - Selecteer
A3:A4en ga met je cursor op het kleine groene vierkantje staan totdat er een plusje verschijnt. - Klik continue op de linkermuisknop en sleep de cursor naar beneden tot
A11(Excel vult nu automatisch de cellen in met stapjes van 0,5).

Met de functie \(N(t) = 300 \cdot e^{2,08t}\) kunnen we op een gewenst tijdstip de hoeveelheid bacteriën berekenen. Het invullen van formules in Excel kan soms lastig zijn als de formule uit meerdere componenten bestaat. In dit geval zijn er 3 componenten. De constante (\(300\)) en de vermenigvuldiging (\(2,08\cdot t\)) zijn makkelijk in te voeren in Excel. Maar hoe rekenen we met de exponent? Excel heeft honderden ingebouwde functies, waaronder ook de EXP() functie.
- Schrijf de formule om het aantal bacterien op tijdstip 0 te berekenen in
B3(zorg ervoor dat je voor \(t\) verwijst naarA3). - Kopieer de formule voor de andere tijdspunten.
- Maak een grafiek van de data.

Exercise 3
Voor een proef heb je 10.000 bacteriën nodig. Probeer uit de grafiek af te lezen na hoeveel tijd er 10.000 bacteriën zijn. Na hoeveel uur is dit het geval?
Klik hier voor het antwoord
Dat is in deze grafiek niet af te lezen.- Maak het verband lineair door de y-as logaritmisch te maken. Dit doe je achtereenvolgens met de rechtermuisknop op de y-as te klikken en vervolgens de optie
Format Axiste selecteren.
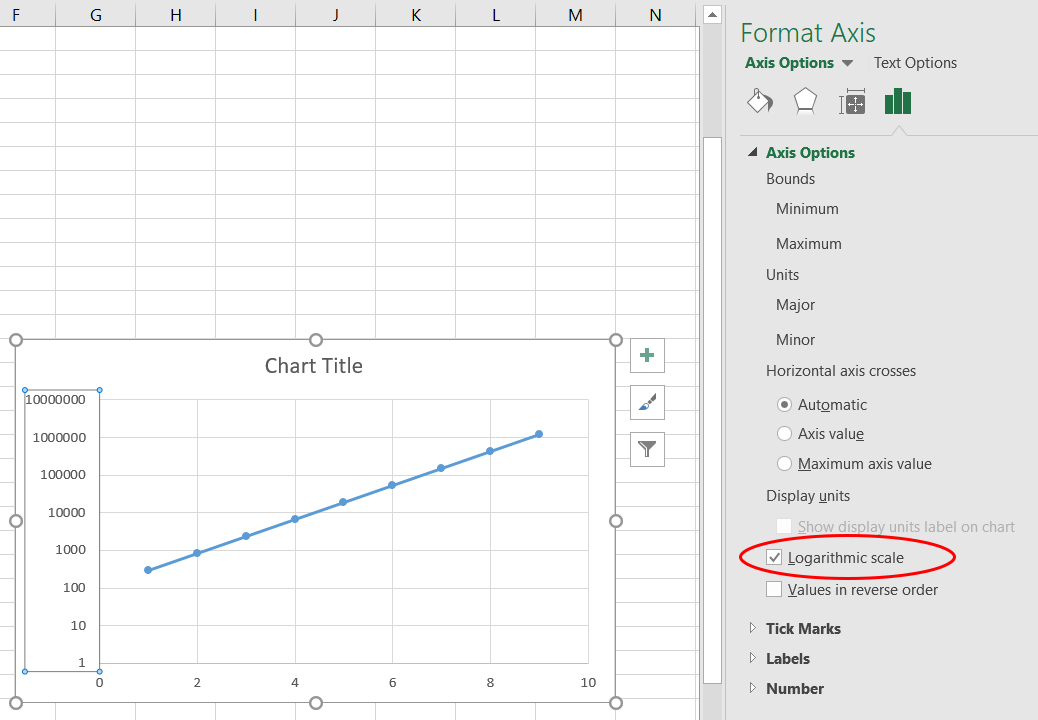
Exercise 3
Lees uit de grafiek af na hoeveel tijd er 10.000 bacteriën zijn. Na hoeveel uur is dit het geval?
Klik hier voor het antwoord
Na 1.75 uur (= 1 uur en 45 minuten).3.3.6 Deel 6 - Lineariseren van verbanden (2)
We gaan nu kijken naar 3 machtsfuncties:
\(f(x) = x^2\)
\(g(x) = x^3\)
\(h(x) = x^{0,5}\)
- Open een nieuw werkblad in Excel.
- Vul een kolom met de getallen 1 t/m 15 (dit zijn de x waardes).
- Bereken \(f(x)\), \(g(x)\) en \(h(x)\). Gebruik de functie
=POWER(in het Nederlands=Macht). - Maak een grafiek (scatter plot with smooth lines) van de gegeven functies.
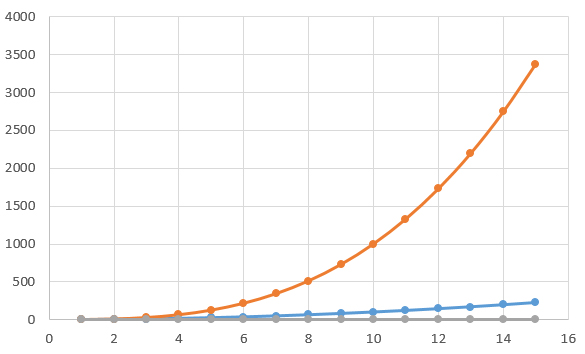
Exercise 3
Hoe maak lineariseer je machtsfuncties?
Klik hier voor het antwoord
Door zowel de x-waarden als de y-waarden op een logaritmische schaal uit te zetten.- Lineariseer de grafiek.
- Voeg major en minor rasterlijnen (gridlines) toe aan je grafiek. Selecteer de grafiek en druk op het groene + rechtsbovenaan.
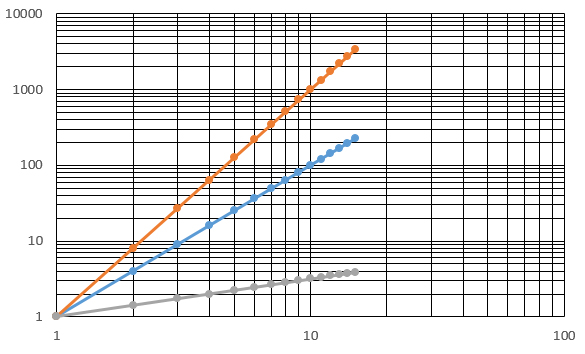
3.3.7 Deel 7 - Lineariseren van verbanden (3)
In een lab staan 10 oplossingen met verschillende HCl oplossingen waarvan de Molariteit (M) is gegeven. De waarden staan in het bestand LineariserenVanVerbanden3.txt.
- Importeer dit bestand in Excel.

We gaan nu de pH uitrekenen met de volgende formule \(pH=−log_{10}[H^+]\).
- Bereken voor iedere concentratie HCl (= H+) de pH. De formule voor een logaritme is ‘log’. Typ
=login een cel en de verschillende log functies verschijnen. Kies de juiste en vergeet het –teken niet toe te voegen!
Exercise 3
Wat is de pH van oplossing 4?
Klik hier voor het antwoord
8,3- Maak nu een grafiek (scatterplots with smooth lines) van de H+ (x-as) en de pH (y-as).
Exercise 3
Welke as(sen) moet je logaritmisch maken om de grafiek te lineariseren?
Klik hier voor het antwoord
De x-as moet logaritmisch worden gemaakt.Exercise 3
Lineariseer de grafiek. Lees af uit de grafiek hoeveel H+ er aanwezig is in een oplossing met pH 6?
Klik hier voor het antwoord
\(1\cdot 10^{-6} M\)3.3.8 Deel 8: correlatie tentamencijfers
In schooljaar 2020/2021 werd de hele cursus online gegeven. Dat heeft veel nadelen, maar ook voordelen: je kunt een boel data verzamelen. Een van jullie docenten vroeg zich bijvoorbeeld af of er een verband is tussen hoe vaak mensen iets in de chat zetten, en hun behaalde cijfer op het tentamen.
De data ziet er ongeveer zo uit:
| Student | Aantal chatberichten | Cijfer |
|---|---|---|
| student 1 | 2 | 2.6 |
| student 2 | 30 | 7.3 |
| student 3 | 14 | 6.2 |
| etc … | … | … |
Open correlatie_cijfers.xlsx. Maak een grafiek en bereken de correlatie-coefficient.
Exercise 3
Wat is de correlatie-coefficient?
Klik hier voor het antwoord
0.155811, dus correct afgerond 0.2
Let op dat de correlatie-coefficient niet die \(R^2\) is die Excel voor je in het grafiekje kan zetten, maar gebruik CORREL().
Let ook op dat je een scatterplot hebt gemaakt met:
- een titel
- astitels
Exercise 3
Is er een verband tussen het aantal chatberichten van een student en het tentamencijfer?
Klik hier voor het antwoord
0.2 is nogal laag. Er lijkt niet echt een verband te zijn tussen het aantal chatberichten en het tentamencijfer van studenten.
3.3.9 Deel 9 - Extra vragen over de lesstof
Exercise 3
Wanneer de verkoop van warme chocomel wordt uitgezet tegen het aantal mensen dat op slippers loopt, wordt een verband gevonden met correlatiecoëfficiënt R van -0,783. Is hier sprake van een causaal en/of statistisch verband?
Klik hier voor het antwoord
Er is sprake van een statistisch verband. Of er ook sprake is van een causaal verband kun je op basis van deze gegevens niet zeggen, maar waarschijnlijk is er een derde factor in het spel, namelijk het weer.Exercise 3
Het verband tussen twee variabelen is zoals weergegeven in onderstaand figuur.

Wat zal de bijbehorende correlatiecoëfficiënt (ongeveer) zijn?
- -0,32
- 0,00
- 0,70
- 0,99
Klik hier voor het antwoord
CExercise 3
Kun je een correlatie-analyse met een correlatiecoëficiënt (r) van 0,8361 gebruiken?
Klik hier voor het antwoord
Jazeker. Er is geen minimale r voor een correlatie-analyse. Een r van 0,8 is zelfs best sterke correlatie.Exercise 3
Hoe moet je een correlatiecoëficiënt (r) van 0,6361 interpreteren?
Klik hier voor het antwoord
Er lijkt wel een verband. Waarschijnlijk geen sterk lineair verband, maar bij een toename van x zal y wel toenemen. Of het nou echt sterk is of niet is moeilijk te zeggen zonder context.
Exercise 3
Hoe interpreteer je een ijklijn met een determinatiecoefficient (\(r^2\)) van 0,790?
Klik hier voor het antwoord
Dit is een slechte ijklijn en de ijklijnformule kan niet gebruikt worden voor het kwantificeren van monsters.Exercise 3
Welke van onderstaande beweringen over de correlatiecoëfficiënt is waar?
- De correlatiecoëfficiënt is een getal tussen 0 en 1 . Dit getal geeft aan hoe sterk het verband is tussen twee variabelen. Een waarde 0 betekent geen correlatie; de waarde 1 betekent een zeer sterke correlatie.
- De correlatiecoëfficiënt is een getal tussen -1 en 1 . Dit getal geeft aan hoe sterk het verband is tussen twee variabelen. Een waarde -1 betekent geen correlatie; de waarde 1 betekent een zeer sterke correlatie.
- De correlatiecoëfficiënt is een getal tussen -1 en 1 . Dit getal geeft aan hoe sterk het verband is tussen twee variabelen. Een waarde 0 betekent geen correlatie; de waarden 1 en -1 betekenen een zeer sterke correlatie.
- De correlatiecoëfficiënt is een getal tussen -1 en 0 . Dit getal geeft aan hoe sterk het verband is tussen twee variabelen. Een waarde 0 betekent geen correlatie; de waarde -1 betekent een zeer sterke correlatie.
Klik hier voor het antwoord
CVOETNOOT: Deze regel geeft soms wat discussie. Sommige labs middelen niet alle herhaalde metingen per concentratie, maar fitten een ijklijn op alle losse datapunten. Het volledige antwoord op die kwestie is: ja, dat zou mogen, maar alleen als de herhaalde metingen volledig onafhankelijk zouden zijn. Meestal zijn ze dat niet, dus zou het niet mogen. Wat “volledig onafhankelijk” precies betekent gaat nu wat ver voor deze cursus, maar je kan er vanuit gaan dat je herhaalde metingen die je tijdens de praktijklessen, projecten en vaardighedenlessen doet dit jaar niet volledig onafhankelijk zijn.↩︎