Les 6 Significantie
6.1 Lesinhoud en leerdoelen
Theorie:
- wat is significantie
- nulhypotheses
- p-waarde
- one sample t-toets
- eenzijdig en tweezijdig toetsen
Vaardigheden:
- one sample t-test in Excel
- oefenen met grote tabellen: Excel het werk laten doen
6.2 Voorbereiding
6.2.1 Significantie
In de vorige les hebben we al gezien dat je verschilvragen kan beantwoorden als je een 95% betrouwbaarheidsinterval berekend hebt. Even voor de herhaling: met een 95% BI heb je dus op basis van een steekproef met steekproefgemiddelde, beschikkking over een schatting van het populatiegemiddelde (ergens in deze range), met een daaraan hangende zekerheid van die schatting (95%).
Als je met genoeg zekerheid weet dat het populatiegemiddelde tussen bepaalde waarden ligt, kun je dus ook met een bepaalde onderliggende zekerheid vragen gaan beantwoorden als “is het populatiegemiddelde …?”, of “is het populatiegemiddelde kleiner dan …?” .
Bijvoorbeeld: De schatting van diastolische bloeddruk bij een groep patienten van een huisartsenpraktijk ligt op (95% BI:) 89 ± 1,3 mmHg. Is de bloeddruk van deze populatie anders dan het Utrechts gemiddelde van 87 mmHg? ja! want 87 zit niet in dit 95% BI.
Weten we dat 100% zeker? Nee, dat niet. Maar we hebben een aardige indicatie: we hebben een schatting met 95% zekerheid dat het populatiegemiddelde tussen de 87,7 en 90,3 mmHg zit. En dat is hoger dan 87.
Als je met genoeg zekerheid zo’n uitspraak kan doen, noemen we dat “significant”. Dus de gemiddeld bloeddruk bij deze praktijk is significant hoger dan 87 mmHg.
6.2.2 Nulhypotheses
Weten we dan wel 95% zeker dat die bloeddruk anders is dan 87 mmHg? Nee, het zit iets lastiger. Dat komt omdat die hele truc er stiekem nog steeds onder zit met die “als we 100 steekproeven zouden doen dan ligt het steekproefgemiddelde in maximaal 5 van de 100 gevallen buiten dit gebied.”
Een iets makkelijkere manier om naar significantie te kijken, is door het gebruik van nul-hypothese-tests. (Die ben je eigenlijk al tegen gekomen bij de Dixon’s Q-test.)
Een nulhypothese (H0) is een testbare hypothese die zegt dat er nul-noppes-data-geen effect is: in dit geval “er is geen verschil tussen de bloeddruk in deze populatie en 87 mmHg.”
Het omgekeerde van de nulhypothese is de alternatieve hypothese (H1): “er is wel een verschil tussen de bloeddruk in deze populatie en 87 mmHg.
Een nul-hypothese-test werkt als volgt:
- Bepaal je onderzoeksvraag (“Is de bloeddruk van deze populatie 87 mmHg?”)
- Bepaal de nulhypothese
- Verzamel data
- Bereken de kans dat je deze data zou vinden, als de nulhypothese zou kloppen. (later meer)
- Is die kans heel klein? Dan noemen we het effect “statistisch significant”.
Wacht, waarom berekenen we niet gewoon de kans op onze data als onze onderzoeks-hypothese klopt? Of zelfs de kans dat onze onderzoekshypothese klopt gezien onze data?
Ja, goeie vraag.
Het korte antwoord is: dan moet je dingen gaan zeggen over de populatie die je niet zeker weet. En daar heb je vervolgens aardig wat computerrekenkracht voor nodig. Of je dat wel of niet zou moeten doen verdeelt de statistici grotendeels in twee kampen. Aangezien het werkveld verwacht dat je deze manier van statistiek in ieder geval begrijpt, en Excel ook niet goed overweg kan met de andere vorm, doen we het zo. Dat betekent dus dat je de kans berekent op je data, als de nulhypothese zou kloppen.
Nulhypotheses vs onderzoekshypotheses
Het woord “hypothese” kennen jullie vooral uit het onderzoek:
- je hebt een onderzoeksvraag, of probleemstelling: wat ben je aan het onderzoeken?
- je hebt een onderzoekshypothese: een logisch verondersteld antwoord voor het probleem dat je onderzoekt
- en dan volgt een verwachting: wat er uit je onderzoek zou komen als je hypothese waar zou zijn.
Nulhypotheses en alternatieve hypotheses zijn geen onderzoekshypotheses, maar dienen echt voor de statistiek die je aan het doen bent. Ze hebben niets te maken met logische antwoorden op je probleemstelling, maar alles met wat je precies kan testen aan je data. Zie bijvoorbeeld de volgende situatie:
- context: patienten met keelpijn drinken te weinig. gemiddeld maar 1 liter per dag.
- onderzoeksvraag: drinken patienten met keelpijn andere hoeveelheden als ze per dag 6 x 500 mg paracetamol gebruiken?
- onderzoekshypothese: paracetamol dempt de pijn en daardoor doet water drinken minder pijn en dat heeft invloed op het water drinken.
- [hier moet je ergens data verzamelen…]
- nulhypothese H0: patienten die paracetamol krijgen drinken niet anders dan 1 liter per dag (er gebeurt niks, nul, noppes, geen effect van paracetamol)
- alternatieve hypothese H1: patienten die paracetamol krijgen, drinken anders dan 1 liter water (wel een effect van paracetamol)
Pas dus op dat je niet per ongeluk onderzoekshypotheses gaat opschrijven als er om een nulhypothese gevraagd wordt.
voorbeelden nulhypotheses bij 1 steekproef, tweezijdig
Nulhypotheses zien er dan bijvoorbeeld zo uit (negeer dat “tweezijdig” even voor nu, daar komen we zo op terug. Die staat er voor jullie overzicht tijdens het leren voor het tentamen):
- Is de lengte van Belgische vrouwen anders dan het Nederlands gemiddelde van 167,4 cm?
- H0: de lengte van Belgische vrouwen is niet anders dan 167,4 cm
- Bevatten deze pilletjes Pain-be-gone wel 500 mg werkzame stof?
- H0: de hoeveelheid werkzame stof is niet anders dan 500mg.
- Verschilt de gemiddelde reistijd met de fiets/auto van op kamers wonende ILC-studenten van het bekende landelijk gemiddelde van studenten in 2003 (18 minuten)?
- H0: er is geen verschil tussen de reistijd van ILC-studenten en 18 minuten.
6.2.3 One sample T-toets
Voor dit soort vragen gebruik je een one sample t-toets. Daarmee kun je testen of het gemiddelde van een groep significant afwijkt van een gegeven ‘criterium’ waarde. Wat je eigenlijk doet, is kijken of je steekproef uit een populatie zou kunnen komen met je criteriumwaarde als gemiddelde. In de voorbeelden hierboven zijn die criteriumwaardes 167,4cm (in voorbeeld 1), 500 mg (in voorbeeld 2) en 18 min. (in voorbeeld 3).

One sample = 1 steekproef. Want je hebt maar 1 steekproef gedaan (alleen de Belgische vrouwen, niet de Nederlandse. Alleen de ILC-studenten, niet alle studenten), etc. Voor de criteriumwaarde had je informatie van iemand anders (hier en hier bijvoorbeeld. Pain-be-gone zogen we uit onze duim)
Opdracht 6
Kan je met behulp van een t-toets statistische analyse doen van een verschilvraag en/of een verbandvraag?
- alleen van een verschilvraag
- alleen van een verbandvraag
- van zowel een verschilvraag als een verbandvraag D voor geen van beide vraagtypes
Klik hier voor het antwoord
A
Voor verbandsvragen moet je een regressie of correlatie gebruiken (les 3).p-waarde
De one-sample t-toets maakt gebruik van de t-verdeling om de kans te berekenen op jouw data of extremer, als de nulhypothese zou kloppen. Die kans heet een p-waarde (“p” voor “probability”). “Extremer” betekent hier: nog verder van wat je zou verwachten bij de nulhypothese. Als die kans erg klein is, dan zal de nulhypothese wel niet kloppen. Dat heet “de nulhypothese verwerpen”. Hoe klein moet die kans dan zijn? Binnen de statistiek is gebruikelijk dat bij een p-waarde lager dan een \(\alpha\) van 0,05 de H0 verworpen mag worden. (Ja, dat is diezelde \(\alpha\) als bij de Z-tabel.)
En als de H0 verworpen kan worden, dan nemen we de H1 aan. Betekent dat dat we hebben bewezen dat de H1 waar is? Nee, dat niet. Maar we hebben wel een lading kansrekening gedaan. Om aan te geven dat we niet zomaar wat zeggen maar er aan gerekend hebben, gebruik je de term “statistisch significant” in je conclusie, als je een p-waarde vindt van minder dan 0,05.
De opties zijn dus:
- p<0.05: we verwerpen H0 en nemen H1 aan.
- p>=0.05: we verwerpen H0 niet
(je neemt H0 dus niet aan, je verwerpt hem of je verwerpt hem niet.)
Let op: de grens is 0.05, en niet 0.5. Soms denken mensen dat de kans op H0 tegen de kans op H1 afgezet wordt, en degene die meer dan 50% kans krijgt, wint. Dat is NIET het geval. Je p-waarde zegt iets over de kans op je data als een nulhypothese zou kloppen, niet andersom!
(Het is ook geen compleet onlogisch idee, maar het is een hele andere tak van statistiek als je dat soort dingen gaat doen.)
Opdracht 6
Een p-waarde van 0.06 betekent:
- Er is 6% kans dat de nulhypothese klopt. We verwerpen de nulhypothese niet.
- Er is een kans van 6% dat de nulhypothese klopt, we nemen de alternatieve hypothese dus aan.
- De kans op onze data als de alternatieve hypothese zou kloppen is 6%. Dat is te groot, we nemen de alternatieve hypothese aan.
- De kans op onze data als de nulhypothese zou kloppen is 6%. Dat is te groot, we verwerpen de nulhypothese niet.
Klik hier voor het antwoord
DStel: Je vraagt je af of Belgische vrouwen 167,4 cm zijn en meet 100 Belgische vrouwen op.
- H0: de lengte van Belgische vrouwen is niet anders dan 167,4 cm
- H1: de lengte van Belgische vrouwen is anders dan 167,4 cm
Net als bij de Z-waardes en de normaalverdeling, zijn we aan het kijken of een bepaalde t-waarde te ver afwijkt van wat je zou verwachten onder de nulhypothese (dus onder de t-verdeling die de populatie zou hebben als de nulhypothese zou kloppen).
Nu kunnen we twee dingen doen:
- Uitrekenen wat de kritische t-waarde zou moeten zijn om een oppervlak onder de curve van precies 5% te krijgen. En dan kijken of de t-waarde van onze resultaten daar overheen gaat.
- Uitrekenen wat het oppervlak onder de curve is voor waarden extremer dan onze t-waarde, en checken of dat minder is dan 5%.
optie 1: kritische t-waarde
Je kan in Excel de functie =T.INV.2T(alpha;vrijheidsgraden) gebruiken om de kritische t-waarde te vinden voor een bepaalde significantie (in dit voorbeeld 0.05) en aantal vrijheidsgraden (in dit voorbeeld 100-1=99)
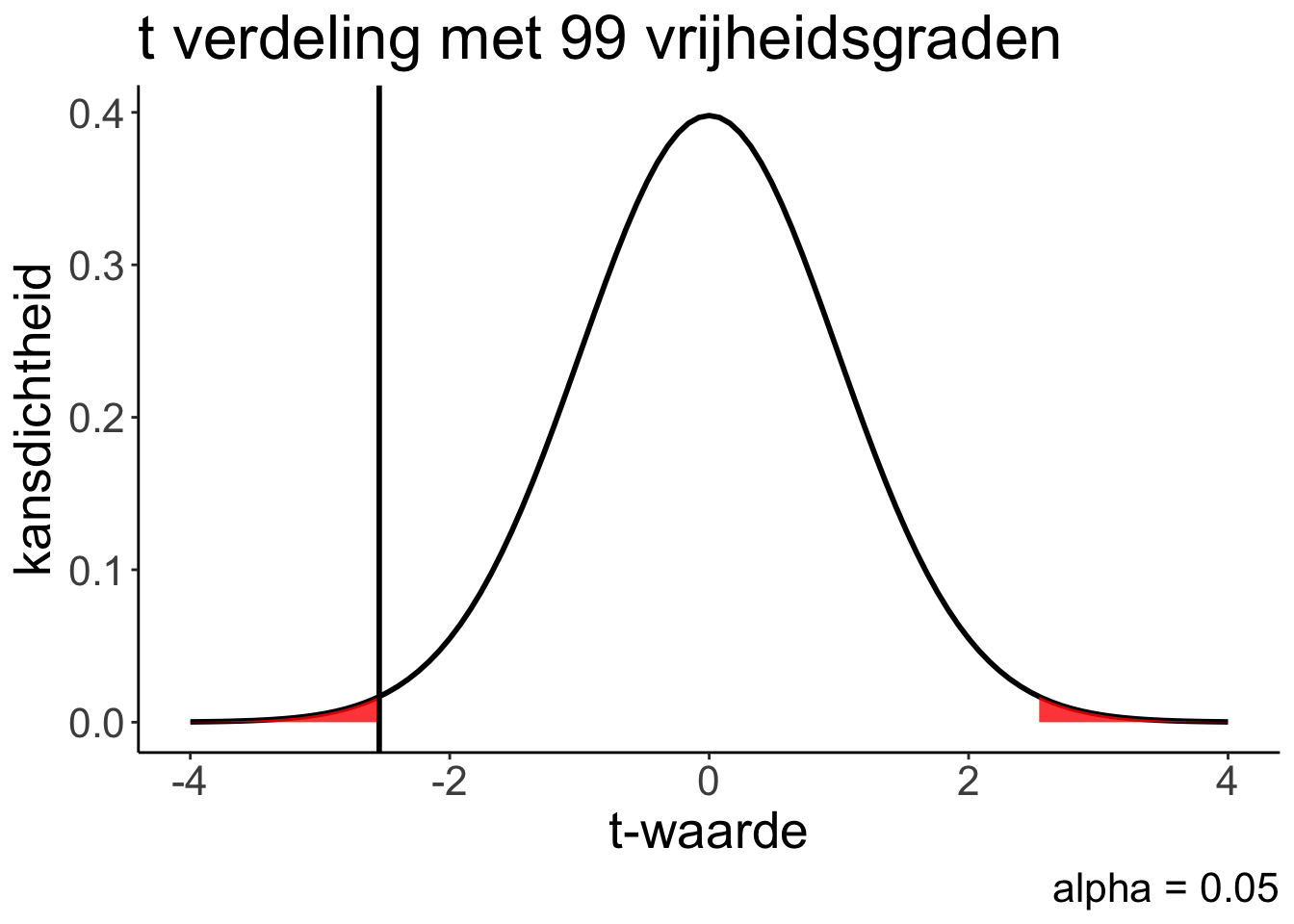
De grijze stukken onder de t-verdeling hieronder zijn de stukken met waarden extremer dan de kritische t-waarde, met samen 5% van het oppervlak. Links 2,5% en rechts 2,5%:

Zoals je ziet moet de t-waarde van het verschil tussen onze steekproef en de criteriumwaarde groter zijn dan in dit geval (hangt af van je aantal vrijheidsgraden) een kritische t-waarde van 1.98 of kleiner dan - 1.98 dan om te kunnen zeggen dat de kans op deze data onder de nulhypothese (letterlijk er onder dus) minder is dan 5%. Dan valt de t-waarde namelijk in een van de twee grijze gebieden.
We moeten dus een t-waarde berekenen. De t-verdeling hadden we in les 4 al gezien.
\(t=\frac{ \overline{x}-\mu}{s/ \sqrt{n}}\)
\(\overline{x}\): het steekproefgemiddelde
\(\mu\): de criteriumwaarde (het gemiddelde van de populatie als de nulhypothese zou kloppen)
\(s\): de steekproefstandaarddeviatie
\(n\): het aantal metingen
In het werkcollege ga je dit zelf narekenen met een dataset van 100 Belgische vrouwenlengtes. Laten we zeggen dat de t-waarde in dit geval -2,54 is.
Als we die t-waarde als verticale streep in de grafiek van net zouden zetten, zie je dat deze t-waarde in een van de twee grijze gebieden valt.
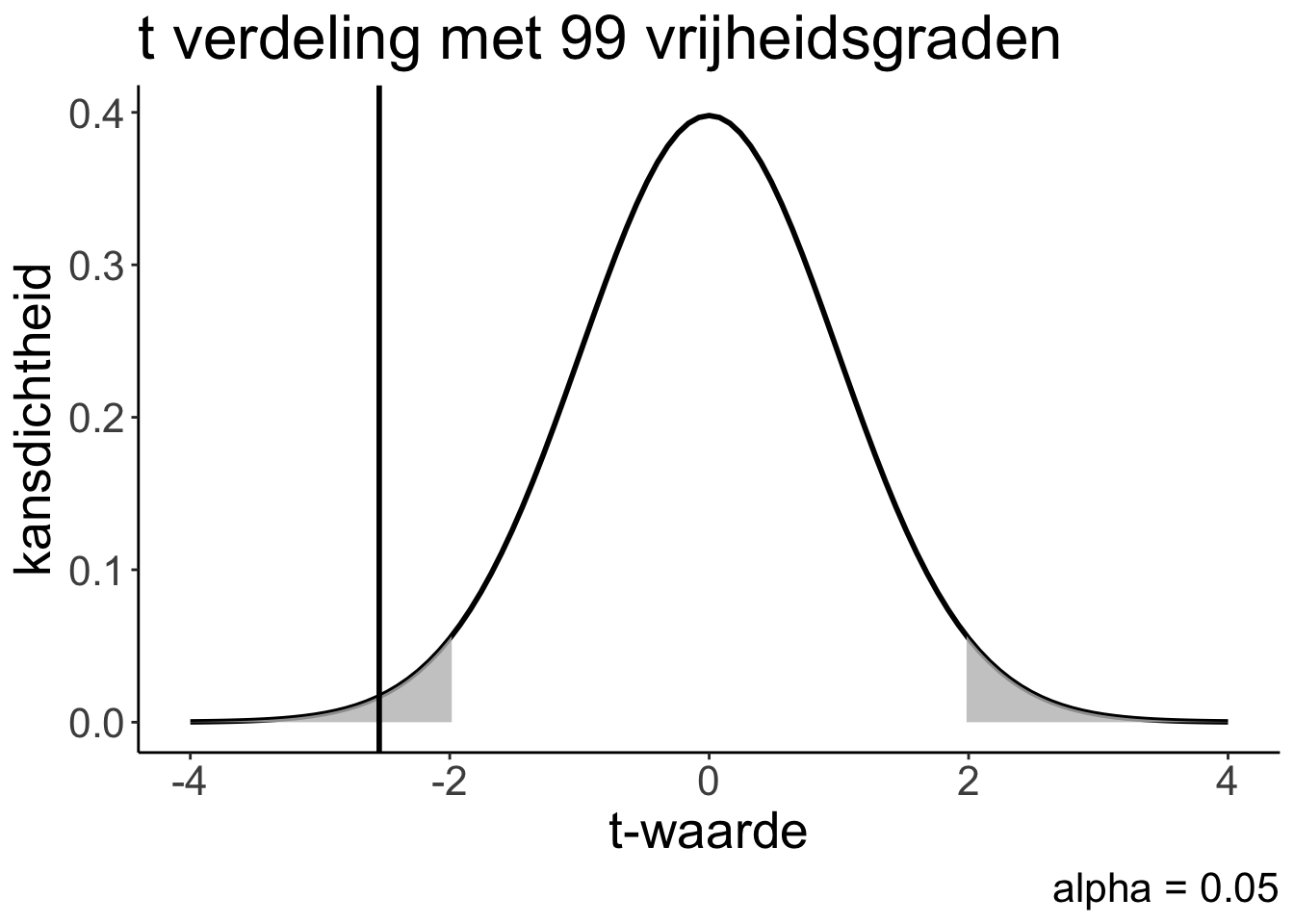
Dat betekent dat de kans op deze data onder de nulhypothese minder moet zijn dan 0.05. We kunnen de H0 verwerpen!
optie 2: p-waarde berekenen
We weten dus eigenlijk al dat we een p-waarde van minder dan 0.05 gaan vinden. Maar hoeveel minder? De meergebruikelijke optie om een p-waarde te gaan berekenen.
Dat is het percentage oppervlak links van die verticale streep is + het oppervlak even zo ver aan de rechter kant (want we hadden niks gevraagd over of Belgische vrouwen keiner of groter zouden zijn, alleen of ze een andere lengte hebben. Dus dat percentage aan de rechter kant telt ook mee).

We vinden vindt een p-waarde van ongeveer p = 0.013. In het werkcollege gaan jullie dit narekenen.
p-waarde < 0,05, dus de conclusie is dat er een significant verschil is tussen de lengte van Belgischie vrouwen en 167,4 cm.
Zo te zien zijn ze significant korter, want het gemiddelde van de Belgische vrouwen was 164.8. Dus ondanks dat je nulhypothese geen richting had, mag je best conclusies trekken met “kleiner” of “groter” er in. Je hebt het alleen moeilijker voor jezelf gemaakt om een p-waarde onder de 0.05 te krijgen (want de twee stukjes rood oppervlak in het grafiekje hierboven moesten samen onder de 5% blijven in plaats van alleen de ene.) Dus je conclusie is hier: Belgische vrouwen zijn significant korter dan Nederlandse vrouwen.
Dat korter of langer blijkt alleen niet uit de p-waarde zelf. Dus daarom moet je in verslagen altijd je steekproefgemiddelde te vermelden.
(Denk je nu “ja, oke, maar wat dan als ik ook 50 Nederlandse vrouwen heb gemeten?” Goeie vraag, daar gaat de volgende les over.)
6.2.4 Eenzijdig en tweezijdig toetsen
Je zag het net al aan de berekening van de p-waarde: het maakt uit hoe je je vraag stelt en je nulhypothese er dus uit ziet.
Kijk nog eens naar onderzoeksvraag of paracetamol iets verandert in het drinkgedrag van keelpijnpatienten, die zonder paracetamol slechts 1 liter per dag drinken. In deze vraag zit geen richting. We vragen ons af of iets “anders is”, maar niet per se hoger of lager. Dit heet tweezijdig, en zo’n vraag ga je tweezijdig toetsen:
tweezijdig
- Drinken keelpijnpatienten anders dan 1 liter als ze paracetamol gebruiken?
- H0: patienten die paracetamol krijgen drinken niet anders dan 1 liter per dag (er gebeurt niks, nul, noppes, geen effect van paracetamol)
- H1: patienten die paracetamol krijgen, drinken ** anders dan** 1 liter water (wel een effect van paracetamol)
Wat dan als mijn hypothese is dat patienten specifiek meer gaan drinken?” Mag dat?
Jazeker, dat mag. Dat heet eenzijdig toetsen. De onderzoeksvraag en nulhypothese krijgen dan een richting:
eenzijdig
- Drinken keelpijnpatienten meer dan 1 liter als ze paracetamol gebruiken?
- H0: patienten gaan niet meer drinken dan 1 liter (dus 1 liter of minder).
- H1: patienten gaan meer drinken dan 1 liter.
Je gebruikt een eenzijdige toets dus wanneer je kijkt naar verschil in een bepaalde richting. Als de p-waarde kleiner is dan 0,05 kun je concluderen dat Patienten inderdaad significant meer drinken dan 1 liter. Maar als de p-waarde groter is dan 0,05, kan dat betekenen dat patienten nog steeds gemiddeld 1 liter drinken, maar het kan ook betekenen dat ze juist minder drinken dan 1 liter!
Vaak weet je als onderzoeker niet welke kant het verschil op zal gaan, maar verwacht je wel een verschil. In dat geval gebruik je een tweezijdige t-toets. Zoals je hierboven zag, tellen dan de oppervlaktes aan beide kanten van de t-verdeling mee, dus “maak je het jezelf moeilijker” om een p-waarde onder de 0.05 te vinden. Over het algemeen is het netjes om het jezelf bij statistiek moeilijk te maken (jeej!).
Gebruik in geval van twijfel dus altijd een tweezijdige t-toets. Zorg dat je onderzoeksvraag en hypothesen ook tweezijdig formuleert (“Is er een verschil tussen … ?” / “Er is een verschil tussen …”).
Is de onderzoeksvraag en hypothese echt heel duidelijk eenzijdig, dan mag je een eenzijdige toets gebruiken.
6.2.4.1 voorbeelden nulhypotheses bij 1 steekproef, eenzijdig
In aanvulling op de tweezijdige nulhypotheses voor one sample t-toetsen hierboven, nu een aantal voorbeelden van eenzijdige:
- Is de lengte van Belgische vrouwen kleiner dan het Nederlands gemiddelde van 167,4 cm?
- H0: de lengte van Belgische vrouwen is niet kleiner dan 167,4 cm
- Bevatten deze pilletjes Pain-be-gone meer dan 500 mg werkzame stof?
- H0: de hoeveelheid werkzame stof is niet meer dan dan 500mg.
- Is de gemiddelde reistijd met de fiets/auto van op kamers wonende ILC-studenten korter dan het bekende landelijk gemiddelde van studenten in 2003 (18 minuten)?
- H0: de reistijd van ILC-studenten is niet korter dan 18 minuten.
6.2.5 Waarom noemen mensen dit soms een student’s t-test?
De t-toets (en de bijbehorende t-verdeling is ontwikkeld door William Sealy Gosset die werkte onder het pseudoniem Student. De toets wordt daarom ook regelmatig als Students t-toets aangeduid. Gosset was werkzaam voor de Guinness brouwerij, waar hij de kwaliteit van het gebrouwen bier in de gaten hield. Hij publiceerde zijn resultaten in 1908 in het statistische tijdschrift Biometrika. Zijn werkgever eiste dat hij dat onder een pseudoniem deed, omdat het gebruik van statistische methoden als ‘bedrijfsgeheim’ gezien werd.
Dit is dus niet speciale “studentestatistiek” of zo, het is the real deal.
6.3 Werkcollege
In dit werkcollege gaan we met de one sample t-test aan de slag.
6.3.1 Deel 1: one sample t-test narekenen
De t-verdeling hadden we in les 4 al gezien.
\(t=\frac{ \overline{x}-\mu}{s/ \sqrt{n}}\)
We hebben dus nodig:
\(\overline{x}\): het steekproefgemiddelde
\(\mu\): de criteriumwaarde (het gemiddelde van de populatie als de nulhypothese zou kloppen)
\(s\): de steekproefstandaarddeviatie
\(n\): het aantal metingen
Exercise 6
Dat zijn allemaal dingen waarvan we al weten hoe we dat moeten berekenen in Excel. We gaan nu het voorbeeld uit de voorbereiding narekenen. De ondrezoeksvraag, H0 en H1 waren:
Je vraagt je af of Belgische vrouwen 167,4 cm lang zijn en meet 100 Belgische vrouwen op.
- H0: de lengte van Belgische vrouwen is niet anders dan 167,4 cm
- H1: de lengte van Belgische vrouwen is anders dan 167,4 cm
Open vrouwenlengte.xlsx en bereken in kolom E:
- steekproefgemiddelde
- criteriumwaarde (die kun je gewoon invullen, hoef je niet aan te rekenen)
- steekproefstandaarddeviatie
- aantal metingen
Klik hier voor het antwoord
Exercise 6
- \(s\) moeten we delen door \(\sqrt{n}\). Die uitkomst heet ook wel de SEM: standard error of the mean.
- En daarna delen we het verschil tussen het steekproefgemiddelde en het populatiegemiddelde onder de nulhypothese (167,4), door de SEM. Dit is de t-waarde. (hou de formule voor de t-verdeling in het oog als je dit even niet volgt.)
Reken de SEM uit in cel E8, en de t-waarde in cel E9
Klik hier voor het antwoord
Exercise 6
- Nu gebruiken we Excel om de p-waarde te berekenen: het percentage oppervlak links van die verticale streep is + het oppervlak even zo ver aan de rechter kant (want we hadden niks gevraagd over of Belgische vrouwen keiner of groter zouden zijn, alleen of ze een andere lengte hebben. Dus dat percentage aan de rechter kant telt ook mee).
- Excel gebruikt daarvoor
=T.DIST.2T(t,deg_freedom)voor een tweezijdige toets enT.DIST.RT(t,deg_freedom)voor een eenzijdige toets. - Deze formule heeft dus nodig: t-waarde (hebben we), vrijheidsgraden (n-1). Net als bij de z-tabel, kan Excel er echter niet tegen als de t-waarde negatief is. Sure, ook de t-verdeling is symmetrisch, dus als Excel dat graag wil, berekenen we dat andere rode stukje oppervlak wel even. Daarvoor nemen we de t-waarde absoluut:
= abs(twaarde)in excel:
Reken de absolute t-waarde uit in cel E10 (t)
Reken het aantal vrijheidsgraden uit in cel E11 (deg_freedom)
Reken de p-waarde uit in cel E12
Klik hier voor het antwoord
Dit is een tweezijdige toets:
Als het goed is kom je op dezelfde p-waarde als in de voorbereiding: p = 0.013.
p-waarde < 0,05, dus de conclusie is dat de lengte van Belgische vrouwen significant verschilt van 167,4 cm.
6.3.1.1 stappenplan one sample t-toets
- Check de voorwaarden:
- Je hebt een verschilvraag
- Je hebt 1 steekproef en een verwachte waarde (criterium?)
- De data zijn interval of ratio (dwz, meetwaarden in de vorm van cijfers)
- De data zijn afkomstig uit een normaal verdeelde populatie (hoe je dat test leer je in jaar 2, je mag er nu vanuit gaan dat het dat is als we je vragen en t-toets te doen.)
- Formuleer de onderzoeksvraag, H0 en H1
- Bereken gemiddelde, standaarddeviatie, n, vrijheidsgraden en SEM in Excel
- Bereken hieruit de t-waarde in Excel
- Bereken hieruit de p-waarde in Excel
- interpreteer de p-waarde:
- p groter of gelijk aan 0.05 –> houd H0
- p kleiner dan 0.05 –> verwerp H0 en accepteer H1
- Formuleer een conclusie op basis van je resultaat
Exercise 6
Probeer wat er gebeurt als je steekproef alleen had bestaan uit de bovenste 20 Belgische vrouwen. Wat was de p-waarde dan geweest? En wat was de conclusie dan geweest?
Klik hier voor het antwoord
Je kan gewoon je hele Excel-sheet kopieren en in de kopie alle data behalve de bovenste 20 datapunten weggooien. Excle rekent automatisch de nieuwe p-waarde uit.
Dan was de lengte van Belgische vrouwen volgens deze steekproef niet statistisch significant anders dan 167,4 cm (p=0.16).
6.3.2 Deel 2: de t-tabel
Je zou natuurlijk ook weer een tabel kunnen maken, met p-waarden voor alle combinaties van aantallen vrijheidsgraden en t-waardes. Dat gaan we in deze opdracht zelf doen, met name om goed met Excel te oefenen. Maar ook om te visualiseren dat hoe groter je t-score is, hoe kleiner de kans dat je deze waarde per toeval tegenkomt.
Je gaat weer gebruik maken van de =T.DIST.2T formule.
- Open een nieuwe tabblad
- Vul in kolom
A3:A502(aangegeven in roze) de reeks in van 0,01 tot 5,00 met stappen van 0,01 (t-scores). Zie de figuur hieronder. (In de figuur staan komma’s als decimal separator. Dit moeten natuurlijk punten zijn.) Vergeet niet dat je een vijftal cellen in kan typen, ze alle vijf selecteren en uittrekken naar beneden zo ver je wilt. Excel rekent zelf verder. - Vul in rij
B2:AX2(aangegeven in geel) de reeks 2 tot en met 50 in met stappen van 1 (vrijheidsgraden) (laat Excel weer het werk doen.) - Nu gaan we de formule intypen zoals aangegeven in de figuur. Bedenk goed waar je de dollar tekens moet zetten
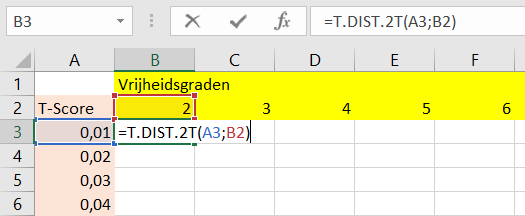
- Vervolgens willen we die formule 49x500 keer herhalen. Oei. Ga dit niet handmatig doen, we doen deze opdracht om te leren hoe je Excel heir het werk laat doen.
- Begin met de bovenste regel. Bedenk nogmaals goed waar de dollar tekens moeten staan en waar niet, selecteer cel B3 en trek hem helemaal naar rechts.
- Selecteer nu de hele bovenste rij 3, en dubbelklik op het zwarte kleine vierkantje rechts onderin je selectievak. Excel bult nu zelf de tabel. Controleer of je waarden kloppen. Zo nee, dan stond er toch ergens een dollar-teken verkeerd! Undo, verander je dollartekens en probeer het nog eens.
Voila: een tabel met p-waarden voor een flinke lading combinatie van t-scores en vrijheidsgraden!
6.3.3 Deel 3: one sample t-test zelf
Open Creatinine.xlsx. Dit bestand bevat de creatinine-concentratie gemeten in de bloedmonsters van 50 patiënten die zijn besmet met hepatitis B. Je wilt weten of besmetting met hepatitis B kan leiden tot een verhoogde creatinine concentratie in het bloed. Je weet al dat gezonde mensen een creatinine concentratie van 92 μmol/l hebben.
De vraag kun je op twee manieren oplossen. De eerste manier is om een 95% betrouwbaarheidsinterval te berekenen van de steekproef en te bepalen of de referentiewaarde van 92 μmol/l daar onder ligt.
Opdracht 6
Is deze toets eenzijdig of tweezijdig?
Klik hier voor het antwoord
eenzijdig, we willen weten of besmetting met hepatitis B kan leiden tot een verhoogde creatinine concentratie in het bloed. Die vraag heeft dus een richting.Opdracht 6
Wat is het 95% B.I. voor de creatinine concentratie in de steekproef?
Klik hier voor het antwoord
Omdat n = 50 gebruiken we de volgende formule voor de berekening van het 95% BI:
\(\bar{x} \pm 1,96 \cdot \frac{s}{\sqrt{n}}\)
Dit geeft een 95% BI van 97 \(\pm\) 6 umol/l (vergeet niet om correct af te ronden!)
Opdracht 6
Valt de referentiewaarde binnen het 95% B.I.?
Klik hier voor het antwoord
Ja, de waarde van 92 μmol/l ligt tussen de ondergrens (91 umol/l) en de bovengrens (103 umol/l) van het 95% B.I.Opdracht 6
Beantwoord op basis van het 95% BI: verhoogt de hepatitis B besmetting de creatinineconcentratie in het bloed van deze patiënten?
Klik hier voor het antwoord
Nee, want het 95% B.I. ligt niet in zijn geheel boven de referentiewaarde.De tweede manier is de one-sample t-test in Excel. Met deze test bepaal je het verschil tussen het steekproefgemiddelde en de referentiewaarde in verhouding tot de spreiding in het steekproefgemiddelde. Hiertoe bereken je eerst het verschil tussen het steekproefgemiddelde \(\bar{x}\) en het populatiegemiddelde \(\mu\). Vervolgens deel je dit verschil door de standaardfout van het steekproefgemiddelde (Standard Error of the Mean (SEM)). De uitkomst van deze berekening is de t-score:
\(t=\frac{ \overline{x}-\mu}{s/ \sqrt{n}}\)
Of (dat is hetzelfde):
\(t\ score = \frac{\bar{x}-\mu}{SEM}\) ; waarbij \(SEM = \frac{s}{\sqrt{n}}\)
Opdracht 6
Wat is de SEM waarde? Geef je antwoord in twee decimalen nauwkeurig.
Klik hier voor het antwoord
\(SEM = 2,93\)Opdracht 6
Wat is de t-score? Geef je antwoord in twee decimalen nauwkeurig.
Klik hier voor het antwoord
\(t\ score = 1,62\)Opdracht 6
Bereken de bijbehorende p-waarde.
Klik hier voor het antwoord
In plaats van T.DIST.2T() gebruik je T.DIST.RT(), want het is een eenzijdige toets.
p = 0.05531
Opdracht 6
deze p-waarde betekent:
- Er is 5,5% kans dat de nulhypothese klopt.
- De kans op onze data als de nulhypothese zou kloppen is 11%.
- De kans op onze data als de nulhypothese zou kloppen is 5,5%.
Klik hier voor het antwoord
COpdracht 6
Verschilt de creatinine-concentratie van hepatitis B-patienten significant van de referentie waarde? Baseer je antwoord op de p-waarde.
Klik hier voor het antwoord
p>0.05, dus er is geen significant verschil tussen de creatinine-concentratie van hepatitis B-patienten en de referentiewaarde.
Opdracht 6
Importeer de data uit koffiedocenten.csv in excel. Hier vind je de hoeveelheid koffie die 25 ILC-docenten per dag dronken in een steekproef. Drinken ILC-docenten minder dan 600 ml koffie per dag?
Klik hier voor het antwoord
p = 0.009
p<0.05, dus ILC-docenten drinken significant minder dan 600 ml koffie per dag.
Opdracht 6
Voor een project over lactose werkte je samen met Teun. Teun staat bekend om zijn enorm slechte pipetteerwerk. Zoals verwacht, liggen de 6 herhaalde metingen van de lactoseconcentratie van een pak huismerk-melk dus nogal ver uit elkaar. De gemiddelde lactoseconcentratie in koemelk is 4,7 gram/l, en jullie vraag was of de lactoseconcentratie in dit pak melk daarvan afwijkt.
Wat is jullie nulhypothese?
Klik hier voor het antwoord
H0: De lactoseconcentratie van het pak melk is (niet anders dan) 4,7 gram/lOpdracht 6
Wat voor test ga je doen om deze vraag te beantwoorden?
Klik hier voor het antwoord
Een one sample t-test, tweezijdig.
Je zou ook een 95% B.I. kunnen berekenen.Opdracht 6
Voor dit deel van het werkcollege heb je de file lactose.txt nodig. Deze zat niet in de zip die je gedownload hebt, download hem hier voor de
voltijd en
deeltijd.
Importeer de data uit lactose.txt. Wijkt de lactoseconcentratie van dit pak melk volgens deze steekproef af van de gemiddelde lactoseconcentratie in koemelk (4,7 gram/l)
Klik hier voor het antwoord
Deze toets is tweezijdig, want er is geen richting aan de onderzoeksvraag. p = 0.41
p>0.05, dus de hoeveelheid lactose in dit pak wijkt niet significant af van de verwachte waarde.
Opdracht 6
Jullie besluiten nog een keer naar het lab te gaan en vinden de volgende meetwaarden:
4.6 ; 4.5 ; 4.4; 5.4; 4.5; 4.6
Wijkt de lactoseconcentratie van dit pak melk volgens deze steekproef dan af van de gemiddelde lactoseconcentratie in koemelk (4,7 gram/l)?
Klik hier voor het antwoord
Er lijkt een outlier in deze dataset te zitten. Doe eerst dixon;s q-test.
n=6, dus \(Q\) = 0.8
\(Q_{kritisch}\) = 0.560 (n=6, alpha=0.05 tenzij er expliciet iets anders gevraagd wordt)
0.8 > 0.560, dus we gooien datapunt met meetwaarde 5.4 eruit! Dat is een outlier.
Dan doen we een one sample t-test, tweezijdig, met de rest van de data. Deze toets is tweezijdig, want er is geen richting aan de onderzoeksvraag.
p = 0.009
p<0.05, dus de hoeveelheid lactose in dit pak wijkt significant af van de verwachte waarde.
Opdracht 6
Zoals je ziet waren de steekproefgemiddeldes \(\overline{x_{1}}\) van Teun en \(\overline{x_{2}}\) van de herhaling gelijk. Toch verschilt de p-waarde. Hoe kan dat?
Klik hier voor het antwoord
De berekening van de p-waarde is afhankelijk van de spreiding van je steekproefdata. De standaarddeviatie zit namelijk in de formule voor de t-waarde.Opdracht 6
Nu je het antwoord op de vorige vraag weet, waarvan is de p-waarde dus nog meer afhankelijk?
Klik hier voor het antwoord
Van het aantal metingen in je steekproef: \(n\).
(denk je nu: “oh, dus als ik 1 miljoen metingen doe vind ik altijd wel wat significants” ? Ja, klopt. Te weinig metingen is niet tof, maar teveel ook niet. Daarom berekenen mensen vaak voor ze een onderzoek doen hoeveel metingen er nodig zijn. Dat zit in cursussen in latere jaren van je studie.)