Les 5 95% Betrouwbaarheidsinterval

5.1 Lesinhoud en leerdoelen

In deze les gaan we aan de slag met 95% betrouwbaarheidsintervallen. Alvast een kleine reminder: random websites op het internet (including soms Wikipedia) maken vaak fouten bij het uitleggen van statistiek. Zeker bij 95% betrouwbaarheidsintervallen.

Theorie:

• steekproeven
• het 95% BI: beschrijvende vragen beantwoorden
  • optie 1: \(\mu\) onbekend, \(\sigma\) bekend
  • optie 2: \(\mu\) onbekend, \(\sigma\) onbekend, 50 metingen of meer
  • optie 3: \(\mu\) onbekend, \(\sigma\) onbekend, <50 metingen
    
• histogrammen vs staafdiagrammen
• verschilvragen beantwoorden met een 95% BI

Vaardigheden:

• steekproefstandaarddeviaties in Excel
• 95% BI berekenen in Excel
• herhaling staafdiagrammen
• kiezen tussen een z-verdeling en een t-verdeling

5.2 Voorbereiding

Deze les gaat over het beantwoorden van beschrijvende vragen en verschilvragen.

In de vorige les hebben we gerekend met Z-scores en met voorbeelden waarbij de lengte van alle Nederlandse mannen bekend was. In de praktijk is dat natuurlijk meestal niet het geval. Ook bij andere experimenten is het vaak onmogelijk om metingen te verrichten aan alle individuen of elementen in de populatie. Denk hierbij bijvoorbeeld aan het bepalen van de gemiddelde brandtijd van een kaars. Bij elke meting gaat immers de kaars verloren (een destructieve meting). In les 1 bespraken we daarom al Steekproeven. Het is realistischer om het populatiegemiddelde te benaderen door de lengte te meten van een relatief kleine groep, een steekproef. Het is wel belangrijk dat die groep representatief is voor de gehele populatie.

5.2.1 Steekproef

In les 1 hadden we het al over steekproeven. Een steekproef doe je als je een vraag hebt over een populatie maar ze niet allemaal kunt meten. Een populatie is alle units waar je een vraag over hebt. Dus vraag je je af hoe lang studenten life sciences studeren voor het tentamen statistiek & excel, dan is je populatie alle studenten life siences. Ze allemaal ondervragen is wat veel werk, dus meestal vraag je er een paar (steekproef) en doet op basis van die paar studenten een uitspraak over de hele populatie (inductieve statistiek).

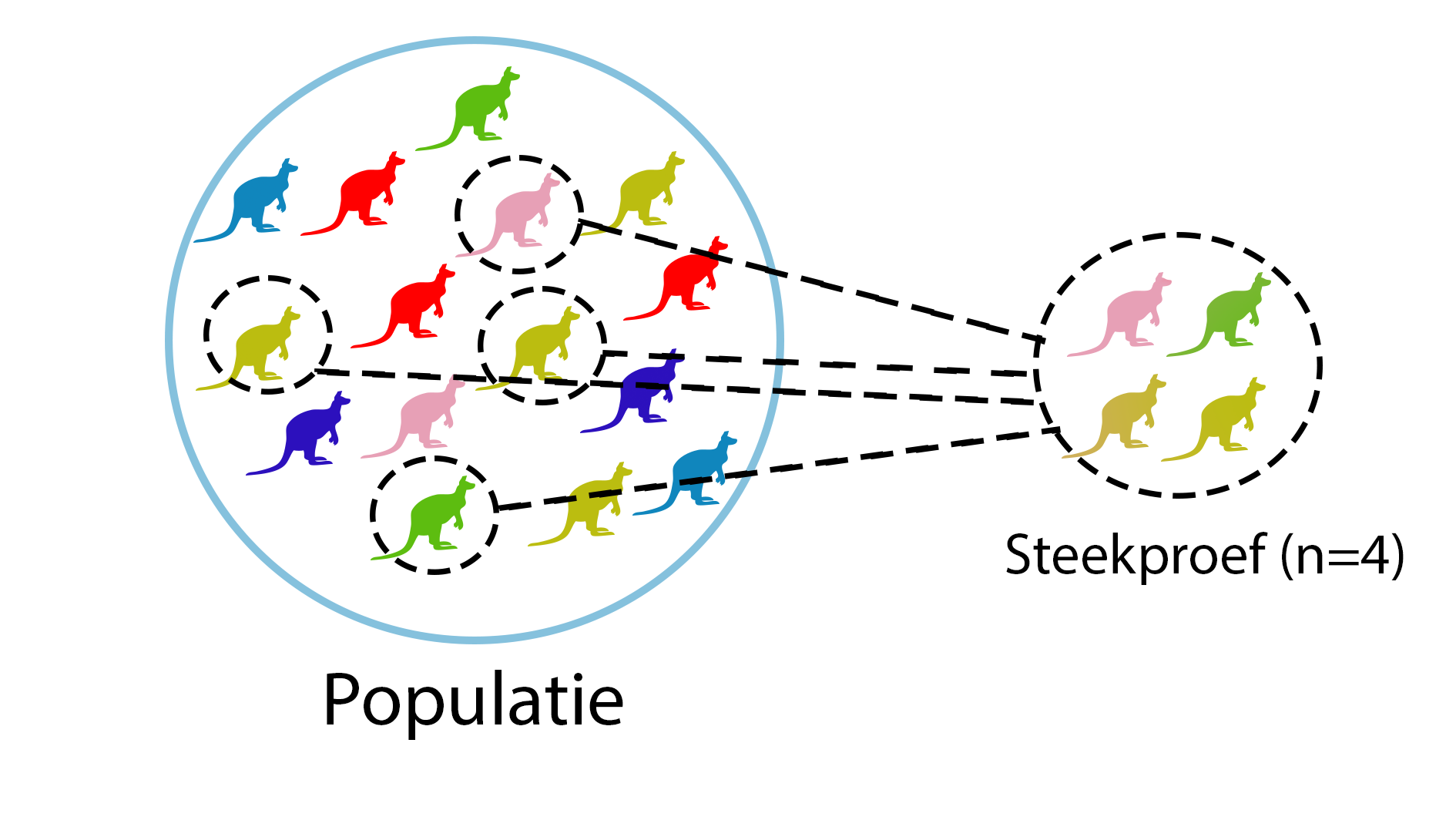
Figure 1.1: Een steekproef van 4 kangaroes uit een totale populatie van 15.

Representatief betekent dat de steekproef ongeveer dezelfde samenstelling heeft als de hele populatie, maar dan in het klein. Dus als je studenten vraagt naar hoe lang ze gestudeerd hebben, moet je niet bijvoorbeeld alleen de studenten vragen die een onoldoende haalden. Je kiest een random steekproef.

Maar, stel je herhaalt je steekproef 5 keer en vraagt steeds random 20 studenten. Dan zul je elke keer net een ander steekproefgemiddelde vinden. Het is dus bijna zeker zo dat als je verschillende steekproeven uit 1 populatie neemt, de data wel wat verschillend is. Onthou dit! Als je dat vergeet kan statistiek verderop verwarrend worden.

5.2.2 Het 95% betrouwbaarheidsinterval

Let op: bij een steekproef met een beschrijvende onderzoeksvraag wil je graag weten wat populatiegemiddelde \(\mu\) is, maar die kunnen we niet precies achterhalen. Daarom bepalen we steekproefgemiddelde \(\overline{x}\) en gaan op basis daarvan een uitspraak (proberen te) doen over \(\mu\)

Stel dat twee studenten ieder een steekproef neemt van 50 Nederlandse mannen. Ze hebben beide dezelfde beschrijvende vraag: hoe lang is de gemiddelde Nederlandse man? De eerste student berekent een steekproefgemiddelde \(\overline{x}\) van 170,6 cm, terwijl de tweede student uitkomt op \(\overline{x}\) = 177,4 cm. Wie heeft er nu gelijk? Nou, allebei, of geen van beiden. Het is heel normaal dat als je twee keer een steekproef doet uit 1 populatie, je niet precies dezelfde data krijgt (attentie, dit is een herhaling. Onthoudt u mee?)

We zetten deze steekproefgemiddelden eens in een histogram (let op dat nu niet aantal metingen maar aantal steekproeven op de y-as staat!):

De twee steekproefgemiddelden uitgezet tegen het aantal steekproeven waarin deze gemiddelden gevonden werden

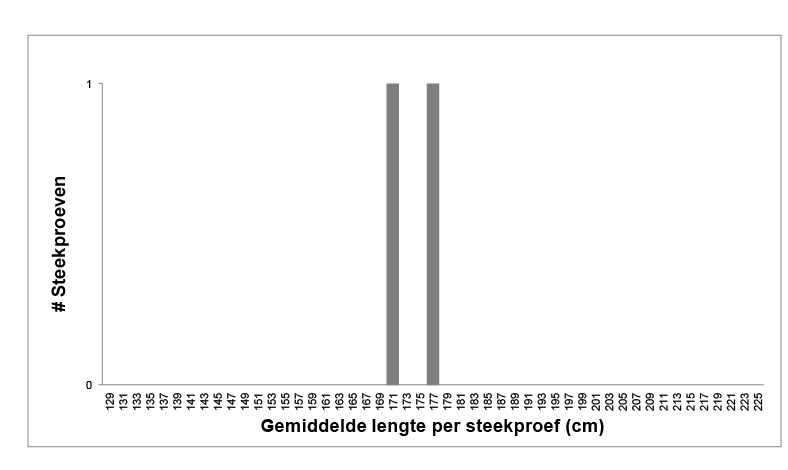
Het herhalen van deze steekproef zal steeds een iets ander gemiddelde laten zien. Er zitten namelijk steeds random andere mannen in. Soms heb je toevallig die ene basketbalspeler van 220 cm, soms heb je toevallig net Joep van 1-meter-62.

Wel zal voor die steekproefgemiddelden gelden dat de meeste waarden rond het populatiegemiddelde \(\mu\) uitkomen, al zullen er ook wel afwijkende waarden zijn. Als je de steekproef van 50 Nederlandse mannen maar vaak genoeg herhaalt en een histogram maakt van alle steekproefgemiddelden, dan zal je zien dat de gemiddelden zich gaan verzamelen in het midden; Het histogram gaat lijken op een normaalverdeling met een piek (laten we hem even \(\overline{x}_{max}\) noemen, dit is het gemiddelde van alle steekproefgemiddelden) ergens in de buurt van het populatiegemiddelde \(\mu\) (175 cm):

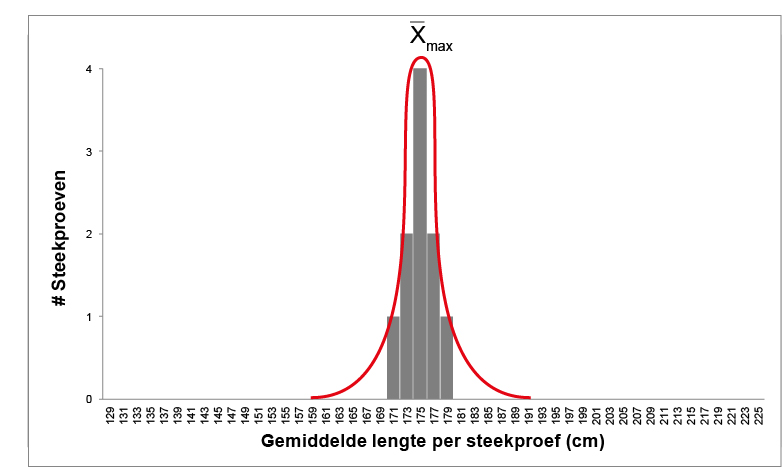Zoals je ziet begint dat aardig op een normaalverdeling te lijken. De breedte van deze verdeling is een maat voor hoe nauwkeurig \(\overline{x}_{max}\) het werkelijke populatiegemiddelde benadert. Het soort statistiek wat we nu aan het doen zijn is dol op dit trucje: stel nou dat je een oneindige hoeveelheid steekproeven doet? Dan hebben we onze geliefde normaalverdeling terug!

Dat komt goed uit, want met normaalverdelingen konden we iets handigs berekenen: d.m.v. de Z-scores hadden we berekend dat 95% van het oppervlak onder een normaalverdeling tussen een z-waarde van 1.96 onder en 1.96 boven het gemiddelde zit. Dus stel dat je je steekproef 100 keer zou herhalen, dan zouden de steekproefgemiddeldes van 95 van die 100 steekproeven tussen de \(\overline{x}_{max} \pm 1,96 * standaarddeviatie\) liggen.

Nou doen we geen 100 steekproeven, we doen er meestal maar 1 (of maar een paar, zoals in de laatste 2 lessen). Maar de truc werkt toch soort van: we hebben een steekproefgemiddelde \(\overline{x}\) en kunnen met die normaalverdeling een schatting gaan geven van \(\mu\). We moeten alleen ook het aantal metingen \(n\) even meenemen.

Die schatting van het populatiegemiddelde \(\mu\) doen we met een 95% betrouwbaarheidsinterval (95% BI). Bijvoorbeeld: op basis van de steekproef hierboven kun je met 95% zekerheid stellen dat het landelijk gemiddelde \(\mu\) ligt tussen 172 en 178 cm, of ook wel: 175 \(\pm\) 3 cm.

Hoe bereken je die grenswaarden?

95% BI Optie 1: \(\sigma\) bekend

Als je de populatie-standaarddeviatie \(\sigma\) wel weet, kun je die gewoon gebruiken. In dat geval, ligt het populatiegemiddelde met 95% zekerheid tussen:

95% BI is \(\overline{x} \pm 1,96 * \frac{\sigma}{\sqrt{n}}\)

• \(\overline{x}\) : steekproefgemiddelde
• \(\sigma\): populatiestandaarddeviatie
• \(n\) : aantal metingen in de steekproef

Stel, we vissen 25 katten van straat in Utrecht en meten hun staart, want we willen weten wat de gemiddelde kattenstaartlengte in Utrecht dit jaar is. Dankzij jarenlang werk van onze vriend Bas weten we dat de populatiestandaarddeviatie van kattenstaartlengte in Utrecht 3 cm is. We vinden een steekproefgemiddelde van 28 cm. Dan is het 95% betrouwbaarheidsinterval:

\(\overline{x} \pm 1,96 * \frac{\sigma}{\sqrt{n}}\)

\(28 \pm 1,96 * \frac{3}{\sqrt{25}} = 28 \pm 1,176\) cm

afronden geeft: \(28 \pm 1\) cm

ondergrens: \(28-1 = 27\) cm

bovengrens: \(28+1 = 29\) cm

Dus het 95% BI is 27 tot 29 cm

We kunnen met 95% zekerheid zeggen dat de gemiddelde kattenstaartlengte van Utrechtse katten (\(\mu\) dus) tussen de 27 en 29 cm ligt. (Vergeet de eenheid niet.)

Leer die manier van uitleggen uit je hoofd. Die 95% gaat over de betrouwbaarheid van jouw schatting en niet over wat anders. Daarom heet het ook een 95% betrouwbaarheidsinterval (of in het Engels: 95% confidence interval: zekerheidsinterval).

• goed: Je kan met 95% zekerheid zeggen dat het populatiegemiddelde ligt tussen …. en …
• fout: Er is een kans van 95% dat het populatiegemiddelde ligt tussen …. en …
• fout: 95% van de datapunten ligt tussen … en …
• fout: 95% van de populatie ligt tussen … en … (dan verwar je het 95% BI met de situatie uit les 4 met die Z-tabel, waarin je het populatiegemiddelde en de populatiestandaarddeviatie weet. )

Merk op dat die 1,96 betekent dat we achter de schermen gebruik maken van de \(Z\)-verdeling.

Dit is dus wel een 95% betrouwbaarheids-interval. Een 95% BI berekenen we alleen als we het populatiegemiddelde niet weten. Als we populatiegemiddelde \(\mu\) weten, hoeven we hem ook niet met 95% betrouwbaarheid te gaan lopen schatten. Tenzij we een \(\mu\) weten, maar we willen controleren of die wel klopt, met een steekproef.

95% BI Optie 2: \(\sigma\) onbekend, >=50 meetpunten

Als je \(\sigma\) niet weet is er gelukkig een backup: we hebben ongetwijfeld wel steekproefstandaarddeviatie \(s\). (Excel: =STDEV.S()) In de vorige les hebben we gezien dat \(s\) afhangt van het aantal metingen.

Bij 50 metingen of meer maakt dat niet zo uit. Dan stoppen we gewoon \(s\) in de plek van \(\sigma\) en is de formule voor het 95% BI dus:

\(\overline{x} \pm 1,96 * \frac{s}{\sqrt{n}}\)

• \(\overline{x}\) : steekproefgemiddelde
• \(s\): steekproefstandaarddeviatie
• \(n\) : aantal metingen in de steekproef

Merk op dat die 1,96 betekent dat we achter de schermen wederom gebruik maken van de \(Z\)-verdeling.

95% BI Optie 3: \(\sigma\) onbekend, <50 meetpunten

Onder de 50 metingen maakt het wel uit. Ook daar is een oplossing voor: de t-verdeling gebruiken. In plaats van 1,96 (die kwam uit de \(Z\)-verdeling), gaan we de schatting van het populatiegemiddelde (want daar waren we mee bezig, remember?) nu een beetje breder maken. Hoeveel breder, hangt af van hoeveel metingen je hebt. We schrijven dus een \(t\) in de formule in plaats van de 1,96 (en die \(t\) is altijd groter dan 1,96):

\(\overline{x} \pm t * \frac{s}{\sqrt{n}}\)

• \(\overline{x}\) : steekproefgemiddelde
• \(t\) : t-waarde
• \(s\): steekproefstandaarddeviatie
• \(n\) : aantal metingen in de steekproef

De \(t-waarde\) moeten we in een tabel opzoeken. Die tabel staat op het formuleblad. In de t-tabel staat steeds de \(t-waarde\) voor een aantal vrijheidsgraden. Dat is het aantal meetpunten min 1:

\(vrijheidsgraden = n-1\)

Dat heeft er mee te maken, dat je bij n metingen, soort van n-1 keuzes hebt. Stel je bijvoorbeeld voor dat je 6 verschillende kleuren Skittles hebt. Je kan 5 keer kiezen welke kleur Skittle je als volgende op gaat eten, maar de 6e keer heb je niks meer te kiezen, er is er nog maar 1 over.

Stel, we vissen 16 katten van straat in Groningen en meten hun staart, want we willen weten wat de gemiddelde kattenstaartlengte in Groningen dit jaar is. We hebben helaas geen idee van de populatiestandaarddeviatie \(\sigma\). We vinden een steekproefgemiddelde \(\overline{x}\) van 26 cm. en een steekproefstandaarddeviatie \(s\) van 5 cm. Dan is het 95% betrouwbaarheidsinterval:

\(\overline{x} \pm t * \frac{s}{\sqrt{n}}\)

dus \(26 \pm t * \frac{5}{\sqrt{16}}\) cm

\(t\) zoeken we op in de tabel bij vrijheidsgraden \(n-1 = 16-1 = 15\). Dat geeft \(t = 2,131\)

\(26 \pm 2,131 * \frac{5}{\sqrt{16}} = 26 \pm 2.66375\) cm

afronden geeft: \(26 \pm 3\) cm

ondergrens: \(26-3 = 23\) cm

bovengrens: \(26+3 = 29\) cm

Dus het 95% BI is 23 tot 29 cm

5.2.2.1 95% BI afronden

Zoals hierboven al te zien was, rond je bij het berekenen van een 95% BI af, zoals je altijd doet bij het geven van een gemiddelde + fout. (Sommige statistici houden er van om alle maten van spreiding “meetfout” te noemen. Andere statistici vinden van niet. Maar voor nu komt het ons best even goed uit: we ronden af net als bij alle “meetfouten”, namelijk:)

• Het steekproefgemiddelde en fout schrijven we als dezelfde macht van 10 (of orde van grootte): \(26 \pm 2.66375\) cm
• We beginnen met het afronden van de meetfout. op 1 significant cijfer :\(26 \pm 3\) cm
• Kijk naar het aantal decimalen die de meetfout nu heeft. Rond je meetwaarde af op hetzelfde aantal decimalen (cijfers na de komma): \(26 \pm 3\) cm (26 had al geen decimalen).
• Wil je het 95% BI dan als een range aangeven, of de ondergrens / bovengrens berekenen, dan werk je verder met de afgeronden getallen: het 95% BI is 23-29 cm.

Let op, als je de ondergrens en bovengrens door Excel laat berekenen, rondt Excel niks af! Dan kom je dus niet goed uit.

95% BI bij tellen: de poissonverdeling

Bij teldata gebruik je geen normaalverdeling of t-verdeling. Als je het aantal UNITS per IETS aan het tellen bent, gebruik je vaak een poissonverdeling (aantal katten/\(km^2\), aantal rode bloedcellen/liter). Het exacte 95% BI bij een poissonverdeling berekenen is wat ingewikkelder en gaan we niet handmatig doen. Er zijn verschillende manieren om het 95% BI bij teldata ongeveer te berekenen.

Je kan weer 1,96 gebruiken, maar het is ook niet ongebruikelijk bij teldata om gewoon 2 te nemen, want het is toch al een benadering.

Bij een Poissonvredeling zijn we aan het tellen, dus N en \(\overline{x}\) zijn hetzelfde. We hebben alleen maar dat ene nummertje om mee te werken. Bij een poissonverdeling geldt dus:

grove schatting van het 95% BI = \(aantal \pm 2*\sqrt{aantal}\)

5.2.3 Herhaling: histogrammen

We hebben al een boel gebruikt gemaakt van histogrammen. We bespraken ze in les 1 al (hierzo) In een histogram laat je zien hoe vaak bepaalde meetwaarden voorkomen. Hieronder hebben we bijvoorbeeld een histogram van kattenstaartlengtes van Siamezen. Op de X-as zie je de staartlengtes, opgedeeld in ranges (15-18 cm, 18-20 cm, 20-22 cm enzovoorts). Op de Y-as zie je hoeveel Siamezen een staartlengte in die range hadden.

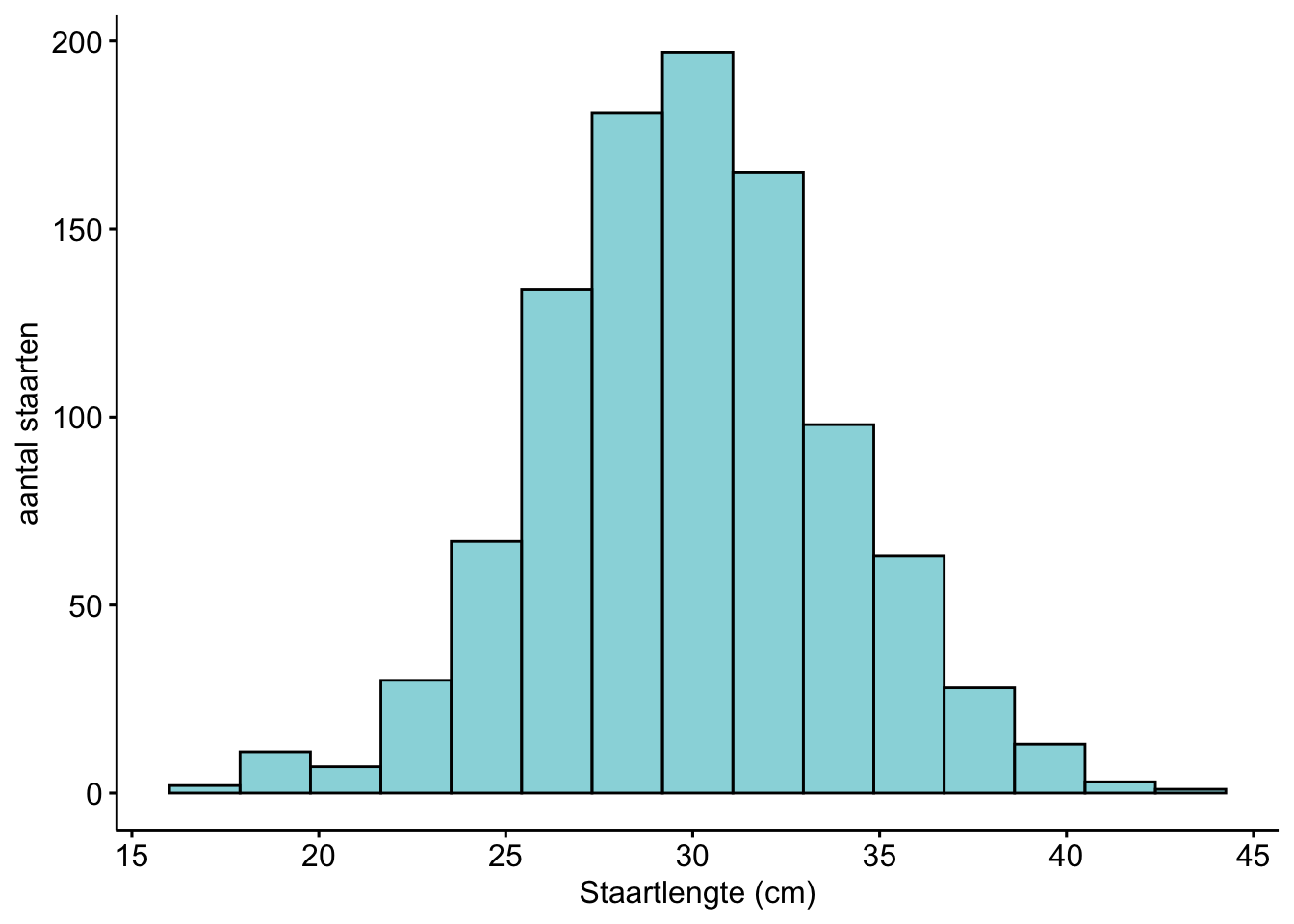
Figure 2.1: Histogram van de staartlengtes van Siamezen. Te zien is dat de gemiddelde siamezenstaart ongeveer 30 cm is.

Een histogram laat dus de kansdichtheid zien voor deze data. Die term heb je wellicht al een paar keer bij een y-as zien staan. Die term heeft te maken met dat het oppervlak van de balken in de grafiek (en dus de hoogte ook) correspondeert met de kans om een kat met een bepaalde staartlengte te meten in deze groep katten.

Een histogram lijkt een beetje op een staafdiagram, maar bij een histogram beschrijf je continue data (een kattenstaart kan 30, maar ook 30,342 cm zijn) en een staafdiagram hoort bij discrete verdelingen. Bijvoorbeeld deze, waarbij de verdeling in diersoort discreet is (een dier is of een kat of een hond. Niet 1,564 kat.). Dit is een staafdiagram:

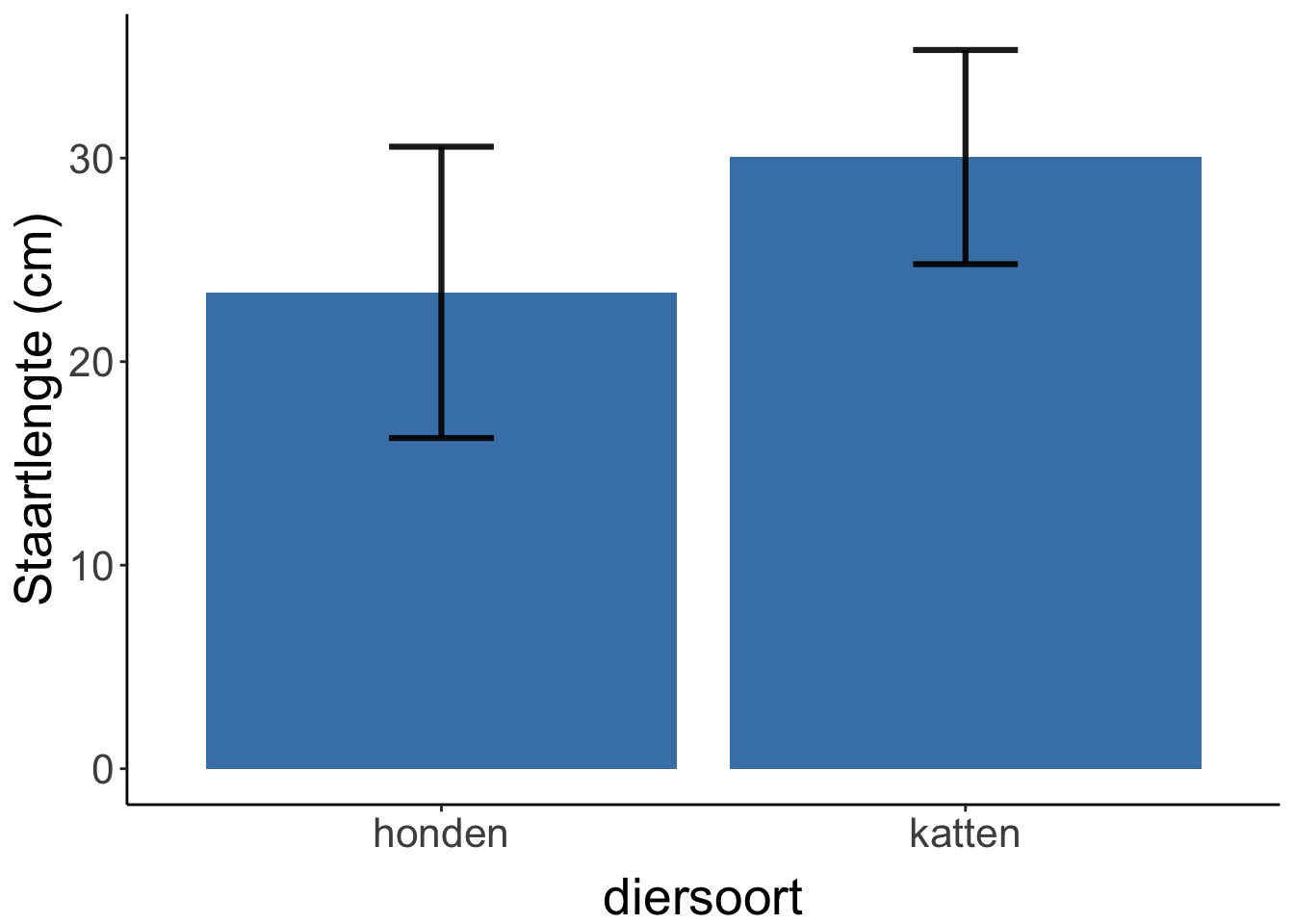
Figure 1.3: Gemiddelde staartlengte van katten en honden op de Uithof. In de foutenbalken staat de standaarddeviatie.

5.2.4 Verschilvragen met een 95% BI beantwoorden

Tot nu toe hebben we gekeken naar het 95% BI in de context van prangende vragen als “wat is de gemiddelde kattenstaartlengte in Utrecht dit jaar?”. Maar je kan het 95% BI ook gebruiken om verschilvragen te beantwoorden. Stel, de gemiddelde kattenstaartlengte in 2020 was 30 centimeter. Dit jaar kunnen we met 95% zekerheid kunnen zeggen dat de gemiddelde kattenstaartlengte van de populatie tussen de 27 en 29 centimeter ligt. Dan weet je dus eigenlijk dat de gemiddelde kattenstaartlengte in Utrecht kleiner is dan vorig jaar! Want de verwachte waarde als er geen verschil zou zijn met vorig jaar (30 cm) ligt buiten het 95% betrouwbaarheidsinterval (27-29 cm).

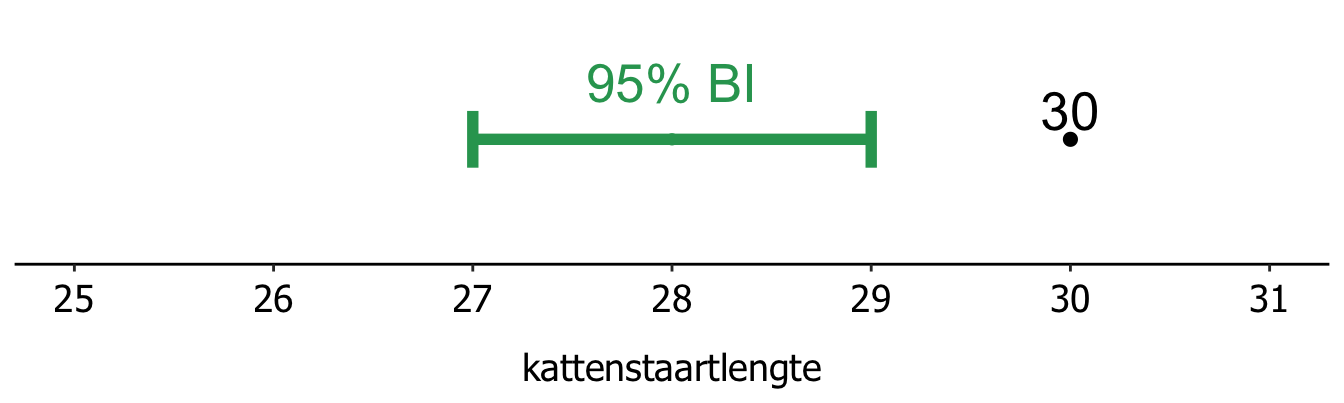
Met een 95% BI kun je dus ook verschilvragen beantwoorden: Is de kattenstaartlengte in Utrecht korter dan vorig jaar? Ja!

5.3 Werkcollege

5.3.1 Deel 1: steekproefstandaarddeviatie

Om het 95% BI uit te rekenen als je de populatiestandaarddeviatie niet weet, moet je de steekproefstandaarddeviatie weten. Dat gaan we eerst nog een keer oefenen. De bedoeling van deze opdracht is niet dat je straks zonder stappenplan handmatig standaarddeviaties kunt berekenen, maar dat je A) meer inzicht krijgt in wat een standaarddeviatie nou precies is en B) meer oefent met berekeningen in Excel.

Stel: Een machine weegt per keer 20 gram suiker af. Een monteur pakt 8 willekeurige bakjes met suiker en weegt ze op weegschaal 1 en op een nieuwe weegschaal 2.

• Open file les5_opdracht1.xlsx
• Bereken het gemiddelde van de 8 bakjes per weegschaal in Excel in B11 en C11

Exercise 5

Wat is het gemiddelde voor zowel weegschaal 1 en weegschaal 2?

Klik hier voor het antwoord

20,0 gram

Vervolgens ga je de standaarddeviatie \(s\) van de metingen op weegschaal 1 handmatig uitrekenen zonder gebruik te maken van de Excel formule voor de standaarddeviatie. Je gebruikt de formule voor standaarddeviatie. Hieronder staat een stappenplan.

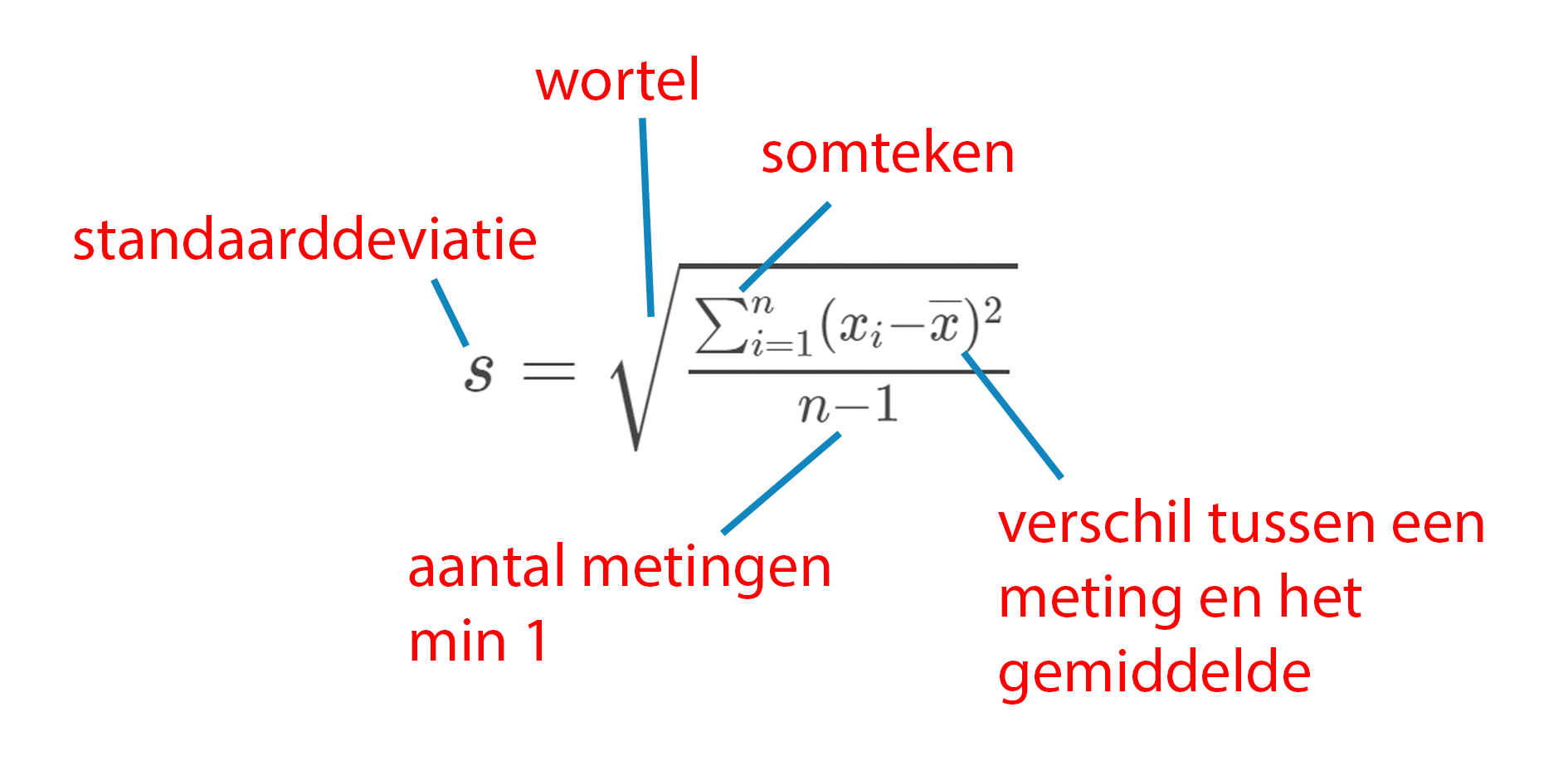
• Als eerste bereken je voor elke losse meting \(x_{i}\) het verschil met het steekproefgemiddelde \(\overline{x}\) in kolommen E en F. Dat is \(x_{i}-\overline{x}\) De antwoorden voor de eerste elementen zijn al gegeven.
• Bereken het kwadraat van de kolommen E en F in de kolommen I en J. In I en J staat dan dus \((x_{i}-\overline{x})^2\)
• Tel alle gekwadrateerde waarden voor weegschaal 1 en weegschaal 2 bij elkaar op in cel I11 en J11 (Nu heb je \(\sum_{i=1}^n(x_{i}-\overline{x})^2\))
• Deel I11 en J11 door \((n-1)\) in I12 en J12. (Je hebt nu \(\frac{\sum_{i=1}^n (x_i - \overline{x})^2 }{n-1}\))
• Neem de wortel van I12 en J12 in I13 en J13 (\(s = \sqrt{\frac{\sum_{i=1}^n (x_i - \overline{x})^2 }{n-1} }\))

Je hebt handmatig de standaardeviaties berekend!

Exercise 5

Wat is de standaarddeviatie van de metingen op weegschaal 1? Geef je antwoord met twee decimalen nauwkeurig.

Klik hier voor het antwoord

5,40 gram

Exercise 5

Wat is de standaarddeviatie van de metingen op weegschaal 2? Geef je antwoord met twee decimalen nauwkeurig.

Klik hier voor het antwoord

1,94 gram

Reken de standaarddeviatie uit met de STDEV.S ( standard deviation of a sample) formule van Excel (in B12 en C12) en vergelijk met de waarde in I13 en J13.

Exercise 5

Zijn de door jou berekende standaardeviaties gelijk aan de standaarddeviaties die door Excel zijn berekend?

Klik hier voor het antwoord

Nou ja, dat hopen we wel. Als niet: controleer je berekeningen!

Heb je bij de excelformule wel =stdev.s() gebruikt? Dit is namelijk een steekproef, en niet de populatie (stdev.p())

We gaan nu een staafdiagram maken met het gemiddelde en error bars op basis van de standaarddeviaties.

Exercise 5

Maak een staafdiagram. Zorg dat de x-as en y-as de juiste titels krijgen. Geef de assen bijschriften. Stel de maximale waarde van de y-as in op 30.

Voeg errorbars toe met de juist standaarddeviatie. Ben je vergeten hoe dat moet, ctrl-klik dan hier: klik

Klik hier voor het antwoord

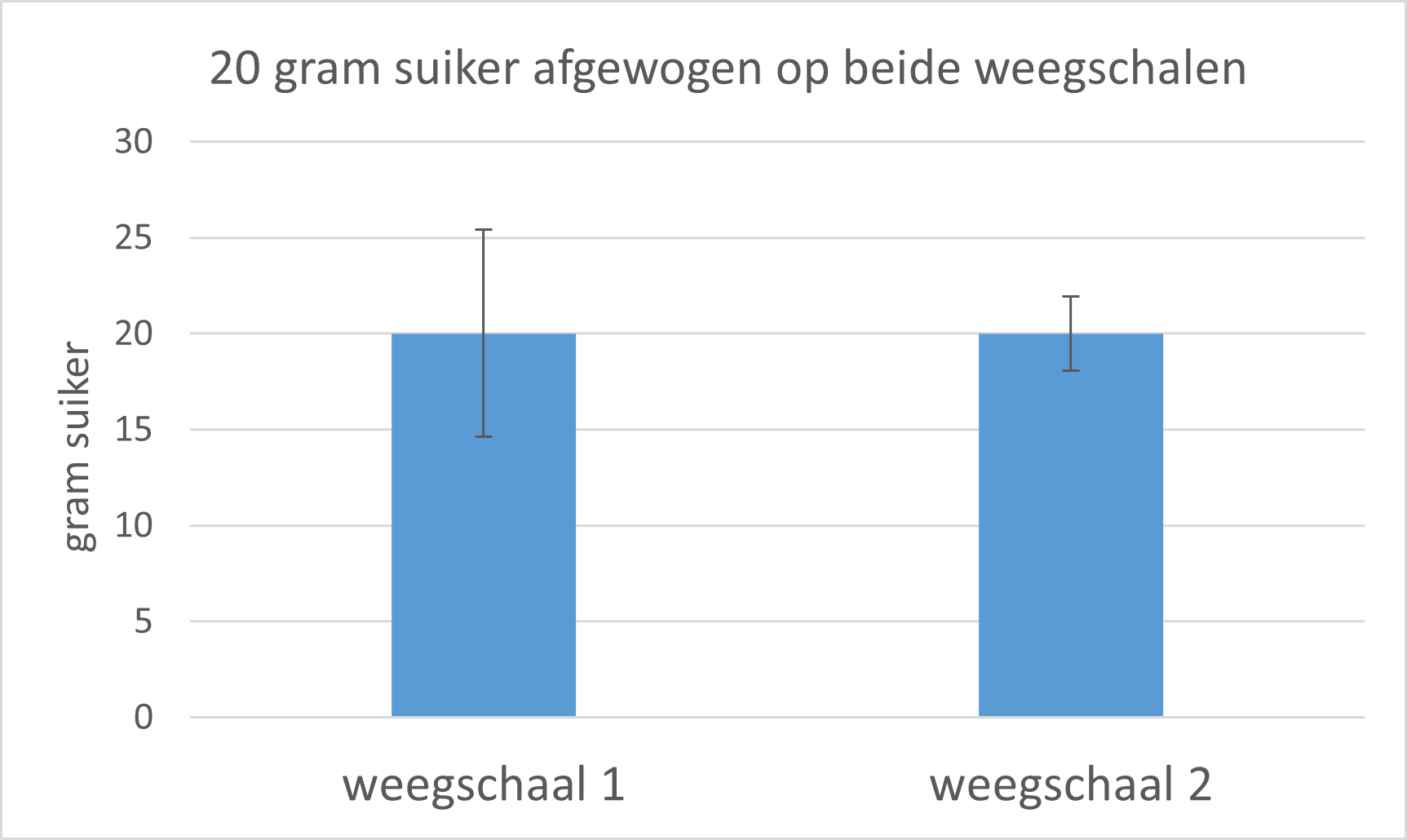
Exercise 5

Welke weegschaal weegt nauwkeuriger?

Klik hier voor het antwoord

weegschaal 2, die heeft de kleinste standaarddeviatie.

5.3.2 Deel 2: 95% BI

Een onderzoeker bepaalt het hemoglobinegehalte van 18 jongens en wil een uitspraak doen over de populatie met 95% betrouwbaarheid.

• Importeer de data uit les5_hemoglobineA.txt (decimal separator is een punt) of les5_hemoglobineB.txt in Excel.
• Bereken het gemiddelde en de standaarddeviatie:

Exercise 5

Wat is het gemiddelde \(\overline{x}\) en standaarddeviatie \(s\) van het hemoglobinegehalte van deze 18 jongens?

1. 9,36 \(\pm\) 0,66 mmol/L
2. 9,37 \(\pm\) 0,66 mmol/L
3. 9,3 \(\pm\) 0,7 mmol/L
4. 9,4 \(\pm\) 0,7 mmol/L

Klik hier voor het antwoord

4. 9,4 \(\pm\) 0,7 mmol/L (vergeet de eenheid niet)

Let dus op dat \(\pm\) tegenkomt bij het noteren van gemiddelde \(\pm\) standaarddeviatie, maar ook bij het berekenen van een 95% BI. \(\pm\) betekent gewoon “eronder en erboven”, en wordt op allerlei plekken gebruikt bij wiskundige notaties. Daarom is het dus belangrijk om altijd duidelijk op te schrijven wat je bedoelt.

De onderzoeker van de vorige vraag heeft alleen maar het gemiddelde en de standaarddeviatie van de steekproef en wil graag een 95% BI uitrekenen.

Exercise 5

Mag de onderzoeker de z-verdeling gebruiken om het 95% B.I. berekenen?

Klik hier voor het antwoord

Nee, de steekproef heeft te weinig meetpunten

De onderzoeker heeft het gemiddelde en de standaarddeviatie gebaseerd op een kleine steekproef (n < 50). De onderzoeker moet dus de t-verdeling gebruiken! Op het formuleblad staan de t-waarden voor het berekenen van een 95% B.I.

Exercise 5

Wat is de waarde van t voor een 95% B.I. ongeveer bij 45 vrijheidsgraden?

1. 1
2. 1.5
3. 2
4. 2.5

Klik hier voor het antwoord

C

Aangezien t-waardes voor vrijheidsgraden 46-49 niet op het formuleblad staan kun je er vanuit gaan dat dat aantal vrijheidsgraden niet bij het beantwoorden van een vraag nodig gaat zijn. Ze bestaan natuurlijk wel.

Exercise 5

Hoe groot verwacht je dat t ongeveer is voor vrijheidsgraden 46 t/m 49??

Klik hier voor het antwoord

ongeveer 2, of tussen de 1,96 en 2,014

Exercise 5

Wat is de t-waarde voor een steekproef van n = 18?

Klik hier voor het antwoord

n = 18 aantal vrijheidsgraden = n - 1 = 17.

t-waarde = 2,110

Exercise 5

Wat zijn de onder- en bovengrens van het 95% betrouwbaarheidsinterval? Geef je antwoord in twee decimalen nauwkeurig.

Klik hier voor het antwoord

\(\sigma\) is onbekend (en \(\mu\) natuurlijk ook, anders berekenden we geen 95% BI), en we hebben minder dan 50 meetpunten. De formule is dus:

\(\overline{x} \pm t * \frac{s}{\sqrt{n}}\)

• \(\overline{x}\) : steekproefgemiddelde
• \(t\) : t-waarde
• \(s\): steekproefstandaarddeviatie
• \(n\) : aantal metingen in de steekproef

De t-waarde was 2,110

afgerond: 9,4 \(\pm\) 0,3

• ondergrens: 9,1
• bovengrens: 9,7

Er is natuurlijk ook een formule in Excel die de grenzen van het 95% B.I. uitrekent. Deze formule =confidence.t().

• De formule begint met G27, de waarde van het steekproefgemiddelde (kijk in je eigen werkblad in welke cel het gemiddelde staat).
• je moet drie dingen invullen:
  • Alpha = 0,05. (vraagje tussendoor: Wat zou je hier invullen als het 99% BI zou zijn?)
  • Standard_dev: Kijk dus in je eigen worksheet waar de Standard_dev staat. Dit kan een andere cel zijn dan G28!
  • Size: is het aantal elementen in de steekproef. In dit geval 18.
• Rond zelf de uitkomst af op 1 significant cijfer.
• Voor de ondergrens trek je de fout af van het gemiddelde. Voor de bovengrens tel je de fout erbij op.

Exercise 5

Laat Excel het 95% BI uitrekenen. Kom je op hetzelfde antwoord als toen je hem handmatig uitrekende?

5.3.3 Deel 3: meer oefenopgaven met het 95% BI

Exercise 5

Je doet een steekproef om te bepalen wat de gemiddelde hoeveelheid paracetamol in huismerk tabletten is. Daarvoor meet je 6 tabletten en vindt de volgende waarden in mg:

508.4

502.5

408.3

407.6

501.3

500.1

Wat is het 95% BI voor je schatting van het populatiegemiddelde?

Klik hier voor het antwoord

471,4 \(\pm\) 51,638…

=

(4,714 \(\pm\) 0,51638 ) * 10\(^2\)

=

afgerond: (4,7 \(\pm\) 0,5 ) * 10\(^2\) mg (seriously, niet die eenheid vergeten)

of

4,2 * 10\(^2\) - 5,2 * 10\(^2\) mg

Exercise 5

Je doet een steekproef om te bepalen wat de gemiddelde hoeveelheid acetylsalicylzuur (de werkzame stof) in aspirine is. Daarvoor meet je 20 tabletten en vindt een gemiddelde hoeveelheid van 514,6 mg en een standaarddeviatie van 3,5 mg. Met welke waarde van t moet je rekenen om het 95%-betrouwbaarheidsinterval te bepalen?

Klik hier voor het antwoord

2,093

Exercise 5

Je doet een steekproef om te bepalen wat de gemiddelde staartlengte is van muizen in de binnenstad. Je vangt 82 muizen en meet hun staart: gemiddeld 6,3 cm met een standaarddeviatie van 1,2 cm. Wat is het 95% BI voor jouw inschatting van de gemiddelde staartlengte van alle muizen in de binnenstad?

Klik hier voor het antwoord

Dit zijn meer dan 50 muizen, dus:

6,3 \(\pm\) 0,2597… cm

dus afgerond: 6,3 \(\pm\) 0,3 cm

ondergrens: 6,0 cm bovengrens 6,6 cm

Exercise 5

Van een populatie gezonde sterke CrossFitters wil je de nuchtere glucosewaarden weten. Je neemt hiervoor de ochtendgroep van 25 man. Je bepaalt op het lab een gemiddelde glucose concentratie van 4,50 mmol/L met een steekproefstandaarddeviatie van 1,5 mmol/L. Wat is het 95%-betrouwbaarheidsinterval voor de gemiddelde concentratie van glucose in deze populatie?

1. 4,5 ± 0,5 mmol/L
2. 4,5 ± 0,6 mmol/L
3. 4,5 ± 2,9 mmol/L
4. 4,5 ± 3,0 mmol/L

Klik hier voor het antwoord

B

Exercise 5

De fabrikant van doosjes pain-be-gone beweert dat de hoeveelheid werkzame stof per pil gemiddeld 300 gram is, met een standaarddeviatie van 0,5 gram.

Je koopt een doosje van 12 pillen pain-be-gone en komt op een steekproefgemiddelde van 299,0 gram. Wat is het 95% betrouwbaarheidsinterval voor deze schatting?

Klik hier voor het antwoord

De populatiestandaarddeviatie is bekend: 0,5. Die gebruik je dus bij de berekening:

299,0 \(\pm\) 0,3 mg

Exercise 5

Je weet dat op Schiermonnikoog de gemiddelde lengte van alle vrouwen boven de 20 jaar, 1.72 beter is, met een standaarddeviatie van 9 cm. Ga je een 95% BI uitrekenen door middel van de z-verdeling?

Klik hier voor het antwoord

Nee, je weet het populatiegemiddelde al, dus je hoeft niet een range te berekenen waar die met een betrouwbaarheid van 95% binnen zal zitten.

Exercise 5

Op een medisch laboratorium is men bezig om te analyseren of de nieren van een patiënt normaal functioneren. Hiervoor wordt de concentratie creatine in het bloed van de patiënt 5 keer bepaald. Uit de analyseresultaten blijkt dat de concentratie creatine gemiddeld 45,8 μmol/L is. De steekproef-standaarddeviatie is 3,8 μmol/L. Binnen welke grenzen ligt met 95% zekerheid het gehalte creatine bij deze patiënt?

Klik hier voor het antwoord

45,8 ± 4.71 µmol/L afronden geeft 46 ± 5 µmol/L

of ook goed: 41-51 µmol/L

eventueel als je Excel gebruikte ook goed: Tussen 41,1 en 50,5 µmol/L

Exercise 5

Je gaat de concentratie van cholesterol in bloed van je laboratoriumratten onderzoeken. Daarom meet je van 10 ratten de concentratie cholesterol in het serum. Je vindt een gemiddelde concentratie van 25,0 mg/dL in deze 10 dieren, met een steekproefstandaarddeviatie van 2,2 mg/dL. Wat is het 95%-betrouwbaarheidsinterval voor de gemiddelde concentratie cholesterol in laboratoriumratten?

Klik hier voor het antwoord

25 ± 2 mg/dL

5.3.4 Deel 4: verschilvragen

Exercise 5

De fabrikant van doosjes pain-be-gone beweert desgevraagd over de mail dat de hoeveelheid werkzame stof per pil gemiddeld 300 mg is, met een standaarddeviatie van 0,5 mg.

Je gelooft er niets van en koopt een doosje van 12 pillen pain-be-gone. Je meet ze en komt op een steekproefgemiddelde van 299 mg.

1. Wat is het 95% betrouwbaarheidsinterval voor deze schatting?

2. Waar is dit een schatting van?

Klik hier voor het antwoord

De populatiestandaarddeviatie is bekend: 0,5. Die gebruik je dus bij de berekening:

299 \(\pm\) 0,2829… mg

afgerond: 299 \(\pm\) 0,3 mg

2. Van het populatiegemiddelde.

Exercise 5

Er is al een populatiegemiddelde bekend. Waarom berekenen we dan hier toch een 95% betrouwbaarheidsinterval? Dat 95% BI was toch om een schatting te geven van een populatiegemiddelde?

Klik hier voor het antwoord

Omdat we het opgegeven populatiegemiddelde willen controleren.

Exercise 5

Heeft de fabrikant gelijk als ze zeggen dat ze pain-be-gone maken met gemiddeld 300 gram werkzame stof met een standaarddeviatie van 0,5 gram?

Klik hier voor het antwoord

Nee, waarschijnlijk niet. 300 mg valt buiten onze schatting van het populatiegemiddelde op basis van de steekproef en de door de fabrikant opgegeven populatie-standaarddeviatie. Dus of hun opgegeven populatiegemiddelde klopt niet, of hun opgegeven populatiestandaarddeviatie klopt niet.

Exercise 5

Je belt de fabrikant op om verhaal te halen. Deze vertelt je dat ze een foutje hebben gemaakt in de mail: de populatiestandaarddeviatie was geen 0,5 gram, maar 5,0 gram. Maar, zo beweren ze, het gemiddelde percentage werkzame stof van 300 gram klopt echt! Klopt dat?

Klik hier voor het antwoord

Met een populatie-standaarddevatie van 5,0 gram kom je op een 95% BI van 296 tot 302 gram. 300 valt hierbinnen, dus de (nieuwe) bewering van de fabrikant zou wel kunnen kloppen.

Exercise 5

We weten dat de inhoud van flesjes Bubbelhup in Nederland 300 ml is. Je koopt 100 flesjes Bubbelhup in Belgie en meet de inhoud. De data staat in bubbelhup.xlsx

• Bedenk dat je in Excel ook naar het gemiddelde van een hele kolom kunt vragen: type =AVERAGE( in een cel in een andere kolom, klik op de letter van de kolom waarvan je het gemiddelde wilt weten, type ) , druk op enter.
• Bevatten flesjes Bubbelhup in Belgie meer ml dan in Nederland?

Klik hier voor het antwoord

Nee, waarschijnlijk niet. We kunnen met 95% zekerheid zeggen dat het populatiegemiddelde in Belgie ligt tussen de 299 en 301 ml. Daar ligt 300 ook tussen, dus de inhoud van flesjes Bubbelhup lijkt niet anders dan in Nederland.

Exercise 5

Bij gezonde volwassenen induceren onder de 40 jaar drie vaccinaties (volgens het standaardschema) een beschermende antistoftiter (anti-HBs≥10 IE/l). Je meet de concentratie anti-HBs bij mr Jansen en vindt een 95% BI van 5,0 - 8,0 IE/l

Welke van de volgende beweringen is waar?

1. De populatie waar deze meting uit komt is waarschijnlijk een andere dan die met een antistoftiter boven de 10 IE/L
2. Deze meting komt waarschijnlijk uit de populatie met mensen die een beschermende antistoftiter hebben.
3. Deze meting moet wel een outlier zijn.
4. We weten 95% zeker dat mr Jansen niet gevaccineerd is tegen hepatitis B.

Klik hier voor het antwoord

A. De populatie waar mr Jansen in zit is een populatie met een niet-hoog-genoege antistoftiter. Een andere populatie dus. Waarom dat bij mr Jansen het geval is weten we niet.