Les 7 T Toetsen

7.1 Lesinhoud en leerdoelen

In deze les behandelen we de two sample t-toets. Deze voer je uit als je een verschilvraag hebt, en twee steekproeven.

Theorie:

two sample t-toets vs one sample t-toets
steekproefgrootte en biologische variatie bij verschilvragen
verschillende typen two sample t-toetsen:
- eenzijdig of tweezijdig
- gepaard of ongepaard
gelijke of ongelijke variantie

Vaardigheden:

two sample t-test in Excel
oefenen met p-waarden

7.2 Voorbereiding

In deze laatste les gaan we kijken naar de two sample t-toets, een t-toets bij 2 steekproeven.

In les 5 heb je geleerd hoe je op basis van een steekproef een 95% betrouwbaarheidsinterval kunt berekenen. Het is dus ook mogelijk om met een zekerheid van 95% te stellen dat een bepaalde waarde niet het gemiddelde kan zijn van de populatie waaruit je steekproef genomen is. In feite vergelijk je dan een referentiewaarde met het 95% betrouwbaarheidsinterval. Dat was een one sample t-toets. Bijvoorbeeld, in een fabriek wordt een nieuwe machine in gebruik genomen om tabletten paracetamol te produceren. Elk tablet moet 400 mg werkzame stof bevatten. Ter controle meet een werknemer in 100 tabletten de hoeveelheid werkzame stof, en bepaald het steekproefgemiddelde en de steekproefstandaarddeviatie. Met behulp van een one sample t-test toetst de werknemer of de schatting van het populatiegemiddelde significant verschilt van de beoogde hoeveelheid werkzame stof.

Maar een t-toets kun je ook doen als je twee steekproeven met elkaar wilt vergelijken! (of eigenlijk wil je de twee populaties met elkaar vergelijken, en daarvoor doe je twee steekproeven.)

Bijvoorbeeld: de werknemer wil weten of de nieuwe machine dezelfde hoeveelheid werkzame stof in tabletten stopt als de oude machine. Daartoe meet hij de hoeveelheid werkzame stof in 100 tabletten die zijn geproduceerd door de nieuwe machine, en 100 tabletten geproduceerd door de oude machine. Beide steekproeven geven een schatting van het werkelijke gemiddelde van de verschillende machines. In dit geval toets hij of de twee populatiegemiddelden (een voor de oude machine, een voor de nieuwe) significant van elkaar verschillen met een two sample t-toets.

7.2.1 Two sample t-toets

Bijvoorbeeld: Hebben Siamezen nou langere staarten dan Abessijnen (ook katten) of niet? (callback naar les 1!)

Je moet twee steekproeven doen: je moet de staarten van een aantal Siamezen opmeten, en de staarten van een aantal Abessijnen. (Je meet dus 1 afhankelijke variabele: staartlengte. De onanfhankelijke variabele hier is kattenras: Siamees of Abessijn. )

In een staafdiagram geef je dan het gemiddelde staartlengte per ras weer (de hoogte van de staaf) en een indicatie van de spreiding (error bars). Op de X-as zet je de onafhankelijke variabele (ras). Op de Y-as zet je de afhankelijke variabele (staartlengte in cm).

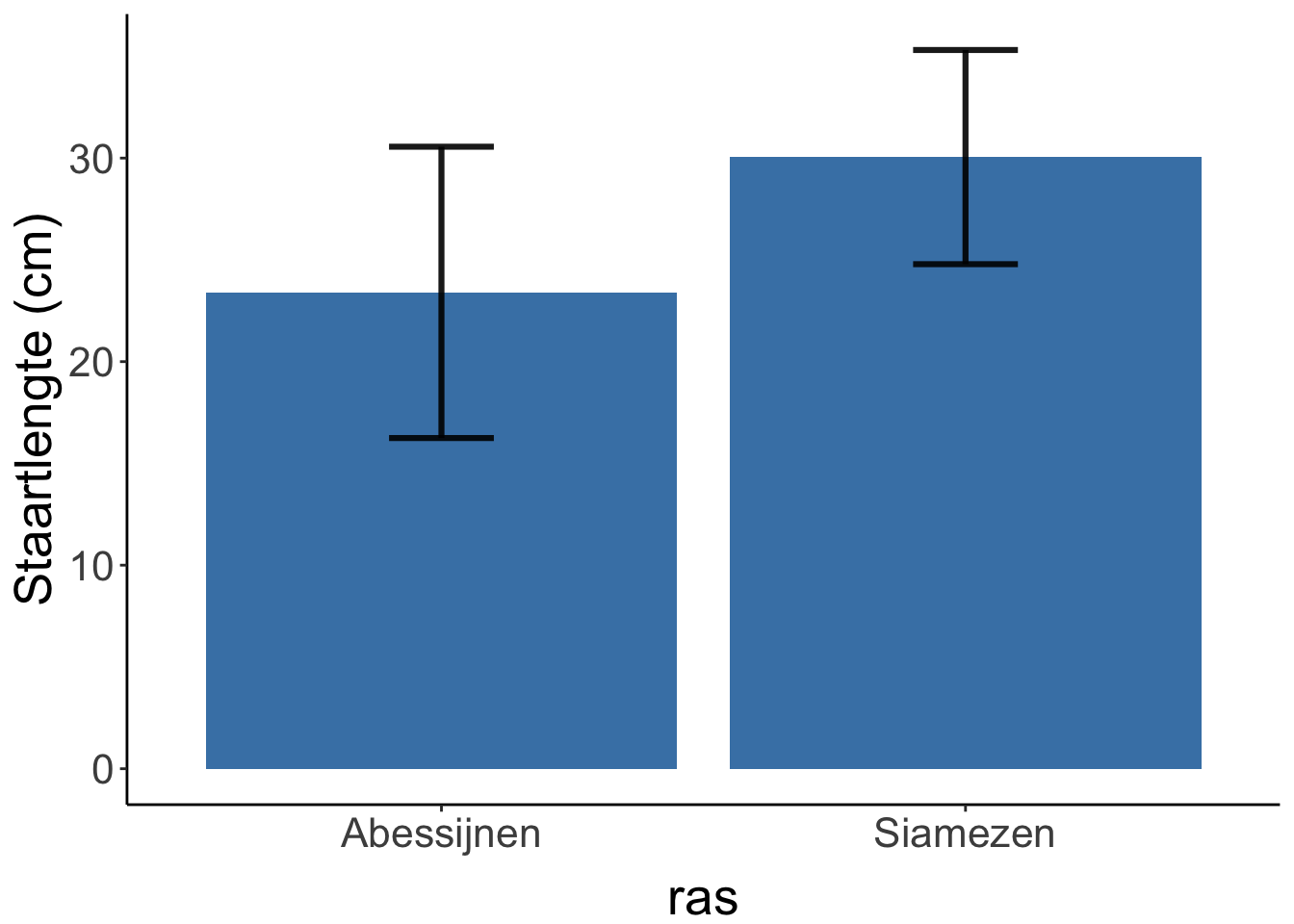
Figure 1.3: Gemiddelde staartlengte van Abesijnen en Siamezen. In de foutenbalken staat de standaarddeviatie.

Oke, top. Maar hebben de populaties katten waar we deze steekproeven uit namen nou even lange staarten? Dat reken je uit met een two sample t-test. Net als bij een one sample t-test stel je een nulhypothese op en krijg je weer een p-waarde.

H0: Siamezen hebben niet langere staarten dan abessijnen.

H1: Siamezen hebben langere staarten dan abessijnen.

Vind je een p-waarde onder de 0.05: verwerp de H0 en neem de H1 aan. Conclusie: Siamezenstaarten zijn significant langer dan abessijnenstaarten.

Vind je een p-waarde op of boven de 0.05: verwerp de H0 niet. Conclusie: Siamezenstaarten zijn NIET significant langer dan abessijnenstaarten.

(\(\alpha\) is nog steeds 0.05! niet opeens 0.5 of 0.1 of zo!)

Nulhypotheses bij two sample t-testen hebben deze vorm:
- Er is geen verschil in [uitkomstmaat] tussen [groep A en groep B]
- [uitkomstmaat] is niet [groter/kleiner] in [groep A] dan in [groep B]
Conclusies bij two sample t-testen hebben deze vorm:
- Er is [wel/niet] een significant verschil in [uitkomstmaat] tussen [groep A en groep B]
- [uitkomstmaat] is [wel/niet] significant [groter/kleiner] in [groep A] dan in [groep B]

Mis je een van de dikgedrukte onderdelen, dan is je nulhypothese/conclusie dus niet in orde.

7.2.2 Hoe werkt een two sample t-toets

In een two sample t-toets vergelijk je dus twee steekproeven. Weer bereken je een p-waarde: de kans op het waargenomen verschil tussen de streekproefgemiddeldes onder aanname dat ze uit dezelfde populatie komen (dat er geen verschil is tussen de onderliggende populaties). Voor de oplettende lezer: stiekem is een two sample t-toets dus inderdaad een one sample t-toets op het verschil tussen de twee steekproeven.

In Excel is er een aparte functie voor: T.TEST(), waar je twee kolommen met data voor nodig hebt in plaats van 1. Hij berekent weer een p-waarde voor je, makkelijker dan bij de one sample t-test. In T.TEST() mag je namelijk gewoon meteen de kolommen met data invoeren. De functie wil een aantal dingen van je weten: T.TEST(array1; array2; tails; type): array 1 en 2 zijn je steekproeven-data. Tails gaat over eenzijdig of tweezijdig en type gaat over gelijke of ongelijke variantie. Die dingen gaan we hieronder eerst inhoudelijk bespreken.

7.2.3 Biologische variatie

Maar wacht. Stel dat we onderzoeken of mensenoren op de uithof en mensenoren in Utrecht-binnenstad even lang zijn. We doen twee steekproeven om dat te onderzoeken. Als de nulhypothese zou kloppen, en er is geen verschil in oorlengte tussen de twee groepen mensen, waarom zou je dan niet twee keer precies hetzelfde steekproefgemiddelde vinden? Dan hoef je toch niet met kansen te gaan rekenen, je kan gewoon kijken of de steekproefgemiddeldes precies hetzelfde zijn?

Helaas, dat klopt niet.

Als twee steekproeven uit dezelfde populatie komen dan heb je misschien de verwachting dat ze dezelfde steekproefgemiddelde hebben, omdat ze allebei een schatting zijn van dezelfde populatiegemiddelde. Maar dat zou alleen werken als er a) helemaal geen variatie in de populatie zou zitten, of b) je de hele populatie zou meten.

Hopelijk heb je onthouden dat de metingen van een steekproef variabel zijn. Als je 5 steekproeven neemt in dezelfde populatie, vind je 5 keer andere data. Want je neemt steeds random n individuen uit de populatie. Als je dus een steekproef met 100 mensen op de Uithof hebt, en een met 100 mensen in de binnenstad, ga je verschillende steekproefgemiddeldes en steekproefstandaarddeviaties vinden, zelfs al zijn de oren van mensen op de uithof gemiddeld even lang als die van mensen in de binnenstad.

De twee steekproefgemiddeldes mogen dus best verschillen, terwijl je geen significant verschil vindt. Sterker nog, meestal zullen ze wat verschillen. Als de standaarddeviatie binnen de steekproeven groot is, dan kan de afwijking ook groot zijn, puur per toeval!

Door meetfouten, biologische variatie, allerlei oorzaken van spreiding, zul je bij een steekproef uit een populatie met populatiegemiddelde \(\mu\) niet steeds een steekproefgemiddelde \(\overline{x} = \mu\) vinden. Je moet dus wel gaan kansberekenen. Gelukkig maar (oke, we geven toe, die link is ancient. Deze is speciaal voor de docenten. Die zijn zo oud.)

7.2.4 Eenzijdige of tweezijdige toetsen

Ook two sample t-toetsen kunnen eenzijdig of tweezijdig zijn. Dat is de “tails” in T.TEST(array1; array2; tails; type) in Excel. Eigenlijk is dit makkelijker dan bij een one sample t toets:

Je gebruikt een eenzijdige toets wederom wanneer je kijkt naar verschil in een bepaalde richting. Je onderzoeksvraag is dan bijvoorbeeld “zijn mannen langer dan vrouwen?”. H0 is dan: Mannen zijn niet langer dan vrouwen. (Dus korter of even lang). en H1: mannen zijn langer dan vrouwen.

Bij een Tweezijdige toets wordt de onderzoeksvraag: “is er verschil in lichaamslengte tussen mannen en vrouwen?”. H0 is dan: Er is geen verschil in lengte tussen mannen en vrouwen. en H1: Er is wel een verschil in lengte tussen mannen en vrouwen.

Gebruik in geval van twijfel nog steeds altijd een tweezijdige t-toets. Zorg dat je onderzoeksvraag en hypothesen ook tweezijdig formuleert.

7.2.5 Gepaarde of ongepaarde steekproeven?

So far so good, dat is hetzelde als bij de one sample t-toets.

Maar bij two sample t-toetsen is er nog een ander ding om rekening mee te houden: hebben de metingen van die twee steekproeven nog met elkaar te maken (dat heet gepaard), of staan ze compleet los van elkaar (ongepaard)?

Stel bijvoorbeeld dat je de amylase-activiteit in het speeksel voor en na het eten van een boterham meet. Je doet sowieso twee steekproeven: 1 voor het eten van een boterham, en 1 na het eten van een boterham.

Doe je dat gepaard: dan meet je bij dezelfde mensen eerst de amylase-activiteit voor de boterham, en dan bi jdezelfde mensen er na. Dus 1 groep in 2 situaties.
Doe je dat ongepaard: dan meet je 2 verschillende groepen mensen. De ene groep mensen heeft geen boterham gegeten, en de andere groep mensen (andere mensen dus!) heeft wel een boterham gegeten.

Why do we care? Het voordeel van een gepaarde proef is dat de biologische variatie die je sowieso vindt in amylase-activiteit wegvalt, omdat je dezelfde mensen in beide steekproeven hebt. Dat maakt de kans groter dat verschillen in amylase-activiteit als gevolg van de boterham duidelijker worden.

Gepaard of ongepaard vul je in bij de “type” in T.TEST(array1; array2; tails; type) in Excel. Meer daarover in het werkcollege.

7.2.6 Proefopzet

Soms heb je de keus om iets gepaard of ongepaard te onderzoeken. Dan heeft gepaard dus de voorkeur. Maar soms heb je geen keus. Wil je bijvoorbeeld kijken of honden en katten in Utrecht even lange oren hebben, dan zul je dat ongepaard moeten onderzoeken. Want de honden in de ene groep kunnen niet even katten worden om in de andere groep te zitten. Welke toets je kunt doen, hangt dus af van je proefopzet! (experimental design):

Ongepaarde proefopzet: twee onafhankelijke groepen waarvan de items / proefpersonen / proefdieren per groep maar 1 keer gemeten worden. Onderzoeken met een controlegroep en een behandelde groep zijn hier een voorbeeld van.
Gepaarde proefopzet: 1 groep die twee keer gemeten worden: bijvoorbeeld voor een behandeling en na een behandeling.

Doe je dus een one sample t test dan moet je kiezen: eenzijdig of tweezijdig (en dat heeft te maken met je vraagstelling, maar niet met je proefopzet).

Doe je een two sample t test dan moet je twee dingen kiezen: eenzijdig of tweezijdig (en dat heeft te maken met je vraagstelling, maar niet met je proefopzet) en gepaard of ongepaard (en dat heeft wel direct te maken met je proefopzet).

7.2.7 Voorbeelden two sample t-toets-situaties

Eenzijdig, gepaard: Verlaagt de experimentele behandeling Bloeddruk-Be-Down de bloeddruk bij een groep patienten met syndroom snufneus-372?

Proefopzet: deze kan gepaard. Je kan dezelfde mensen twee keer meten: een keer voor de behandeling en een keer er na.
Data: je meet de bloeddruk van een x aantal patienten. Daarna starten de patienten met de behandeling. Daarna meet je dezelfde patienten nog een keer. Je zorg dat de data van 1 patient in dezelfde rij in Excel staat.
Onderzoeksvraag: eenzijdig. Er is een richting aan de vraag (“lager”).
Welke toets: two sample t toets, eenzijdig, gepaard.
H0: de bloeddruk van de patienten na de behandeling is niet lager dan de bloeddruk voor de behandeling.
H1: de bloeddruk van de patienten na de behandeling is lager dan de bloeddruk voor de behandeling.

Tweezijdig, gepaard: Verandert de experimentele behandeling Bloeddruk-Be-Down de bloeddruk bij een groep patienten met syndroom snufneus-372?

Proefopzet: zelfde als hierboven
Data: zelfde als hierboven
Onderzoeksvraag: tweezijdig. Er is geen richting aan de vraag
Welke toets: two sample t toets, tweezijdig, gepaard.
H0: er is geen verschil tussen de bloeddruk van de patienten na de behandeling en voor de behandeling.
H1: er is wel een verschil tussen de bloeddruk van de patienten na de behandeling en voor de behandeling.

Eenzijdig, ongepaard: Zijn de ijsjes bij ijssalon Toscana kouder dan de ijsjes bij ijssalon Venetia?

Proefopzet: ongepaard. Ijsjes van Toscala zijn geen ijsjes van Venetia.
Data: je meet de temperatuur van een x aantal ijsjes bij Toscana, en de temperatuur van een x aantal ijsjes bij Venetia
Onderzoeksvraag: eenzijdig. Er is een richting aan de vraag (“kouder”).
welke toets: two sample t toets, eenzijdig, ongepaard.
H0: ijsjes bij Toscala zijn niet kouder dan ijsjes bij Venetia
H1: ijsjes bij Toscana zijn kouder dan ijsjes bij Venetia.

Tweezijdig, ongepaard: Hebben de ijsjes bij ijssalon Toscana een andere temperatuur dan de ijsjes bij ijssalon Venetia? (of: is er een verschil in temperatuur tussen ijsjes bij ijssalon Toscana en ijsjes bij ijssalon Venetia?)

Proefopzet: zelfde als hierboven. Ijsjes van Toscala zijn nog steeds geen ijsjes van Venetia. Ook niet als we tweezijdig toetsen.
Data: zelfde als hierboven.
Onderzoeksvraag: tweezijdig. Er is geen richting aan de vraag.
welke toets: two sample t toets, tweezijdig, ongepaard.
H0: ijsjes bij Toscana hebben geen andere temperatuur dan ijsjes bij Venetia / er is geen verschil in temperatuur tussen ijsjes bij Toscana en ijsjes bij Venetia.
H1: ijsjes bij Toscana hebben wel een andere temperatuur dan ijsjes bij Venetia / er is wel een verschil in temperatuur tussen ijsjes bij Toscana en ijsjes bij Venetia.

7.2.8 Fouten bij hypothesetests

Moeten we bij Toscana dan altijd evenveel ijsjes meten als bij Venetia? Nou, precies evenveel is bij een ongepaarde meting niet per se nodig (maar wel beter). (Bij een gepaarde meting heb je automatisch evenveel metingen in beide steekproeven.) Als het aantal metingen heel erg verschilt, neemt de kans toe dat je concludeert dat er een significant verschil in ijstemperatuur is, terwijl dat in werkelijkheid niet klopt.

We hebben al gezien dat statistiek te maken heeft met kansberekening, en met het stellen van een drempelwaarde aan die kansen (0.05). Dat betekent dus automatisch dat we ook wel eens fouten gaan maken. Fouten heb je in twee smaken: Type 1 (false positive) en Type 2 (false negative):

Stel, je zoekt panda’s.

Type 1 error: “Dit is een panda!”

In werkelijkheid is dit geen panda. Die vis ook niet. Foto van Carl Chapman from Phoenix, usa, CC BY 2.0, Wikipedia

Type 2 error: “Dit is geen panda!”

In werkelijkheid is dit juist wel een panda. Foto van Fernando Revilla, Wikipedia

Je moet dus ongeveer evenveel metingen hebben in beide steekproeven om een two sample t-test te mogen doen. Een paar metingen verschil is niet zo’n ramp.

7.2.9 Gelijke variantie

Als we twee t-verdelingen met elkaar aan het vergelijken zijn, moeten die dan even breed zijn? Of in mensentaal: is het noodzakelijk dat de spreiding in de steekproef ijsjes van Toscana even groot is als de spreiding in de steekproef ijsjes bij Venetia? Want anders hebben onze schattingen van het populatiegemiddelde een verschillende nauwkeurigheid toch? En die t-toetsen hadden iets te maken met een 95% betrouwbaarheidsinterval, dus dat maakt vast uit?

Inderdaad, dat maakt uit. Daarom bereken je de p-waarde in een t-test bij ongelijke variantie iets anders. De meest gebruikte manier is om de hoeveelheid vrijheidsgraden in je berekeningen iets te verlagen als er een verschil is in variantie, om te compenseren. Dit doet Excel allemaal voor je, je moet alleen wel even zelf aangeven of de varianties van de steekproeven gelijk zijn. Dat vul je ook in bij de “type” in T.TEST(array1; array2; tails; type) in Excel. Meer daarover in het werkcollege.

Hoe weet je dat dan? Nou, het eerlijke antwoord is dat je daar weer een nulhypothesetest voor moet uitvoeren, met H0: de varianties zijn niet verschillend en H1: de varianties zijn verschillend. Het houdt je van de straat, die statistiek… Voor deze cursus laten we deze toets even voor wat het is, en kun je de volgende vuistregel gebruiken:

Bereken voor beide steekproeven (groepen) de steekproefstandaarddeviatie \(s\). Als de grootste steekproefstandaarddeviatie minder dan drie keer de kleinste steekproefstandaarddeviatie is, zijn de resultaten nog wel oke als je uitgaat van gelijke variantie.

Dus als \(s_{grootste} / s_{kleinste} < 3\) : min of meer gelijke varianties

als \(s_{grootste} / s_{kleinste} > 3\) : ongelijke varianties

7.3 Werkcollege

Als je twee steekproeven met elkaar wilt vergelijken moet er aan een aantal voorwaarde voldaan zijn:

Je hebt een verschilvraag
Je hebt 2 steekproeven (heb je er maar 1, dan doe je een one sample t test)
De data zijn interval of ratio (dwz, meetwaarden in de vorm van cijfers)
Beide steekproeven zijn afkomstig uit een normaal verdeelde populatie (hoe je dat test leer je ook in jaar 2, je mag er nu vanuit gaan dat het dat is als we je vragen en t-toets te doen.)
je hebt ongeveer evenveel metingen in beide steekproeven

Als je twee steekproeven met elkaar vergelijkt gebruik je in Excel de =T.TEST formule:

Deze formule bestaat uit de volgende onderdelen:

Array 1: Meetwaarden van steekproef 1.
Array 2: Meetwaarden van steekproef 2.
Tails: eenzijdig (1) of tweezijdig (2).
Type: Gepaard (1), ongepaard met gelijke variantie (2) of ongepaard met ongelijke variantie (3).

7.3.1 Deel 1 - Data sorteren in Excel

Soms heb je data in kolommen staan in een volgorde die je niet bevalt. Alles door elkaar bijvoorbeeld. Wil je data in kolommen sorteren, dan kan Excel dat voor je doen.

Download van Canvas het bestand Sorteerdata.xlsx. download hem hier voor de voltijd en deeltijd.

In het eerste werkblad zie je de data van de screenshots hieronder. Doe mee met de volgende stappen:

Selecteer de tabel die je wilt sorteren:

Klik op het tabblad Data op het knopje Sort

Selecteer bij Column de kolom op basis waarvan je wilt sorteren (in dit geval: groep):

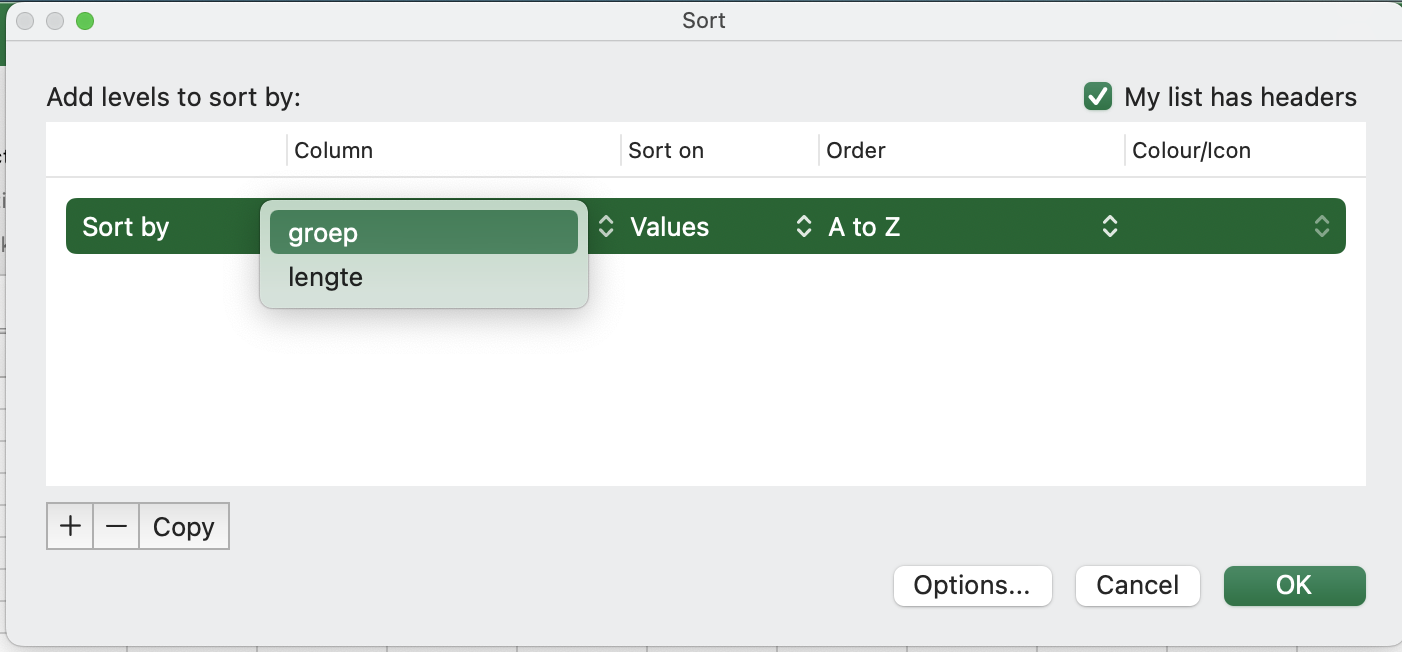
Bij Order kun je kiezen of je van klein naar groot of van groot naar klein wilt sorteren.

Klik OK en je data is gesorteerd!

Opdracht 7

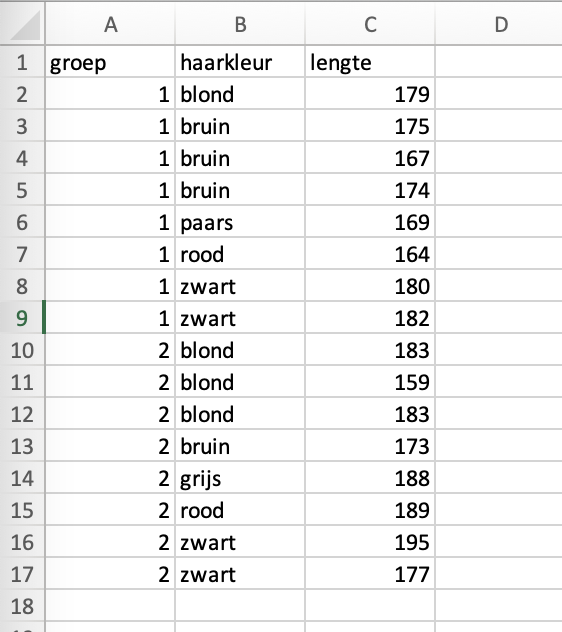
In het tweede werkblad vind je data waar ook gegevens over haarkleur in zitten. We willen graag deze data op groep-, en vervolgens op haarkleur sorteren.

Als je in het schermpje van net op het plusje linksonderin klikt, kun je nog een kolom toevoegen waarop je wilt sorteren.

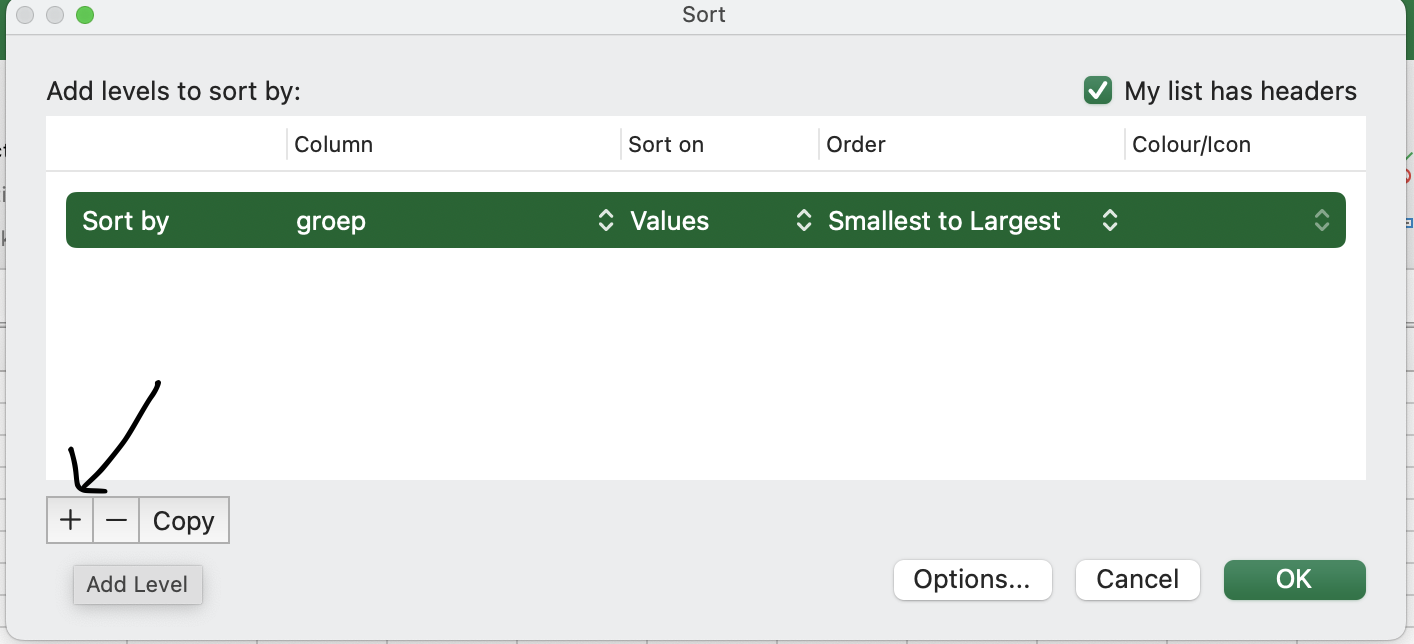
Probeer de data te sorteren op groep en op haarkleur.

Klik hier voor het antwoord

Als het gelukt is, zag het schermpje er zo uit:

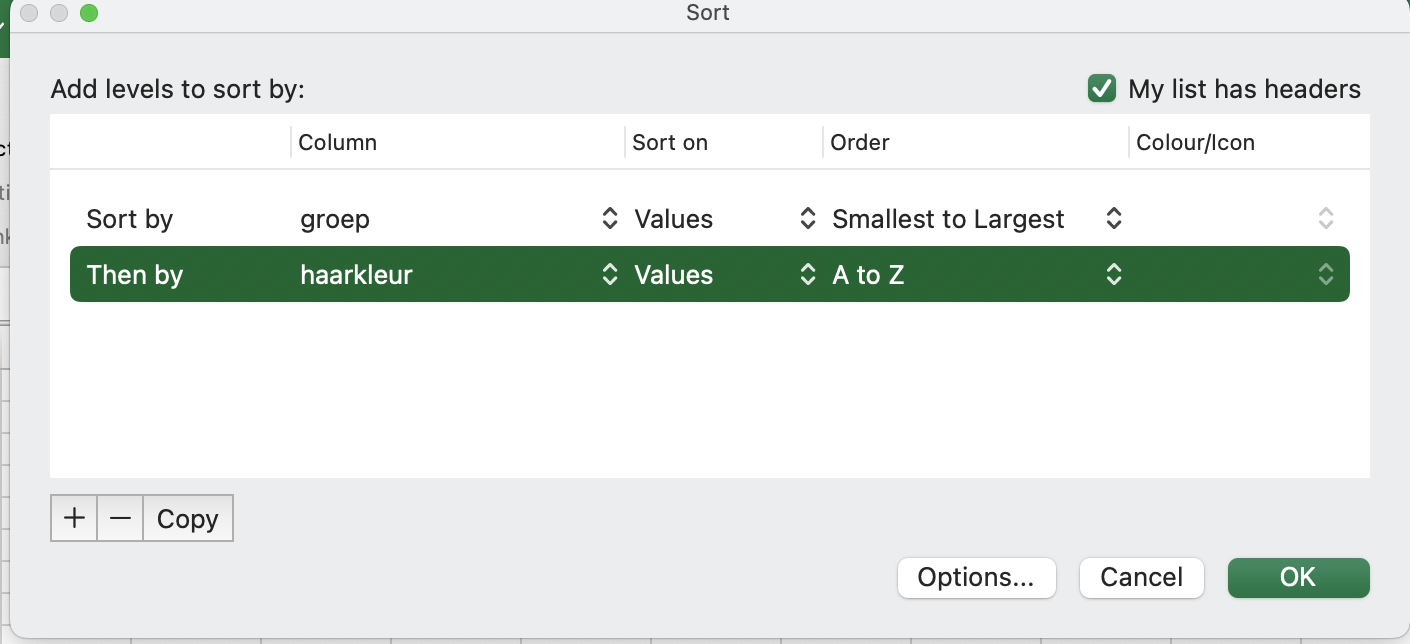
En de data nu zo:

7.3.2 Deel 2 - Ferritine

Open Ferritine.xlsx. In deze file staan de ferritine waardes in het bloed van verschillende groepen patiënten. Ferritine is een ijzerbindend eiwit dat het transport en opslag van ijzer regelt. Een tekort aan ferritine kan betekenen dat er een tekort aan ijzer is in het bloed.

In de eerste twee experimenten bestaan groep 1 en 2 uit verschillende personen. Van al die personen is de ferritine-concentratie één keer gemeten. De vraag is of de ferritine-concentratie van deze patiëntenpopulaties verschilt.

Opdracht 7

Bereken de gemiddelden en standaard deviaties voor de twee groepen. Bereken ook de p-waarden voor de verschillende t-toetsen in B4:B6. Zijn de p-waarden van de verschillende testen hetzelfde?

Klik hier voor het antwoord

Nee, elke t-toets levert een andere p-waarde op.

Je moet dus goed begrijpen welke je moet kiezen!

Opdracht 7

Zouden we gepaard of ongepaard moeten testen?

Klik hier voor het antwoord

ongepaard. Mensen zijn maar 1 keer gemeten, ze zitten in de ene steekproef OF in de andere, niet in allebei.

Opdracht 7

Is de spreiding binnen de twee groepen gelijk (“equal variance”) of niet (“non equal variance”)? Maak een schatting

Klik hier voor het antwoord

4,0 / 3,4 < 3, dus wel ongeveer gelijk genoeg.

Opdracht 7

Wat is de (juiste) p-waarde voor het verschil tussen beide groepen? Geef je antwoord in 4 decimalen nauwkeurig.

Klik hier voor het antwoord

\(p = 0,0499\)

De spreiding van de groepen in het tweede experiment is juist niet gelijk. De proefopzet en vraag waren hetzelfde als in experiment 1.

Opdracht 7

Reken na dat de spreiding niet gelijk is (unequal variances).

Klik hier voor het antwoord

6,0 / 0,8 > 3, dus inderdaad niet gelijk genoeg.

Opdracht 7

Bereken de gemiddelden en standaard deviaties voor de twee groepen. Bereken ook de p-waarden voor de verschillende t-toetsen in F4:F6. Zijn de p-waarden van de verschillende testen hetzelfde?

Klik hier voor het antwoord

Nee, elke t-toets levert een andere p-waarde op.

Opdracht 7

Wat is de (juiste) p-waarde voor het verschil tussen beide groepen? Geef je antwoord in 4 decimalen nauwkeurig.

Klik hier voor het antwoord

\(0,0528\)

Opdracht 7

Is het verschil tussen beide groepen in experiment 2 significant?

Klik hier voor het antwoord

Nee, want \(p > 0,05\).

Opdracht 7

Als de spreiding in beide groepen gelijk was geweest, was je conclusie dan anders geweest?

Klik hier voor het antwoord

Ja, je vindt dan een significant verschil tussen de groepen (\(p < 0,05\)).

Experiment 3 is anders opgezet. In plaats van twee onafhankelijke groepen te vergelijken zijn hier de ferritine-waarden van patiënten vergeleken voor en na behandeling met medicijnen. Dezelfde groep patiënten is dus twee keer gemeten: voor de behandeling en na de behandeling met het medicijn. Dit is een gepaarde meeting.

Opdracht 7

Bereken de gemiddelden en standaard deviaties voor de “voor” en “na” groep. Bereken ook de p-waarden voor de verschillende t-toetsen in J4:J6. Zijn de p-waarden van de verschillende testen hetzelfde?

Klik hier voor het antwoord

Nee, elke t-toets levert een andere p-waarde op.

Opdracht 7

Wat is de (juiste) p-waarde voor het verschil tussen beide groepen? Geef je antwoord in 4 decimalen nauwkeurig.

Klik hier voor het antwoord

\(0,0836\)

Opdracht 7

Is er een statistisch significant effect van de behandeling?

Klik hier voor het antwoord

Nee, want \(p > 0,05\).

7.3.3 Deel 3 - Eindelijk, die kattenstaarten

We zitten al sinds les 1 in spanning: hebben siamezen nou langere staarten dan abessijnen? Jullie docenten hebben ijverig doorgewerkt (alles voor de wetenschap en onze studenten he) en in beide groepen 100 kattenstaarten gemeten. Hier is de data! Open kattenstaarten.xlsx.

Opdracht 7

Wat is de nulhypothese?

Klik hier voor het antwoord

H0: siamezen hebben niet langere staarten dan abessijnen

Opdracht 7

Wat voor test ga je doen

Klik hier voor het antwoord

Dit is duidelijk een eenzijdige vraagstelling, en een ongepaarde proefopzet:

Een ongepaarde, eenzijdige two sample t-toets.

Opdracht 7

Wat is je conclusie?

Klik hier voor het antwoord

De proefopzet is ongepaard, dus we moeten kiezen of we “equal variances” evronderstellen of niet. Bereken van beide groepen de standaarddeviatie en deel de grootste door de kleinste:

7/5 < 3, dus we doen equal variances.

=T.TEST(A:A;B:B;1;2) geeft 1.15977E-12

oftewel 1,15977 * 10\(^{-12}\)

Dat is een heel stuk minder dan 0.05, dus we verwerpen H0!

Conclusie: Siamezenstaarten zijn significant langer dan abessijnenstaarten.

7.3.4 Deel 4 - Extra vragen over de lesstof

Opdracht 7

In een experiment bepaal je hoeveel amylase activiteit speeksel bevat door te meten hoeveel zetmeel er omgezet wordt door speeksel in 5 minuten. Je wilt weten of er verschil is in amylase activiteit tussen mensen die in het afgelopen uur gegeten hebben en mensen die langer geleden gegeten hebben. Je kunt dit experiment zowel gepaard als ongepaard opzetten. Wat heeft de voorkeur, en waarom?

Klik hier voor het antwoord

Gepaard, want dan heeft de biologische variatie geen invloed.

Opdracht 7

Je wilt weten of er verschil is in lichaamslengte tussen \(1^{ste}\) jaars en \(2^{de}\) jaars studenten aan het ILC. Je dataset bestaat uit 15 meetpunten per leerjaar en de data zijn normaal verdeeld. Welke t-toets ga je toepassen?

Klik hier voor het antwoord

two sample t-toets, ongepaard, tweezijdig.

Opdracht 7

Je onderzoekt een eventueel verschil in tijdsbesteding aan uiterlijke verzorging (in minuten per week) tussen mannen en vrouwen. Formuleer een nul-hypothese om dit statistisch te testen.

Klik hier voor het antwoord

Er is geen verschil in tijdsbesteding aan uiterlijke verzorging tussen mannen en vrouwen.

Opdracht 7

Je wilt weten of er een verschil is in lichaamsgewicht tussen rokers en niet-rokers. Je gaat je hypothese statistisch toetsen met een t-toets. Wat is je nul-hypothese?

Klik hier voor het antwoord

Er is geen verschil in massa tussen rokers en niet-rokers.

Opdracht 7

Je wilt weten of er een verschil is in lichaamsgewicht tussen rokers en niet-rokers. Je gaat je hypothese statistisch toetsen met een t-toets. De t-toets levert een p-waarde op van 0,006. Is er sprake van een statistisch significant verschil in lichaamsgewicht tussen rokers en niet-rokers?

Klik hier voor het antwoord

Ja, want \(p < 0,05\), dus er is sprake van een statistisch significant verschil.

Opdracht 7

Formuleer je conclusie bij de gegevens van de vorige vraag

Klik hier voor het antwoord

Er is een significant verschil in lichaamsgewicht tussen rokers en niet-rokers (p=0,006).

Opdracht 7

Je wilt weten of er verschil is in de gemiddelde temperatuur tussen de maanden juli en augustus. Stel de nul-hypothese op.

Klik hier voor het antwoord

Er is geen verschil in (gemiddelde) temperatuur tussen de maanden juli en augustus.

Opdracht 7

Je doet een tweezijdige, ongepaarde two sample t-toets en vindt een p-waarde van 0.80. Wat is je conclusie?

Klik hier voor het antwoord

Er is geen significant verschil in (gemiddelde) temperatuur tussen de maanden juli en augustus.

(dat “significant” geeft aan de lezer aan: ik roep niet zomaar wat, I actually did the math en ik heb data!)

Opdracht 7

In een experiment bepaal je hoeveel amylase activiteit speeksel bevat door te meten hoeveel zetmeel er omgezet wordt door speeksel in 5 minuten. Je wilt weten of er verschil is in amylase activiteit tussen mensen die in het afgelopen uur gegeten hebben en mensen die langer geleden gegeten hebben. Je wilt dit graag in een gepaarde opzet doen. Hoe kun je deze proef opzetten?

Klik hier voor het antwoord

Aan de proef neemt 1 groep mensen deel. Van deze groep wordt speeksel afgenomen voor en na het eten en de amylaseactiviteit in beide monsters wordt vergeleken.

Opdracht 7

In een experiment bepaal je hoeveel amylase activiteit speeksel bevat door te meten hoeveel zetmeel er omgezet wordt door speeksel in 5 minuten. Je wilt weten of er verschil is in amylase activiteit tussen mensen die in het afgelopen uur gegeten hebben en mensen die langer geleden gegeten hebben. Je wilt dit graag in een ongepaarde opzet doen. Hoe kun je deze proef opzetten?

Klik hier voor het antwoord

Aan de proef nemen twee groepen mensen deel. Van de ene groep wordt speeksel afgenomen zonder dat de personen vooraf hebben gegeten. Van de andere groep wordt speeksel afgenomen nadat de personen gegeten hebben. De amylaseactiviteit in beide groepen wordt vergeleken.

Opdracht 7

Je onderzoekt een eventueel verschil in tijdsbesteding aan uiterlijke verzorging (in minuten per week) tussen mannen en vrouwen. Je vindt een p-waarde van 0,67. Is er sprake van een statistisch significant verschil in tijdsbesteding aan uiterlijke verzorging (in minuten per week) tussen mannen en vrouwen?

Klik hier voor het antwoord

Nee, want \(p > 0,05\), dus er geen sprake van een statistisch significant tijdsbesteding aan uiterlijke verzorging (in minuten per week) tussen mannen en vrouwen.

Opdracht 7

Kan je met behulp van een t-toets statistische analyse doen van een verschilvraag en/of een verbandvraag?

Klik hier voor het antwoord

Alleen van een verschilvraag.

Opdracht 7

Aan welke voorwaarde(n) moet worden voldaan om een t-toets te mogen uitvoeren?

Klik hier voor het antwoord

Er is sprake van een verschilvraag.
De data moet normaal verdeeld zijn voor alle datasets.
De data moet van het type ratio of interval zijn.