Oefenopgaven
Hier vind je een aantal random extra oefenopgaven. Ze zijn zeker niet allemaal representatief voor het tentamen en vormen ook als geheel niet zoiets als een oefententamen (zie daarvoor de oefentoets op testvision). Dus garantie tot aan de deur! Maar het zijn een aantal onderwerpen die voorbij kwamen bij de inzages en over de mail, dus we hebben wat extra oefenopgaven gemaakt.
Exercise 9
Een fokprogramma wordt opgezet om een type cavia’s voort te brengen als huisdieren. De populatiestandaarddeviatie van het gewicht van deze cavia’s is 90g. We weten dat de 2% zwaarste dieren meer dan 1500g wegen. We willen het populatiegemiddelde weten. Welke van de volgende dingen moet je daarvoor gebruiken?
- een 95% betrouwbaarheidsinterval
- een q-test
- een t-test
- een Z-waarde
antwoord
- een Z-waarde. We weten dingen over de hele populatie: zowel dat percentage als de populatie-standaarddeviatie.
Exercise 9
Bereken het gezochte populatiegemiddelde in de vorige vraag.
antwoord
Z-waarde bij 2% (zoek op in de tabel op het formuleblad) is 2.05.
Z = (x-mu)/sigma
Dus 2.05 = (1500-mu)/90
mu = 1315g
Exercise 9
We willen het gemiddelde antilichaamtiter bepalen in het bloed van ex-coronapatiënten en we doen een steekproef (N = 5). Met de steekproef vinden we een gemiddelde van 12 mM en een standaarddeviatie van 2,2 mM.
Welke van de volgende dingen kunnen we met deze gegevens berekenen?
- een 95% betrouwbaarheidsinterval
- een q-test
- een correlatie-coefficient
- een Z-waarde
antwoord
- Een 95% BI. We hebben gegevens over een steekproef. We hebben geen ruwe data (dus q-test kan niet), we hebben maar 1 afhankelijke variabele en ook geen verbandsvraag (dus correlatie kan niet), we hebben geen gegevens over de populatie (dus Z-waarde kan niet).
Exercise 9
(vervolgvraag:) Welke t-waarde moet je hierbij gebruiken?
antwoord
n = 5, dus het aantal vrijheidsgraden is n-1=4
t zoek je op in de tabel en is 2,776
Exercise 9
Stel, we schatten de lengte van de haren van Golden Retrievers. We doen een steekproef en vinden een 95% betrouwbaarheidsintervan van 5 ± 1 cm.
Wat zegt dit over de haarlengte van de populatie Golden Retrievers?
antwoord
Dat we met 95% zekerheid kunnen zeggen dat de gemiddelde haarlengte (dus niet alle haarlengtes, maar het gemiddelde) van de hele populatie Golden Retrievers tussen de 4 en 6 cm ligt.
Exercise 9
(vervolgvraag:) Kun je op basis van dit 95% betrouwbaarheidsinterval ook zeggen dat Golden Retrievers dus nooit langere haren dan 6 cm hebben?
antwoord
Nee, dat kan niet. De boven- en ondergrens die je berekend hebt zijn de grenzen van je schatting van het populatiegemiddelde. Ze zeggen niets over de spreiding in de populatie.
Exercise 9
Zijn die grenzen van het 95% BI gelijk aan het hoogste en laagste datapunt in je steekproef?
antwoord
Nee. Het zijn de grenzen van je schatting, niet van je data (zie ook vorige vraag).
Exercise 9
Je wilt een correlationeel onderzoek doen (een correlatie uitzoeken) naar het verband tussen staartlengte en snuitlengte bij Golden Retrievers. Hoeveel afhankelijke variabelen heb je nodig?
antwoord
2: staartlengte en snuitlengte zijn allebei afhankelijke variabelen.
Exercise 9
Je onderzoekt of er een verschil is in snuitlengte tussen honden in Utrecht en honden in Amersfoort. Welke statistische test / methode ga je doen?
antwoord
We hebben een verschilvraag, en die vraag is tweezijdig. Er zijn twee groepen honden, een hond in Utrecht woont niet ook in Amersfoort.
Dus een two sample t test, tweezijdig, ongepaard.
Exercise 9
Je vindt een p-waarde van 0.032
Hou een alpha van 0.05 aan. Hebben honden in Utrecht een andere snuitlengte dan honden in Amersfoort, volgens jouw onderzoek?
antwoord
Ja, want p<0.05
Exercise 9
We willen onderzoeken of er een verband is tussen snuitlengte en staartlengte bij honden in Amersfoort. Welke statistische test / methode ga je doen?
antwoord
We hebben een verbandvraag, met twee onafhankelijke variabelen. We doen een correlationeel onderzoek: maak een scatterplot (geen regressielijn) en bereken een correlatie-coefficient.
Exercise 9
Is de volgende bedachte data ongeveer normaal verdeeld?
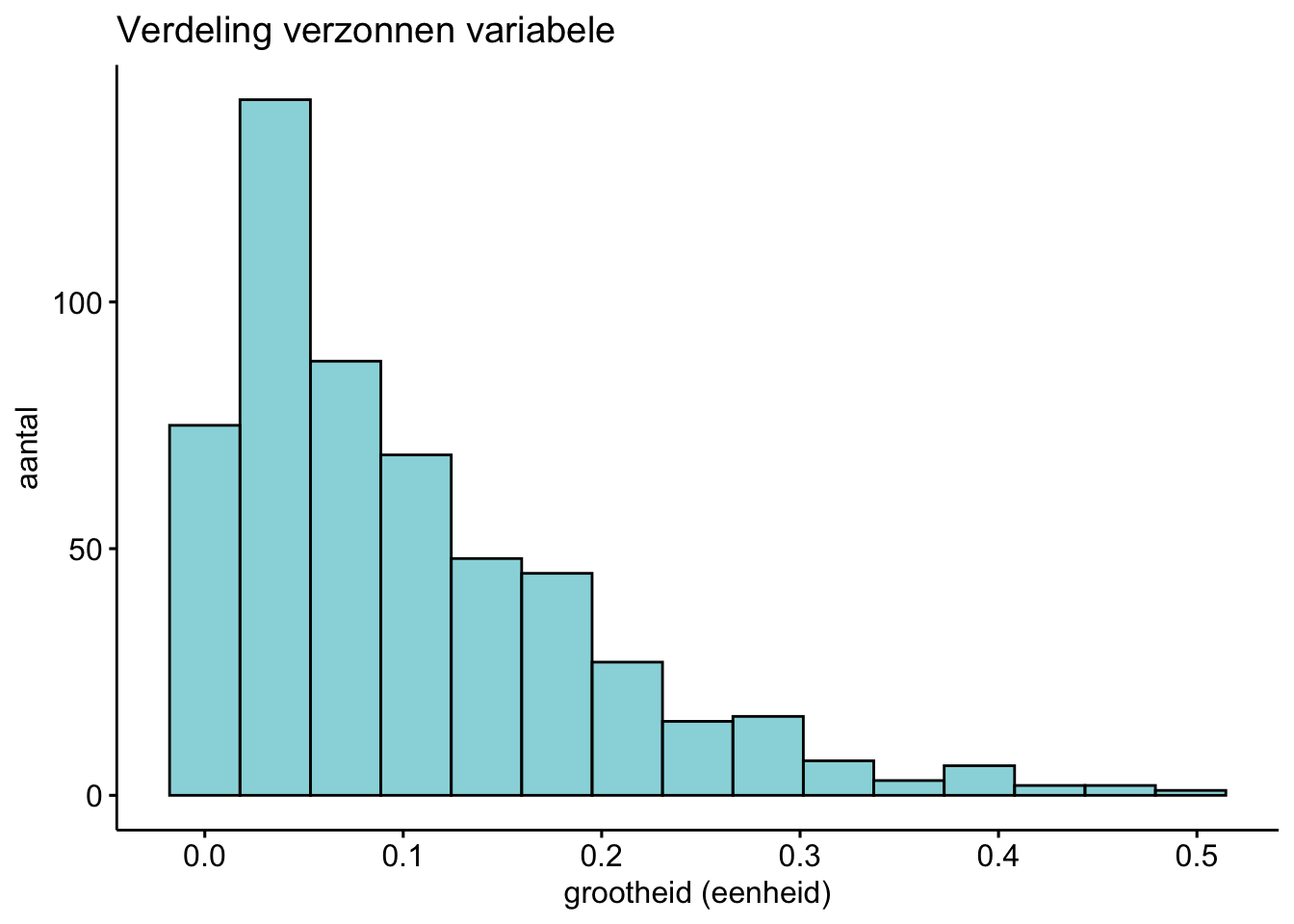
antwoord
Dit is niet ongeveer normaal verdeeld.
Een normaalverdeling is symmetrisch en heeft het hoogste punt in het midden. Deze verdeling is niet symmetrischExercise 9
We meten bij 4 Golden Retrievers de snuiten op en vinden de volgende lengtes:
- 10 cm,
- 12 cm,
- 90 cm,
- 10 cm
Van welke meetfout is hier waarschijnlijk sprake bij meting drie?
antwoord
Een vermijdbare fout. Die 90 is waarschijnlijk een typefout.Exercise 9
Je vraagt je af of studenten tijdens hun vakantie meer cola drinken per dag dan tijdens de tentamenweek. Wat is je nulhypothese?
antwoord
Studenten drinken tijdens hun vakantie niet meer cola per dag dan tijdens hun tentamenweek.Exercise 9
Van de fabrikant van flesjes azijnzuur is bekend dat de populatiestandaarddeviatie van de inhoud van de flesjes 2ml is, en volgens de fabrikant stoppen zij 300 ml in een flesje. Je wilt weten tussen welke waarden de inhoud van 95% van de flesjes zit. Welke van de volgende dingen moet je daarvoor gebruiken?
- een 95% betrouwbaarheidsinterval
- een q-test
- een t-test
- een Z-waarde
antwoord
- een Z-waarde. We weten dingen over de hele populatie: zowel het populatiegemiddelde als de populatie-standaarddeviatie. Laat je niet in de war maken doordat we toevallig 95% kozen als percentage. Teken Z-waarden-vragen altijd even op papier: Teken een normaalverdeling en kleur het stuk oppervlak dat je wilt weten.
Exercise 9
Je vraagt je af hoeveel cola er in een glas cola van je favoriete cafe zit. Je besteld een maand (31 dagen) lang elke dag een glas cola, en meet de inhoud. Je komt op een steekproefstandaarddeviatie van 10 ml en een steekproefgemiddelde van 247ml. Wat kun je met de gegevens uit deze opdracht berekenen?
- een 95% betrouwbaarheidsinterval
- een q-test
- een steekproefgemiddelde en steekproefstandaarddeviatie
- een Z-waarde
antwoord
- een 95% betrouwbaarheidsinterval. We hebben alle gegevens die we daar voor nodig hebben (steekproefgemiddelde, steekproefstandaarddeviatie, aantal metingen).
Exercise 9
Als je weet dat de populatie konijnen in Utrecht gemiddeld 200 gram wortels per dag eet, met een standaarddeviatie van 20 gram. Wat heb je dan nodig om te berekenen hoeveel procent van de konijnen meer eet dan 220 gram?
- een 95% betrouwbaarheidsinterval
- een q-test
- een steekproefgemiddelde en steekproefstandaarddeviatie
- een Z-waarde
antwoord
- een Z-waarde
Exercise 9
Je vraagt je af of jouw Konijnen Flappie, Minous, Jaap, en Barbara, meer eten dan 220 gram. Je meet van elk konijn hoeveel wortels ze op krijgen. Je berekent in Excel een steekproefgemiddelde en steekproefstandaarddeviatie. Welke van de volgende dingen kun je nu berekenen om je vraag te beantwoorden?
- een 95% betrouwbaarheidsinterval
- een q-test
- een steekproefgemiddelde en steekproefstandaarddeviatie
- een Z-waarde
antwoord
- een 95% betrouwbaarheidsinterval.
Exercise 9
Is de volgende bedachte data ongeveer normaal verdeeld?
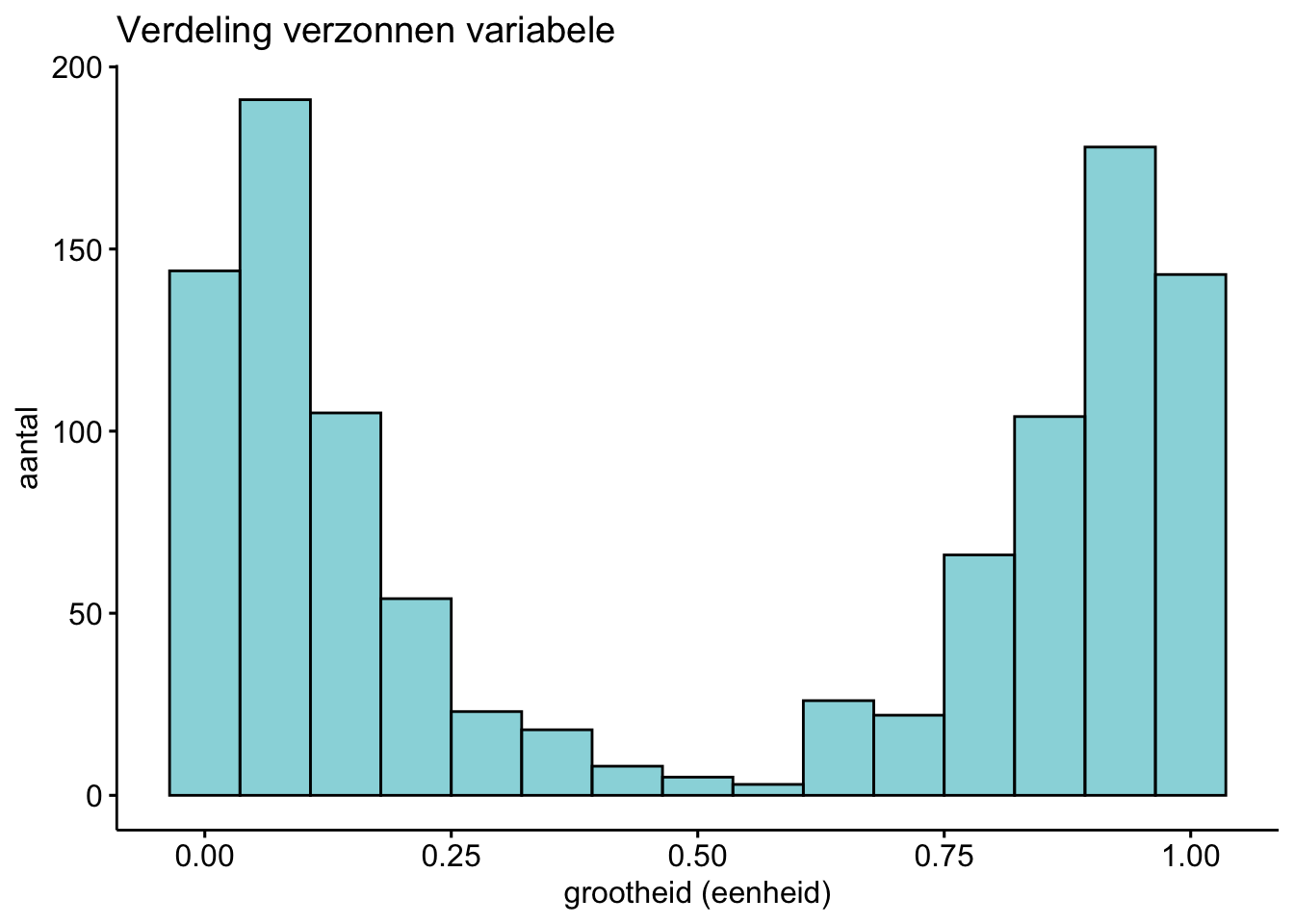
antwoord
Dit is niet ongeveer normaal verdeeld.
Een normaalverdeling is symmetrisch en heeft het hoogste punt in het midden. Deze verdeling is wel symmetrich, maar het hoogste punt ligt niet in het midden.Exercise 9
Is de volgende bedachte data ongeveer normaal verdeeld?
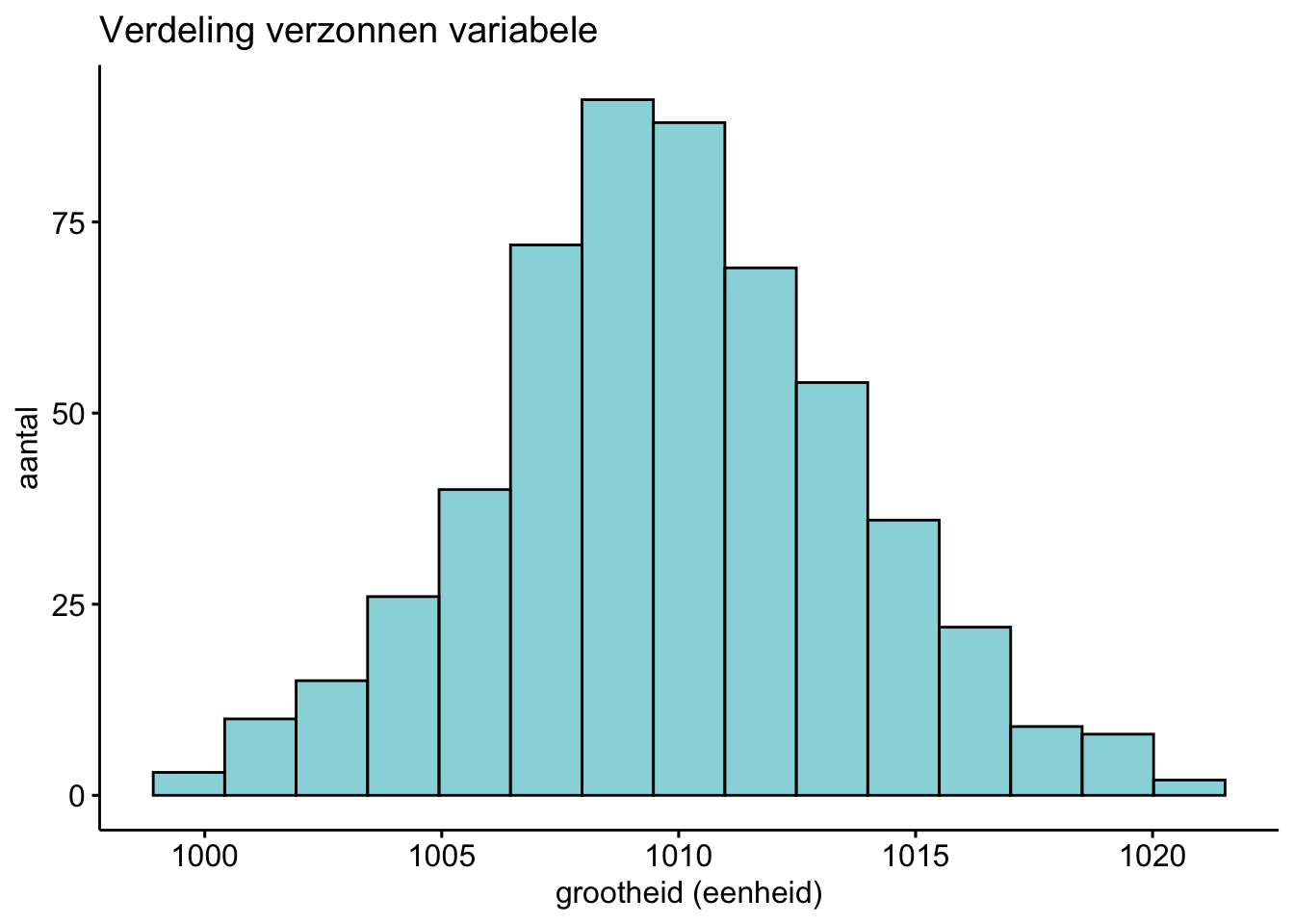
antwoord
Dit is wel ongeveer normaal verdeeld.
Een normaalverdeling is symmetrisch en heeft het hoogste punt in het midden. We hebben zo te zien niet heel erg veel data, dus precies, exact op de millimeter symmetrisch is hij niet. Maar wel ongeveer.Exercise 9
Je vraagt je af of jouw Konijnen Flappie, Minous, Jaap, en Barbara, meer eten dan 220 gram. Wat voor soort vraag is dat?
- een beschrijvende vraag
- een verbandvraag
- een verschilvraag
antwoord
Een verschilvraag. Je vraagt je af of ze verschillend-en-dan-specifiek-meer eten dan 220 gram.