Les 4 Kansverdeling en outliers

4.1 Lesinhoud en leerdoelen

Tijdens deze gaan we verderkijken naar de normaalverdeling, en gebruiken we de Z-tabel om percentages te berekenen onder een standaard normaalverdeling.

Theorie:

• z formule en z tabel
• normaal verdeelde en niet normaal verdeelde data
• outliers

Vaardigheden:

• Een z-tabel gebruiken
• outliers vinden in Excel

4.2 Voorbereiding

4.2.1 Normaalverdeling

We hebben het al eerder gehad over de normaalverdeling hier in les 2.

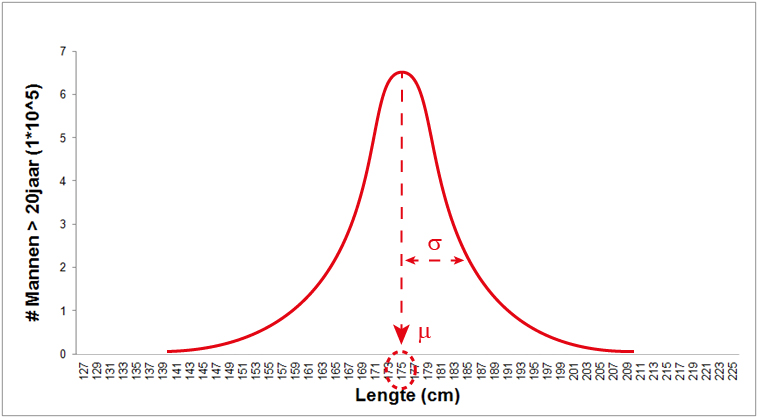
In dit figuur hadden we bijvoorbeel normaal verdeelde data van de lengtes van Nederlandse mannen boven de 20, met:

• Het populatiegemiddelde (\(\mu\)), de gemiddelde lengte van de populatie. Deze is gelijk aan de x-waarde, de lengte, op het hoogste punt van de grafiek (zie onderstaande figuur). Dit betekent dat als je de lengte van willekeurig persoon meet de kans het grootst is dat die lengte rond de 1,75 meter zal uitvallen.
• De populatiestandaarddeviatie (\(\sigma\)), de variatie van de meetwaarden binnen de populatie (zie onderstaande figuur). Deze waarde bepaalt de breedte van de curve.

4.2.2 Oppervlak onder de normaalverdeling

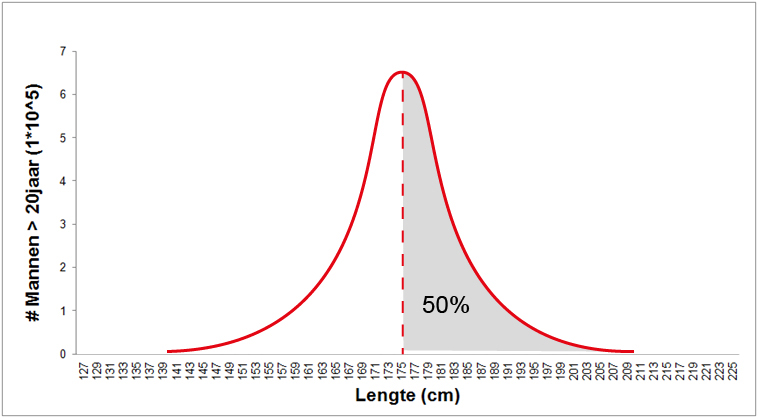
In de grafiek hierboven zitten alle mannen ergens onder die curve, ze zijn allemaal geteld. Het oppervlak onder de curve is dus 100% van de populatie. Dat is handig, want daar kunnen we mee gaan rekenen.

Zo is 50% van de mannen groter dan 1,75 meter, want 1.75 ligt precies in het midden, en de normaalcurve is symmetrisch. 50% is het percentage oppervlak onder de curve tussen 1,75 meter en \(\infty\) (zie onderstaande figuur).

Dat werkt met elk stukje oppervlak onder de curve: Stel je plukt een random man van straat en je vraagt je af hoe groot de kans is dat hij tussen de 157 (\(x_1\)) en 162 cm (\(x_2\)) is, dan is dat dus gelijk aan het percentage oppervlak onder de curve tussen (\(x_1\) en \(x_2\)).

4.2.3 Z-waardes

Als je het populatiegemiddelde (\(\mu\)) en de populatiestandaarddeviatie (\(\sigma\)) kent, kun je dit oppervlak en daarmee de kans op een waarde uit het interval \(x_1\) en \(x_2\) berekenen. Dit is een best veel voorkomend soort vraag. Hoeveel procent van de Nederlandse mannen is bijvoorbeeld langer dan 190 cm?

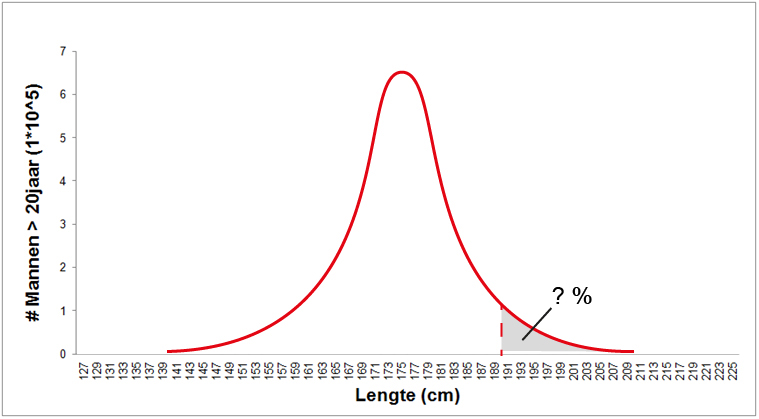
Om hier antwoord op te kunnen geven zou je de computer kunnen laten rekenen:

Hoeveel procent van de mannen is groter dan 190 cm bijvoorbeeld?

En groter dan 185 cm?

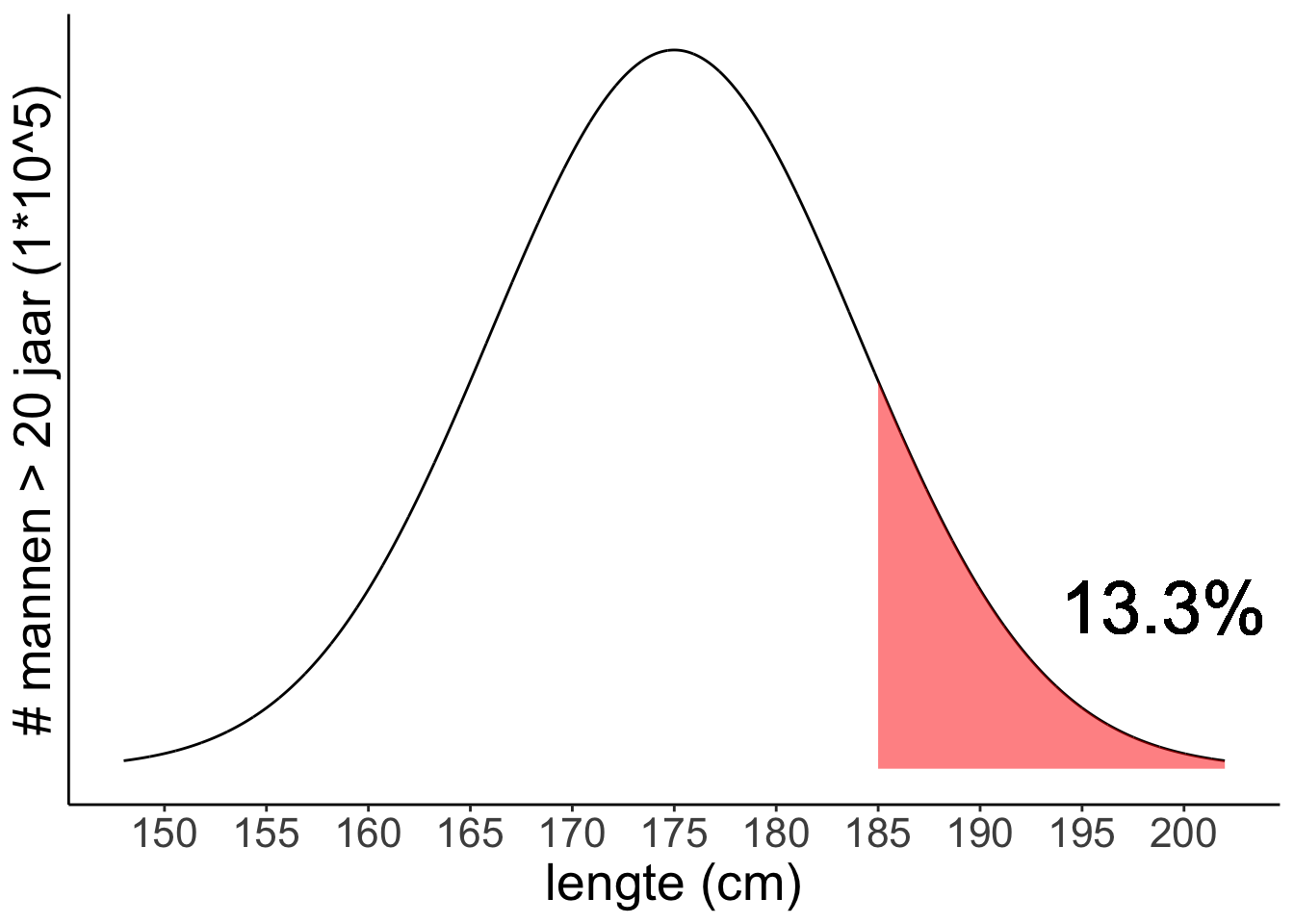
En kleiner dan 165 cm?

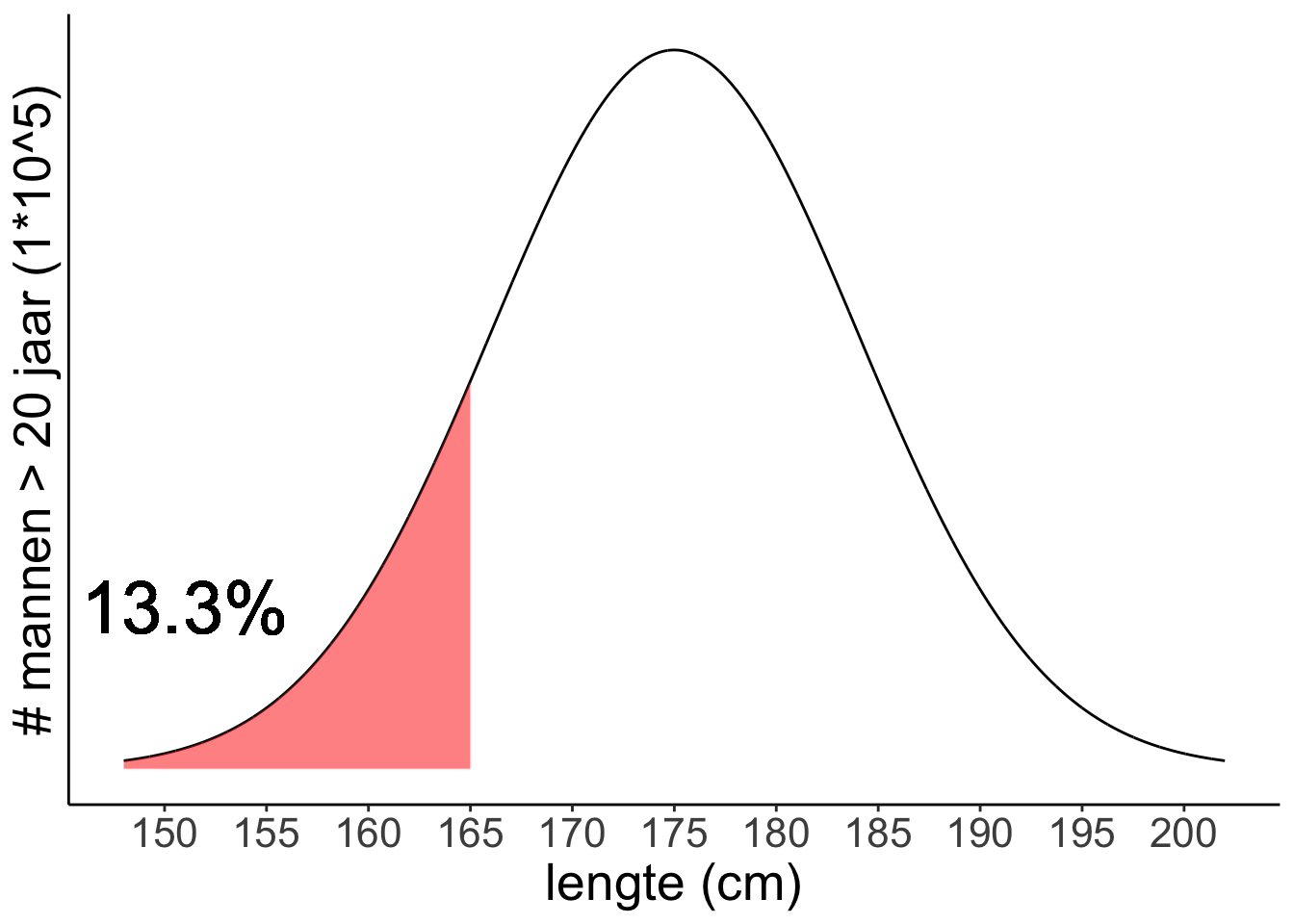(Merk op dat dat percentage net zo groot is al het percentage mannen langer dan 185 cm. 185 ligt namelijk net zo ver van het gemiddelde (175) als 165. En de normaalverdeling is symmetrisch.)

Maar handiger zou zijn als we gewoon een tabel hadden liggen met oppervlaktes boven of onder een hoeveelheid cm op de x-as er in. Zodat we even in de tabel konden kijken: “ah, het percentage mannen langer dan 190 cm is zoveel procent!”

Probleempje: als we dat in een tabel willen gaan zetten, heb je heel veel tabellen nodig. Voor elke mogelijke normaalverdeling met een ander gemiddelde of standaarddeviatie een andere… Want nu bekijken we lengte van mannen, maar volgende keer weer kattenstaarten… Dat zou een heel boekwerk worden.

Oplossing: We maken 1 tabel, voor een standaard-normaalverdeling met \(\mu=0\) en \(\sigma=1\). Die standaard-normaalverdeling noemen we de z-verdeling. Door die z-verdeling te gebruiken, kunnen we de tabel gebruiken voor elke willekeurige normaalverdeling met hele anders gemiddelde en standaarddeviatie. We moeten alleen even de waarde waar we in geinteresseerd zijn (“Hoeveel % van de populatie is langer dan …[waarde]… cm?”) omschalen naar die nieuwe Z-verdeling.

Dat doe je door de waarde niet meer in de eenheid van de x-as uit te drukken (bijv bij 185 cm: “10 cm van het gemiddelde”), maar in \(\sigma\)’s (“1.11 standaarddeviaties van het gemiddelde”). Dat heet dan de Z-waarde:

\(z=\frac{x-\mu}{\sigma}\)

(Oftewel: Z = afstand waarde tot het gemiddelde, uitgedrukt in \(\sigma\)’s.)

Bij een normaalverdeling met populatiegemiddelde \(\mu=175\) en populatiestandaarddeviatie \(\sigma = 9\), is een waarde van 185 (x) dus:

\(z=\frac{185-175}{9}\) \(= 1.11\)

Dus 1.11 standaarddeviaties van het gemiddelde.

4.2.4 Z-tabel : “hoeveel procent is groter dan [x>gemiddelde] ?”

In de Z-tabel staat vervolgens voor elke z-waarde welk percentage van de populatie groter is dan die z-waarde.

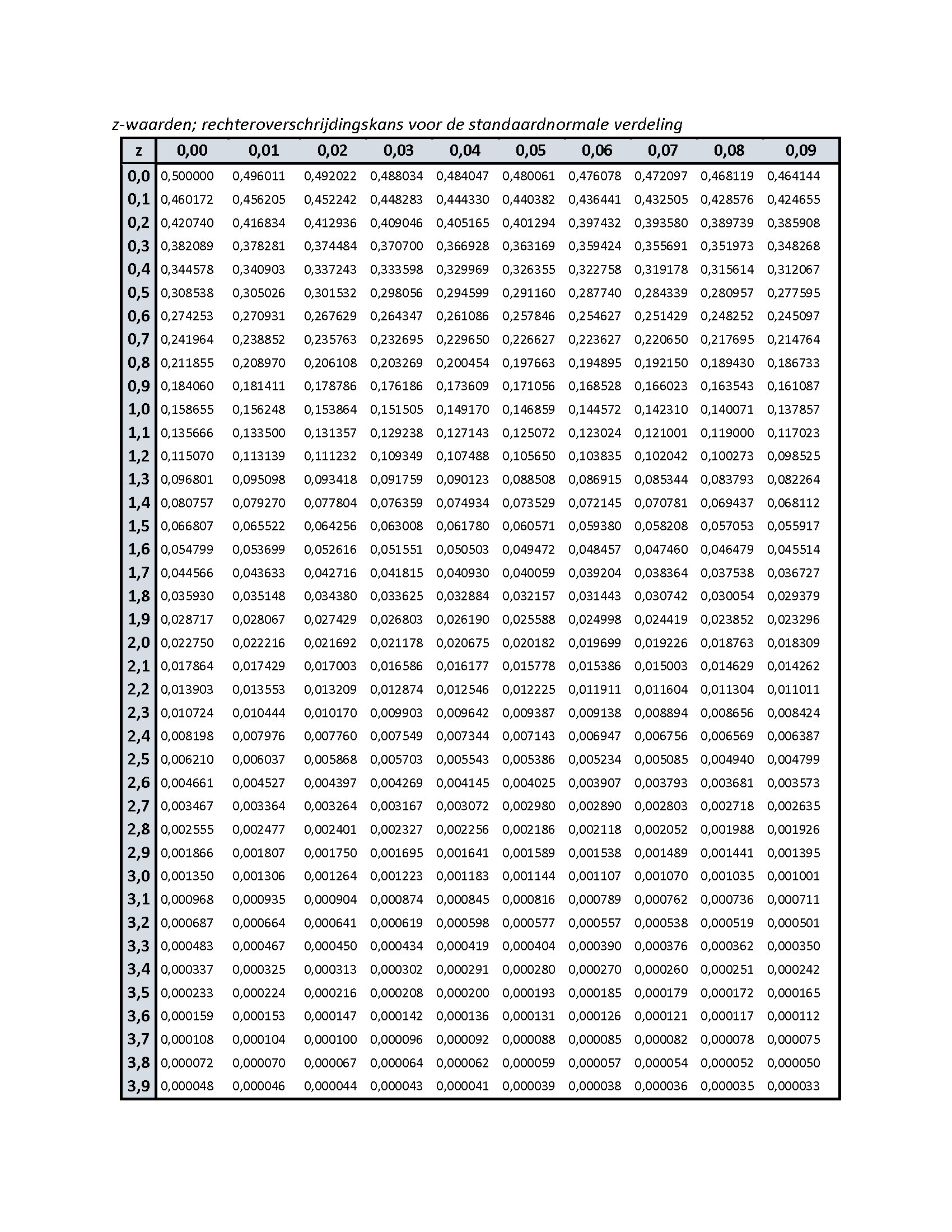
Op de formulekaart (hier is hij) staat de z-tabel. Zoals je ziet begint de tabel linksboven in de hoek bij een Z van 0,00 en geeft dan een percentage van 50%. Dat klopt, want een Z-score van 0,00 is 0 standaarddeviaties van het gemiddelde, oftewel, precies op het gemiddelde!

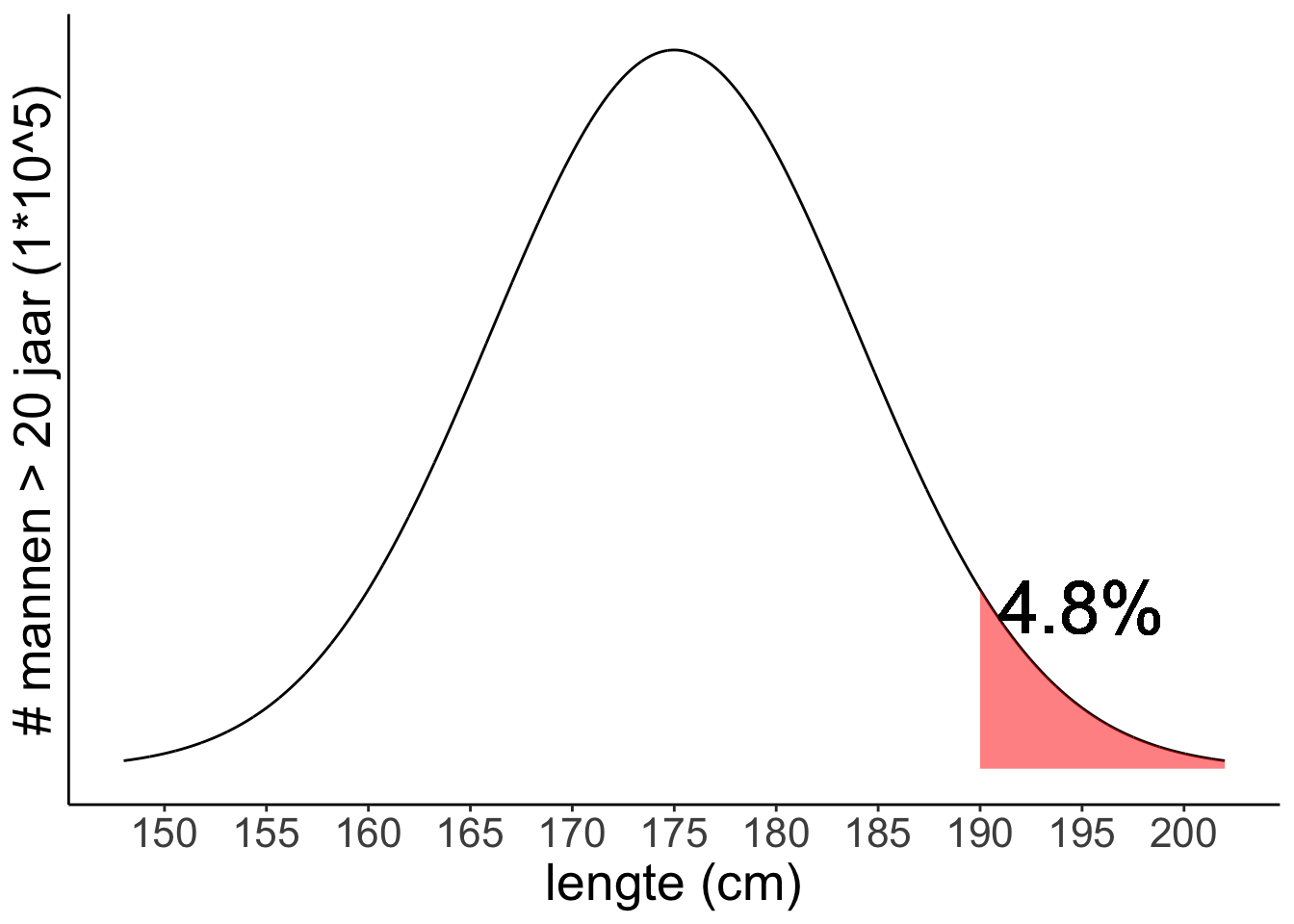
Uit het volgende voorbeeld blijkt hoe we de z-verdeling en de tabel kunnen gebruiken. Een onderzoeker vraagt zich af hoeveel procent van de Nederlandse populatie langer is dan 1,90 meter. Het populatiegemiddelde (\(\mu\)) is 1,75 m, en de populatiestandaarddeviatie (\(\sigma\)) is afgerond 0,09 meter. In de onderstaande figuur vertaalt deze vraag zich als: wat is het percentage van het gearceerde oppervlak ten opzichte van het totale oppervlak?

Om dit aan de hand van de z-tabel te kunnen bepalen, bereken je de zogenaamde z-waarde met behulp van de formule:

\(z=\frac{x-\mu}{\sigma}\)

Je vindt dan:

\(z=\frac{1,90-1,75}{0,09}=1,66...\)

Je zoekt in de z-tabel in de rij 1,6 en kolom 0,07 (samen 1,67) en vindt de waarde 0,047460. Je kunt dan concluderen dat het gearceerde deel in de grafiek gelijk is aan 4,8% van het totale oppervlak; 4,8% van de Nederlanders is dus langer dan 1,90 meter (dat klopt met wat we de computer net uit hadden laten rekenen hier , ctrl-klik om in een nieuwe tab te openen.)

4.2.5 Z-tabel : “hoeveel procent is groter/kleiner dan… ?”

In het voorbeeld van net hadden we het makkelijk. Er werd gevraagd naar het percentage groter dan een waarde hoger dan het gemiddelde. Dat is precies wat in de z-tabel staat.

Maar stel dat de vraag is “welk perentage van de mannen is langer dan 163 cm?”.

\(z=\frac{x-\mu}{\sigma}\)

Je vindt dan:

\(z=\frac{1,63-1,75}{0,09}= -1,33...\)

Negatieve Z-waarden staan niet in de tabel. Maar, de normaalcurve is symmetrisch! Dus het percentage oppervlak lager dan Z=-1.33, is even groot als het percentage oppervlak boven de Z=1.33.

Exercise 4

Zoek in de tabel op welk percentage hoort bij Z=1.33

Dit is het percentage oppervlak rechts van de waarde 1,87 m (want dat is net zo ver van het gemiddelde als 1,63 m.). We zochten echter het percentage langer dan 1,63m. Hoe groot is dat percentage?

Klik hier voor het antwoord

ongeveer 90.8%

het percentage dat groter is dan Z=1.33 is 0,091759*100= 9,1759 %

Dat is dus hetzelfde als het percentage dat kleiner is dan Z=-1.33. Begrijp je dit niet, teken dan de normaalcurve op een stuk papier en kleur de oppervlaktes groter dan 1,87 m en kleiner dan 1,63m in. Zoals je ziet zijn die hetzelfde.

We zochten echter het percentage mannen groter dan Z=-1.33. Aangezien het totaal 100% is, is dit percentage 100- 9,1759 = ongeveer 90.8%

4.2.6 Z-tabel : “hoe lang is de grootste …% ?”

Omgekeerd werkt het ook. Als je wilt weten hoe lang de langste 2,5% van de Nederlandse man minstens is, dan zoek je in de tabel de z-waarde op die hoort bij 2,5% of daar het dichtst bij ligt (z = 1,96). Vervolgens vul je de formule in, en maakt de \(x\) vrij. Hieruit volgt:

\(x = \mu + 1,96\sigma\)

Dus \(x\) is gelijk aan het gemiddelde plus 1,96 * de populatiestandaard deviatie:

\(x=1,75+1,96\cdot 0,09=1,93\)

Dus de langste 2,5% van de mannen is tenminste 1,93 meter lang. Als je 1,96 * de standaarddeviatie van het gemiddelde aftrekt, dan berekenen je juist wat de maximale grootte is van de kleinste 2,5% van de Nederlanders:

\(x=μ−1,96\cdot σ\)

4.2.7 Oppervlak tussen twee waardes

Op deze manier kun je ook de oppervlakte tussen twee waardes vinden. Zo zit 95% van de populatie bij een normaalverdeling tussen een z-waarde van 1.96 onder en boven het gemiddelde. We hebben net namelijk al opgezocht dat 2,5% van de populatie groter is dan een z-waarde van 1,96 boven het gemiddelde. Omdat de normaalverdeling symmetrisch is, is ook ook precies 2,5% KLEINER dan een z-waarde van 1.96 ONDER het gemiddelde.

100 - 2,5 - 2,5 = 95% hou je over, dus die 95% zit er precies tussenin.

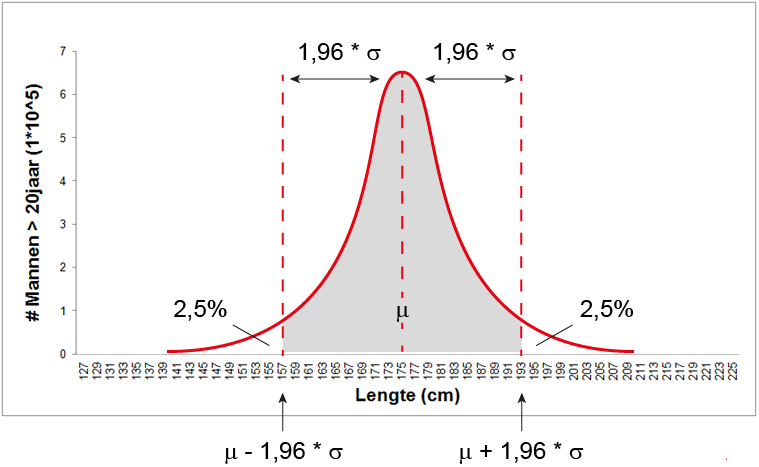
Als je terug wilt rekenen naar lengtes, moet je die z-waarde weer omrekenen: de grenzen liggen dus op \(x=μ−1,96⋅σ\) en \(x=μ+1,96⋅σ\). Het oppervlak onder de curve tussen deze twee grenzen omvat 95% van de populatie. Je mag dan ook stellen dat 95% van de populatie tussen de 1,57 en 1,93 meter lang is. Zo kun je ook zeggen dat als je op straat een willekeurig iemand opmeet, de kans 95% is dat diens lengte tussen 1,57 en 1,93 meter zal uitvallen.

Alleen als de hele populatie bekend is , oftewel je weet het populatiegemiddelde (\(\mu\)) en de populatiestandaarddeviatie (\(\sigma\)), kun je met de z-tabel berekenen tussen welke twee waarden met een zekerheid van 95% de waarde van een willekeurige meting uit die populatie zal zitten. Dit is NIET een 95% betrouwbaarheids-interval, dat komen we later nog tegen.

4.2.8 Andere verdelingen

De normaalverdeling is ons lievelingetje, maar er zijn natuurlijk veel andere verdelingen.

Normaalverdeling

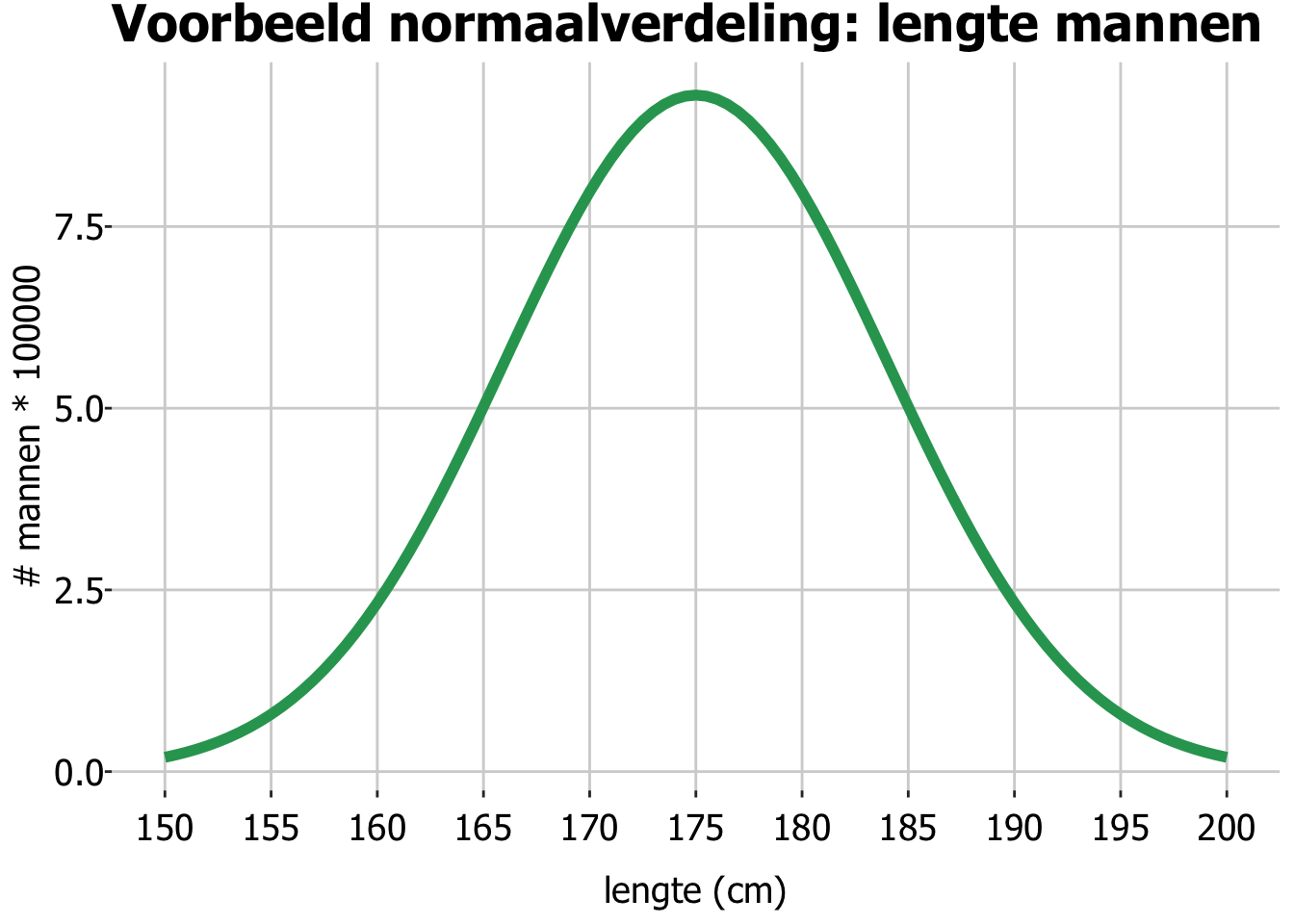
in de normaalverdeling, zijn meetwaarden rond het gemiddelde het meest waarschijnlijk, en een waarde -zeg- 5 eenheden boven het gemiddelde is even waarschijnlijk als een waarde 5 eenheden onder het gemiddelde. Oftewel: de normaalverdeling is symmetrisch.

z-verdeling

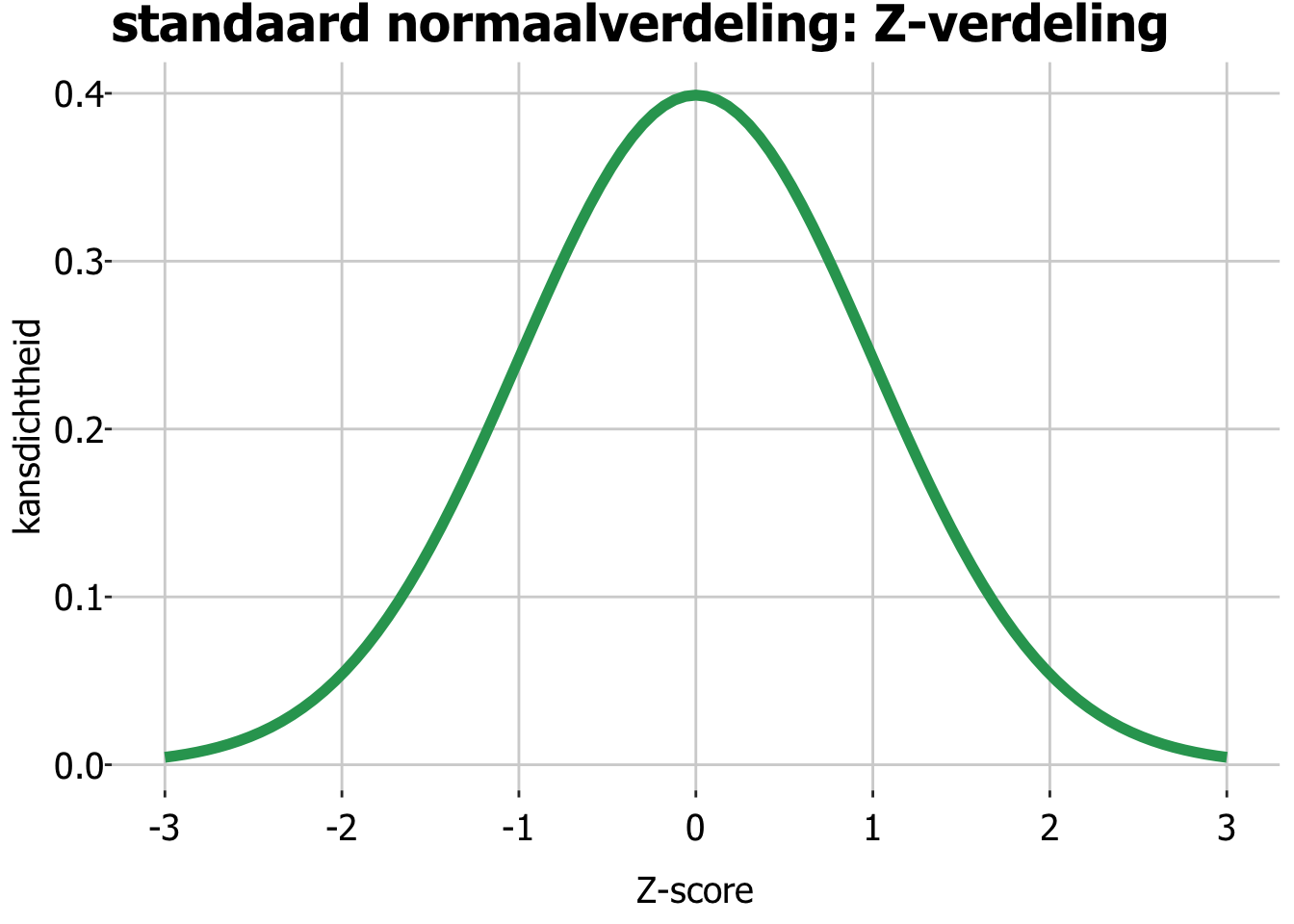
De z-verdeling is een normaalverdeling met gemiddelde 0 en standaarddeviatie 1. Het heet ook wel de standaard-normaalverdeling. Door normaalverdelingen om te rekenen naar een z-verdeling (met de z-waarde) kun je percentages vinden met een z-tabel.

t-verdeling

Dat werkt heel leuk met die normaalverdeing, en die Z-scores:

\(z=\frac{x-\mu}{\sigma}\)

Maar er is wel een probleempje: de standaarddeviatie \(\sigma\) en gemiddelde \(\mu\) van de hele populatie weten we vaak helemaal niet! Dat is net de lol van inductieve statistiek: we proberen vaak op basis van een steekproef iets te zeggen over de populatie. Hoe dan verder?

Zo’n steekproef heeft een aantal metingen (n). De steekproef-standaarddeviatie hangt af van je aantal metingen… Als je minder metingen hebt, vindt je een grotere standaarddeviatie dan als je meer metingen hebt. Dat is logisch ook: bij minder metingen weet je minder nauwkeurig waar dat gemiddelde ergens zou liggen. Heb je minder dan 50 metingen, dan is dat een probleem!

Het steekproefgemiddelde zelf hangt trouwens niet per se af van het aantal metingen. Bij meer metingen verschuift je schatting van het gemiddelde niet, we weten het alleen met een hogere nauwkeurigheid.

De truc hierbij is om bij minder dan 50 metingen niet een Z-verdeling te gebruiken maar een t-verdeling (ook wel student’s t-verdeling, naar de bijnaam van degene die hem uitvond). de formule voor \(t\) lijkt op die van \(z\), maar je gebruikt de steekproefstandaarddeviatie \(s\) ipv de populatiestandaarddeviatie \(\sigma\). En je gooit de wortel van het aantal metingen er in om te compenseren:

\(t=\frac{ \overline{x}-\mu}{s/ \sqrt{n}}\)

(Reminder: je hoeft geen formules uit je hoofd te leren.)

Dan krijg je een verdeling die lijkt op de normaalverdeling, maar met dikkere zijkanten als je minder metingen \(n\) hebt:

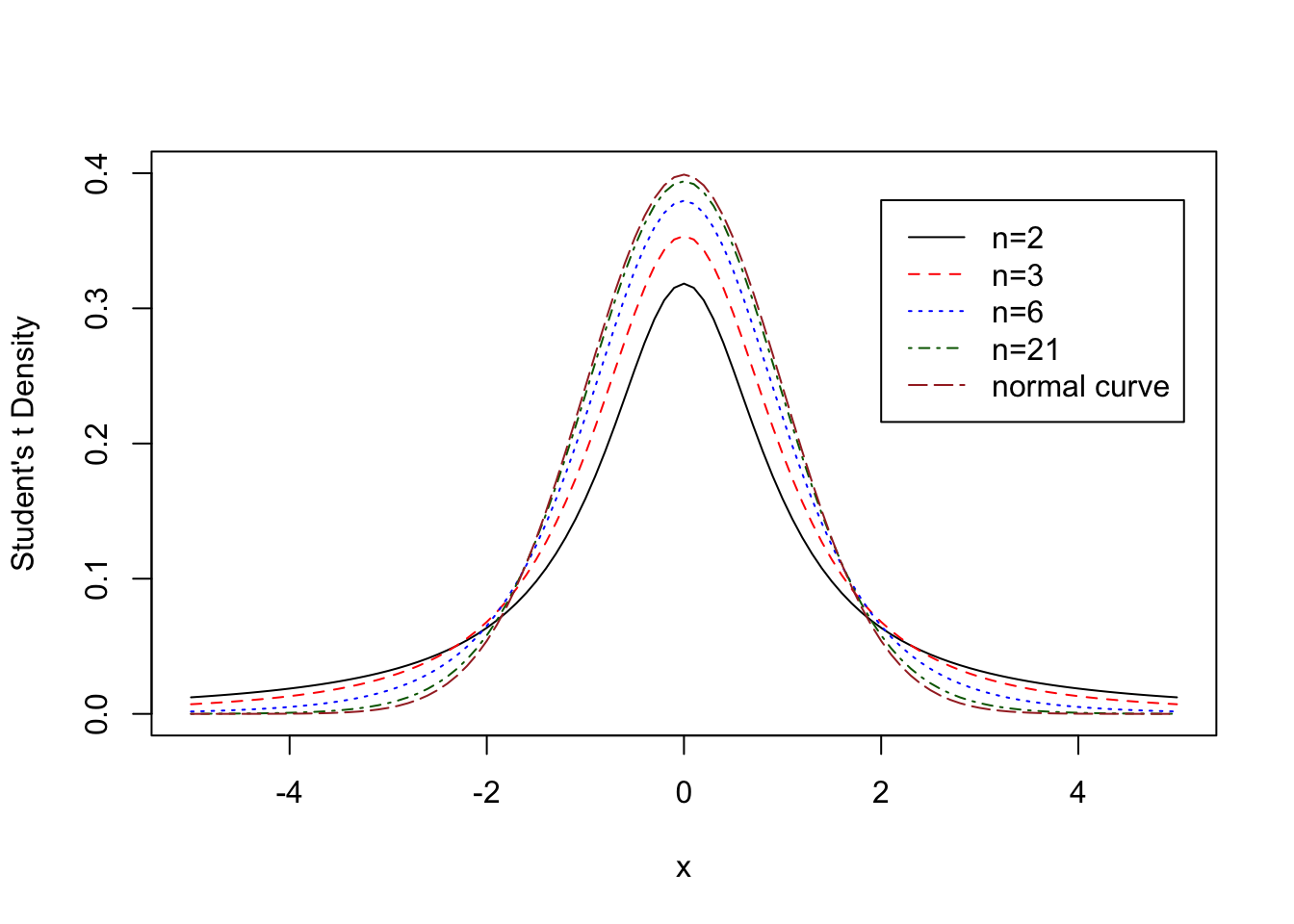
Figure 1.7: thanks to Yuk Tung Liu for the graph

Zoals je in de grafiek ziet, lijkt de t-verdeling bij n=21 al behoorlijk op de z-verdeling. Bij n=50 lijkt hij er zoveel op, dat je gewoon weer een z-verdeling kunt gebruiken. In de volgende les gaan we hiermee bezig.

Kleine preview: De t-distributie gebruik je bij kleinere steekproeven (volgende les) en is ook heel handig voor het doen van t-test (de les daarna). Speel hier met de t-verdeling om te zien hoe hij gaat lijken op een normaalverdeling als je genoeg meetpunten hebt.

Uniforme verdeling

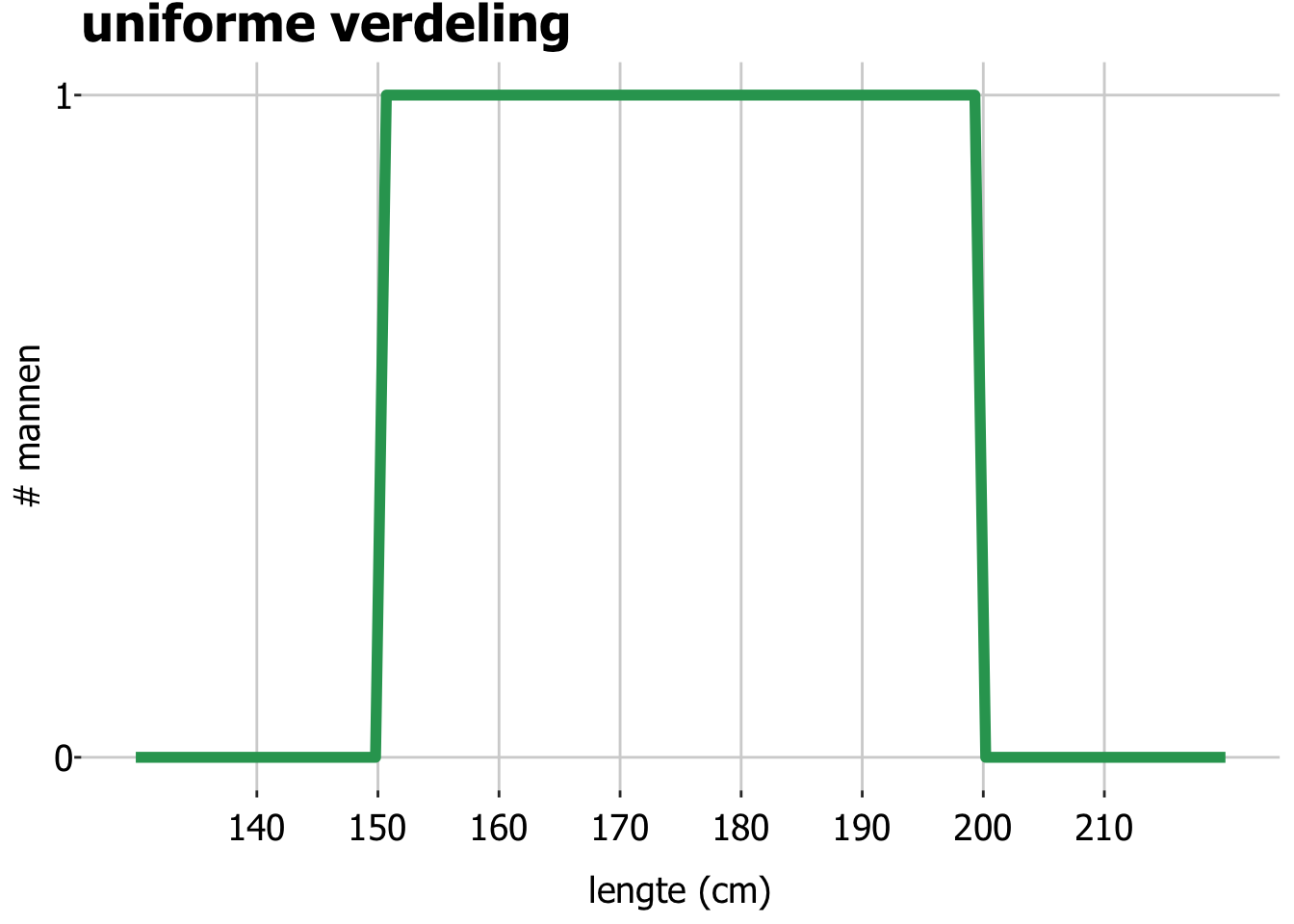
Stel je nu voor dat we 50 mannen hebben gezocht, voor elke cm tussen 150 en 200 cm lengte precies 1 man met die lengte. Dus 1 man met een lengte tussen de 150 en de 151 cm, 1 man met een lengte tussen de 151 en 152 cm, etc. Hoe beschrijf je deze groep mannen met een functie? Die functie ziet er zo uit, alle lengtes tussen 150 en 200 cm komen even vaak voor:

Poissonverdeling

Hierboven hadden we continue data. Een continue variabele zoals lichaamslengte kan (binnen bepaalde grenzen) iedere waarde aannemen, niet alleen hele centimeters.

Als je niet aan het meten bent, maar aan het tellen, gebruik je een andere kansverdeling. De Poissonverdeling (uitgevonden door Siméon Poisson) gebruik je als je het aantal van iets per tijdseenheid/oppervlakte/afstand/volume etc aan het tellen bent. Bijvoorbeeld:

• het aantal vissen dat per dag door de sluis in Utrecht zwemt
• het aantal bomen in de berm per hectometer singel
• het aantal rodebloedcellen per microliter bloed (onthoud die, die komt bij het vak hematologie terug)
• het aantal konijnen per vierkante kilometer op de uithof

Deze verdeling wordt alleen bepaald door de verwachtingswaarde \(\lambda\) (bijv: het verwachte aantal vissen per uur).

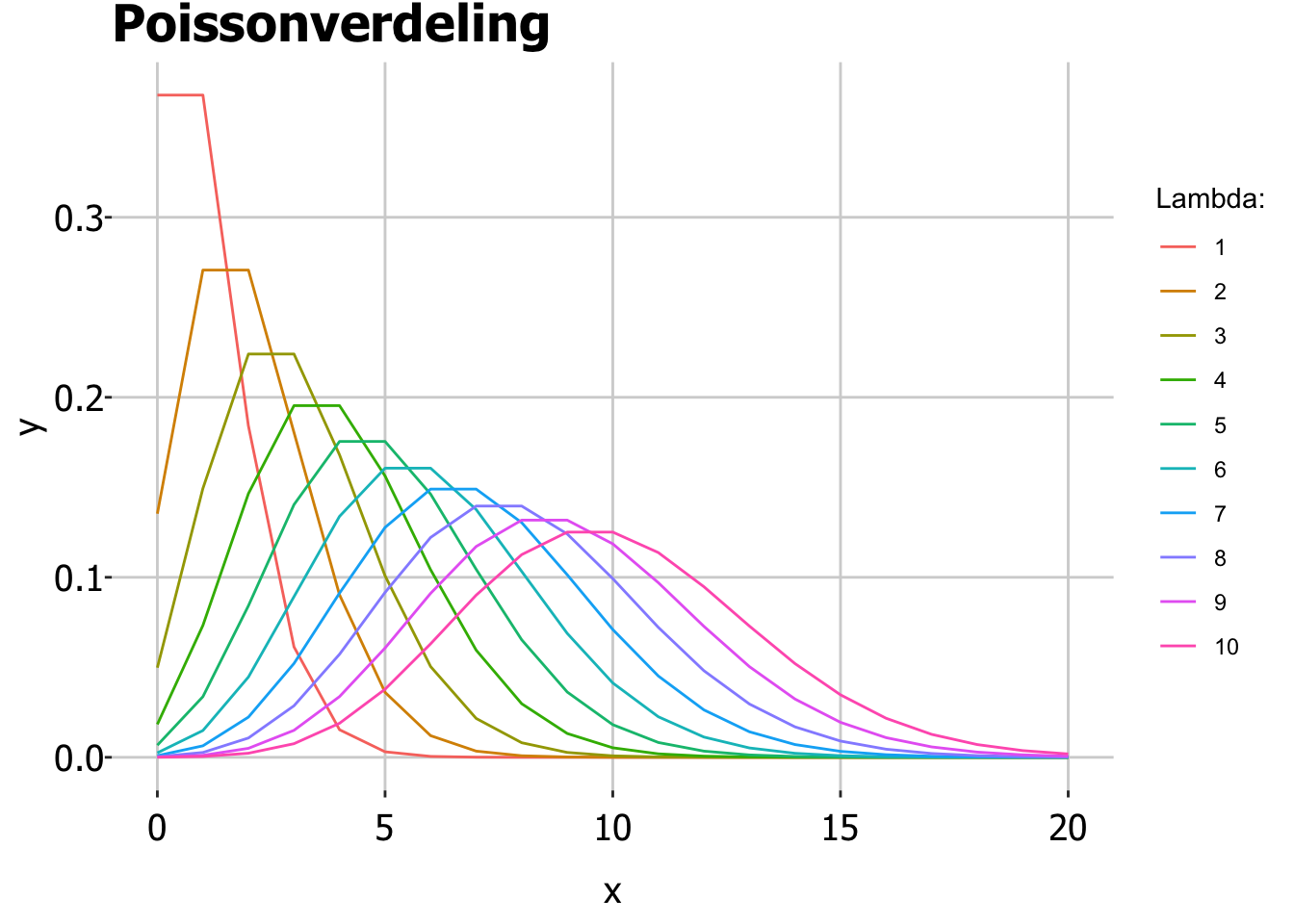
Bereken je de standaarddeviatie, dan gaat dit dus ook anders dan bij de normaalverdeling. Bij de normaalverdeling hing de standaarddevaitie af van (de wortel van het kwadraat van) de verschillen tussen individuen in de populatie en het gemiddelde, en het aantal metingen in je steekproef.

Bij de Poissonverdeling is de steekproefstandaarddeviatie gelijk aan de wortel uit het getelde aantal:

\(s = \sqrt{aantal}\)

Stel je telt 50 leukocyten per 0,01 microliter bloed, dan is de standaarddeviatie \(s = \sqrt{50} = 7,07\).

Scheve verdelingen

De Poissonverdeling lijkt redelijk symmetrisch, maar is het niet. En aantallen tellen onder de nul zit er ook niet in: -5 vissen per uur kan niet!

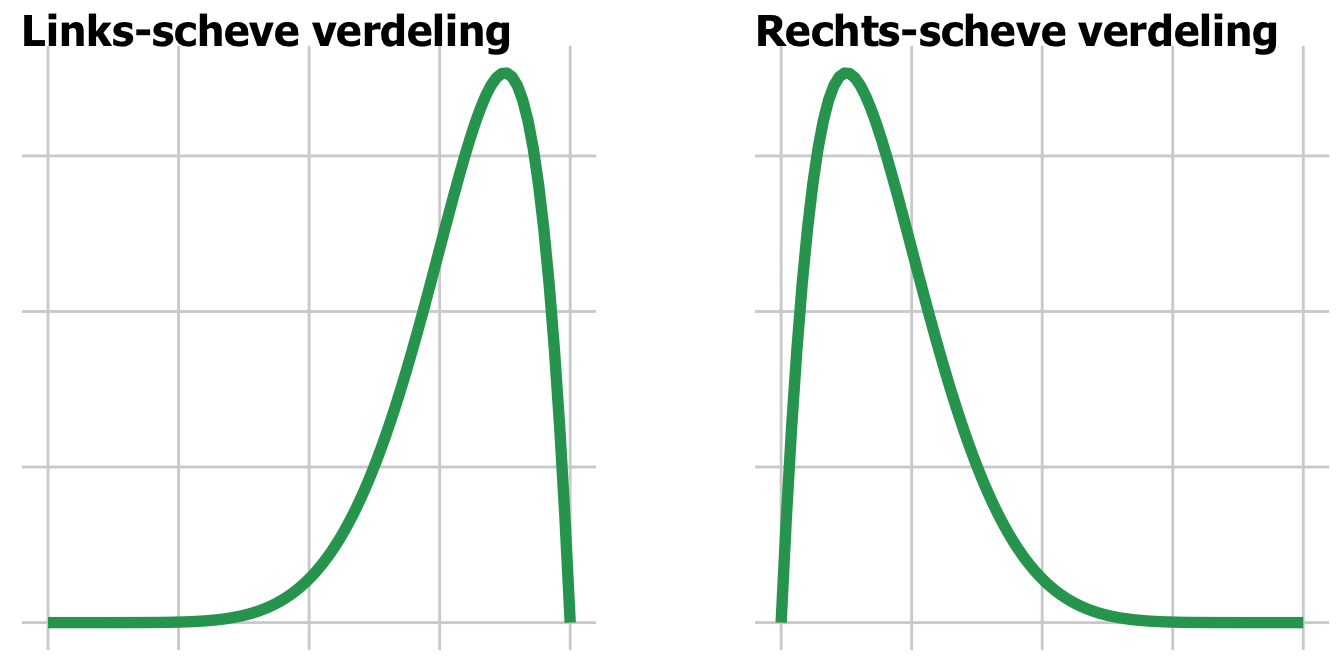
Verdelingen kunnen dus ook scheef zijn. Dan is de kansverdeling rondom de piek niet meer symmetrisch, maar een van de staarten is langer.

Bij een links-scheve verdeling (left-skewed) is de linker staart langer. Er zijn dan meer metingen met relatief lage waarden. Het gemiddelde ligt dan links van de piek.

Bij een rechts-scheve verdeling (right-skewed) is de rechter staart langer. Er zijn dan meer metingen met relatief hoge waarden. Het gemiddelde ligt dan rechts van de top,

Is dit nou normaal?

Een normaalverdeling herken je aan de piek in het midden en de symmetrische staarten. Het lijkt een beetje op zo’n oude klok, dus we noemen de normaalverdeling ook wel klokvormig (of bell shaped in het Engels).

hier is de grootste klok van de domtoren, foto door Pepijntje, Public domain, via Wikimedia Commons

Vaak is de vraag “is dit nou normaal verdeeld?”, omdat je met normaal verdeelde data andere dingen kunt dan met niet-normaal verdeelde data. Hoe herken je dan niet-normaal verdeelde data?

• Ten eerste: Je kunt dus naar de verdeling kijken. Lijkt hij niet op een normaalverdeling (geen klok-vorm) met de piek in het midden en symmetrische staarten? Dan is het waarschijnlijk niet normaal verdeeld. Ongelijke staarten en de piek niet in het midden zijn duidelijke aanwijzingingen dat de data niet normaal verdeeld is. Vergeet echter niet dat er altijd wat variatie in je data zit, dus bij een steekproef met normaal verdeelde data zal de grafiek ongeveer symmetrisch zijn met ongeveer de piek in het midden.
• Ten tweede: als het kwalitatieve data is, dan is het niet normaal verdeeld. Ben je aan het tellen ipv meten? niet normaal verdeeld.
• Ten derde: je kan statistisch testen of data normaal verdeeld is. Dat leren jullie in het tweede jaar.

4.2.9 outliers (Outliers)

Je hebt hierboven gezien dat onder verschillende verdelingen, de ene meetwaarde vaak waarschijnlijker is dan de andere.

Soms is een waarde zo afwijkend dat het de vraag is of je die wel mee moet nemen in je verdere analyse. De vraag is dan dus hoe (on)waarschijnlijk die meting is.

Stel, je bepaalt de concentratie van een stof in een bloedmonster afkomstig van een proefdier in vijfvoud; je vindt de waarden 4,4; 5,3; 4,4;4,6 en 4,6. (Vaak meet je een grootheid een aantal malen om nauwkeurige(r) uitspraken te kunnen doen over de gemiddelde waarde.)

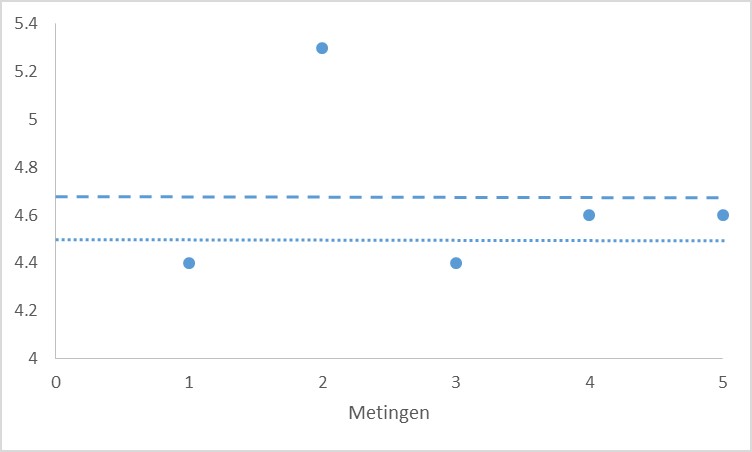
Als je deze waarden gebruikt in je berekeningen vind je een gemiddelde van 4,66. De tweede waarde (5,3) valt echter uit de toon. Zonder deze waarde zou je een ander (en waarschijnlijk beter) gemiddelde vinden. Kijk ook eens naar de metingen die je zelf tijdens de eerste les vaardigheden hebt verricht. Zitten daar ‘verdachte’ waarden tussen?

Soms weet je nog dat er wat mis ging op het lab, en kun je daarom je datapunt met goede reden weggooien. Dat lukt echter lang niet altijd (wel een goede reden om dus altijd echt een goed labjournaal bij te houden!).

Maar je kan een datapunt niet zomaar weggooien omdat hij je niet bevalt. Er is altijd een kans dat de verdachte waarde geen echte outlier is maar werd veroorzaakt door zuiver toeval. Waar trek je de grens, en wanneer noem je iets een outlier? Statistiek kan hierbij helpen: je kunt op basis van een kansberekening gaan kiezen of het datapunt mee mag blijven doen of niet. Een methode hiervoor is de methode van Dixon (ook vaak de Q-test genoemd). Die is geschikt als je weinig datapunten hebt (maximaal 25, meestal bij minder dan 10).

Waarschuwing vooraf: de Q-test kun je niet gebruiken als je:

• maar 1 of 2 datapunten hebt
• maar 3 datapunten hebt, en daarvan zijn er twee precies hetzelfde. Of datapunten en daarvan zijn er 3 precies hetzelfde. etc (dus als n-1 datapunten precies hetzelfde zijn).

Dixons Q-test

De Dixons Q-test is specifiek bedoeld voor de situatie dat je weinig herhaalde metingen hebt, en er is er eentje wel erg vreemd. Dus stel, je meet 5 keer het suikerpercentage van een flesje cola, en een van de 5 metingen is twee keer zo hoog als de andere vier.

Herhaalde metingen zijn meerdere metingen van dezelfde variabele bij hetzelfde flesje cola, hetzelfde pak sinaasappelsap, dezelfde persoon, patient, proefdier etc. Doe je een steekproef met 50 metingen, en is 1 van je metingen wel erg vreemd, dan heb je daar weer andere tests voor. Die behandelen we niet in deze cursus.

Bekijk hier een kennisclip over de Dixons Q-test (let op dat de formule voor Q verschilt per hoeveel metingen (n) je hebt. Check je formulekaart voor de juist formule):

De gegevens voor de Q-test staan op je formuleblad:

1. Pak je formuleblad erbij en ga naar blz 2 (“Kritische waarden voor de Dixon-test voor outliers).
2. Je moet een zgn. \(Q-waarde\) berekenen. De manier waarop deze \(Q\) moet worden berekend is afhankelijk van een aantal meetpunten. De berekening staat als formule in tabel voor de Dixon test voor outliers, in de meest linker kolom. Zo is voor 3 t/m 7 meetpunten de berekening als volgt gedefinieerd (r10 in de de tabel mag je gewoon lezen als ‘Q’):

\(Q=\frac{x2−x1}{xn−x1}\)

De betekenis van de diverse “x-jes” in de formule is als volgt: Je hebt n metingen verricht. In gedachten rangschik je alle metingen op zo’n manier dat je begint met de outlier. Als je een mogelijke outlier naar beneden hebt, begin je dus met de kleinste waarde x1, dan de één na kleinste x2, tot de grootste waarde die dan xn heet. Als je een outlier naar boven wilt testen, stelt x1 de grootste waarde voor, x2 de op één na grootste, en uiteindelijk xn de kleinste waarde.

Exercise 4

De waarden in het grafiekje hierboven waren 4,4; 5,3; 4,4; 4,6 en 4,6 welke is onze verdachte?

hoeveel is N?

Klik hier voor het antwoord

5.3 is de mogelijke outlier, naar boven toe

N is 5 (5 metingen)

Exercise 4

Zet de waarden in volgorde, en vul in:

• x1 =
• x2 =
• x3 =
• x4 =
• x5 =

Reken vervolgens \(Q\) uit met de juiste formule in de tabel op het formuleblad.

Klik hier voor het antwoord

• x1 = 5,3
• x2 = 4,6
• x3 = 4,6
• x4 = 4,4
• x5 = 4,4

\(Q\) = (4,6-5,3) / (4,4-5,3) = 0,778

Met die Q-waarde kunnen we een hypothesetest gaan doen. Hypothesetests gaan we in de volgende lessen nog vaker tegenkomen. Stel, we willen die verdachte waarde er graag uit gooien. Dan wil je graag weten hoe groot de kans zou zijn dat je dit punt zou vinden en het is geen outlier. Is die kans nou heel klein, dan kun je hem rustig weg gooien. Meestal spreken we af dat die kans kleiner moet zijn dan 5%, dat heet een significantiewaarde \(\alpha = 0.05\).

In de Q-test hoef je die kans niet zelf uit te rekenen. De waarde die Q moet overstijgen (=de kritische Q-waarde of \(Q_{kritisch}\)) om onder een bepaalde \(\alpha\) te komen staan in de tabel op je formuleblad.

3. Je zoekt \(Q_{kritisch}\) op in de tabel in de juiste kolom en de juiste regel. Kies de kolom voor de \(\alpha\)-waarde die je wilt (meestal 0.05). Kies de regel met het aantal metingen dat je hebt (in dit geval n=5). In de kolom α=0,05 vinden we dan \(Q_{kritisch}=0,642\). Dit is de waarde waar jouw Q-waarde overheen moet om bij een \(\alpha\)-waarde van 0.05 als outlier bestempeld te worden.
4. Vergelijk deze \(Q_{kritisch}\) met jouw berekende \(Q\). Is je berekende \(Q\) groter, dan is het een outlier.

Exercise 4

Was de meetwaarde van 5.3 een outlier bij een \(\alpha\)-waarde van 0.05?

Klik hier voor het antwoord

ja.

\(Q\) = 0,778 \(Q_{kritisch}\)=0,642

0,778 > 0,642, dus het is een outlier

Merk op dat de waarde van \(Q_{kritisch}\) in de tabel toeneemt naarmate α kleiner wordt.

Exercise 4

Was de meetwaarde van 5.3 een outlier bij een \(\alpha\)-waarde van 0.01?

Klik hier voor het antwoord

nee

\(Q\) = 0,778 \(Q_{kritisch}\)=0,780

0,778 < 0,780, dus het is geen outlier

Of je iets een outlier gaat noemen, hangt er dus vanaf met welke betrouwbaarheid je dat wilt doen. Wil je een \(\alpha\)-waarde van 0.05, dan zeggen we ook wel dat je met een betrouwbaarheid van 95% bepaald of iets een outlier is (0.05 is 5%, 100-5 = 95%).

stappenplan Dixons Q-test

1. wijs je verdachte waarde aan. Dit is \(X1\).
2. controleer of niet al je andere metingen precies gelijk aan elkaar zijn. Is dat het geval (bijvoorbeeld je metingen zijn: 4.1; 4.1; 4.1 en 4.3) dan kun je geen Q-test doen en moet je je verdachte waarde gewoon meenemen.
3. bepaal je aantal metingen \(n\)
4. Zet je waarden in oplopende of aflopende volgorde, te beginnen met verdachte waarde \(X1\). Vind \(X2\) en \(Xn\).
5. zoek de berekening voor \(Q\) op op je formuleblad en bereken \(Q\)
6. Kies een \(alpha\) (meestal 0.05) en zoek de juiste \(Q_{kritisch}\)
7. Kijk of \(Q > Q_{kritisch}\). Ja? dan is het een outlier.
8. Gooi je outlier uit je dataset. Die doet niet meer mee voor verdere berekeningen.
9. Einde. Je mag het niet nog een keer doen met dezelfde dataset.

Opmerkingen Q-test

• Het is hoe dan ook fout een waarde zonder verdere uitleg te negeren! Als je een waarde niet meeneemt in je berekeningen is het belangrijk te vermelden welke waarde dit is en waarom je die waarde niet meeneemt in je berekening (statistische reden, fout of vergissing tijdens experiment, etc.).
• Als je al weet dat je waarde afwijkt omdat je een fout hebt gemaakt op het lab (per ongeluk reagens vergeten toe te voegen of zo), dan hoef je geen Q-test te doen.
• De methode van Dixon werkt alleen maar goed als je te maken hebt met een set metingen waar maar 1 outlier in zit. Als er meerdere outliers in zitten is deze methode te simpel en heb je andere technieken nodig die we hier niet zullen behandelen.
• Wanneer een waarde wordt weggelaten moeten gemiddelde en andere statistische parameters zoals het 95% betrouwbaarheidsinterval, dat we in volgende lessen behandelen, weer opnieuw worden berekend (het aantal meetpunten is nu immers 1 kleiner).
• De methode van Dixon is alleen geldig voor herhaalde metingen van dezelfde waarde.
• Er zijn nog andere methoden voor outlierdetectie. Eén van de op met name laboratoria gebruikte methoden is de Methode van Grubbs.

4.3 Werkcollege

4.3.1 Deel 1 - Z-scores

Het oppervlak onder de normaalcurve tussen twee meetwaarden (x1 en x2) is de kans om een waarde uit dat interval tegen te komen. De kans om een meetwaarde tegen te komen tussen de minimale en maximale waarde van de populatie is dus 100%. We zeggen ook wel dat de oppervlakte onder de grafiek 1 is, of 100%.

Als je een willekeurig iemand meet uit de populatie dan is de grootste kans om een lengte tegen te komen die dicht bij het gemiddelde is (daar zijn er immers het meeste van). Hoe verder je verwijderd bent van het gemiddelde (b.v. een persoon van 230 cm) hoe kleiner de kans om die waarde (in dit geval de lengte) tegen te komen. De afstand van een meetwaarde t.o.v. het gemiddelde kun je uitdrukken in eenheden (in dit geval cm.) maar ook in standaarddeviaties, dan heet het de Z-score:

\(z=\frac{x-\mu}{\sigma}\)

Bereken in Excel de Z-score van iemand met een lengte van 195 cm uit een populatie van μ = 180 cm en σ = 10 cm d.m.v. bovenstaande formule

Exercise 4

Wat is de Z-score?

Klik hier voor het antwoord

1.5

Exercise 4

Wat is de rechter overschrijdingskans van deze Z-score? Maak gebruik van de Z-tabel

Klik hier voor het antwoord

6,7%

Exercise 4

Wat betekent deze rechter overschrijdingskans?

1. Dit is de kans dat een willekeurig iemand groter is dan 195cm
2. Dit is de kans dat een willekeurig iemand kleiner is dan 195cm
3. Dit is de kans dat een willekeurig iemand precies 195cm lang is

Klik hier voor het antwoord

A

Exercise 4

Klopt de onderstaande stelling?

‘De Z-score neemt af met een toenemende \(\sigma\)’

Klik hier voor het antwoord

ja

Exercise 4

Klopt de onderstaande stelling?

‘Wanneer \(\sigma\) toeneemt wordt de kans kleiner dat je iemand ontmoet die langer is dan 195cm’

Klik hier voor het antwoord

nee

Exercise 4

Volgens een fabrikant geldt voor het volume van een maatkolf dat het populatiegemiddelde μ = 150 mL en de populatiestandaarddeviatie σ = 3 mL. Welk volume heeft de kleinste 2,5 % van de maatkolven die uit de fabriek komen maximaal?

Klik hier voor het antwoord

Je zoekt x-aswaarde (volume) waar de kleinste 2,5% links van zit. We zitten kleiner dan het gemiddelde en we zoeken het oppervlakte links van een bepaalde waarde.

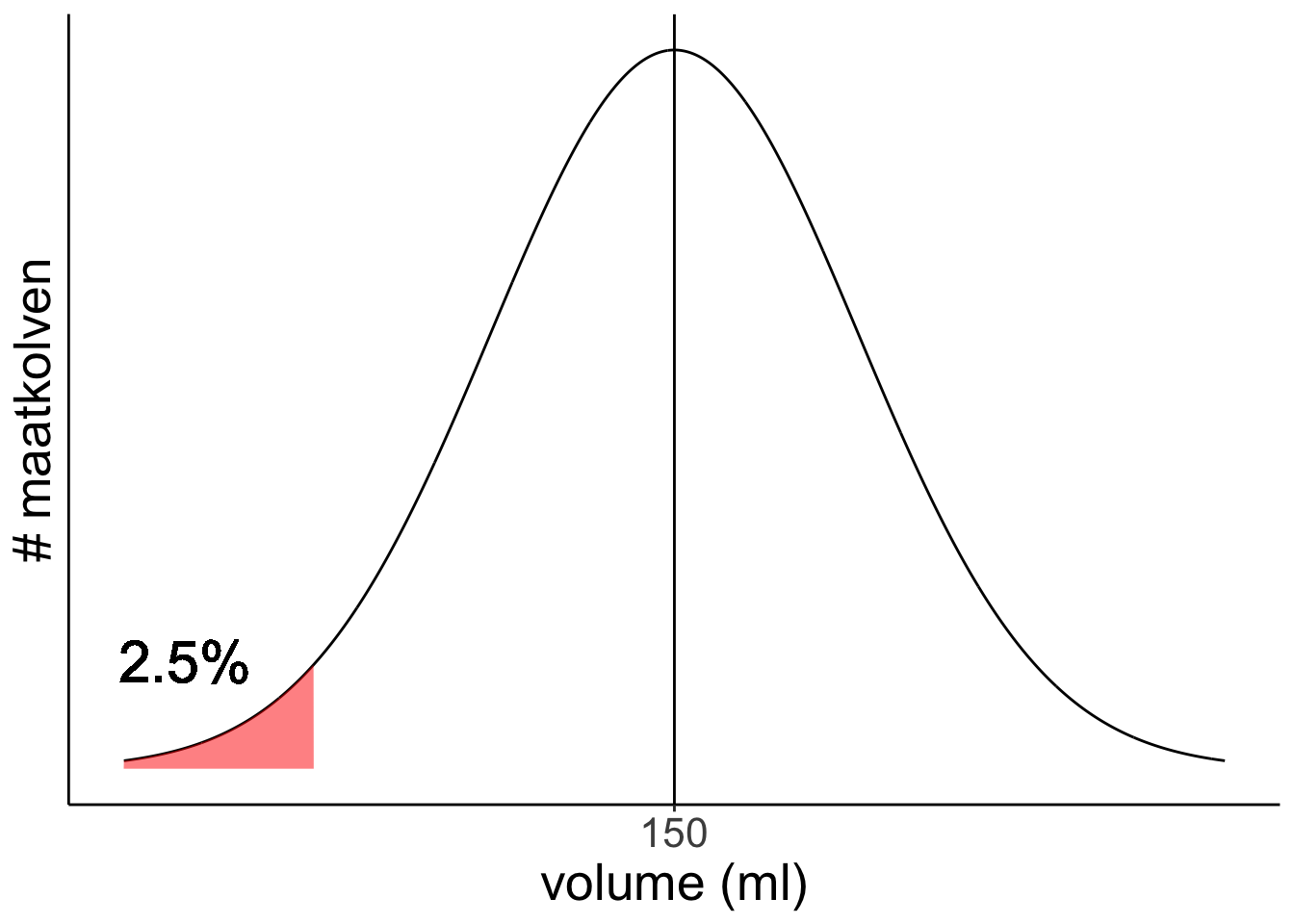
Maar de linker kant van de z-verdeling staat niet in de tabel, we kunnen alleen opzoeken wat de oppervlakte is verder naar rechts dan een waarde groter dan het gemiddelde. Gelukkig is de normaalverdeling symmetrisch, dus we kunnen ook de waarde op de x-as zoeken waar 2,5% boven zit.

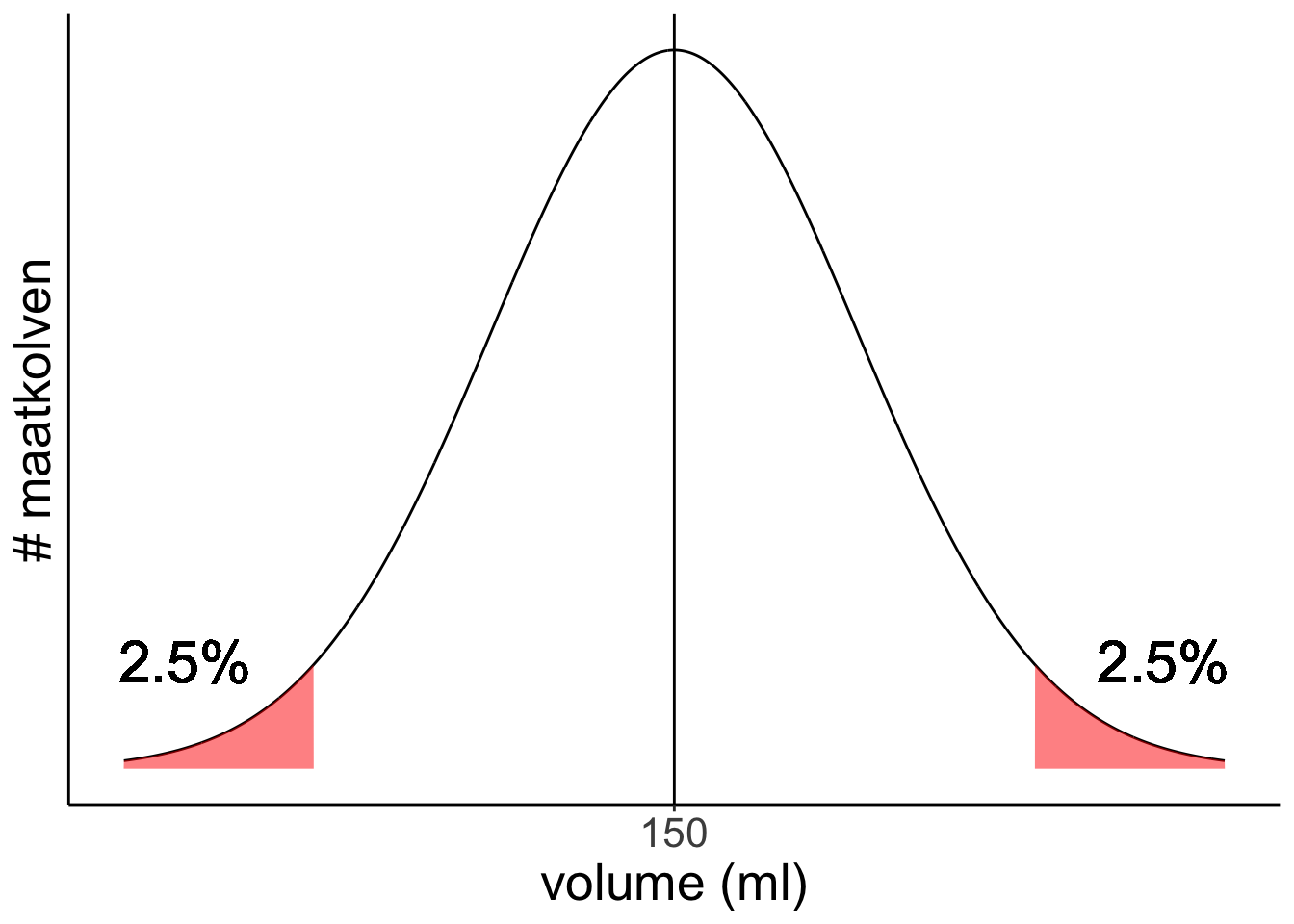
Zoek 2,5% op in de tabel: je vindt Z= 1,96

\(z=\frac{x-\mu}{\sigma}\)

1,96 = (x - 150)/3

x = 155,9 ml

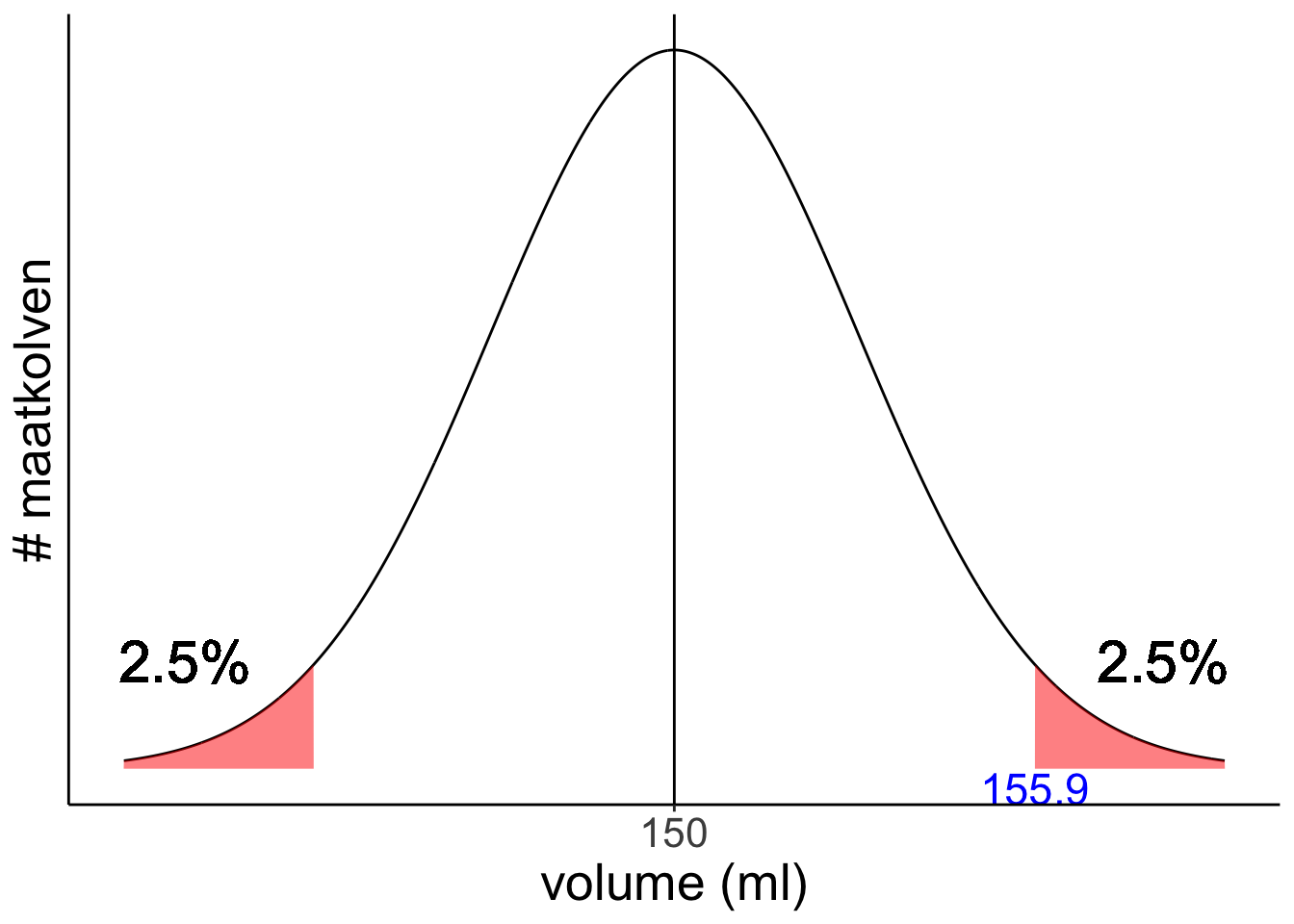
De afstand tot het gemiddelde die we zoeken is net zo groot, maar dan onder het gemiddeld in plaats van erboven: 155,9 - 150 = 5,9 ml.

150 - 5,9 ml = 144,1

antwoord: 144,1 ml

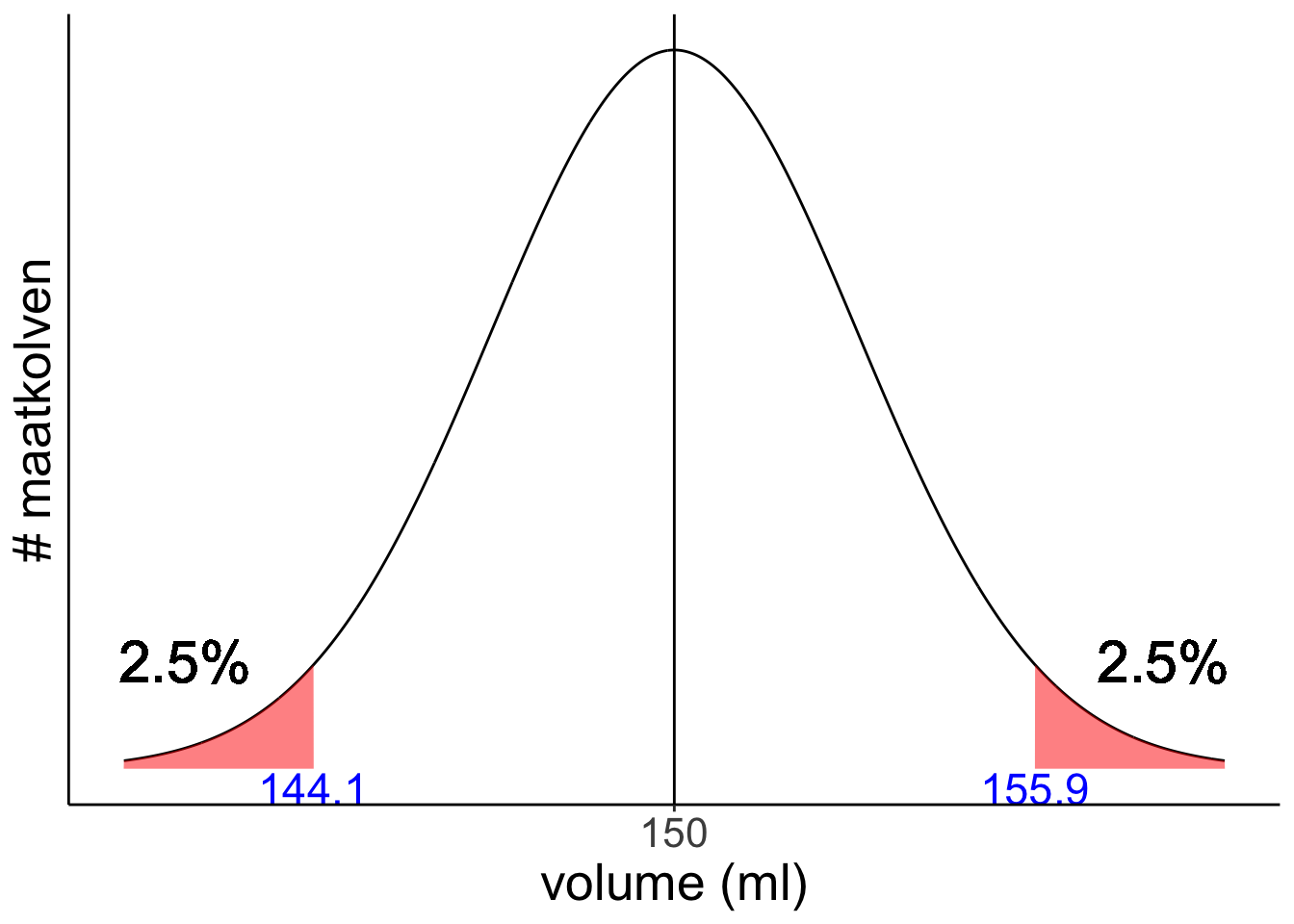
Exercise 4

Een machine die weegdoosjes vult heeft een gemiddelde μ van 20,0 mg en een populatiestandaarddeviatie σ van 0,306 mg. Hoeveel procent van de afgevulde weegdoosjes zal meer dan 20,6 mg bevatten?

Klik hier voor het antwoord

Vul de formule in: \(z=\frac{x-\mu}{\sigma}\)

Zoek het bijbehorende percentage op in de tabel: 2,5%

Exercise 4

De gemiddelde glucoseconcentratie in het bloed is 5,2 nmol/L voor normale, nuchtere en gezonde mensen. De populatiestandaarddeviatie is 0,8 nmol/L. Binnen welke grenzen zal een willekeurige meting met 95% zekerheid liggen?

Klik hier voor het antwoord

Tussen de 3,6 en 6,8 nmol/L

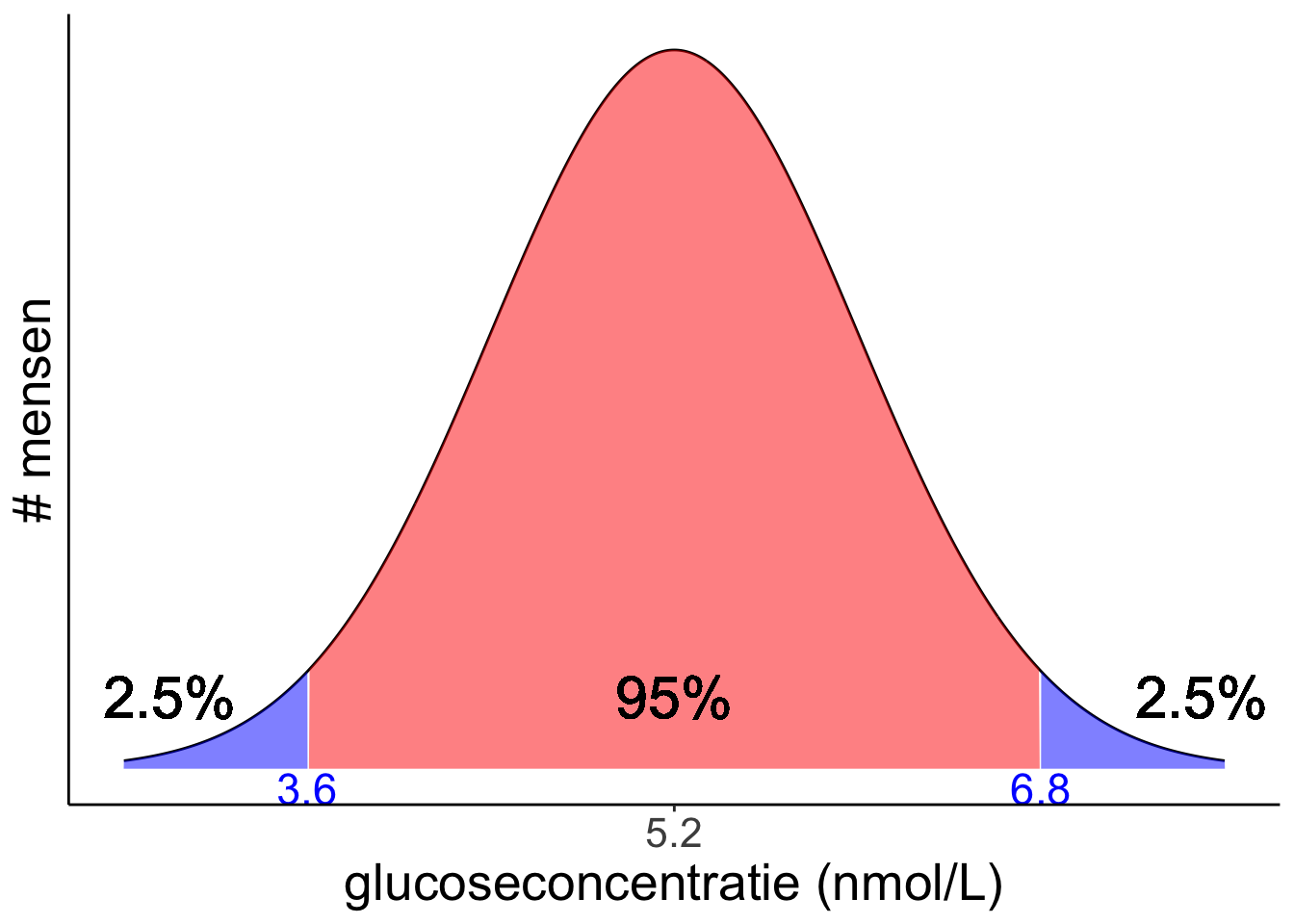
Exercise 4

Volgens de fabrikant geldt voor het volume van Cola Zero dat het populatiegemiddelde 𝜇 = 330 ml en de populatiestandaarddeviatie 𝜎 = 3 ml. Dat betekent dat 2,5 % van de flesjes die uit de fabriek komen minder bevatten dan:

Klik hier voor het antwoord

324,1 ml

Exercise 4

Een bedrijf synthetiseert een farmaceutisch middel met een zuiverheid van μ = 98,2 %. De standaardafwijking van de zuiverheid is σ = 1,6 %. Hoe groot is de kans dat het bedrijf (met deze gegevens) een onzuiverheid krijgt die kleiner is dan 95%?

HINT

Laat je niet in de war brengen door die procenten. Hier is de “eenheid” percentage.

Dus:

μ = 98,2

σ = 1,6

x = 95

Klik hier voor het antwoord

2,28%

4.3.2 Deel 2 - kansverdelingen

Exercise 4

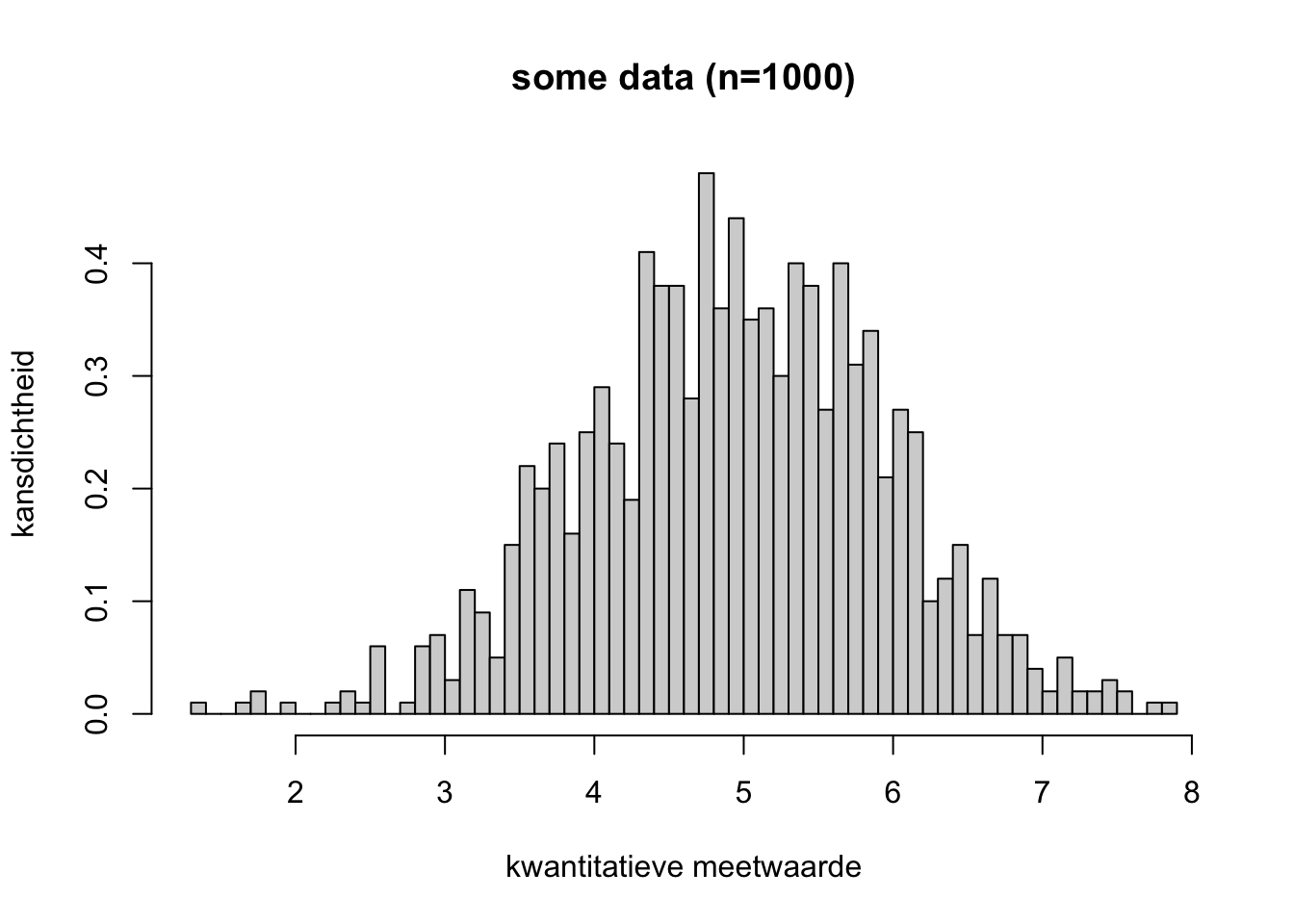
Is de volgende data denk je waarschijnlijk normaal verdeeld? Leg uit waarom.

Klik hier voor het antwoord

Waarschijnlijk wel. Het histogram heeft een klokvorm, met het hoogste punt in het midden en is symmetrisch.

Exercise 4

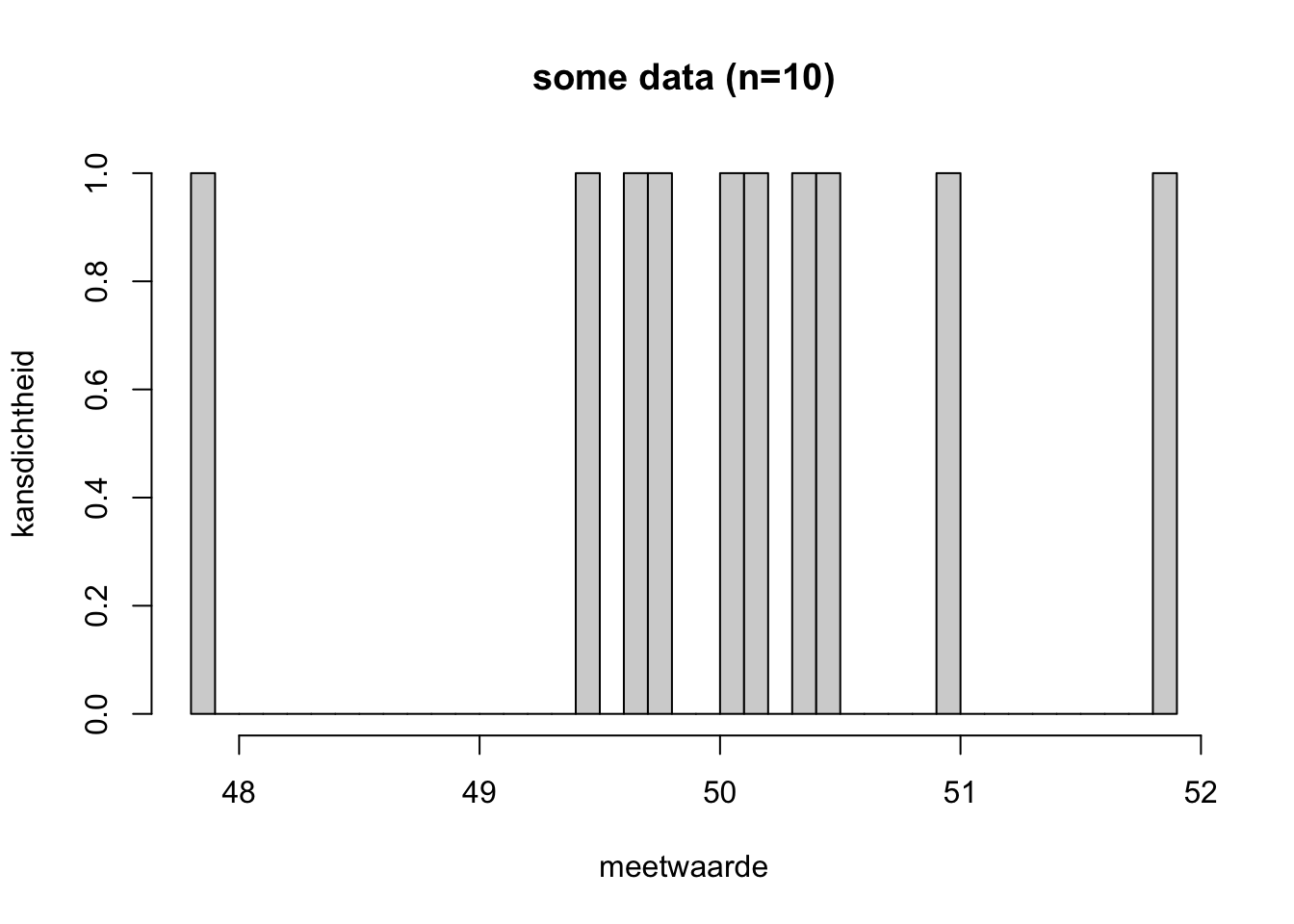
Is de volgende data denk je waarschijnlijk normaal verdeeld? Leg uit waarom.

Klik hier voor het antwoord

Neh. Deze dataset ziet er niet normaal verdeeld uit. Het zijn wel wat weinig datapunten, dus als je antwoord was “dat kun je niet echt zeggen met zo weinig datapunten” hadden we het ook prima gevonden.

Exercise 4

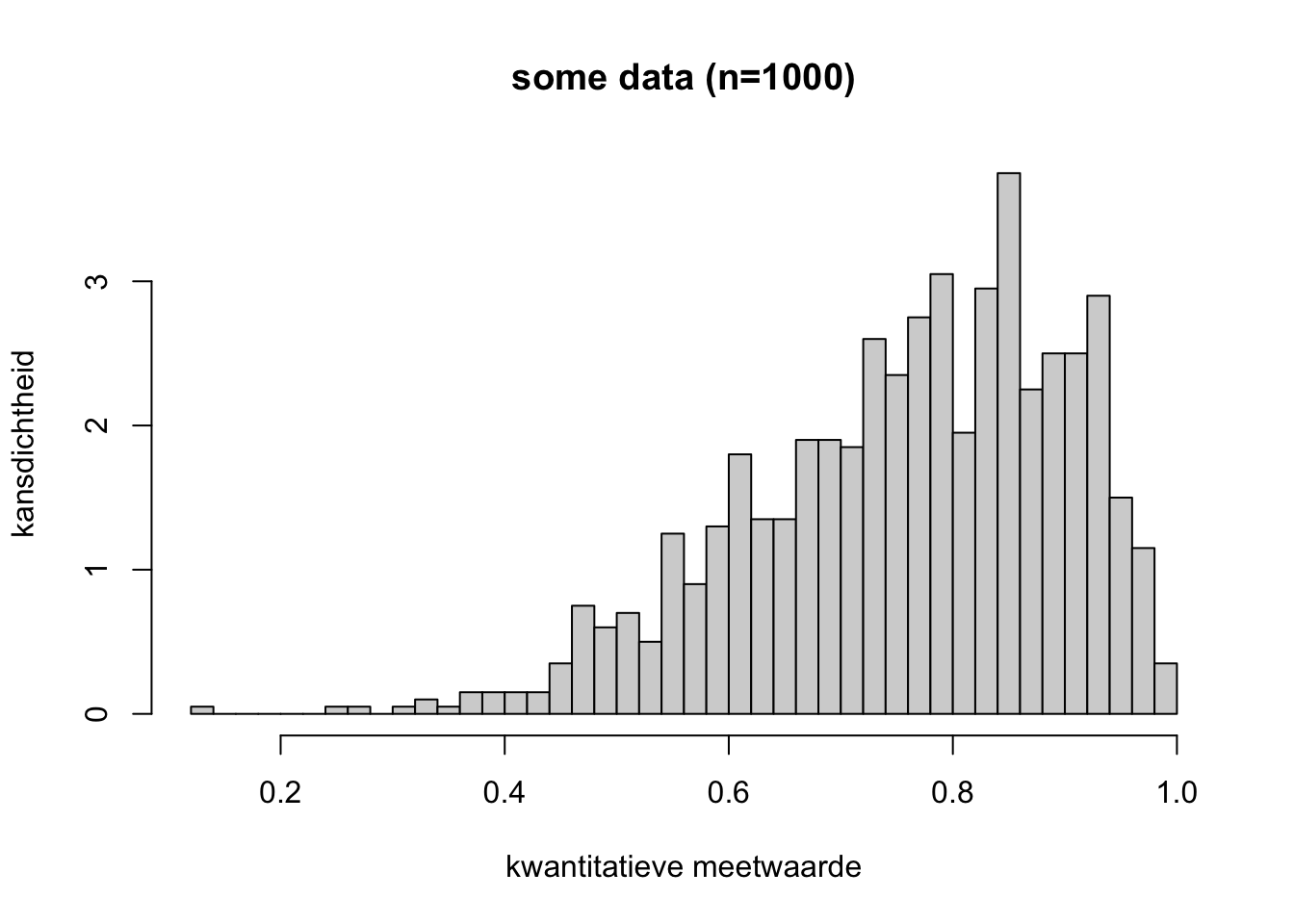
Is de volgende data denk je waarschijnlijk normaal verdeeld? Leg uit waarom.

Klik hier voor het antwoord

Nee, dit ziet er niet normaal verdeeld uit. Het histogram heeft een klokvorm, maar is scheef: het hoogste punt zit niet in het midden en het histogram is niet symmetrisch. Deze verdeling ziet er links-scheef uit.

4.3.3 Deel 3 - Outliers

Een groep studenten meet het alcoholpercentage van dezelfde fles wijn. Alle studenten meten 1 keer en slaan de data op in een text bestand.

• Gebruik het bestand dixonstest_data1.txt
• Importeer de data in Excel
• Zorg dat je een nette tabel met data krijgt

Het lijkt dat de meetwaardes van student 6 afwijkt van de andere meetwaardes. Student 6 heeft geen labjournaal bijgehouden, dus we hebben geen idee wat er gebeurd is. Mogen we dit meetpunt negeren?

Bereken met m.b.v. de Dixon’s Q-test in Excel of deze waarde significant afwijkt van de andere waardes in de groep bij een significantie niveau a = 0,05. Gebruik hiervoor de Dixon’s Q-test. De tabel staat op je formuleblad. Beantwoord de volgende vragen:

Exercise 4

Is de meetwaarde van student 6 een outlier?

HINT

Zoek in de tabel op het formuleblad op wat de formule is bij n=11 meetpunten. r21 mag je lezen als \(Q\). Is de \(Q\) die je krijgt groter dan \(Q_{kritisch}\) ?

Klik hier voor het antwoord

\(Q=\frac{x3−x1}{x_{n-1}−x1}\)

zet je meetwaarden onder elkaar en sorteer de data met Excel van groot naar klein.

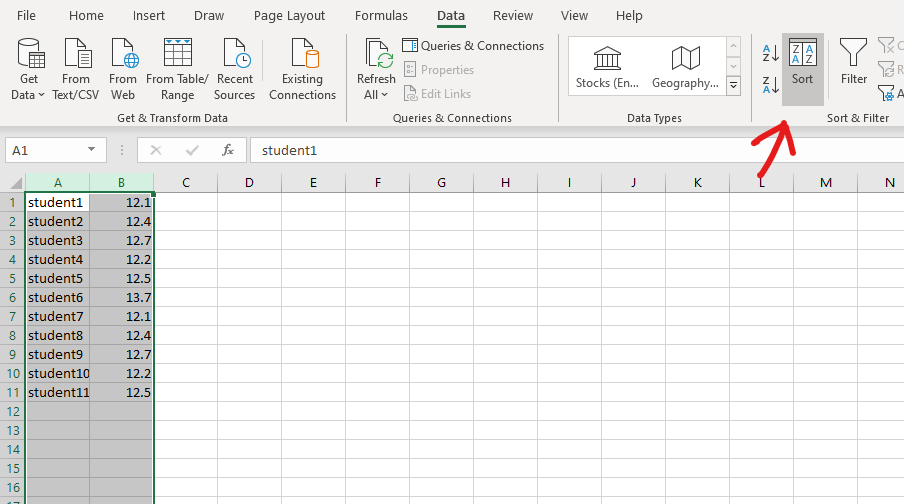
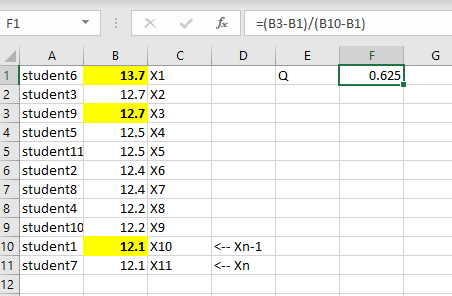
\(Q\) = 0,625 \(Q_{kritisch}\)=0,576

0,625 > 0,576, dus het is een outlier

Exercise 4

Kun je berekenen of de meetwaarde van student 3 en 9 ook een outlier is volgens de Dixon’s Q-test?

Klik hier voor het antwoord

Dat kan je niet berekenen, je mag de Dixon’s Q-test gebruiken voor maximaal 1 (een, uno, one) outlier per dataset.

Exercise 4

Vanaf welk significantieniveau zou de waarde van student 6 geen outlier zijn?

Klik hier voor het antwoord

Kijk welke kolom in de tabel (bij n=11), als eerste groter is dan 0,625.

Dat is bij een \(\alpha\) (=significantieniveau) van 0.02.

Exercise 4

Een andere groep studenten meet de voetlengte van een medestudent met maat 39. Ze vinden de volgende meetwaarden:

student	gemeten_voetlengte_cm
1	25.1
2	25.2
3	25.1
4	25.3
5	25.7
6	24.9

Met welke maximale betrouwbaarheid zou je kunnen zeggen dat de meting van student 5 een outlier is?

Klik hier voor het antwoord

n=6

\(Q=\frac{x_{2}−x_{1}}{x_{n}−x_{1}} = 0.5\)

Welke kolom haalt deze Q nog bij n=6? Dat is de kolom met \(\alpha\) = 0,10 en een \(Q_{kritisch}\) van 0,482.

De kolom met \(\alpha\) = 0.05 en een \(Q_{kritisch}\) van 0,560 gaat onze berekende \(Q\)-waarde niet meer overheen.

Je kan dus met een maximale betrouwbaarheid van 90% zeggen dat de meting van student 5 een outlier is. (want \(\alpha\) = 0,10 = 10%. en 100-10 = 90%)

Exercise 4

Drie docenten zijn weer bezig met hun grote hobby: kattenstaarten meten. Ze besluiten eens alle drie de staart van kat Minoes te meten:

docent	gemeten_staartlengte_cm
Bas	20.1
Alyanne	15.2
Rolinka	20.1

Is de meetwaarde van Alyanne een outlier?

Klik hier voor het antwoord

Zou best kunnen, maar op basis van de Dixon’s Q-test kun je dat niet bepalen, omdat de andere twee meetwaarden precies even groot zijn. We hebben dus geen idee van de spreiding, en dus ook niet of de meetwaarde van Alyanne erg vreemd is ten opzichte van de spreiding.

Exercise 4

Ze vertrouwen Alyanne’s meetpunt voor geen meter. De docenten besluiten om elk de staart van 5 buurtkatten op te meten. De data ziet er als volgt uit. Duidelijk is, dat Alyanne’s meetlint niet helemaal in orde is. Dat kan kloppen, want haar kinderen hebben er onlangs aan lopen trekken.

kat	Bas	Alyanne	Rolinka
Zorro	25.1	18.8	25.2
Joep	28.2	21.1	28.1
Mikkie	27.5	20.6	27.5
Muis	21.0	15.8	21.1
Elsa	29.6	22.2	29.7

Wat voor type meetfout is dit?

Klopt het dat je meetwaarden lager uitvallen als iemand je meetlint uitgerekt heeft?

Klik hier voor het antwoord

Systematische fout. Zie les 2

Ja, dat zou kunnen kloppen.

Exercise 4

Stel je hebt de glucoseconcentratie in een sample 8 keer bepaald. Je wilt kijken of een van je meetwaarden een outlier is.

Wat zal er met \(Q_{kritisch}\) gebeuren als je zou eisen dat \(\alpha=0\), en dus een betrouwbaarheid van 100%? Dus dan zou je dus helemaal nooit een toevallig sterk afwijkende waarde ten onrechte bestempelen als outlier?

Klik hier voor het antwoord

Dan wordt \(Q_{kritisch}\) 1. Aangezien je Q-waarde nooit groter gaat zijn dan 1 (vervang de afwijkende waarde in een van de vragen hierboven maar eens voor iets belachelijk hoogs. 200 of zo. en reken Q maar uit), is de consequentie dat je nooit iets als een outlier zult bestempelen. Daar hebben we dus niks aan. Statistiek betekent risico’s nemen!

Nu weet je meteen waarom je geen Q-test kunt doen als al je metingen, behalve die ene verdachte, precies gelijk aan elkaar zijn. Dan is \(Q\) namelijk wel altijd 1! Dus wat die verdachte waarde ook is, hij zou altijd als outlier bestempeld worden. Dat mag dus niet.