1 Un recorrido por la Estadística Espacial

Los estadísticos son patriotas, ¡luchan por la independencia!

1.1 Introducción

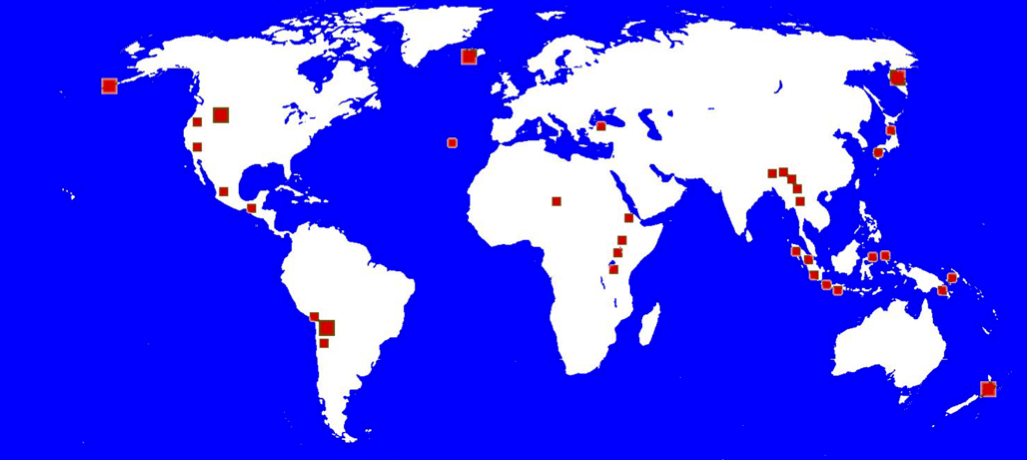
¿Se puede ver todo desde una perspectiva espacial?

require(dplyr)
leaflet::leaflet() %>%
  leaflet::addTiles() %>%  
  leaflet::addMarkers(lng=-78.4708585, lat=-0.1683198, popup="Más allá de la independencia")

Evolución

  • idd: Sean \(X_1\ldots X_n\) v.a. independientes e idénticamente distribuidas.

  • Mediciones repetidas: datos pareados.

  • Series de tiempo.

  • Correlación <-> Autocorrelación <-> Autocorrelación Espacial

Cressie (2015), publicado por primera vez en 1993

1.1.0.1 Datos Geoestadísticos

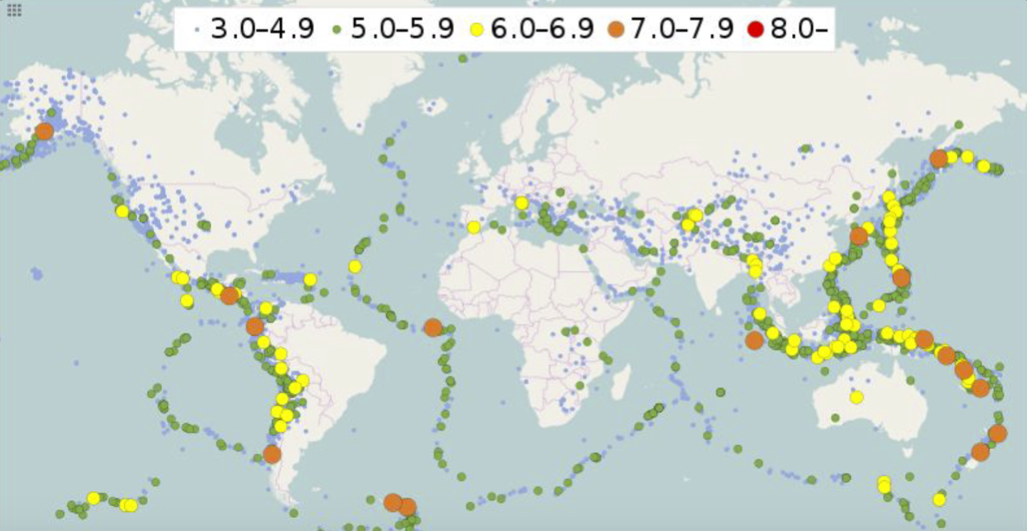
drawing

1.1.0.2 Lattice data

drawing

1.1.0.3 Point patterns

drawing

Sea \(\mathbf{s}\in\mathbb{R}^d\) un dato genérico de posición en un espacio ecuclideano \(d\)-dimensional y suponga que el dato observado en \(\mathbf{s}\), \(\mathbf{Z(s)}\), es una variable aleatoria. Permítase a \(\mathbf{Z(s)}\) variar sobre el conjunto índice \(D\subset \mathbb{R}^d\) tal que genera el proceso aleatorio (campo aleatorio) \[ \{\mathbf{Z(s)}:\mathbf{s}\in D\} \]

Usualemente se asume a \(D\) fijo, pero podría ser un conjunto aleatorio. Es decir, tanto \(\mathbf{Z}\) como \(D\) pueden variar en cada realización.

  • Datos Geoestadísticos: \(D\) es un subconunto fijo de \(\mathbb{R}^d\) que contiene un rectángulo d-dimensional de volumen positivo; \(\mathbf{Z(s)}\) es un vector aleatorio en la ubicación \(\mathbf{s}\in D\).

  • Datos lattice: \(D\) es una colección fija (regular o irregular) de puntos de \(\mathbb{R}^d\); \(\mathbf{Z(s)}\) es un vector aleatorio en la ubicación \(\mathbf{s}\in D\)

  • Patrones de puntos: \(D\) es un proceso en \(\mathbb{R}^d\) o un subconjunto de \(\mathbb{R}^d\); \(\mathbf{Z(s)}\) es un vector aleatorio en la ubicación \(\mathbf{s}\in D\)

1.1.0.4 Ignorando la correlación espacial

  • \(E(\bar{Z})=\mu\)
  • \(V(\bar{Z})=\frac{\sigma^2_0}{n}\)

1.1.0.5 Considerando la correlación espacial

  • \(E(\bar{Z})=\mu\)
  • \(V(\bar{Z})=\frac{\sigma^2_0}{n}\left(1+\frac{2}{n}\sum_{i<j}^{n}\left(\frac{3}{2}\frac{h}{110}-\frac{1}{2}\frac{h^3}{110^3} \right) \right)\)
  • \(C(h) = \sigma^2_0\left(1- \left(\frac{3}{2}\frac{h}{110}-\frac{1}{2}\frac{h^3}{110^3}\right) \right)\)

1.1.1 Datos espaciales

  • Son datos que tienen una referencia especial: valores de las coordenadas y un sistema de referencia (long/lat o UTM).

  • Hacer un mapa adecuado que no distorsione los datos subyacentes es desafiante: How to lie with maps (Monmonier (2018))

  • El análisis de datos espaciales va más allá de lo que se ve en un mapa, trata de responder a la pregunta: ¿cuál es el proceso hipotético que que generado los datos observados?

  • Las instituciones están cada vez más preocupadas por este tipo de datos, por ejemplo, el Banco Mundial:

Datos de acceso libre del Banco Mundial

En R

  • Inicialmente R no podía manejar datos espaciales, particularmente los sistemas de coordenadas.

  • Desarrolladores crearon el paquete sp que maneja clases y métodos para datos espaciales.

  • sp trabaja con puntos, líneas, polígonos y cuadrículas (grids).

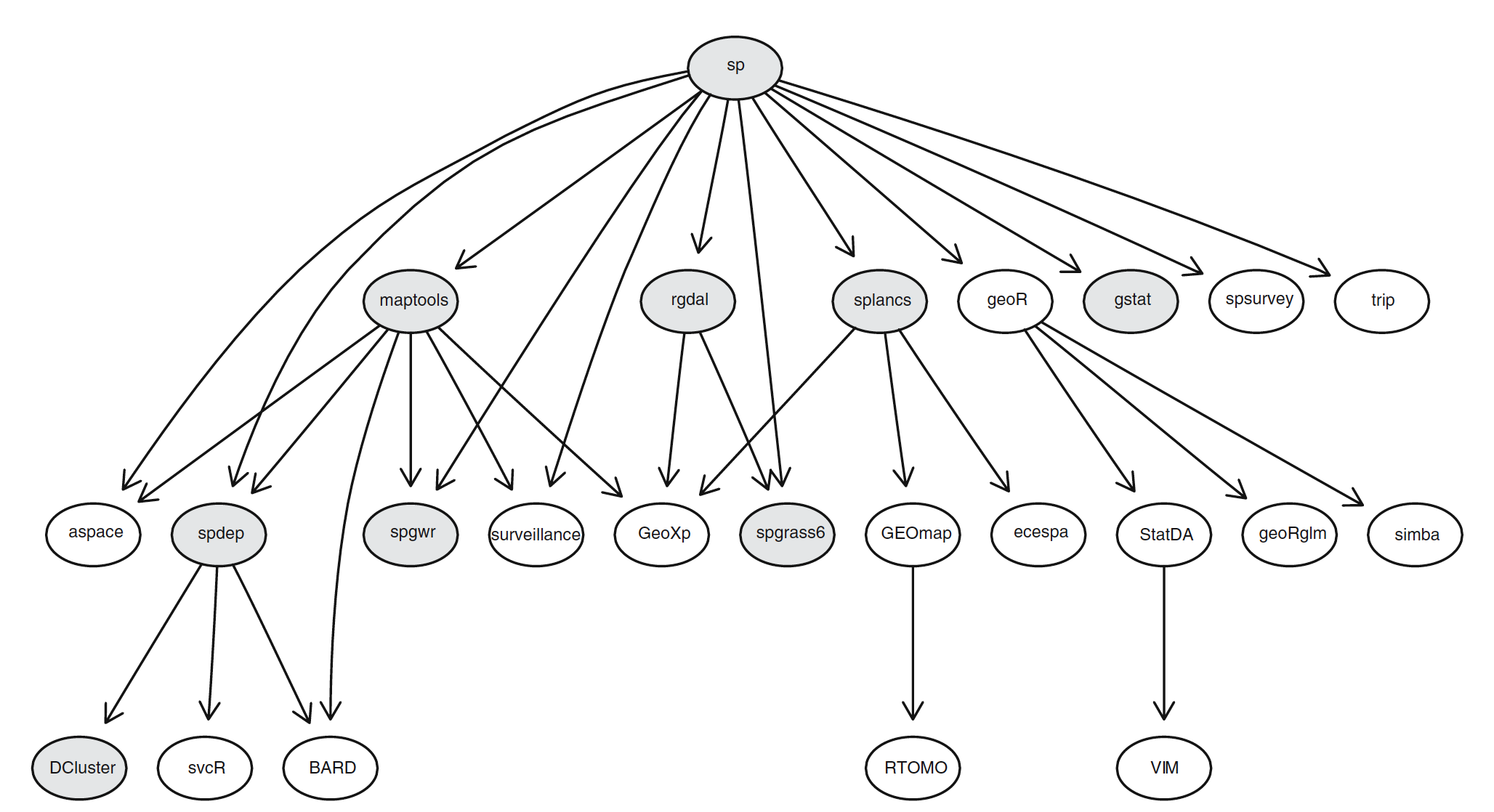
Paquetes de R en CRAN dependiendo de sp o importándolo directa o indirectamente (fecha 2008-04-06). Fuente: R. S. Bivand et al. (2008)
  • sf es el nuevo estándar
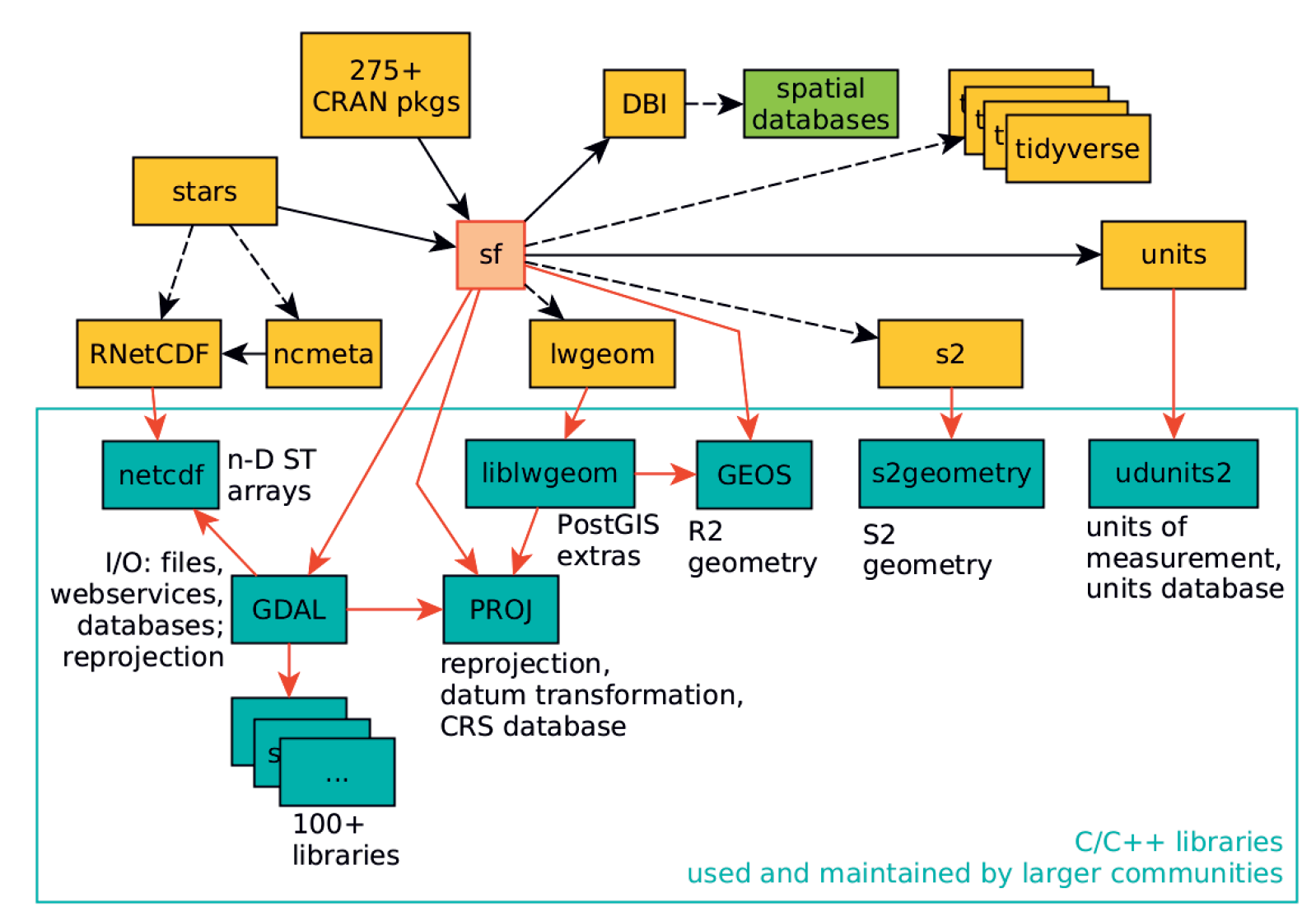
Paquetes de R en CRAN dependiendo de sf; las flechas indican dependencia fuerte, las flechas discontinuas dependencia débil. Fuente: Pebesma and Bivand (2023)

1.2 Modelización

1.2.1 Geoestadística

La clase de modelos estables de correlación están datos por:

\[ \rho(||\boldsymbol{h}||,\alpha,\beta) = exp\left\{ -\left(\frac{||\boldsymbol{h}||}{\alpha}\right)^{\beta} \right\} \]

donde \(||\boldsymbol{h}||\geq0\),\(\alpha>0\),\(0<\beta\leq2\).

En GeoModels (Bevilacqua and Morales-Oñate (2018)), este modelo de correlación corresponde a:

  • Exponential, exponential, exp o exponential son las especificaciones en el parámetro corrmodel. This is \(\beta = 1\)
  • Gauss, gauss, Gaussian and gaussian son las especificaciones en el parámetro corrmodel. This is \(\beta = 2\)
  • Stable o stable con las especificaciones en el parámetro corrmodel. En este caso ambos parámetros son libres.
CorFunStable <- function(lag,R_power,scale)
{
  rho=exp(-R_pow(lag/scale,R_power))
  return (rho)
}

Ejemplo:

scale = 1.2/3
R_power = 1
curve(CorFunStable(x,R_power,scale), ylab=expression(paste(rho,"(",h,")")),0,2)
abline(v=scale*3)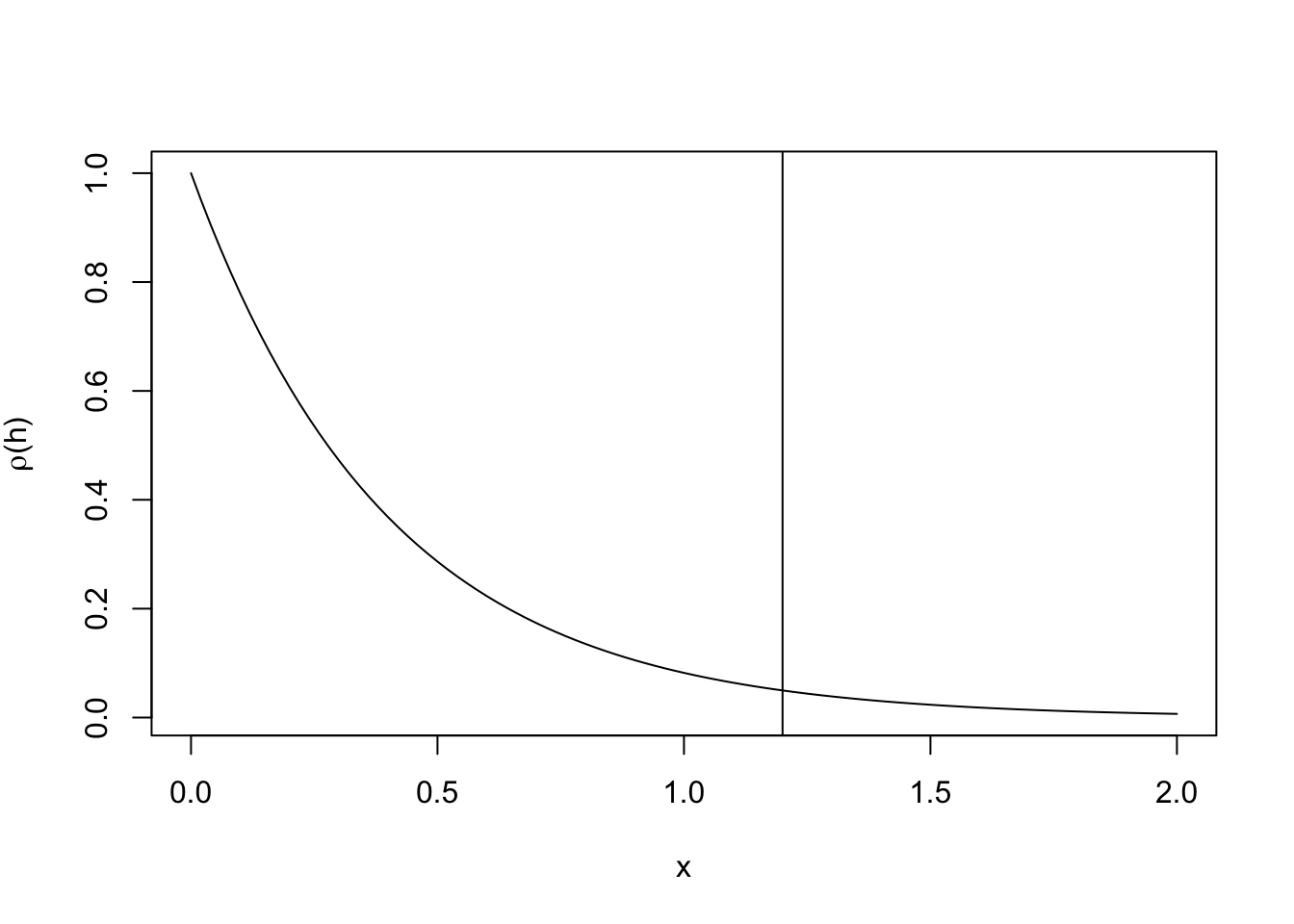

1.3 Aplicaciones

1.3.1 Point patterns

  • Baddeley et al. (2008) es una excelente introducción en el análisis point patterns a través del paquete spatstat (Baddeley and Turner (2005))

  • A continuación se muestran los datos de emergencias reportadas en ECU 911 en el mes de diciembre del 2014 en la zona urbana de Ambato (Padilla, 2015):

## Reading layer `PARROQUIA_URBANA' from data source 
##   `/private/var/folders/0p/n_r_hl095sv7nktfp_8n9n_80000gn/T/Rtmp4EHXgX/file2ca63214340/PARROQUIA_URBANA.shp' 
##   using driver `ESRI Shapefile'
## Simple feature collection with 9 features and 5 fields
## Geometry type: POLYGON
## Dimension:     XY
## Bounding box:  xmin: 761357 ymin: 9855965 xmax: 770602.4 ymax: 9865474
## Projected CRS: WGS 84 / UTM zone 17S
##     OBJECTID     NOMBRE           DPA_PARROQ          Shape_Leng      Shape_Area               geometry
##  Min.   : 6   Length:9           Length:9           Min.   : 3995   Min.   : 525448   POLYGON      :9  
##  1st Qu.: 8   Class :character   Class :character   1st Qu.: 9998   1st Qu.:3281191   epsg:32717   :0  
##  Median :10   Mode  :character   Mode  :character   Median :11578   Median :3819908   +proj=utm ...:0  
##  Mean   :10                                         Mean   :11540   Mean   :3597053                    
##  3rd Qu.:12                                         3rd Qu.:13884   3rd Qu.:4256663                    
##  Max.   :14                                         Max.   :17746   Max.   :5416222

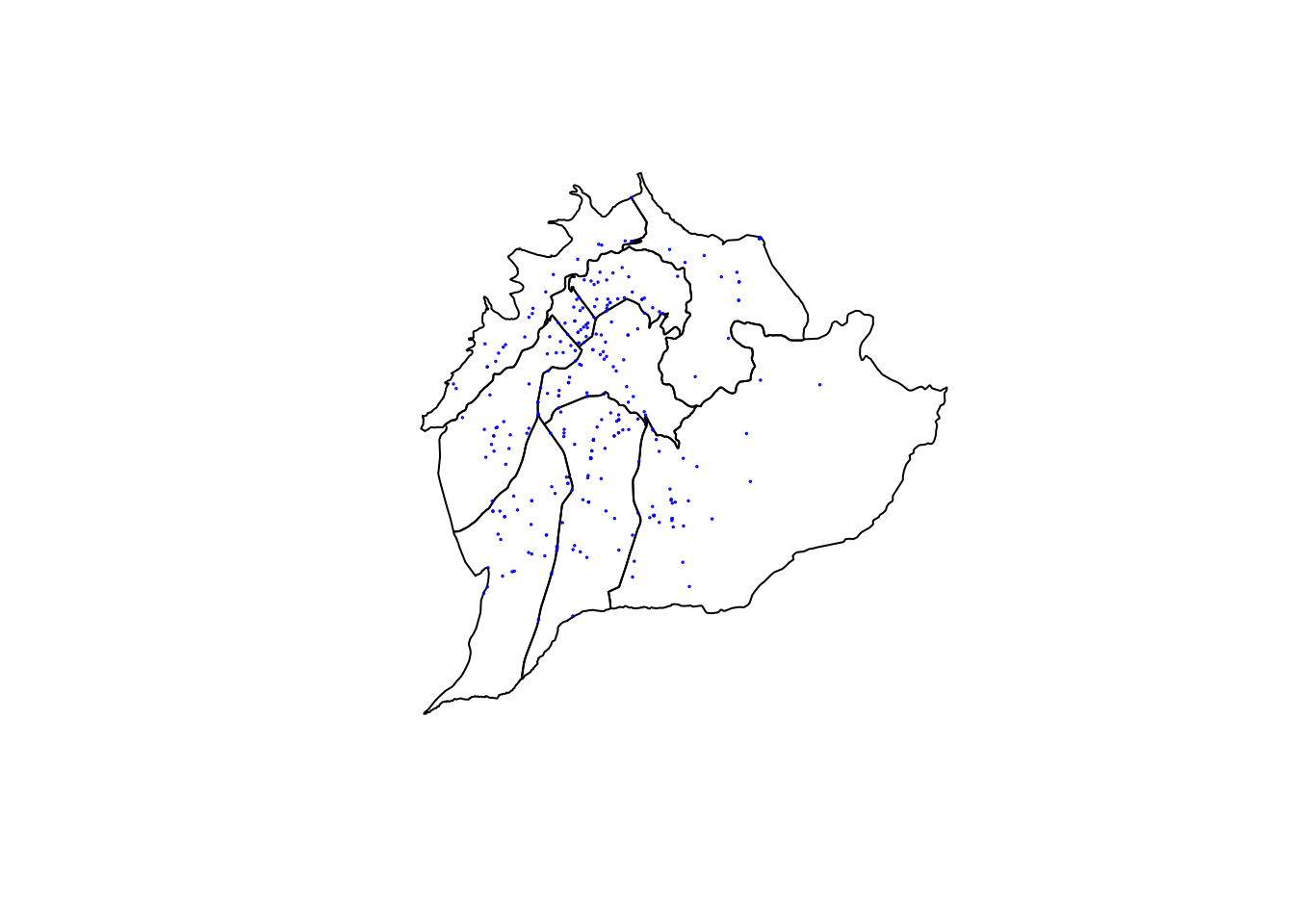
  • Ahora, después de convertir los datos a un planar point pattern, determinamos si se trata de un proceso aleatorio:
#https://spatstat.org/news.html
library(sf)
summary(cc)
## Planar point pattern:  281 points
## Average intensity 3.196119e-06 points per square unit
## 
## *Pattern contains duplicated points*
## 
## Coordinates are given to 10 decimal places
## 
## Window: rectangle = [761357, 770602.4] x [9855965, 9865474] units
##                     (9245 x 9510 units)
## Window area = 87919100 square units
(M <- spatstat.explore::quadrat.test(cc, nx = 5, ny = 5))
## 
##  Chi-squared test of CSR using quadrat counts
## 
## data:  cc
## X2 = 692.04, df = 24, p-value < 2.2e-16
## alternative hypothesis: two.sided
## 
## Quadrats: 5 by 5 grid of tiles
plot(st_geometry(poligonos))
points(cc, pch = 1, cex = 0.1,col = "blue")
plot(M, add = TRUE, cex = 0.5)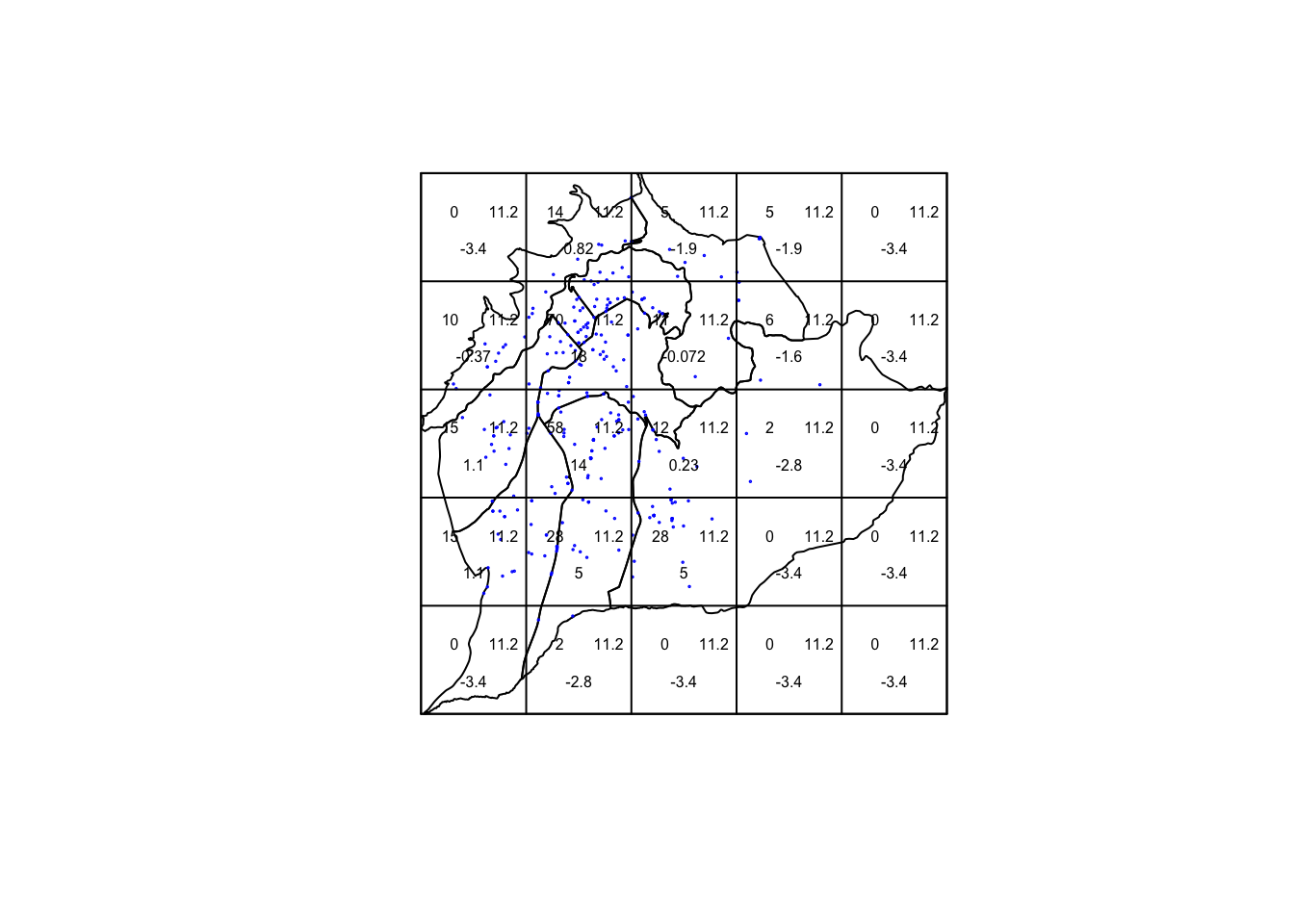

1.3.2 Clasificación

  • El enfoque espacial incluso puede trascender el enfoque tradicional:
Póster presentado en la X Escuela de Verano Latinoamericana de Inteligencia Artificial, 2014. Ganador del segundo lugar.
  • La distribución espacial de las especies de peces analizada es:
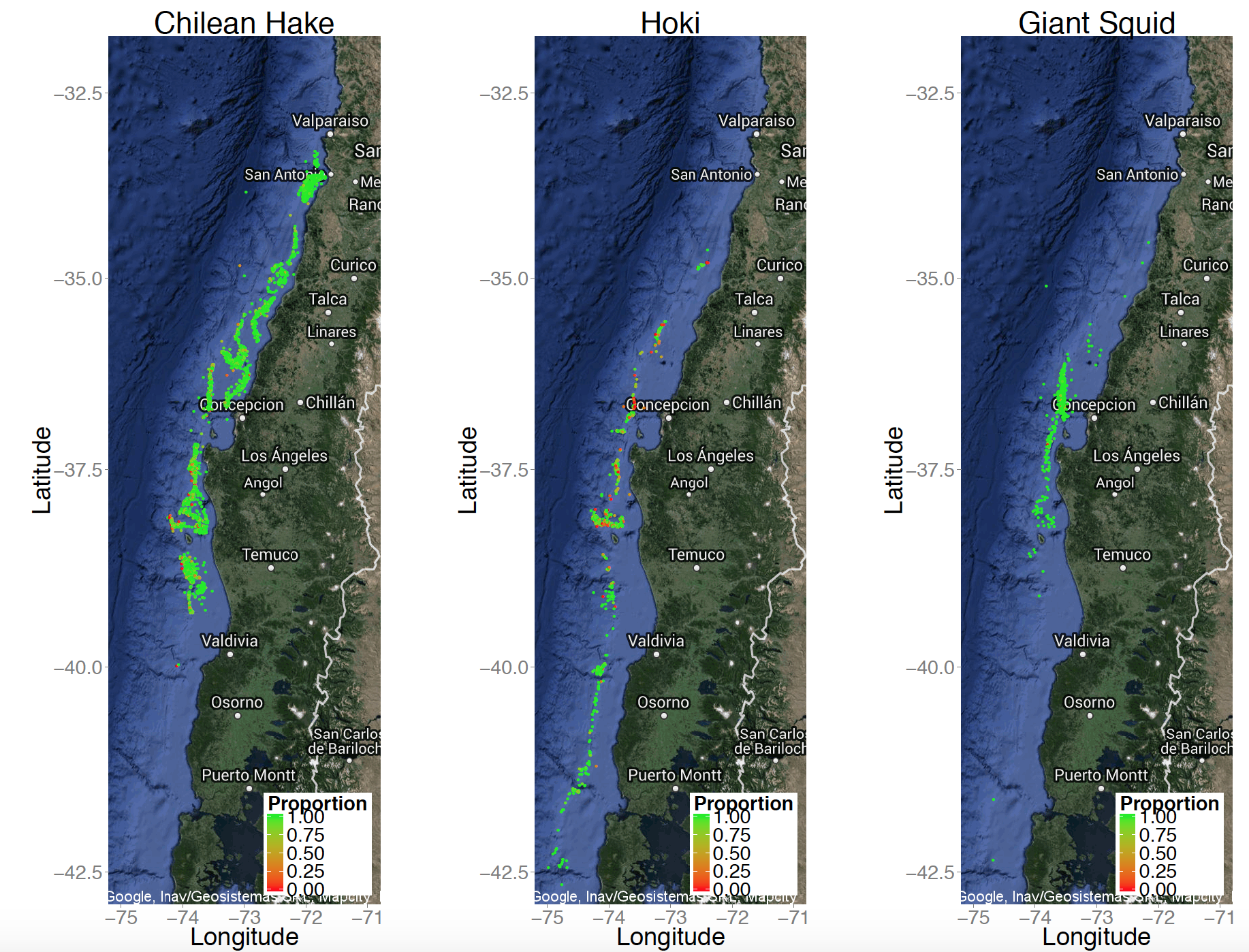
Distribución de especies en la costa chilena.
  • Algunos resultados:
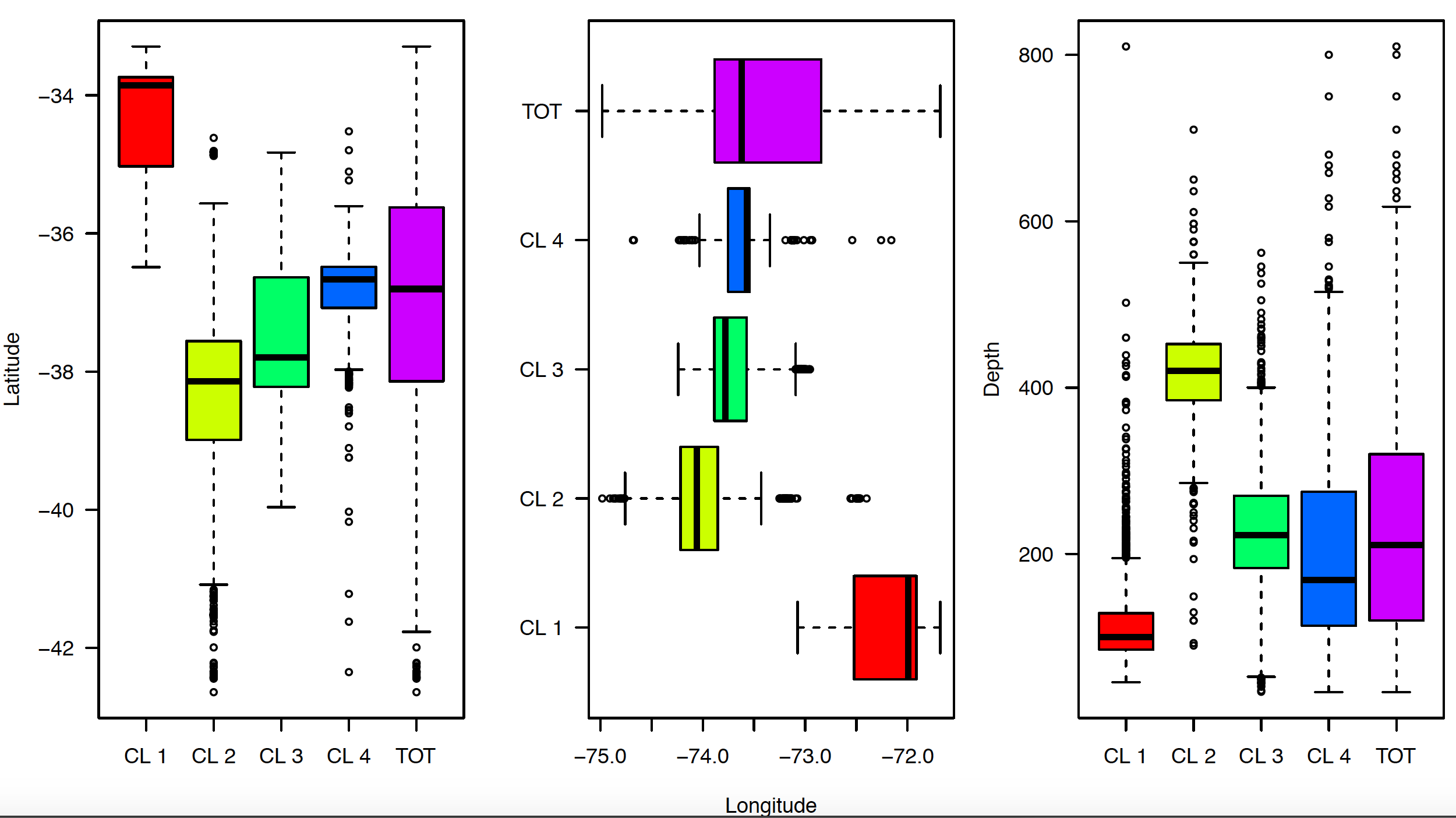
Distribución de lances en longitud, latitud y profundidad.

Conclusiones

  • Las mayores diferencias entre los cuatro grupos identificados (tácticas de pesca) se determinaron por el arte de la pesca, la profundidad y la latitud de la pesca.

  • La aplicación del clasificador fuzzy nos permitió discriminar entre tipos de lances, el objetivo de este documento.

1.3.3 Geoestadística

library(GeoModels)

###############################################################
############ Ejemplos de campos aleatorios gauseanos
################      espaciales    ################
###############################################################


# Definimos las coordenadas espaciales de los puntos:
set.seed(3)
N=400  # número de locaciones
x <- runif(N, 0, 1)
set.seed(6)
y <- runif(N, 0, 1)
coords <- cbind(x,y)

# Se define la matriz de covariables espaciales
X=cbind(rep(1,N),runif(N))

# Definición de los parámetros de covarianza:
corrmodel <- "Exp"
mean <- 0.2
mean1 <- -0.5
sill <- 1
nugget <- 0
scale <- 0.2/3
param <- list(mean=mean,mean1=mean1,sill=sill,nugget=nugget,scale=scale)

# Simulación del campo aleatorio:
data <- GeoSim(coordx=coords,corrmodel=corrmodel, param=param,X=X)$data

# Parámetros fijos:
fixed<-list(nugget=nugget)
# Valores iniciales para los parámetros a estimase
start<-list(mean=mean,mean1=mean1,scale=scale,sill=sill)

################################################################
###
### Ejemplo 1. Ajuste de máxima verosimilitud por parejas
### de un campo aleatorio con correlación exponencial
###
###############################################################
fit1 <- GeoFit(data=data,coordx=coords,corrmodel=corrmodel, 
                    maxdist=0.05,likelihood="Marginal",type="Pairwise",
                    start=start,fixed=fixed,X=X)
print(fit1)
## 
## ##################################################################
## Maximum  Composite-Likelihood Fitting of Gaussian Random Fields
## 
## Setting: Marginal Composite-Likelihood 
## 
## Model: Gaussian 
## 
## Distance: Eucl 
## 
## Type of the likelihood objects: Pairwise 
## 
## Covariance model: Exp 
## 
## Optimizer: Nelder-Mead 
## 
## Number of spatial coordinates: 400 
## Type of the random field: univariate 
## Number of estimated parameters: 4 
## 
## Type of convergence: Successful 
## Maximum log-Composite-Likelihood value: -2963.17
## 
## Estimated parameters:
##     mean     mean1     scale      sill  
##  0.16799  -0.41887   0.08109   1.10017  
## 
## ##################################################################

1.3.4 Lattice Data

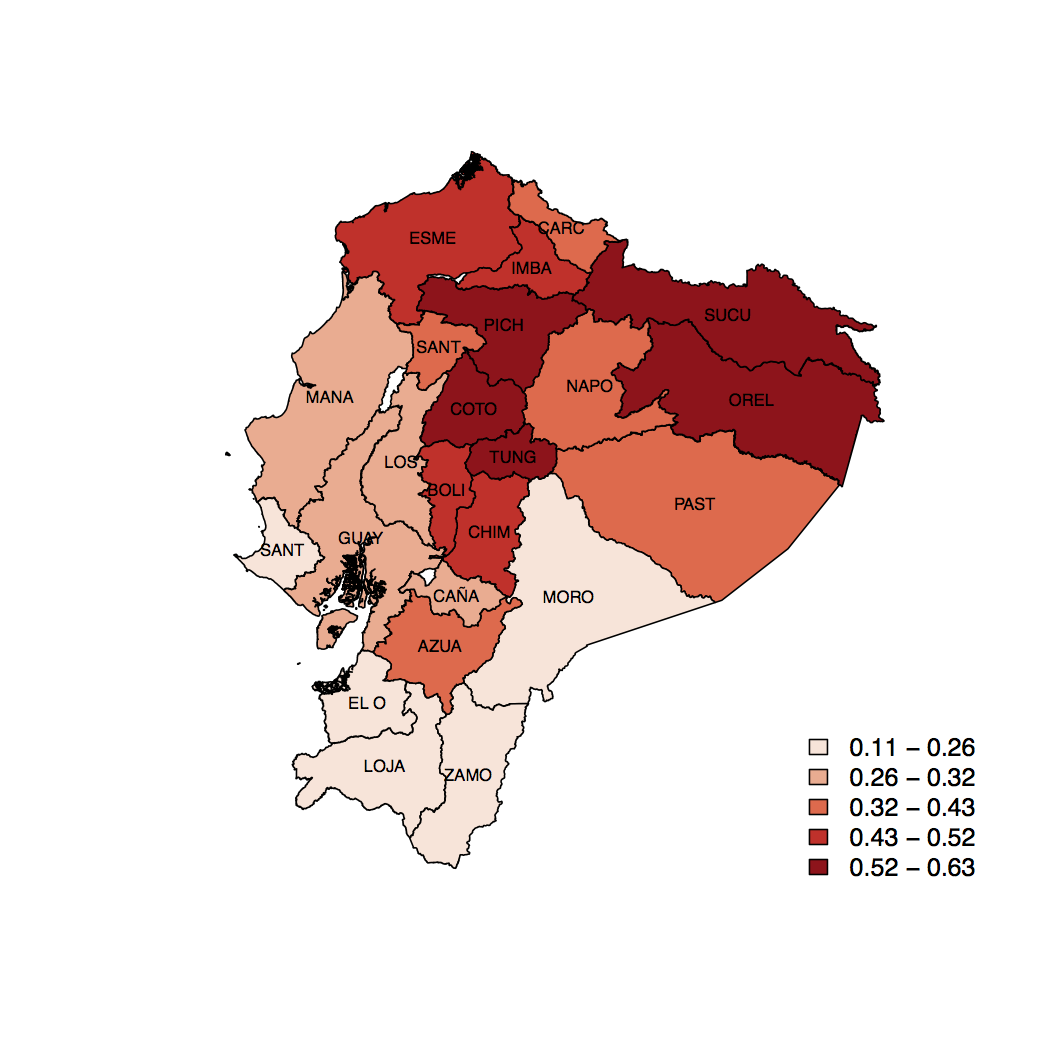
Distribución espacial del porcentaje de éxito en innovación por provincia drawing

  • Se ha encontrado que el componente espacial es significativo en el éxito innovador. Esto implica que existen spillovers en la innovación. La cercanía geográfica de las empresas es significativa tanto desde un puntos de vista descriptivo como desde la modelización.

  • En modelo estimado sugiere que se debe enfocar la política de innovación hacia el componente externo. Sin embargo, al mismo tiempo sugiere que la dinámica de innovación de las fuentes internas y de otros rubros en la innovación que actualmente persisten deben ser mitigados.

1.4 Conclusiones

Hacia a la Ciencia de Datos Espaciales

Métodos:

  • Estadística espacio-temporal (geoestadística, patrones de puntos, métodos de estimación).

  • Nuevas fuentes de datos espaciales (redes sociales, Google, remotos).

  • Geometría estocástica, teselados, procesos de puntos.

  • Modelización causal.

  • Modelización predictiva.

  • Calidad de datos espaciales e incertidumbre.

hay que aprender a juzgar una sociedad por sus ruidos, por su arte y por sus fiestas más que por sus estadísticas (Attali (1995))