7 Pruebas de autocorrelación
Tomado de Kopczewska (2020), sección 4.5.
Librerías usadas:
spdepgstat
7.1 Introducción
Los métodos de estadística espacial también se denominan análisis exploratorio de datos espaciales (ESDA). Las estadística espacial comprende métodos para probar la existencia de procesos de autocorrelación espacial. Las medidas de autocorrelación espacial se utilizan para evaluar la correlación de variables con respecto a la ubicación espacial.
La autocorrelación espacial significa que las observaciones geográficamente cercanas son más similares entre sí que las distantes. Esto hace posible predecir valores en un punto dado, conociendo los valores en otras ubicaciones.
La medida de autocorrelación espacial se puede utilizar de varias formas: para probar la existencia de autocorrelación espacial y características de la población; para determinar el grado de autocorrelación, por ejemplo, la distancia por encima de la cual las observaciones son independientes; determinar el modelo teórico apropiado para la estructura espacial observada o concluir sobre el proceso espacial.
Con base en las conclusiones de la ESDA, se puede rechazar la hipótesis de la aleatoriedad espacial, lo que abre el camino a la búsqueda de conglomerados espaciales (Anselin, 1999). Las conclusiones de la ESDA también son la base para la especificación espacial de los modelos.
En estadística espacial se utilizan dos tipos de medidas: medidas globales y locales.
Por un lado, las medidas globales se plasman en un indicador de autocorrelación espacial o similitud general de regiones. Su ventaja es que es un indicador sintética y su desventaja es promediar.
Por otro lado, gracias a las estadísticas locales, que se determinan para cada región, se puede responder a la pregunta de si la región está rodeada de regiones con valores altos o bajos o si es similar/diferente a las regiones vecinas. Los valores de las estadísticas locales no se generalizan para toda el área analizada y se trabaja con información sobre la posición de cada región en relación con los vecinos.
El uso de técnicas ESDA es el primer paso en el análisis de datos espaciales y permite la detección de patrones de autocorrelación espacial globales y locales en los datos.
La autocorrelación global se puede medir mediante las estadísticas I de Moran global (Moran, 1950; Cliff & Ord, 1981) y C de Geary.
Las medidas locales más utilizadas incluyen las estadísticas locales Moran’s II y las estadísticas locales Geary’s Ci, que forman parte del llamado indicador local de asociación espacial (LISA) (Anselin, 1995) y las estadísticas locales G Getis-Ord (Ord & Getis, 1995).
Las estadísticas globales pueden identificar conglomerados y relaciones espaciales solo para todo el sistema. Sin embargo, estas estadísticas se pueden desagregar en estadísticas locales, gracias a las cuales se pueden detectar patrones de relaciones espaciales locales entre las regiones y sus vecinos.
El cálculo de LISA permite detectar cuál de las regiones influye fuertemente en la formación de conglomerados locales y examinar los conglomerados locales no aleatorios, los denominados puntos calientes/fríos (hot spots o cold spots), inestabilidad local (heterocedasticidad), observaciones atípicas significativas (Ministeri, 2003). La siguiente tabla resume algunas de las características listadas:
| Estadístico | Tipo | Tipo de medición | Interpretación | Funciones en R |
|---|---|---|---|---|
| Moran’s I | Global | Una medida de autocorrelación espacial | I>0: autocorrelación espacial positiva, los valores de observación a la distancia d son similares I<0: autocorrelación espacial negativa, los valores de observación a la distancia d son diferentes I=0: los valores de observación a la distancia d se distribuyen aleatoriamente |
moran ()moran.test ()moran.mc ()moran.plot () |
| Geary’s C | Global | Una medida de autocorrelación espacial | 0<C<1: autocorrelación espacial positiva, los valores de observación a la distancia d son similares 1<C<2: autocorrelación espacial negativa, los valores de observación a la distancia d son diferentes |
geary ()geary.test () geary.mc () |
| Join-count | Global en grupos | Una medida de autocorrelación espacial | H0 asume que no hay autocorrelación espacial, el valor p>α confirma esta hipótesis H1 asume la existencia de autocorrelación espacial, valor p<α confirma esta hipótesis |
joincount.test () joincount.mc () joincount.multi () |
| Local Moran’s Ii | Local | Junto con Local Geary, crea LISA, una medida de relaciones espaciales. | valor p<α: rodeado por valores relativamente altos, un grupo de valores altos valor p>(1−α): un área rodeada por valores relativamente bajos, un grupo de valores bajos |
local.moran () localmoran.sad () |
| Local Geary’s Ci | Local | Junto con Local Moran, crea LISA, una medida de diversidad espacial | valor p>(1−α): positivo, región rodeada de observaciones similares valor p<α: negativo, región rodeada por diferentes observaciones | Existe el comando usdm::lisa() que permite al usuario calcular este estadístico, pero para rásteres. |
| Local Gi, G∗ | Local | Medida de relaciones espaciales | Gi>0: área rodeada por valores relativamente altos, clúster de alto valor Gi<0: área rodeada por valores relativamente bajos, clúster de valor bajo |
localG () |
| Local Hi, LOSH | Local | Medida de relaciones espaciales | Interpretado junto con las estadísticas G∗. Valores altos indican un entorno heterogéneo; valores bajos indican homogeneidad local. | LOSH() |
| Empirical Bayes index | Local | Medida de relaciones espaciales | Interpretado como las estadísticas I de Moran, utilizadas por interés (por ejemplo, número de casos / población) | EBImoran.mc() |
Supuestos:
La estadística espacial se basa en varios supuestos. El más importante de ellos es la estacionariedad, lo que significa que los datos analizados deben tener una distribución normal con promedio y varianza constantes.
Sin embargo, las estructuras de autocorrelación espacial no siempre son constantes en toda el área de estudio, por lo que es suficiente satisfacer una estacionariedad débil, donde la media y la varianza son constantes, mientras que la autocorrelación depende solo de la distancia entre los objetos probados.
Los patrones espaciales deben ser isotrópicos; es decir, no deben depender de la dirección del estudio. Además, la forma del área estudiada afecta la intensidad, alcance y tipo de proceso espacial estimado, así como su importancia.
También existen los llamados efectos de borde (Fortin, Dale y Ver Hoef, 2002). Este problema se revela durante las observaciones en el borde del área de estudio. Estas regiones tienen menos vecinos que los objetos ubicados en el medio. Como resultado de este efecto, pueden aparecer diferencias en las estimaciones dependiendo de la matriz de vecindad adoptada (por ejemplo, de primer o segundo orden) (Cressie, 1993b).
Un elemento común en econometría espacial es el llamado retardo/rezago espacial, que se determina para la variable examinada. El operador de rezago espacial es un promedio ponderado del valor de la variable en las regiones vecinas, de acuerdo con la matriz de ponderaciones espaciales declarada W.
Cuando se utiliza la matriz de vecindad de primer orden para el cálculo según el criterio de contigüidad, el rezago espacial será el promedio de los valores en las regiones limítrofes con el área examinada. Si se adoptara la matriz de segundo orden, el rezago espacial se determinaría a partir de los valores de los vecinos de estos vecinos. Una interpretación análoga ocurre cuando se usa la matriz de distancia o la matriz k de los vecinos más cercanos.
En las siguientes secciones usaremos datos de Valor agregado anual por cantones del Ecuador tomados del Banco Central del Ecuador y el indicador de Necesidades Básicas Insatisfechas por personas.
# leo los datos
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/VABNoPetroleroCantones2007-2019.csv"
datos <- read.csv(uu,sep = ",")
datos$COD_CANT[nchar(datos$COD_CANT)==3] = paste("0",datos$COD_CANT[nchar(datos$COD_CANT)==3],sep = "")
datos <- subset(datos,datos$YEAR == 2019)
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/proyeccion_cantonal_total_2010-2020.csv"
poblacion <- read.csv(uu,sep = ";")
poblacion$CODIGO[nchar(poblacion$CODIGO)==3] = paste("0",poblacion$CODIGO[nchar(poblacion$CODIGO)==3],sep = "")
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/NBI_PER_CANT.csv"
NBI <- read.csv(uu, sep = ";")
NBI$CODIGO[nchar(NBI$CODIGO)==3] = paste("0",NBI$CODIGO[nchar(NBI$CODIGO)==3],sep = "")
datos <- merge(datos,poblacion[,c("CODIGO","A_2019")],by.x = "COD_CANT",by.y = "CODIGO",all.x = TRUE)
datos <- merge(datos,NBI[,c("CODIGO","POBRES_P")],by.x = "COD_CANT",by.y = "CODIGO",all.x = TRUE)
datos$VAB_PC <- datos$VAB/datos$A_2019 #miles de USD / pob
uu <- "https://github.com/vmoprojs/DataLectures/raw/master/SpatialData/2012_nxcantones.zip"
poligonos <- read_git_shp(uu)## Reading layer `nxcantones' from data source
## `/private/var/folders/0p/n_r_hl095sv7nktfp_8n9n_80000gn/T/RtmpJEd1fK/file5c5539dc6d21/nxcantones.shp'
## using driver `ESRI Shapefile'
## Simple feature collection with 224 features and 6 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -732143.5 ymin: 9445216 xmax: 1147852 ymax: 10189400
## Projected CRS: WGS 84 / UTM zone 17Spoligonos <- poligonos[poligonos$DPA_PROVIN!="90",]
poligonos <- poligonos[poligonos$DPA_PROVIN!="20",]
poligonos = merge(poligonos,datos,by.x ="DPA_CANTON",by.y = "COD_CANT",all.x=TRUE)
# Me quedo con los datos que no son perdidos:
poligonos <- poligonos[!is.na(poligonos$POBRES_P),]
library(spdep)
set.ZeroPolicyOption(TRUE)## [1] TRUE7.2 Estadísticos Globales
Las medidas globales en estadística espacial permiten determinar la tendencia espacial general en la región. Su análisis permite una visión sintética de los datos. También proporcionan una buena base para una evaluación posterior más detallada del fenómeno.
7.2.1 Estadístico global: I de Moran
El estadístico global I de Moran es probablemente la medida espacial más antigua, introducida por Moran en 1950 (Moran (1950)) y se usa para realizar pruebas de hipótesis de autocorrelación global.
Es una prueba basada en la covarianza, similar a una prueba de Pearson y el estadístico tiene la siguiente fórmula:
I=∑i∑jwijzizj/S0∑iz2i/n
donde zi=xi−ˉx, S0=∑i∑jwij. xi es la observación en la unidad espacial i, ˉx es el promedio de todas las unidades espaciales, n es el total de unidades espaciales y wij es un elemento de la matriz de pesos espaciales W. La matriz de pesos espaciales W se suele estandarizar por fila (las filas suman 1).
7.2.1.1 Inferencia
La significancia de estadístico I de Moran puede evaluarse desde un enfoque paramétrico o no paramétrico; en este texto se adopta el enfoque no paramétrico. Para este objetivo se obtiene una distribución de la permutación del estadístico basado en una simulación de Monte Carlo de 10000 permutaciones.
La hipótesis nula asumida es la ausencia de autocorrelación, es decir, una distribución aleatoria de los valores.
## $I
## [1] 0.3155373
##
## $K
## [1] 3.410684##
## Moran I test under randomisation
##
## data: poligonos$POBRES_P
## weights: cont.listw
## n reduced by no-neighbour observations
##
## Moran I statistic standard deviate = 5.8776, p-value = 2.081e-09
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic Expectation Variance
## 0.297925901 -0.004950495 0.002655377## Moran I statistic
## 5.877631##
## Moran I test under normality
##
## data: poligonos$POBRES_P
## weights: cont.listw
## n reduced by no-neighbour observations
##
## Moran I statistic standard deviate = 5.8711, p-value = 2.164e-09
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic Expectation Variance
## 0.297925901 -0.004950495 0.002661278## Moran I statistic
## 5.871112#pvalue para Moran's I (distribucion normal)
pval.norm <- 1-pnorm(MInorm$statistic, mean=0, sd=1)
pval.norm## Moran I statistic standard deviate
## 2.164412e-09##
## Monte-Carlo simulation of Moran I
##
## data: poligonos$POBRES_P
## weights: cont.listw
## number of simulations + 1: 1000
##
## statistic = 0.29793, observed rank = 1000, p-value = 0.001
## alternative hypothesis: greater## statistic
## 6.046479Sol <- t(rbind(c(MIran$estimate,MIran$statistic,MIran$p.value),
c(MInorm$estimate,MInorm$statistic,MInorm$p.value),
c(MImc$statistic,mean(MImc$res),var(MImc$res),Zmi,MImc$p.value)))
rownames(Sol) <- c("MI","E[MI]","V[MI]","z-value","p-value")
colnames(Sol) <- c("Randomization","Normal","Monte Carlo")
Sol## Randomization Normal Monte Carlo
## MI 2.979259e-01 2.979259e-01 0.297925901
## E[MI] -4.950495e-03 -4.950495e-03 -0.001553044
## V[MI] 2.655377e-03 2.661278e-03 0.002453169
## z-value 5.877631e+00 5.871112e+00 6.046479456
## p-value 2.080891e-09 2.164412e-09 0.0010000007.2.2 Interpretación de MI
- Su media teórica es ˉI=−1(n−1) y tiende a 0.
- Signo positivo y significativo: conglomerados de valores similares. Es decir, puede ser valores altos, bajos, o ambos.
- Signo negativo y significativo: valores que alternan. Puede deberse a ouliers espaciales, puede deberse a heterogeneidad espacial (un patrón parecido a un tablero de ajedrez).
7.2.3 Comparando MI’s
- El estadístico de moran depende de la matriz de pesos espaciales W.
- Se puede comparar variables con la misma matriz de pesos espaciales, pero no se puede comprar variables (incluso la misma variable) con distintas matrices de pesos espaciales.
- Para comparabilidad, incluso cuando usas diferentes pesos espaciales, puedes usar valores estandarizados como z−value del ejemplo anterior.
Recuerda que el estadístico de Moran es global, es decir que da cuenta de un patrón general en los datos, pero no da cuenta de la ubicación de los patrones. Por ejemplo, si es positivo indica que existe autocorrelación y que las unidades espaciales se agrupan en en valores similares, pero no indica dónde están esos grupos.
La existencia de correlación positiva indica la existencia de conglomerados, pero no el por qué se dan estos conglomerados. El por qué puede deberse a dos motivos:
- contagio verdadero: evidencia de conglomerados debido a interacción espacial. Por ejemplo, si una persona contagia a otras de gripe en un lugar cerrado.
- contagio aparente: evidencia de conglomerados debido a heterogeneidad espacial. Por ejemplo, si un grupo de personas se reúne en un lugar cerrado que ya estaba contaminado.
7.2.4 Gráfico de Moran
El gráfico de Moran nos permite empezar a conectar la idea de estadísiticos globales y locales. También es una guía para reconocer el tipo de autocorrelación con la que estamos tratando.
variable <- poligonos$POBRES_P
variable.std <- ((variable-mean(variable))/sd(variable))
moran.plot(variable.std, cont.listw, labels=as.character(poligonos$DPA_CANTON),pch=19,quiet=F) # 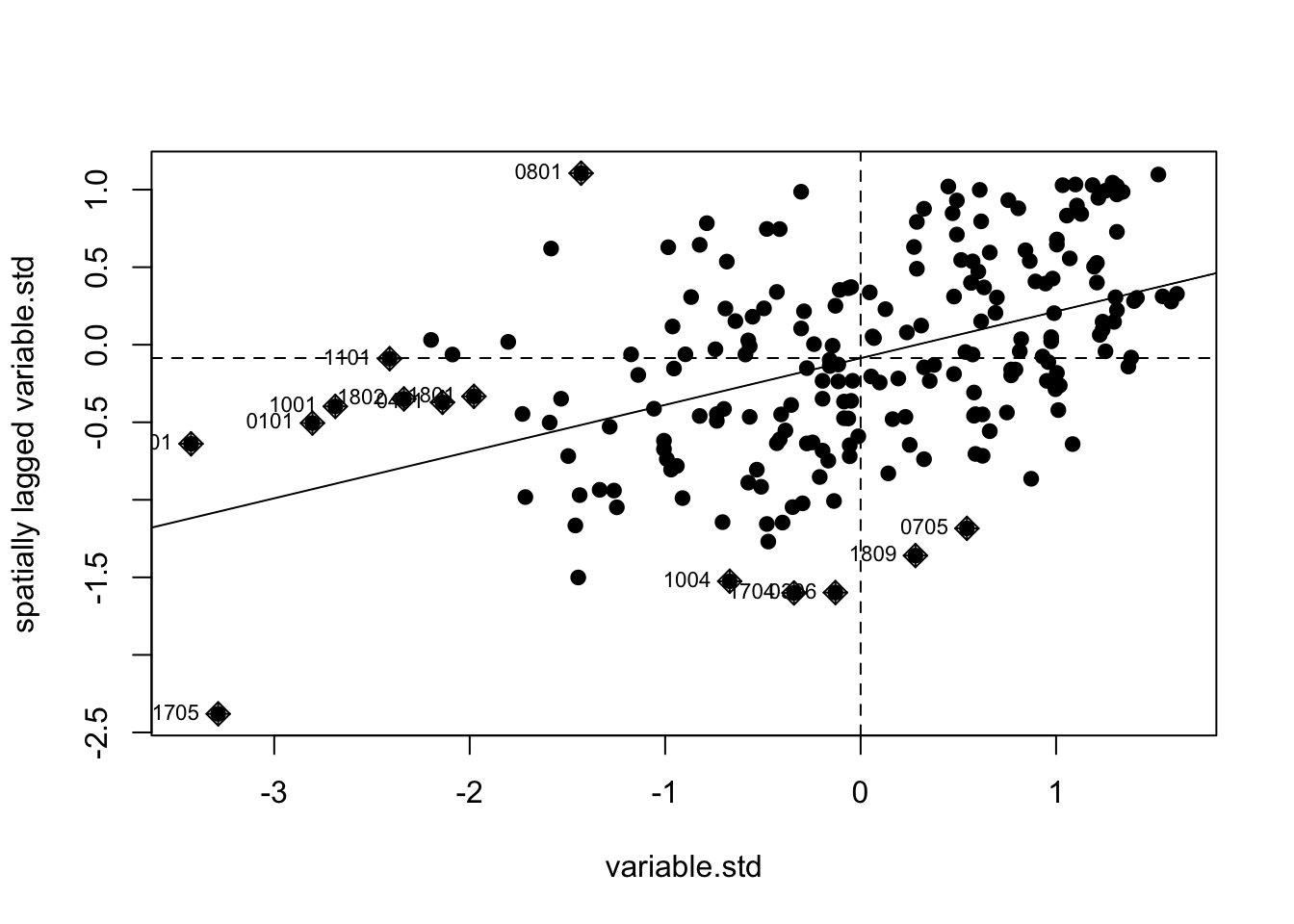
## Potentially influential observations of
## lm(formula = wx ~ x) :
##
## dfb.1_ dfb.x dffit cov.r cook.d hat
## 0101 0.05 -0.13 0.14 1.05_* 0.01 0.04_*
## 0306 -0.17 0.02 -0.17 0.96_* 0.01 0.00
## 0401 0.04 -0.08 0.09 1.03_* 0.00 0.03
## 0801 0.19 -0.27 0.32_* 0.96_* 0.05 0.01
## 0901 0.04 -0.08 0.09 1.03_* 0.00 0.03
## 1001 0.06 -0.15 0.16 1.04_* 0.01 0.04_*
## 1101 0.08 -0.20 0.21 1.03_* 0.02 0.03_*
## 1308 0.18 -0.29 0.34_* 0.96_* 0.06 0.02
## 1701 0.05 -0.17 0.18 1.07_* 0.02 0.06_*
## 1704 -0.16 0.06 -0.17 0.96_* 0.01 0.01
## 1705 -0.16 0.53 -0.55_* 1.02 0.15 0.06_*
## 1707 -0.20 0.01 -0.20 0.94_* 0.02 0.00
## 1708 0.16 -0.04 0.16 0.97_* 0.01 0.00
## 1802 0.05 -0.11 0.12 1.04_* 0.01 0.03_*
## 1809 -0.15 -0.04 -0.15 0.97_* 0.01 0.01Se puede tipificar los cuadrantes:
Cuadrante I & III:
Autocorrelación positiva.
Conglomerados de valores similares.
Unidades espaciales que son similares a sus vecinos.
Cuadrante II & IV:
Autocorrelación negativa.
outliers espaciales.
Unidades espaciales que son diferentes a sus vecinos.
Otra forma de entender los cuadrantes es mediante el tipo de autocorrelación:
- Cuadrante I: High-High, unidades espaciales que están sobre su media, rodeadas de vecinas que están sobre su media.
- Cuadrante II: Low-High, unidades espaciales que están debajo de su media, rodeadas de vecinas que están debajo de su media. Este cuadrante marca unidades espaciales candidatas a outliers espaciales.
- Cuadrante III: Low-Low, unidades espaciales que están debajo su media, rodeadas de vecinas que están debajo de su media.
- Cuadrante IV: High-Low, unidades espaciales que están sobre su media, rodeadas de vecinas que están debajo de su media. Este cuadrante marca unidades espaciales candidatas a outliers espaciales.
¿Cuáles de estas señales de los cuadrantes son significativas? Esto se aborda con estadísticos locales.
Veamos el gráfico de Moran como una regresión lineal:
x <- poligonos$POBRES_P# extraemos la variable
zx <- scale(x) # se estandariza la variable
mean(zx) # controlamos que el promedio sea correcto## [1] -4.67039e-17## [1] 1wzx <- lag.listw(cont.listw, zx) # rezago espacial de x
morlm <- lm(wzx~zx) # regression
slope <- morlm$coefficients[2] # pendiente
intercept <- morlm$coefficients[1] # término constante
par(pty="s") # ventana cuadrada
plot(zx, wzx, xlab="zx",ylab="Rezago espacial de zx", pch="*")
abline(intercept, slope) # linea de regresion
abline(h=0, lty=2) # linea horizontal en y = 0
abline(v=0, lty=2) # linea vertical en x = 0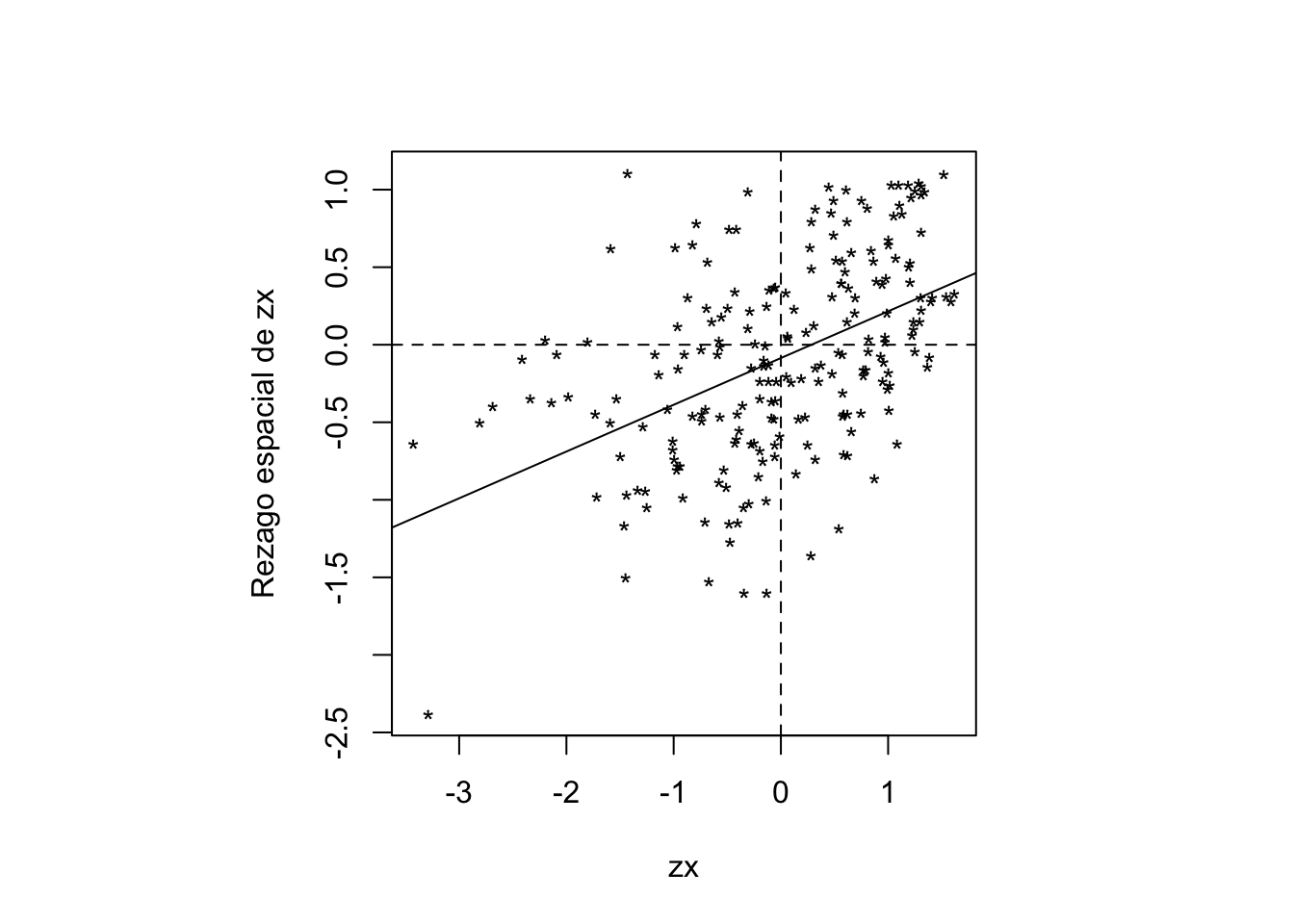
Graficamos las unidades espaciales según el cuadrante al que pertenecen en el gráfico de Moran:
# map of belonging to the quarters of the Moran scatterplot
# creating a variable for analysis
x <- poligonos$POBRES_P# creating a variable for analysis
zx <- scale(x) # variable standardisation
wzx <- lag.listw(cont.listw, zx) # spatial lag of x
cond1 <- ifelse(zx>=0 & wzx>=0, 1,0) # I quarter
cond2 <- ifelse(zx>=0 & wzx<0, 2,0) # II quarter
cond3 <- ifelse(zx<0 & wzx<0, 3,0) # III quarter
cond4 <- ifelse(zx<0 & wzx>=0, 4,0) # IV quarter
cond.all <- as.data.frame(cond1+cond2+cond3+cond4)
# chart - colour map, Figure 10b
brks <- c(1,2,3,4)
cols <- c("royalblue", "springgreen", "yellow", "red")
par(mar=c(5.1,1,4.1,1))
plot(st_geometry(poligonos), col=cols[findInterval(cond.all$V1, brks)])
legend("bottomleft", legend=c("I - HH - high rodeado por high",
"II - LH - low rodeado por high", "III - LL - low
rodeado por low", "IV exercise - HL - high rodeado por low"),
fill=cols, bty="n", cex=0.8)
title(main="Regiones según cuadrantes del gráfico de Moran")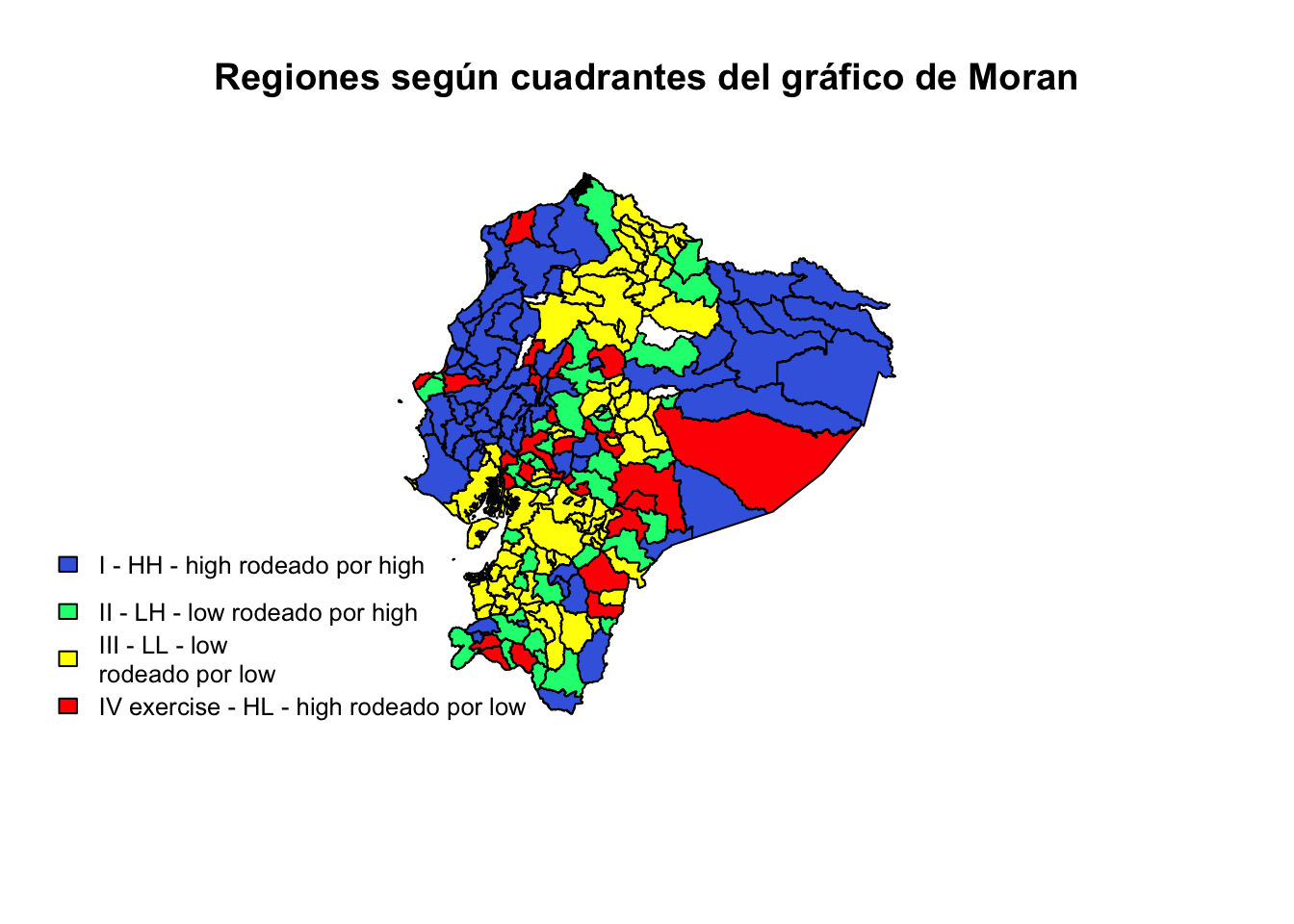
7.2.5 Estadístico Global de Geary
Propuesto por Geary en 1954, se basa en la noción de disimilaridad:
C=(n−1)2S0∑i∑jwij(xi−xj)2∑iz2i
donde zi=xi−ˉx, S0=∑i∑jwij. xi es la observación en la unidad espacial i, xj es la observación en la unidad espacial j, ˉx es el promedio de todas las unidades espaciales, n es el total de unidades espaciales y wij es un elemento de la matriz de pesos espaciales W.
- El valor de C está comprendido entre 0 y 2, asintóticamente sigue una distribución normal.
- Asumiendo ausencia de autocorrelación espacial, el valor esperado de C es 1.
- Si 0<C≤1 indica regiones similares (autocorrelación positiva). Esto es equivalente a que su valor z sea negativo, z<0.
- Si 1<C≤2 indica regiones con valores alternantes (autocorrelación negativa). Esto es equivalente a que su valor z sea positivo, z>0.
- El estadístico C asume una matriz de pesos espaciales simétrica, en el caso de asimetría (como en el caso de los vecinos más cercanos), el estadísitico puede no ser de utilidad.
7.2.5.1 Inferencia
La significancia de estadístico C de Geary puede evaluarse desde un enfoque paramétrico o no paramétrico; en este texto se adopta principalemente el enfoque no paramétrico. Para este objetivo se obtiene una distribución de la permutación del estadístico basado en una simulación de Monte Carlo de 10000 permutaciones.
La hipótesis nula asumida es la ausencia de autocorrelación, es decir, una distribución aleatoria de los valores.
## $C
## [1] 0.7708447
##
## $K
## [1] 3.410684##
## Geary C test under randomisation
##
## data: poligonos$POBRES_P
## weights: cont.listw
## n reduced by no-neighbour observations
##
## Geary C statistic standard deviate = 4.8761, p-value = 5.409e-07
## alternative hypothesis: Expectation greater than statistic
## sample estimates:
## Geary C statistic Expectation Variance
## 0.727619784 1.000000000 0.003120314##
## Geary C test under normality
##
## data: poligonos$POBRES_P
## weights: cont.listw
## n reduced by no-neighbour observations
##
## Geary C statistic standard deviate = 4.9216, p-value = 4.292e-07
## alternative hypothesis: Expectation greater than statistic
## sample estimates:
## Geary C statistic Expectation Variance
## 0.727619784 1.000000000 0.003062941##
## Monte-Carlo simulation of Geary C
##
## data: poligonos$POBRES_P
## weights: cont.listw
## number of simulations + 1: 1000
##
## statistic = 0.72762, observed rank = 1, p-value = 0.001
## alternative hypothesis: greater## statistic
## -3.704493Un resumen de los resultados
Sol <- t(rbind(c(GCran$estimate,GCran$statistic*-1,GCran$p.value),
c(GCnorm$estimate,GCnorm$statistic*-1,GCnorm$p.value),
c(GCmc$statistic,mean(GCmc$res),var(GCmc$res),Zgc,GCmc$p.value)))
rownames(Sol) <- c("C","E[C]","V[C]","z-value","p-value")
colnames(Sol) <- c("Randomization","Normal","Monte Carlo")
Sol## Randomization Normal Monte Carlo
## C 7.276198e-01 7.276198e-01 0.727619784
## E[C] 1.000000e+00 1.000000e+00 0.944124452
## V[C] 3.120314e-03 3.062941e-03 0.003415679
## z-value -4.876143e+00 -4.921599e+00 -3.704492722
## p-value 5.409010e-07 4.291999e-07 0.0010000007.3 Estadísticos Locales
Anselin (1995) propuso indicadores locales de relaciones espaciales (local indicators of spatial association - LISA). LISA incluye estadísticos locales: Ii de Moran y Ci de Geary.
El estadístico de Moran local permite la identificación de efectos de aglomeración espacial (similar al estadístico G Getis-Ord), mientras que el Geary local muestra similitudes y diferencias espaciales.
Las estadísticas locales de Moran brindan información sobre grupos de valor bajo o alto, mientras que los estadísticos locales de Geary muestran diferencias promedio entre el objeto y los vecinos, lo que ayuda a encontrar valores atípicos y patrones de similitud/diferencia.
Estos estadísticos están relacionadas con sus contrapartes globales y se pueden utilizar para estimar el impacto de las estadísticas individuales en sus contrapartes globales.
Gracias a LISA, es posible identificar los denominados puntos calientes, es decir, centros con valores altos rodeados de valores bajos, así como clusters locales en ausencia de autocorrelación global. Las islas de alto valor pueden interpretarse no solo como puntos calientes, sino también como valores atípicos. Entonces, los estadísticos locales son un indicador de inestabilidad local y desviaciones locales del patrón de autocorrelación global.
En resumen, los LISA nos presentan dos componentes:
un estadístico para cada unidad espacial que puede ser sujeto a pruebas de significancia.
cuantifica la relación entre el estadístico global y el local: la suma de los estadísticos locales es proporcional al estadístico global.
7.3.1 Estadístico local: I de Moran
Ii=(xi−ˉx)∑nj=1wij(xj−ˉx)∑ni=1(xi−ˉx)2/n Para evaluar la significancia se evalúa los valores
p−value<α: las unidades espaciales que cumplen con esta condición indican tienen un índice local de Moran positivo y significativo. Esto significa que éstas unidades están rodeadas de valores altos de la variable analizada.
p−value>1−α: las unidades espaciales que cumplen con esta condición indican tienen un índice local de Moran negativo y significativo. Esto significa que éstas unidades están rodeadas de valores bajos de la variable analizada.
locM <- localmoran(poligonos$POBRES_P, cont.listw,alternative = "greater")
# locM <- localmoran_perm(poligonos$POBRES_P, cont.listw)
oid1 <- order(poligonos$DPA_CANTON)
locMorMat <- printCoefmat(data.frame(locM[oid1,], row.names=poligonos$DPA_CANTON[oid1]), check.names=FALSE)## Ii E.Ii Var.Ii Z.Ii Pr.z...E.Ii..
## 0101 1.4232e+00 -3.6921e-02 5.5495e-01 1.9600e+00 0.0250
## 0102 7.5646e-01 -4.3472e-03 1.8262e-01 1.7803e+00 0.0375
## 0103 4.1197e-01 -1.3237e-03 4.6259e-02 1.9216e+00 0.0273
## 0104 2.9734e-02 -3.1669e-03 9.4230e-02 1.0718e-01 0.4573
## 0105 6.3380e-01 -1.0482e-03 5.5490e-02 2.6950e+00 0.0035
## 0106 -6.9801e-01 -5.5214e-03 2.3168e-01 -1.4387e+00 0.9249
## 0107 2.1783e+00 -9.7991e-03 6.8885e-01 2.6364e+00 0.0042
## 0108 3.3034e-01 -2.5409e-03 6.5874e-02 1.2970e+00 0.0973
## 0109 -1.6297e-01 -2.9613e-04 8.8367e-03 -1.7305e+00 0.9582
## 0110 4.0086e-01 -1.0390e-03 7.3689e-02 1.4805e+00 0.0694
## 0111 2.1691e-02 -2.5916e-03 1.8351e-01 5.6683e-02 0.4774
## 0112 2.8064e-01 -5.2482e-03 2.7666e-01 5.4352e-01 0.2934
## 0113 2.2088e-01 -8.0482e-04 3.3930e-02 1.2035e+00 0.1144
## 0114 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 0115 9.5611e-03 -6.7624e-07 2.3663e-05 1.9656e+00 0.0247
## 0201 -2.0744e-02 -4.4763e-05 1.3361e-03 -5.6630e-01 0.7144
## 0202 2.7062e-01 -1.7852e-03 7.5186e-02 9.9346e-01 0.1602
## 0203 1.3075e-02 -1.7806e-04 9.4340e-03 1.3645e-01 0.4457
## 0204 9.2173e-02 -2.2469e-03 2.3987e-01 1.9279e-01 0.4236
## 0205 -3.2540e-02 -7.8076e-05 2.7318e-03 -6.2108e-01 0.7327
## 0206 6.2311e-01 -3.7731e-03 8.0817e-01 6.9732e-01 0.2428
## 0207 6.4246e-02 -1.8708e-03 1.9979e-01 1.4792e-01 0.4412
## 0301 8.0199e-01 -1.1883e-02 3.5047e-01 1.3748e+00 0.0846
## 0302 4.6022e-01 -7.4899e-04 3.9662e-02 2.3147e+00 0.0103
## 0303 4.8237e-02 -1.8734e-05 6.5555e-04 1.8847e+00 0.0297
## 0304 4.1862e-01 -8.6266e-04 6.1191e-02 1.6958e+00 0.0450
## 0305 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 0306 2.0707e-01 -7.8076e-05 5.5424e-03 2.7825e+00 0.0027
## 0307 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 0401 7.9820e-01 -2.1483e-02 7.3559e-01 9.5571e-01 0.1696
## 0402 -1.1792e-01 -9.4006e-05 3.2892e-03 -2.0545e+00 0.9800
## 0403 7.3819e-01 -4.1514e-03 2.1908e-01 1.5860e+00 0.0564
## 0404 1.3795e-01 -8.7178e-05 3.6779e-03 2.2761e+00 0.0114
## 0405 7.3430e-01 -4.6154e-03 1.9384e-01 1.6783e+00 0.0466
## 0406 9.0538e-01 -3.8972e-03 2.7560e-01 1.7320e+00 0.0416
## 0501 -2.6796e-01 -3.5310e-03 1.0503e-01 -8.1595e-01 0.7927
## 0502 -3.1079e-01 -4.3500e-04 3.0869e-02 -1.7664e+00 0.9613
## 0503 1.9973e-01 -4.5285e-03 3.2004e-01 3.6106e-01 0.3590
## 0504 -3.4475e-02 -3.1108e-03 8.0603e-02 -1.1047e-01 0.5440
## 0505 4.0525e-02 -3.3999e-05 1.4345e-03 1.0709e+00 0.1421
## 0506 2.2713e-01 -1.5012e-03 1.0642e-01 7.0085e-01 0.2417
## 0507 -2.6961e-01 -7.3661e-03 2.5586e-01 -5.1845e-01 0.6979
## 0601 -3.0974e-01 -2.2674e-02 7.7542e-01 -3.2600e-01 0.6278
## 0602 -1.9153e-01 -2.7846e-03 6.3844e-02 -7.4701e-01 0.7725
## 0603 -5.6079e-02 -7.0262e-03 2.9437e-01 -9.0410e-02 0.5360
## 0604 5.5120e-02 -1.0809e-03 2.3214e-01 1.1664e-01 0.4536
## 0605 -3.8011e-02 -5.3780e-05 5.7539e-03 -5.0039e-01 0.6916
## 0606 -3.4452e-01 -8.9949e-03 4.7238e-01 -4.8819e-01 0.6873
## 0607 -2.4045e-01 -4.9360e-04 1.7264e-02 -1.8263e+00 0.9661
## 0608 3.7750e-01 -1.7431e-03 3.7411e-01 6.2003e-01 0.2676
## 0609 2.1041e-01 -2.0579e-04 8.6811e-03 2.2605e+00 0.0119
## 0610 4.4567e-02 -1.4353e-03 1.0175e-01 1.4421e-01 0.4427
## 0701 1.4002e+00 -9.7001e-03 6.8197e-01 1.7073e+00 0.0439
## 0702 3.6635e-01 -5.6938e-04 2.4010e-02 2.3680e+00 0.0089
## 0703 1.6626e+00 -7.4768e-03 3.9326e-01 2.6632e+00 0.0039
## 0704 4.6848e-01 -1.2167e-03 8.6270e-02 1.5991e+00 0.0549
## 0705 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 0706 1.2427e-01 -1.2860e-04 5.4254e-03 1.6889e+00 0.0456
## 0707 6.8139e-02 -1.7806e-04 3.8275e-02 3.4920e-01 0.3635
## 0708 7.7546e-01 -1.4048e-02 5.8439e-01 1.0328e+00 0.1509
## 0709 9.1281e-01 -7.7390e-03 2.6871e-01 1.7759e+00 0.0379
## 0710 1.0788e+00 -1.0505e-02 2.3900e-01 2.2281e+00 0.0129
## 0711 1.3140e+00 -7.3046e-03 3.0595e-01 2.3888e+00 0.0085
## 0712 1.7088e+00 -9.9984e-03 4.1764e-01 2.6597e+00 0.0039
## 0713 8.3417e-01 -4.7526e-03 1.2294e-01 2.3926e+00 0.0084
## 0714 1.3877e-01 -5.9354e-04 3.1435e-02 7.8603e-01 0.2159
## 0801 -1.5897e+00 -9.6017e-03 5.0394e-01 -2.2258e+00 0.9870
## 0802 9.5908e-01 -8.0699e-03 4.2420e-01 1.4849e+00 0.0688
## 0803 4.4467e-01 -1.1852e-02 6.2061e-01 5.7949e-01 0.2811
## 0804 8.8291e-01 -5.2277e-03 1.5523e-01 2.2542e+00 0.0121
## 0805 -4.1547e-01 -1.6199e-03 5.6592e-02 -1.7396e+00 0.9590
## 0806 1.8862e-02 -2.6266e-04 2.8096e-02 1.1409e-01 0.4546
## 0807 4.8440e-01 -1.1206e-02 7.8667e-01 5.5878e-01 0.2882
## 0901 7.4895e-01 -2.0468e-02 8.4591e-01 8.3657e-01 0.2014
## 0902 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 0903 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 0904 1.2650e+00 -5.0127e-03 3.5408e-01 2.1342e+00 0.0164
## 0905 1.2292e+00 -6.6126e-03 4.6635e-01 1.8096e+00 0.0352
## 0906 9.9345e-02 -6.1377e-05 4.3571e-03 1.5060e+00 0.0660
## 0907 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 0908 2.6733e-01 -5.3735e-03 3.7944e-01 4.4272e-01 0.3290
## 0909 -1.1205e-01 -6.6168e-04 7.0749e-02 -4.1878e-01 0.6623
## 0910 -2.9233e-01 -8.6266e-04 9.2221e-02 -9.5977e-01 0.8314
## 0911 3.5261e-02 -1.1066e-05 5.8643e-04 1.4565e+00 0.0726
## 0912 1.7565e-01 -1.5122e-03 1.6156e-01 4.4077e-01 0.3297
## 0913 4.9856e-01 -9.4443e-04 2.0286e-01 1.1090e+00 0.1337
## 0914 1.2121e+00 -7.8022e-03 5.4959e-01 1.6455e+00 0.0499
## 0916 3.0509e-01 -1.5260e-02 6.3404e-01 4.0231e-01 0.3437
## 0918 9.7254e-01 -5.7470e-03 4.0565e-01 1.5360e+00 0.0623
## 0919 -1.3560e-01 -7.8909e-03 3.3031e-01 -2.2221e-01 0.5879
## 0920 -2.6992e-01 -5.8663e-04 4.1623e-02 -1.3202e+00 0.9066
## 0921 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 0922 -3.6236e-01 -4.7330e-03 5.0401e-01 -5.0375e-01 0.6928
## 0923 1.3672e-02 -7.9849e-06 4.2314e-04 6.6505e-01 0.2530
## 0924 6.5884e-01 -3.5142e-03 2.4861e-01 1.3284e+00 0.0920
## 0925 -1.5696e-01 -9.6781e-05 1.0354e-02 -1.5416e+00 0.9384
## 0927 2.2365e-01 -1.5514e-03 1.0997e-01 6.7909e-01 0.2485
## 0928 8.0262e-01 -8.0699e-03 5.6829e-01 1.0754e+00 0.1411
## 1001 1.0735e+00 -3.3906e-02 8.5140e-01 1.2002e+00 0.1150
## 1002 1.6929e+00 -1.3811e-02 7.2180e-01 2.0088e+00 0.0223
## 1003 1.9394e-01 -3.5544e-04 1.2433e-02 1.7425e+00 0.0407
## 1004 1.0264e+00 -2.1068e-03 7.3565e-02 3.7922e+00 0.0001
## 1005 2.1376e-01 -6.9517e-04 2.9310e-02 1.2527e+00 0.1052
## 1006 3.0522e-01 -4.1436e-04 2.1949e-02 2.0630e+00 0.0196
## 1101 2.1782e-01 -2.7259e-02 6.0965e-01 3.1388e-01 0.3768
## 1102 -3.5999e-01 -1.0809e-03 4.5557e-02 -1.6816e+00 0.9537
## 1103 1.4711e-01 -4.2815e-03 1.4918e-01 3.9196e-01 0.3475
## 1104 -2.3130e-02 -1.8734e-05 6.5555e-04 -9.0267e-01 0.8166
## 1105 -2.8155e-01 -1.8277e-03 7.6976e-02 -1.0082e+00 0.8433
## 1106 -2.8726e-01 -4.6643e-03 1.9588e-01 -6.3851e-01 0.7384
## 1107 -3.6983e-01 -2.0481e-03 8.6239e-02 -1.2524e+00 0.8948
## 1108 -6.2179e-01 -4.5476e-03 3.2139e-01 -1.0888e+00 0.8619
## 1109 -9.0553e-02 -1.0716e-03 1.8188e-02 -6.6350e-01 0.7465
## 1110 1.5755e-02 -1.0141e-05 4.2788e-04 7.6215e-01 0.2230
## 1111 -3.2851e-01 -2.6283e-03 7.8245e-02 -1.1650e+00 0.8780
## 1112 -2.6851e-01 -4.8718e-03 2.5691e-01 -5.2014e-01 0.6985
## 1113 -7.1049e-02 -4.0689e-03 2.1475e-01 -1.4454e-01 0.5575
## 1114 2.1342e-01 -2.2811e-03 1.6157e-01 5.3663e-01 0.2958
## 1115 -1.7953e-01 -1.5798e-03 8.3587e-02 -6.1551e-01 0.7309
## 1116 4.7905e-02 -4.4613e-03 3.1531e-01 9.3257e-02 0.4628
## 1201 -9.6740e-02 -3.9422e-04 8.1143e-03 -1.0696e+00 0.8576
## 1202 6.0386e-01 -6.6943e-03 3.5238e-01 1.0285e+00 0.1518
## 1203 -1.1050e-02 -1.3582e-05 9.6422e-04 -3.5543e-01 0.6389
## 1204 2.8237e-01 -1.2418e-03 5.2330e-02 1.2398e+00 0.1075
## 1205 -2.2002e-01 -8.0482e-04 5.7092e-02 -9.1746e-01 0.8205
## 1206 2.0376e-01 -2.7846e-03 1.9714e-01 4.6518e-01 0.3209
## 1207 1.9356e-01 -1.5012e-03 7.9434e-02 6.9209e-01 0.2444
## 1208 4.7065e-01 -1.1382e-03 4.7967e-02 2.1542e+00 0.0156
## 1209 1.1548e+00 -5.9770e-03 6.3569e-01 1.4559e+00 0.0727
## 1210 -8.0908e-03 -1.1066e-05 7.8564e-04 -2.8826e-01 0.6134
## 1211 8.8911e-01 -4.5962e-03 9.8363e-01 9.0111e-01 0.1838
## 1212 1.0903e+00 -4.7330e-03 5.0401e-01 1.5424e+00 0.0615
## 1213 7.2818e-01 -3.7557e-03 4.0033e-01 1.1568e+00 0.1237
## 1301 -6.5524e-01 -3.1829e-03 1.1102e-01 -1.9570e+00 0.9748
## 1302 3.0457e-01 -4.1977e-03 2.2152e-01 6.5603e-01 0.2559
## 1303 2.8105e-01 -4.9360e-04 1.1343e-02 2.6435e+00 0.0041
## 1304 1.4162e-01 -3.8859e-04 2.7577e-02 8.5512e-01 0.1962
## 1305 4.0079e-01 -7.9802e-03 8.4703e-01 4.4415e-01 0.3285
## 1306 3.5153e-01 -1.1382e-03 3.3935e-02 1.9145e+00 0.0278
## 1307 8.7927e-02 -2.2335e-03 4.7913e-01 1.3025e-01 0.4482
## 1308 -1.6091e+00 -1.1774e-02 2.5015e+00 -1.0099e+00 0.8437
## 1309 -6.4849e-01 -4.8022e-03 3.3929e-01 -1.1051e+00 0.8654
## 1310 1.2166e+00 -8.0699e-03 3.3774e-01 2.1074e+00 0.0175
## 1311 5.1804e-01 -6.8593e-03 2.8742e-01 9.7908e-01 0.1638
## 1312 8.7927e-02 -7.5584e-05 1.6249e-02 6.9036e-01 0.2450
## 1313 3.4353e-01 -1.7852e-03 9.4433e-02 1.1237e+00 0.1306
## 1314 8.8096e-02 -1.0716e-03 5.6725e-02 3.7438e-01 0.3541
## 1315 3.4644e-01 -1.5403e-03 8.1497e-02 1.2189e+00 0.1114
## 1316 1.0863e+00 -8.4339e-03 5.9370e-01 1.4208e+00 0.0777
## 1317 1.2452e+00 -7.3661e-03 5.1909e-01 1.7385e+00 0.0411
## 1318 1.5811e+00 -1.0890e-02 2.3160e+00 1.0461e+00 0.1477
## 1319 4.8698e-01 -6.8593e-03 7.2887e-01 5.7844e-01 0.2815
## 1320 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 1321 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 1322 3.0410e-01 -2.0481e-03 1.4511e-01 8.0368e-01 0.2108
## 1401 -7.2109e-01 -2.9066e-03 8.6508e-02 -2.4418e+00 0.9927
## 1402 -1.1646e-01 -1.1478e-03 3.4221e-02 -6.2336e-01 0.7335
## 1403 -4.2120e-02 -1.7428e-04 4.5291e-03 -6.2327e-01 0.7334
## 1404 4.1840e-01 -2.5409e-03 1.0693e-01 1.2873e+00 0.0990
## 1405 -3.2097e-02 -4.3500e-04 1.2979e-02 -2.7793e-01 0.6095
## 1406 -1.1384e-01 -4.3472e-03 2.2937e-01 -2.2861e-01 0.5904
## 1407 -2.0259e-01 -8.8059e-03 4.6254e-01 -2.8493e-01 0.6122
## 1408 4.1712e-02 -3.5544e-04 3.8017e-02 2.1575e-01 0.4146
## 1409 5.3306e-01 -1.2292e-02 6.4337e-01 6.7990e-01 0.2483
## 1410 -1.2735e-01 -2.9454e-03 1.5563e-01 -3.1534e-01 0.6237
## 1411 5.5120e-02 -6.1377e-05 1.3195e-02 4.8038e-01 0.3155
## 1412 4.2930e-01 -9.3789e-03 3.9201e-01 7.0065e-01 0.2418
## 1501 2.9430e-03 -2.1969e-05 4.5236e-04 1.3940e-01 0.4446
## 1503 -7.5764e-01 -3.5738e-03 1.5025e-01 -1.9454e+00 0.9741
## 1504 3.8000e-01 -3.1829e-03 1.3387e-01 1.0473e+00 0.1475
## 1601 -3.6877e-01 -2.1997e-03 7.6803e-02 -1.3227e+00 0.9070
## 1602 7.8428e-01 -4.4135e-03 2.3285e-01 1.6344e+00 0.0511
## 1603 -2.5172e-02 -1.3500e-03 7.1442e-02 -8.9125e-02 0.5355
## 1604 3.9610e-01 -9.1859e-03 3.8401e-01 6.5401e-01 0.2566
## 1701 2.3332e+00 -5.5095e-02 1.0720e+00 2.3067e+00 0.0105
## 1702 8.1193e-01 -2.3429e-03 6.9770e-02 3.0827e+00 0.0010
## 1703 1.2548e+00 -8.3681e-03 2.9037e-01 2.3441e+00 0.0095
## 1704 5.4829e-01 -5.4573e-04 3.8722e-02 2.7891e+00 0.0026
## 1705 7.8604e+00 -5.0718e-02 5.1513e+00 3.4856e+00 0.0002
## 1707 1.0057e-01 -1.4650e-05 1.5674e-03 2.5406e+00 0.0055
## 1708 -3.0586e-01 -2.8391e-04 6.1024e-02 -1.2370e+00 0.8920
## 1709 5.0330e-01 -7.1951e-03 7.6431e-01 5.8393e-01 0.2796
## 1801 3.9677e-01 -1.8375e-02 4.1470e-01 6.4466e-01 0.2596
## 1802 8.2037e-01 -2.5630e-02 8.7387e-01 9.0499e-01 0.1827
## 1803 0.0000e+00 0.0000e+00 0.0000e+00 NaN NaN
## 1804 1.1313e-01 -1.5122e-03 8.0016e-02 4.0528e-01 0.3426
## 1805 1.3357e-01 -1.7806e-04 9.4340e-03 1.3770e+00 0.0843
## 1806 -5.8117e-02 -1.5798e-03 1.1198e-01 -1.6895e-01 0.5671
## 1807 3.3844e-02 -1.4650e-05 4.3727e-04 1.6192e+00 0.0527
## 1808 1.8353e-01 -7.7666e-04 3.2744e-02 1.0185e+00 0.1542
## 1809 -3.5859e-01 -3.6910e-04 3.9477e-02 -1.8029e+00 0.9643
## 1901 7.3294e-02 -6.4736e-03 1.9198e-01 1.8205e-01 0.4278
## 1902 2.2895e-01 -3.8859e-04 4.1562e-02 1.1249e+00 0.1303
## 1903 3.3015e-03 -1.7525e-05 9.2866e-04 1.0892e-01 0.4566
## 1904 2.1655e-02 -4.4613e-03 1.5542e-01 6.6247e-02 0.4736
## 1905 -9.1963e-04 -2.6729e-04 9.3504e-03 -6.7462e-03 0.5027
## 1906 3.1337e-02 -3.3999e-05 3.6377e-03 5.2014e-01 0.3015
## 1907 1.5559e-02 -1.1749e-04 6.2256e-03 1.9868e-01 0.4213
## 1908 -2.6419e-01 -1.6199e-03 6.8237e-02 -1.0052e+00 0.8426
## 1909 -1.0795e-01 -4.3285e-03 3.0597e-01 -1.8734e-01 0.5743
## [ reached getOption("max.print") -- omitted 15 rows ]# Veamos los valores significativos <0.05
la <- na.omit(locMorMat[which(locMorMat$Pr.z...E.Ii..<0.05),])
la## Ii E.Ii Var.Ii Z.Ii Pr.z...E.Ii..
## 0101 1.423198641 -3.692141e-02 5.549471e-01 1.960030 2.499613e-02
## 0102 0.756463161 -4.347248e-03 1.826238e-01 1.780319 3.751191e-02
## 0103 0.411967658 -1.323733e-03 4.625897e-02 1.921580 2.732934e-02
## 0105 0.633803003 -1.048224e-03 5.549026e-02 2.695030 3.519115e-03
## 0107 2.178341892 -9.799055e-03 6.888547e-01 2.636401 4.189531e-03
## 0115 0.009561077 -6.762369e-07 2.366298e-05 1.965635 2.467042e-02
## 0302 0.460220557 -7.489922e-04 3.966158e-02 2.314660 1.031577e-02
## 0303 0.048236647 -1.873445e-05 6.555467e-04 1.884707 2.973468e-02
## 0304 0.418618575 -8.626643e-04 6.119093e-02 1.695778 4.496396e-02
## 0306 0.207070303 -7.807556e-05 5.542443e-03 2.782473 2.697320e-03
## 0404 0.137946442 -8.717759e-05 3.677919e-03 2.276061 1.142119e-02
## 0405 0.734301998 -4.615448e-03 1.938384e-01 1.678325 4.664186e-02
## 0406 0.905376489 -3.897213e-03 2.755995e-01 1.732030 4.163410e-02
## 0609 0.210407065 -2.057921e-04 8.681096e-03 2.260464 1.189623e-02
## 0701 1.400221371 -9.700147e-03 6.819697e-01 1.707310 4.388222e-02
## 0702 0.366352187 -5.693821e-04 2.400997e-02 2.367977 8.942826e-03
## 0703 1.662604548 -7.476848e-03 3.932578e-01 2.663170 3.870410e-03
## 0706 0.124274200 -1.286028e-04 5.425376e-03 1.688944 4.561509e-02
## 0709 0.912812890 -7.738957e-03 2.687072e-01 1.775860 3.787804e-02
## 0710 1.078784401 -1.050547e-02 2.390006e-01 2.228148 1.293533e-02
## 0711 1.314018893 -7.304618e-03 3.059487e-01 2.388828 8.451112e-03
## 0712 1.708811210 -9.998378e-03 4.176386e-01 2.659668 3.910883e-03
## 0713 0.834167542 -4.752558e-03 1.229404e-01 2.392618 8.364331e-03
## 0804 0.882912875 -5.227679e-03 1.552257e-01 2.254238 1.209059e-02
## 0904 1.264952819 -5.012657e-03 3.540834e-01 2.134220 1.641240e-02
## 0905 1.229163627 -6.612634e-03 4.663513e-01 1.809603 3.517870e-02
## 0914 1.212075739 -7.802205e-03 5.495860e-01 1.645502 4.993312e-02
## 1002 1.692850407 -1.381139e-02 7.217977e-01 2.008814 2.227843e-02
## 1003 0.193941255 -3.554418e-04 1.243326e-02 1.742500 4.071046e-02
## 1004 1.026444488 -2.106756e-03 7.356465e-02 3.792201 7.465899e-05
## 1006 0.305215194 -4.143559e-04 2.194885e-02 2.062954 1.955851e-02
## 1208 0.470653766 -1.138168e-03 4.796750e-02 2.154155 1.561400e-02
## 1303 0.281052040 -4.935975e-04 1.134302e-02 2.643531 4.102312e-03
## 1306 0.351531905 -1.138168e-03 3.393463e-02 1.914463 2.778049e-02
## 1310 1.216646570 -8.069907e-03 3.377417e-01 2.107382 1.754226e-02
## 1317 1.245171688 -7.366070e-03 5.190928e-01 1.738475 4.106362e-02
## 1701 2.333227062 -5.509453e-02 1.071978e+00 2.306746 1.053448e-02
## 1702 0.811926994 -2.342917e-03 6.977010e-02 3.082717 1.025599e-03
## 1703 1.254776109 -8.368103e-03 2.903678e-01 2.344114 9.536171e-03
## 1704 0.548290735 -5.457303e-04 3.872229e-02 2.789089 2.642824e-03
## 1705 7.860444147 -5.071773e-02 5.151336e+00 3.485622 2.454969e-04
## 1707 0.100567280 -1.464956e-05 1.567411e-03 2.540554 5.533843e-03
## 2101 0.707771356 -2.679882e-03 1.127679e-01 2.115639 1.718776e-02
## 2104 0.713049959 -3.055168e-03 1.285113e-01 1.997589 2.288063e-02
## 2107 1.276825052 -8.069907e-03 4.241972e-01 1.972803 2.425900e-02
## 2201 0.172969489 -3.501038e-04 8.046647e-03 1.932147 2.667068e-02
## 2202 1.157487885 -6.942477e-03 3.653482e-01 1.926460 2.702348e-02# Veamos los valores significativos > 0.95
lb <- na.omit(locMorMat[locMorMat$Pr.z...E.Ii..>0.95,])
lb## Ii E.Ii Var.Ii Z.Ii Pr.z...E.Ii..
## 0109 -0.1629696 -2.961322e-04 0.00883666 -1.730504 0.9582299
## 0402 -0.1179247 -9.400557e-05 0.00328915 -2.054549 0.9800387
## 0502 -0.3107868 -4.349973e-04 0.03086865 -1.766426 0.9613378
## 0607 -0.2404519 -4.935975e-04 0.01726353 -1.826295 0.9660971
## 0801 -1.5896726 -9.601739e-03 0.50393897 -2.225807 0.9869865
## 0805 -0.4154653 -1.619892e-03 0.05659173 -1.739649 0.9590397
## 1102 -0.3599929 -1.080906e-03 0.04555684 -1.681556 0.9536725
## 1301 -0.6552416 -3.182922e-03 0.11102285 -1.956953 0.9748235
## 1401 -0.7210903 -2.906623e-03 0.08650789 -2.441786 0.9926926
## 1503 -0.7576409 -3.573802e-03 0.15024869 -1.945381 0.9741354
## 1809 -0.3585922 -3.690978e-04 0.03947715 -1.802938 0.9643010Veamos el mapa de significancia del estadístico de Moran local de las unidades espaciales.
names(locMorMat)[5]<-"Prob"
brks <- c(min(locMorMat[,5],na.rm = TRUE), 0.05000, 0.95000, max(locMorMat[,5],na.rm = TRUE))
cols <- c("grey30", "grey90", "grey60")
cols <- c("royalblue", "springgreen", "yellow")
plot(st_geometry(poligonos), col=cols[findInterval((locMorMat[,5]), brks)])
legend("bottomleft", legend=c("rodeado de relativamente altos valores,
locM>0", "no significativo", "rodeado de relativamente bajos valores, locM<0"),
fill = cols, bty="n", cex=0.75)
title(main=" Estadístico local de Moran ", cex=0.7)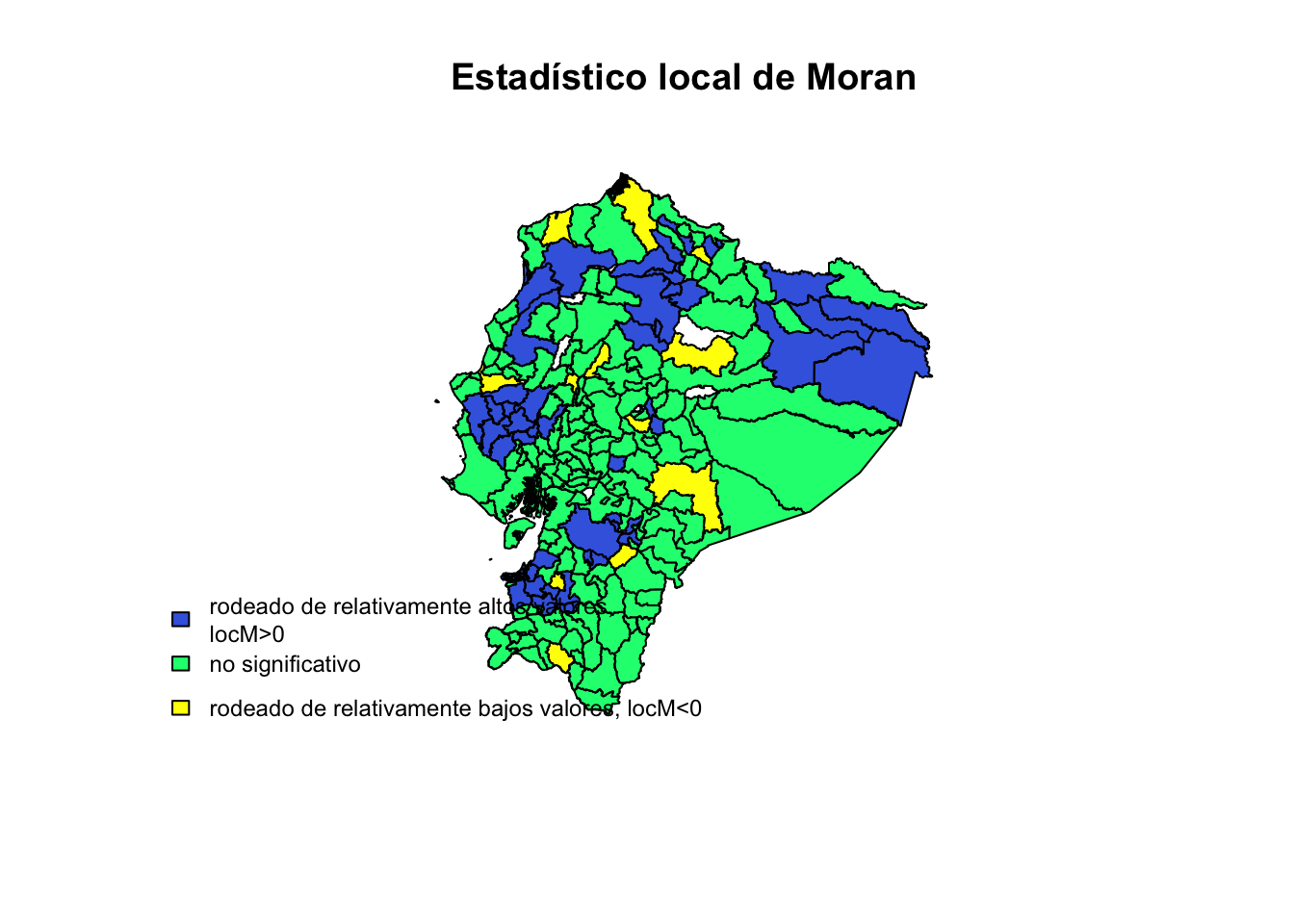
7.3.2 Estadístico Local de Geary
El estadístico local de Geary se define como
Ci=1m2∑jwij(xi−xj) donde m2=n−1∑i(xi−ˉx)2. El valor esperado del Geary local se obtiene de la siguiente manera bajo aleatorización:
E(Ci)=2nwi(n−1)
7.3.3 Estadístico Local: Getis-Ord Gi y G∗i
Los estadísticos Gi y G∗i también son LISA y están dados por:
Gi=∑j≠iwijxj∑j≠ixj
G∗i=∑jwijxj∑jxj donde xi es la observación en la unidad espacial i y wij es un elemento de la matriz de pesos espaciales W. Note que G∗i incluye a la unidad espacial analizada, mientras Gi no. Tanto Gi como G∗i requieren que x sea positivo.
Inferencia
Para la inferencia se asume una distribución t para Gi y G∗i. La hipótesis nula es que Gi=0.
Valores positivos y significativos en la unidad espacial significan una agrupación de unidad espacial de alto valor (unidad analizada y vecinas), el llamado cluster de alto valor.
Valores negativos del estadístico Gi indican la existencia de un grupo de regiones con valores bajos de la variable examinada, es decir, la unidad espacial i está rodeada por unidades espaciales similares de valor bajo.
Valores positivos y significativas de Getis-Ord tienen un valor p por debajo de 0.05, mientras que las estadísticas negativas y significativas tienen un valor p por encima de 0.95.
Veamos su cálculo:
# local Gi y Gi^*
locG <- localG(poligonos$POBRES_P, cont.listw,zero.policy = TRUE)
locGstar<-localG(poligonos$POBRES_P, nb2listw(include.self(cont.nb)))
summary(locG)## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## -3.7922 -1.2921 -0.1873 -0.2282 0.8355 2.6435 12## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -4.6790 -1.3271 -0.1812 -0.1894 0.9642 2.6196Revisamos la significancia:
# significancia con la prueba t para n=100
sig <- ifelse(locG<=-3.289 | locG>=3.289, "*", " ")
which(sig=="*")## [1] 102 179## [1] 102 179En este caso no tenemos significancia.
val <- qt(0.975,df=length(poligonos$POBRES_P)-1)
# significancia con la prueba t para n=100
sig <- ifelse(locG<=-val | locG>=val, "*", " ")
which(sig=="*")## [1] 5 7 24 28 31 33 51 54 55 62 63 64 65 67 70 77 100 102 104 128 136 143
## [23] 156 175 176 177 178 179 180 201 204 207## [1] 1 2 3 5 7 24 28 33 51 53 54 55 61 62 63 64 65 67 70 77 99 100
## [23] 102 104 128 136 143 156 175 176 177 178 179 180 201 204 207En este caso si tenemos significancia. Veamos el mapa de las unidades espaciales:
# graph of significant locG statistics
brks<-c(-10,-val, val, 10)
cols<-c("grey40", "grey85", "grey55")
cols<-c("red", "grey85", "green")
plot(st_geometry(poligonos), col=cols[findInterval(locG, brks)])
legend("bottomleft", legend=c("G significativo - rodeado de valores relativamente bajos", "G no significativo", "G significativo - rodeado por valores relativamente altos"), fill=cols, bty="n", cex=0.75)
title(main="Valores G significativos")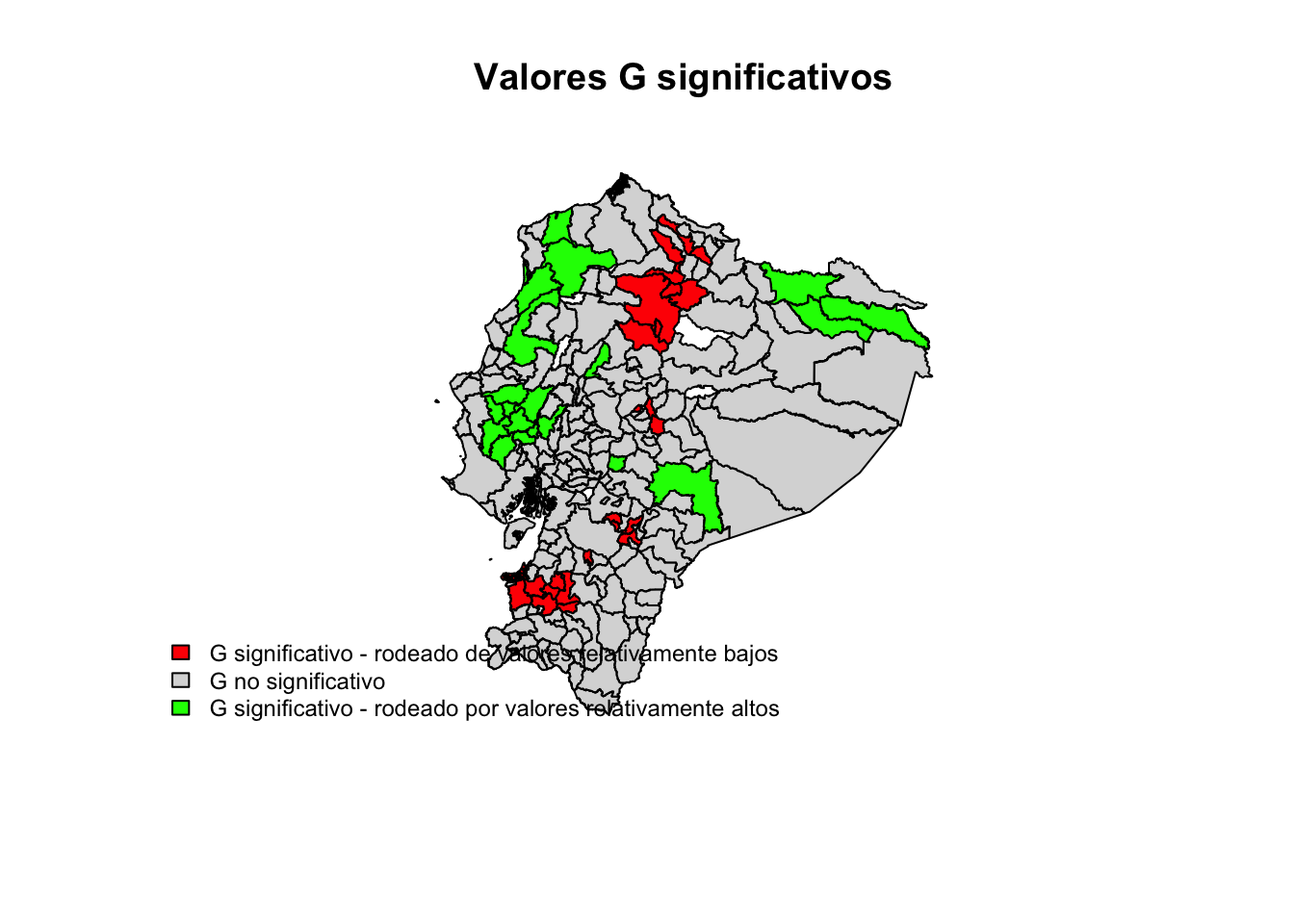
7.3.4 Heterocedasticidad espacial local
Es posible extender el análisis de similitud de vecindades mediante la estabilidad de una variable en el espacio utilizando la medida de heterocedasticidad espacial local (LOSH) (Hi) (heterocedasticidad espacial local), complementaria a la Gi.
El análisis combinado de ambos indicadores permite medir la similitud e inestabilidad de una variable en el espacio. El estadístico Hi mide la varianza de una variable en la vecindad, indicando áreas con variabilidad uniforme y no uniforme, de manera análoga a la medida de autocorrelación en el indicador Gi.
La medida local de heterocedasticidad espacial LOSH (Hi) viene dada por la fórmula:
Hi=∑jwij|ej|α∑jwij donde ej=xj−¯xj, wij es un elemento de la matriz de pesos espaciales W. Si α=1, Hi corresponde a una medida de desviación absoluta, si α=2, Hi corresponde a una medida de varianza.
La interpretación combinada se la puede apreciar en la siguiente tabla:
| Hi alto | Hi bajo | |
|---|---|---|
| Gi alto | Un punto caliente con condiciones locales heterogéneas |
Un punto caliente con unidades espaciales similares |
| Gi bajo | Condiciones locales heterogéneas pero a un nivel medio bajo (poco frecuente) |
Condiciones locales homogéneas y un nivel medio bajo |
Veamos el cálculo del estadístico:
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## -3.7922 -1.2921 -0.1873 -0.2282 0.8355 2.6435 12Notemos que la siguiente función presenta un problema por valores perdidos:
#Hi LOSH local
locH <- LOSH(poligonos$POBRES_P, cont.listw, a=2, var_hi=TRUE, zero.policy=TRUE,na.action=na.exclude)Creamos LOSH1 para arreglar el problema:
LOSH1 <- function (x, listw, a = 2, var_hi = TRUE, zero.policy = NULL,
na.action = na.fail, spChk = NULL)
{
if (is.null(zero.policy))
zero.policy <- get("zeroPolicy", envir = .spdepOptions)
stopifnot(is.logical(zero.policy))
n <- length(listw$neighbours)
if (n != length(x))
stop("Different numbers of observations")
NAOK <- deparse(substitute(na.action)) == "na.pass"
NAOK <- TRUE
if (var_hi) {
res <- matrix(nrow = n, ncol = 6)
colnames(res) <- c("Hi", "E.Hi", "Var.Hi", "Z.Hi", "x_bar_i",
"ei")
}
else {
res <- matrix(nrow = n, ncol = 3)
colnames(res) <- c("Hi", "x_bar_i", "ei")
}
Wi <- vapply(listw$weights, sum, FUN.VALUE = 0)
res[, "x_bar_i"] <- lag.listw(listw, x, zero.policy = zero.policy,
NAOK = NAOK)/Wi
res[, "ei"] <- abs(x - res[, "x_bar_i"])^a
denom_hi <- mean(res[, "ei"],na.rm = TRUE) * Wi
res[, "Hi"] <- lag.listw(listw, res[, "ei"], zero.policy = zero.policy,
NAOK = NAOK)/denom_hi
if (var_hi) {
var_ei <- (sum(res[, "ei"]^2,na.rm = TRUE)/n) - mean(res[, "ei"],na.rm = TRUE)^2
res[, "Var.Hi"] <- (n - 1)^(-1) * denom_hi^(-2) * var_ei *
(n * vapply(listw$weights, function(y) sum(y^2),
FUN.VALUE = 0) - Wi^2)
res[, "Z.Hi"] <- (2 * res[, "Hi"])/res[, "Var.Hi"]
res[, "E.Hi"] <- 1
}
res
}#Hi LOSH local
locH <- LOSH1(poligonos$POBRES_P, cont.listw, a=2, var_hi=TRUE, zero.policy=TRUE,na.action=na.exclude)
summary(locH)## Hi E.Hi Var.Hi Z.Hi x_bar_i
## Min. :0.008121 Min. :1 Min. :0.1456 Min. : 0.008101 Min. :0.4400
## 1st Qu.:0.371345 1st Qu.:1 1st Qu.:0.3263 1st Qu.: 1.330049 1st Qu.:0.6896
## Median :0.927097 Median :1 Median :0.4942 Median : 4.132274 Median :0.7520
## Mean :1.112421 Mean :1 Mean :0.6005 Mean : 5.263507 Mean :0.7555
## 3rd Qu.:1.642660 3rd Qu.:1 3rd Qu.:0.6621 3rd Qu.: 8.735031 3rd Qu.:0.8247
## Max. :4.683636 Max. :1 Max. :2.0049 Max. :18.275086 Max. :0.9350
## NA's :12 NA's :12 NA's :12 NA's :12
## ei
## Min. :0.000001
## 1st Qu.:0.001230
## Median :0.006360
## Mean :0.016284
## 3rd Qu.:0.022016
## Max. :0.141301
## NA's :12Guardamos los valores relevantes del estadístico Hi:
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.008121 0.371345 0.927097 1.112421 1.642660 4.683636 12Veamos el gráfico conjunto de Gi y Hi:
par(mfrow = c(1,2))
# mapa de Gi
brks <- c(a[1], a[2], a[3], a[5], a[6])
colfunc <- colorRampPalette(c("royalblue", "springgreen", "yellow", "red"))
coli <- colfunc(5)
plot(st_geometry(poligonos), col=coli[findInterval(locG, brks)], main=" Gi statistics")
legend("bottomright", legend=c("Very low", "Low", "Medium", "High", "Very
high"), fill=coli, bty="n")
# mapa de LOSH
brks <- c(b[1], b[2], b[3], b[5], b[6])
plot(st_geometry(poligonos), col=coli[findInterval(locH[,"Hi"], brks)])
legend("bottomright", legend=c("Very low", "Low", "Medium", "High", "Very
high"), fill=coli, bty="n")
title(main="Hi statistics")
7.4 Cross correlación espacial entre dos variables
Global
Introducido por Chen (2015), el índice de cross-correlación espacial global (GSCI por sus siglas en inglés) está dado por:
Rc=xTWy y es un estadístico escalado entre [−1,1]; x y y son las variables estudiadas y W es la matriz de pesos espaciales.
Este es una medida indirecta que calcula correlación relacionada con distancia.
También se tiene una relación entre correlación tradicional de dos variables y Rc:
R0=Rc+Rp
donde R0 es un índice de correlación de Pearson, donde la dependencia consiste de relación entre valores de la variable y relaciones en el espacio. Rc es el coeficiente GSCI y Rp es una cross-correlación parcial, que expresa la influencia directa de las variables sin efectos espaciales.
Local
También se tiene medidas locales de cross-correlación, el índice de cross-correlación espacial local (LSCI por sus siglas en inglés):
R(xy)i=xi∑jwijyj R(yx)j=yi∑jwijxj donde i y j son diferentes unidades espaciales y wij son elementos de la matriz de pesos espaciales W.
El GSCI refleja la suma de correlaciones cruzadas entre dos (todos) elementos cualesquiera, mientras que el LSCI mide la correlación cruzada entre un elemento dado y todos los demás en el sistema.
library(spatialEco) # crossCorrelation()
centroides <- st_coordinates(st_centroid(poligonos))
cont.mat <- as.matrix(dist(centroides))
x1 <- poligonos$VAB_PC
x2 <- poligonos$POBRES_P
# versión con W
ii <- crossCorrelation(x1, x2, w=cont.mat, type=c("LSCI", "GSCI"), k=999,
scale.xy=TRUE, scale.partial=TRUE, scale.matrix=TRUE, alpha=0.05)
ii## Moran's-I under randomization assumptions...
## First-order Moran's-I: -0.00739955
## First-order p-value: 147
## Chen's SCI under randomization assumptions...
##
## Summary statistics of local partial cross-correlation [xy]
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -1.0000 0.6051 0.6411 0.6288 0.6675 1.0000
##
## p-value based on 2-tailed t-test: 0.04804805
## p-value based on 2-tailed t-test observations above/below CI: 0.0960961
##
## Counts of cluster types
## High.High High.Low Low.High Low.Low
## 32 39 45 99scale.partial: estandariza el estadístico entre -1 y 1.scale.matrix: estandariza W tal que sus filas sumen 1.alpha: nivel de significancia.knúmero de simulaciones.scale.xyestandarización de las variables analizadas.LSCI: local spatial cross-correlation index.GSCI: global spatial cross-correlation index.
Los resultados muestran que el GSCI es -0.0073996 y su p-valor es 147, lo que indica que las dos variables no están correlacionadas en el espacio.
Veamos la correlación de pearson:
## [1] -0.3547163Según las expresiones anteriores, tenemos que R0=−0.3547, Rc=0.00006 y Rp=R0−Rc.
Respecto a la correlación local LSCI, vemos que con un α=.1 si es significativo porque su p-valor es 0.048048. Veamos algunos resultados:
## lsci.xy lsci.yx
## 1 0.4608829 0.09533135
## 2 0.7018634 0.27924013
## 3 0.7216789 0.06764266
## 4 0.7348345 0.06408113
## 5 0.7146435 -0.14035150
## 6 0.7723176 0.21886699Las estadísticas locales lsci.xy deben interpretarse como la influencia de x sobre y.
A continuación se calcula la correlación basándonos en las distancias en los centroides:
# version with coordinates and distance
X <- centroides
# colnames(X) <- c("x","y")
# X <- as.matrix(dist(X))
iii <- crossCorrelation(x1, x2, coords=X, type = c("LSCI","GSCI"), k=999, dist.function="inv.power", scale.xy=TRUE, scale.partial=TRUE, scale.matrix=FALSE, alpha=0.05)
iii## Moran's-I under randomization assumptions...
## First-order Moran's-I: -0.00739955
## First-order p-value: 143
## Chen's SCI under randomization assumptions...
##
## Summary statistics of local partial cross-correlation [xy]
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -1.0000 0.6051 0.6411 0.6288 0.6675 1.0000
##
## p-value based on 2-tailed t-test: 0.04404404
## p-value based on 2-tailed t-test observations above/below CI: 0.08808809
##
## Counts of cluster types
## High.High High.Low Low.High Low.Low
## 32 39 45 99# library(tmap)
# library(tmaptools)
# tmap_mode("plot")
# tm_shape(poligonos) +
# tm_fill("cross_cor", style = "quantile", palette = "-RdYlBu",
# title = "Matriz de contiguidad: w=cont.mat") +
# tm_borders()
library(dplyr)
poligonos$cross_cor <- ii$SCI[,"lsci.xy"]
poligonos <- poligonos %>%
mutate(quantile_bin = cut(cross_cor, breaks = quantile(cross_cor, probs = seq(0, 1, by = 0.2), na.rm = TRUE), include.lowest = TRUE))
ggplot(data = poligonos) +
geom_sf(aes(fill = quantile_bin)) +
scale_fill_brewer(palette = "YlGnBu") + # Choose a color palette
theme_minimal() +
labs(fill = "w=cont.matY - Quantiles", title = "Matriz de contiguidad")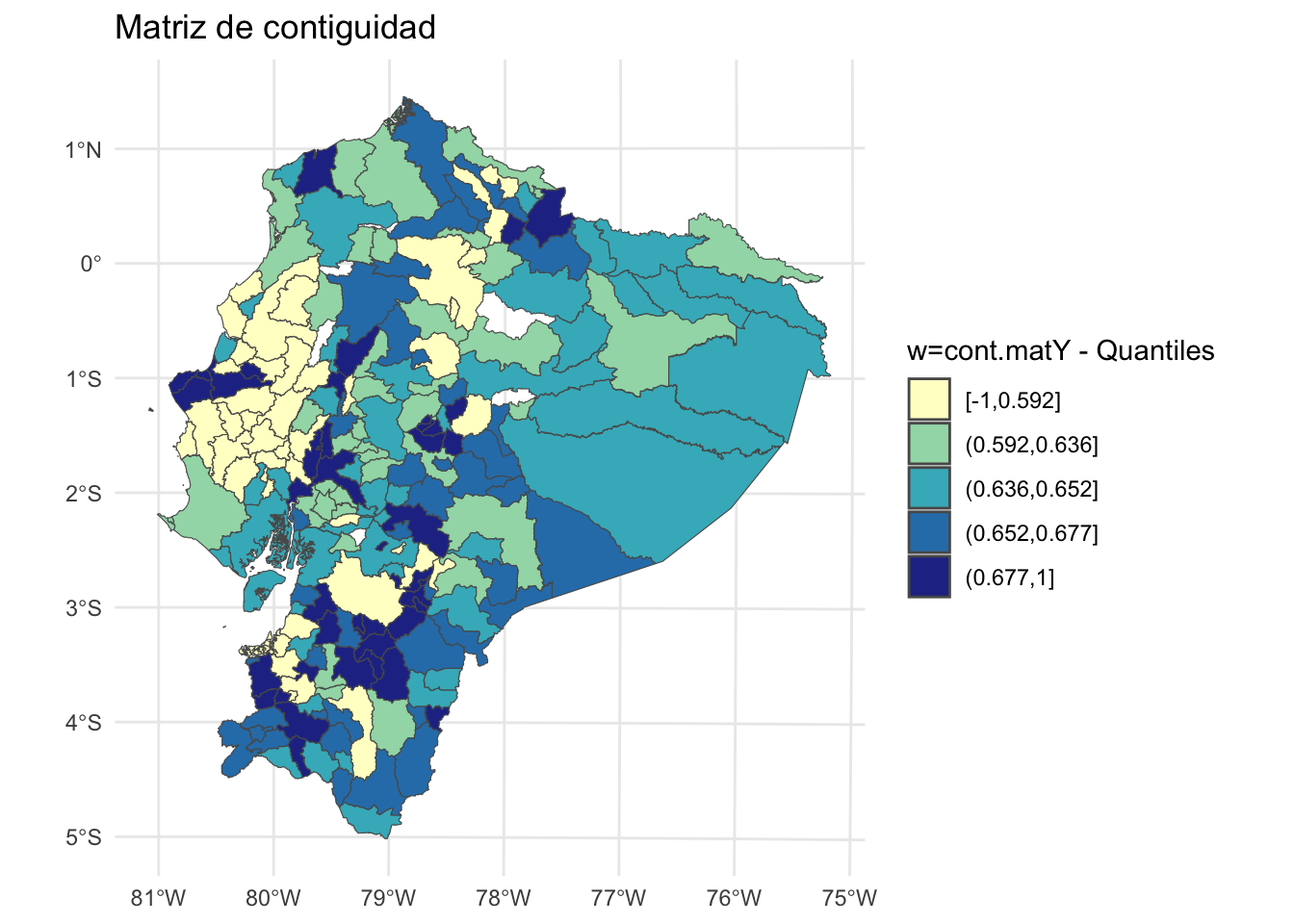
# mapa de los resultados de iii
poligonos$cross_cor_id <- iii$SCI[,"lsci.xy"]
# tm_shape(poligonos) +
# tm_fill("cross_cor_id", style = "quantile", palette = "-RdYlBu",
# title = "Matriz de distancia inversa al cuadrado: dist.function='inv.power'") +
# tm_borders()
poligonos <- poligonos %>%
mutate(quantile_bin_id = cut(cross_cor_id, breaks = quantile(cross_cor_id, probs = seq(0, 1, by = 0.2), na.rm = TRUE), include.lowest = TRUE))
ggplot(data = poligonos) +
geom_sf(aes(fill = quantile_bin_id)) +
scale_fill_brewer(palette = "YlGnBu") + # Choose a color palette
theme_minimal() +
labs(fill = "dist.function='inv.power' - Quantiles", title = "Matriz de distancia inversa al cuadrado")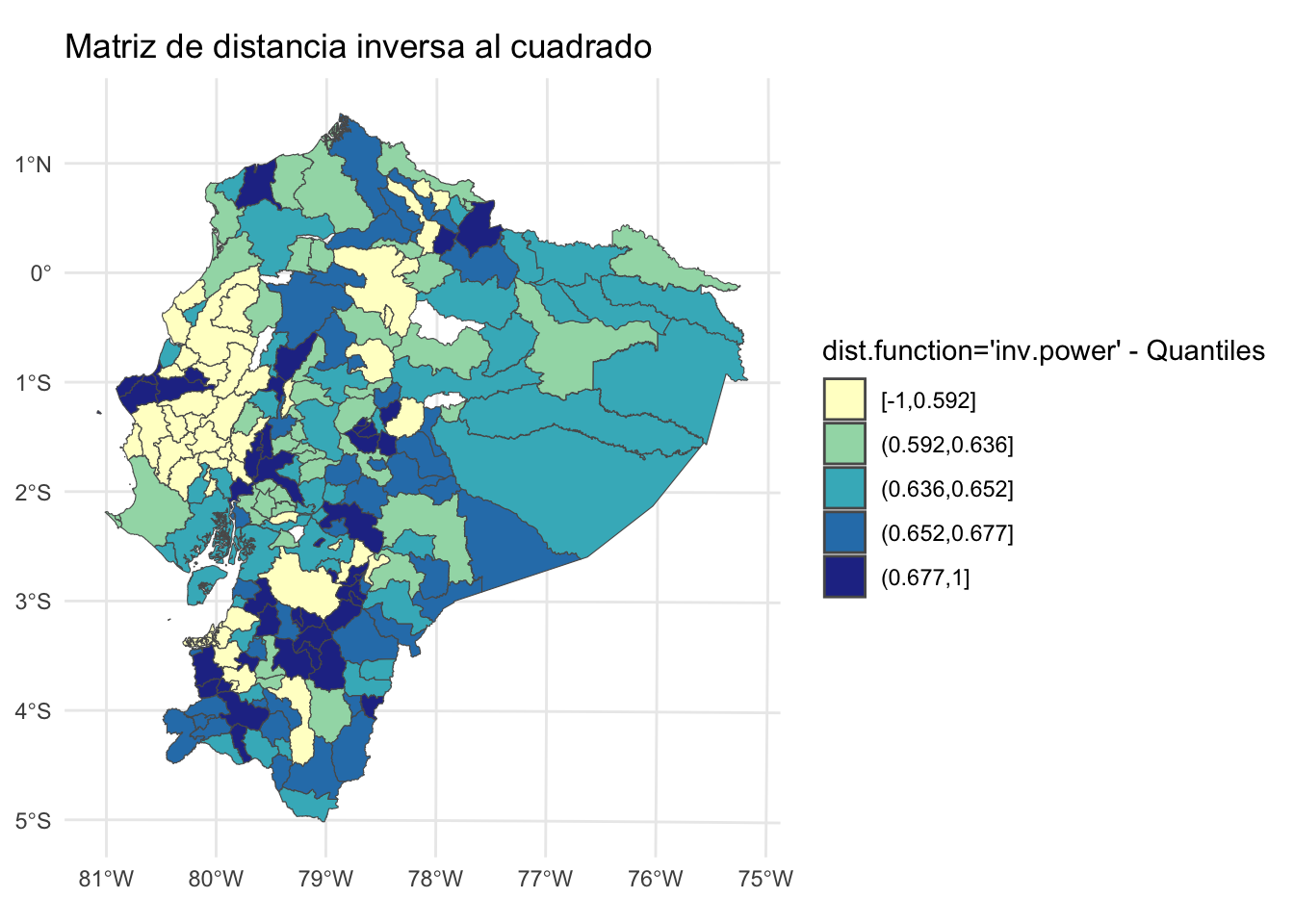
En los gráficos son visibles agrupaciones de valores altos y bajos. Las áreas claras (correlación cruzada espacial negativa fuerte) significan una diferenciación espacial mucho más fuerte (relación de las variables y efectos espaciales) que los campos más oscuros (correlación cruzada espacial negativa media).