3 Objetos espaciales

Tomado de Pebesma and Bivand (2023), espefíficamente de las viñetas(https://r-spatial.github.io/sf/index.html)

Librerías usadas:

• sf

3.1 Atributos simples

Atributos simples o acceso simple a atributos se refiere a un estándar formal (ISO 19125-1:2004) que describe:

1. cómo los objetos del mundo real se pueden representar en computadoras, con énfasis en la geometría espacial de estos objetos.
2. cómo dichos objetos pueden almacenarse y extraerse de bases de datos, y
3. qué operaciones geométricas deben definirse para ellos.

El estándar se implementa ampliamente en bases de datos espaciales (como PostGIS), Sistemas de Información Geográfica -SIG comerciales (por ejemplo, ESRI ArcGIS) y forma la base de datos vectoriales para bibliotecas como GDAL. Un subconjunto de funciones simples forma el estándar GeoJSON.

R tiene clases bien soportadas para almacenar datos espaciales (sp) y conectarse a los entornos mencionados anteriormente (rgdal,rgeos), pero hasta ahora ha carecido de una implementación completa de características simples, lo que hace que las conversiones a veces sean complicadas, ineficientes o incompletas. El paquete sf intenta llenar este vacío y apunta a suceder al sp a largo plazo.

3.2 ¿Qué es una característica (feature)?

Una característica se considera una cosa o un objeto del mundo real, como un edificio o un árbol. Como ocurre con los objetos, a menudo se componen de otros objetos. Este también es el caso de las características: un conjunto de características puede formar una sola característica. Una masa forestal puede ser una característica, un bosque puede ser una característica, una ciudad puede ser una característica. Un píxel de una imagen de satélite puede ser una característica, y una imagen completa también puede ser una característica.

Las entidades tienen una geometría que describe en qué lugar de la Tierra se encuentra la entidad y tienen atributos que describen otras propiedades. La geometría de un árbol puede ser la delimitación de su copa, de su tallo o el punto que indica su centro. Otras propiedades pueden incluir su altura, color, diámetro a la altura del pecho en una fecha determinada, etc.

3.2.1 Dimensiones

Todas las geometrías están compuestas de puntos. Los puntos son coordenadas en un espacio de 2, 3 o 4 dimensiones. Todos los puntos de una geometría tienen la misma dimensionalidad. Además de las coordenadas \(X\) e \(Y\), existen dos dimensiones adicionales opcionales:

• una coordenada \(Z\) que denota altura.
• una coordenada \(M\) (rara vez utilizada), que denota alguna medida asociada con el punto, en lugar de con la característica en su conjunto; algunos ejemplos podrían ser el tiempo de medición o el error de medición de las coordenadas.

Los cuatro casos posibles se denota como:

1. Los puntos bidimensionales se refieren a x e y, este y norte, o longitud y latitud, nos referimos a ellos como \(XY\).
2. puntos tridimensionales como \(XYZ\).
3. puntos tridimensionales como \(XYM\).
4. puntos en cuatro dimensiones como \(XYZM\).

3.2.2 Tipos de geometría de entidades simples

Los siguientes siete tipos de funciones simples son los más comunes y, por ejemplo, los únicos que se utilizan para GeoJSON:

type	description
POINT	geometría de dimensión cero que contiene un solo punto
LINESTRING	secuencia de puntos conectados por líneas rectas que no se cruzan entre sí; geometría unidimensional
POLYGON	geometría con área positiva (bidimensional); la secuencia de puntos forma un anillo cerrado que no se cruza entre sí; el primer anillo indica el anillo exterior, cero o más anillos posteriores indican agujeros en este anillo exterior
MULTIPOINT	set of points; a MULTIPOINT is simple if no two Points in the MULTIPOINT are equal
MULTILINESTRING	set of linestrings
MULTIPOLYGON	set of polygons
GEOMETRYCOLLECTION	set of geometries of any type except GEOMETRYCOLLECTION

Cada uno de los tipos de geometría también puede ser un conjunto vacío, que contiene coordenadas cero (para PUNTO, el estándar no está claro cómo representar la geometría vacía). Se puede considerar que las geometrías vacías son análogas a los atributos faltantes (NA), los valores NULL o las listas vacías.

3.2.3 Sistema de Referencia de Coordenadas

Coordenadas polares y cartesianas:

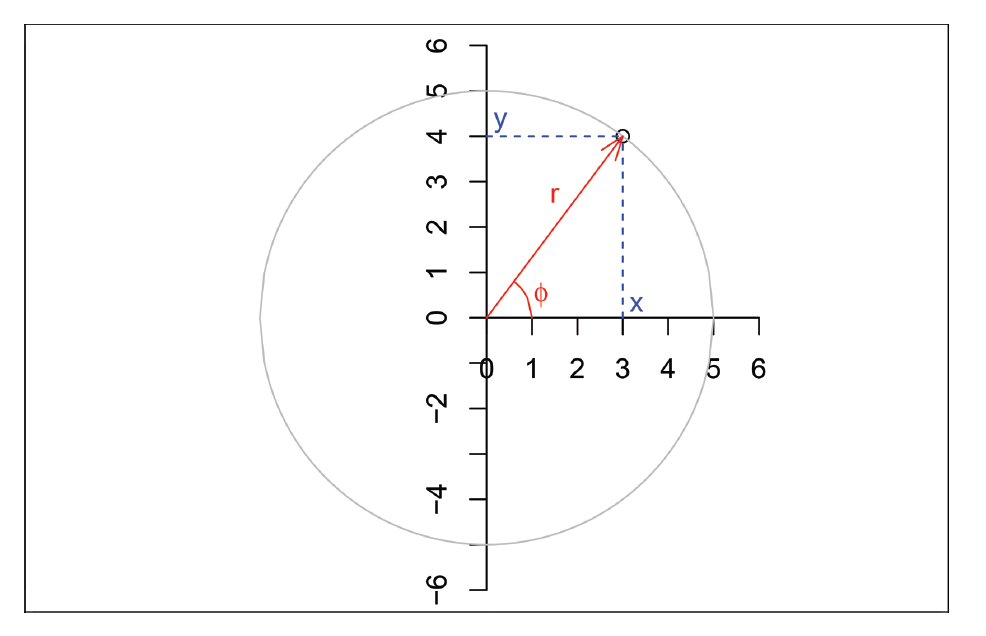
\[x = r \cos \phi, y = r \sin \phi\] \[r = \sqrt{x^2+y^2}, \phi = atan2(x,y)\]

Donde atan2: La función arcotangente de dos parámetros devuelve el ángulo formado entre el eje \(x\) positivo y la recta que conecta el origen con un punto de coordenadas \((x,y)\neq(0,0)\) del plano euclidiano, expresado en radianes.

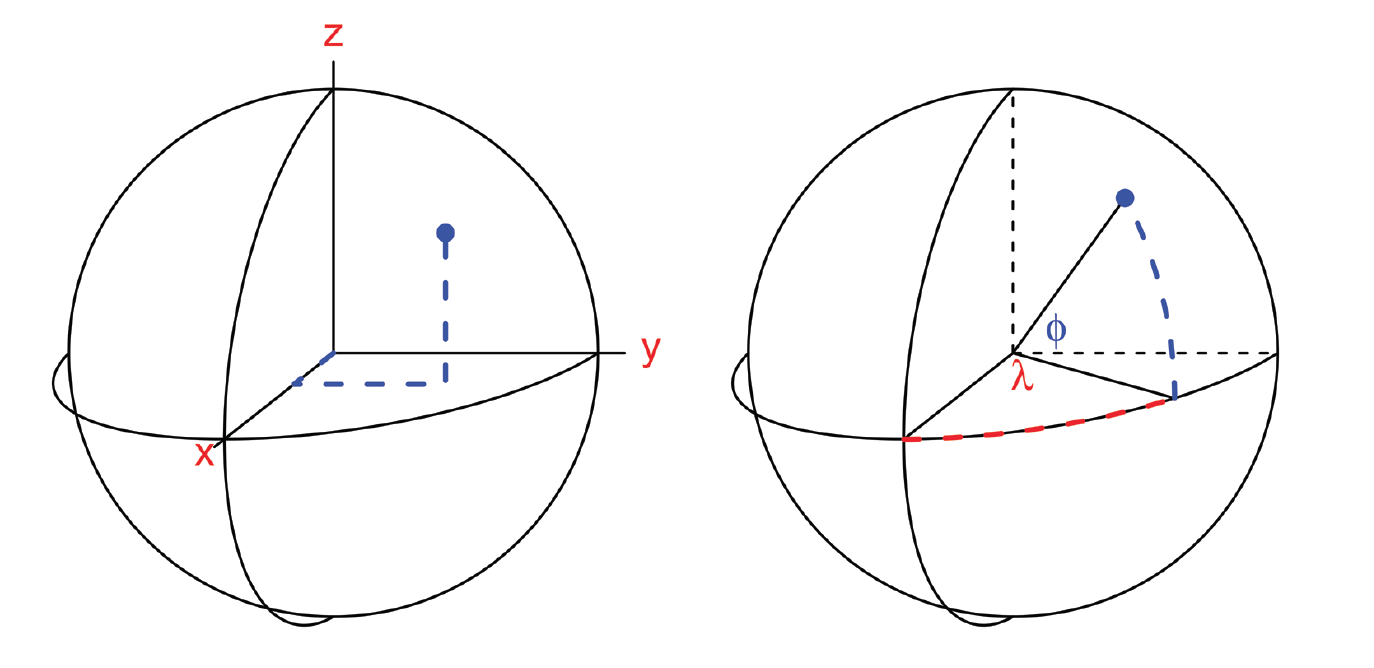
Coordenadas esféricas:

En tres dimensiones las coordenadas cartesianas se expresan como \((x,y,z)\), las coordenadas esféricas se expresan con \((r,\lambda,\phi)\) donde

• \(r\) es el radio de la esfera,
• \(\lambda\) es la longitud, medida en el plano \((x,y)\) en contra de las manecillas del reloj desde el eje \(x\) positivo
• \(\phi\) es la latitud, el ángulo entre el vector y el plano \((x,y)\).

• \(-180º\leq\lambda\leq180º\) (o \(0º\leq\lambda\leq360º\)).
• \(-90º\leq\phi\leq90º\).
• Si estamos interesados en un punto de la esfera, se suele omitir \(r\) porque en ese caso \((\lambda,\phi)\) son suficientes para identificar el punto.

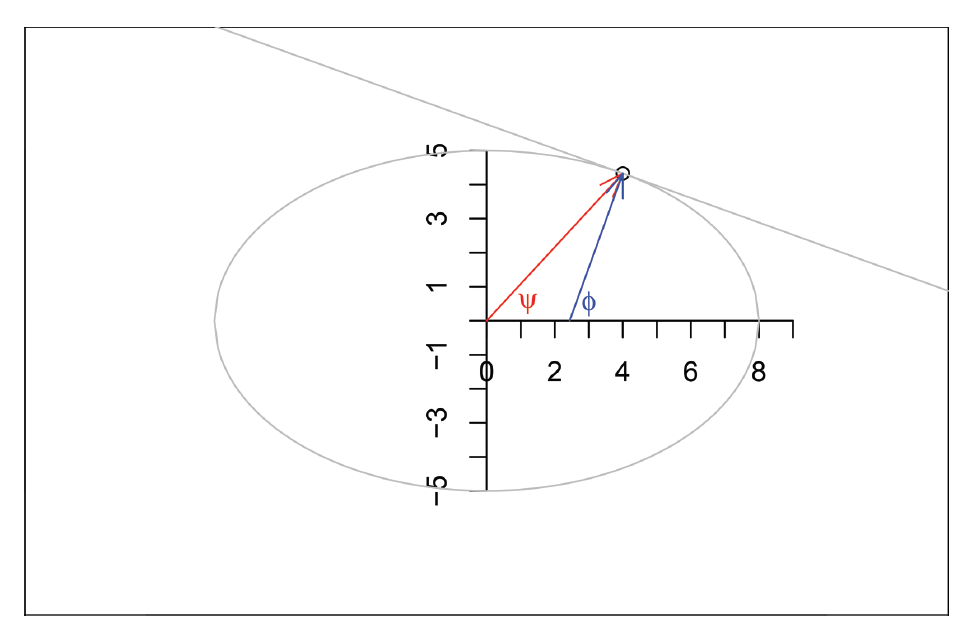
Coordenadas en la elipse:

Hay dos maneras en las que un ángulo puede expresarse:

• medido desde el centro de la elipse (\(\psi\)) o,
• medido perpendicular a la tangente de la elipse en el punto de medición (\(\phi\)).

• Un sistema de coordenadas es un conjunto de reglas matemáticas para especificar cómo se asignarán las coordenadas a los puntos.
• Un datum es un parámetro o conjunto de parámetros que definen la posición del origen, la escala, y la orientación del sistema de coordenadas.
• Un geodetic datum o datum geodésico es un datum que describe la relación de un sistema de coordenadas a la tierra.
• Un sistema de referencia de coordenadas es un sistema de coordenadas que está relacionado a un objeto (a la tierra en el caso geodésico) por un datum.

Video: https://www.youtube.com/watch?v=SaFrbKVC1Yw

Las coordenadas sólo se pueden colocar en la superficie de la Tierra cuando se conoce su sistema de referencia de coordenadas (CRS); este puede ser

• un CRS esferoide como WGS84,
• un CRS bidimensional (cartesiano) proyectado como una zona UTM o Web Mercator,
• o un CRS en tres dimensiones, o incluyendo el tiempo.

3.3 Cómo se organizan los atributos simples

El paquete sf representa características simples como objetos R nativos. De manera similar a PostGIS, todas las funciones y métodos en sf que operan con datos espaciales tienen el prefijo st_, que se refiere al tipo espacial; esto hace que sean fáciles de encontrar.

Las funciones simples se implementan como datos nativos de R, utilizando estructuras de datos simples (clases S3, listas, matrices, vectores). El uso típico implica leer, manipular y escribir conjuntos de características, con atributos y geometrías.

Como los atributos generalmente se almacenan en objetos data.frame (o el muy similar tbl_df), también almacenaremos geometrías de características en una columna data.frame.

Dado que las geometrías no tienen un solo valor, se colocan en una columna de lista, una lista de longitud igual al número de registros en el marco de datos, y cada elemento de la lista contiene la geometría de característica simple de esa característica.

Las tres clases utilizadas para representar características simples son:

• sf, la tabla (data.frame) con atributos de características y geometrías de características, que contiene
• sfc, la lista-columna con las geometrías para cada característica (registro), que se compone de
• sfg, la geometría de característica de una característica simple individual.

library(sf)
nc <- st_read(system.file("shape/nc.shp", package="sf"))

## Reading layer `nc' from data source 
##   `/Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/library/sf/shape/nc.shp' using driver `ESRI Shapefile'
## Simple feature collection with 100 features and 14 fields
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -84.32385 ymin: 33.88199 xmax: -75.45698 ymax: 36.58965
## Geodetic CRS:  NAD27

Veamos su clase

class(nc)

## [1] "sf"         "data.frame"

Para identificar el nombre de la columna que tiene las geometrías:

attr(nc, "sf_column")

## [1] "geometry"

Si se imprime tres valores

print(nc[9:15], n = 3)

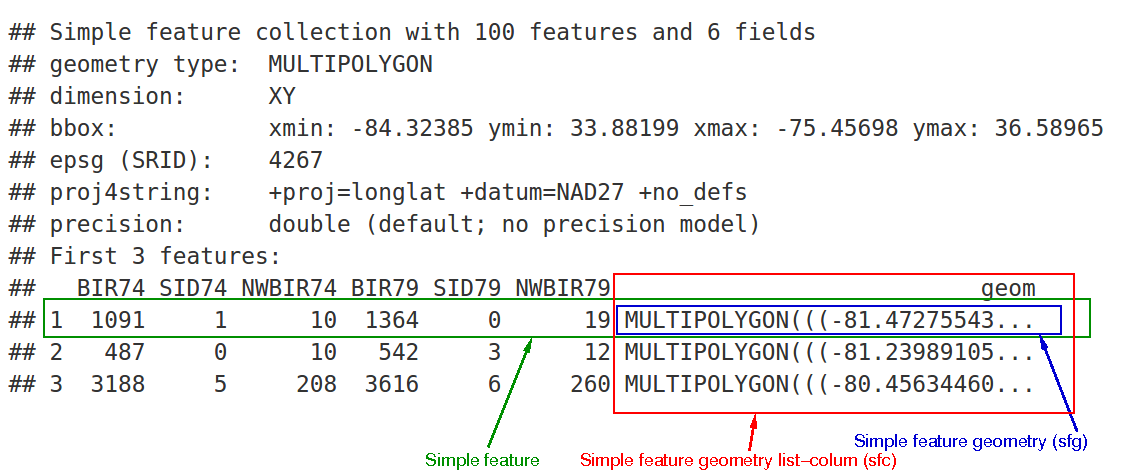
En la salida vemos:

• en verde una característica simple: un único registro, o fila del data.frame, que consta de atributos y geometría
• en azul una característica simple (un objeto de clase sfg)
• en rojo, una columna de lista de características simples (un objeto de clase sfc, que es una columna en el data.frame)

Los métodos para objetos sf son:

methods(class = "sf")

##   [1] [                            [[<-                         [<-                         
##   [4] $<-                          aggregate                    anti_join                   
##   [7] arrange                      as.data.frame                cbind                       
##  [10] coerce                       dbDataType                   dbWriteTable                
##  [13] distinct                     dplyr_reconstruct            drop_na                     
##  [16] duplicated                   filter                       full_join                   
##  [19] gather                       group_by                     group_split                 
##  [22] identify                     idw                          initialize                  
##  [25] inner_join                   krige                        krige.cv                    
##  [28] left_join                    merge                        mutate                      
##  [31] nest                         pivot_longer                 pivot_wider                 
##  [34] plot                         print                        rbind                       
##  [37] rename_with                  rename                       right_join                  
##  [40] rowwise                      sample_frac                  sample_n                    
##  [43] select                       semi_join                    separate_rows               
##  [46] separate                     show                         slice                       
##  [49] slotsFromS3                  spread                       st_agr                      
##  [52] st_agr<-                     st_area                      st_as_s2                    
##  [55] st_as_sf                     st_as_sfc                    st_bbox                     
##  [58] st_boundary                  st_break_antimeridian        st_buffer                   
##  [61] st_cast                      st_centroid                  st_collection_extract       
##  [64] st_concave_hull              st_convex_hull               st_coordinates              
##  [67] st_crop                      st_crs                       st_crs<-                    
##  [70] st_difference                st_drop_geometry             st_filter                   
##  [73] st_geometry                  st_geometry<-                st_inscribed_circle         
##  [76] st_interpolate_aw            st_intersection              st_intersects               
##  [79] st_is_valid                  st_is                        st_join                     
##  [82] st_line_merge                st_m_range                   st_make_valid               
##  [85] st_minimum_rotated_rectangle st_nearest_points            st_node                     
##  [88] st_normalize                 st_point_on_surface          st_polygonize               
##  [91] st_precision                 st_reverse                   st_sample                   
##  [94] st_segmentize                st_set_precision             st_shift_longitude          
##  [97] st_simplify                  st_snap                      st_sym_difference           
## [100] st_transform                 st_triangulate_constrained   st_triangulate              
## [103] st_union                     st_voronoi                   st_wrap_dateline            
## [106] st_write                     st_z_range                   st_zm                       
## [109] summarise                    transform                    transmute                   
## [112] ungroup                      unite                        unnest                      
## see '?methods' for accessing help and source code

Podemos transformar un objeto sf a data.frame (se pierde las características sf por lo que ya no aplicarían los métodos anteriores)

nc.no_sf <- as.data.frame(nc)
class(nc.no_sf)

## [1] "data.frame"

Cheatsheet: https://github.com/rstudio/cheatsheets/blob/main/sf.pdf

3.4 sfc: la columna con la geometría simple

La columna en el sf data.frame que contiene las geometrías es una lista, de clase sfc. Podemos recuperar la columna de lista de geometría en este caso mediante nc$geom o nc[[15]], pero la forma más general usa `st_geometry()```:

nc$geometry

## Geometry set for 100 features 
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -84.32385 ymin: 33.88199 xmax: -75.45698 ymax: 36.58965
## Geodetic CRS:  NAD27
## First 5 geometries:

## MULTIPOLYGON (((-81.47276 36.23436, -81.54084 3...

## MULTIPOLYGON (((-81.23989 36.36536, -81.24069 3...

## MULTIPOLYGON (((-80.45634 36.24256, -80.47639 3...

## MULTIPOLYGON (((-76.00897 36.3196, -76.01735 36...

## MULTIPOLYGON (((-77.21767 36.24098, -77.23461 3...

(nc_geom <- st_geometry(nc))

## Geometry set for 100 features 
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -84.32385 ymin: 33.88199 xmax: -75.45698 ymax: 36.58965
## Geodetic CRS:  NAD27
## First 5 geometries:

## MULTIPOLYGON (((-81.47276 36.23436, -81.54084 3...

## MULTIPOLYGON (((-81.23989 36.36536, -81.24069 3...

## MULTIPOLYGON (((-80.45634 36.24256, -80.47639 3...

## MULTIPOLYGON (((-76.00897 36.3196, -76.01735 36...

## MULTIPOLYGON (((-77.21767 36.24098, -77.23461 3...

Las geometrías se imprimen en forma abreviada, pero podemos ver una geometría completa seleccionándola, p.e. el primero por:

nc_geom[[1]]

## MULTIPOLYGON (((-81.47276 36.23436, -81.54084 36.27251, -81.56198 36.27359, -81.63306 36.34069, -81.74107 36.39178, -81.69828 36.47178, -81.7028 36.51934, -81.67 36.58965, -81.3453 36.57286, -81.34754 36.53791, -81.32478 36.51368, -81.31332 36.4807, -81.26624 36.43721, -81.26284 36.40504, -81.24069 36.37942, -81.23989 36.36536, -81.26424 36.35241, -81.32899 36.3635, -81.36137 36.35316, -81.36569 36.33905, -81.35413 36.29972, -81.36745 36.2787, -81.40639 36.28505, -81.41233 36.26729, -81.43104 36.26072, -81.45289 36.23959, -81.47276 36.23436)))

La clumna de geometrías tiene su propia clase:

class(nc_geom)

## [1] "sfc_MULTIPOLYGON" "sfc"

Con los siguientes métodos:

methods(class = 'sfc')

##  [1] [                            [<-                          as.data.frame               
##  [4] c                            coerce                       format                      
##  [7] fortify                      identify                     initialize                  
## [10] Ops                          print                        rep                         
## [13] scale_type                   show                         slotsFromS3                 
## [16] st_area                      st_as_binary                 st_as_grob                  
## [19] st_as_s2                     st_as_sf                     st_as_text                  
## [22] st_bbox                      st_boundary                  st_break_antimeridian       
## [25] st_buffer                    st_cast                      st_centroid                 
## [28] st_collection_extract        st_concave_hull              st_convex_hull              
## [31] st_coordinates               st_crop                      st_crs                      
## [34] st_crs<-                     st_difference                st_geometry                 
## [37] st_inscribed_circle          st_intersection              st_intersects               
## [40] st_is_valid                  st_is                        st_line_merge               
## [43] st_m_range                   st_make_valid                st_minimum_rotated_rectangle
## [46] st_nearest_points            st_node                      st_normalize                
## [49] st_point_on_surface          st_polygonize                st_precision                
## [52] st_reverse                   st_sample                    st_segmentize               
## [55] st_set_precision             st_shift_longitude           st_simplify                 
## [58] st_snap                      st_sym_difference            st_transform                
## [61] st_triangulate_constrained   st_triangulate               st_union                    
## [64] st_voronoi                   st_wrap_dateline             st_write                    
## [67] st_z_range                   st_zm                        str                         
## [70] summary                      type_sum                     vec_cast.sfc                
## [73] vec_ptype2.sfc              
## see '?methods' for accessing help and source code

Atributos

attributes(nc_geom)

## $n_empty
## [1] 0
## 
## $crs
## Coordinate Reference System:
##   User input: NAD27 
##   wkt:
## GEOGCRS["NAD27",
##     DATUM["North American Datum 1927",
##         ELLIPSOID["Clarke 1866",6378206.4,294.978698213898,
##             LENGTHUNIT["metre",1]]],
##     PRIMEM["Greenwich",0,
##         ANGLEUNIT["degree",0.0174532925199433]],
##     CS[ellipsoidal,2],
##         AXIS["latitude",north,
##             ORDER[1],
##             ANGLEUNIT["degree",0.0174532925199433]],
##         AXIS["longitude",east,
##             ORDER[2],
##             ANGLEUNIT["degree",0.0174532925199433]],
##     ID["EPSG",4267]]
## 
## $class
## [1] "sfc_MULTIPOLYGON" "sfc"             
## 
## $precision
## [1] 0
## 
## $bbox
##      xmin      ymin      xmax      ymax 
## -84.32385  33.88199 -75.45698  36.58965

3.5 sfg Geometría de caracterísitia simple

Los objetos de geometría de característica simple (sfg) llevan la geometría de una sola característica: un punto, cadena lineal (LINESTRING) o polígono.

Las características simples se implementan en R con tipos nativos, siguiendo las siguientes reglas:

1. un solo POINT es un vector numérico
2. un conjunto de puntos (como LINESTRING o POLYGON) es una matriz, donde cada fila contiene un punto.
3. cualquier otro conjunto es list.

Como ejemplo:

(x <- st_point(c(1,2)))

## POINT (1 2)

(x <- st_point(c(1,2,3)))

## POINT Z (1 2 3)

Veamos otros ejemplos:

p <- rbind(c(3.2,4), c(3,4.6), c(3.8,4.4), c(3.5,3.8), c(3.4,3.6), c(3.9,4.5))
(mp <- st_multipoint(p))

## MULTIPOINT ((3.2 4), (3 4.6), (3.8 4.4), (3.5 3.8), (3.4 3.6), (3.9 4.5))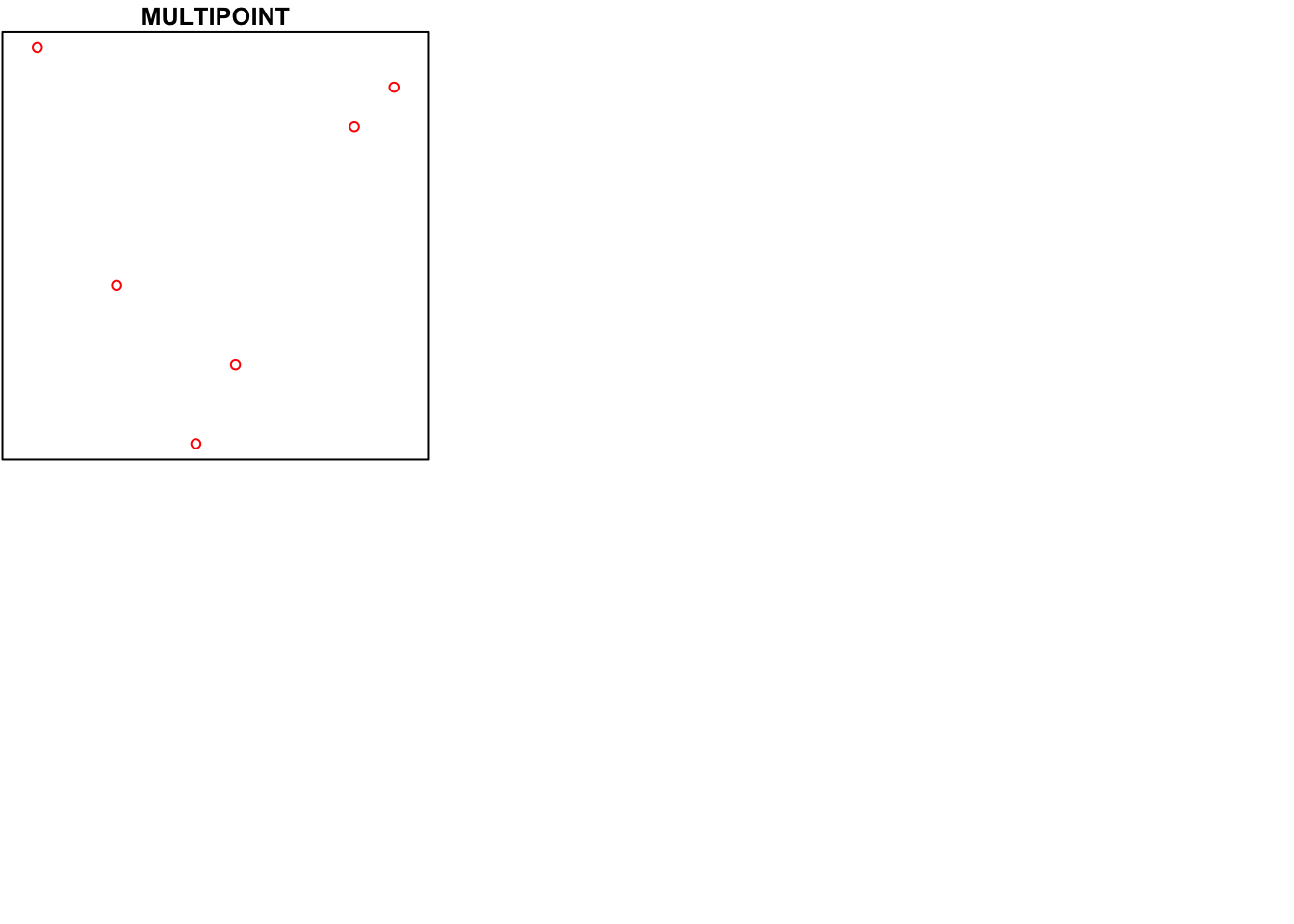

par(mar = c(0.1, 0.1, 1.3, 0.1), mfrow = c(2, 3))
plot(mp, col = 'red')
box()
title("MULTIPOINT")

s1 <- rbind(c(0,3),c(0,4),c(1,5),c(2,5))
(ls <- st_linestring(s1))

## LINESTRING (0 3, 0 4, 1 5, 2 5)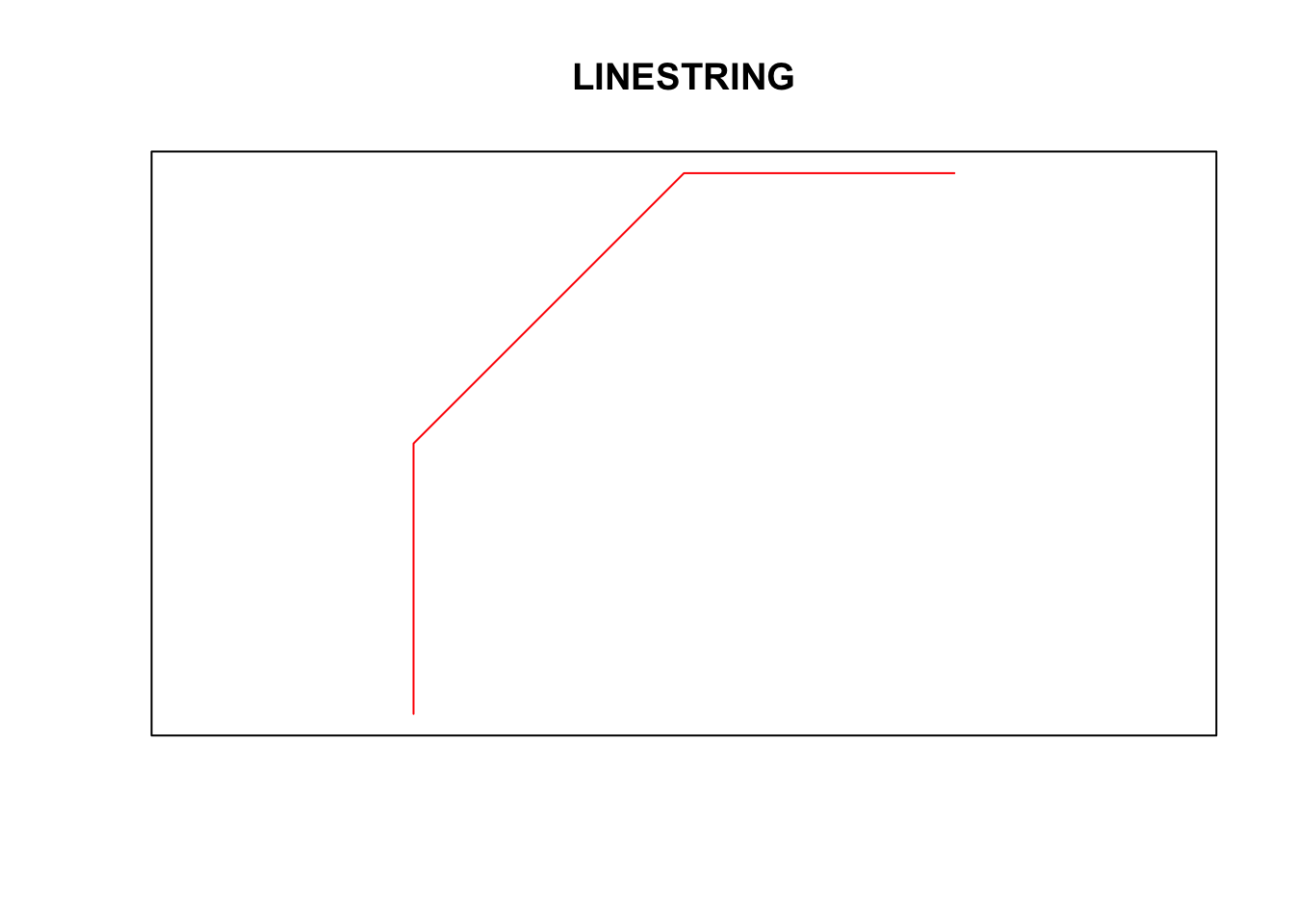

plot(ls, col = 'red')
box()
title("LINESTRING")

s2 <- rbind(c(0.2,3), c(0.2,4), c(1,4.8), c(2,4.8))
s3 <- rbind(c(0,4.4), c(0.6,5))
(mls <- st_multilinestring(list(s1,s2,s3)))

## MULTILINESTRING ((0 3, 0 4, 1 5, 2 5), (0.2 3, 0.2 4, 1 4.8, 2 4.8), (0 4.4, 0.6 5))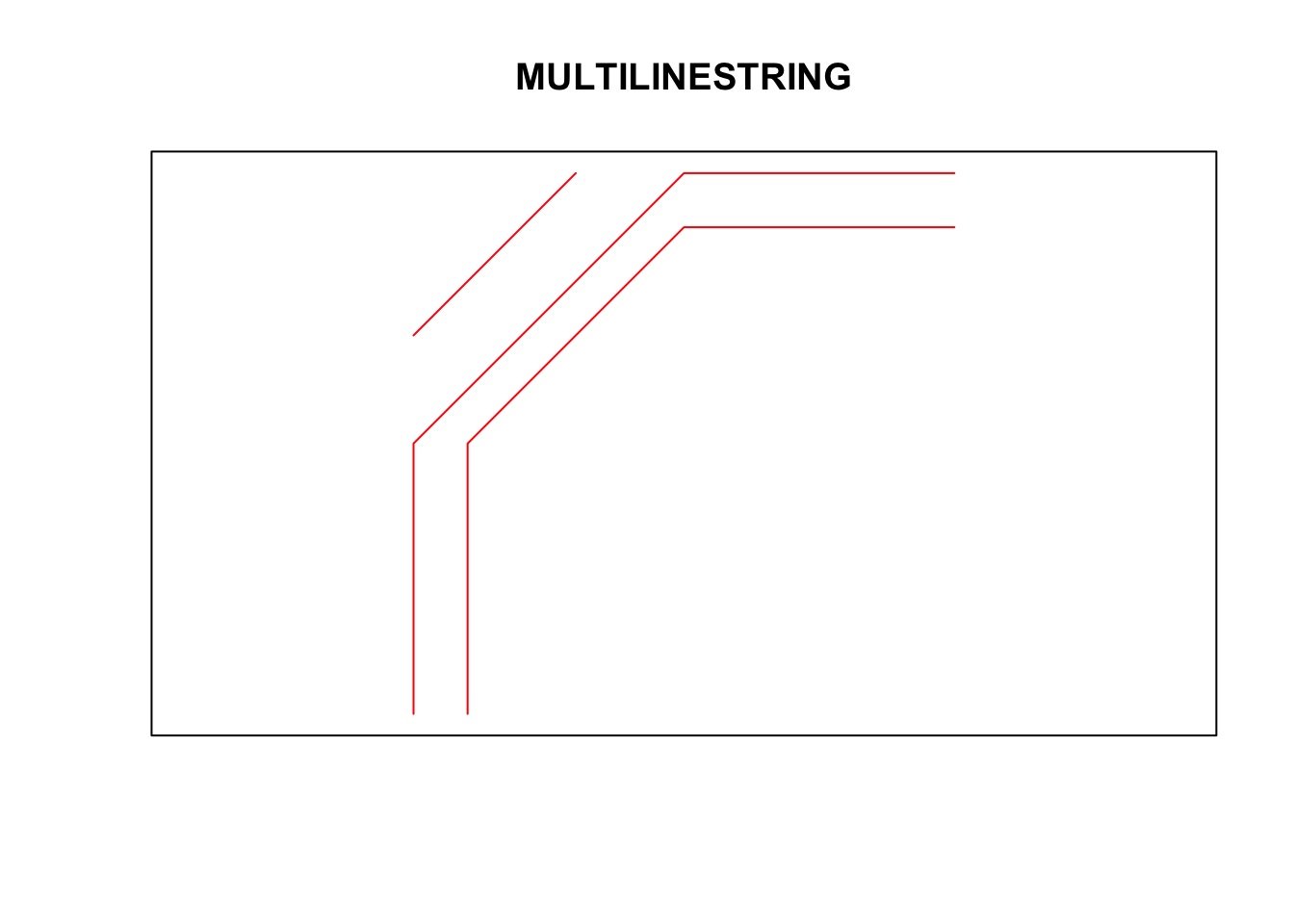

plot(mls, col = 'red')
box()
title("MULTILINESTRING")

Los objetos creados se muestra a continuación:

p1 <- rbind(c(0,0), c(1,0), c(3,2), c(2,4), c(1,4), c(0,0))
p2 <- rbind(c(1,1), c(1,2), c(2,2), c(1,1))
pol <-st_polygon(list(p1,p2))
plot(pol, border = 'red', col = 'grey', xlim = c(0,4))
box()
title("POLYGON")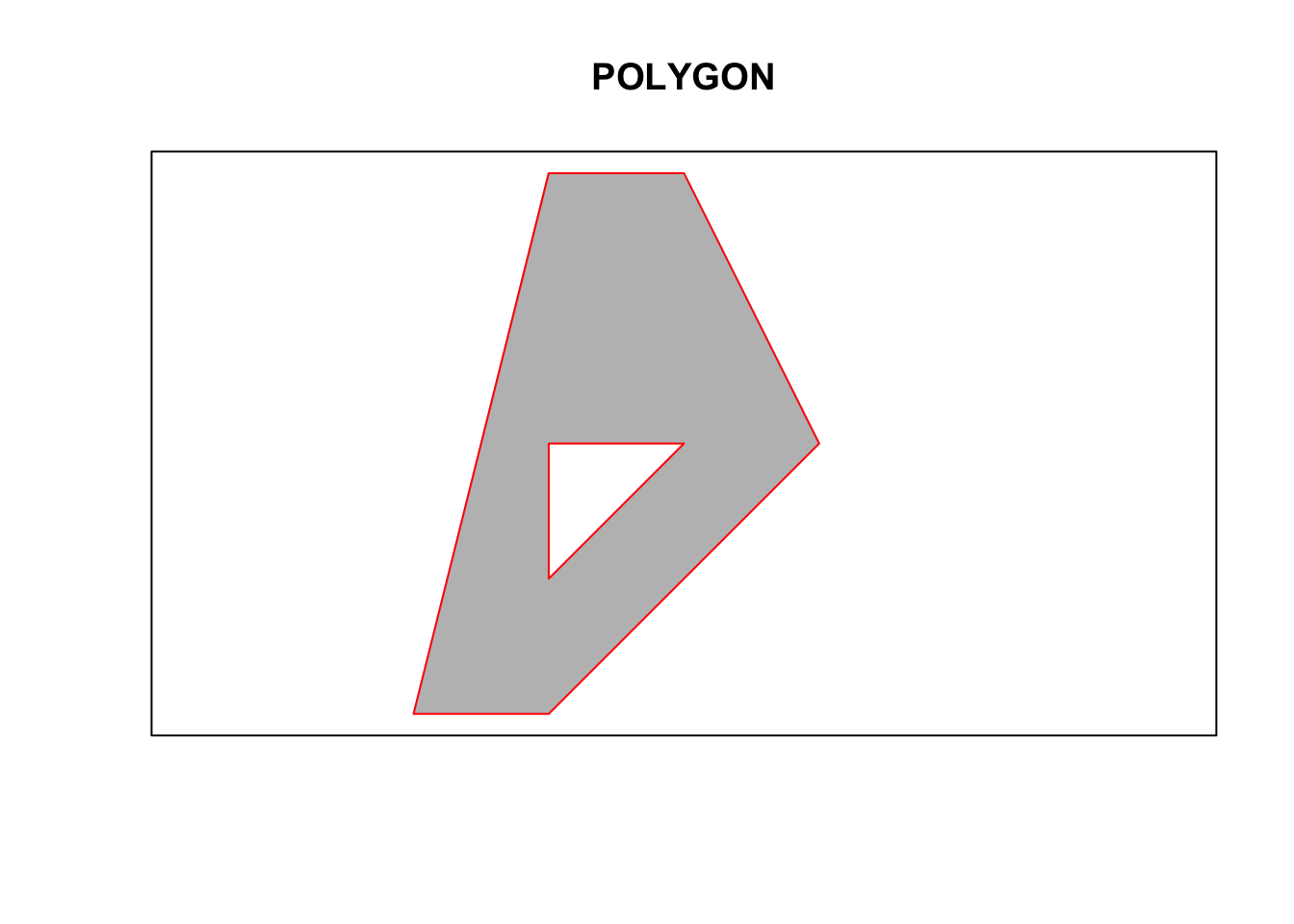

p3 <- rbind(c(3,0), c(4,0), c(4,1), c(3,1), c(3,0))
p4 <- rbind(c(3.3,0.3), c(3.8,0.3), c(3.8,0.8), c(3.3,0.8), c(3.3,0.3))[5:1,]
p5 <- rbind(c(3,3), c(4,2), c(4,3), c(3,3))
(mpol <- st_multipolygon(list(list(p1,p2), list(p3,p4), list(p5))))

## MULTIPOLYGON (((0 0, 1 0, 3 2, 2 4, 1 4, 0 0), (1 1, 1 2, 2 2, 1 1)), ((3 0, 4 0, 4 1, 3 1, 3 0), (3.3 0.3, 3.3 0.8, 3.8 0.8, 3.8 0.3, 3.3 0.3)), ((3 3, 4 2, 4 3, 3 3)))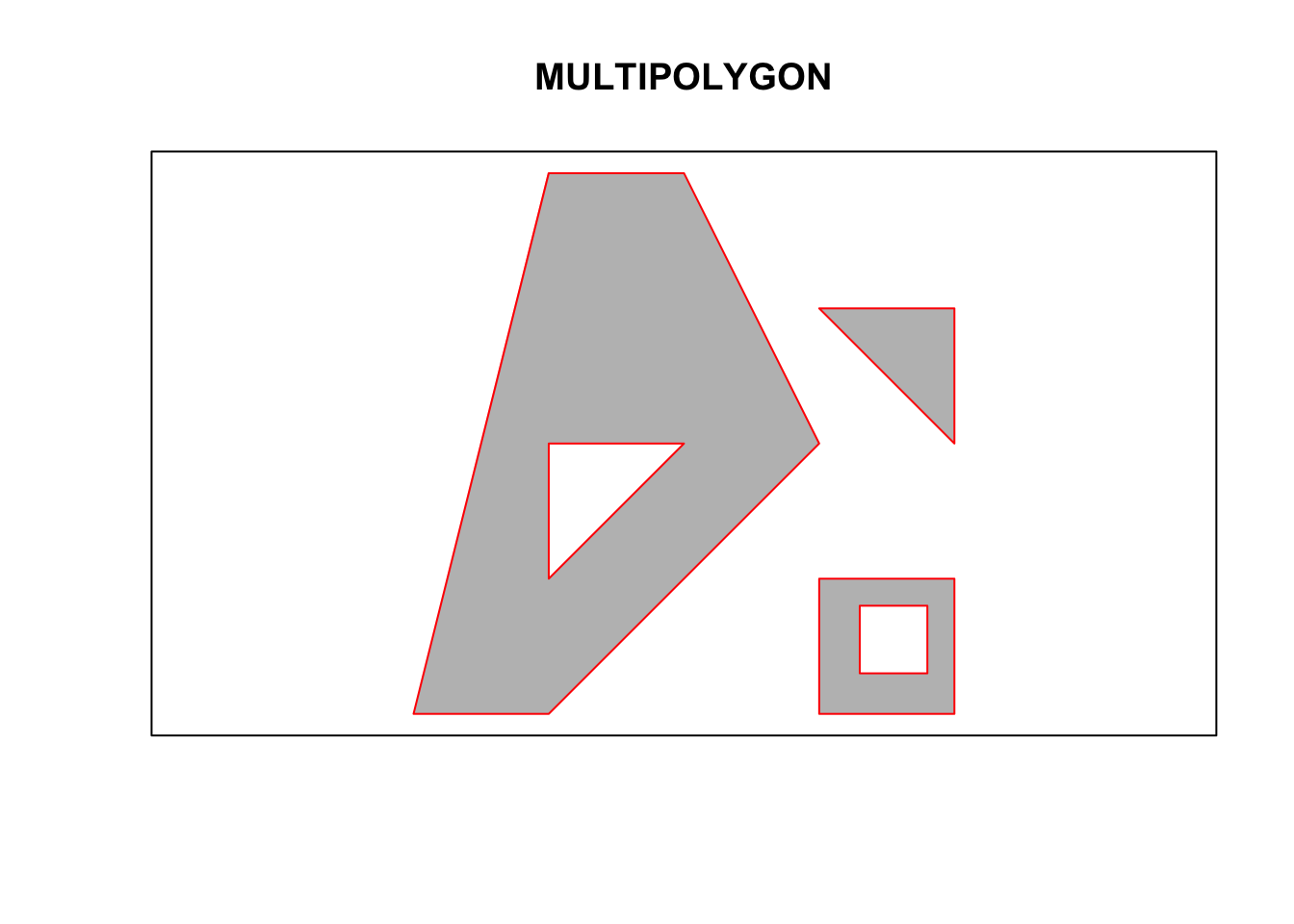

plot(mpol, border = 'red', col = 'grey')
box()
title("MULTIPOLYGON")

(gc <- st_geometrycollection(list(mp, mpol, ls)))

## GEOMETRYCOLLECTION (MULTIPOINT ((3.2 4), (3 4.6), (3.8 4.4), (3.5 3.8), (3.4 3.6), (3.9 4.5)), MULTIPOLYGON (((0 0, 1 0, 3 2, 2 4, 1 4, 0 0), (1 1, 1 2, 2 2, 1 1)), ((3 0, 4 0, 4 1, 3 1, 3 0), (3.3 0.3, 3.3 0.8, 3.8 0.8, 3.8 0.3, 3.3 0.3)), ((3 3, 4 2, 4 3, 3 3))), LINESTRING (0 3, 0 4, 1 5, 2 5))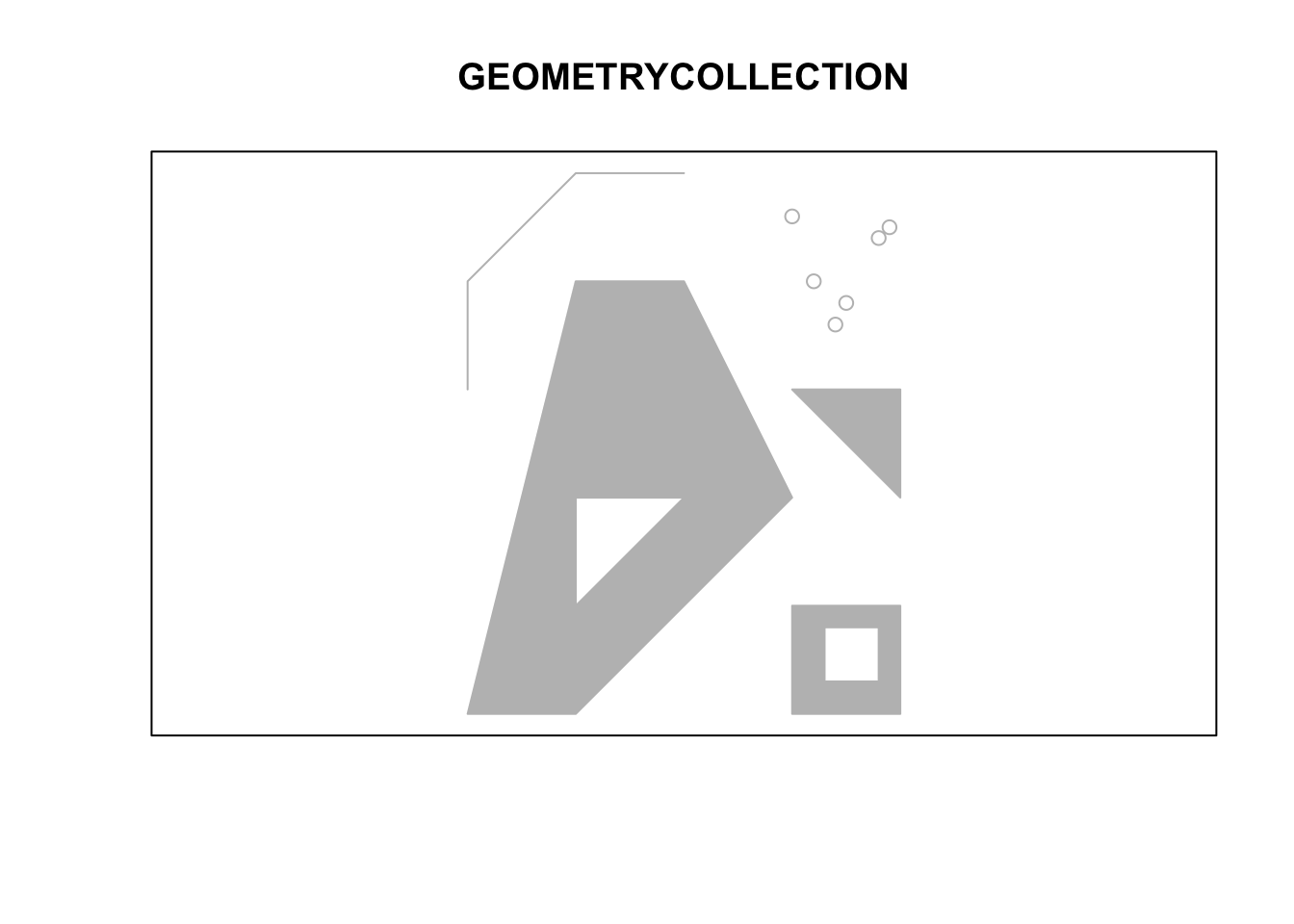

plot(gc, border = 'grey', col = 'grey')
box()
title("GEOMETRYCOLLECTION")

par(mfrow = c(1, 1))

3.6 Lectura y escritura

Como vimos antes, se indica la dirección del archivo en filename:

filename <- system.file("shape/nc.shp", package="sf")
nc <- st_read(filename)

## Reading layer `nc' from data source 
##   `/Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/library/sf/shape/nc.shp' using driver `ESRI Shapefile'
## Simple feature collection with 100 features and 14 fields
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -84.32385 ymin: 33.88199 xmax: -75.45698 ymax: 36.58965
## Geodetic CRS:  NAD27

Podemos omitir la información de salida con quiet=TRUE o usando una función equivalente read_sf:

nc <- st_read(filename,quiet=TRUE)
nc <- read_sf(filename)

Se puede escribir usando:

st_write(nc, "nc.shp")
write_sf(nc, "nc.shp") # con quiet