6 Autocorrelación
Tomado de L. Anselin (1988), capítulo 2 y 3.
Librerías usadas:
spspdep
6.1 El alcance de la Econometría Espacial
6.1.1 Econometría Espacial y Ciencia Regional
Las ciencias regionales se formulan problemáticas sobre el comportamiento espacial de la sociedad, generalmente desde un punto de vista teórico.
Las teorías deben ser expresadas operativamente a través de modelos. Así, los conceptos y relaciones se expresan en especificaciones matemáticas formales, se le da significado a las variables en función de los datos y se necesita hacer estimación, pruebas de hipótesis y predicción. Aquí aparecen las metodologías basadas en estadística o econometría.
El conjunto de técnicas que manejan las peculiaridades causadas por el espacio en el análisis estadístico de los modelos de las ciencias regionales, es el dominio de la econometría espacial.
A principios de 1970, Jean Paelinck es quien acuña el término “econometría espacial”.

En su libro Spatial Econometrics (Paelinck et al. (1979)) señalan 5 características del campo de estudio:
- El rol de la interdependencia espacial en los modelos espaciales.
- La asimetría en las relaciones espaciales.
- La importancia de los factores explicativos localizados en otros espacios.
- Modelización explícita del espacio.
De todos modos, la necesidad de un nuevo campo de estudio es a veces cuestionado debido a que no es siempre claro lo que distingue a la econometría espacial de:
- la econometría estándar, y
- la estadística espacial.
6.1.1.1 Econometría Espacial & Econometría Estándar
Por un lado, algunos aspectos analizados en econometría espacial como la interacción espacial o la densidad usan métodos de la econometría estándar, por lo que en este primer punto no habría mayor distinción.
Por otro lado, en lo espacial hay aspectos específicos de los datos y los modelos en ciencias regionales que imposibilitan la aplicación de los métodos econométricos estándar. A estos aspectos los llamaremos efectos espaciales que son de dos tipos:
- dependencia espacial,
- heterogeneidad espacial.
En términos generales, la dependencia espacial o autocorrelación espacial suele entenderse como la falta de independencia en los datos de corte transversal. La dependencia está en el núcleo de las ciencias regionales, como lo expresa Tobbler (1979) en la primera ley de la geografía:
Todas las cosas están relacionadas entre sí, pero las cosas más próximas en el espacio tienen una relación mayor que las distantes.
En este sentido, la dependencia espacial está determinada por la noción de espacio relativo por lo que el efecto de la distancia adquiere relevancia.
Si se extiende la noción de espacio más allá del espacio en dideano (incluyendo el espacio político, distancia interpersonal, redes sociales, etc), es claro que la dependencia espacial es un fenómeno con una amplia gama de aplicaciones en las ciencias sociales.
La dependencia espacial puede ser causada por dos elementos:
Problemas de medición:
- medición arbitraria de unidades espaciales de observación (zonas censales, fronteras entre regiones)
- Agregación espacial: Presencia de externalidades espaciales y efectos spill over.
Estructura espacial inherente:
- Fenómenos espaciales en terminos de flujos, patrones, estructura, procesos.
Es parcialmente verdad que la dependencia estudiada en series de tiempo es similar a la espacial. Difieren principalmente por la naturaleza multidireccional de la dependencia espacial, mientras que en el tiempo es claramente unidireccional.
En libros clásicos de econometría como Mandala (1977) no se enuncia el problema de autocorrelación espacial. Incluso en métodos de datos de panel se suele dar mayor énfasis a la dimensión temporal mientras la potencial dependencia transversal se asume ausente.
El segundo tipo de efecto espacial, la heterogeneidad espacial, se refiere a la falta de estabilidad sobre el espacio del comportamiento o las relaciones bajo estudio. Más precisamente, implica que las formas funcionales y los parámetros varían con la posición y no es homogéneo en el conjunto de datos.
Por ejemplo, esto ocurre cuando hay regiones ricas en el norte y regiones pobres en el sur. A diferencia de lo que sucede en el caso de la dependencia espacial, la heterogeneidad espacial (en su mayoría), sí puede ser resuelta por técnicas de econometría estándar. Sin embargo, tener conocimiento teórico de la estructura espacial puede llevar a resultados más eficientes.
Los casos donde se combinan flujos espaciales y estructura espacial pueden generar dependencia combinado con heterogeneidad. Este problema solo se resuelve con métodos de econometría espacial.
En resumen:
La econometría espacial es un subconjunto de métodos econométricos que se encarga de aspectos espaciales presentes en observaciones de corte transversal y espacio-temporales. Variables relacionadas a posición, distancia y estructura (topología) son tratadas explícitamente en la especificación, estimación, diagnóstico y predicción de modelos.
6.1.1.2 Econometría Espacial & Estadística Espacial
La distinción entre estos dos campos es menos fácil de hacer. Generalmente depende de la preferencia personal del investigador. Una discusión entre Haining (1986) y Aselin (1986) sugiere esta distinción:
- estadística espacial: (data-driven) motivada por los datos.
- econometía espacial: (model-driven) motivada por el modelo.
Representantes en Estadística Espacial:
- Andrew Cliff y Keith Ord.
- Maurice Stevenson Bartlett.
- Daniel A. Griffith.
- Brian D. Ripley.
Representantes en Econometría Espacial:
- Leen Hordijk.
- Jean Paelinck.
- Leitner Nigkamp.
- Luc Aselin.
Otra distinción suele ser el campo de estudio:
- econometría espacial: economía regional y urbana.
- estadística espacial: fenómenos físicos en biología y geología (análisis de patrones de puntos, Krigging).
6.1.2 Efectos espaciales
6.1.2.1 Dependencia espacial
En la mayoría de ejercicios de ciencias regionales, los datos se obtienen a partir de observaciones que están ordenados en el tiempo y el espacio. En este caso, se puede caracterizar las observaciones a través de sus posiciones (usando un sistema de coordenadas), o por su posición relativa usando una métrica de distancia.
Ejemplos:
- Zonas censales, provincias, etc: población, empleo, actividad económica.
- Mapas digitales: satélites, se hacen rejillas artificiales.
En este contexto, la existencia de dependencia espacial es uno de los temas que debe ser abordado por el investigador. La dependencia espacial puede considerarse como la existencia de una relación funcional entre lo que pasa en un punto del espacio y lo que pasa en otro lugar.
Esto sucede por dos condiciones en general:
- Producto de errores de medición para observaciones en unidades espaciales continuas.
- Existencia de una variedad de fenómenos de interacción espacial (más relacionado a las ciencias regionales y la geografía humana).
En el primer caso, los datos son recogidos a nivel agregado (provincias). Por lo tanto, puede haber poca correspondencia entre el fenómeno estudiado y la delineación geográfica elegida. Como consecuencia, los errores pueden ocurrir. Además los errores tenderán a tener un efecto de desbordamiento (spillover effect) entre unidades espaciales. Como resultado, los errores de la unidad espacial i, tienen probabilidad de estar relacionados con los de la unidad j. Este spillover espacial es una razón para que exista dependencia.
En el contexto de regresión, esto puede llevar a que se tenga términos de perturbación no esféricos (que la distribución normal multivariada de los errores no forme esferas en su contorno proyectado). En la figura, las áreas verdaderas estudiadas son A, B y C, mientras que las mediciones son resultado de agregar 1 y 2. Como resultado la variable observada Y1, será el agregado de YA y parte de YB y la variable observada Y2 será el agregado YC y el resto de YB:
Y1=YA+λYB
Y2=YC+(1−λ)YB
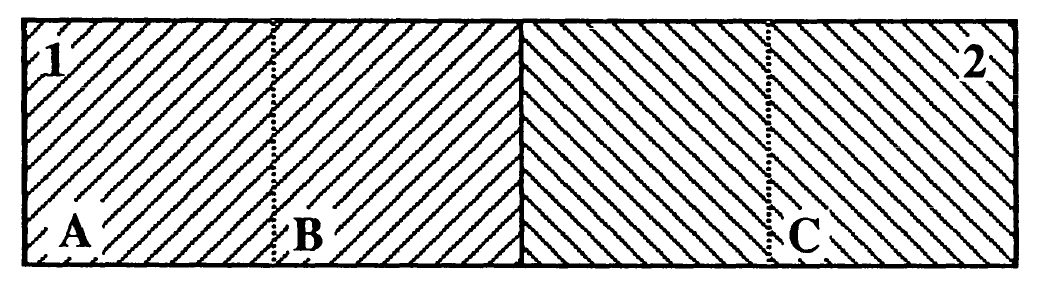
Es posible que esta agregación sufra de errores en el parámetro de ponderación λ, que está presente en Y1, como en Y2. Como resultado, estos errores de medición van a generar un patrón que exhiba dependencia espacial.
El segundo factor que puede causar dependencia espacial es más fundamental y se deriva de la importancia del espacio como un elemento en la estructura explicativa del comportamiento humano.
Las teorías de interacción espacial, procesos de difusión y las jerarquías espaciales arrojan marcos formales para la estructura y dependencia entre fenómenos en diferentes lugares del espacio.
Como resultado, lo que pasa en un punto es determinado (en parte) por lo que pasa en todo el sistema. Esto puede ser expresado formalmente:
yi=f(y1,y2,…,yN)
Aquí, cada observación de la variable y en i∈S (con S como el conjunto de todas las unidades espaciales de observación) está relacionada formalmente a través de la función f a las magnitudes de la variable en otras unidades espaciales del sistema.
Notemos que esa ecuación no es muy útil en lo práctico, dado que nos llevaría a un sistema no identificado, con muchos más parámetros (potencialmente N2−N) que observaciones (N).
Imponiendo una estructura en las relaciones funcionales dentro de f (esto es, una forma particular en el proceso espacial) un número limitado de características de la dependencia espacial puede ser estimado y testeado empíricamente.
Recordemos los dos enfoques de modelización de la dependencia espacial:
- Parte de la teoría, e impone una estructura para la dependencia espacial a priori. Esta estructura se incorpora en una especificación formal del modelo que luego se usa en análisis estadístico.
- Parte de los datos, el investigador trata de inferir la forma funcional apropiada para la dependencia a partir de indicadores, como la autocorrelación y la cross-correlación.
6.1.2.2 Heterogeneidad Espacial
En la literatura se encuentra gran evidencia de falta de uniformidad en los efectos espaciales. Se suele lidiar con este tema mediante
- considerar parámetros que cambian
- coeficientes aleatorios
- formas de cambio estructural
Además, las observaciones en sí mismas no son homogéneas:
- unidades espaciales con diferente área y forma.
- diferentes poblaciones
- diferente desarrollo tecnológico
Todo esto puede verse reflejado en heterocedasticidad. Veamos el problema en la siguiente formulación
yit=fit(xit,βit,ϵit)
i se refiere a la unidad espacial y t al periodo de tiempo. fit es una forma funcional especifica espacio temporal. Este modelo no es operacional porque hay más parámetros que observaciones (problema de identificabilidad de los parámetros).
Para poder hacer estimación e inferencia, y asegurar la identificabilidad, se necesita imponer restricciones sobre el modelo. Hay un trade-off entre especificidad espacial para identificabilidad de los parámetros y la forma funcional dentro de las restricciones de los datos.
6.2 Efectos espaciales, un enfoque formal
6.2.1 Conectividad en el espacio
En el caso de series de tiempo, la idea de una variable rezagada no es ambigua, en el espacio las cosas pueden complicarse.
En lo siguiente se asumen que las observaciones están organizadas en unidades espaciales, que pueden ser puntos en un grid regular o irregular, o regiones en un mapa.
6.2.1.1 Vecinos en el espacio
El concepto de dependencia espacial implica la necesidad de determinar qué otras unidades en el sistema espacial tienen influencia en la unidad particular que se está considerando. Formalmente, esto se expresa en los conceptos de la topología como vecindad y vecino más cercano.
Consideremos un sistema S de N unidades espaciales, etiquetadas i=1,2,…N, y una variable x observada para cada una de estas unidades espaciales. El conjunto de vecinos J para la unidad espacial i, para el cual:
P[xi|x]=P[xi|xJ]
donde xJ es el vector de observaciones para xj∀j∈J, y x es el vector que tiene todos los valores del sistema. De forma menos estricta, el conjunto de vecinos j para la unidad espacial i puede ser:
{j|P[xi]≠P[xi|xj]}
es decir, como las posiciones para las que la probabilidad marginal condicional para xi no es igual a la probabilidad marginal no condicional. Note que hasta el momento no se ha mencionado nada respecto a las posiciones relativas de las unidades espaciales, solo la influencia a través de probabilidades condicionales.
Para introducir el aspecto espacial en estas definiciones de vecinos, se tiene esta definición:
{j|P[xi]≠P[xi|xj],dij<ϵi}
donde dij es una medida de distancia entre i y j en un espacio apropiadamente estructurado (espacios euclideanos, espacios métricos, etc), y ϵi es un punto de corte crítico para cada unidad espacial i, que puede ser el mismo para todas las unidades espaciales.
Esta definción alternativa de vecindad introduce más estructura en el conjunto de datos espaciales, combinando una noción de dependencia estadística (relacionando magnitudes) con la noción de espacio (distancia y posición relativa).
El conjunto de vecinos espaciales puede representarse en una estructura de grafo con una matriz de conectividad asociada.
6.2.1.2 Matrices de contiguidad espacial
Las medidas originales de dependencia propuestas por Moran y Geary se basaban en contiguidad binaria entre unidades espaciales.
Si dos unidades espaciales tienen un borde común de longitud no nula, se consideran contiguos, y se asigna el valor 1.
Esta definición obviamente asume la existencia de un mapa del que los bordes pueden discernirse. Sin embargo, cuando se ubican en un grid, la contiguidad no es única.
Por ejemplo, considere la siguiente figura con sus respectivos centroides:
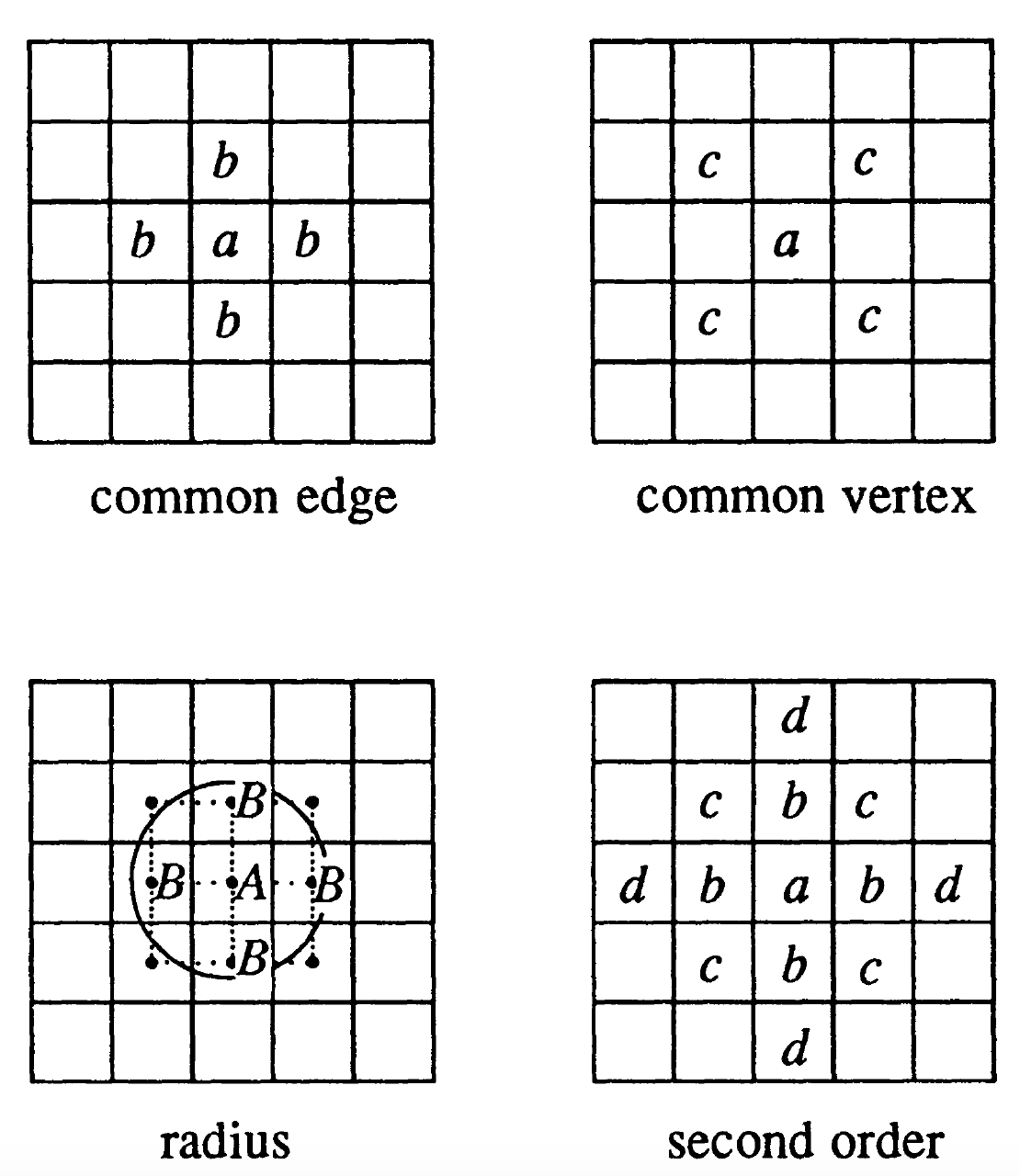
Un borde común entre la celda a y celdas aledañas puede considerarse de diferentes maneras. Por ejemplo:
- Si se toma el criterio del lado común (common edge), las celdas b son contiguas. Análogo al movimiento de la torre en ajedrez (rook case).
- Si se toma el criterio de vértice común (common vertex), entonces las celdas c son contiguas. Análogo al movimiento del alfil en ajedrez (bishop case).
- Una combinación de las dos, donde las celdas b y c resultan contiguas. Análogo al movimiento de la reina en ajedrez (queen case).
- Criterio del camino más corto como criterio de contigüidad (radius). Los puntos se consideran vecinos si están dentro de un determinado radio o distancia uno de otro. Los puntos B están dentro del radio d del centroide A se pueden considerar vecinos de A.
También se puede considerar órdenes de contiguidad. Esto se logra de manera recursiva:
- definiendo el orden de contigüidad k-ésimo cuando las unidades espaciales son contiguas de primer orden a la unidad espacial de orden (k−1)-ésimo.
En un grid cuadrado, esto es una serie de bandas concéntricas alrededor de la unidad espacial en consideración. Por ejemplo: las celdas c y d son contiguas de segundo orden a a de acuerdo al criterio de la torre, porque c y d son contiguos de primer orden a b.
La estructura espacial resultante se expresa formalmente en una matriz de contiguidad o conectividad. Esta matriz tiene tantas filas y columnas como unidades espaciales existan. En cada fila, una columna distinta de cero corresponde a unidades espaciales contiguas.
Por ejemplo, las 9 celdas en el centro de la figura anterior (numeradas de izquierda a derecha y de arriba hacia abajo) se presenta en la siguiente tabla usando el criterio de la torre.
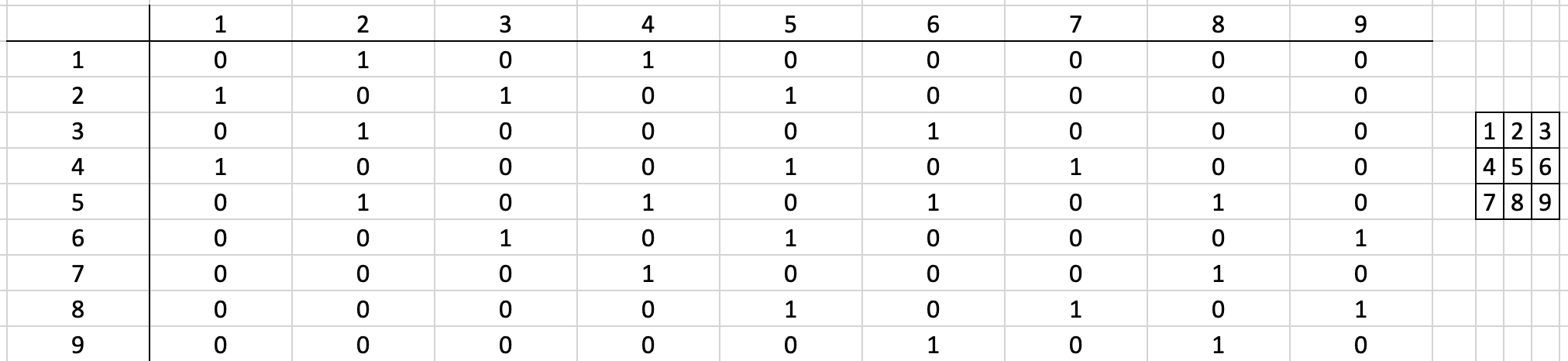
Claramente, el tener varias formas de definir contiguidad no es una cualidad deseable:
- Es una representación limitada de las posibles interacciones espaciales que pueden formularse.
- La misma matriz de contigüidad puede representar varios arreglos de unidades espaciales.
6.2.1.3 Matrices de pesos espaciales
La idea de contiguidad binaria fue extendida para incluir interacciones potenciales entre dos unidades espaciales. La determinación de una especificación apropiada para esta matriz, wij, es uno de los temas metodológicos más difíciles y controversiales en econometría espacial.
La sugerencia original de Cliff y Ord consiste en usar una combinación medidas de distancia (distancia inversa, o exponenciales negativos de la distancia) y la longitud relativa del borde común entre dos unidades espaciales, en el sentido del porcentaje en el total de la longitud del borde que es ocupado por la otra unidad en consideración.
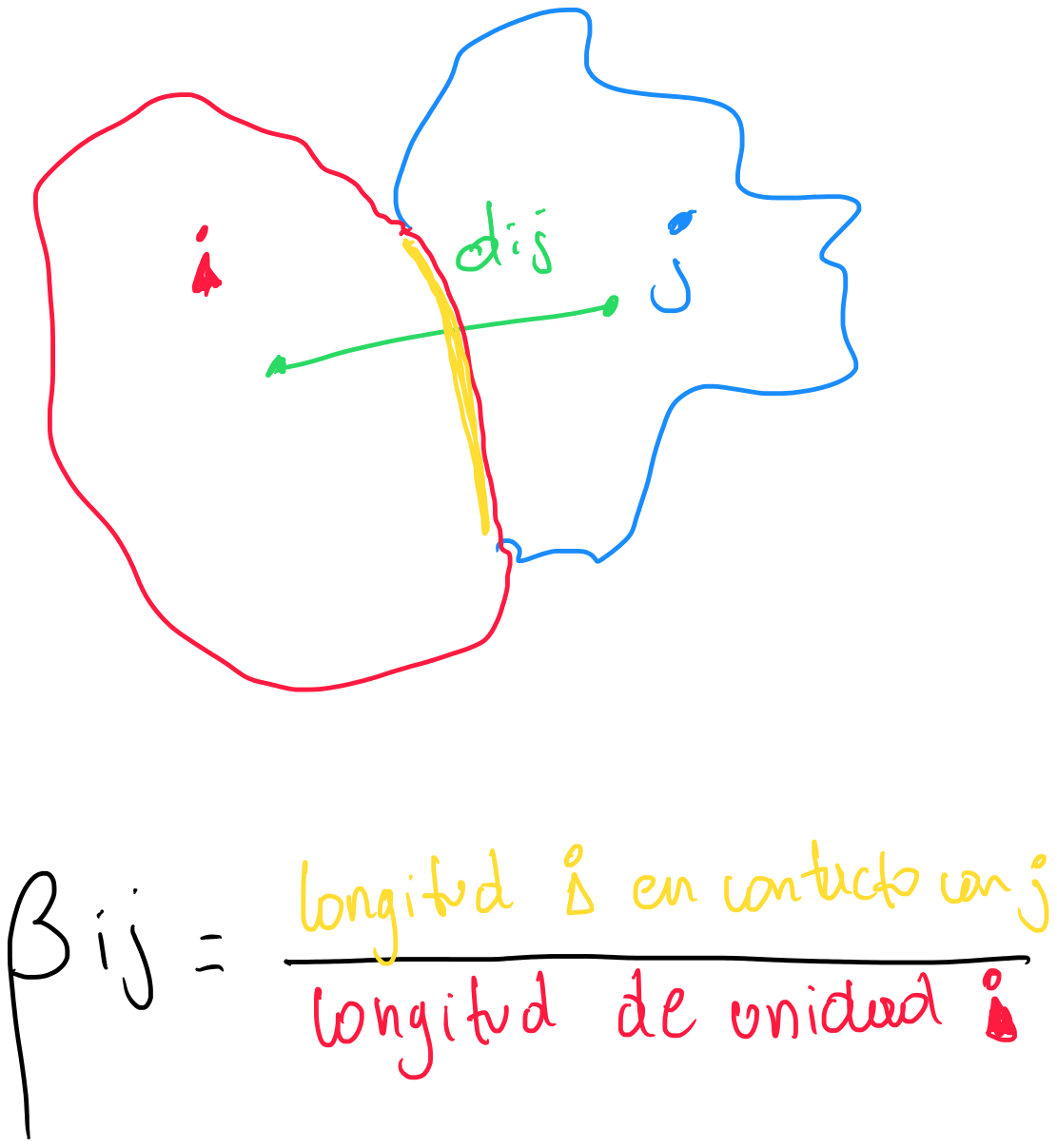
Los pesos resultantes serán asimétricos, a menos que ambas unidades espaciales tengan la misma longitud de borde. Formalmente.
wij=[dij]−a[βij]b
con dij como la distancia entre la unidad espacial i y j, βij como la proporción del borde de la unidad i que está en contacto con la unidad j, y a y b como parámetros.
De manera similar, Dacey sugirió pesos que también toman en cuenta el área relativa de las unidades espaciales:
wij=dijαiβij
con dij como un factor binario de contigüidad, αi como el porcentaje de la unidad espacial i sobre el total de todas las unidades espaciales en el sistema, y βij como la medida de borde usada antes.
Ambos pesos están estrechamente vinculados a las características físicas de las unidades espaciales en un mapa. Al igual que con las medidas de contigüidad binaria, son menos útiles cuando las unidades espaciales consisten en puntos, ya que entonces las nociones de longitud y área del borde son en gran medida artificiales y están determinadas por un algoritmo de teselación particular. También son menos significativos cuando el fenómeno de interacción espacial en consideración está determinado por factores tales como variables puramente económicas, que pueden tener poco que ver con la configuración espacial de los límites en un mapa físico.
En este sendito, por ejemplo Bodson y Peeters proponen unos pesos de accesibilidad (calibrados entre 0 y 1), que combina en una función logística la influencia de varios canales de comunicación entre unidades espaciales, como carreteras, tren, y otros enlaces de comunicación. Formalmente,
wij=∑jkj(a1+be−cjdij) donde kj muestra la importancia relativa del medio de comunicación j. La suma es sobre los j medios de comunicación, que separan las unidades espaciales por una distancia dij. a, b y cj son parámtros a estimarse.
En la mayoría de las aplicaciones de la ciencia regional, la matriz de ponderaciones se basa en alguna combinación de relaciones de distancia y contigüidad simple. Las distancias involucradas son en el sentido más general y pueden basarse en el tiempo de viaje, o derivarse de un análisis de escala multidimensional. En la mayoría de las aplicaciones sociológicas del análisis espacial, la matriz de peso está determinada por conceptos de la teoría de redes sociales.
Un problema importante resulta de la incorporación de parámetros en los pesos. Normalmente, estos pesos se consideran exógenos y los valores de los parámetros se determinan a priori, o en un paso separado del resto del análisis espacial. Esto crea problemas para la estimación e interpretación de los resultados. En particular, podría conducir potencialmente a la inferencia de relaciones espurias, ya que la validez de las estimaciones está condicionada previamente por la medida en que la estructura espacial se refleja correctamente en las ponderaciones. Más importante aún, podría resultar en un razonamiento circular, en el que la estructura espacial, que el analista puede desear descubrir en los datos, debe suponerse conocida antes de llevar a cabo el análisis de datos. En el contexto de pruebas de hipótesis, dado que la hipótesis nula es de independencia espacial, la matriz de ponderaciones debe relacionarse con la hipótesis alternativa relevante de dependencia espacial, con el fin de maximizar la potencia de la prueba. Sin embargo, incluso con una matriz de ponderación especificada incorrectamente, el rechazo de la hipótesis nula solo implicará una falta de independencia, y no un tipo particular de dependencia. Aunque la potencia de la prueba se verá afectada, la posibilidad de conclusiones falsas no es tan grande como en la especificación funcional de un modelo.
6.2.1.4 Operadores de rezago espacial
El objetivo del uso de una matriz de ponderación espacial en la especificación de modelos econométricos espaciales es relacionar una variable en un punto del espacio con las observaciones de esa variable en otras unidades espaciales del sistema.
En un contexto de series de tiempo, esto se logra mediante el uso de un operador de retardo o rezago, que desplaza la variable en uno o más períodos en el tiempo. Por ejemplo:
yt−k=Lky muestra la variable y rezagada k periodos desde t, como la potencia k-ésima del operador de rezagos L.
En el espacio, debido a las infinitas direcciones que se puede girar, las cosas se complican. Por ejemplo, considere la siguiente figura:
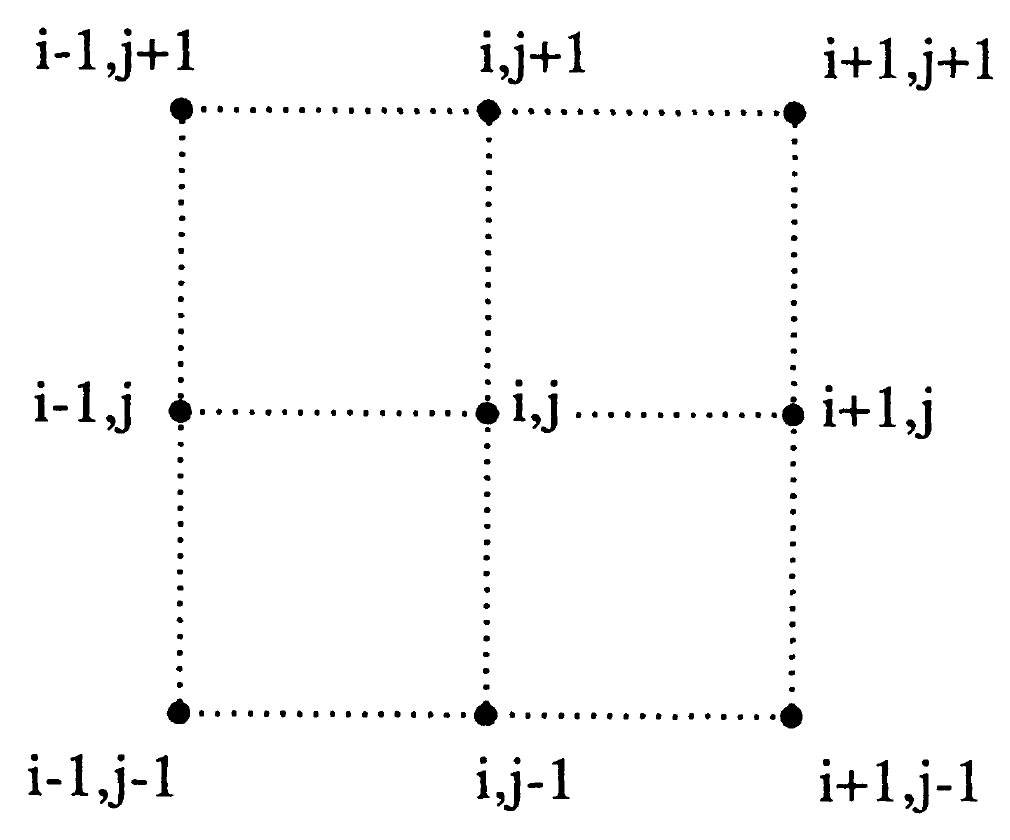
La variable x observada en la posición i,j puede girarse de las siguientes maneras:
- usando el criterio de la torre:
xi−1,j;xi,j−1;xi+1,j;xi,j+1;
- usando el criterio del alfil:
xi−1,j−1;xi+1,j−1;xi+1,j+1;xi−1,j+1;
Para el criterio de la reina se tiene 8 posibles movimientos.
En las aplicaciones no suele existir una justificación apriori para guiar la elección de la dependencia. Además, si es un grid irregular las posibilidades son infinitas y el número de grados de libertad disponibles pueden ser insuficientes para tener estimaciones eficientes.
Este problema se resuelve considerando una suma ponderada de todos los valores que pertenecen a una clase de contigüidad, en lugar de tomarlos de manera individual. Los términos de la suma se obtienen multiplicando las observaciones por el peso asociado de la matriz de pesos espaciales. Formalmente:
Lsxi=∑jwijxj∀j∈Ji
donde Ls es el operador de rezago asociado con la clase de contigüidad s para i, y wij son las ponderaciones espaciales. En notación matricial:
Lsx=Wsx.
Los pesos wij se consideran como dados, pero estimar los pesos y la asociación estadísitica en conjunto se vuelve un problema no lineal. Al fijarlos previamente el problema es lineal.
Un rezago espacial menos restrictivo puede construirse de la noción de accesibilidad potencial, como:
fi=∑jq(dij,θ)xj
donde fi es el potencial en i, y q es una función de distancia dij entre i y j, parametrizada en términos de un vector de coeficientes θ. Dado que la expresión resultante es no lineal, la estimación y las pruebas de hipótesis pueden ser más complejas.
6.2.1.4.1 En R
Creamos un teselado regular:
library(sp)
x <- c(1,2,2,1,1)
y <- c(1,1,2,2,1)
vl1 <- cbind(x,y);vl2 <- cbind(x-1,y+1);vl3 <- cbind(x,y+1);vl4 <- cbind(x+1,y+1);vl5 <- cbind(x-1,y);vl6 <- cbind(x+1,y);vl7 <- cbind(x-1,y-1);vl8 <- cbind(x,y-1);vl9 <- cbind(x+1,y-1)
Sr1 <- sp::Polygon(vl1)
Sr2 <- sp::Polygon(vl2)
Sr3 <- sp::Polygon(vl3)
Sr4 <- sp::Polygon(vl4)
Sr5 <- sp::Polygon(vl5)
Sr6 <- sp::Polygon(vl6)
Sr7 <- sp::Polygon(vl7)
Sr8 <- sp::Polygon(vl8)
Sr9 <- sp::Polygon(vl9)
Srs1 <- sp::Polygons(list(Sr1), "s1")
Srs2 <- sp::Polygons(list(Sr2), "s2")
Srs3 <- sp::Polygons(list(Sr3), "s3")
Srs4 <- sp::Polygons(list(Sr4), "s4")
Srs5 <- sp::Polygons(list(Sr5), "s5")
Srs6 <- sp::Polygons(list(Sr6), "s6")
Srs7 <- sp::Polygons(list(Sr7), "s7")
Srs8 <- sp::Polygons(list(Sr8), "s8")
Srs9 <- sp::Polygons(list(Sr9), "s9")
SpP <- SpatialPolygons(list(Srs1,Srs2,Srs3,Srs4,Srs5,Srs6,Srs7,Srs8,Srs9))
sp::plot(SpP, col = 1:9, pbg="white")
text(coordinates(SpP),paste("s",1:9,sep = ""),col = "white")
Calculamos los vecinos del teselado:
## Neighbour list object:
## Number of regions: 9
## Number of nonzero links: 24
## Percentage nonzero weights: 29.62963
## Average number of links: 2.666667## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## s1 0 0 1 0 1 1 0 1 0
## s2 0 0 1 0 1 0 0 0 0
## s3 1 1 0 1 0 0 0 0 0
## s4 0 0 1 0 0 1 0 0 0
## s5 1 1 0 0 0 0 1 0 0
## s6 1 0 0 1 0 0 0 0 1
## s7 0 0 0 0 1 0 0 1 0
## s8 1 0 0 0 0 0 1 0 1
## s9 0 0 0 0 0 1 0 1 0
## attr(,"call")
## nb2mat(neighbours = wr, style = "B", zero.policy = TRUE)Graficamos los enlaces entre los polígonos:
sp::plot(SpP, col='gray', border='blue')
xy <- coordinates(SpP)
sp::plot(wr, xy, col='red', lwd=2, add=TRUE)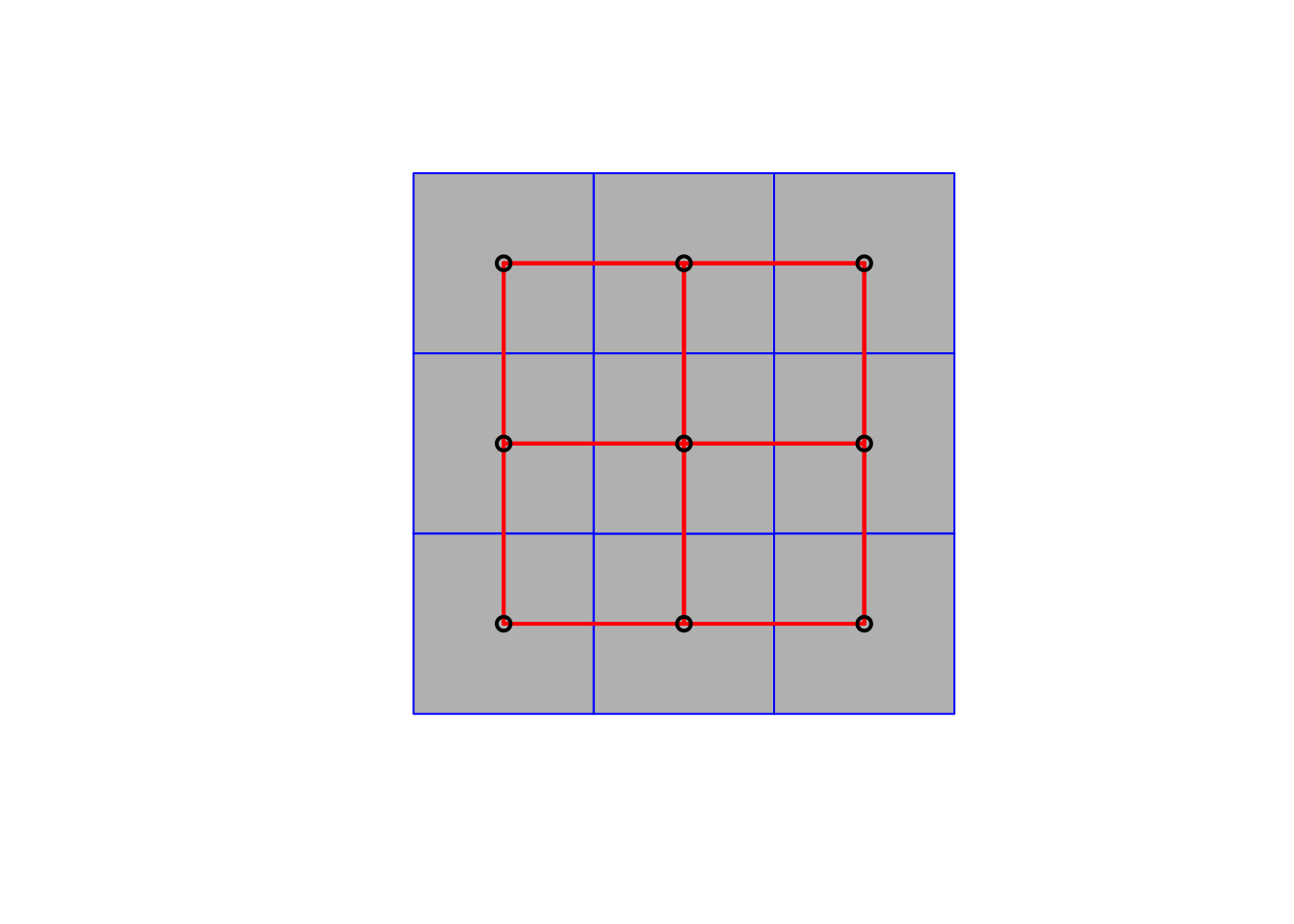
Otras formas de influencia entre polígonos:
- Basado en la distancia:
# dnearneigh: Neighbourhood contiguity by distance
wd10 <- dnearneigh(xy, 0, 10)
wd25 <- dnearneigh(xy, 0, 25, longlat=TRUE)- Vecino más cercano:
- Rezago de segundo orden:
wr2 <- wr
for (i in 1:length(wr)) {
lag1 <- wr[[i]] # vecinos de i
lag2 <- wr[lag1] # tomo a los vecinos de los vecinos de i
lag2 <- sort(unique(unlist(lag2))) # val unicos de vec de vec de i
lag2 <- lag2[!(lag2 %in% c(wr[[i]], i))] #evito el doble conteo
wr2[[i]] <- lag2
}Graficamos todas las influencias con la función plotit:
plotit <- function(nb, lab='') {
sp::plot(SpP, col='gray', border='white')
sp::plot(nb, xy, add=TRUE, pch=20)
text(2.5, 2.8, paste0('(', lab, ')'), cex=1.25)
}
par(mfrow=c(2, 3), mai=c(0,0,0,0))
plotit(wr, 'adjacency')
plotit(wr2, 'lag-2 adj.')
plotit(wd10, '10 km')
plotit(wd25, '25 km')
plotit(k3, 'k=3')
plotit(k6, 'k=6')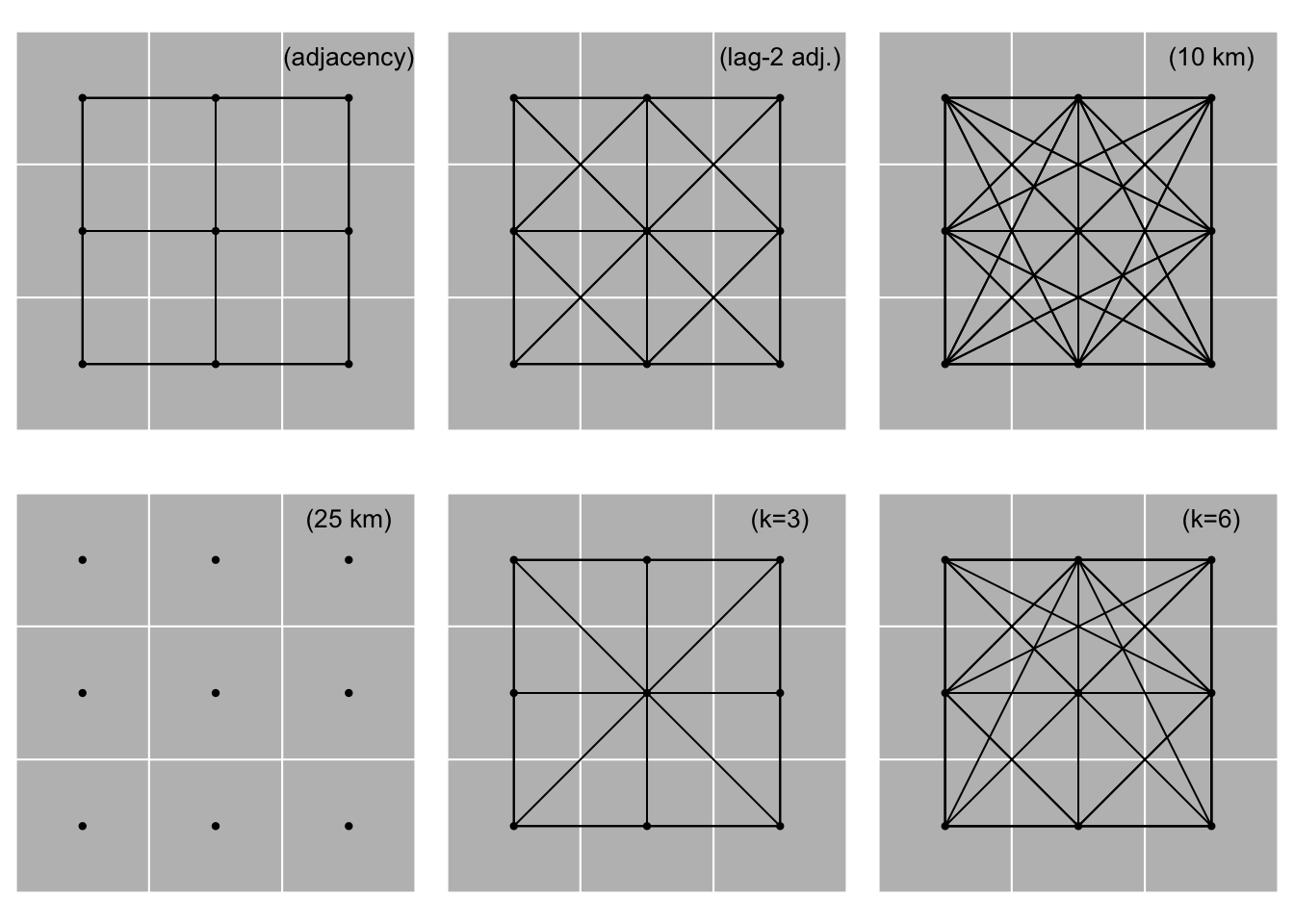
6.2.1.5 Propiedades de las matrices de ponderaciones espaciales
La intrincada relación entre las medidas de asociación espacial y la elección de una matriz de conectividad tiene varias implicaciones para el desempeño de los estimadores y las estadísticas de prueba.
Desde un punto de vista puramente metodológico, es importante relacionar las propiedades de estas diversas técnicas con el grado de conexión espacial o dependencia espacial inherente que puede estar presente en los datos. Esto es particularmente relevante para el diseño de experimentos de simulación de Monte Carlo para evaluar el desempeño de estimadores y pruebas en situaciones que imitan contextos empíricos realistas.
6.2.2 Estadístico de Autocorrelación: una forma general
Medida de similaridad
El producto vectorial: yiyj
- Bajo aleatoriedad, el producto vectorial no es sistemáticamente grande o pequeño.
- Cuando valores altos están sistemáticamente juntos, el producto vectorial será grande y vice versa.
Medidas de DIsimilaridad
Dos medidas comunides de disimilaridad son:
- diferencia al cuadrado (yi−yj)2
- diferencia absoluta |yi−yj|
- Bajo aleatoriedad, la medida de disimilitud no es sistemáticamente grande o pequeño.
- Cuando valores altos están sistemáticamente juntos, el producto vectorial será grande y vice versa.
Similaridad posicional
Los pesos espaciales wij formalizan la noción de vecinos (vecinos en algún sentido).
Una forma en que se puede plantear un estadístico general de autocorrelación como
suma de todas las parejas del producto de una medida de similaridad de la variable y un indicador de vecindad (peso espacial)
Estadístico = \sum_i\sum_jf(x_ix_j)w_{ij}
donde f(x_ix_j) denota una forma funcional de la similaridad entre i y j para la variable x. w_{ij} es el peso espacial entre i y j.
