8 Heterogeneidad
Librerías usadas
spdepggplot2
Como se mencionó en 6.1.1.1, la heterogeneidad espacial se puede abordar desde métodos de la econometría estándar. A continuación, la exploraremos desde el gráfico de Moran y desde la prueba de Levene habiendo agregado las unidades espaciales.
8.1 Gráfico de moran
Importamos los datos y hacemos el gráfico de Moran:
# leo los datos
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/VABNoPetroleroCantones2007-2019.csv"
datos <- read.csv(uu,sep = ",")
datos$COD_CANT[nchar(datos$COD_CANT)==3] = paste("0",datos$COD_CANT[nchar(datos$COD_CANT)==3],sep = "")
datos <- subset(datos,datos$YEAR == 2019)
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/proyeccion_cantonal_total_2010-2020.csv"
poblacion <- read.csv(uu,sep = ";")
poblacion$CODIGO[nchar(poblacion$CODIGO)==3] = paste("0",poblacion$CODIGO[nchar(poblacion$CODIGO)==3],sep = "")
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/NBI_PER_CANT.csv"
NBI <- read.csv(uu, sep = ";")
NBI$CODIGO[nchar(NBI$CODIGO)==3] = paste("0",NBI$CODIGO[nchar(NBI$CODIGO)==3],sep = "")
datos <- merge(datos,poblacion[,c("CODIGO","A_2019")],by.x = "COD_CANT",by.y = "CODIGO",all.x = TRUE)
datos <- merge(datos,NBI[,c("CODIGO","POBRES_P")],by.x = "COD_CANT",by.y = "CODIGO",all.x = TRUE)
datos$VAB_PC <- datos$VAB/datos$A_2019 #miles de USD / pob
# setwd("~/Documents/DataBase/MAPAS/2012_nxcantones")
uu <- "https://github.com/vmoprojs/DataLectures/raw/master/SpatialData/2012_nxcantones.zip"
poligonos <- read_git_shp(uu)## Reading layer `nxcantones' from data source
## `/private/var/folders/0p/n_r_hl095sv7nktfp_8n9n_80000gn/T/RtmpJEd1fK/file5c5530aee693/nxcantones.shp'
## using driver `ESRI Shapefile'
## Simple feature collection with 224 features and 6 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -732143.5 ymin: 9445216 xmax: 1147852 ymax: 10189400
## Projected CRS: WGS 84 / UTM zone 17Spoligonos <- poligonos[poligonos$DPA_PROVIN!="90",]
poligonos <- poligonos[poligonos$DPA_PROVIN!="20",]
poligonos = merge(poligonos,datos,by.x ="DPA_CANTON",by.y = "COD_CANT",all.x=TRUE)
# Me quedo con los datos que no son perdidos:
poligonos <- poligonos[!is.na(poligonos$POBRES_P),]
library(spdep)
set.ZeroPolicyOption(TRUE)## [1] TRUE# Se construye la lista de vecinos
cont.nb <- poly2nb(poligonos)
# Se construye la matriz de pesos espaciales
cont.listw <- nb2listw(cont.nb, style="W",zero.policy = TRUE)Vemos el gráfico que también se muestra en 7.2.4 pero se le ha agregado un suavizamiento LOESS (suavizado de ponderación local) y una tendencia lineal.
variable <- poligonos$POBRES_P
variable.std <- ((variable-mean(variable))/sd(variable))
mp <- moran.plot(variable.std, cont.listw, labels=as.character(poligonos$DPA_CANTON),pch=19,quiet=TRUE,plot=FALSE) #
library(ggplot2)
xname <- attr(mp, "xname")
ggplot(mp, aes(x=x, y=wx)) + geom_point(shape=1) +
geom_smooth(formula=y ~ x, method="loess") +
geom_smooth(formula=y ~ x, method="lm",se = FALSE,colour = "lightblue") +
geom_hline(yintercept=mean(mp$wx), lty=2) +
geom_vline(xintercept=mean(mp$x), lty=2) + theme_minimal() +
geom_point(data=mp[mp$is_inf,], aes(x=x, y=wx), shape=9) +
geom_text(data=mp[mp$is_inf,], aes(x=x, y=wx, label=labels, vjust=1.5)) +
xlab(xname) + ylab(paste0("Rezago espacial ", xname))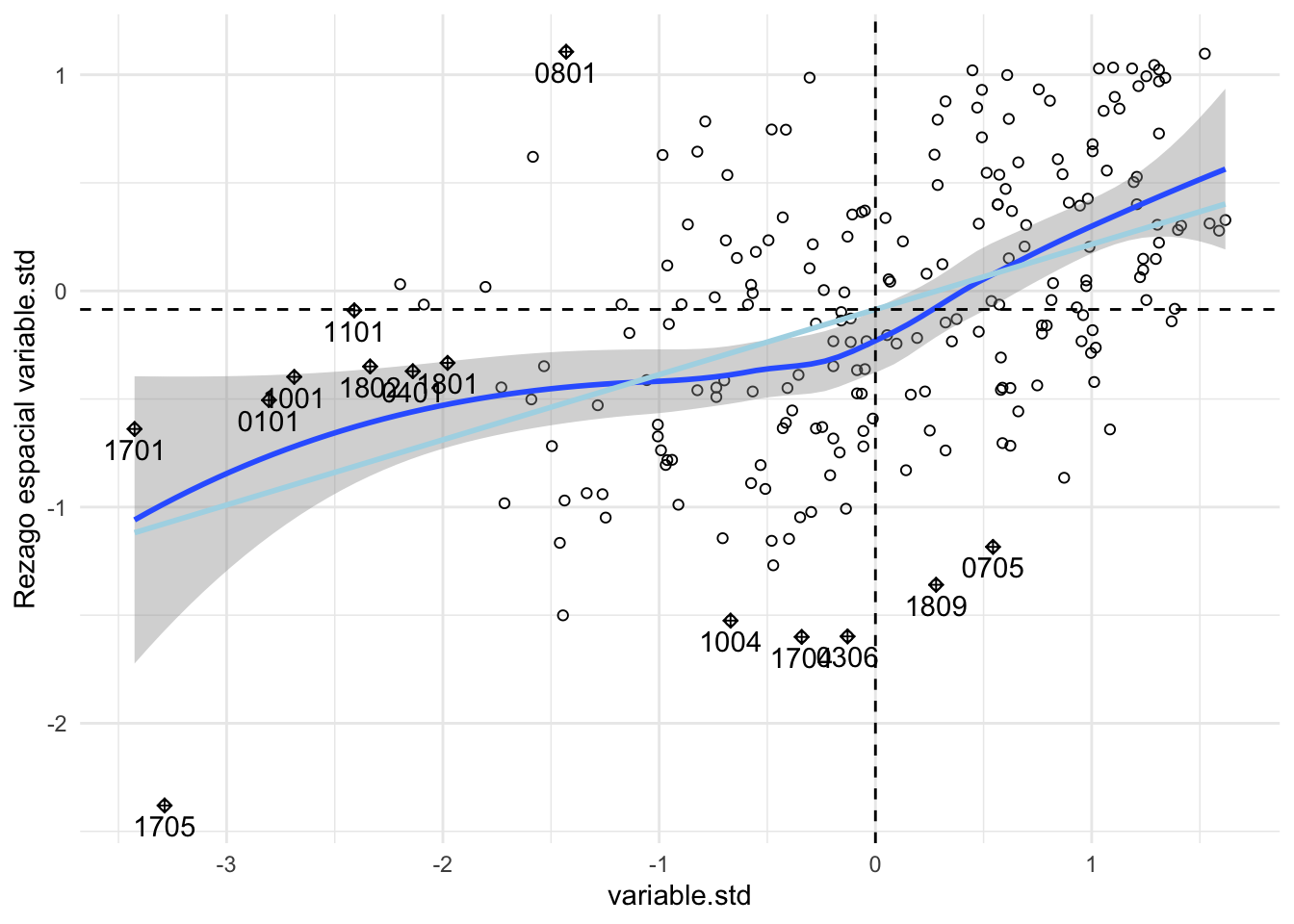
El suavizador de Loess se puede explorar para identificar posibles rupturas estructurales en el patrón de autocorrelación espacial, es decir, heterogeneidad espacial.
La tendencia lineal indica es el punto de referencia sobre el cual podemos comparar los resultados del suavizamiento local. Mientras más nos alejamos de la tendencia lineal, se tiene evidencia de mayor heterogeneidad en los datos (Luc Anselin, Syabri, and Kho (2010)).
Por ejemplo, en algunas partes del conjunto de datos, la curva puede ser muy pronunciada y positiva, lo que sugiere una fuerte autocorrelación espacial positiva, mientras que en otras partes, puede ser plana, lo que indica que no hay autocorrelación.
En nuestro ejemplo, la pendiente negativa de la curva para los valores más pequeños de \(z\) (hasta \(-1\) aproximadamente) sugiere un efecto de los valores atípico (modificando la pendiente I de Moran). Esto se puede evaluar de manera más formal mediante el estudio de valores atípicos e influyentes.
¿Qué pasaría si nos quedamos son los valores marcados como influyentes?
8.2 Agregación espacial
Otra forma en la que exploramos la heterogeneridad espacial es mediante la agregación de unidades espaciales. De este modo se puede hacer pruebas de diferencias en medias y varianzas.
Por ejemplo, en el caso ecuatoriano podemos agregar la información en Costa, Sierra y Amazonía.
costa <- c("07","08","09","12","13","23","24")
sierra <- c("01","02","03","04","05","06","10","11","17","18")
amazonia <- c("14","15","16","19","21","22")
fil <- poligonos$DPA_PROVIN %in% costa
poligonos$Region[fil] <- "Costa"
fil <- poligonos$DPA_PROVIN %in% sierra
poligonos$Region[fil] <- "Sierra"
fil <- poligonos$DPA_PROVIN %in% amazonia
poligonos$Region[fil] <- "Amazonia"
datH <- poligonos[,c("Region","POBRES_P")]
kruskal.test(datH$POBRES_P,datH$Region)##
## Kruskal-Wallis rank sum test
##
## data: datH$POBRES_P and datH$Region
## Kruskal-Wallis chi-squared = 16.192, df = 2, p-value = 0.0003048La prueba de Kruskal-Wallis tiene la hipótesis nula la igualdad en las medias de las distribuciones. Vemos que se rechaza esta hipótesis en nuestro conjunto de datos.
Veamos la exploración gráfica de la distribución de la variable sobre las regiones analizadas:
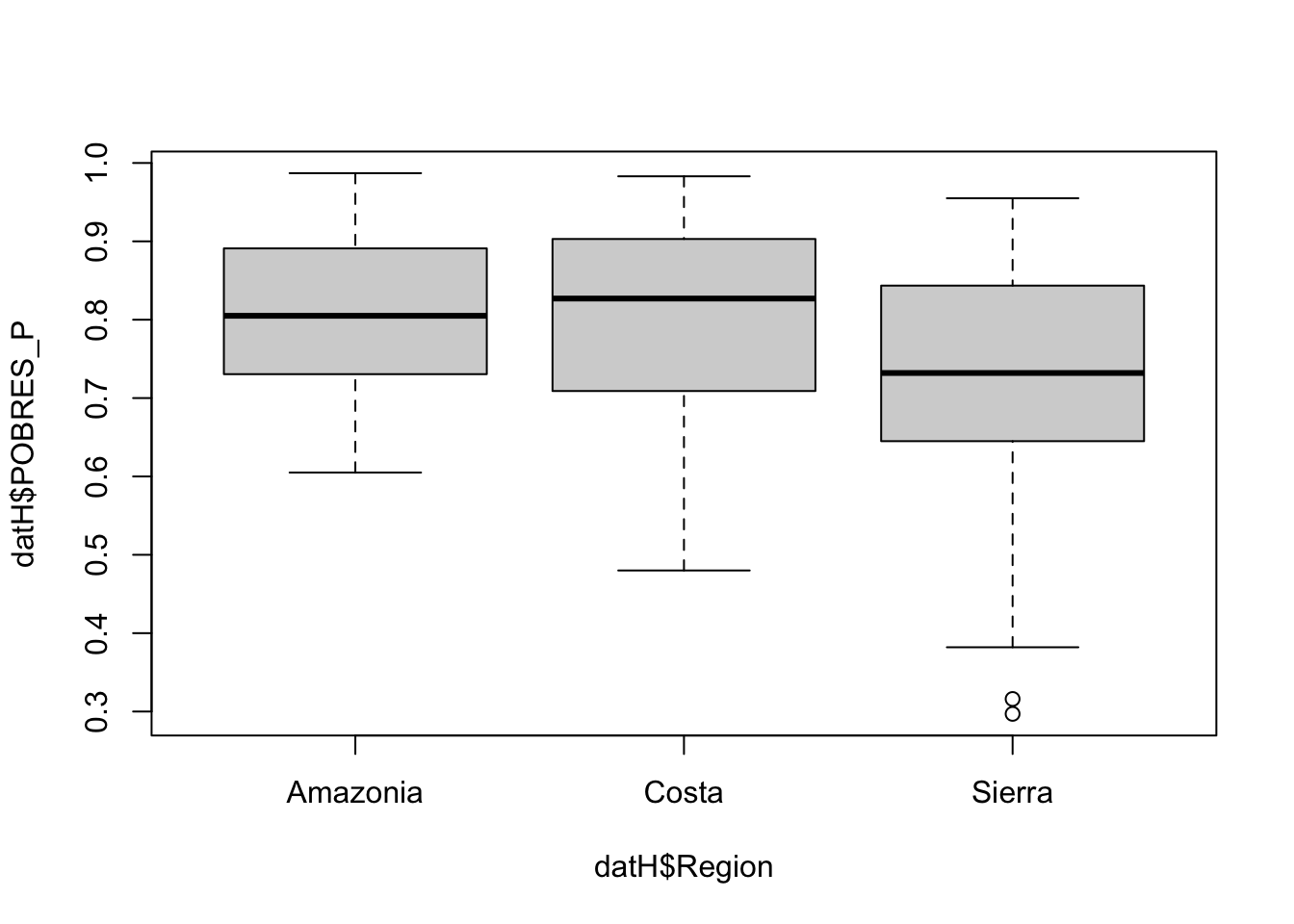
Veamos ahora una prueba de igualdad de varianzas, la prueba de Levene:
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 1.2161 0.2722
## 128## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 0.0515 0.8207
## 174## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 1.0788 0.301
## 122La prueba de Levene indica que no hay diferencias estadísticamente significativas en las varianzas entre regiones.